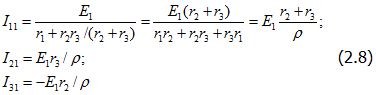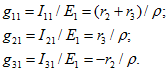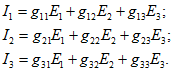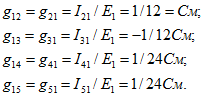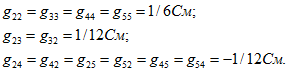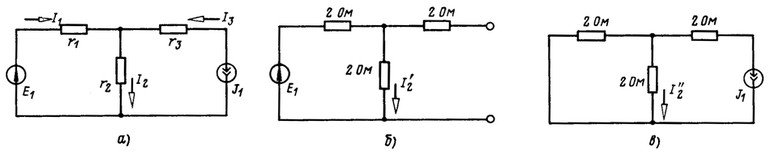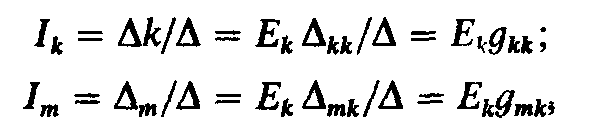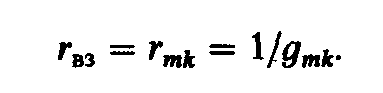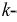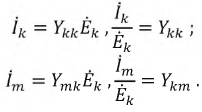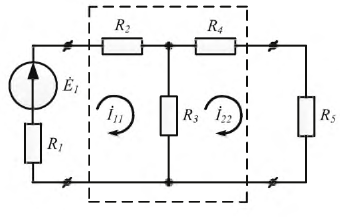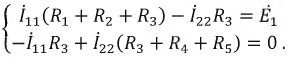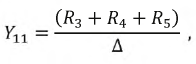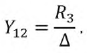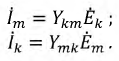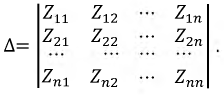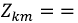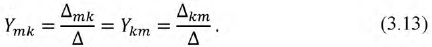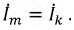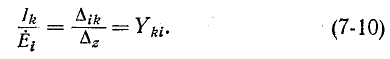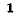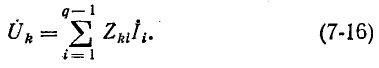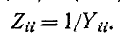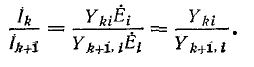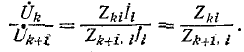
Приравняем ЭДС E2 и E3 нулю (рис. 2.4,6), при этом токи в ветвях
где
Из (2.8) определим:
Аналогично рассчитываются входные и взаимные проводимости второй и третьей ветвей:
Если взаимные проводимости найдены, то легко определить токи во всех ветвях при любых значениях ЭДС. Так, для схемы рис. 2.4, а
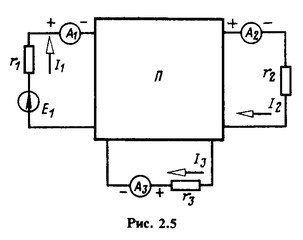
Аналогично определяются входные и взаимные проводимости других ветвей.
Пример 2.2.
Определить входные и взаимные проводимости ветвей схемы рис. 2.6, а, если
Решение.
Для определения входной проводимости и взаимных проводимостей между первой и остальными ветвями положим Е3 = E5 = 0 (рис. 2.6, б). Затем можно задаться E1 и найти все токи. Однако для данной схемы проще задать ток в ветви с сопротивлением r4 или r5, например I51 = = 1 А, и найти необходимую ЭДС E1 и токи в остальных ветвях.
Так как r4 = r5, то I41 = I51 и I31 = — (I51 + I41) = — 2 А. На выводах элемента с сопротивлением r2 напряжение ; токи
и ЭДС, при действии которой ток I51 = 1 А, а остальные токи равны найденным значениям,
.
Входная проводимость первой ветви .
Взаимные проводимости между первой и остальными ветвями
Аналогично определяются входные и взаимные проводимости остальных ветвей:
При определении проводимостей следует включить ЭДС Е2 в ветвь 2, направленную так же, как и ток I2, а при определении
ЭДС E4 в ветвь 4.
Пример 2.3.
В условиях предыдущей задачи (см. пример 2.2) определить токи во всех ветвях, если ЭДС Е1 = 24 В, E3 = 12 В и E5 = 24 В.
Решение.
Зная входные и взаимные проводимости ветвей, легко определить в них токи, пользуясь принципом наложения:
и т.д.
Если кроме источников ЭДС схема содержит и источники тока, то по принципу наложения к частичным токам, обусловленным действием источников ЭДС, добавятся частичные токи, обусловленные каждым из источников тока:
При определении входных и взаимных проводимостей все токи следует считать равными нулю (источники тока не действуют), а ветви с источниками тока разорвать (идеальные источники тока). При расчете коэффициентов передачи следует считать все ЭДС
.
Пример 2.4.
Составить зависимость при r1 = r2 = r3 = 2 Ом в схеме рис. 2.7, а.
Решение.
Ток Проводимость
определяется расчетом режима в схеме рис. 2.7, б. Ток
. Коэффициент
определяется расчетом режима в схеме рис. 2.7, в. Ток

Параллельным соединением резисторов (или приемников энергии, ветвей, сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).
Рис. 1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении
Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений
Для двух параллельно соединенных сопротивлений
Для ветвей с одинаковым сопротивлением где n количество ветвей
.
Ток при параллельном соединении
Мощность при параллельном соединении
Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам
Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:
Эквивалентная проводимость
(1)
т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость
и эквивалентное сопротивление
.
Для двух резисторов
Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой
в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
.
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
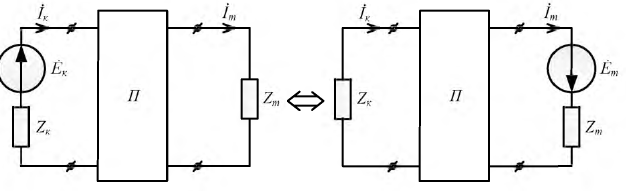
Рассмотрим
сложную цепь с одной действующей э. д.
с., выделив в
ней две ветви с сопротивлениями rk
и
rm,
в
одной
из которых имеется
источник э. д. с. Ek.
Остальную
часть цепи представим в виде пассивного
четырехполюсника П (рис. 1.21, а),
который
подключен к ней с
помощью входных (1,
1’)
и
выходных (2, 2′) зажимов. Э. д. с. Ek
вызывает
ток как в ветви k,
так
и в ветви т:
где
∆kk
— алгебраическое дополнение, которое
получается в результате вычеркивания
k-й
строки и k-го
столбца в определителе ∆k;
∆ — определитель
системы; ∆mk
— алгебраическое
дополнение, получаемое путем
вычеркивания k-й
строки и т-го
столбца
в определителе ∆m.
Коэффициенты
пропорциональности gkk
и
gmk
имеют
размерность проводимостей.
Коэффициент с одинаковыми индексами
gkk
называется входной
проводимостью и
численно равен току на входе цепи, когда
действующая
э. д. с. на входе равна 1 В:
(1.40)
С
входная проводимость любой ветви
представляет
собой
отношение тока к э. д. с. в данной ветви
(при э. д. с. в остальных ветвях,
равных нулю). Величина, обратная входной
проводимости, называется
входным
сопротивлением:
(1.41)
Коэффициент
с разными индексами gmk
называется
взаимной
или
передаточной
(между
ветвями т
и
k)
проводимостью.
Взаимную проводимость
можно определить как величину, равную
отношению выходного
тока к входному напряжению. Взаимная
проводимость численно равна
току в выходной ветви т,
когда
э. д. с., действующая во входной
ветви k,
равна
1 В:
(1.42)
Итак,
взаимные проводимости двух любых ветвей
можно определить
как отношение тока в одной ветви к э. д.
с. в другой ветви, когда
э.д. с. в остальных ветвях цепи равны
нулю. Величину, обратную
взаимной проводимости, называют взаимным
сопротивлением этих
ветвей:
(1.43)
Входные
и взаимные проводимости могут быть
определены расчетным путем или
экспериментально. Определяя входные и
взаимные проводимости расчетным
путем, необходимо для рассматриваемых
ветвей схемы составить уравнения по
методу контурных токов, причем необходимо
соблюдать условие, чтобы каждая из этих
ветвей входила только в
один, свой, контур. Затем, найдя определитель
системы ∆ и алгебраические
дополнения, находят проводимости:
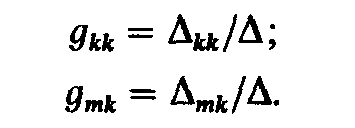
Экспериментальное
определение gkk
и
gmk
рассмотрим
на примере цепи рис.
1.21, а.
В
ветвь k
включим
э. д. с. Ek,
а в ветвь т
— амперметр
для измерения
тока. Сняв показания с амперметра,
разделим ток ветви т
на
э. д. с. Ek
и
найдем значение gmk:
Im/Ek
= gmk.
Для
определения входной
проводимости gkk
ветви k
необходимо
измерить ток в ветви k,
создаваемый
э. д. с.
Ek,
включенной
в ветвь k:
gkk
=
Ik/Ek.
Входные
и взаимные проводимости ветвей могут
быть использованы
при расчете цепей методами наложения
и контурных токов, а также
при выводе основных уравнений
четырехполюсников и т. д. При передаче
сигналов в электрических цепях с одним
источником питания важными
параметрами, характеризующими режим
работы цепи, являются коэффициенты
передачи по напряжению и току. Коэффициентом
передачи
по напряжению называется
отношение напряжения приемника к
напряжению источника э. д. с. цепи, а
коэффициентом
передачи по току
— отношение
тока в приемнике к току источника тока
цепи.
В общем виде
коэффициент передачи по напряжению
коэффициент
передачи по току
Входные и взаимные проводимости:
Пусть дана некоторая электрическая цепь, содержащая единственный источник ЭДС в
Рис. 3.4. Схема пассивного четырехполюсника
Определим 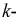
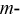
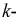
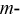
Если 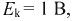
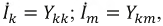
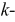
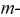
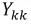
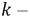
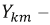
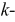
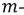
Рис. 3.5. Схема замещения пассивного четырехполюсника
Представим пассивный четырехполюсник в виде схемы рис. 3.5 и составим для нее уравнения по методу контурных токов.
Тогда входная проводимость первой ветви будет:
а взаимная проводимость первой и второй ветвей:
Свойство взаимности
Рассмотрим еще одно важное свойство, имеющее место в линейных электрических цепях. Оно базируется на понятиях входных и взаимных проводимостей.
Используя понятие взаимных проводимостей, можно выразить токи в первой и второй схемах рис. 3.6 следующим образом:
Докажем, что взаимные проводимости 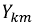
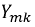
Этот определитель всегда симметричен относительно главной диагонали, проходящей через элементы 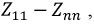
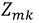
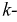
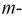
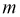
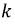
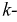
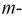
Пусть 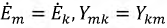
Свойство взаимности: если ЭДС 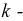
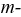
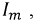
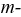
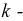
Цепи, обладающие такими свойствами, носят название обратимых цепей. Все линейные цепи обратимы.
Входные и передаточные проводимости и сопротивления
В электротехнике, радиотехнике и теории автоматического регулирования широко используются понятия о входных и передаточных функциях.
Условимся называть источник э. д. с. независимым или автономным (самостоятельным), если э. д. с. источника не зависит от напряжений и токов в цепи.
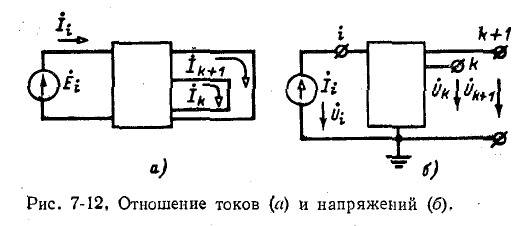
Пусть в какую-либо ветвь контура электрической цепи включен независимый источник э. д. с. 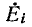
только контуру i. Если вся остальная часть электрической цепи не содержит независимых источников электрической энергии, то в соответствии с формулой (7-4) заданная э. д. с. 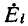
и
Отношение контурного тока к э. д. с., действующей в том же контуре, при отсутствии независимых источников во всех остальных контурах называется входной проводимостью электрической цепи:
В свою очередь отношение контурного тока к э. д. с., действующей в другом контуре, при отсутствии независимых источников во всех остальных контурах называется передаточной (или взаимной) проводимостью контуров:
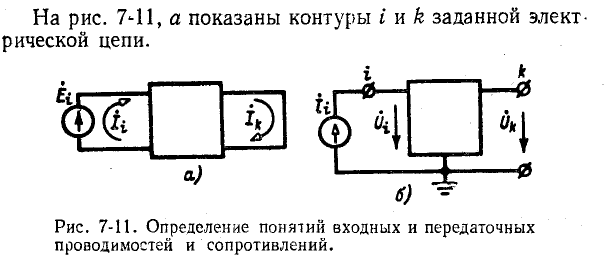
Элементами определителя системы и алгебраических дополнений в выражениях (7-9) и (7-10) служат собственные и общие сопротивления контуров заданной электрической цепи. Определитель 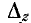
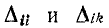
На основании (7-9) и (7-10) заключаем, что входная и передаточная проводимости численно равны токам в контурах i и k, когда в контуре i действует э. д. с., равная 1 В.
С учетом обозначений (7-9) и (7-10) выражения для токов (7-4) принимают вид:
Аналогичные рассуждения могут быть проведены и в отношении узлов i и к электрической цепи в предположении, что к узлу i подключен независимый источник тока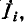
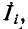
и
Отношение напряжения в узле к току, заданному в том же узле, при отсутствии в схеме других независимых источников называется входным сопротивлением электрической цепи:
соответственно отношение напряжения в узле к току, заданному в другом узле, при отсутствии в схеме других источников называется передаточным (или взаимным) сопротивлением узлов:
Элементами определителя системы и алгебраических дополнений в (7-14) и (7-15) служат собственные и общие проводимости узлов заданной электрической цепи.
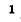
Определитель 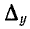
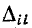
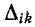
На основании (7-14) и (7-15) заключаем, что входное и передаточное сопротивления узлов численно равны напряжениям в узлах i и k (относительно базисного узла), когда в узле i задан ток, равный 1 А.
С учетом обозначений (7-14) и (7-15) выражения для напряжений (7-6) принимают вид:
Следует иметь в виду, что входным сопротивлением может также называться величина, обратная выражению (7-9), а входной проводимостью — величина, обратная выражению (7-14).
Очевидно, что для одной и той же пары выводов электрической цепи, не содержащей источников, величины 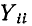
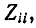
Отношение двух контурных токов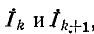
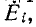
Аналогично отношение двух узловых напряжений и 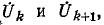
- Преобразование треугольника сопротивлений в эквивалентную звезду
- Метод контурных токов
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
В методе узловых потенциалов за вспомогательные расчетные величины принимают потенциалы узлов схемы. При этом потенциалом одного из узлов задаются, обычно считая его равным нулю (заземляют). Этот узел называют опорным узлом. Затем для каждого узла схемы, кроме опорного узла, составляют систему уравнений методом узловых потенциалов. По найденным потенциалам узлов находят токи ветвей по обобщенному закону Ома (закону Ома для ветви с ЭДС).
Отметим, что метод узловых потенциалов без предварительного преобразования схемы не применим к схемам с взаимной индукцией.
Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), не имеющих общего узла нужно применять особые способы составления системы уравнений метода узловых потенциалов.
Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), имеющих общий узел, этот общий узел принимают за опорный узел (заземляют). Тогда потенциалы узлов, соединенных этими идеальными источниками ЭДС без пассивных элементов с опорным узлом, равны ЭДС этих идеальных источников (+E, если идеальный источник ЭДС направлен от опорного узла и –E в противном случае).
Метод двух узлов является частным случаем метода узловых потенциалов. Он применяется для определения токов в ветвях схемы с двумя узлами и произвольным числом параллельных активных и пассивных ветвей.
Решение задач методом узловых потенциалов и методом двух узлов
Задача 1.4.1 Рассчитать цепь рис. 1.4.1 методом узловых, потенциалов.
Рис. 1.4.1
Решение. В рассматриваемой схеме четыре узла. Заземлим узел 4 (опорный узел)
φ 4 =0.
Тогда
φ 3 = φ 4 + E 2 =200 B.
Необходимо найти потенциалы узлов 1 и 2. Составим систему уравнений по методу узловых потенциалов для узлов 1 и 2.
Рассматривая узел 1, получим
φ 1 ⋅ g 11 − φ 2 ⋅ g 12 − φ 3 ⋅ g 13 =J+ E 1 R 1 + R ′ 1
или
φ 1 ⋅ g 11 − φ 2 ⋅ g 12 =J+ E 1 R 1 + R ′ 1 + E 1 ⋅ g 13 .
В правой части этого уравнения оба слагаемых учтены со знаком плюс, так как J и E1 направлены к узлу 1.
Рассматривая узел 2 (правая часть уравнения равна нулю, так как в ветвях, подсоединенных к узлу 2, нет источников энергии), получим
Индивидуалка Лиза (25 лет) т.8 929 529-57-81 Москва, метро Полянка.
− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 − φ 3 ⋅ g 23 =0
или
− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = E 2 ⋅ g 23 .
Найдем собственную проводимость первого узла
g 11 = 1 R 6 + 1 R 1 + R ′ 1 + 1 R ИТ + 1 R 2 + 1 R 5 = 1 20 + 1 25 + 1 25 + 1 40 =0,155 См.
Проводимость ветви с идеальным источником тока равна нулю, так как внутреннее сопротивление идеального источника тока RИТ равно бесконечности.
Собственная проводимость узла 2
g 22 = 1 R 2 + 1 R 3 + 1 R 4 = 1 25 + 1 30 + 1 35 =0,102 См.
Взаимные проводимости между узлами
g 13 = 1 R 6 + 1 R 1 + R ′ 1 = 1 20 + 1 25 =0,09 См; g 21 = g 12 = 1 R 2 = 1 25 =0,04 См; g 23 = 1 R 3 = 1 30 =0,033 См.
Подставив в уравнения известные величины, получим
{ φ 1 ⋅0,155− φ 2 ⋅0,04=39 − φ 1 ⋅0,04+ φ 2 ⋅0,102=6,6
Для решения этой системы используем метод определителей. Главный определитель системы
Δ=| 0,155 −0,04 −0,04 0,102 |=0,01421.
Частные определители
Δ 1 =| 39 −0,04 6,6 0,102 |=4,242; Δ 2 =| 0,155 39 −0,04 6,6 |=2,583.
Находим потенциалы узлов
φ 1 = Δ 1 Δ = 4,242 0,01421 =298,6 В; φ 2 = Δ 2 Δ = 2,583 0,01421 =181,8 В.
Определяем токи в ветвях (положительные направления токов в ветвях с ЭДС выбираем по направлению ЭДС, в остальных ветвях произвольно)
I 1 = φ 3 − φ 1 + E 1 R 1 + R ′ 1 = 200−298,6+150 10+15 =2,056 А.
В числителе этого выражения от потенциала узла 3, из которого вытекает ток I1, вычитается потенциал узла 1, к которому ток подтекает. Если ЭДС ветви совпадает (не совпадает) с выбранным направлением тока, то она учитывается со знаком плюс (минус). В знаменателе выражения учитываются сопротивления ветви.
Аналогично определяем другие токи (направления токов указаны на схеме рис. 1.4.1)
I 1 = φ 3 − φ 1 R 6 = 200−298,6 20 =−4,93 А; I 2 = φ 1 − φ 2 R 2 = 298,6−181,8 25 =4,67 А; I 3 = φ 3 − φ 2 R 3 = 200−181,8 30 =0,607 А; I 4 = φ 2 − φ 4 R 4 = 181,8−0 35 =5,194 А.
Для определения тока в ветви с идеальной ЭДС зададимся направлением тока I7. По первому закону Кирхгофа для узла 3 составим уравнение
− I 7 + I 3 + I 1 + I 6 =0.
Откуда
I 7 = I 3 + I 1 + I 6 =0,607+2,056−4,98=−2,317 A.
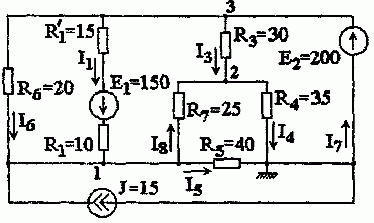
Задача 1.4.2 Определить токи в схеме рис. 1.4.2 методом узлового напряжения.
Рис. 1.4.2
Решение
1 Находим напряжение между двумя узлами по методу двух узлов
U ab = φ a − φ b = E 1 ⋅ g 1 +J g 1 + g 2 + g 3 = 32⋅ 1 1 +18 1 1 + 1 6 + 1 2 =30 B.
При составлении этого уравнения по методу двух узлов в числителе необходимо брать произведение ЭДС на проводимость своей ветви со знаком плюс, если ЭДС направлена к узлу a, и минус — если направлена от узла a к узлу b.
Аналогичное правило определяет и знаки токов источников тока.
2 Находим токи по закону Ома (по закону Ома для ветви с ЭДС)
I 1 = E 1 + φ b − φ a R 1 = E 1 − U ab R 1 = 32−30 1 =2 А; I 2 = U ab R 2 = 30 6 =5 А; I 3 = U ab R 3 = 30 2 =15 А.
Правильность решения проверим по первому закону Кирхгофа
I 1 − I 2 + I 3 +J=0; 2−5−15+18=0.
Метод узловых потенциалов в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи

метод двух узлов,
метод узловых напряжений,
метод узловых потенциалов,
собственная проводимость,
взаимная проводимость