Поговорим о том, как найти протоны, нейтроны и электроны. В атоме существует три вида элементарных частиц, причем у каждой есть свой элементарный заряд, масса.
Строение ядра
Для того чтобы понять, как найти протоны, нейтроны и электроны, представим особенности строения ядра. Оно является основной частью атома. Внутри ядра располагаются протоны и нейтроны, именуемые нуклонами. Внутри ядра эти частицы могут переходить друг в друга.
Например, чтобы найти протоны, нейтроны и электроны в атоме водорода, необходимо знать его порядковый номер. Если учесть, что именно этот элемент возглавляет периодическую систему, то в его ядре содержится один протон.
Диаметр атомного ядра составляет десятитысячную долю всего размера атома. В нем сосредоточена основная масса всего атома. По массе ядро превышает в тысячи раз сумму всех электронов, имеющихся в атоме.
Характеристика частиц
Рассмотрим, как найти протоны, нейтроны и электроны в атоме, и узнаем об их особенностях. Протон — это элементарная частица, которая соответствует ядру атома водорода. Его масса превышает электрон в 1836 раз. Для определения единицы электричества, проходящего через проводник с заданным поперечным сечением, используют электрический заряд.
У каждого атома в ядре располагается определенное количество протонов. Оно является постоянной величиной, характеризует химические и физические свойства данного элемента.
Как найти протоны, нейтроны и электроны в атоме углерода? Порядковый номер данного химического элемента 6, следовательно, в ядре содержится шесть протонов. Согласно планетарной модели строения атома, вокруг ядра по орбитам движется шесть электронов. Для определения количество нейтронов из значения относительной атомной массы углерода (12) вычитаем количество протонов (6), получаем шесть нейтронов.
Для атома железа число протонов соответствует 26, то есть этот элемент имеет 26-й порядковый номер в таблице Менделеева.
Нейтрон является электрически нейтральной частицей, нестабильной в свободном состоянии. Нейтрон способен самопроизвольно превращаться в положительно заряженный протон, испуская при этом антинейтрино и электрон. Средний период его полураспада составляет 12 минут. Массовое число — это суммарное значение количества протонов и нейтронов внутри ядра атома. Попробуем выяснить, как найти протоны, нейтроны и электроны в ионе? Если атом во время химического взаимодействия с другим элементом приобретает положительную степень окисления, то число протонов и нейтронов в нем не изменяется, меньше становится только электронов.
Заключение
Существовало несколько теорий, касающихся строения атома, но ни одна из них не была жизнеспособной. До версии, созданной Резерфордом, не было детального пояснения о расположении внутри ядра протонов и нейтронов, а также о вращении по круговым орбитам электронов. После появления теории планетарного строения атома у исследователей появилась возможность не только определять количество элементарных частиц в атоме, но и предсказывать физические и химические свойства конкретного химического элемента.
Нахождение числа нейтронов, протонов и электронов в атоме .
Атом состоит из ядра и вращающихся вокруг ядра электронов.
Ядро состоит из протонов и нейтронов
Протон- положительно заряженная частица
масса протона равна единице, заряд протона равен единице
Нейтрон-нейтральная частица
масса нейтрона равна единице, заряд нейтрона равен нулю
Электрон- отрицательно заряженная частица
Заряд электрона равен -1, а масса электрона равна нулю
Порядковый номер элемента в таблице Менделеева указывает на число электронов в атоме
Количество протонов в атоме равно количеству электронов , так как атом электрически нейтрален
Масса атома складывается из числа протонов и числа нейтронов, масса электрона не учитывается
Рассмотрим фрагмент таблицы Менделеева и найдем количество протонов, нейтронов и электронов
в атоме водорода
После чего начертим модель атома водорода
Порядковый номер атома водорода равен единице, значит атом имеет:
1 электрон
1 протон
Для нахождения количества нейтронов нужно из массы вычесть число протонов
Масса атома водорода равна единице
Количество нейтронов=1-1=0
В атоме водорода нет нейтронов
Модель атома водорода:
Рассмотрим фрагмент таблицы Менделеева и найдем количество протонов, нейтронов и электронов
в атоме гелия
После чего начертим модель атома гелия
Порядковый номер атома гелия равен 2, значит атом имеет:
2 электрона
2 протона
Для нахождения количества нейтронов нужно из массы вычесть число протонов
Масса атома гелия равна 4
Количество нейтронов=4-2=2
В атоме гелия 2 нейтрона
Модель атома гелия:
Задача 1.
С помощью фрагмента таблицы Менделеева найти количество протонов, нейтронов и электронов в атоме лития
Массу атома округлить до 7.
Показать ответ
Показать решение
Видеорешение
Задача 2.
С помощью фрагмента таблицы Менделеева найти количество протонов, нейтронов и электронов в атоме углерода.
Показать ответ
Показать решение
Видеорешение
Задача 3.
С помощью фрагмента таблицы Менделеева найти количество протонов, нейтронов и электронов в атоме азота.
Показать ответ
Показать решение
Видеорешение
Задача 4.
С помощью фрагмента таблицы Менделеева найти количество протонов, нейтронов и электронов в атоме кислорода.
Атомную массу округлить до 16.
Показать ответ
Показать решение
Видеорешение
Как мы видим в таблице Менделеева выше стоит порядковый номер, то есть заряд, который равен числу протонов
и электронов , а под ним расположена атомная масса.
Из каких-то непонятных соображений в ядерных реакциях или просто в одиночном обозначении элемента
сверху стоит масса, а снизу заряд(номер).
То есть все наоборот
( _{6}^{12}textrm{C} ;;;;;;;;; ) (12) это масса, (6) это заряд (номер)
( _{Z}^{M}textrm{C} ;;;;;;;;; ) (M) это масса, (Z) это заряд (номер)
Задача 5.
Найти количество протонов, нейтронов и электронов в атоме фтора
( _{9}^{19}textrm{F} )
Показать ответ
Показать решение
Видеорешение
Задача 6.
Найти количество протонов, нейтронов и электронов в атоме алюминия
( _{13}^{27}textrm{Al} )
Показать ответ
Показать решение
Видеорешение
Изотопы это атомы одного и того же химического элемента, они имеют одинаковый заряд,
но разное количество нейтронов
Изотопы кислорода:
( _{8}^{16}textrm{O} , ;;;; _{8}^{17}textrm{O} , ;;;; _{8}^{18}textrm{O} )
Да, друзья мои, атом делим! Эту радостную новость я вам сообщаю сразу.
Атом тоже являет собой составную конструкцию. Получается, что детальки тоже устроены из деталек, только более мелких. Почему же греки называли атом неделимым? Мы уже знаем ответ: потому что деление мельчайшей крошки вещества – атома – приводит к тому, что вещество перестает существовать в своем привычном виде! Как перестает существовать автомобиль, если его разобрать на отдельные части – колеса, поршни, гайки, рычаги…
Все в мире сделано, как мы уже выяснили, из примерно сотни атомов (химических элементов). А сами атомы? Они состоят всего из трех деталек, только в разных сочетаниях.
Всего из трех!
В это трудно поверить, но все многообразие окружающей нас природы – звезды, планеты, мама с папой, хлеб, собака, воздух – это всего лишь разные наборы трех частичек, которые сначала складываются в атомы, а уж затем атомы составляют молекулы, строящие мир. Но в основе мира – всего три частицы. Частицы эти называются элементарными.
Опять возникает это слово «элементарные»!
Простейшие химические вещества, которые занесены в таблицу Менделеева, называют химическими элементами. И частицы, из которых сделаны эти элементы, тоже называются элементарными.
А имена у них есть?
Есть. Знакомьтесь:
Содержание
- Протон, Нейтрон, Электрон. Вся святая троица.
- А что такое электрический ток?
- А почему, собственно говоря, разноименные заряды притягиваются? И почему одноименные отталкиваются?
- Ну, вот, собственно, и все! Вся природа у нас в кармане! Теперь нами понят ее главный принцип.
- Иногда еще атомную массу называют атомным весом.
- Когда происходит подобное? Из-за чего атомы могут, например, терять электроны?
Протон, Нейтрон, Электрон. Вся святая троица.
Но прежде, чем рассказать про них подробнее, я отвечу на закономерный вопрос, который должен был снова у вас возникнуть: а из чего сделаны элементарные частицы? Может, они тоже из каких-то еще более мелких деталюшек состоят?
Не вдаваясь в ненужные подробности, отвечу так: нет! Не состоят!
– Позвольте! – скажет мне какой-нибудь умный ребенок, поправляя пальчиком круглые очки. – Позвольте! Весь мой опыт говорит о том, что если по чему-то сильно стукнуть, оно развалится на части. Чашка на осколки, молекула на атомы, атомы – на эти ваши элементарные частицы. А если стукнуть по частицам, на что они развалятся, гражданин хороший?
– Какой умный мальчик! – отвечу я с некоторой робостью. – Проник в самую суть вещей! Стукнуть, говорит, надо. Именно так и поступают физики, когда изучают частицы! Они разгоняют их в специальных ускорителях и стукают друг об друга. А чем их еще стукнуть, чтобы разломать, если они – самые маленькие в мире? Вот их друг об друга и стукают.
И как вы думаете, что получается?
Элементарные частицы не разваливаются на составляющие, а превращаются в другие элементарные частицы. Причем эти превращения, которые называют ядерными реакциями, зависят от скорости, до которой разогнали частицы. То есть от той энергии, которую частицам сообщили. Дело в том, что энергия (скорость) может превращаться в вещество, в массу. И более того – при глубоком рассмотрении оказывается, что это одно и то же – энергия и масса, представляете! Мир един. Но об этом мы поговорим позже.
А сейчас познакомимся поближе с элементарными частицами. Они ужасно милые! (Вообще говоря, элементарных частиц довольно много. Но главных, из которых сделано все вещество в мире, всего три, как уже было сказано. Ими мы и займемся, а остальной вселенский мусор оставим взрослым физикам.)
С чего начнем?
Давайте с электрона. Он самый маленький, а маленьких обижать нельзя.
Итак, под свет прожекторов на сцену нашего внимания, раскланиваясь, выходит электрон. Что мы можем о нем сказать? Какого он цвета? Он шершавый? Он влажный, твердый, газообразный? Он теплоемкий?
Нет! Все те свойства, к которым мы привыкли в нашем большом мире (он называется макромир), не имеют никакого отношения к миру элементарных частиц (микромиру). Нет в микромире ни цвета, ни запаха, ни шершавости, ни твердости. Это все свойства макромира. Все эти свойства складываются из множества частиц, это макросвойства. А по отдельности частицы этих свойств не имеют.
А что же они имеют?
Ну, что есть у того же электрона? Ведь какие-то свойства у него должны быть! Иначе бы его не существовало! Ведь существовать – это значит проявлять себя как-то, то есть иметь свойства!
Да, некоторые свойства у электрона есть. У него есть масса. Про нее мы уже говорили – электрон очень легонький, самый легонький из всей троицы.
Электрон в 1820 раз легче протона. Для сравнения: если протон – это танк, то электрон – это одна канистра с топливом. Если протон – человек, то электрон – это авторучка в его кармане. Вот такая разница в массе.
Заметили, кстати, новый физический термин необыкновенной сложности – «масса»? Я его как бы между делом ввел. Надеюсь, не огорчил.
Что это такое? Масса – это просто количество вещества. Чем тело тяжелее, тем оно массивнее. Папа массивнее ребенка. Танк массивнее автомобиля. Солнце массивнее Земли.
Массу не нужно путать с весом. Хотя многие взрослые путают. Даже генералы и начальники. А, может, и сам президент. Между тем это совершенно разные вещи! Вес – это сила, с которой Земля притягивает массу. Сила, с которой массивное тело давит на опору, на которой лежит, или растягивает подвес, на котором висит. В космосе, в невесомости никакого веса нет, потому невесомость так и называется. Но все равно даже в невесомости толстый космонавт гораздо массивнее щуплого. И если они оттолкнутся друг от друга, то полетят в разные стороны с разными скоростями – толстый медленно, а щуплый быстро! Потому что количество вещества в их телах разное, в толстом вещества много, а в худом кот наплакал.
Вес и масса физиками даже измеряются в разных единицах – масса в килограммах, а сила в особых единицах – ньютонах. Массу определяют с помощью весов, а силу с помощью специальных приборов – ньютонометров. Усекли?
Массу ученые люди еще называют мерой инертности тела. Действительно, массивное тело очень инертное, чтобы его разогнать, нужно много усилий потратить. А легкое тело и разогнать легче, его инертность мала.
Электрон очень легок. Его масса составляет столь мизерную величину, что ее написание потребует от меня особой внимательности – чтобы в нулях не ошибиться:
0,0000000000000000000000000009 грамма – вот сколько весит электрон.
А еще у электрона есть размер. Он тоже крохотный:
0,00000000000000001 миллиметра – вот какого электрон диаметра.
Электрон можно представить себе, как маленький шарик, который вращается вокруг своей оси. Этакая малюсенькая планетка.
Причем, как вы понимаете, электрончик может вращаться или в одну сторону, или в другую, как это показано на рисунке ниже. И это тоже одно из свойств электрона – левое вращение или правое. По-научному вращение электрона называют спином. Не спиной, поскольку никакой спины у шарика нет, а спином. Спин – это собственное вращение электрона, от английского слова «spin» (вращение).
Если в винтовочном стволе правая нарезка, то вылетевшая из ствола пуля будет иметь вращение вправо. А если левая – влево. Теперь представьте, что мы стреляем в мишень, свободно закрепленную в центре и могущую вращаться. В этом случае пули с правым вращением, впиваясь в мишень, будут передавать ей свое вращение, постепенно раскручивая в ту же сторону – примерно как отвертка крутит винт.
Если мы не знаем, в какую сторону крутятся вылетающие из ствола пули, можно поставить опыт, стреляя по крутящейся мишени. В какую сторону она завертится, в такую и пули крутятся.
Но спин – это сущая ерунда по сравнению с последним и самым загадочным свойством электрона. Свойство это называется зарядом. Но заряд не в том смысле, что электрон чем-то заряжен, как винтовка патроном, потому что патрон из винтовки можно вынуть. А этот загадочный заряд из электрона вынуть нельзя. Он ему присущ, он его часть. Он – главное его свойство. Электрон, собственно говоря, и есть заряд!
Что же такое заряд?
Этого никто не знает. Но зато мы знаем, как загадочный заряд проявляет себя. И вы сейчас это узнаете.
Давным давно люди заметили, что если кусочек янтаря натереть шерстяной тканью, он начнет притягивать маленькие кусочки бумажки. Янтарь – это окаменевшая сосновая смола. Наверняка у вашей мамы есть янтарные безделушки – кулончик или сережки. Безделушки надо приспособить к делу! Возьмите кулон, тщательно выковыряйте из оправы желтоватый янтарь (маме он больше не понадобится), возьмите шерстяной носок, нарвите бумагу на крохотные кусочки. После чего, потерев янтарь, попробуйте притянуть им бумажные клочки.
Надеюсь, вам не влетит за смелые исследования.
На указанное явление впервые обратили внимание те же древние греки, весьма вдумчивый народец. По-гречески янтарь – «электрон». И вы, наверное, уже догадались, что за притягивание бумажек отвечают электроны, раз эти частички физиками были названы в честь янтаря.
Действительно, в этом простом эксперименте человечество впервые столкнулось с действием электрических сил, которые обусловлены электрическим зарядом.
Теперь-то мы к электричеству привыкли. Теперь мы без него жить не можем. Теперь у нас кругом розетки, которые больно бьют током догадливых детей, додумавшихся сунуть туда свой тонкий пальчик. Теперь нас просто окружает электричество, без коего и шагу не ступить. Стиральные машины, лифты, лампы, холодильники, троллейбусы и электрички, радиоприемники и телевизоры, заводы и фабрики – все работает на электричестве. Линии электропередач передают потребителям электрический ток, который вырабатывается электростанциями.
А что такое электрический ток?
Нет ничего проще! Поток электронов – вот что такое электроток. Как река – это течение триллионов и биллионов молекул воды по руслу, так и электрический ток – это течение миллиардов электронов по металлическому проводу. Все металлы очень хорошо проводят ток. Это отличительное свойство металлов, на которое ученые давно обратили внимание. Сегодня в кристаллической решетке металла мы умеем организовывать организованное течение мириадов элементарных частичек под названием электроны. Греки добывали чуть-чуть электричества, натирая шерстью янтарь. У нас же теперь – целые электростанции, которые занимаются производством электроэнергии. Уйму тока дают!
Короче говоря, заряд электрона – это некое свойство, которое характеризуется… чем? Ясно, чем характеризуется масса. Инертностью! Чем массивнее тело, тем труднее его разгонять. Попробовали потолкать – ого! тяжеленное! А заряд как обнаружить?
А заряд проявляет себя тем, что он притягивается к другому заряду – противоположному.
Существуют два вида зарядов – положительный и отрицательный. Ничего положительного и отрицательного в бытовом смысле в них нет, они не хорошие и не плохие, просто их так назвали когда-то да и все. Обозначают положительный заряд знаком плюс – «+», а отрицательный знаком минус – «-». Эти знаки вы тыщу раз видели на разных батарейках. А если не видели, сходите да посмотрите. Мне кажется, лучше всего попробовать выломать батарейку из папиных часов с помощью молотка и отвертки.
Электрон является носителем отрицательного заряда, а протон – положительного. Разноименные заряды притягиваются друг к другу, одноименные отталкиваются. Это прекрасно видно на рисунке.
Вот так мы и к протону незаметно перешли. Посмотрим-ка на него внимательно.
Если электрон маленький, легонький и электроотрицательный (минус), то протон большой, тяжелый и электроположительный (плюс). Полная противоположность! При этом протон и электрон притягиваются друг к другу.
А почему, собственно говоря, разноименные заряды притягиваются? И почему одноименные отталкиваются?
Этого никто не знает. Но это так! Уж такое это свойство – электрический заряд. Именно так оно себя проявляет. Понять, почему именно так, на современном этапе развития науки нельзя, можно только привыкнуть. Привычка вполне заменят понимание. Можно сказать, что привычка и есть понимание. Привык – и вроде как понимаешь.
Электрон и протон – на вид очень разные ребята. И масса, и размер у них разные. А вот заряд одинаковый – заряд протона в точности равен заряду электрона, только знак имеет противоположный.
Что еще сказать о протоне? По сравнению с электроном он просто гигант! Если вы забыли, я напомню – протон в 1820 раз тяжелее электрона. И по размерам, соответственно, больше.
Поскольку плюс и минус притягиваются, протон и электрон притягиваются друг к другу и могут образовать пару, напоминающую звездную систему. Только в звездной системе планета кружится вокруг светила, а тут электрон будет кружиться вокруг протона.
Самая простая подобного рода система состоит из одного протона, вокруг которого крутится один электрон.
Аналогичные, казалось бы, системы. Только одна из них (звездная) существует в макромире, а другая (атомная) в микромире. Но разница, тем не менее, есть. И состоит она, главным образом в том, что планета и звезда электронейтральны, то есть не обладают зарядом (никто еще не догадался потереть Солнце шерстяной тряпочкой). А электрон и протон обладают зарядом, то есть их притягивает друг к другу электрический заряд. А планету к звезде притягивает сила всемирного тяготения, которая действует на все массивные тела. Та самая, которая бросает вас на землю, когда вы спотыкаетесь и падаете. Та самая, которая неудержимо влечет вниз любимую мамину чашку, которую вы взяли без разрешения и уронили. Почему она на пол-то летит, свинья такая?
Притягивается.
Все тела, имеющие массу, притягиваются друг к другу. И чем больше масса, тем сильнее.
Вообще-то говоря, электрон и протон тоже имеют массу и потому притягиваются друг к другу без всякого заряда. Но их массы такие крошечные, что не смогли бы устроить между ними устойчивую связь без помощи зарядов.
А знаете, что это такое у нас получилось – ну, когда один электрон мы запустили крутиться вокруг одного протона?
Это атом водорода.
Самый легкий химический элемент. Самое простое вещество на свете. Номер первый в таблице Менделеева. Всего-навсего один протон и один электрон – и вот мы уже имеем газ водород. Вообще-то, строго говоря, в атомарном состоянии водород как газ не встречается. Он существует в виде молекулы из двух атомов водорода – Н2. Два атома водорода сцепляются вместе и образуют молекулу газа по имени водород. Но это уже мелочи. Главное, что нам удалось собрать всего из двух элементарных частиц первое химическое вещество. Для этого даже третья элементарная частица не понадобилась – нейтрон.
Нейтрон – парень скромный. Он не обладает таким ярким характером, как протон, хотя они очень похожи. У нейтрона почти такая же масса, как у протона, и практически такой же размер. Но заряда у нейтрона нет. Он нейтральный.
А на фиг он тогда нужен?
И вправду, мы вон вполне удачно собрали первое, правда, пока самое простое вещество всего из двух элементарных частичек. Так зачем нужен нейтрон?
Разгадку этой загадки я открою чуть позже. А пока скажу обтекаемо: природе нейтрон зачем-то понадобился. И уже в следующем химическом элементе он присутствует.
Давайте попробуем собрать что-нибудь посложнее водорода!
Как? Простая логика подсказывает: если у нас в простейшем веществе две частички, надо добавить еще одну – третью. Вот вокруг нашего Солнца вращается около десятка планет. И поскольку атом напоминает планетную систему, давайте запустим вокруг протона еще несколько электронов.
Это будет сложновато! Я ведь не зря выше сказал, что заряды протона и электрона равны. Положительный заряд протона уже скомпенсирован отрицательным зарядом электрона, который кружится вокруг него. У протона уже силенки не хватит притянуть и удержать еще один электрон.
К тому же надо вот на что внимание обратить – атом водорода электронейтрален, то есть минусовый заряд электрона компенсируется в нем плюсовым зарядом протона. Потому и говорят, что для внешнего наблюдателя атом нейтрален. Все вещество, которое нас окружает, электронейтрально. А если случайно на нем накопится заряд, как на синтетической кофте, которую снимают через голову, или на янтаре, когда его шерстью потрешь, то вещество начнет притягивать мелкие предметы, потрескивать и даже искрить. Потрите резиновый воздушный шарик о голову, и он начнет волосы притягивать. Но это редкость, обычно вещество у нас в руках не искрит, не трещит, никуда ничего не притягивает и вообще ведет себя прилично. Нейтрально.
Поэтому если нам надо создать вещество, поимеем в виду, что оно должно быть электронейтрально, то есть число плюсиков в его атоме должно быть равно числу минусиков.
Значит, чтобы собрать что-то посложнее водорода, нужно в дополнение ко второму электрону на орбите всобачить ему в центр (в ядро) еще один протон. Потому что один протон два электрона не удержит, заряда не хватит. А два протона запросто удержат два электрона. И тогда все уравновесится – в ядре атома будет два плюсовых заряда от двух протонов, а вокруг будут крутиться два электрона с двумя минусовыми зарядиками. И в целом атом останется электронейтральным.
И таким образом что у нас получилось?
У нас почти получился гелий – вещество номер 2 в таблице Менделеева. До настоящего гелия ему не хватает только двух нейтронов в ядре. Добавим их, и получится гелий.
Природа устроила так, что количеству протонов в ядре атома приблизительно соответствует количество нейтронов. То есть если мы будем сооружать атом, например, с 10 протонами в ядре и 10 электронами на орбитах, то нам придется вдуть в ядро еще с десяток нейтронов. Балласт.
Поскольку протоны и нейтроны очень похожи (за исключением заряда), их часто называют одним словом – нуклоны. Ядро атома состоит из нуклонов, а вокруг кружатся в бесконечном вальсе электроны. Прелестно!
Ну, вот, собственно, и все! Вся природа у нас в кармане! Теперь нами понят ее главный принцип.
Как собрать следующий, третий по счету химический элемент в таблице Менделеева? Очень просто. Берем три протона, три нейтрона и три электрона. Нуклоны скатываем, как снежок, в одно ядро, вокруг запускаем три штучки электрончиков – и получаем литий. Литий – это уже не газ. Это уже легкий металл. Самый легкий металл на свете.
Вы, надеюсь, уже нашли водород, гелий и литий в таблице Менделеева…
А теперь поступим так. Найдите-ка в таблице наше родное и всеми горячо любимое золото. Стойте!.. Лучше, чтобы вы не листали книгу туда-сюда, я просто сам перенесу из таблицы Менделеева клеточку с золотом сюда. И расположу ее чуть ниже золотых слитков.
Мы видим тут значок золота – Au (аурум) – и две цифры. Верхняя – это порядковый номер элемента в таблице Менделеева. У золота № 79. Почему такой?
Отчего золото оказалось в периодической таблице элементов под номером 79?
Не знаете? А могли бы и догадаться! Вспомните, как мы строили первые три простейшие вещества. У первого, водорода – один протон и один электрон. У второго, гелия – по два. У третьего, лития – по три. Уловили закономерность? Порядковый номер – это количество протонов в ядре атома и электронов на орбите, вот и все! Если элемент стоит в таблице Менделеева пятым, то это только потому, что у него пять протонов в ядре, а вокруг кружатся 5 электронов.
А вторая цифра, которая внизу, что значит? Выглядит она страшно, но пугаться не стоит. Это атомная масса. Только выражена она не в килограммах или граммах, а в атомных единицах, где гирькой служит нуклон. 1 нуклон – это одна единица массы. Два нуклона – две единицы атомной массы. Крайне просто.
Иногда еще атомную массу называют атомным весом.
Мы знаем, что вес и масса – разные вещи, но так сложилось в науке, что атомный вес является синонимом атомной массы. Примем это как данность. Жалко что ли? Мы же говорим «чайник закипел», хотя кипит вовсе не чайник, а вода в чайнике.
Так вот, каков атомный вес водорода? Одна атомная единица! Потому что в его ядре один нуклон. А у гелия? Четыре! Потому что в ядре гелия четыре нуклона – две гирьки протонов, а еще и две гирьки нейтронов. (Электроны при определении атомного веса не учитываются из-за чрезвычайной легкости.)
Проще говоря, атомная масса, которая указана возле каждого элемента в таблице Менделеева до запятой – это общее количество нуклонов (протонов и нейтронов) в его ядре.
Посмотрите, в ядре атома золота 196 частиц. Протонов там, как мы уже выяснили, 79 штук. Все остальное – нейтроны. Возьмите калькулятор и посчитайте… Не хотите? Ну, ладно, я за вас посчитаю:
196 – 79 = 117
Получается, у золота 117 нейтронов в атоме.
Внимательный детский глаз может, еще раз оглядев клеточку золота, вырезанную из менделеевской таблицы, послать сигнал в хитрый детский мозг, и мозг озаботится ненужным вопросом:
– Дяденька писатель! А что там еще за цифры стоят после запятой? Ну, после 196?
Ох, не хотел я вам этого говорить, дети, хотел утаить, но раз к стенке приперли, придется расколоться.
Это очень трудно, друзья мои! Не каждый взрослый об этом знает! А вы поймете за одну минуту.
В обычном нормальном атоме золота, как мы уже выяснили, 117 нейтронов и 79 протонов. Но иногда встречаются атомы-уродцы. Довольно редко. У них есть лишние нейтроны. Как иногда у людей бывает по шесть пальцев на руках. Нечастое явление.
Предположим, на тысячу нормальных атомов приходится один дефектный. И если в норме в атоме золота 117 нейтронов, то иногда встречаются «вспухшие» уродливые атомы, в которых 118 нейтронов. Все помидорчики как помидорчики, а у одного помидора какой-то уродский вырост на боку. Ничего, мы и такой съедим.
Атомы-уродцы называют изотопами. Именно из-за них, кособоких паразитов средний вес всех атомов отличается от целого числа. Что понятно: если у нас из десяти атомов все десять имеют атомный вес в 6 единиц, то и средний атомный вес будет равен ровно шести:
(6+6+6+6+6+6+6+6+6+6): 10 = 6
А вот если один из десяти атомов имеет вес в 7 единиц, средний вес изменится:
(6+6+6+6+6+7+6+6+6+6): 10 = 6, 1
Видите, после запятой появилась циферка, которая говорит о том, что не «все шестерки одинаковы».
Если вы внимательно посмотрите на атомные веса элементов в таблице Менделеева, то увидите, что все они не являются целыми числами. Значит, каждое элементарное вещество имеет уродливые атомы. Даже водород. Хотя, казалось бы, проще водорода ничего быть не может – один протон, вокруг которого крутится один электрон, вот и весь атом. Эта не какой-нибудь свинец, у которого в ядре больше двух сотен нуклонов, а вокруг этого огромного ядра кружится больше восьмидесяти электронов!
Однако все же бывают атомы водорода, в ядре которых, кроме протона, есть еще и нейтрон. Один. А порой и два! Такой водород называют тяжелым. Потому что его атом тяжелее обычного.
На рисунке ниже нарисованы атомы нормального водорода и редкие уродики, а также написано, как эти уродики называются.
Но так как атомы-уродцы встречаются редко, говорить мы о них пока прекращаем. Я рассказал вам про изотопы лишь затем, чтобы объяснить наличие циферок после запятой. Вы на эти циферки просто внимания не обращайте да и все.
Вы теперь и так знаете слишком много! Вы представляете, по каким принципам строится вещество. Берите любой атом из таблицы Менделеева и рассказывайте про него маме или даже папе. Задавайте контрольные вопросы. Проверяйте усвоенный материал.
А пока взрослые морщат лоб и мычат в свое оправдание что-то типа «я, конечно, в школе учи-и-ил, но забы-ы-ыл», мы с вами возьмем сейчас тот же хлор и натрий, из которого ранее соль поваренную делали, и посмотрим, что тут к чему.
Натрий. Легкий металл. Как он сделан? Его номер 11-й. Значит, 11 протонов и 11 электронов. Атомный вес натрия – 22. То есть в ядре 22 нуклона.
22 нуклона минус 11 протонов = 11 нейтронов. Все. Атом натрия готов.
Теперь хлор надо собрать по инструкции дяденьки Менделеева.
У хлора номер 17. То есть 17 протонов и 17 электронов. Атомный вес (число нуклонов в ядре) – 35.
35 – 17 = 18 нейтронов. Все, собрали хлор.
Теперь соединяем два этих атома – хлора и натрия, – зацепив один за другой колечками самых дальних электронных орбит, и получаем сложное вещество – молекулу поваренной соли.
Так строятся все вещества – сцепляясь дальними орбитами электронов. При этом дальние электрончики, которые крутились на этих орбитах, становятся как бы общими для обоих ядер.
Все, можно стереть пот со лба. Мы освоили химию и физику элементарных частиц. Слава Менделееву! Науке слава!
Теперь осталась одна маленькая деталь, которую нужно знать каждому приличному ребенку. Один маленький штрих, который завершит картину мироздания, сделав ее в ваших блестящих глазах более полной и блестящей.
Итак, мы знаем, что практически все окружающее нас вещество электронейтрально. Если вы дотрагиваетесь до шкафа, он не бьет вас током. Потому что в веществе шкафа количество положительных зарядов равно количеству отрицательных. Его атомы электронейтральны.
Но что будет, если атом потеряет один или два электрона? Вот такой рассеянный атом. Может такое быть? Может! Какое-нибудь сильное воздействие может парочку электрончиков у атома оторвать.
Вы скажете (подсмотрев в таблицу Менделеева):
– Ха! Даже если такое случится, невелика потеря! Вокруг ядра атома могут крутиться под сотню электронов! Например, у радия их 88. Некисло так! Подумаешь, пару потеряет…
Однако потеря даже одного отрицательного заряда означает избыток заряда положительного. Если атом теряет электрон, значит у него остается один «лишний», нескомпенсированный протон. И атом в целом таким образом приобретает положительный заряд +1.
А если атом теряет два электрона, то он приобретает заряд +2.
Бывает и наоборот – когда к атому присоседится какой-нибудь приблудный лишний электрон. В этом случае атом получает один отрицательный заряд —1.
Такие заряженные атомы называются ионами.
Когда происходит подобное? Из-за чего атомы могут, например, терять электроны?
Это бывает при высоких температурах, то есть тогда, когда атомы газа имеют большую энергию и скорости, носятся, как сумасшедшие, сталкиваются друг с другом. Мы ведь с вами помним, что частота и скорость соударений и есть температура. В обычном воздухе скорость соударений молекул невелика. А вот на Солнце раскаленный газ имеет температуру в тысячи (на поверхности Солнца) и даже десятки миллионов градусов (внутри нашего светила). Я сказал «на Солнце»? Это немного неточно. Скорее, «в Солнце». Потому что Солнце представляет собой раскаленный газовый шар. В основном оно состоит из водорода с небольшой примесью гелия.
Так вот в этих условиях скорость соударения атомов водорода такова, что «крышу срывает» у атомов на всю катушку. Атомы разрушаются, электроны слетают со своих орбит и начинают метаться одни, так же, как и протоны. Получается хаотическая электронно-протонная смесь или, иначе говоря, ионизированная плазма.
Плазма – горячая смесь ионов. Огонь – это тоже плазма. Только в обычном пламени костра или свечи содержание ионов не такое большое, как на Солнце, потому что температура ниже.
Я загрузил вас новыми словами – «ионы», «плазма». Но зато теперь вы можете похвастаться тем, что знаете целых четыре состояния вещества!
Первое – твердое. Атомы и молекулы в таком веществе крепко держатся друг за друга, никуда не бегают, а только чуть-чуть дрожат и топчутся на одном месте, образуя кристаллическую решетку.
Второе состояние вещества – жидкое. Здесь уже энергетика частичек вещества такова, что они ломают кристаллическую структуру, рушат тесные ряды и начинают хаотически бродить, будучи не в силах удержаться в твердой структуре. Растекаются. Но еще не разлетаются друг от друга.
Разлетаться они начнут в третьем состоянии вещества – газообразном, которое наступит при дальнейшем нагреве, то есть дальнейшей накачке вещества энергией. Тогда скорость атомов станет уже такой, что силы их притяжения не смогут сдерживать энергичность расшалившихся атомов. Они просто разлетятся друг от друга и рассеются в пространстве.
Если же газ собрать в каком-то закрытом объеме или просто удерживать мощной силой гравитации (как на Солнце) и продолжать нагревать, то энергетика атомов станет уже такой огромной, что при столкновении друг с другом будут разрушаться уже сами атомы – с них начнет срывать электронные шубы. И останутся только ионы, ионизированный газ – плазма. При этом газ начнет светиться, что говорит о его высокой температуре.
Плазма – это прекрасно. Мы любим смотреть на плазму…
Глава 3. Как устроен атом и вообще весь мир
3.3 (66.41%) 128 votes
Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a0 = 0,529 Å.
Атом водорода имеет специальное значение в квантовой механике и релятивистской квантовой механике, поскольку для него проблема двух тел имеет точное или приближенное аналитическое решения. Эти решения применимы для разных изотопов водорода, с соответствующей коррекцией.
В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощенно рассматривается как электрон в электростатическом поле бесконечно тяжёлого атомного ядра, не участвующего в движении (или просто в кулоновском электростатическом потенциале вида 1/r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.
В 1913 году Нильс Бор предложил модель атома водорода, имеющую множество предположений и упрощений, и вывел из неё спектр излучения водорода. Предположения модели не были полностью правильны, но тем не менее приводили к верным значениям энергетических уровней атома.
Результаты расчётов Бора были подтверждены в 1925—1926 годах строгим квантово-механическим анализом, основанном на уравнении Шрёдингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра выводится в аналитической форме. Оно описывает не только уровни энергии электрона и спектр излучения, но и форму атомных орбиталей.
Содержание
- 1 Решение уравнения Шрёдингера
- 2 Математическое описание атома водорода
- 2.1 Энергетический спектр
- 2.2 Волновые функции
- 2.3 Угловой момент
- 3 Нахождение энергии электрона из модели Бора
- 4 Визуализация орбиталей атома водорода
- 5 Строение и свойства атома водорода
- 5.1 Образование атома водорода и его спектр излучения
- 5.2 Возбуждение и ионизация атома водорода
- 5.3 Строение атома водорода в основном состоянии
- 5.4 Атом водорода в электрическом поле
- 5.5 Взаимодействие атома водорода с протоном
- 5.6 Взаимодействие атома водорода с электроном
- 5.7 Рекомбинация атомов водорода
- 6 Примечания
- 7 См. также
- 8 Ссылки
Решение уравнения Шрёдингера[править | править исходный текст]
Решение уравнения Шрёдингера для водородного атома использует факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны, их зависимость от угловой координаты следуют полностью из изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента. Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Отсюда следует, что собственные состояния гамильтониана задаются двумя квантовыми числами углового момента l и m (целые числа). Квантовое число углового момента l может принимать значения 0, 1, 2… и определяет величину углового момента. Магнитное квантовое число может принимать m = −l, …, +l; оно определяет проекцию углового момента на (произвольно выбранную) ось z.
В дополнение к математическим выражениям для волновых функций полного углового момента и проекции углового момента, нужно найти выражение для радиальной зависимости волновой функции. В потенциале 1/r радиальные волновые функции записываются с использованием полиномов Лагерра). Это приводит к третьему квантовому числу, которое называется основным квантовым числом n и может принимать значения 1, 2, 3… Основное квантовое число в атоме водорода связано с полной энергией атома. Заметим, что максимальное значение квантового числа углового момента ограничено основным квантовым числом: оно может изменяться только до n − 1, то есть l = 0, 1, …, n−1.
Из-за сохранения углового момента состояния с одинаковыми l, но различными m в отсутствие магнитного поля имеют одну и ту же энергию (это выполняется для всех задач с аксиальной симметрией). Кроме того, для водородного атома состояния с одинаковыми n, но разными l также вырождены (то есть имеют одинаковую энергию). Однако это свойство — особенность лишь атома водорода (и водородоподобных атомов), оно не выполняется для более сложных атомов, которые имеют (эффективный) потенциал, отличающийся от кулоновского (из-за присутствия внутренних электронов, экранирующих потенциал ядра).
Если мы примем во внимание спин электрона, то появится последнее, четвёртое квантовое число, определяющее состояния атома водорода — проекция углового момента собственного вращения электрона на ось Z. Эта проекция может принимать два значения. Любое собственное состояние электрона в водородном атоме полностью описывается четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это объясняет также, почему выбор оси Z для квантования направления вектора углового момента является несущественным: орбиталь для данных l и 

Рассмотрим сейчас решение уравнения Шрёдингера для атома водорода. Так как потенциальная функция электрона в атоме водорода имеет вид 
Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, 


Уравнение Шрёдингера в сферических координатах:
В этом уравнении 




После подстановки значений частных производных в уравнение Шрёдингера получим:
Умножим уравнение на
Второе слагаемое тут зависит только от φ. Перенесём его в правую часть равенства.
Равенство возможно, когда обе части равны какой-то постоянной величине. Обозначим её 
Решением этого уравнения являются функции
Угол φ может изменяться от 0 до 2π. Функция 


Далее, интегрируя квадрат модуля функции 
Далее рассмотрим левую часть уравнения (1). Она, конечно, равна
Разделим уравнение на
После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через 
Решение этих двух последних уравнений приводит к значениям l и n соответственно. Три квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода.
Модуль полной энергии электрона в стационарном состоянии в атоме водорода обратно пропорционален 

Число l называется азимутальным квантовым числом и определяет орбитальный момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).
Магнитное квантовое число 
Математическое описание атома водорода[править | править исходный текст]
Энергетический спектр[править | править исходный текст]
Энергетические уровни атома водорода, включая подуровни тонкой структуры, записываются в виде
-
- где
— постоянная тонкой структуры,
— собственное значение оператора полного момента импульса.
Энергию 

-
(в системе СИ),
где h — постоянная Планка, 
Волновые функции[править | править исходный текст]
В сферических координатах волновые функции имеют вид:
где:
— Боровский радиус.
— обобщённые полиномы Лагерра степени
от функции
— нормированные на единицу сферические функции.
Угловой момент[править | править исходный текст]
Собственные значения для оператора углового момента:
Нахождение энергии электрона из модели Бора[править | править исходный текст]
Вычислим уровни энергии атома водорода без учёта тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Приравнивая кулоновскую силу притяжения 

Здесь 



Отсюда кинетическая энергия электрона
где 
Потенциальная его энергия
Полная энергия, соответственно, равна
Для нахождения радиуса rn стационарной орбиты с номером n рассмотрим систему уравнений, в которой второе уравнение есть математическое выражение первого постулата Бора
Отсюда получаем выражение для радиуса стационарной орбиты с номером n:
Радиус первой орбиты оказывается равным 
Подставляя это значение в выражение для энергии, получим, что
Отсюда мы можем найти волновое число (по определению это обратная длина волны или число длин волн, укладывающихся на 1 см) фотона, излучаемого атомом водорода за один переход из возбужденного состояния с главным квантовым числом 
где 
Визуализация орбиталей атома водорода[править | править исходный текст]
Плотность вероятности для электрона при различных квантовых числах (l)
Изображение справа показывает первые несколько орбиталей атома водорода (собственные функции гамильтониана). Они представляют собой поперечные сечения плотности вероятности, величина которой отражена цветом (чёрный цвет соответствует минимальной плотности вероятности а белый — максимальной). Квантовое число углового момента l обозначено в каждой колонке, используя обычные спектроскопические обозначения (s означает l = 0; p: l = 1; d: l = 2). Главное квантовое число n (= 1, 2, 3…) отмечено справа от каждого ряда. Для всех картин магнитное квантовое число m равно 0, и сечение взято в плоскости — XZ, Z — вертикальная ось. Плотность вероятности в трёхмерном пространстве получается при вращении картинки вокруг оси Z.
Основное состояние, то есть состояние самой низкой энергии, в котором обычно находится электрон, является первым, состоянием 1s (n = 1, l = 0). Изображение с большим количеством орбиталей доступно до более высоких чисел n и l. Отметим наличие чёрных линий, которые появляются на каждой картинке, за исключением первой. Они — узловые линии (которые являются фактически узловыми поверхностями в трёх измерениях). Их общее количество всегда равно n − 1, которое является суммой числа радиальных узлов (равного n − l − 1) и числа угловых узлов (равного l).
Строение и свойства атома водорода[править | править исходный текст]
Образование атома водорода и его спектр излучения[править | править исходный текст]
При попадании в электрическое поле положительно заряженного протона отрицательно заряженного электрона происходит захват последнего протоном — образуется атом водорода. Образовавшийся атом водорода находится в возбуждённом состоянии. Время жизни атома водорода в возбуждённом состоянии — ничтожные доли секунды (10−8 — 10−10сек)[2], однако очень высоковозбуждённые атомы в бесстолкновительной среде могут существовать до секунд. Снятие возбуждения атома происходит за счёт излучения фотонов с фиксированной энергией, проявляющихся в характерном спектре излучения водорода. Поскольку газообразный атомарный водород содержит множество атомов в различных степенях возбуждения, спектр состоит из большого числа линий.
Схема происхождения спектра атомарного водорода представлена на рисунке.[3].
Линии спектра серии Лаймана обусловлены переходом электронов на нижний уровень с квантовым числом n = 1 с уровней с квантовыми числами n = 2, 3, 4, 5, 6… Линии Лаймана лежат в ультрафиолетовой области спектра. Линии спектра серии Бальмера обусловлены переходом электронов на уровень с квантовым числом n = 2 с уровней с квантовыми числами n = 3, 4, 5, 6… и лежат в видимой области спектра.
Линии спектра серий Пашена, Брэкета и Пфунда обусловлены переходом электронов на уровни с квантовыми числами n, равными 3, 4 и 5 (соответственно), и расположены в инфракрасной области спектра.[4].
В нормальном (основном) состоянии (главное квантовое число n = 1) атом водорода в изолированном виде может существовать неограниченное время. Согласно квантохимическим расчетам, радиус мест наибольшей вероятности нахождения электрона в атоме водорода в нормальном состоянии (главное квантовое число n = 1) равен 0,529 Å. Этот радиус является одной из основных атомных констант, он получил название боровский радиус (см. выше). При возбуждении атома водорода электрон проходит на более высокий квантовый уровень (n = 2, 3, 4 и т. д.), при этом радиус мест наибольшей вероятности нахождения электрона в атоме возрастает пропорционально квадрату главного квантового числа:
- rn = a0 · n2.
Возбуждение и ионизация атома водорода[править | править исходный текст]
Возбуждение атома водорода происходит при нагревании, электроразряде, поглощении света и т. д., причём в любом случае атом водорода поглощает определённые порции — кванты энергии, соответствующие разности энергетических уровней электронов. Обратный переход электрона сопровождается выделением точно такой же порции энергии. Квантовые переходы электрона соответствуют скачкообразному изменению концентрического шарового слоя вокруг ядра атома водорода, в котором преимущественно находится электрон (шаровым слой является только при нулевом значении азимутального квантового числа l).
Согласно квантовомеханическим расчётам, наиболее вероятное расстояние электрона от ядра в атоме водорода равно боровскому радиусу ~ 0,53 Å при n = 1; 2,12 Å — при n = 2; 4,77 Å — при n = 3 и так далее. Значения этих радиусов относятся как квадраты натуральных чисел (главного квантового числа) 12 : 22 : 32…. В очень разреженных средах (например, в межзвёздной среде) наблюдаются атомы водорода с главными квантовыми числами до 1000 (ридберговские атомы), чьи радиусы достигают сотых долей миллиметра.
Если электрону в основном состоянии придать дополнительную энергию, превышающую энергию связи E0 ≈ 13,6 эВ, происходит ионизация атома водорода — распад атома на протон и электрон.
Радиальное распределение вероятности нахождения электрона в атоме.
Строение атома водорода в основном состоянии[править | править исходный текст]
Радиальная зависимость dp(r)/dr плотности вероятности нахождения электрона в атоме водорода, находящемся в основном состоянии, представлена на рисунке. Эта зависимость даёт вероятность того, что электрон будет обнаружен в тонком шаровом слое радиуса r толщиной dr с центром в ядре. Площадь этого слоя равна S = 4πr2, его объём dV = 4πr2dr. Общая вероятность нахождения электрона в слое равна (4πr2dr) ψ2, поскольку в основном состоянии волновая функция электрона сферически симметрична (то есть постоянна в рассматриваемом шаровом слое). Рисунок выражает зависимость dp(r)/dr = 4πr2ψ2. Кривая радиального распределения плотности вероятности dp(r)/dr нахождения электрона в атоме водорода имеет максимум при a0. Этот наиболее вероятный радиус совпадает с боровским радиусом. Размытое облако плотности вероятности, полученное при квантовомеханическом рассмотрении, значительно отличается от результатов теории Бора и согласуется с принципом неопределённости Гейзенберга. Это размытое сферически симметричное распределение плотности вероятности нахождения электрона, называемое электронной оболочкой, экранирует ядро и делает физическую систему протон-электрон электронейтральной и сферически симметричной — у атома водорода в основном состоянии отсутствуют электрический и магнитный дипольные моменты (как и моменты более высоких порядков), если пренебречь спинами электрона и ядра. Следует отметить, что максимум объёмной плотности вероятности ψ2 достигается не при r = a0, как для радиальной зависимости, а при r = 0.
Атом водорода в электрическом поле[править | править исходный текст]
По теории деформационной поляризации, нейтральный атом водорода, попадая во внешнее электрическое поле, подвергается деформации — центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L, что приводит к появлению в атоме водорода наведённого электрического дипольного момента μ[5]. Величина наведённого дипольного момента прямо пропорциональна напряжённости внешнего электрического поля E:
- μ = αeE = Lq.
Коэффициент пропорциональности αe носит название электронной поляризуемости. Электронная поляризуемость атома водорода составляет 0,66 Å3.[6]
Чем выше напряжённость приложенного электрического поля, тем больше смещение центра электронной оболочки от центра атома водорода и, собственно, длина наведённого диполя
- L = αe E/q,
где q — величина заряда ядра атома водорода.
При высоких значениях напряжённости приложенного электрического поля атом водорода подвергается ионизации полем с образованием свободных протона и электрона.
Взаимодействие атома водорода с протоном[править | править исходный текст]
Деформационная поляризация атома водорода в электрическом поле протона
Протон, обладая положительным элементарным электрическим зарядом q = 1,602•10 −19 Кл, как и всякий точечный электрический заряд создаёт вокруг себя электрическое поле с напряжённостью E. E = q/R2, Где R — расстояние точки поля до протона.
Нейтральный атом водорода, попадая в электрическое поле протона, подвергается деформационной поляризации (рис.1.). Длина наведённого электрического диполя атома водорода обратно пропорциональна квадрату расстояния между атомом водорода и протоном L = αe E/q = αe/R2 = 0,66/R2
Отрицательный полюс наведённого электрического диполя атома водорода ориентируется в сторону протона. В результате чего начинает проявляться электростатическое притяжение между атомом водорода и протоном. Сближение частиц (атома водорода и протона) возможно до тех пор, пока центр плотности вероятности нахождения электрона станет равноудалённым от обоих протонов. В этом предельном случае d=R=2L. Центр области вероятного нахождения электрона совпадает с центром симметрии образовавшейся системы H2+ — молекулярного иона водорода, при этом d=R=2L=³√2αe = ³√2•0,66 = 1,097 Å.
Найденная величина d = 1,097 Å близка к экспериментальной величине межъядерного расстояния в молекулярном ионе водорода H2+ — 1,06 Å.[7]
Взаимодействуя с протоном, атом водорода образует молекулярный ион водорода
H2+,H + H + -> H2+ + Q,
Характеризующийся простейшей одноэлектронной ковалентной химической связью.
Взаимодействие атома водорода с электроном[править | править исходный текст]
Рис. Деформационная поляризация атома водорода под действием приближающегося электрона и модель гидрид-иона H—
Электрон, обладая элементарным электрическим зарядом, как и протон создаёт вокруг себя электрическое поле, но в отличие от электрического поля протона с отрицательным знаком. Нейтральный атом водорода, попадая в электрическое поле электрона подвергается деформационной поляризации. Центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L в противоположную сторону к приближающемуся электрону. Приближающийся электрон как бы вытесняет из атома водорода находящийся в нём электрон, подготавливая место для второго электрона. Величина смещения центра электронной оболочки атома водорода L обратно пропорциональна квадрату расстояния атома водорода к приближающемуся электрону R:
L = αe/R2 = 0.66/R2 (рис)
Сближение атома водорода и электрона возможно до тех пор, пока центры областей плотностей вероятности нахождения обоих электронов не станут равноудалёнными от ядра объединённой системы — отрицательно заряженного иона водорода. Такое состояние системы имеет место при:
re = L = R = 3√0,66 = 0,871 Å.
Где re — орбитальный радиус двухэлектронной оболочки гидрид-иона H—.
Таким образом, атом водорода проявляет своеобразную амфотерность, он может взаимодействовать как с положительно заряженной частицей (протоном), образуя молекулярный ион водорода H2+, так и с отрицательно заряженной частицей (электроном), образуя гидрид-ион H—.
Рекомбинация атомов водорода[править | править исходный текст]
Рекомбинация атомов водорода обсуловлена силами межатомного взаимодействия. Происхождение сил, вызывающих притяжение электрически нейтральных атомов друг к другу, было объяснено в 1930 году Ф.Лондоном. Межатомное притяжение возникает вследствие флуктуации электрических зарядов в двух атомах, находящихся близко друг от друга. Поскольку электроны в атомах движутся, то каждый атом обладает мгновенным электрическим дипольным моментом, отличным от нуля. Мгновенный диполь (электродинамика) на одном атоме наводит противоположно направленный диполь в соседнем атоме. Наступает синхронизация колебаний двух атомов — двух осцилляторов, частоты которых совпадают. Результатом этого процесса является образование молекулы водорода.
Наличие мгновенного электрического дипольного момента у атома водорода выражается в характерной особенности атома водорода, проявляющейся в крайней реакционной способности атомарного водорода и склонности его к рекомбинации. Время существования атомного водорода составляет около 1 сек. Под давлением в 0.2 мм рт. ст. Рекомбинация атомов водорода имеет место, если образующаяся молекула водорода быстро освобождается от избытка энергии, выделяющейся при взаимодействии атомов водорода путём тройного столкновения. Соединение атомов водорода в молекулу протекает значительно быстрее на поверхности различных металлов, чем в самом газе. При этом металл воспринимает ту энергию, которая выделяется при образовании молекул водорода, и нагревается до очень высоких температур. Тепловой эффект реакции образования молекулярного водорода из атомов водорода составляет 103 ккал/моль.
На принципе рекомбинации атомов водорода разработана атомно-водородная сварка. Между двумя вольфрамовыми стержнями создаётся электрическая дуга, через которую по облегающим стержни трубкам пропускается ток водорода. При этом часть молекул водорода распадается на атомы, которые затем вновь соединяются на металлической поверхности, помещаемой на небольшом расстоянии от дуги. Металл может быть таким путём нагрет до температуры выше 3500° C[8].
Константы реакции диссоциации молекулярного водорода (Kp) и степень превращения водорода в атомарное состояние (α) в зависимости от абсолютной температуры (T) представлены в таблице[9]:
| T, к | 2000 | 3000 | 4000 | 5000 | 6000 | 8000 |
|---|---|---|---|---|---|---|
| Кр | 2,62 · 10-6 | 2,47 · 10-2 | 2,52 | 4,09 · 10 | 2,62 · 102 | 2,70 · 103 |
| α | 8,10 · 10-4 | 7,83 · 10-2 | 0,621 | 0,954 | 0,992 | 0,999 |
Примечания[править | править исходный текст]
- ↑ Сивухин Д. В. § 13. Спектр водорода // Общий курс физики. — М.: Наука, 1986. — Т. V. Атомная и ядерная физика. Часть 1: Атомная физика. — С. 68. — 416 с. — ISBN 5-02-014053-8
- ↑ Ахметов Н. С. Неорганическая химия. Учебное пособие для вузов с ил. — 2-е изд., перераб. и доп. — М.: «Высшая школа», 1975. — 672 с.
- ↑ Некрасов Б. В. Курс общей химии. — 14-е изд. — М.: ГНТИ химической литературы, 1962. — С. 113. — 976 с.
- ↑ Даниэльс Ф., Олберти Р. Физическая химия. — пер. с англ. под ред. д. х. н., проф. К. В. Топчиевой. — М.: «Мир», 1978. — С. 369-370. — 645 с.
- ↑ Потапов А. А. Деформационная поляризация: Поиск оптимальных моделей. — Новосибирск: «Наука», 2004. — 511 с. — ISBN 5-02-032065-X
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: Издательство химической литературы, 1962. — Т. 1. — С. 385. — 1071 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: Издательство химической литературы, 1962. — Т. 1. — С. 388. — 1071 с.
- ↑ Некрасов Б. В. Курс общей химии. — 14-е изд. — М.: ГНТИ химической литературы, 1962. — С. 110. — 976 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: «Химия», 1964. — Т. 3. — С. 24. — 1008 с. — 65 000 экз.
См. также[править | править исходный текст]
- Водород
- Водородоподобный атом
- Квантовая механика
- Квантовая химия
- Квантовая теория поля
- Квантовое состояние
- Принцип неопределённости
- Волновая функция
- Электронное облако
- Ридберговский атом
Ссылки[править | править исходный текст]
- Griffiths David J. Introduction to Quantum Mechanics. — Upper Saddle River, NJ: Prentice Hall, 1995. — ISBN ISBN 0-13-111892-7
Параграф 4.2 описывает атом водорода, а вся глава 4 имеет отношение к теме.
- Bransden B.H. Physics of Atoms and Molecules. — London: Longman, 1983. — ISBN ISBN 0-582-44401-2
- Физика атома водорода на Scienceworld
- Графическое представление орбиталей
- Апплет изображающий орбитали атома водорода
ru:Протий
This article is about the physics of the hydrogen atom. For a chemical description, see hydrogen. For monatomic hydrogen, see Hydrogen § Atomic hydrogen.
 |
|
| General | |
|---|---|
| Symbol | 1H |
| Names | hydrogen atom, 1H, H-1, protium |
| Protons (Z) | 1 |
| Neutrons (N) | 0 |
| Nuclide data | |
| Natural abundance | 99.985% |
| Half-life (t1/2) | stable |
| Isotope mass | 1.007825 Da |
| Spin | 1/2 |
| Excess energy | 7288.969±0.001 keV |
| Binding energy | 0.000±0.0000 keV |
| Isotopes of hydrogen Complete table of nuclides |
Depiction of a hydrogen atom showing the diameter as about twice the Bohr model radius. (Image not to scale)
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.[1]
In everyday life on Earth, isolated hydrogen atoms (called «atomic hydrogen») are extremely rare. Instead, a hydrogen atom tends to combine with other atoms in compounds, or with another hydrogen atom to form ordinary (diatomic) hydrogen gas, H2. «Atomic hydrogen» and «hydrogen atom» in ordinary English use have overlapping, yet distinct, meanings. For example, a water molecule contains two hydrogen atoms, but does not contain atomic hydrogen (which would refer to isolated hydrogen atoms).
Atomic spectroscopy shows that there is a discrete infinite set of states in which a hydrogen (or any) atom can exist, contrary to the predictions of classical physics. Attempts to develop a theoretical understanding of the states of the hydrogen atom have been important to the history of quantum mechanics, since all other atoms can be roughly understood by knowing in detail about this simplest atomic structure.
Isotopes[edit]
The most abundant isotope, hydrogen-1, protium, or light hydrogen, contains no neutrons and is simply a proton and an electron. Protium is stable and makes up 99.985% of naturally occurring hydrogen atoms.[2]
Deuterium (2H) contains one neutron and one proton in its nucleus. Deuterium is stable and makes up 0.0156% of naturally occurring hydrogen[2] and is used in industrial processes like nuclear reactors and Nuclear Magnetic Resonance.
Tritium (3H) contains two neutrons and one proton in its nucleus and is not stable, decaying with a half-life of 12.32 years. Because of its short half-life, tritium does not exist in nature except in trace amounts.
Heavier isotopes of hydrogen are only created artificially in particle accelerators and have half-lives on the order of 10−22 seconds. They are unbound resonances located beyond the neutron drip line; this results in prompt emission of a neutron.
The formulas below are valid for all three isotopes of hydrogen, but slightly different values of the Rydberg constant (correction formula given below) must be used for each hydrogen isotope.
Hydrogen ion[edit]
Lone neutral hydrogen atoms are rare under normal conditions. However, neutral hydrogen is common when it is covalently bound to another atom, and hydrogen atoms can also exist in cationic and anionic forms.
If a neutral hydrogen atom loses its electron, it becomes a cation. The resulting ion, which consists solely of a proton for the usual isotope, is written as «H+» and sometimes called hydron. Free protons are common in the interstellar medium, and solar wind. In the context of aqueous solutions of classical Brønsted–Lowry acids, such as hydrochloric acid, it is actually hydronium, H3O+, that is meant. Instead of a literal ionized single hydrogen atom being formed, the acid transfers the hydrogen to H2O, forming H3O+.
If instead a hydrogen atom gains a second electron, it becomes an anion. The hydrogen anion is written as «H–» and called hydride.
Theoretical analysis[edit]
The hydrogen atom has special significance in quantum mechanics and quantum field theory as a simple two-body problem physical system which has yielded many simple analytical solutions in closed-form.
Failed classical description[edit]
Experiments by Ernest Rutherford in 1909 showed the structure of the atom to be a dense, positive nucleus with a tenuous negative charge cloud around it. This immediately raised questions about how such a system could be stable. Classical electromagnetism had shown that any accelerating charge radiates energy, as shown by the Larmor formula. If the electron is assumed to orbit in a perfect circle and radiates energy continuously, the electron would rapidly spiral into the nucleus with a fall time of:[3]
where 

Bohr–Sommerfeld Model[edit]
In 1913, Niels Bohr obtained the energy levels and spectral frequencies of the hydrogen atom after making a number of simple assumptions in order to correct the failed classical model. The assumptions included:
- Electrons can only be in certain, discrete circular orbits or stationary states, thereby having a discrete set of possible radii and energies.
- Electrons do not emit radiation while in one of these stationary states.
- An electron can gain or lose energy by jumping from one discrete orbit to another.
Bohr supposed that the electron’s angular momentum is quantized with possible values:
where
and 

where 



For 
is called the Rydberg unit of energy. It is related to the Rydberg constant 
The exact value of the Rydberg constant assumes that the nucleus is infinitely massive with respect to the electron. For hydrogen-1, hydrogen-2 (deuterium), and hydrogen-3 (tritium) which have finite mass, the constant must be slightly modified to use the reduced mass of the system, rather than simply the mass of the electron. This includes the kinetic energy of the nucleus in the problem, because the total (electron plus nuclear) kinetic energy is equivalent to the kinetic energy of the reduced mass moving with a velocity equal to the electron velocity relative to the nucleus. However, since the nucleus is much heavier than the electron, the electron mass and reduced mass are nearly the same. The Rydberg constant RM for a hydrogen atom (one electron), R is given by
where 

There were still problems with Bohr’s model:
- it failed to predict other spectral details such as fine structure and hyperfine structure
- it could only predict energy levels with any accuracy for single–electron atoms (hydrogen-like atoms)
- the predicted values were only correct to
, where
is the fine-structure constant.
Most of these shortcomings were resolved by Arnold Sommerfeld’s modification of the Bohr model. Sommerfeld introduced two additional degrees of freedom, allowing an electron to move on an elliptical orbit characterized by its eccentricity and declination with respect to a chosen axis. This introduced two additional quantum numbers, which correspond to the orbital angular momentum and its projection on the chosen axis. Thus the correct multiplicity of states (except for the factor 2 accounting for the yet unknown electron spin) was found. Further, by applying special relativity to the elliptic orbits, Sommerfeld succeeded in deriving the correct expression for the fine structure of hydrogen spectra (which happens to be exactly the same as in the most elaborate Dirac theory). However, some observed phenomena, such as the anomalous Zeeman effect, remained unexplained. These issues were resolved with the full development of quantum mechanics and the Dirac equation. It is often alleged that the Schrödinger equation is superior to the Bohr–Sommerfeld theory in describing hydrogen atom. This is not the case, as most of the results of both approaches coincide or are very close (a remarkable exception is the problem of hydrogen atom in crossed electric and magnetic fields, which cannot be self-consistently solved in the framework of the Bohr–Sommerfeld theory), and in both theories the main shortcomings result from the absence of the electron spin. It was the complete failure of the Bohr–Sommerfeld theory to explain many-electron systems (such as helium atom or hydrogen molecule) which demonstrated its inadequacy in describing quantum phenomena.
Schrödinger equation[edit]
The Schrödinger equation allows one to calculate the stationary states and also the time evolution of quantum systems. Exact analytical answers are available for the nonrelativistic hydrogen atom. Before we go to present a formal account, here we give an elementary overview.
Given that the hydrogen atom contains a nucleus and an electron, quantum mechanics allows one to predict the probability of finding the electron at any given radial distance 

Here, 

The 





It turns out that this is a maximum at 


probability indicated by the square of the wavefunction. Since the probability of finding the electron somewhere in the whole volume is unity, the integral of 
As discussed below, the ground state 








and there are three 
An electron in the 

Wavefunction[edit]
The Hamiltonian of the hydrogen atom is the radial kinetic energy operator and Coulomb attraction force between the positive proton and negative electron. Using the time-independent Schrödinger equation, ignoring all spin-coupling interactions and using the reduced mass 
Expanding the Laplacian in spherical coordinates:
This is a separable, partial differential equation which can be solved in terms of special functions. When the wavefunction is separated as product of functions 


- radial:
- polar:
- azimuth:
The normalized position wavefunctions, given in spherical coordinates are:
3D illustration of the eigenstate 
where:
The quantum numbers can take the following values:
Additionally, these wavefunctions are normalized (i.e., the integral of their modulus square equals 1) and orthogonal:
where 


The wavefunctions in momentum space are related to the wavefunctions in position space through a Fourier transform
which, for the bound states, results in[12]
where 


The solutions to the Schrödinger equation for hydrogen are analytical, giving a simple expression for the hydrogen energy levels and thus the frequencies of the hydrogen spectral lines and fully reproduced the Bohr model and went beyond it. It also yields two other quantum numbers and the shape of the electron’s wave function («orbital») for the various possible quantum-mechanical states, thus explaining the anisotropic character of atomic bonds.
The Schrödinger equation also applies to more complicated atoms and molecules. When there is more than one electron or nucleus the solution is not analytical and either computer calculations are necessary or simplifying assumptions must be made.
Since the Schrödinger equation is only valid for non-relativistic quantum mechanics, the solutions it yields for the hydrogen atom are not entirely correct. The Dirac equation of relativistic quantum theory improves these solutions (see below).
Results of Schrödinger equation[edit]
The solution of the Schrödinger equation (wave equation) for the hydrogen atom uses the fact that the Coulomb potential produced by the nucleus is isotropic (it is radially symmetric in space and only depends on the distance to the nucleus). Although the resulting energy eigenfunctions (the orbitals) are not necessarily isotropic themselves, their dependence on the angular coordinates follows completely generally from this isotropy of the underlying potential: the eigenstates of the Hamiltonian (that is, the energy eigenstates) can be chosen as simultaneous eigenstates of the angular momentum operator. This corresponds to the fact that angular momentum is conserved in the orbital motion of the electron around the nucleus. Therefore, the energy eigenstates may be classified by two angular momentum quantum numbers, 




In addition to mathematical expressions for total angular momentum and angular momentum projection of wavefunctions, an expression for the radial dependence of the wave functions must be found. It is only here that the details of the 


Note that the maximum value of the angular momentum quantum number is limited by the principal quantum number: it can run only up to 

Due to angular momentum conservation, states of the same 




Taking into account the spin of the electron adds a last quantum number, the projection of the electron’s spin angular momentum along the 







Mathematical summary of eigenstates of hydrogen atom[edit]
In 1928, Paul Dirac found an equation that was fully compatible with special relativity, and (as a consequence) made the wave function a 4-component «Dirac spinor» including «up» and «down» spin components, with both positive and «negative» energy (or matter and antimatter). The solution to this equation gave the following results, more accurate than the Schrödinger solution.
Energy levels[edit]
The energy levels of hydrogen, including fine structure (excluding Lamb shift and hyperfine structure), are given by the Sommerfeld fine-structure expression:[13]
where 


Coherent states[edit]
The coherent states have been proposed as[15]
which satisfies 
Visualizing the hydrogen electron orbitals[edit]
Probability densities through the xz-plane for the electron at different quantum numbers (ℓ, across top; n, down side; m = 0)
The image to the right shows the first few hydrogen atom orbitals (energy eigenfunctions). These are cross-sections of the probability density that are color-coded (black represents zero density and white represents the highest density). The angular momentum (orbital) quantum number ℓ is denoted in each column, using the usual spectroscopic letter code (s means ℓ = 0, p means ℓ = 1, d means ℓ = 2). The main (principal) quantum number n (= 1, 2, 3, …) is marked to the right of each row. For all pictures the magnetic quantum number m has been set to 0, and the cross-sectional plane is the xz-plane (z is the vertical axis). The probability density in three-dimensional space is obtained by rotating the one shown here around the z-axis.
The «ground state», i.e. the state of lowest energy, in which the electron is usually found, is the first one, the 1s state (principal quantum level n = 1, ℓ = 0).
Black lines occur in each but the first orbital: these are the nodes of the wavefunction, i.e. where the probability density is zero. (More precisely, the nodes are spherical harmonics that appear as a result of solving the Schrödinger equation in spherical coordinates.)
The quantum numbers determine the layout of these nodes.[16] There are:
Features going beyond the Schrödinger solution[edit]
There are several important effects that are neglected by the Schrödinger equation and which are responsible for certain small but measurable deviations of the real spectral lines from the predicted ones:
- Although the mean speed of the electron in hydrogen is only 1/137th of the speed of light, many modern experiments are sufficiently precise that a complete theoretical explanation requires a fully relativistic treatment of the problem. A relativistic treatment results in a momentum increase of about 1 part in 37,000 for the electron. Since the electron’s wavelength is determined by its momentum, orbitals containing higher speed electrons show contraction due to smaller wavelengths.
- Even when there is no external magnetic field, in the inertial frame of the moving electron, the electromagnetic field of the nucleus has a magnetic component. The spin of the electron has an associated magnetic moment which interacts with this magnetic field. This effect is also explained by special relativity, and it leads to the so-called spin–orbit coupling, i.e., an interaction between the electron’s orbital motion around the nucleus, and its spin.
Both of these features (and more) are incorporated in the relativistic Dirac equation, with predictions that come still closer to experiment. Again the Dirac equation may be solved analytically in the special case of a two-body system, such as the hydrogen atom. The resulting solution quantum states now must be classified by the total angular momentum number j (arising through the coupling between electron spin and orbital angular momentum). States of the same j and the same n are still degenerate. Thus, direct analytical solution of Dirac equation predicts 2S(1/2) and 2P(1/2) levels of hydrogen to have exactly the same energy, which is in a contradiction with observations (Lamb–Retherford experiment).
- There are always vacuum fluctuations of the electromagnetic field, according to quantum mechanics. Due to such fluctuations degeneracy between states of the same j but different l is lifted, giving them slightly different energies. This has been demonstrated in the famous Lamb–Retherford experiment and was the starting point for the development of the theory of quantum electrodynamics (which is able to deal with these vacuum fluctuations and employs the famous Feynman diagrams for approximations using perturbation theory). This effect is now called Lamb shift.
For these developments, it was essential that the solution of the Dirac equation for the hydrogen atom could be worked out exactly, such that any experimentally observed deviation had to be taken seriously as a signal of failure of the theory.
Alternatives to the Schrödinger theory[edit]
In the language of Heisenberg’s matrix mechanics, the hydrogen atom was first solved by Wolfgang Pauli[17] using a rotational symmetry in four dimensions [O(4)-symmetry] generated by the angular momentum
and the Laplace–Runge–Lenz vector. By extending the symmetry group O(4) to the dynamical group O(4,2),
the entire spectrum and all transitions were embedded in a single irreducible group representation.[18]
In 1979 the (non-relativistic) hydrogen atom was solved for the first time within Feynman’s path integral formulation
of quantum mechanics by Duru and Kleinert.[19][20] This work greatly extended the range of applicability of Feynman’s method.
See also[edit]
- Antihydrogen
- Atomic orbital
- Balmer series
- Helium atom
- Lithium atom
- Hydrogen molecular ion
- Proton decay
- Quantum chemistry
- Quantum state
- Theoretical and experimental justification for the Schrödinger equation
- Trihydrogen cation
- List of quantum-mechanical systems with analytical solutions
References[edit]
- ^
Palmer, D. (13 September 1997). «Hydrogen in the Universe». NASA. Archived from the original on 29 October 2014. Retrieved 23 February 2017. - ^ a b Housecroft, Catherine E.; Sharpe, Alan G. (2005). Inorganic Chemistry (2nd ed.). Pearson Prentice-Hall. p. 237. ISBN 0130-39913-2.
- ^ Olsen, James; McDonald, Kirk (7 March 2005). «Classical Lifetime of a Bohr Atom» (PDF). Joseph Henry Laboratories, Princeton University. Archived from the original (PDF) on 9 September 2019. Retrieved 11 December 2015.
- ^ «Derivation of Bohr’s Equations for the One-electron Atom» (PDF). University of Massachusetts Boston.
- ^ Eite Tiesinga, Peter J. Mohr, David B. Newell, and Barry N. Taylor (2019), «The 2018 CODATA Recommended Values of the Fundamental Physical Constants» (Web Version 8.0). Database developed by J. Baker, M. Douma, and S. Kotochigova. Available at http://physics.nist.gov/constants, National Institute of Standards and Technology, Gaithersburg, MD 20899. Link to R∞, Link to hcR∞
- ^ «Solving Schrödinger’s equation for the hydrogen atom :: Atomic Physics :: Rudi Winter’s web space». users.aber.ac.uk. Retrieved 30 November 2020.
- ^ Messiah, Albert (1999). Quantum Mechanics. New York: Dover. p. 1136. ISBN 0-486-40924-4.
- ^ LaguerreL. Wolfram Mathematica page
- ^ Griffiths, p. 152
- ^ Condon and Shortley (1963). The Theory of Atomic Spectra. London: Cambridge. p. 441.
- ^ Griffiths, Ch. 4 p. 89
- ^ Bransden, B. H.; Joachain, C. J. (1983). Physics of Atoms and Molecules. Longman. p. Appendix 5. ISBN 0-582-44401-2.
- ^ Sommerfeld, Arnold (1919). Atombau und Spektrallinien [Atomic Structure and Spectral Lines]. Braunschweig: Friedrich Vieweg und Sohn. ISBN 3-87144-484-7. German English
- ^ Atkins, Peter; de Paula, Julio (2006). Physical Chemistry (8th ed.). W. H. Freeman. p. 349. ISBN 0-7167-8759-8.
- ^ Klauder, John R (21 June 1996). «Coherent states for the hydrogen atom». Journal of Physics A: Mathematical and General. 29 (12): L293–L298. arXiv:quant-ph/9511033. doi:10.1088/0305-4470/29/12/002. S2CID 14124660.
- ^ Summary of atomic quantum numbers. Lecture notes. 28 July 2006
- ^
Pauli, W (1926). «Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik». Zeitschrift für Physik. 36 (5): 336–363. Bibcode:1926ZPhy…36..336P. doi:10.1007/BF01450175. S2CID 128132824. - ^
Kleinert H. (1968). «Group Dynamics of the Hydrogen Atom» (PDF). Lectures in Theoretical Physics, Edited by W.E. Brittin and A.O. Barut, Gordon and Breach, N.Y. 1968: 427–482. - ^
Duru I.H., Kleinert H. (1979). «Solution of the path integral for the H-atom» (PDF). Physics Letters B. 84 (2): 185–188. Bibcode:1979PhLB…84..185D. doi:10.1016/0370-2693(79)90280-6. - ^
Duru I.H., Kleinert H. (1982). «Quantum Mechanics of H-Atom from Path Integrals» (PDF). Fortschr. Phys. 30 (2): 401–435. Bibcode:1982ForPh..30..401D. doi:10.1002/prop.19820300802.
Books[edit]
- Griffiths, David J. (1995). Introduction to Quantum Mechanics. Prentice Hall. ISBN 0-13-111892-7. Section 4.2 deals with the hydrogen atom specifically, but all of Chapter 4 is relevant.
- Kleinert, H. (2009). Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, Worldscibooks.com, World Scientific, Singapore (also available online physik.fu-berlin.de)
External links[edit]
- The Hydrogen Atom and The Periodic Table — The Feynman Lectures on Physics
- Physics of hydrogen atom on Scienceworld

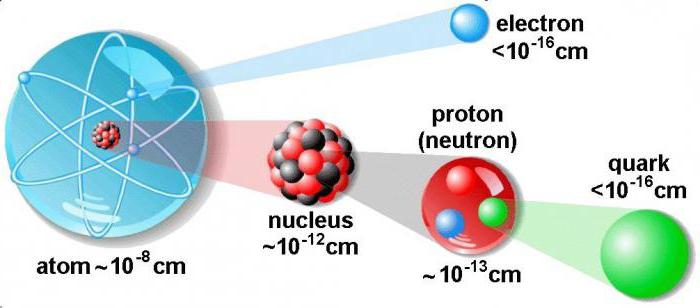
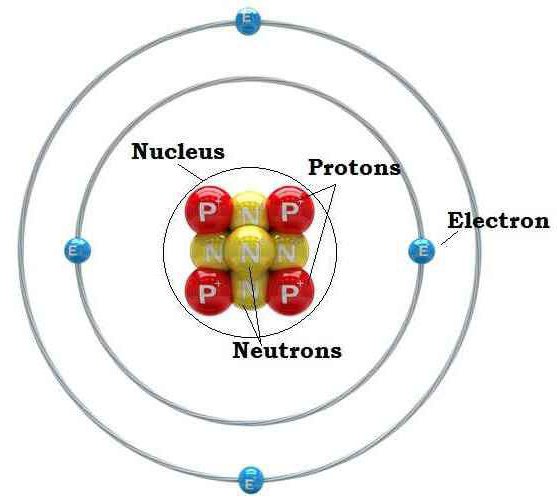
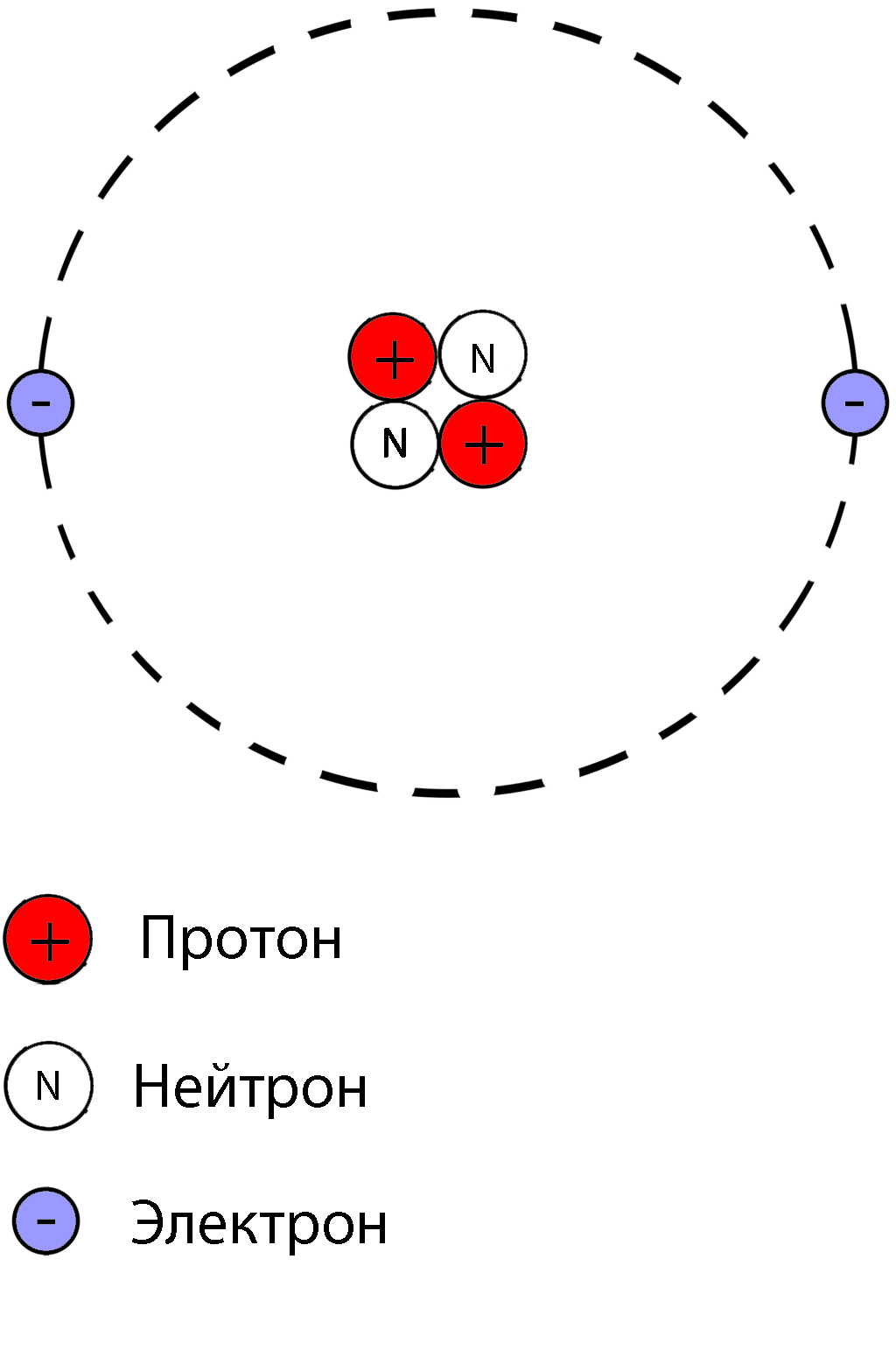

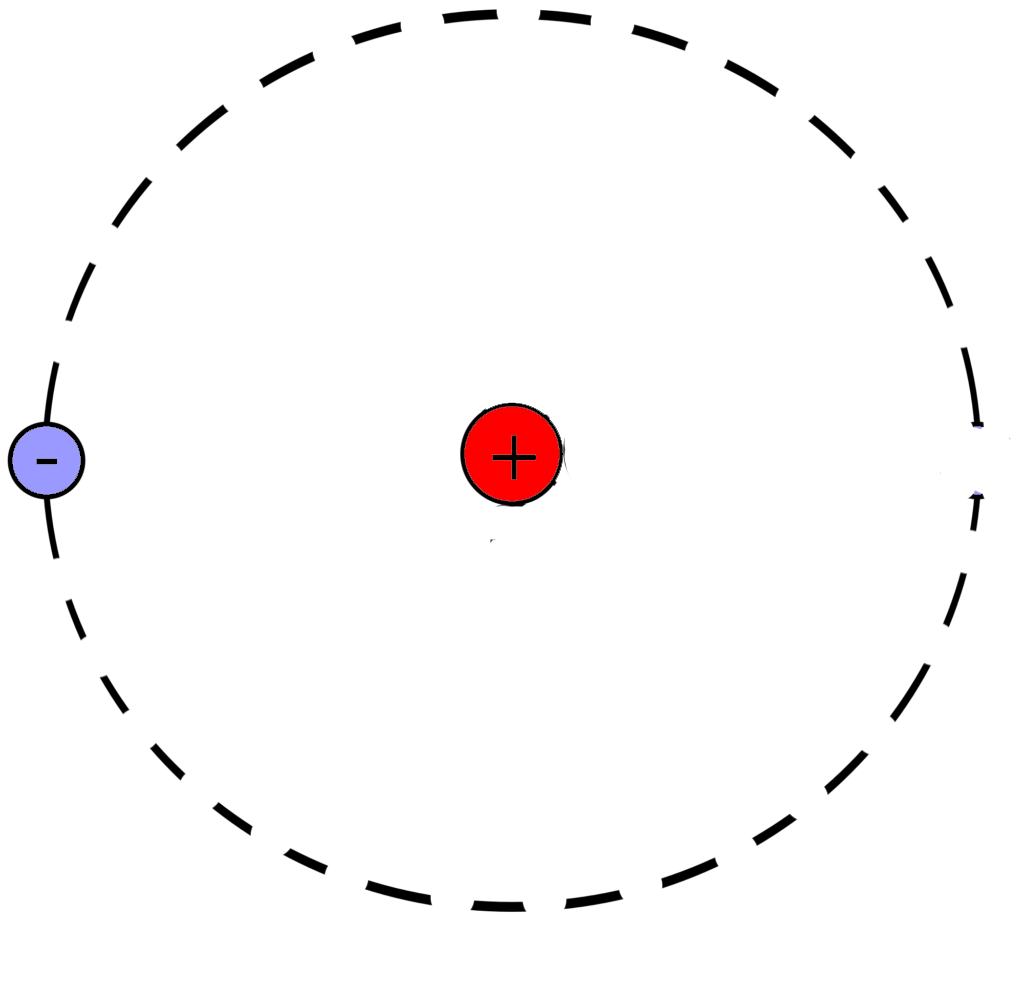
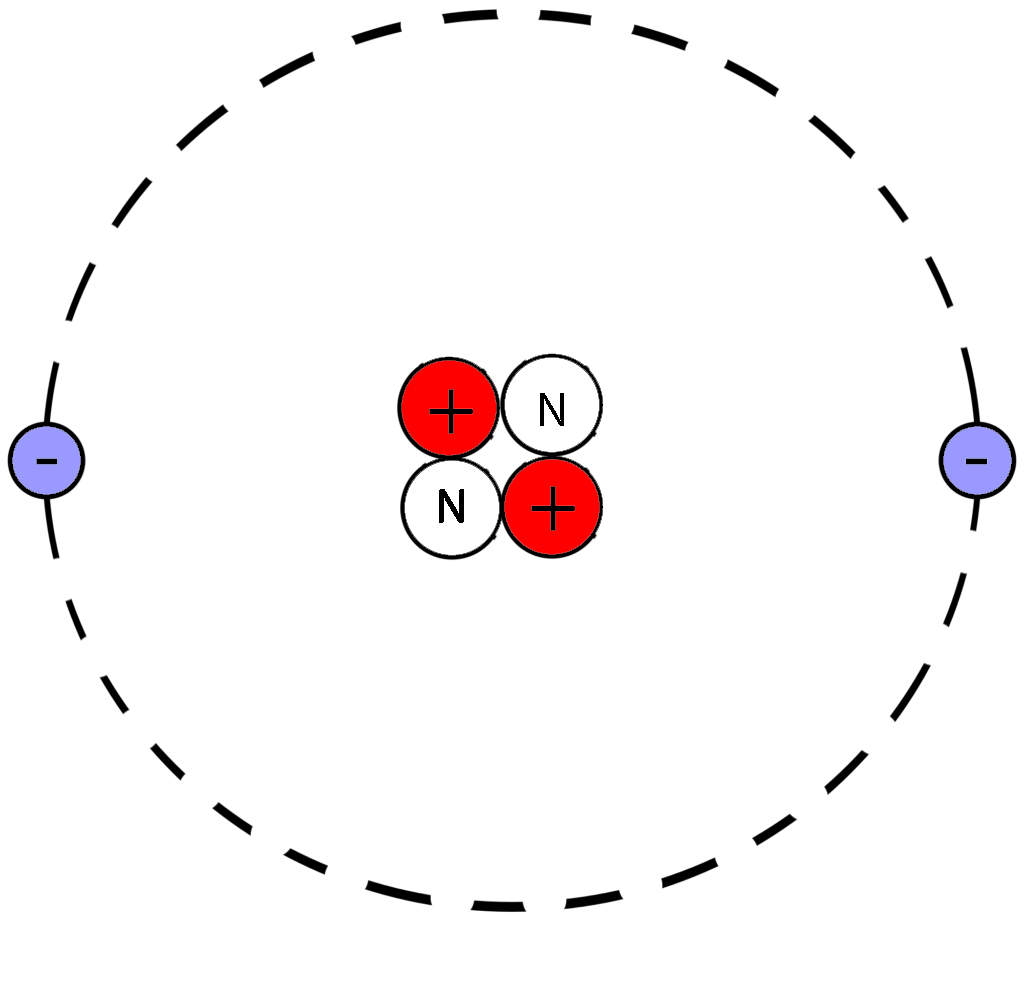




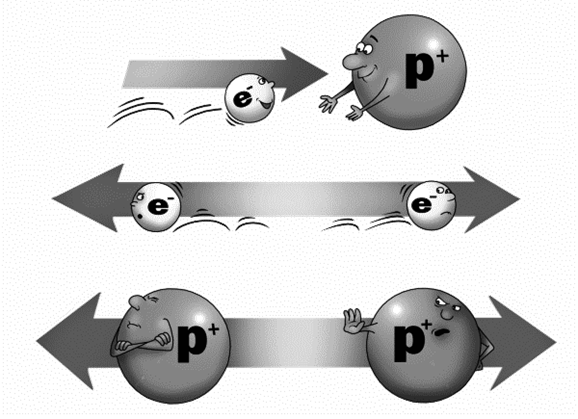
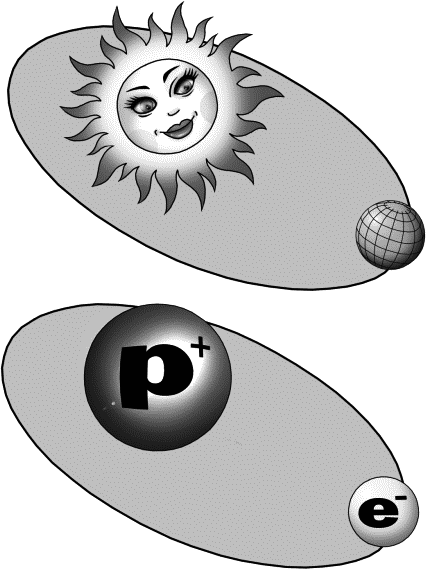
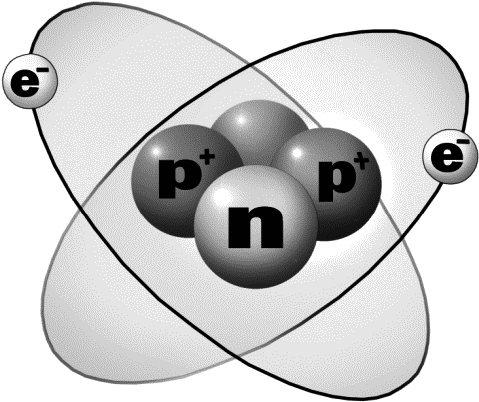



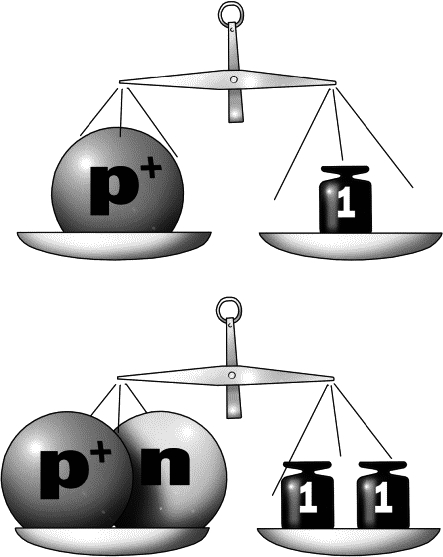
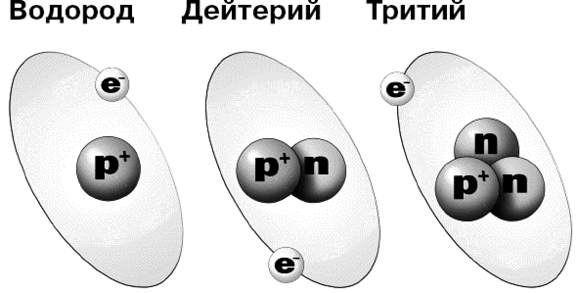
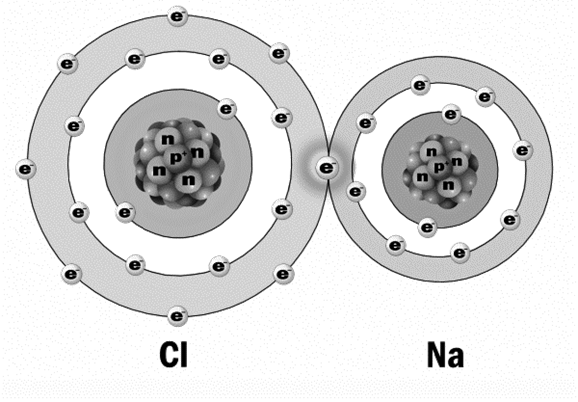
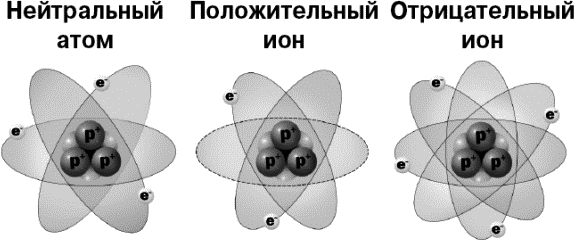



















 — постоянная тонкой структуры,
— постоянная тонкой структуры, — собственное значение оператора полного момента импульса.
— собственное значение оператора полного момента импульса. (в системе СИ),
(в системе СИ),![psi_{nlm}(r,theta,varphi) = sqrt {{left ( frac{2}{n a_0} right )}^3frac{(n-l-1)!}{2n {cdot} [(n+l)!]} } {cdot} exp{ left( {- frac{r}{n a_0}} right) } {cdot} {left( frac{2r}{n a_0} right)}^{l} L_{n-l-1}^{2l+1}{ left( frac{2r}{n a_0} right)} cdot Y_{l,m}(theta, varphi ),](https://web.archive.org/web/20140424195751im_/http://upload.wikimedia.org/math/0/9/3/093b5cbbb032288e8f67849d576d6768.png)
 — Боровский радиус.
— Боровский радиус. — обобщённые полиномы Лагерра степени
— обобщённые полиномы Лагерра степени  от функции
от функции 
 — нормированные на единицу сферические функции.
— нормированные на единицу сферические функции.
















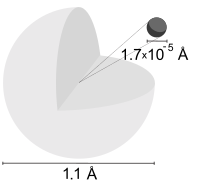














![{displaystyle -{frac {hbar ^{2}}{2mu }}left[{frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial psi }{partial r}}right)+{frac {1}{r^{2}sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial psi }{partial theta }}right)+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}psi }{partial varphi ^{2}}}right]-{frac {e^{2}}{4pi varepsilon _{0}r}}psi =Epsi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed150abb1693ab2493937b669446a54865b9562)




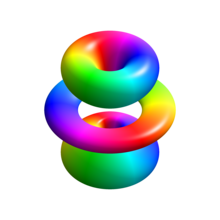



![{displaystyle {begin{aligned}E_{j,n}={}&-mu c^{2}left[1-left(1+left[{frac {alpha }{n-j-{frac {1}{2}}+{sqrt {left(j+{frac {1}{2}}right)^{2}-alpha ^{2}}}}}right]^{2}right)^{-1/2}right]\approx {}&-{frac {mu c^{2}alpha ^{2}}{2n^{2}}}left[1+{frac {alpha ^{2}}{n^{2}}}left({frac {n}{j+{frac {1}{2}}}}-{frac {3}{4}}right)right],end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e54f0064eafaeab9e7d8b3e5e41e667a3138a7b)

![{displaystyle {begin{aligned}langle r,theta ,varphi mid s,gamma ,{bar {Omega }}rangle ={}&e^{-s^{2}/2}sum _{n=0}^{infty }(s^{n}e^{igamma /(n+1)^{2}}/{sqrt {n!}})\&{}times ,sum _{ell =0}^{n}u_{n+1}^{ell }(r)sum _{m=-ell }^{ell }left[{frac {(2ell )!}{(ell +m)!(ell -m)!}}right]^{1/2}left(sin {frac {bar {theta }}{2}}right)^{ell -m}left(cos {frac {bar {theta }}{2}}right)^{ell +m}\&{}times ,e^{-i(m{bar {varphi }}+ell {bar {psi }})}Y_{ell m}(theta ,varphi ){sqrt {2ell +1}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb48ff266b61e92b9bdfcd39d562729c3910e97a)
