Время на прочтение
6 мин
Количество просмотров 35K
Представьте, что вам нужно сгенерировать равномерно распределённое случайное число от 1 до 10. То есть целое число от 1 до 10 включительно, с равной вероятностью (10%) появления каждого. Но, скажем, без доступа к монетам, компьютерам, радиоактивному материалу или другим подобным источникам (псевдо) случайных чисел. У вас есть только комната с людьми.
Предположим, что в этой комнате чуть более 8500 студентов.
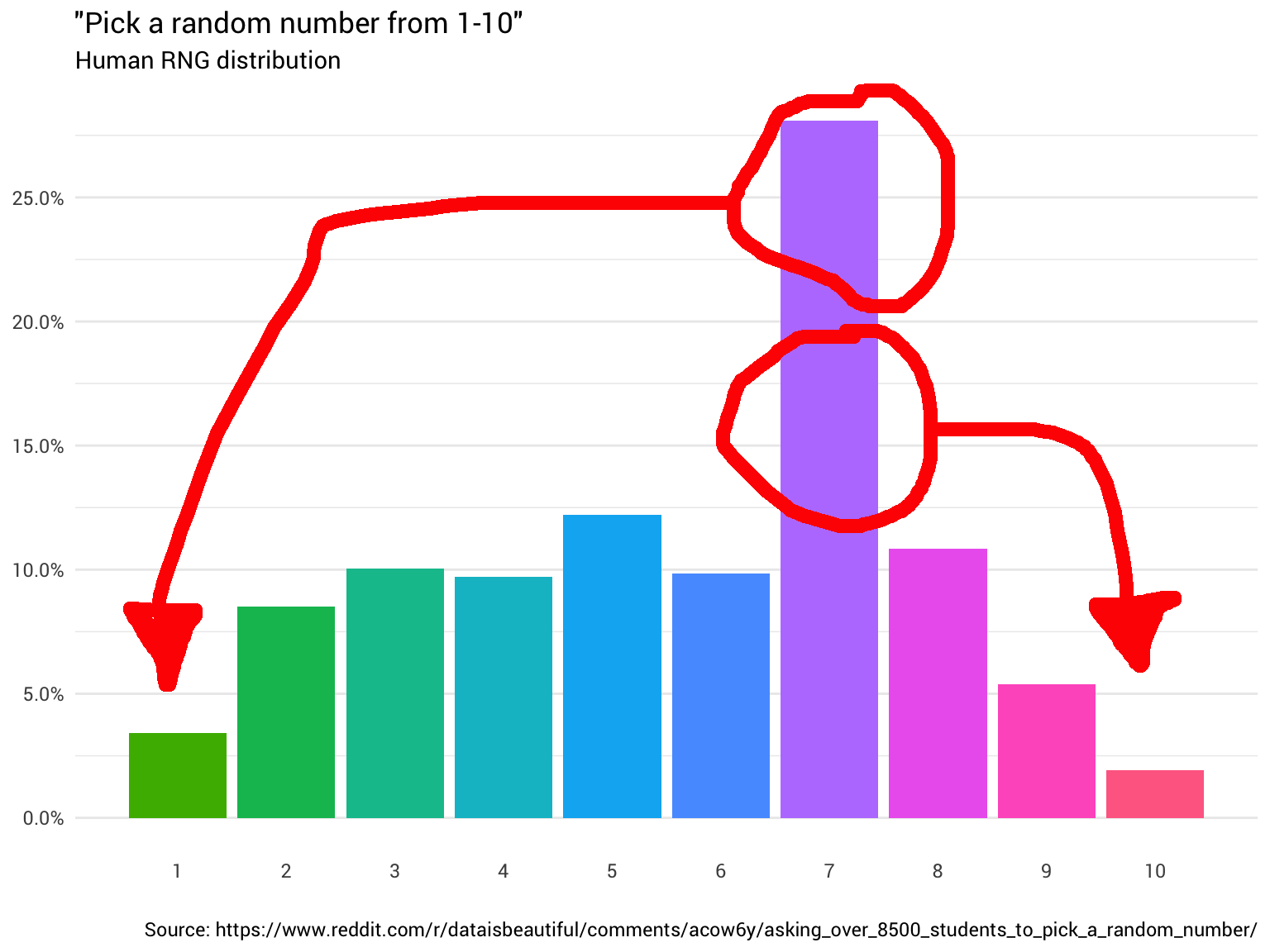
Самое простое — попросить кого-нибудь: «Эй, выбери случайное число от одного до десяти!». Человек отвечает: «Семь!». Отлично! Теперь у вас есть число. Однако вы начинаете задаваться вопросом, является ли оно равномерно распределённым?
Поэтому вы решили спросить ещё несколько человек. Вы продолжаете их спрашивать и считать их ответы, округляя дробные числа и игнорируя тех, кто думает, что диапазон от 1 до 10 включает 0. В конце концов вы начинаете видеть, что распределение вообще не равномерное:
library(tidyverse)
probabilities <-
read_csv("https://git.io/fjoZ2") %>%
count(outcome = round(pick_a_random_number_from_1_10)) %>%
filter(!is.na(outcome),
outcome != 0) %>%
mutate(p = n / sum(n))
probabilities %>%
ggplot(aes(x = outcome, y = p)) +
geom_col(aes(fill = as.factor(outcome))) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(labels = scales::percent_format(),
breaks = seq(0, 1, 0.05)) +
scale_fill_discrete(h = c(120, 360)) +
theme_minimal(base_family = "Roboto") +
theme(legend.position = "none",
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank()) +
labs(title = '"Pick a random number from 1-10"',
subtitle = "Human RNG distribution",
x = "",
y = NULL,
caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/")
Данные с Reddit
Вы хлопаете себя по лбу. Ну конечно, оно не будет случайным. В конце концов, нельзя доверять людям.
Итак, что делать?
Вот бы найти какую-то функцию, которая преобразует распределение «человеческого ГСЧ» в равномерное распределение…
Интуиция тут относительно проста. Нужно всего лишь взять массу распределения оттуда, где она выше 10%, и переместить туда, где она меньше 10%. Так, чтобы все столбцы на графике были одного уровня:
По идее, такая функция должна существовать. Фактически, должно быть много различных функций (для перестановки). В крайнем случае, можно «разрезать» каждый столбец на бесконечно малые блоки и построить распределение любой формы (как кирпичики Lego).
Конечно, такой экстремальный пример немного громоздок. В идеале мы хотим сохранить как можно больше исходного распределения (т. е. сделать как можно меньше измельчений и перемещений).
Как найти такую функцию?
Ну, наше объяснение выше звучит очень похоже на линейное программирование. Из Википедии:
Линейное программирование (LP, также именуется линейной оптимизацией) — метод достижения наилучшего результата… в математической модели, требования которой представлены линейными отношениями… Стандартная форма представляет собой обычную и наиболее интуитивную форму описания задачи линейного программирования. Она состоит из трёх частей:
- Линейная функция, которую необходимо максимизировать
- Проблемные ограничения следующей формы
- Неотрицательные переменные
Аналогично можно сформулировать и проблему перераспределения.
Представление проблемы
У нас есть набор переменных
, каждая из которых кодирует долю вероятности, перераспределённую от целого числа
(от 1 до 10) к целому числу
(от 1 до 10). Поэтому, если
, то нам нужно перенести 20% ответов от семёрки к единице.
variables <-
crossing(from = probabilities$outcome,
to = probabilities$outcome) %>%
mutate(name = glue::glue("x({from},{to})"),
ix = row_number())
variables## # A tibble: 100 x 4 ## from to name ix ## <dbl> <dbl> <glue> <int> ## 1 1 1 x(1,1) 1 ## 2 1 2 x(1,2) 2 ## 3 1 3 x(1,3) 3 ## 4 1 4 x(1,4) 4 ## 5 1 5 x(1,5) 5 ## 6 1 6 x(1,6) 6 ## 7 1 7 x(1,7) 7 ## 8 1 8 x(1,8) 8 ## 9 1 9 x(1,9) 9 ## 10 1 10 x(1,10) 10 ## # … with 90 more rows
Мы хотим ограничить эти переменные таким образом, чтобы все перераспределённые вероятности суммировались в 10%. Другими словами, для каждого
от 1 до 10:
Можем представить эти ограничения в виде списка массивов в R. Позже свяжем их в матрицу.
fill_array <- function(indices,
weights,
dimensions = c(1, max(variables$ix))) {
init <- array(0, dim = dimensions)
if (length(weights) == 1) {
weights <- rep_len(1, length(indices))
}
reduce2(indices, weights, function(a, i, v) {
a[1, i] <- v
a
}, .init = init)
}
constrain_uniform_output <-
probabilities %>%
pmap(function(outcome, p, ...) {
x <-
variables %>%
filter(to == outcome) %>%
left_join(probabilities, by = c("from" = "outcome"))
fill_array(x$ix, x$p)
})Мы также должны убедиться, что сохраняется вся масса вероятностей из исходного распределения. Так что для каждого
в диапазоне от 1 до 10:
one_hot <- partial(fill_array, weights = 1)
constrain_original_conserved <-
probabilities %>%
pmap(function(outcome, p, ...) {
variables %>%
filter(from == outcome) %>%
pull(ix) %>%
one_hot()
})Как уже говорилось, мы хотим максимизировать сохранение исходного распределения. Это наша цель (objective):
maximise_original_distribution_reuse <-
probabilities %>%
pmap(function(outcome, p, ...) {
variables %>%
filter(from == outcome,
to == outcome) %>%
pull(ix) %>%
one_hot()
})
objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums()Затем передаём проблему солверу, например, пакету lpSolve в R, объединив созданные ограничения в одну матрицу:
# Make results reproducible...
set.seed(23756434)
solved <- lpSolve::lp(
direction = "max",
objective.in = objective,
const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)),
const.dir = c(rep_len("==", length(constrain_original_conserved)),
rep_len("==", length(constrain_uniform_output))),
const.rhs = c(rep_len(1, length(constrain_original_conserved)),
rep_len(1 / nrow(probabilities), length(constrain_uniform_output)))
)
balanced_probabilities <-
variables %>%
mutate(p = solved$solution) %>%
left_join(probabilities,
by = c("from" = "outcome"),
suffix = c("_redistributed", "_original"))Возвращается следующее перераспределение:
library(gganimate)
redistribute_anim <-
bind_rows(balanced_probabilities %>%
mutate(key = from,
state = "Before"),
balanced_probabilities %>%
mutate(key = to,
state = "After")) %>%
ggplot(aes(x = key, y = p_redistributed * p_original)) +
geom_col(aes(fill = as.factor(from)),
position = position_stack()) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(labels = scales::percent_format(),
breaks = seq(0, 1, 0.05)) +
scale_fill_discrete(h = c(120, 360)) +
theme_minimal(base_family = "Roboto") +
theme(legend.position = "none",
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank()) +
labs(title = 'Balancing the "Human RNG distribution"',
subtitle = "{closest_state}",
x = "",
y = NULL) +
transition_states(
state,
transition_length = 4,
state_length = 3
) +
ease_aes('cubic-in-out')
animate(
redistribute_anim,
start_pause = 8,
end_pause = 8
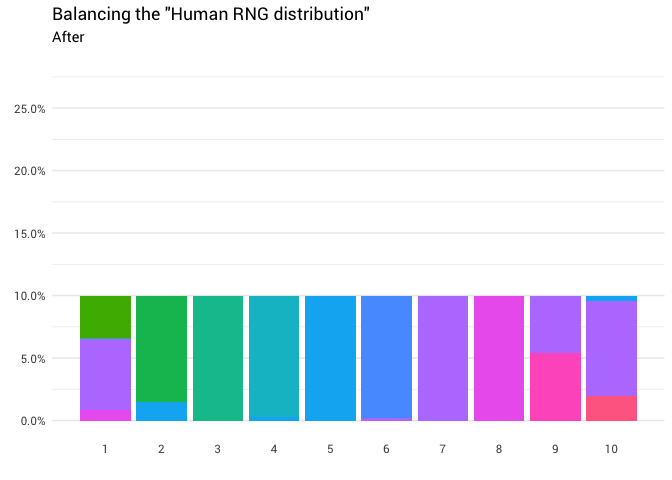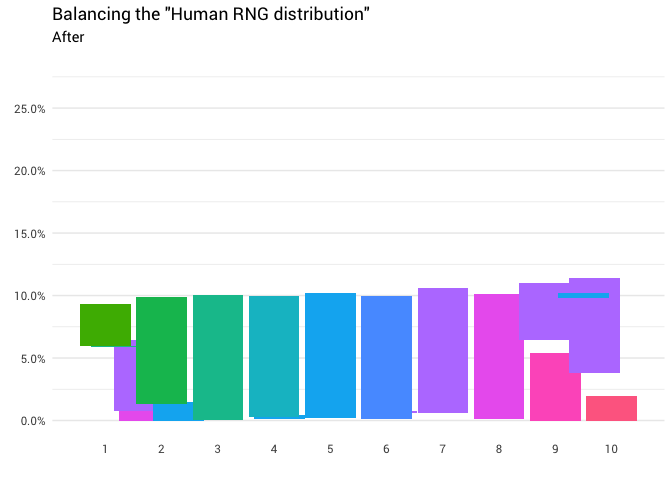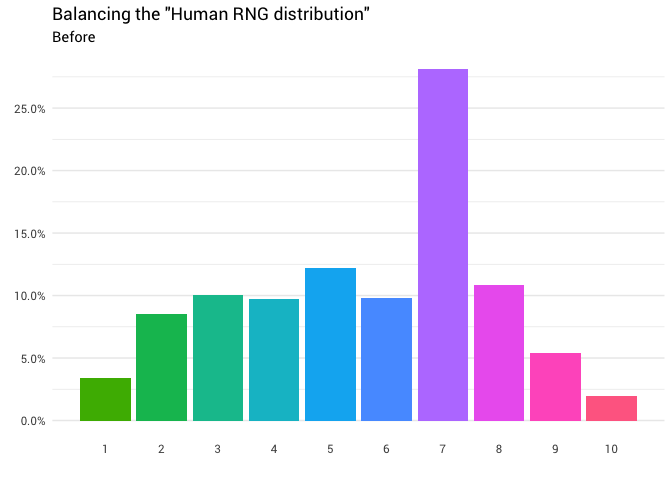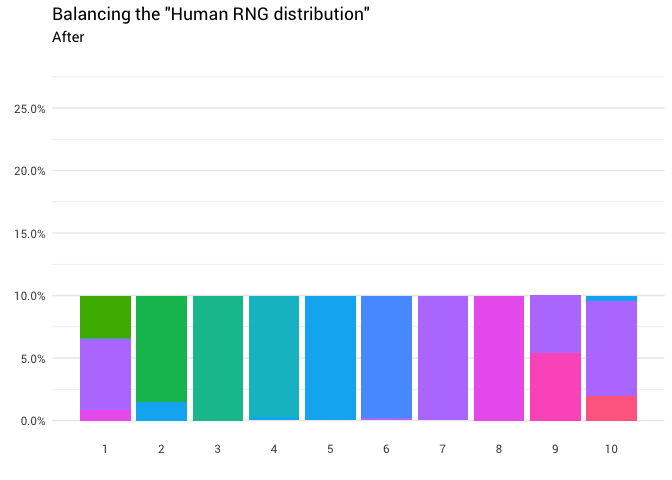
)Отлично! Теперь у нас есть функция перераспределения. Давайте поближе посмотрим, как именно движется масса:
balanced_probabilities %>%
ggplot(aes(x = from, y = to)) +
geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) +
geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) +
scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) +
scale_fill_discrete(h = c(120, 360)) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(breaks = 1:10) +
theme_minimal(base_family = "Roboto") +
theme(panel.grid.minor = element_blank(),
panel.grid.major = element_line(linetype = "dotted"),
legend.position = "none") +
labs(title = "Probability mass redistribution",
x = "Original number",
y = "Redistributed number")Эта диаграмма говорит, что примерно в 8% случаев, когда кто-то называет восемь в качестве случайного числа, вам нужно воспринимать ответ как единицу. В остальных 92% случаев он остаётся восьмёркой.
Было бы довольно просто решить задачу, если бы у нас был доступ к генератору равномерно распределённых случайных чисел (от 0 до 1). Но у нас только комната, полная людей. К счастью, если вы готовы примириться с несколькими небольшими неточностями, то из людей можно сделать довольно хороший ГСЧ, не спрашивая более двух раз.
Возвращаясь к нашему исходному распределению, у нас есть следующие вероятности для каждого числа, которые можно использовать для повторного назначения любой вероятности, если необходимо.
probabilities %>%
transmute(number = outcome,
probability = scales::percent(p))## # A tibble: 10 x 2 ## number probability ## <dbl> <chr> ## 1 1 3.4% ## 2 2 8.5% ## 3 3 10.0% ## 4 4 9.7% ## 5 5 12.2% ## 6 6 9.8% ## 7 7 28.1% ## 8 8 10.9% ## 9 9 5.4% ## 10 10 1.9%
Например, когда кто-то даёт нам восемь в качестве случайного числа, нужно определить, должна ли эта восьмёрка стать единицей или нет (вероятность 8%). Если мы спросим другого человека о случайном числе, то с вероятностью 8,5% он ответит «два». Так что если это второе число равно 2, мы знаем, что должны вернуть 1 как равномерно распределённое случайное число.
Распространив эту логику на все числа, получаем следующий алгоритм:
По этому алгоритму вы можете использовать группу людей для получения чего-то близкого к генератору равномерно распределённых случайных чисел от 1 до 10!
И так, человеку крайне сложно получить случайное число, тем более если нужно сгенерировать более 1 000, а то и 1 000 000 чисел. Поэтому мы придумали алгоритмы генерации чисел. Случайное число можно получить 2-мя видами либо с помощью физики, либо математике.
Но есть одна проблема, любой алгоритм можно предугадать и он начнет зацикливаться, так в 1983г на шоу «Поймай свою удачу», водитель грузовика Майкл Ларсон он выиграл просто блять сумасшедшие деньги просчитав алгоритм случайных числе этой передачи. После этого случая появился сайт random.org, который генерирует по настоящему рандомное число.
Давайте разберем, как он их получает. Получает этот сайт благодаря матушки природы, да-да наша природа которую мы порой блять недооцениваем, потому-что только матушка природа способна получить хаос который мы не можем предугадать, точнее можем, но это будет пиздец как не скоро, т.к. надо будет рассчитать движение каждого атома во вселенной. Сайт random.org генерирует свои основываясь на данных атмосферных шумов.
Окей, нахуя я тут распинался и рассказывал про этот сайт рандом орг?
Благодаря природе, наш цифровой мир находиться под защитой. Случайные коды которые приходят при платежах ваших банков, основаны на подобных алгоритмах, то есть ни один хакер в мире не сможет предугадать код и спиздить ваши 300р на последний дошик, в военной промышленности тоже эта хрень используется, поэтому, что вы сейчас прочитали, не так уж и не нужно.
Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite
Что такое произвольное число?
Е. чисел, содержащих целую и дробную части, осуществляется в два этапа.
Отдельно переводится целая часть, отдельно — дробная.
В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).
Изобразите на координатной плоскости все точки (х ; у) такие, что у = 3, х — произвольное число?
Изобразите на координатной плоскости все точки (х ; у) такие, что у = 3, х — произвольное число.
Р вопрос по математике.
Что такое произвольные функции?
Что такое произвольные функции.
Число записано с помощью трехсот единиц и произвольного количества нулей, может ли оно быть квадратом натурального числа?
Число записано с помощью трехсот единиц и произвольного количества нулей, может ли оно быть квадратом натурального числа?
Изобразите на координатной плоскости все точки (x ; y) такие, что x = 5, y – произвольное число?
Изобразите на координатной плоскости все точки (x ; y) такие, что x = 5, y – произвольное число.
Что такое произвольный треугольник?
Что такое произвольный треугольник.
Изобразите на координатной плоскости все точки (х ; у) такие, что х равен 2, у — произвольное число?
Изобразите на координатной плоскости все точки (х ; у) такие, что х равен 2, у — произвольное число.
Натуральное число можно умножать на два и произвольным образом переставлять в нем цифры (запрещается лишь ставить ноль на первое место)?
Натуральное число можно умножать на два и произвольным образом переставлять в нем цифры (запрещается лишь ставить ноль на первое место).
Докажите, что превратить число 1 в число 8412 с помощью таких операций невозможно.
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры( нельзя только ставить нуль на первое место)?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры( нельзя только ставить нуль на первое место).
Можно ли с помощью таких операций из 1 получить 74?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры (нельзя только ставить нуль на первое место)?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры (нельзя только ставить нуль на первое место).
Можно ли с помощью таких операций из 1 получить 74?

С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры ( нельзя только ставить нуль на первое место)?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры ( нельзя только ставить нуль на первое место).
Можно ли с помощью таких операций из 1 получить 78?
На этой странице находится вопрос Что такое произвольное число?. Здесь же – ответы на него, и похожие вопросы в категории Математика, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.
Производная функции
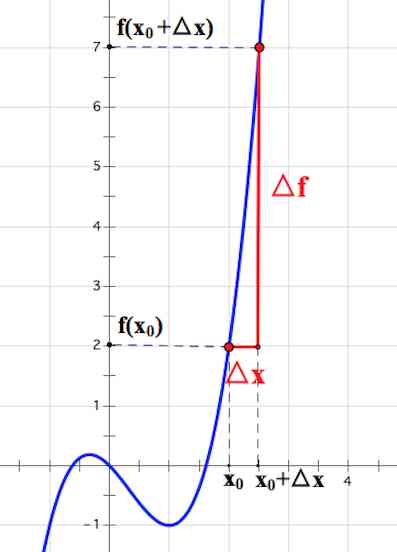
Производной функции в точке называется предел отношения приращения функции к приращению аргумента при , если этот предел существует.
Но нет необходимости каждый раз пользоваться этим определением для нахождения производной…
Геометрический смысл производной
Если мы рассмотрим прямоугольный треугольник , то заметим, что есть .
А при стремлении к нулю, точка будет приближаться к точке и секущая «превратится» в касательную к графику функции в точке .
Производная в точке равна тангенсу угла наклона касательной к графику функции в этой точке:
где – угол наклона касательной (проведенной к в т. )
Физический смысл производной
Если точка движется вдоль оси и ее координаты изменяются по закону , то мгновенная скорость точки :
Пример. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени .
Математика
Квадратный корень из двух приблизительно равен 1.4142135624. Запоминить его значение можно с помощью следующей запоминалки:
Я Катя, я дура, но я вот нашла корень из двух.
Производная произведения
Формула дифференцирования произведения: d(UV) = U∙dV + V∙dU. Запомнить эту формулу можно заменив ее правую часть фразой: «Удавить – и в воду».
Умножение и деление положительных и отрицательных чисел
Если под плюсом понимать друга, а под минусом — врага, то получится такая система:
Друг(+) моего врага(-)= мой враг(-)
Враг(-) моего друга(+)= мой враг(-)
Враг(-) моего врага(-)= мой друг(+)
Друг(+) моего друга(+)= мой друг(+)
Вот такое простой способ позволяет не запутаться в правилах запоминания чисел с разными знаками — положительных и отрицательных.
Числитель и знаменатель
Для тех, кто путает местами числитель и знаменатель существует следующая запоминалка:
Числитель, как и Чердак, находится сверху, поэтому знаменатель — снизу.
Цифры римской системы нумерации
Для запоминания цифр римской системы нумерации можно пользоваться одним из мнемонических правил:
| Mы | 1000 |
| Dаем | 500 |
| Cоветы | 100 |
| Lишь | 50 |
| Xорошо | 10 |
| Vоспитанным | 5 |
| Iндивидам | 1 |
| Mы | 1000 |
| Dарим | 500 |
| Cочные | 100 |
| Lимоны | 50 |
| Xватит | 10 |
| Vсем | 5 |
| Iх | 1 |
Неравенство треугольника
Для каждого треугольника выполняется следующее правило — сумма длин любых двух сторон треугольника больше длины третьей. Для запоминания можно использовать такое стихотворение:
Знает даже каждый школьник,
Что такое треугольник.
Но совсем не каждый знает
Замечательный закон:
Сторона его любая,
Даже самая большая,
Меньше суммы двух сторон.
Биссектриса
Биссектриса — это такая крыса, которая бегает по углам и делит углы пополам.
Медиана
Медиана – обезьяна, она идет по сторонам и делит стороны пополам.
Определение синуса и косинуса
Синус и косинус угла задаётся на основе соотношений в прямоугольном треугольнике.
Синус угла определяется как отношение противолежащего, к данному углу, катета к гипотенузе
Косинус это как отношение прилежащего катета к гипотенузе.
Чтобы не запутаться что используется с чем можно использовать следующую ассоциацию:
Косинус – косяк – дверь – дверь приложена (прилежащий катет) к косяку. Т.е. Косинус угла это отношение прилежащего катета к гипотенузе. Ну а противолежащий достаётся синусу.
Производные синуса и косинуса
Производные синуса и косинуса находятся по формулам: (sin a)’ = cos a и (cos a)’ = -sin a. Всё очень просто: нужно синус заменить на косинус, косинус на синус и не запутаться со знаком. Эти формулы можно записать в следующем виде:
Рандомайзер
Генератор Случайных чисел онлайн генерирует рандомные числа в заданном диапазоне. Количество и диапазон рандомных чисел можно изменить в настройках. Генератор позволяет задать порядок случайных чисел, удалить повторы
Случайное число
Попыток генерации: 0 (сброс)
Диапазон случайных чисел:
от
до
дополнит. настройки
исключить повторы
включить анимацию
сохранять статистику
Случайное число

Генератор Случайных чисел позволяет генерировать от 1 до 250 случайных чисел в диапазоне от 1 до 999999999. Дополнительные настройки рандомайзера позволяют исключать повторы при генерации случайных чисел, упорядочить полученные числа в порядке возрастания или убывания, задать разделители, изменить размер шрифта. Все сделанные Вами изменения генератора случайных чисел сохраняются для последующего использования.
Читать еще…
Сгенерированные числа можно скопировать из отдельного окна.
Вы можете сохранять и редактировать статистику генерации случайных чисел.
Результаты работы Генератора, статистика и настройки никуда не передаются. Все данные хранятся в кукисах, памяти Вашего браузера и доступны только Вам.
Скрыть…

Для работы проектов iXBT.com нужны файлы cookie и сервисы аналитики.
Продолжая посещать сайты проектов вы соглашаетесь с нашей
Политикой в отношении файлов cookie
Подбрасывая монетку, можно быть уверенным, что шансы выпадения орла и решки одинаковы. Но можно зайти на сайт с генерацией рандомных чисел или скачать приложение на телефон, в котором будет возможность имитировать бросок монетки. Однако будет ли в таком случае результат действительно случайным, или же программа подберет число/результат, который заранее был известен?
В большинстве случаев результат не будет действительно случайным, он будет получен алгоритмом, выдающим последовательность чисел близкую к случайной. Подобных алгоритмов очень много, и все они используют различные формулы, однако они все зацикливаются и могут выдать ограниченное количество цепочек «случайных» чисел.
Хорошим и простым примером будет один из самых ранних алгоритмов для генерации псевдослучайных чисел. Например, трехзначное число возводится в квадрат, затем из середины квадрата числа берётся трехзначное число, которое и становится результатом. А производя подобные вычисления несколько раз подряд, получается цепочка псевдослучайных чисел. Выглядит это так: допустим начальное значение 111, в таком случае 111² = 12321, получаем результат 232, после чего повторяем процедуру — 232² = 53824 и результатом становится 382. Чтобы подбор чисел не был постоянно одинаковым, важно чтобы начальное значение было разным при запуске алгоритма. Так, например, программы могут брать начальное значение исходя из даты и времени, когда был запущен алгоритм/приложение.
Большинство игр, приложений и сайтов используют именно генераторы псевдослучайных чисел, поскольку это значительно проще в реализации, а результат может быть получен мгновенно и без подключения к сети. Однако предсказуемость подобного генератора совершенно не подходит для использования его в целях шифрования данных. Тут на помощь приходит генератор истинно случайных чисел.
Простейшим истинным генератором случайных чисел является игральный кубик. Однако создать большой массив данных кидая кубик едва ли получится, а чтобы узнать результат даже одного броска, требуется время. Поэтому современные генераторы случайных чисел используют данные, полученные измерением различных физических процессов. Например, используют шум в электрических цепях, атмосферный шум, космическое излучение, колебания электромагнитного поля вакуума или шум радиоактивного распада атомов. Полученные данные являются абсолютно случайными и никак не могут быть предсказаны.
Недостатком подобноных генераторов является относительно медленная скорость выдачи результата, все же передача данных занимает больше времени, чем получение результата путем расчета по алгоритму. Однако уверенность в получении случайного числа важна во многих сферах. Но несмотря на сложность генераторов случайных чисел ими может воспользоваться каждый. Есть большое количество сайтов предоставляющих такую возможность (обычно, если сайт использует генератор истинно случайных чисел, то об этом есть информация).
Сейчас на главной
Новости
Публикации

Продолжаем серию обзоров на портативные
аккумуляторы Perfeo
Mountains
и на этот раз модель на 30 А*ч с максимальной выходной мощностью 22.5 Вт. Из
протоколов доступны PD3.0,
AFC
12V,
PE+2.0….

Купил себе по очень хорошей цене аккумуляторную цепную пилу Ryobi P2502BTL, немного попользовался и решил
рассказать читателям. Ну и отвечу на главный вопрос: может ли она заменить
бензиновую…

Как сказали в компании TempoTec, посмотрели они на рынок наушников, всплакнули и решили для своего плеера V6 делать что-то самостоятельно. Вот так и появилась гибридная 5-драйверная модель…

В наше время найти беспроводные наушники,
подходящие для активных занятий спортом, — довольно сложная задача. Нужно,
чтобы они имели компактный крепкий кейс, который не будет занимать слишком…

Портативные аккумуляторы перестали быть чем-то диковинным, они есть почти у всех, а у некоторых и не один. Форм-фактор тоже разный, у кого-то это здоровая коробка на 20-30 Ач, а у кого-то…

Еще один представитель длинных домов в Москве. Дали наводку в комментариях, оказалась неподалеку, заехала посмотреть. Дом расположен на улице Сталеваров в районе Ивановское Восточного…