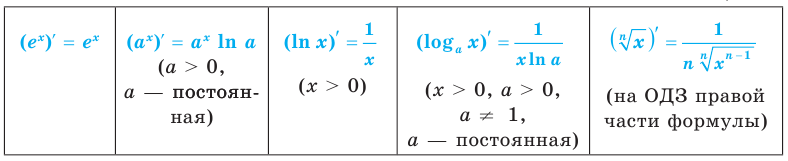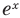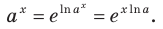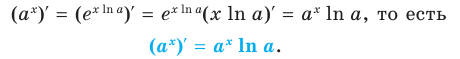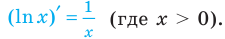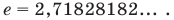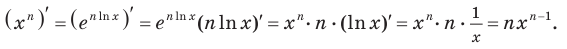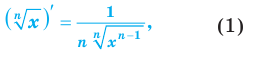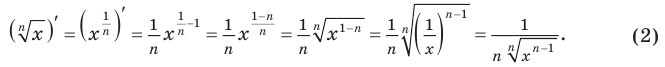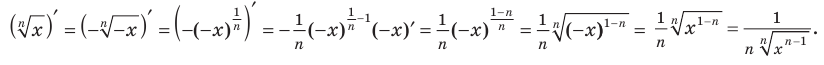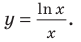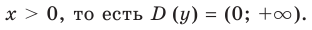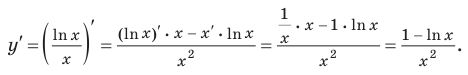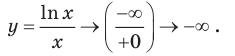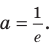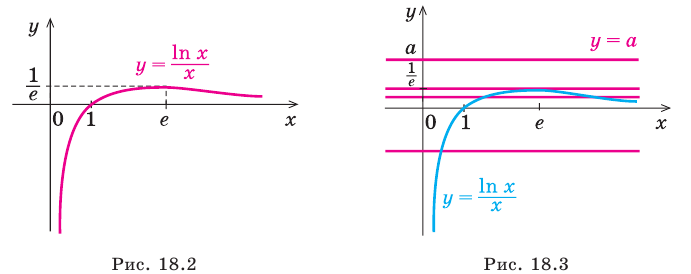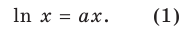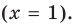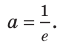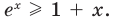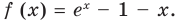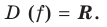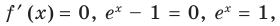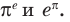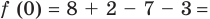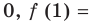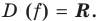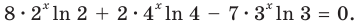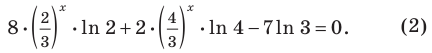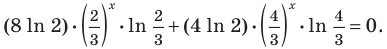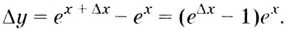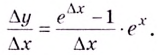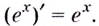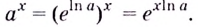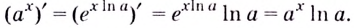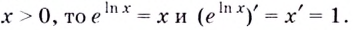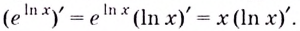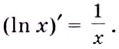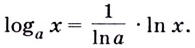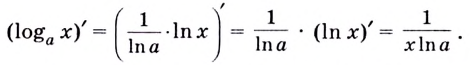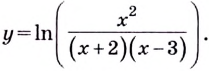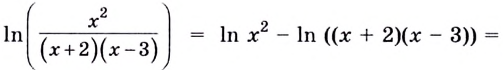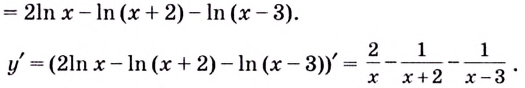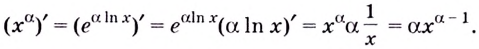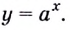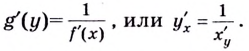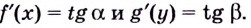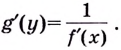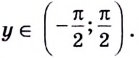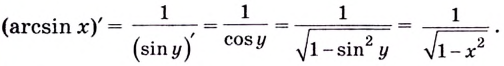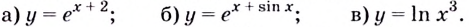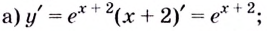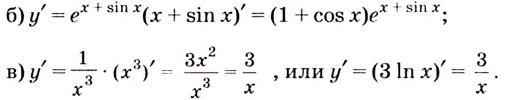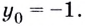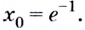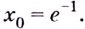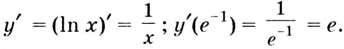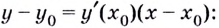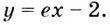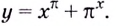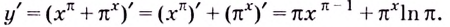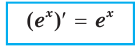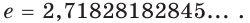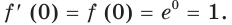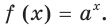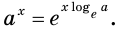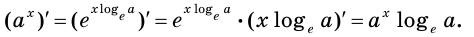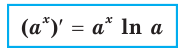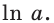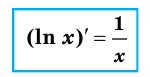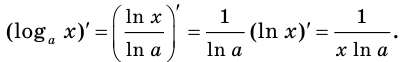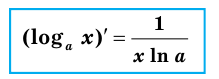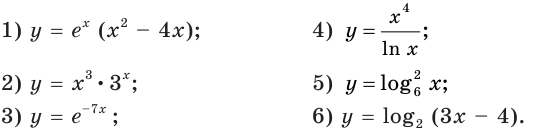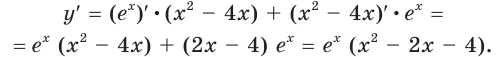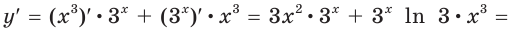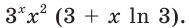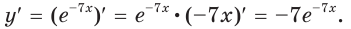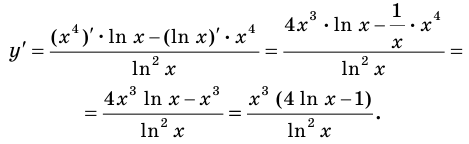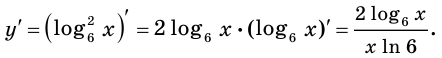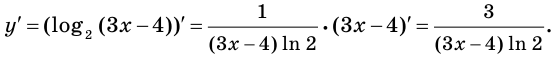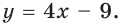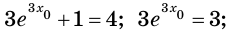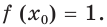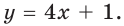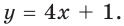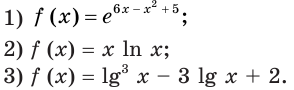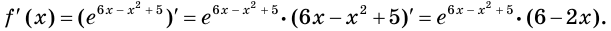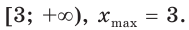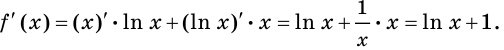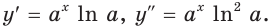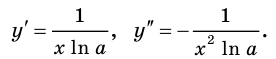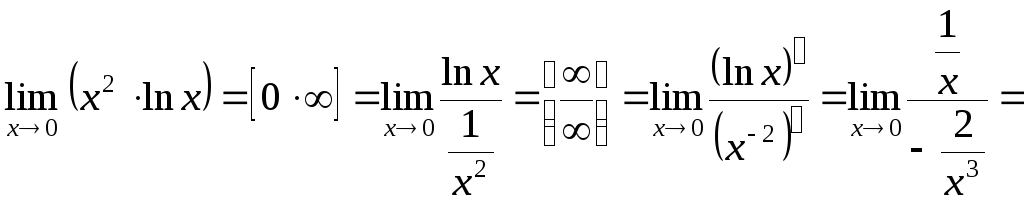Простое объяснение принципов решения логарифмического дифференцирования и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения логарифмического дифференцирования
В некоторых случаях нахождение производной функции значительно упрощается, если сначала произвести логарифмирование исходной функции, а уже затем произвести дифференцирование. Такой приём носит название логарифмического дифференцирования.
Правило нахождения степенно-показательной функции
Таблица основных производных
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Примеры решения логарифмического дифференцирования
Задача
Найти производную функции .
Решение
Найдём логарифм функции
.
Дифференцируем это равенство по :
Выразим :
Ответ
Задача
Найти производную функции .
Решение
Используя формулу , получаем:
Ответ
Задача
Найти производную функции .
Решение
Найдём логарифм функции
Дифференцируем это равенство по :
Ответ
Задача
Найти производную функции
.
Решение
Найдём логарифм функции
Дифференцируем это равенство по :
Ответ
Задача
Найти производную функции
.
Решение
Найдём логарифм функции
Дифференцируем это равенство по :
Ответ
Задача
Найти производную функции .
Решение
Найдём логарифм функции
.
Дифференцируем это равенство по :
Выразим :
Ответ
Задача
Найти производную функции
.
Решение
Найдём логарифм функции
Дифференцируем это равенство по :
Выразим :
Ответ
Задача
Найти производную функции
.
Решение
Возьмём натуральные логарифмы от обеих частей равенства, получим:
Дифференцируем это равенство по :
Выразим :
Ответ
Задача
Найти производную функции
Решение
Возьмём натуральные логарифмы от обеих частей равенства, получим:
Дифференцируем это равенство по :
Выразим :
Ответ
Задача
Найти производную функции
.
Решение
Найдём логарифм функции
Дифференцируем это равенство по :
Выразим :
Ответ
Содержание:
- Суть метода логарифмического дифференцирования
- Производная показательно-степенной функции
Для функций вида $y(x)=frac{u_{1}(x) cdot u_{2}(x) cdot ldots cdot u_{k}(x)}{v_{1}(x) cdot v_{2}(x) cdot ldots cdot v_{m}(x)}$ для упрощения нахождения
производной рациональнее использовать логарифмическое дифференцирование.
Суть метода логарифмического дифференцирования
Суть такого дифференцирования заключается в следующем: вначале находится
логарифм заданной функции, а уже затем
вычисляется от него производная. Пусть задана некоторая функция
$y=f(x)$. Прологарифмируем левую и правую части данного выражения:
$$ln y=ln f(x)$$
Далее продифференцируем полученное равенство при условии, что
$y$ является функцией от $x$, то есть найдем
производную сложной функции:
$$(ln y)^{prime}=(ln f(x))^{prime} Rightarrow frac{1}{y} cdot y^{prime}=(ln f(x))^{prime}$$
А тогда, выражая искомую производную $y^{prime}$, в
результате имеем:
$$y^{prime}=y cdot(ln f(x))^{prime}$$
Пример
Задание. Найти производную функции
$y=frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}$
Решение. Если находить производную данной функции, используя
таблицу производных и
правила дифференцирования, то процесс будет очень трудоемким. Производную будем находить с помощью логарифмического
дифференцирования. Прологарифмируем левую и правую части заданной функции:
$$ln y=ln frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}$$
Используя свойства логарифмов, преобразуем правую часть полученного равенства к следующему виду:
$$begin{array}{c}
ln frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}= \
=ln left[(x+2)^{2}(x-4) sqrt{x^{2}+1}right]-ln left[(x-2)^{3}(x-4)^{5}right]= \
=ln (x+2)^{2}+ln (x-4)+ln sqrt{x^{2}+1}-ln (x-2)^{3}-ln (x-4)^{5}= \
=2 ln (x+2)+ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)-5 ln (x-4)= \
=2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)
end{array}$$
$$ln y=2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)$$
Дифференцируем левую и правую часть последнего равенства, не забывая, что
$y$ является функцией переменной
$x$:
$$begin{array}{c}
(ln y)^{prime}=left(2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)right)^{prime} \
frac{y^{prime}}{y}=(2 ln (x+2))^{prime}-(4 ln (x-4))^{prime}+left(frac{1}{2} ln left(x^{2}+1right)^{prime}-right. \
-(3 ln (x-2))^{prime}=2(ln (x+2))^{prime}-4(ln (x-4))^{prime}+frac{1}{2}left(ln left(x^{2}+1right)right)^{prime}- \
-3(ln (x-2))^{prime}=2 cdot frac{1}{x+2} cdot(x+2)^{prime}-4 cdot frac{1}{x-4} cdot(x-4)^{prime}+ \
+frac{1}{2} cdot frac{1}{x^{2}+1} cdotleft(x^{2}+1right)^{prime}-3 cdot frac{1}{x-2} cdot(x-2)^{prime}= \
=frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}
end{array}$$
Итак,
$$frac{y^{prime}}{y}=frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}$$
Отсюда
$$y^{prime}=yleft(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$$
Подставляя вместо функции $y$ ее выражение,
окончательно будем иметь, что
$$y^{prime}=frac{(x+2)^{2} sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{4}}left(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$$
Ответ. $y^{prime}=frac{(x+2)^{2} sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{4}}left(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$
Производная показательно-степенной функции
Рационально использовать логарифмическое дифференцирование и при нахождении
производной показательно-степенной
(или степенно-показательной) функции или «функции в степени функция», то есть в случае, когда заданная функция имеет
вид $y(x)=u(x)^{v(x)}$. Логарифмируем левую и правую часть:
$$ln y(x)=ln u(x)^{v(x)}$$
$$ln y(x)=v(x) cdot ln u(x)$$
Тогда
$$(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime}$$
Производную в левой части равенства находим как производную сложной функции, а в правой — как производную произведения:
$$begin{array}{c}
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)} Rightarrow \
Rightarrow y^{prime}(x)=y(x) cdotleft(v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)}right)
end{array}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти производную функции $y(x)=(sin x)^{x}$
Решение. Применим логарифмическое дифференцирование:
$$begin{array}{l}
ln y(x)=ln (sin x)^{x} \
ln y(x)=x ln (sin x)
end{array}$$
Тогда, продифференцировав левую и правую часть, будем иметь:
$$begin{array}{c}
(ln y(x))^{prime}=(x ln (sin x))^{prime} \
frac{y^{prime}(x)}{y(x)}=(x)^{prime} cdot ln sin x+x cdot(ln sin x)^{prime}= \
=1 cdot ln sin x+x cdot frac{1}{sin x} cdot(sin x)^{prime}=ln sin x+frac{x}{sin x} cdot cos x= \
=ln sin x+x cdot operatorname{ctg} x
end{array}$$
Отсюда получаем, что
$$y^{prime}(x)=y(x)(ln sin x+x operatorname{ctg} x)=(sin x)^{x} cdot(ln sin x+x operatorname{ctg} x)$$
Ответ. $y^{prime}(x)=(sin x)^{x} cdot(ln sin x+x operatorname{ctg} x)$
Читать дальше: производная степенно-показательной функции.
В данной публикации мы рассмотрим производные логарифмических функций, а также разберем примеры решения задач для закрепления материала.
- Виды логарифмов
- Общая формула производной логарифма
-
Производная натурального логарифма
- Примеры задач
Виды логарифмов
Прежде, чем перейти к формулам производных, напомним, что для некоторых логарифмов предусмотрены отдельные названия:
1. Десятичный логарифм (lg x)
lg x = log10x
Т.е. это логарифм числа x основанию 10.
2. Натуральный логарифм (ln x)
ln x = loge x
Т.е. это логарифм числа x по основанию e (экспонента).
Общая формула производной логарифма
Производная логарифма x по основанию a равняется числу 1, разделенному на произведение натурального логарифма a и числа x.
Производная натурального логарифма
Производная от натурального логарифма числа x равняется единице, разделенной на x.
Данная формула получена следующим образом:
Сокращение ln e в данном случае возможно благодаря свойству логарифма:
Производная натурального логарифма сложной функции u = u (x):
Примеры задач
Задание 1:
Найдите производную функции y(x) = log4x.
Решение:
Используя общую формулу производной получаем:
Задание 2:
Вычислите производную функции y = ln x / 5.
Решение:
Применим свойство производной, согласно которой константу можно вынести за знак производной, и далее воспользуемся формулой для натурального логарифма:
Содержание:
Производные показательной и логарифмической функций:
Объяснение и обоснование
Чтобы обосновать формулы производных показательных и логарифмических функций, используем без доказательства свойство функции
При а > 0 по основному логарифмическому тождеству имеем
Тогда по правилу нахождения производной сложной функции:
По полученной формуле мы можем найти значение производной показательной функции для любого значения 
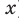
Для логарифмической функции сначала найдем производную функции 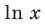
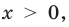
При 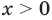
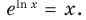
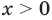
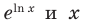
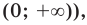
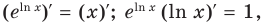
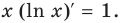
Поскольку 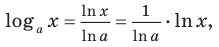
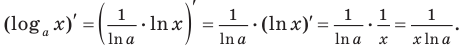
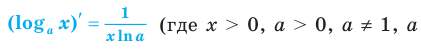
Замечание. Формула 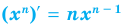
*Напомним , что 
Если 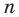
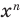
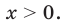
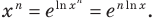
Следовательно, далее формулой 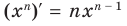
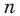
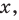
Опираясь на полученный результат, обоснуем также формулу
которую можно использовать при тех значениях 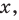
Если 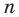
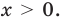
Если 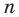
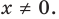

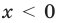
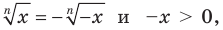
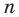
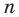
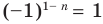
Следовательно, и для нечетного 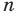
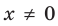
В последнем случае такие громоздкие преобразования пришлось вы- 1 полнить вследствие того, что при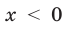
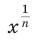
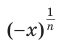
Примеры решения задач
Пример №1
Найдите производную функции:
Решение:
Комментарий:
Последовательно определяем, от какого выражения берется производная (ориентируясь на результат последнего действия). В задании 1 сначала берется производная суммы: 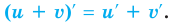
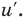
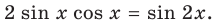
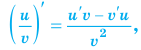

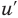
Пример №2
Найдите уравнение касательной к графику функции 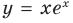
Решение:
Если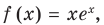
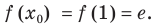
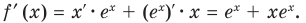
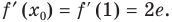
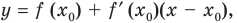
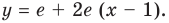
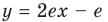
Комментарий:
Уравнение касательной к графику функции 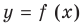
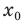
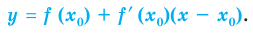
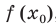
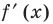
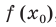
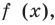
Пример №3
1) Постройте график функции 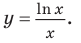
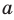
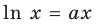
Комментарий:
Для выполнения задания 1 исследуем функцию 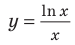
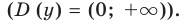
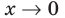
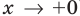
Тогда 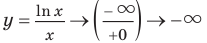
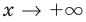
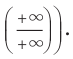
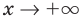
При выполнении задания 2 целесообразно использовать графическую иллюстрацию решения. Это можно сделать двумя способами:
Решение:
1) Исследуем функцию
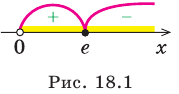
1. Область определения:
2. Функция ни четная, ни нечетная, поскольку ее область определения не симметрична относительно точки 0. 3. Точки пересечения графика с осями координат. График не пересекает ось 
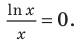

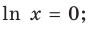
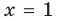
Производная существует на всей области определения функции 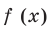
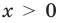
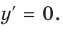
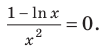
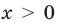
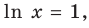
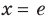
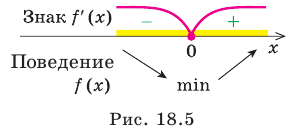
5. Отмечаем критические точки на области определения функции и находим знак 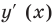
Составляем таблицу, в которой отмечаем промежутки возрастания, убывания и экстремумы функции.
6. Найдем координаты еще нескольких точек графика функции:
Заметим, что при 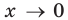

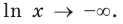
7. Используя результаты исследования, строим график функции 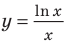
I способ решения задания 2
Область допустимых значений данного уравнения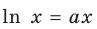
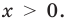
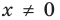
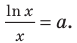
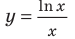
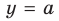
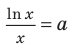

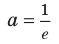
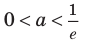
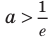
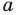
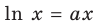
II способ решения задания 2
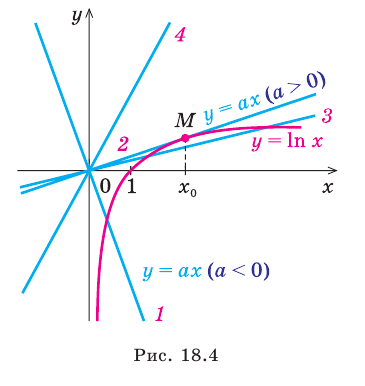
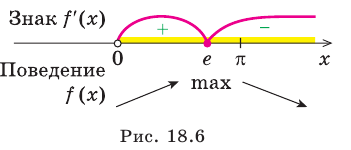
Рассмотрим графическую иллюстрацию (рис. 18.4) решения данного уравнения
Функция 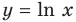
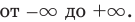
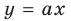
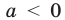
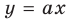
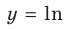
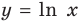
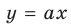
При 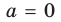
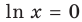
При 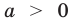
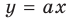
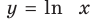
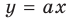
Тогда уравнение (1) будет иметь два корня. Если же прямая 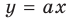
Выясним, когда прямая 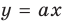
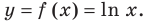
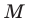
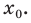
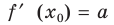
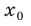
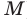
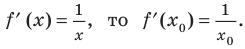
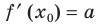
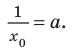
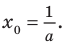
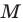
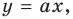
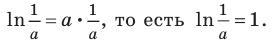
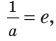
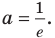
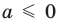
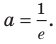
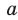
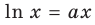
Пример №4
Докажите, что при всех действительных значениях 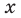
Решение:
Рассмотрим функцию
Область определения:
Производная 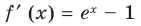
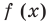
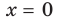
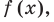
Как видим, непрерывная функция 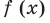
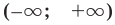
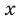
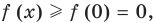

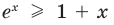
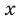
Комментарий:
Используем производную для доказательства данного неравенства. Для этого исследуем функцию 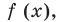
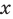
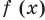
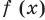
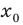
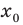
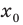
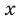

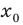
При доказательстве числовых неравенств или для сравнения двух чисел часто бывает удобно перейти к более общему функциональному неравенству
Пример №5
Сравните числа
Комментарий:
Чтобы составить план решения, можно рассуждать следующим образом. Мы не знаем, какое из данных чисел больше: 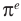
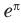

Затем заменим знак «
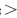
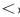




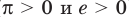
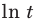
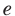
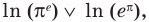

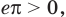
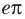
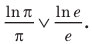
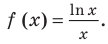
Далее, учитывая, что 
Решение:
Рассмотрим функцию 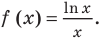
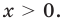
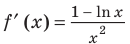
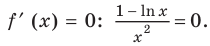
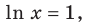
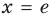
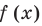
Функция 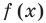
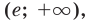
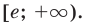

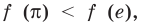
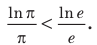
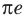
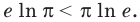
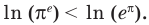
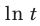
Ответ:
Пример №6
Решите уравнение
Комментарий:
Если попытаться применить к данному уравнению схему решения показательных уравнений (см. с. 178), то удается реализовать только первый ее пункт — избавиться от числовых слагаемых в показателях степеней. А привести все степени к одному основанию (с удобными показателями) или к двум основаниям так, чтобы получить однородное уравнение, или перенести все члены в одну сторону и разложить полученное выражение на множители — не удается. Попробуем применить свойства соответствующих функций. Но и на этом пути нам не удается использовать конечность ОДЗ (она бесконечна), оценку значений левой и правой частей уравнения (они обе в пределах от 
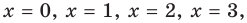
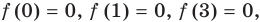
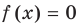
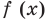
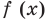
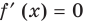
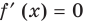
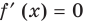
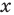
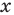
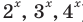
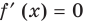
Решение:
Данное уравнение равносильно уравнению 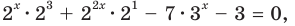
Обозначим 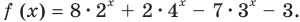
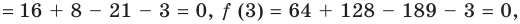
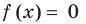
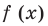
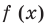
Производная 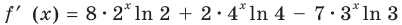
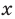
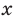
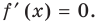
Поскольку 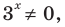
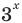
Чтобы доказать, что уравнение (2) имеет не больше двух корней, достаточно доказать, что функция 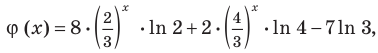
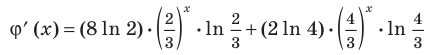
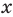
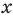
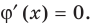
Поскольку 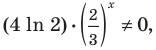
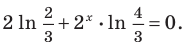
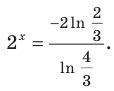
- Заказать решение задач по высшей математике
Производные показательной и логарифмической функций — формулы и доказательство
Докажем следующие формулы производных:
1. Пусть дана функция 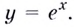
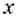
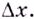
Следовательно,
Если 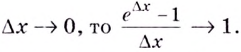
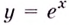
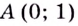
Если значение 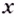
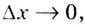
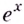
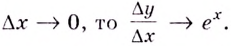
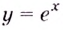
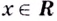
2.Как известно, при каждом 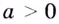
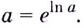
По теореме о производной сложной функции
Итак, формула 2 доказана.
3. Если
А по теореме о производной сложной функции
Следовательно, 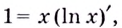
4. При каждом 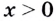
Следовательно,
По доказанным формулам можно находить производные любых показательных или логарифмических функций, а значит, и исследовать эти функции.
Обратите внимание! Если функция содержит логарифм сложного выражения, то прежде чем находить её производную, целесообразно это выражение прологарифмировать.
Пример №7
Найдите производную функции
Решение:
Теперь можно вывести формулу производной степенной функции 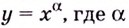
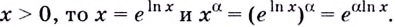
Итак, формула 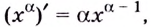
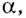
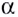
Формулу для нахождения производной логарифмической функции можно вывести иначе, используя тот факт, что функция 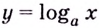
Выясним, как связаны между собой производные взаимно обратных функций.
Теорема. Если функция 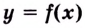
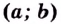
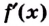
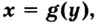
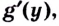
Обоснуем эти формулы, используя геометрический смысл производной.
Пусть 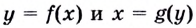
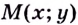
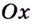
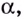
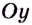
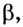
Поскольку 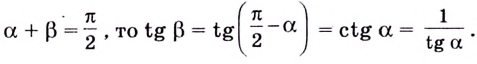
Строгое доказательство этой теоремы рассматривается в университетском курсе математического анализа.
Применим формулу 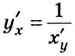
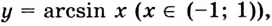
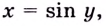
Получим:
Пример №8
Найдите производную функции:
Решение:
Пример №9
Запишите уравнение касательной к графику функции 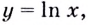
Решение:
Найдём абсциссу точки касания: 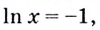
Найдём производную функции 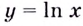
Уравнение касательной запишем в виде 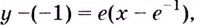
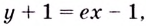
Пример №10
Найдите производную функции
Решение:
Заданная функция является суммой степенной и показательной функций. Для нахождения её производной воспользуемся соответствующими формулами:
Определение производной показательной и логарифмической функций
Существует ли функция, производная которой равна самой функции? Ответить на этот вопрос легко. Например, функция, которая является нулевой константой, обладает этим свойством.
А можно ли указать такую функцию 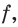
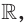
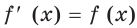
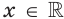
Оказывается, что среди показательных функций 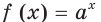
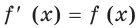
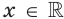
основанием степени, обозначают буквой 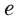
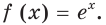
Установлено, что число 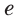
Функцию 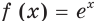
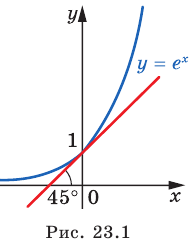
Отметим одну особенность графика экспоненты.
Имеем:
Следовательно, касательная к графику экспоненты в точке с абсциссой, равной нулю, имеет угловой коэффициент, равный 1. То есть эта касательная образует угол 45° с положительным направлением оси абсцисс (рис. 23.1).
Выведем формулу для нахождения производной показательной функции
Имеем: 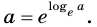
Пользуясь правилом вычисления производной сложной функции, запишем:
Логарифм по основанию 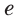
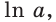
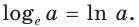
Эта формула показывает, что между значением производной показательной функции и соответствующим значением самой функции существует прямая пропорциональная зависимость. Коэффициент пропорциональности равен
В пункте 20 мы определили, что логарифмическая функция 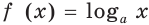
Для любого 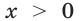
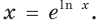
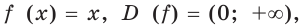
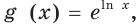
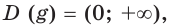
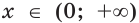
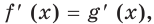
Левая часть этого равенства равна 1. В правой части получаем: 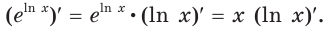
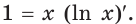
Имеем:
Следовательно,
Пример №11
Найдите производную функции:
Решение:
1) Применяя теорему о производной произведения двух функций, получаем:
2) Имеем:
3) Используя теорему о производной сложной функции, запишем:
4) Имеем:
5) Применив теорему о производной сложной функции, получаем:
6) Имеем:
Пример №12
Составьте уравнение касательной к графику функции 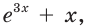
Решение:
Поскольку угловой коэффициент прямой 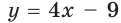
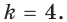
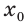
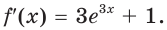
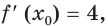
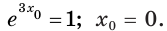
Тогда искомое уравнение имеет вид
Ответ:
Ответ: у = 4х + 1.
Пример №13
Найдите промежутки возрастания и убывания и точки экстремума функции:
Решение:
1) Имеем:
Исследовав знак производной функции 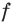
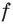
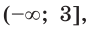
2) Имеем:
Исследуем знак 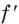
Имеем: 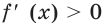
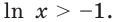
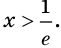
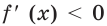
Получаем, что функция 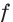
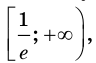
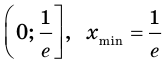
3) Имеем:
Тогда 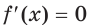
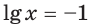
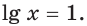
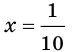
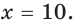
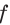
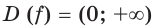
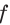
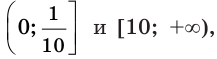
Пример №14
Докажите, что: 1) показательная функция 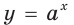
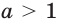
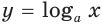
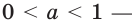
Решение:
1) Имеем:
Поскольку 
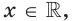
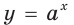
2) Запишем:
Если 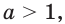
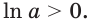
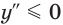
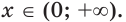
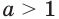
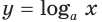
При 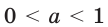
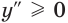
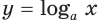
- Показательно-степенные уравнения и неравенства
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция — определение и вычисление
- Дифференциальная геометрия
- Логарифмическая функция, её свойства и график
- Логарифмические выражения
- Показательная функция, её график и свойства
Логарифмическое дифференцирование
При
вычислении производной от логарифма
произведения, частного, степени или
корня, для упрощения нахождения
производной проводят предварительное
преобразование (см. Пример 10(и)).
В
ряде случаев для нахождения производной
целесообразно заданную функцию сначала
прологарифмировать (по умолчанию имеется
в виду натуральный логарифм). Затем
найти производную от этого логарифма
и по ней отыскать производную от заданной
функции. Такой прием называется
логарифмическим
дифференцированием.
Метод логарифмического
дифференцирования позволяет легко
найти производную показательно-степенной
функции вида
,
где
и
– дифференцируемые функции аргумента
.
Пример 14.
Найти
производную функции
.
Решение.
Прологарифмируем
обе части функции и преобразуем выражение:
.
Теперь дифференцируем
уравнение, как неявно заданную функцию:
;
;
;
;
Так
как
,
то окончательно получаем:
.
Производные высших порядков
Производной
2-го порядка от функции
называется производная от её первой
производной, т.е.
.
Аналогично,
производной 3-го порядка от функции
называется
производная от её второй производной,
т.е.
.
Таким
образом, производной
-го
порядка от функции
называется производная от производной
-го
порядка, т.е.
.
Следовательно,
для нахождения производной
-го
порядка необходимо последовательно
найти производную первого, затем второго,
затем третьего и т.д. до-го
порядка.
Пример 15.
Найти
третью производную
функции
.
Решение.
;
;
.
2.3. Дифференциал функции
Из определения
производной и свойств пределов следует,
что если
то
,
где
–
бесконечно малая величина ().
Выражаем
и получаем, что:
.
Так как,
то в дальнейшем ее можно не учитывать
и мы получим:
Главная
часть приращения функции, линейная
относительно приращения независимой
переменной
,
называется дифференциалом
функции
и обозначается
или
:
.
Т.
к. дифференциал
,
то дифференциал
функции равен произведению производной
функции на дифференциал аргумента:
.
Таким
образом, для нахождения дифференциала
функции, необходимо найти производную
и умножить её
на дифференциал независимой переменной
.
Пример
16.
Найти
дифференциал функции
.
Решение.
.
2.4. Применение дифференциального исчисления функции одной переменной
2.4.1. Применение производной при вычислении пределов.
Правило Лопиталя
При
вычислении предела функции подстановка
предельного значения аргумента часто
приводит к неопределенностям вида
,
,
от которых невозможно избавиться при
помощи ранее изученных приемов. Теорема,
известная под названиемправило
Лопиталя,
является одним из основных инструментов
для раскрытия таких неопределенностей.
Правило
Лопиталя:
Пусть в некоторой окрестности точки
функции
и
дифференцируемы и
.
Еслии
одновременно являются бесконечно малыми
или бесконечно большими функциями при
,
то
,
при условии, что
предел отношения производных существует.
Эта
теорема справедлива также и для
односторонних пределов, и в случае,
когда
.
В
некоторых случаях раскрытие
неопределенностей вида
может потребовать неоднократного
применения правила Лопиталя.
Неопределенности
,
,
,
,
,
сводятся к
неопределенностям вида
путем алгебраических преобразований.
Пример 17.
Вычислить с помощью
правила Лопиталя пределы:
а); б)
; в)
.
Решение.
а)
.
б)
.
в)
.
Обозначим
искомый предел через
и прологарифмируем выражение:
;
или
.
Тогда:
.
Так
как
,
то искомый предел.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #