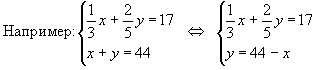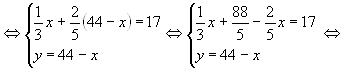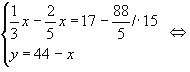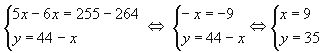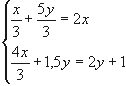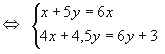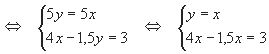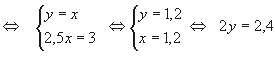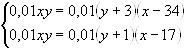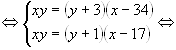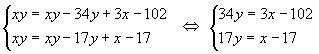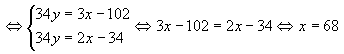Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Пропорция: 400 кг сплава — 100%
56 кг цинка — х%
х = 56 * 100 : 400 = 14% — процент содержания цинка
Ответ: сплав содержит 14% цинка.
Отмена
Нелли Масновиева
Отвечено 28 сентября 2019
-
Комментариев (0)
Добавить
Отмена
Контрольные задания > Найдите процент содержания цинка в сплаве, если 400 кг сплава содержат 56 кг цинка.
Ответ:
[frac{56}{400} cdot 100% = frac{56 cdot 100}{400}% = frac{56 cdot 1}{4}% =]
[= 14% — содержание цинка в сплаве.]
[Ответ:14%. ]
Семён Туманов
16 ноября, 03:22
0
Задача решается простейшей математической пропорцией.
Массу всего сплава (400 кг) обозначаем за 100%, а массу цинка в сплаве (56 кг) за x.
Получаем пропорцию: 400 кг — 100 %
56 кг — х %.
Выражаем х. Получаем: 56 * 100 / 400 = 14 %.
Ответ: массовая доля 56 кг цинка в 400 кг сплава равна 14 процентов.
- Комментировать
- Жалоба
- Ссылка
Задачи, связанные с понятием “концентрация” и “процентное содержание”,
являются традиционно трудными для обучающихся. В них речь идет о сплавах,
растворах и смесях, которые получаются при сплавлении или смешивании различных
веществ. При решении таких задач принимаются некоторые допущения. Первое: если
смешиваются два раствора, объем которых х и у, то получившаяся
смесь будет иметь объем х +
у. Второе: получившиеся смеси и сплавы имеют однородную консистенцию.
В смесях и растворах содержится некоторый объем чистого вещества. Отношение
объема чистого вещества к объему всего раствора называется объемной
концентрацией. (Содержание чистого вещества в единице объема).
Концентрация, выраженная в процентах, называется процентным содержанием.
При решении таких задач удобно пользоваться таблицей, которая помогает понять
задачу и по которой легче составить уравнение или систему. В работе приведены
решения нескольких задач, а также предложены задачи для самостоятельного
решения. Для удобства к задачам прилагаются ответы.
1. Некоторый сплав состоит из
двух металлов, входящих в отношении 1 : 2, а другой содержит те же металлы в
отношении 2 : 3. Из скольких частей обоих сплавов можно получить третий сплав,
содержащий те же металлы в отношении 17 : 27?
Решение: Пусть взято х частей
первого сплава и у частей второго. В х
частях первого сплава содержится
частей первого металла и
частей второго. В
y частях второго сплава содержится
частей первого металла и
частей второго.
Составим таблицу:
Из таблицы видно, что можно получить три уравнения. 1)
х + у = 44 , 2)
3) . Решив систему из
двух уравнений, получим ответ.
Ответ: 9 частей первого сплава и 35 частей второго сплава.
2. Имеется два слитка, представляющие собой сплавы цинка с медью. Масса первого
слитка 2 кг, масса второго – 3 кг. Эти два слитка сплавили вместе с 5 кг сплава
цинка с медью, в котором цинка было 45 %, и получили сплав цинка с медью, в
котором цинка стало 50%. Если бы процентное содержание цинка в первом слитке
было бы равно процентному содержанию цинка во втором, а процентное содержание
цинка во втором такое же как в первом, то сплавив эти два слитка с 5 кг сплава,
в котором содержится 60% цинка, мы бы получили сплав, в котором цинка содержится
55%. Найдите процентное содержание цинка в первом и втором слитках.
Решение: Составим по условию задачи следующую таблицу
| 1 случай | 2 случай | ||||
| масса | Zn (%) |
Zn (кг) |
Zn (%) |
Zn (кг) |
|
| 1 сплав | 2кг | х % | 0,02 х кг |
у % |
0,02 у кг |
| 2 сплав | 3кг | у % | 0,03 у кг |
х % | 0,03 х кг |
| 3 сплав | 5кг | 45% | 2,25 кг | 60% | 3 кг |
| 4 сплав | 10кг | 50% | 5 кг | 55% | 5,5 кг |
По таблице составим систему уравнений
прибавим к первому уравнению второе, получим
Ответ: 40% и 65%.
Имеется два разных сплава меди со свинцом. Если взять 1 кг первого сплава и 1
кг второго сплава и переплавить их, то получится сплав с содержанием 65% меди.
Известно, что если взять кусок № 1 и кусок № 2 первого и второго сплавов
соответственно, имеющих суммарную массу 7 кг, и переплавить их, то получится
сплав с содержанием 60% меди. Какова масса меди, содержащаяся в сплаве,
получающемся при совместной переплавке куска первого сплава, равного по массе
куску № 2, и куска второго сплава, равного по массе куску № 1?
Решение: Составим по условию задачи следующую таблицу
| 1случай | 2 случай | 3 случай | |||||
| масса | Cu (%) |
Cu (кг) |
масса | Cu (кг) |
масса | Cu (кг) |
|
| 1 сплав | 1 кг | n% | 0,01n кг |
х кг | 0,01n кг |
у кг | 0,01n у кг |
| 2 сплав | 1 кг | m% | 0,01m кг |
у кг | 0,01m у кг |
х кг | 0,01m х кг |
| 3 сплав | 2 кг | 65% | 1,3 кг |
7 кг | 60% или 4,2 кг |
По данным таблицы составим систему уравнений
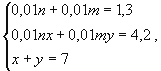
у + 0,01m
х.
Представим его в виде 0,01(n у
+ m х).
Решим систему уравнений.
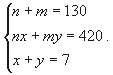
уравнение на третье и вычтем второе.
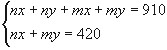
Ответ: 4,9 кг.
4. Имеется два слитка сплавов золота и меди. В первом слитке отношение золота к
меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с 5/6 второго,
то в получившемся слитке окажется столько золота, сколько было бы в первом меди,
а если 2/3 первого слитка сплавить с половиной второго, то в получившемся слитке
окажется меди на 1 кг больше, чем было золота во втором слитке. Сколько золота в
каждом слитке?
Решение: Пусть в первом слитке содержится х кг
золота и 2х кг меди.
Тогда масса всего слитка 3х кг. Пусть во втором
слитке содержится 2у кг
золота и 3у кг меди. Тогда
масса всего слитка 5у кг. Составим
таблицу:
| 1 случай | 2 случай | ||||||
| Масса всего сплава | Масса части сплава |
Золото (кг) |
Медь (кг) |
Масса части сплава |
Золото (кг) |
Медь (кг) |
|
| 1 сплав | 3х кг | х кг | 2х кг | ||||
| 2 сплав | 5у кг | 2,5у кг | у кг | 1,5 у кг | |||
| 3 сплав | 2х | (2у + 1) кг |
По данным таблицы составим систему уравнений
Ответ: 1,2 кг и 2,4 кг.
5. Имеется три слитка: первый слиток – сплав меди с никелем, второй – никель с
цинком, третий цинка с медью. Если сплавить первый кусок со вторым, то процент
меди в получившемся слитке будет в два раза меньше, чем он был в первом слитке.
Если сплавить второй слиток с третьим, то процент никеля в получившемся слитке
будет в три раза меньше, чем он был во втором слитке. Какой процент цинка будет
содержать слиток, получившийся при сплаве всех трех слитков, если во втором
слитке было 6% цинка, а в третьем – 11%?
Решение: Заметим, что во втором слитке нет меди, а если его сплавить с
первым, в котором есть медь, то процент меди в новом сплаве будет в 2 раза меньше, чем он был в
первом слитке, значит масса первого слитка равна массе второго. Пусть их масса будет
х.
Если сплавить второй слиток, в котором есть никель, с третьим слитком, в котором
никеля нет, то процент никеля в новом сплаве будет в 3 раза меньше, чем он был
во втором слитке. Значит второй слиток по массе в 2 раза больше второго. Значит
его масса будет 2х. Занесем данные в
таблицу:
| Масса слитка |
Zn (%) | Zn (масса) | |
| 1 слиток | х | нет | нет |
| 2 слиток | х | 6% | 0,06х |
| 3 слиток | 2х | 11% | 0,22х |
| 4 слиток | 4х | y % | 0,28х |
Ответ: 7%
6. В сосуде находится определенное количество смеси
воды с кислотой. Чтобы уменьшить концентрацию кислоты на 34% (было p%, а стало
p-34%) в сосуд надо долить 3 л воды, а чтобы уменьшить её на 17%, надо долить 1
л воды. Какова концентрация кислоты в сосуде?
Решение: Составим по условию задачи следующую таблицу:
|
Кол-во смеси |
Кислота в % |
Кислота в литрах |
y л |
х% |
0,01xy |
|
(y + 3) л |
(x – 34) % |
0,01(y + 3)(x – 34) |
|
(y +1) л |
(x – 17) % |
0,01(y + 1)(x – 17) |
Если к раствору кислоты добавить чистую воду, то изменится
концентрация кислоты, а количество кислоты не меняется. На этом основании составим
систему уравнений:
Ответ: 68%.
7. Имеется три слитка золота массой 2 кг, 3 кг и 5 кг с
различным процентным содержанием золота. Каждый слиток разделен на три куска и
из 9 получившихся кусков получили три слитка массой 2 кг, 3 кг и 5 кг, но уже с
равным процентным содержанием золота. На какие части следует разделить каждый
слиток, чтобы гарантировать равное процентное содержание золота в получившихся
слитках независимо от его содержания в исходных слитках.
Решение: Процентное содержание золота в новых
получившихся слитках 2 кг, 3 кг и 5 кг будет равно процентному содержанию золота в слитке, который
получится если просто сплавить исходные слитки массой 2 кг, 3 кг и 5 кг в
десятикилограммовый кусок. Тогда золото входит в каждый новый слиток в отношении 2 : 3 :
5 . Значит нужно Каждый исходный слиток разделить на части пропорциональные
этим числам. Всего частей 10. Получим
2 : 10 * 2 = 0,4; 2 : 10 * 3 = 0,6; 2 : 10 * 5 = 1
и т.д. Представим этот результат в виде таблицы.
| Масса слитка | 1часть | 2часть | 3часть | |
| 1 слиток | 2 кг | 0,4 кг | 0,6 кг | 1 кг |
| 2 слиток | 3 кг | 0,6 кг | 0,9 кг | 1,5 кг |
| 3 слиток | 5 кг | 1 кг | 1,5 кг | 2,5 кг |
Задачи для самостоятельного решения
8. Из трех кусков сплавов меди и никеля с соотношением по массе этих
металлов 2 : 1, 3 : 1, 5 : 1 получили новый сплав. Его масса оказалась равной 12
кг, а соотношение меди и никеля в нем составило 4:1. Найти массу каждого
исходного куска, если первый весил вдвое больше второго.
Ответ: 1,92 кг,
0,96 кг, 9,12 кг.
9. Из трех кусков сплавов серебра и меди с соотношением масс этих металлов
3:2, 2:3, 1:4 получили новый сплав. Его масса оказалась равной 22 кг, а
соотношение серебра и меди в нем составило 1:1. Найти массу каждого
исходного куска, если второй весил вдвое больше третьего. Ответ: 13,75 кг,
5,5 кг, 2,75 кг.
10. Из трех кусков сплавов олова и свинца с соотношением масс этих металлов
4 : 1, 1 : 1, 1 : 4 получили новый сплав. Его масса оказалась равной 24 кг, а
соотношение олова и свинца в нем составило 2 : 3. Найти массу каждого
исходного куска, если первый весил вдвое больше второго.
Ответ: 6,4 кг, 3,2
кг, 14,4 кг.
11. Из трех кусков сплавов золота и серебра с соотношением масс этих
металлов 1 : 1, 1 : 5, 5 : 1 получили новый сплав. Его масса оказалась равной 24
кг, а соотношение золота и серебра в нем составило 2 : 1. Найти массу каждого
исходного куска, если третий кусок весил втрое больше первого.
12. Имеются два сплава, в одном из которых содержится 20%, в другом 30%
олова. Сколько нужно взять первого и второго сплава, чтобы получить 10 кг
нового сплава, содержащего 27% олова?
Ответ: 3 кг , 7 кг.
13. Имеются два сплава, в одном из которых содержится 40%, а во втором 20%
серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы
получить сплав, содержащий 32% серебра?
14. Имеются два сплава, в одном из которых содержится 10%, а в другом
– 20%
меди. Сколько нужно взять первого и второго сплавов, чтобы получить 15 кг
нового сплава, содержащего 14% меди?
Ответ: 9 кг и 6 кг.
15. Имеются два сплава, в одном из которых содержится 30%, а в другом
– 50%
золота. Сколько кг второго сплава нужно добавить к 10 кг первого, чтобы
получить сплав, содержащий 42% золота?
Ответ: 15 кг.
16. Из молока, жирность которого 5%, делают творог, жирностью 0,5%.
Определить, сколько творога получается из 1 тонны молока?
Ответ: 300 кг.
17. При смешивании растворов, содержащих 25% и 60% кислоты, получился
раствор, содержащий 39% кислоты. Определить в какой пропорции были смешаны
растворы?
Ответ: 3 : 2.
18. Добытая руда содержит 21% меди, а обогащенная – 45%. Известно, что в
процессе обогащения 60% добытой руды идет в отходы. Определить процентное
содержание меди в отходах.
Ответ: 5%.
19. В 100 граммов 20%-ного раствора соли добавили 300 граммов ее 10%-ного
раствора. Определить концентрацию полученного раствора.
Ответ: 12,5%.
20. Какое количество воды надо добавить к 100 граммам 70%-ной уксусной
эссенции, чтобы получить 5% раствор уксуса?
Ответ: 1300 гр.
21. Процентное содержание соли в растворе сначала снизилось на 20%, а затем
повысилась на 20%. На сколько процентов изменилось первоначальное содержание
соли?
Ответ: на 4%.
22. Морская вода содержит 5% соли. Сколько килограммов пресной воды надо
добавить к 40 кг морской воды, чтобы содержание соли в последней составляло
2%.
Ответ: 60 кг.
23. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра
составляет
веса меди. Сколько килограммов серебра в данном сплаве?
Ответ: 0,25 кг.
24. Имеется лом стали двух сортов с содержанием никеля 5% и 40% . Сколько
нужно взять каждого из этих сортов металлолома, чтобы получить 140т стали с
содержанием никеля 30%.
Ответ: 40 т и 100 т.
25. Кусок сплава меди с оловом весом 2 кг содержит 45% меди. Сколько чистого
олова надо прибавить к этому куску, чтобы получившийся новый сплав имел 40%
меди?
Ответ: 1,5 кг.
26. Сколько чистого спирта надо прибавить к 735 г 16%-ного раствора йода в
спирте, чтобы получить 10%-ный раствор?
Ответ: 441 г.
27. Сплав из меди и цинка весом в 24 кг при погружении в воду потерял в
своем весе
Определить количество меди и цинка в этом сплаве, если известно, что медь
теряет в воде
своего веса, а цинк
своего веса.
Ответ: 17 кг и 7 кг.
28. Имеются два сплава золота и серебра. В одном количество этих металлов
находится в отношении 2 : 3, а в другом в отношении 3 : 7. Сколько нужно взять
от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и
серебро были бы в отношении 5 : 11?
Ответ: 1 кг, 7 кг.
29. Одна бочка содержит смесь спирта с водой в отношении 2 : 3, а другая в
отношении 3 : 7. По сколько ведер надо взять из каждой бочки, чтобы составить
12 ведер смеси, в которой спирт и вода были бы в отношении 3 : 5?
Ответ: 9
ведер из первой и 3 ведра из второй.
30. Два раствора, из которых первый содержал 800 г безводной серной кислоты,
а второй 600 г безводной серной кислоты, соединили вместе и получили 10 кг
нового раствора серной кислоты. Определить вес первого и второго растворов,
вошедших в смесь, если известно, что процент содержания безводной серной
кислоты в первом растворе на 10% больше, чем процент содержания безводной
серной кислоты во втором.
Ответ: 4 кг и 6 кг.
31. Имелось два разных сплава меди. Процент содержания меди в первом сплаве
был на 40 меньше, чем процент содержания меди во втором сплаве. После того
как их сплавили вместе, получили сплав, содержащий 36% меди. Определить
процентное содержание меди в первом и втором сплавах, если известно,
содержание меди в первом сплаве было 6 кг, а во втором 12 кг.
Ответ: 20% и
60%.
32. 36 г цинка в воде весят 31 г, а 23 г свинца в воде весят 21 г. Сплав
цинка и свинца массой 292 г в воде весит 261 г. Сколько цинка и сколько
свинца содержится в сплаве?
Ответ: 108 г цинка и 184 г свинца.
33. В двух одинаковых сосудах, объемом по 30 л каждый, содержится всего 30 л
кислоты. Первый сосуд доливают доверху водой и полученной смесью дополняют
второй сосуд, затем из второго сосуда отливают в первый 12 литров смеси.
Сколько кислоты было первоначально в первом сосуде, если во втором сосуде
после переливаний оказалось на 2 л меньше кислоты, чем в первом?
Ответ: 20
литров.
34. Имеется два слитка сплавов золота и меди. В первом слитке отношение
золота к меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с
5/6 второго, то в получившемся слитке окажется столько золота, сколько было
бы в первом меди, а если 2/3 первого слитка сплавить с половиной второго, то
в получившемся слитке окажется меди на 1 кг больше, чем было золота во
втором слитке. Сколько золота в каждом слитке?
Ответ: 1,2 кг и 2,4 кг.
35. Имеется два сосуда. В одном содержится три литра 100%-ной серной
кислоты, а в другом два литра воды. Из первого сосуда во второй перелили
один стакан кислоты, а затем из второго в первый – один стакан смеси. Эту
операцию повторили еще два раза. В результате во втором сосуде образовалась
42%-ная кислота. Сколько серной кислоты в процентах содержится теперь в
первом сосуде?
Ответ: 72%.
36. Имеется два куска металла массой 1 кг и 2 кг. Из этих кусков сделали два
других: первый массой 0,5 кг, содержащий 40% меди, а второй массой 2,5 кг,
содержащий 88% меди. Каково процентное содержание меди в исходных кусках?
Ответ: 40% и 100%.
37. Из колбы в пробирку отлили
раствора соли. Раствор в пробирке выпаривали, пока процентное содержание
соли в нем не увеличилось в два раза. Получившийся раствор вернули в колбу, что
увеличило процентное содержание соли в находившемся в колбе растворе на 2 %.
Какое процентное содержание соли было в растворе первоначально?
Ответ: 10%.
Литература:
- Шарыгин И.Ф. “Математика для поступающих в ВУЗы”. Москва, Дрофа, 2000 г.
- Сканави М.И. “2500 задач по математике для поступающих в ВУЗы”.
Москва, Оникс, 2003 г. - Черкасов О., Якушев А. “Математика”. Москва, Айрис, 2000 г.
- Белоносов В.С., Фокин М.В. “Задачи вступительных экзаменов по
математике.” Новосибирск, издательство НГУ, 1995 г.