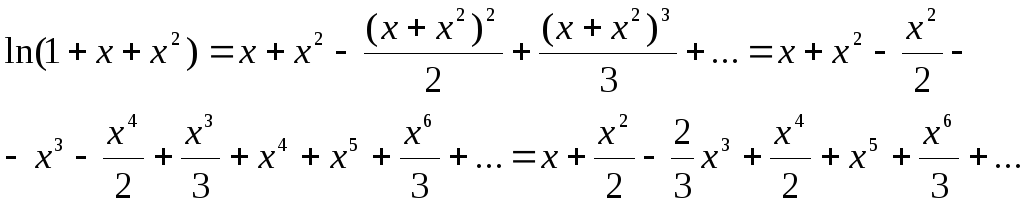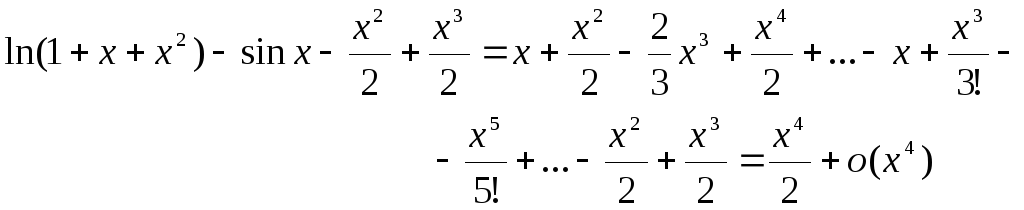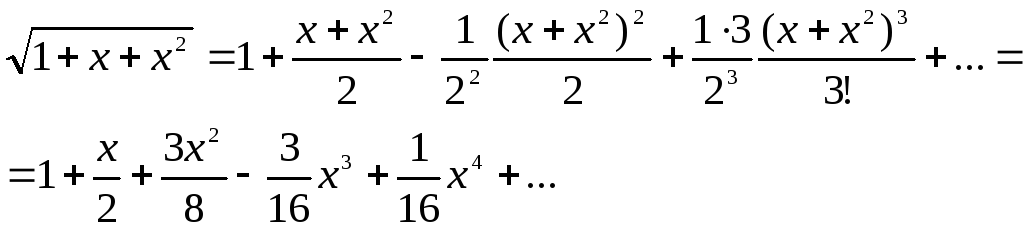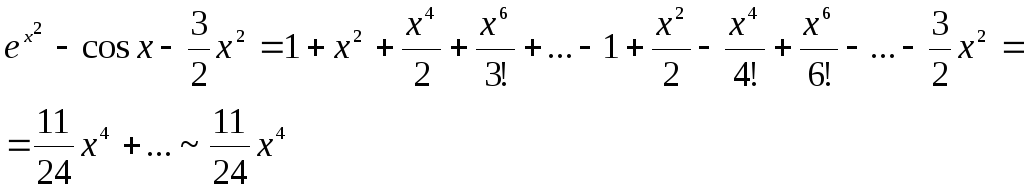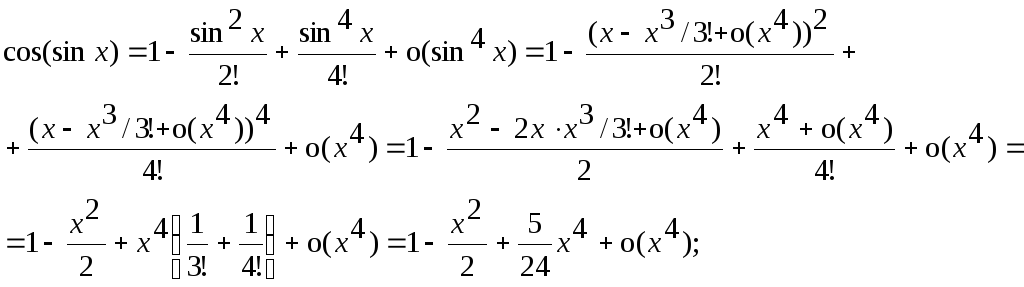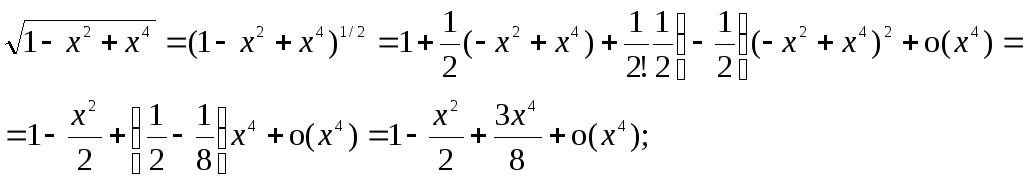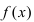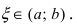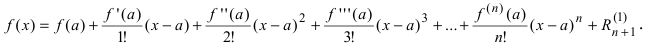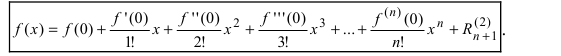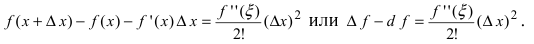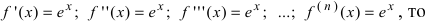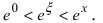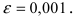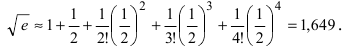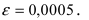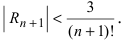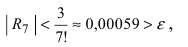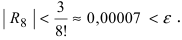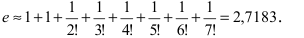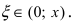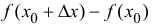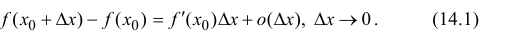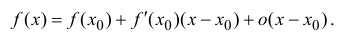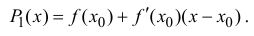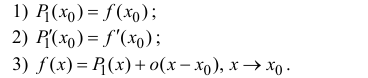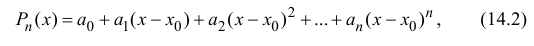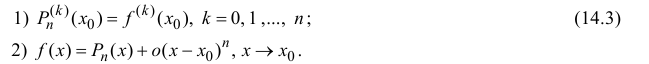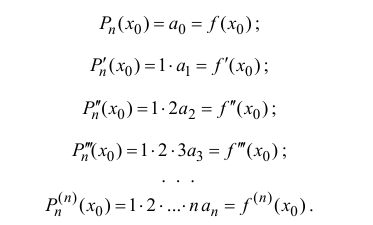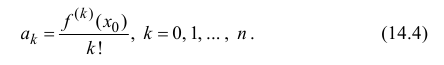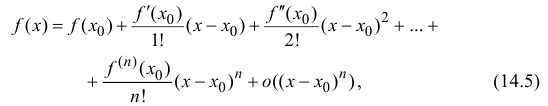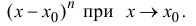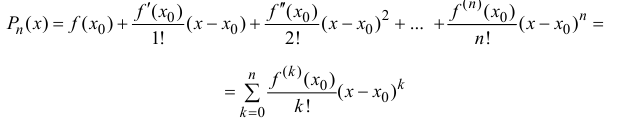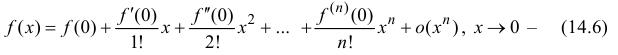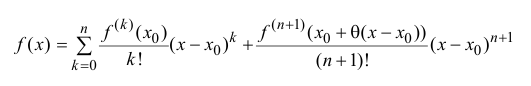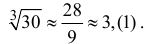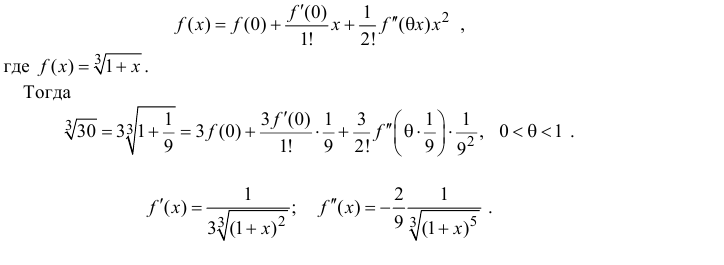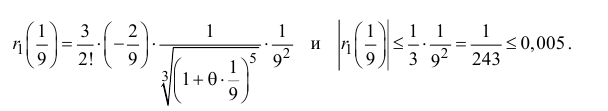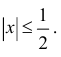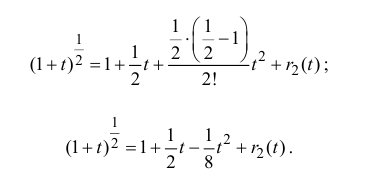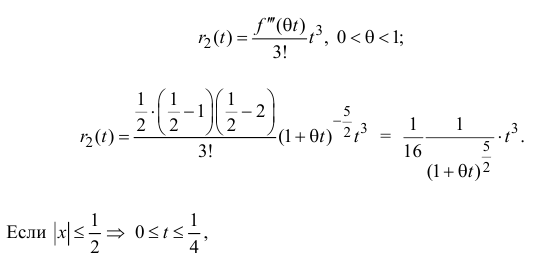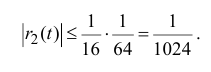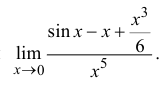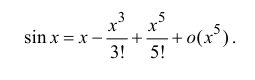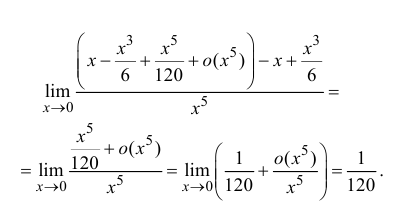Формула Тейлора.
Определение. Пусть функция $f(z)$ определена в окрестности точки $x_0$ и имеет в этой окрестности производные до $(n-1)$ порядка включительно, и пусть существует $f^{(n)}(x_0).$ Тогда
$$f(x)=f(x_0)+frac{f'(x_0)}{1!}(x-x_0)+frac{f»(x_0)}{2!}(x-x_0)^2+…+$$ $$+frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n)$$ при $xrightarrow x_0. $
То есть $$f(x)=sumlimits_{k=0}^{n}frac{f^{(k)}(x_0)}{k!}(x-x_0)^k+o((x-x_0)^n),qquad xrightarrow x_0.$$
Многочлен $P_n(x)=sumlimits_{k=0}^{n}frac{f^{(k)}(x_0)}{k!}(x-x_0)^k $ — многочлен Тейлора. $r_n=f(x)-P_n(x)$ — остаточный член $n$-го порядка формулы Тейлора.
При $x_0=0$ $f(x)=sumlimits_{k=0}^nfrac{f^{(k)}(0)}{k!}x^k+o(x^n) -$ формула Маклорена.
Формулы Тейлора в окрестности точки $x_0=0$ для основных элементарных функций.
$$e^x=1+x+frac{x^2}{2!}+…+frac{x^n}{n!}+o(x^n);quad xrightarrow 0$$
$$sin x=x-frac{x^3}{3!}+frac{x^5}{5!}+…+frac{(-1)^nx^{2n+1}}{(2n+1)!}+o(x^{2n+2}); quad xrightarrow 0$$
$$cos x=1-frac{x^2}{2!}+frac{x^4}{4!}+…+(-1)^nfrac{x^{2n}}{(2n)!}+o(x^{2n+1});quad xrightarrow 0$$
$$(1+x)^alpha=1+alpha x+frac{alpha(alpha-1)}{2!}x^2+…+$$ $$+frac{alpha(alpha-1)…(alpha-(n-1))}{n!}x^n+o(x^n);quad xrightarrow 0$$
$$frac{1}{1+x}=sumlimits_{k=0}^n (-1)^kx^k+o(x^n);quad xrightarrow 0$$
$$frac{1}{1-x}=sumlimits_{k=0}^n x^k+o(x^n);quad xrightarrow 0$$
$$ln(1+x)=x-frac{x^2}{2}+frac{x^3}{3}+…+frac{(-1)^{n-1}x^n}{n}+o(x^n);quad xrightarrow 0$$
$$ln(1-x)=-sumlimits_{k=0}^n frac{x^k}{k}+o(x^n)quad xrightarrow 0.$$
$$tg x = x+frac{x^3}{3}+frac{x^5}{15}+overline{o}(x^5) quad xrightarrow 0$$
$$arcsin x = x+sumlimits_{k=1}^nfrac{(2k-1)!!}{2^k k!(2k+1)}x^{2k+1}+overline{o}(x^{2n+2}), quad xrightarrow 0$$
Примеры.
Разложить по формуле Маклорена до $o(x^n)$ функции
${bf 1. e^{5x-1}}$
Решение.
$$e^{5x-1}=frac{e^{5x}}{e}=sumlimits_{k=0}^nfrac{(5x)^k}{k!e}+o(x^n).$$
${bf 2. sin(2x+3)}$
Решение.
$$sin(2x+3)=sin 2xcos 3+sin 3cos 2x=$$
$$cos 3sumlimits_{k=0}^n(-1)^kfrac{(2x)^{2k+1}}{(2k+1)!}+sin 3sumlimits_{k=0}^n(-1)^kfrac{(2x)^{2k}}{(2k)!}+o(x^{2n+1})$$
${bf 3.}cosleft(frac{x}{2}+2right)$
Решение.
$$cos^{(k)}left(frac{x}{2}+2right)=frac{1}{2^k}cosleft(frac{x}{2}+2+frac{pi}{2}kright)$$
$$cosleft(frac{x}{2}+2right)=sumlimits_{k=0}^nfrac{1}{2^k}frac{cos(2+frac{pi}{2}k)}{k!}x^k+o(x^k).$$
${bf 4. frac{1}{1-2x}}$
Решение.
$$frac{1}{1-2x}=sumlimits_{k=0}^n 2^kx^k+o(x^n).$$
${bf 5. frac{1}{3x+4}}$
Решение.
$$frac{1}{3x+4}=frac{1}{4}frac{1}{frac{3}{4}x+1}=frac{1}{4}sumlimits_{k=0}^n(-1)^kleft(frac{3}{4}right)^kx^k+o(x^n).$$
Вычисление пределов с помощью формулы Тейлора.
Пусть требуется найти $limlimits_{xrightarrow 0}frac{f(x)}{g(x)},$ где $f(0)=g(0)=0.$ Предполагая, что функции $f(x)$ и $g(x)$ можно разложить по формуле Маклорена, ограничимся
первыми отличными от нуля членами в разложении этих функций:
$f(x)=ax^n+o(x^n),$ $aneq 0,$ $g(x)=bx^m+o(x^m),$ $bneq 0.$
Если $m=n,$ то
$$limlimits_{xrightarrow 0}frac{f(x)}{g(x)}=limlimits_{xrightarrow 0}frac{f(x)}{g(x)}=limlimits_{xrightarrow 0}frac{ax^n+o(x^n)}{bx^n+o(x^n)}=frac{a}{b};$$
Если $n>m$ , то $$limlimits_{xrightarrow 0}frac{f(x)}{g(x)}=0;$$
если же $m>n$ ,то $$limlimits_{xrightarrow 0}frac{f(x)}{g(x)}=infty.$$
Примеры.
Вычислить пределы, используя формулу Тейлора.
1. $limlimits_{xrightarrow 0}frac{ln (1+x)-x}{x^2}.$
Решение.
$$limlimits_{xrightarrow 0}frac{ln (1+x)-x}{x^2}=limlimits_{xrightarrow 0}frac{x-frac{x^2}{2}-x}{x^2}=-frac{1}{2}.$$
{jumi[*4]}
2. $limlimits_{xrightarrow 0}frac{e^x-1-x}{x^2}.$
Решение.
$$limlimits_{xrightarrow 0}frac{e^x-1-x}{x^2}=limlimits_{xrightarrow 0}frac{1+x+frac{x^2}{2}-1-x}{x^2}=frac{1}{2}.$$
3. $limlimits_{xrightarrow 0}frac{cos x-1+frac{x^2}{2}}{x^4}.$
Решение.
$$limlimits_{xrightarrow 0}frac{cos x-1+frac{x^2}{2}}{x^4}=limlimits_{xrightarrow 0}frac{1-frac{x^2}{2}+frac{x^4}{4!}-1+frac{x^2}{2}}{x^4}=frac{1}{24}.$$
4. $limlimits_{xrightarrow 0}frac{tg x-sin x}{x^3}.$
Решение.
$$limlimits_{xrightarrow 0}frac{tg x-sin x}{x^3}=limlimits_{xrightarrow 0}frac{x+frac{x^3}{3}-x+frac{x^3}{3}}{x^3}=frac{2}{3}.$$
5. $limlimits_{xrightarrow 0}frac{sqrt{1+2tg x}-e^x+x^2}{arctg x-sin x}.$
Решение.
Разложим числитель по формуле Тейлора:
$tg x=x+frac{x^3}{3}+o(x^3),,, xrightarrow 0$
$2tg x=2x+frac{2x^3}{3}+o(x^3),,, xrightarrow 0$
$sqrt{1+t}=(1+t)^{frac{1}{2}}=1+frac{1}{2}t-frac{1}{8}t^2+frac{1}{16}t^3+o(t^3),,, trightarrow 0;$
Таким образом,
$$sqrt{1+2tg x}=1+frac{1}{2}2 tg x-frac{1}{8}(2 tg x)^2+frac{1}{16}(2 tg x)^3+o(tg^3x)=$$
$$=1+tg x-frac{1}{2}tg^2 x+frac{1}{2}tg^3+o(tg^3x)=$$
$$=1+x+frac{x^3}{3}-frac{1}{2}x^2+frac{x^3}{2}+o(x^3)=1+x-frac{1}{2}x^2+frac{5}{6}x^3+o(x^3).$$
Учитывая, что $e^x=1+x+frac{x^2}{2}+frac{x^3}{6}+o(x^3)$ находим, по формуле Маклорена числитель дроби
$$sqrt{1+2tg x}-e^x+x^2=$$ $$=1+x-frac{1}{2}x^2+frac{5}{6}x^3-1-x-frac{x^2}{2}-frac{x^3}{6}+x^2+o(x^3)=$$ $$=frac{2}{3}x^3+o(x^3),,,,xrightarrow 0.$$
Далее раскладываем знаменатель:
$sin x= x-frac{x^3}{6}+o(x^3);$
$arcsin x=x+frac{x^3}{6}+o(x^3).$
Отсюда $arcsin x-sin x=frac{x^3}{3}+o(x^3).$
Таким образом, дробь представляется в виде $$frac{frac{2}{3}x^3+o(x^3)}{frac{1}{3}x^3+o(x^3)}.$$
Отсюда
$$limlimits_{xrightarrow 0}frac{sqrt{1+2tg x}-e^x+x^2}{arctg x-sin x}=2.$$
Ответ: 2.
Степенные ряды в форме рядов Тейлора и Маклорена
Степенные ряды и, в частности, ряды Тейлора являются одним из видов функциональных рядов.
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots — постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости, когда для частичных сумм Sn(x)S_n(x) существует предел, сумма ряда S(x)S(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n,limn→∞Sn(x)=S(x)S_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n, quad limlimits_{n to infty } S_n (x) = S (x)
Возьмем функцию действительной переменной f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{»}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{»}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно записать в другом виде. Полагая:
x−x0=t,f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
ряд Тейлора
f(x)=f(x0+t)=f(0)+f′(x0)1!t+f′′(x0)2!t2+…+f(n)(x0)n!tn+…=∑k=0∞f(k)(x0)k!tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{»}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
сводится к ряду Маклорена:
g(t)=g(0)+g′(0)1!t+…+g(n)(0)n!tn+…=∑k=0∞g(k)(0)k!tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Как и в случае произвольного степенного ряда, ряды Тейлора и Маклорена имеют интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=1xf(x)=dfrac{1}{x}
в окрестности точки x0=1x_0=1.
С помощью замены:
x−x0=x−1=tx-x_0=x-1=t
функция сводится к виду:
f(x)=f(t+1)=11+tf(x)=f(t+1)=dfrac {1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
11+t=1−t+t2−t3+…+(−1)ntn+…=∑k=0∞(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−1)(x-1):
1x=1−(x−1)+(x−1)2−(x−1)3+…+(−1)n(x−1)n+…=∑k=0∞(−1)k(x−1)k,∣x−1∣<1dfrac {1}{x}=1-(x-1)+ (x-1)^2-(x-1)^3+ldots+(-1)^{n}(x-1)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-1)^{k}, quad |x-1|<1
Формула Тейлора
Следствием разложения функции в степенной ряд является соответствующая формула Тейлора. Если функция f(x)f(x) имеет в точке x0x_0 производные до nn –го порядка включительно, то функцию f(x)f(x) можно представить с помощью формулы Тейлора:
f(x)=f(x0)+f′(x0)1!(x−x0)+…+f(n)(x0)n!(x−x0)n+Rn(x)f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n (x)
или
f(x)=∑k=0nf(k)(x0)k!(x−x0)k+Rn(x)f(x)= sumlimits_{k=0}^{n} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k +R_n (x),
где функция Rn(x)R_n (x) называется остаточным членом.
Формы остаточного члена
Существует несколько форм для остаточного члена. В частности, если f(x)f(x) дифференцируема (n+1)(n+1) раз в окрестности x0x_0, то Rn(x)R_n (x) может быть представлена в форме Лагранжа:
Rn(x)=f(n+1)(ξ)(n+1)!xn+1,x<ξ<x0R_n (x)=dfrac {f^{(n+1)}(xi)}{(n+1)!} x^{n+1}, quad x<xi<x_0 или x<ξ<x0x<xi<x_0.
Если функция f(x)f(x) дифференцируема (n−1)(n-1) раз в окрестности x0=0x_0=0, то Rn(x)R_n(x) может быть представлена в форме Пеано:
Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n).
Учитывая, что ряд Тейлора можно свести к ряду Маклорена, запишем формулу Тейлора для основных элементарных функций в окрестности x0=0x_0=0 и укажем соответствующие интервалы сходимости.
Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+o(xn),∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+o(x^n),quad |x|<infty
Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+o(x2n),∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ o(x^{2n}),quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+o(x2n+1),∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ o(x^{2n+1}),quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+o(x2n+2),∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ o(x^{2n+2}),quad |x|le{1}
Логарифмическая функция:
ln(1+x)=x1!−x22!+x33!−…+(−1)n+1xnn!+o(xn),x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ o(x^n),quad xin (-1;1]
Степенная функция:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+o(xn)(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ o(x^n)
Пример 1
Разложим, используя формулу Тейлора, функцию
f(x)=(x+1)ln(x2+2x+2)f(x)=(x+1)ln (x^2+2x+2)
в окрестности точки x0=−1x_0=-1 с точностью до o((x+1)7)o((x+1)^7).
Выполнив замену переменной
x−x0=x+1=tx-x_0=x+1=t
получаем:
g(t)=tln(1+t2)g(t)=tln(1+t^2)
Используя разложение логарифмической функции, получаем:
g(t)=t(t21!−(t2)22!+(t2)33!+o((t2)3))=t3−t52+t76+o(t7)g(t)=t left( dfrac{t^2}{1!}-dfrac{(t^2)^2}{2!}+dfrac{(t^2)^3}{3!}+o((t^2)^3) right)=t^3-dfrac{t^5}{2}+dfrac{t^7}{6}+o(t^7)
Выполняем далее обратную замену переменной:
f(x)=(x+1)3−(x+1)52+(x+1)76+o((x+1)7)f(x)= (x+1)^3-dfrac{(x+1)^5}{2}+dfrac{(x+1)^7}{6}+o((x+1)^7)
Пример 2
Разложим, используя формулу Тейлора, функцию
f(x)=(x2−4x)cos(2x−4)f(x)=(x^2-4x)cos{(2x-4)}
в окрестности точки x0=2x_0=2 с точностью до o((x−5)5)o((x-5)^5).
Выполнив замену переменной:
x−x0=x−2=t,x=t+2x-x_0=x-2=t, quad x=t+2
получаем:
g(t)=(t2−4)cos2tg(t)=(t^2-4)cos{2t}
Используя разложение тригонометрической функции, получаем:
g(t)=(t2−4)(1−(2t)22!−(2t)44!+o(t5))=(t2−4)(1−2t2+2t43+o(t5))g(t) =(t^2-4) left( 1-dfrac{(2t)^2}{2!}-dfrac{(2t)^4}{4!}+o(t^5) right) =(t^2-4) left( 1-2t^2+dfrac{2t^4}{3}+o(t^5) right)
Раскрываем скобки, ограничиваясь слагаемыми со степенью t не выше пяти:
g(t)=(t2−2t4)−(4−8t2+8t43+o(t5))=−4+9t2−143t4+o(t5)g(t) =(t^2-2t^4)- left( 4-8t^2+dfrac{8t^4}{3}+o(t^5) right) =-4+9t^2-dfrac{14}{3} t^4+o(t^5)
Выполняя обратную замену переменной, получаем:
f(x)=−4+9(x−2)2−143(x−2)4+o((x−2)5)f(x)=-4+9(x-2)^2-dfrac{14}{3}(x-2)^4+o((x-2)^5)
Применение формулы Тейлора при x, стремящемся к бесконечности
При необходимости представить функцию с помощью формулы Тейлора при x→∞x to infty с точностью до o(1xn)oleft( dfrac {1} {x^n}right), последовательно:
- выполняем замену переменной t=1xt=dfrac{1}{x};
- полученную функцию g(t)g(t) представляем с помощью формулы Тейлора с необходимой точностью;
- с помощью обратной замены переменных находим искомое выражение для f(x)f(x).
Пример
Разложим, используя формулу Тейлора, функцию
f(x)=2x−x2−1f(x)=2x-sqrt{x^2-1}
с точностью до o(1×3)oleft( dfrac {1} {x^3}right) при x→+∞x to +infty.
Выполнив замену переменной
t=1x,x=1tt=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=2t−1t2−1=2−(1−t2)1/2tg(t)=dfrac {2}{t}-sqrt {dfrac{1}{t^2}-1}=dfrac{2-(1-t^2)^{1/2}}{t}
Учитывая требуемую точность o(t3)o(t^3), используем разложение степенной функции в ряд Тейлора с точностью до o(t4)o(t^4):
g(t)=2−(1−t22−t48)+o(t4)t=1t+t2−t38+o(t3)g(t)=dfrac {2-left( 1-dfrac{t^2}{2}-dfrac{t^4}{8}right)+o(t^4)}{t}=dfrac{1}{t}+dfrac{t}{2}-dfrac{t^3}{8}+o(t^3)
Выполняя обратную замену переменной, находим:
f(x)=x+12x−18×3+o(1×3),x→+∞f(x)=x+dfrac{1}{2x}- dfrac {1}{8x^3}+ oleft( dfrac {1} {x^3}right), quad x to +infty
Применение формула Тейлора при вычислении пределов
С помощью разложения функции с использованием формулы Тейлора при вычислении пределов можно избавиться от неопределённостями различного вида. Проиллюстрируем использование формулы Тейлора на примере вычисления предела функции с неопределенностью вида (00)left( dfrac {0} {0}right).
Пример 1
Вычислим, используя формулу Тейлора, предел:
limx→1ex−ecos(x−1)sin(x−1)limlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}
Заменим ex{e^{x}} и тригонометрические функции их разложениями в степенные ряды в окрестности x0=1x_0=1, находим:
limx→1ex−ecos(x−1)sin(x−1)=limx→1(e+e(x−1)+e(x−1)22!+e(x−1)33!+…)−e(1−(x−1)22!+…)(x−1)−(x−1)33!+…=elimx→1(x−1)+(x−1)2+(x−1)36+…(x−1)−(x−1)36+…=elimx→11+(x−1)+(x−1)26+…1−(x−1)26+…=elimlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}=limlimits_{x to 1} dfrac {left(e+e(x-1)+dfrac{e(x-1)^2}{2!}+dfrac{e(x-1)^3}{3!} +ldots right)-eleft( 1-dfrac{(x-1)^2}{2!}+ ldots right)} {(x-1)-dfrac{(x-1)^3}{3!}+ ldots}= elimlimits_{x to 1 } dfrac {(x-1)+(x-1)^2+ dfrac{(x-1)^3}{6}+ldots} {(x-1)- dfrac{(x-1)^3}{6}+ldots} =e limlimits_{x to 1 } dfrac {1+(x-1) +dfrac{(x-1)^2}{6}+ldots} {1- dfrac{(x-1)^2}{6}+ldots} =e
Тест по теме «Формула и ряд Тейлора»
При
вычислении пределов широко используются
эквивалентные бесконечно малые. Если
использовать формулу Тейлора, то таблицу
эквивалентных бесконечно малых можно
бесконечно расширить.
Запишем еще раз
формулу Тейлора.
Так
как
то
при
назовем эквивалентностью 1-го порядка.
Аналогично,
так как

то
при
назовем эквивалентностью 2-го порядка.
И
вообще эквивалентность n+1-го
порядка имеет вид:
Используя
формулы Тейлора для элементарных функций
1-10, можно значительно расширить таблицу
эквивалентных бесконечно малых
(эквивалентность п+1-го
порядка). Получим таблицу эквивалентности
(формулы 11- 20 ).
11.
12.
13.
14.
15
16.
17.
18.
19.
20.
Применим эти
формулы для вычисления пределов.
Типовые
примеры
Вычислить пределы.
а)
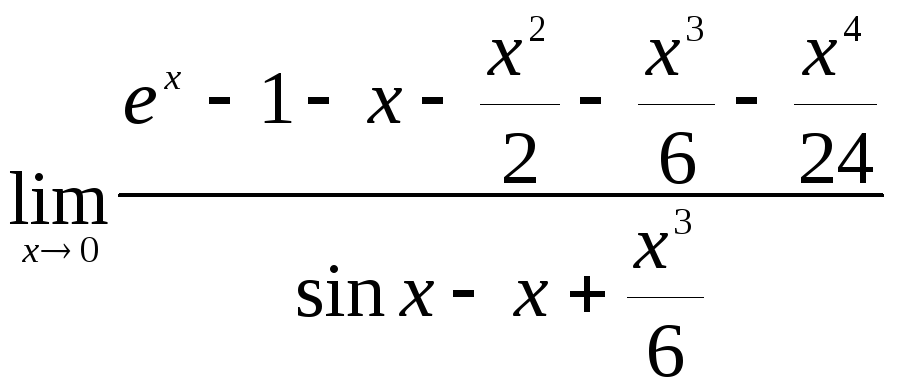
б)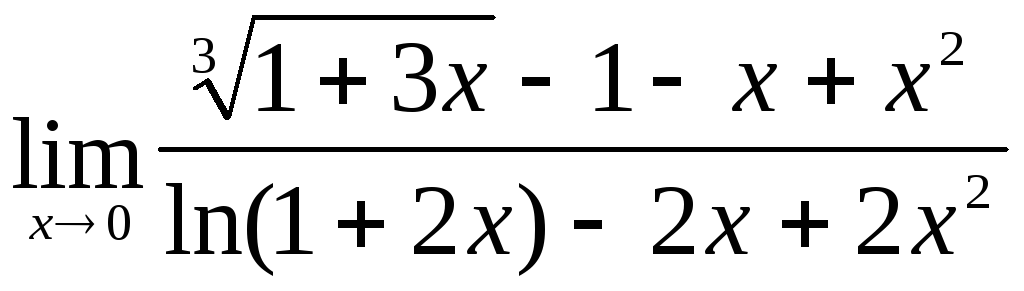
Отметим,
что в обоих случаях мы имеем неопределенность
.
►а)
Здесь применяем формулы 11 и 12.
;
Тогда
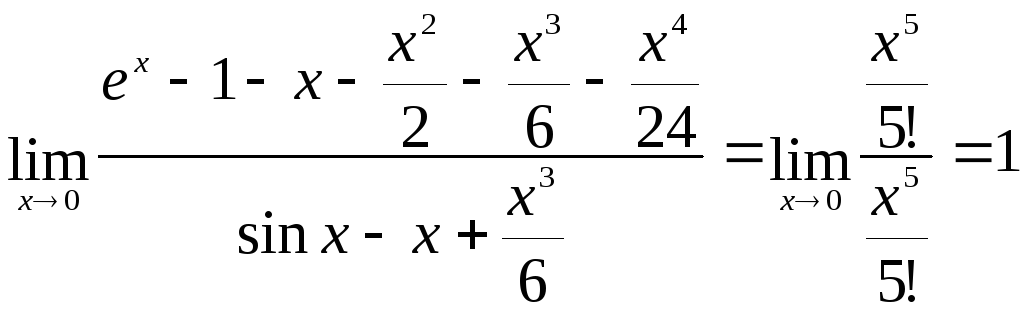
►б)
Так как
,
то
.
Так как,
то
.
Получим
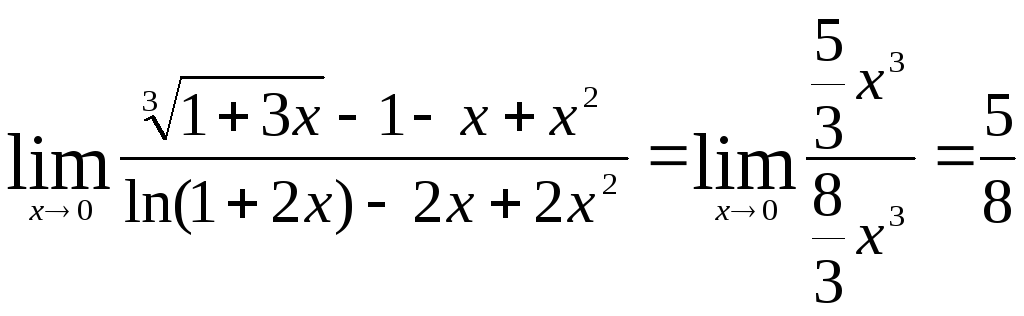
Отметим,
что в рассмотренных примерах эквивалентность
применялась, как и положено, ко всему
числителю и ко всему знаменателю. Если
эквивалентность применять к отдельным
слагаемым в числителе или знаменателе,
то можно допустить ошибку. Так, если в
примере б) в числителе применить формулу
эквивалентности
и в знаменателе применить эквивалентность
,
то получим неверный результат:.
На самом деле, как мы видели выше, предел
этот равен. Применение эквивалентности к отдельным
слагаемым может привести к серьезным
ошибкам. Конечно, надежнее всего применять
эквивалентность к числителю и знаменателю.
Но это, чаще всего, не так просто сделать.
Рассмотренный выше пример был специально
подобран так, чтобы это можно было
сделать легко. Если применение
эквивалентности для всего числителя
(или знаменателя) затруднено, то следует
применять сами формулы Тейлора. Весь
вопрос в этом случае, сколько членов в
формуле Тейлора взять за основу? Например,
формулу 1 можно применить в виде:,
или,
илии т. д.
Надо
помнить основное очень простое правило.
Главным
членом бесконечно малого многочлена,
то есть стремящегося к нулю при
,
является младший член (с наименьшим
показателем степени). Например, приглавным членом многочлена
является член -7х2
.
При
применении формулы Тейлора к отдельным
членам числителя (или знаменателя) надо
выбирать столько членов для каждого
слагаемого, чтобы не потерять главный
член.
Типовой
пример
Найти
главные члены для функций
и
и найти предел
.
►Напишем
формулы Тейлора для sinx
и cosx.
,
.
Так как,
то ясно, что для нахождения главной
части функциидостаточно взять по два члена в разложении
функцийsinx
и cosx,
т.е.
.
Итак, главная часть функции f(x)
при
равна
.
Для функцииимеем:
,
,
,
.
Здесь
главная часть равна
.
Тогда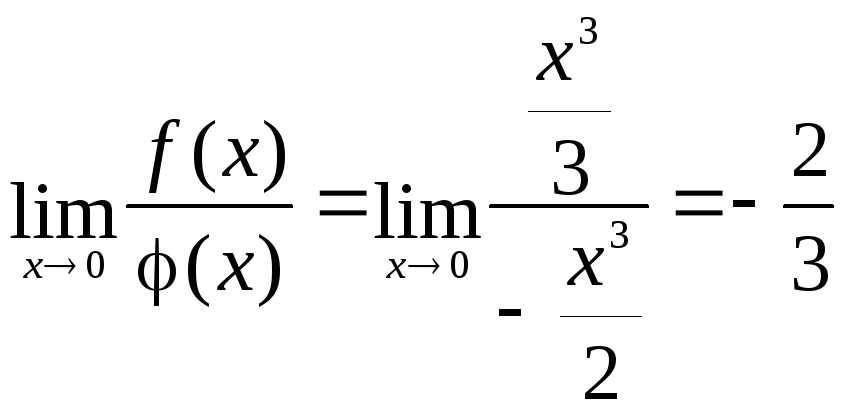
Типовые
примеры.
1)
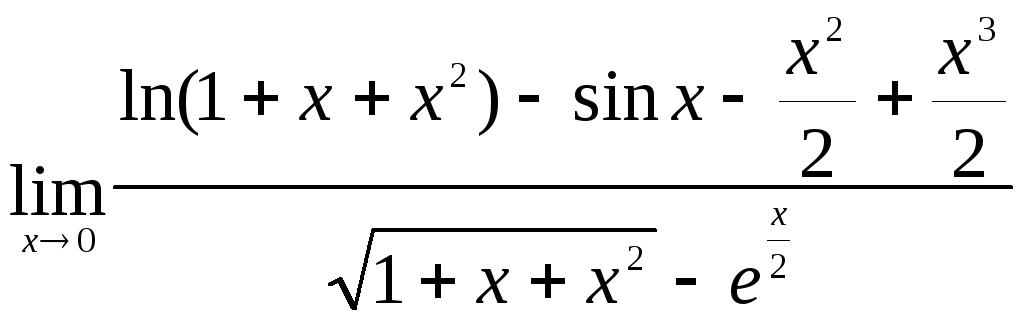
►Имеем
при
:
Числитель примет
вид:
Для знаменателя
имеем:
Окончательно
получим:
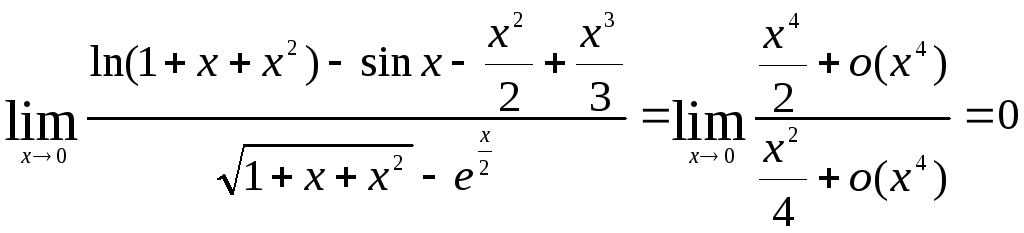
2)
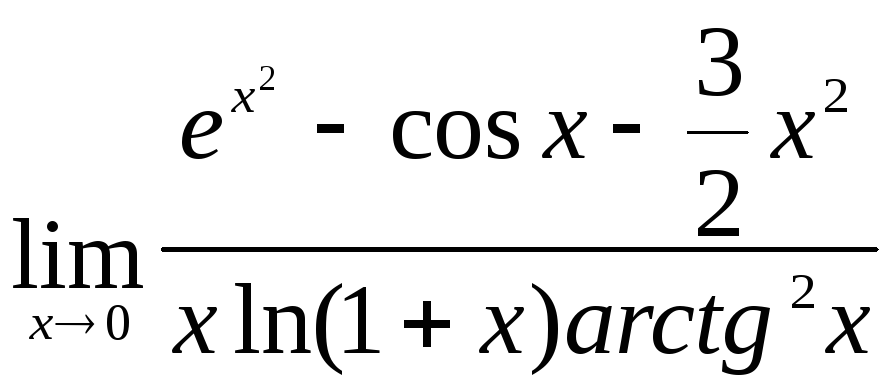
►Здесь,
как впрочем и во всех предыдущих примерах,
имеем неопределенность
.
Так как знаменатель одночлен, то можно
применить эквивалентность 1-го порядка:
Для числителя
имеем:
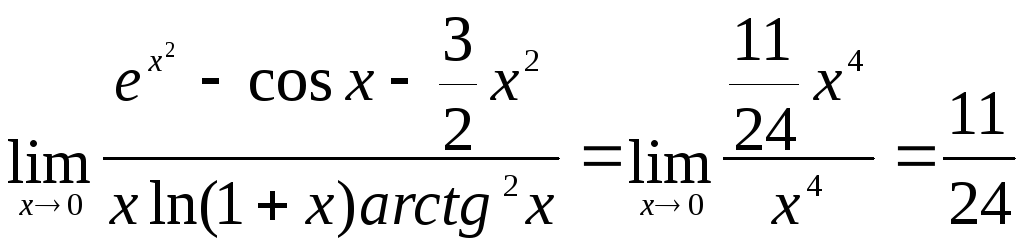
3)
.
►Так
как в знаменателе стоит х5,
то при представлении функций, стоящих
в числителе, по формуле Маклорена, мы
должны брать многочлены не ниже пятой
степени:
;
(следующий
член разложения имеет шестую степень)
,
◄
4)
.
►Здесь
мы в выкладках обязаны удерживать члены
до четвёртой степени:
поэтому
.◄
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формула Тейлора
5 разделов
от теории до практики
12 примеров
Примеры решения задач
видео
Примеры решения задач
-
Формула Тейлора с остаточным членом в форме Лагранжа.
Начать изучение
-
Формула Тейлора с остаточным членом в форме Пеано.
Начать изучение
-
Разложение основных элементарных функций по формуле Тейлора.
Начать изучение
-
Показательная функция.
Начать изучение
-
Гиперболические функции.
Начать изучение
-
Тригонометрические функции.
Начать изучение
-
Степенная функция.
Начать изучение
-
Логарифмическая функция.
Начать изучение
-
Примеры разложения функций по формулам Тейлора и Маклорена.
Начать изучение
-
Вычисление пределов с помощью формулы Тейлора.
Начать изучение
Формула Тейлора с остаточным членом в форме Лагранжа.
Лемма 1.
Если функция f(x) имеет в точке x_{0} производную n-го порядка, то существует многочлен P_{n}(x) степени не выше n такой, что tag{1} P_n(x_0)=f(x_{0}), P_{n}^{(k)}(x_{0})=f^{(k)}(x_{0}), k=overline{1,n}.
Этот многочлен представляется в виде tag{2}P_n(x)=f(x_{0})+frac{f'(x_{0})}{1!}(x-x_0)+frac{f″(x)}{2!}(x-x_0)^2+ldots+frac{f^{(n)}(x_0)}{n!}(x-x_0)^n.
Доказательство.
circ Пусть varphi(x)=(x-x_0)^m, где minmathbb{N}. Тогда varphi(x_0)=0,
tag{3}varphi^{(k)}(x_{0})=left{begin{array}{ll} 0, & если kneq m,\ k!, & если k=m.end{array}right. Из (3) следует, что многочлен P_n(x), заданный формулой (2), удовлетворяет условиям (1). Этот многочлен называют многочленом Тейлора n-го порядка для функции f(x) в точке x_{0}. bullet
Лемма 2.
Пусть функции f(x) и psi(x) определены в delta-окрестности точки x_0 и удовлетворяют следующим условиям:
- для каждого xin U_{delta}(x_0) существуют varphi^{(n+1)}(x) и psi^{(n+1)};
- tag{4}begin{array}{cc}varphi(x_0)=varphi'(x_0)=ldots=varphi^{(n)}(x_0)=0,\ psi(x_0)=psi'(x_0)=ldots=psi^{(n)}(x_0)=0;end{array}
- psi(x)neq 0, psi^{(k)}(x)neq 0 для xindot{U}_{delta}(x_{0}) и для k=overline{1,n+1}.
Тогда для каждого xindot{U}_{delta}(x_{0}) существует точка xi, принадлежащая интервалу с концами x_0 и x такая, что tag{5}frac{varphi(x)}{psi(x)}=frac{varphi^{(n+1)}(xi)}{psi^{(n+1)}(xi)}.
Доказательство.
circ Пусть, например, xin(x_0,x_0+delta). Тогда, применяя к функциям varphi и psi на отрезке [x_0,x] теорему Коши и учитывая, что varphi(x_0)=psi(x_0)=0 в силу условий (4), получаем tag{6}frac{varphi(x)}{psi(x)}=frac{varphi(x)-varphi(x_0)}{psi(x)-psi(x_0)}=frac{varphi'(xi_1)}{psi'(xi_1)}quad x_0 < xi_1 < x.
Аналогично, применяя к функциям varphi’ и psi’ на отрезке [x_{0},xi_{1}] теорему Коши, находим tag{7}frac{varphi'(xi_1)}{psi'(xi_1)}=frac{varphi'(xi_1)-varphi'(x_0)}{psi'(xi_1)-psi'(x_0)}=frac{varphi″(xi_2)}{psi'(xi_2)}quad x_0 < xi_1 < xi_2.
Из равенств (6) и (7) следует, что
frac{varphi(x)}{psi(x)}=frac{varphi'(xi_1)}{psi'(xi_1)}=frac{varphi″(xi_2)}{psi″(xi_2)},quad x_0 < xi_2 < xi_1 < x < x_0+delta.
Применяя теорему Коши последовательно к функциям varphi″ и psi″, varphi^{(3)} и psi^{(3)},ldots,varphi^{(n)} и psi^{(n)} на соответствующих отрезках, получаем
frac{varphi(x)}{psi(x)}=frac{varphi'(xi_1)}{psi'(xi_1)}=ldots=frac{varphi^{(n)}(xi_n)}{psi^{(n)}(xi_n)}=frac{varphi^{(n+1)}(xi)}{psi^{(n+1)}(xi)},
где x_0 < xi < xi_{n} < ldots < xi_{1} < x < x_0+delta.
Равенство (5) доказано для случая, когда xin(x_0,x_0+delta). Аналогично рассматривается случай, когда xin(x_0-delta,x_0). bullet
Теорема 1.
Пусть существует delta >0 такое, что функция f(x) имеет в delta-окрестности точки x_0 производные до (n+1)-го порядка включительно.
Тогда для любого xindot{U}_delta(x_0) найдется точка xi, принадлежащая интервалу Delta с концами x_{0} и x, такая, что
tag{8}f(x)=f(x_0)+frac{f'(x_{0})}{1!}(x-x_0)+ldots+frac{f^{(n)}(x_{0})}{n!}(x-x_0)^n+frac{f^{(n+1)}(xi)}{(n+1)!}(x-x_{0})^{n+1}.
Доказательство.
circ Пусть xindot{U}_delta(x_0), P_n(x)=displaystylesum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_0)^k — многочлен Тейлора для функции f(x). Обозначим
tag{9}r_{n}(x)=f(x)-P_n(x).
Так как многочлен P_{n}(x) удовлетворяет в силу леммы 1 условиям (1), то из равенства (9) следует, что
tag{10}r_n(x_0)=r_n'(x_0)=ldots=r_{n}^{(n)}(x_{0})=0.
Рассмотрим функции varphi(x)=r_n(x), psi(x)=(x-x_0)^{n+1}. Эти функции удовлетворяют условиям леммы 2, и поэтому для них выполняется равенство (5), то есть
tag{11}frac{varphi(x)}{psi(x)}=frac{r_n(x)}{(x-x_0)^{n+1}}=frac{r_n^{(n+1)}(xi)}{(n+1)!}=frac{f^{(n+1)}(xi)}{(n+1)!},quadxiinDelta,
так как P_n^{(n+1)}(x)equiv 0, psi^{(n+1)}(x)=(n+1)! Из равенств (11) и (9) следует формула (8). bullet
Замечание 1.
Функцию r_n(x)=displaystyle frac{f^{(n+1)}(xi)}{(n+1)!}(x-x_0)^{n+1} называют остаточным членом формулы Тейлора в форме Лагранжа. Формула (8) справедлива и при x=x_{0}.
Следствие.
Если функции varphi и psi дифференцируемы n раз при xgeq x_{0} и удовлетворяют условиям varphi^{(k)}(x_{0})=psi^{(k)}(x_{0}), k=overline{0,n-1}, varphi^{(n)}(x)>psi^{(n)}(x) при x > x_0, то varphi(x) > psi(x) при x > x_{0}.
circ Для n=1 утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим f(x)=varphi(x)-psi(x). Тогда f^{(k)}(x_{0})=0 при k=overline{0,n-1}0, и по формуле (8) получаем f(x)=frac{1}{n!}(x-x_{0})^{n}f^{(n)}(xi).
Если x> x_{0}, то xi > x_0, f^{(n)}(xi)=varphi^{(n)}(xi)-psi^{(n)}(xi) > 0, и поэтому f(x) > 0, то есть varphi(x) > psi(x) при x > x_{0}. bullet
Пример 1.
Доказать, что:
- |sin t-t|leqdisplaystylefrac{t^2}{2} для tinmathbb{R};
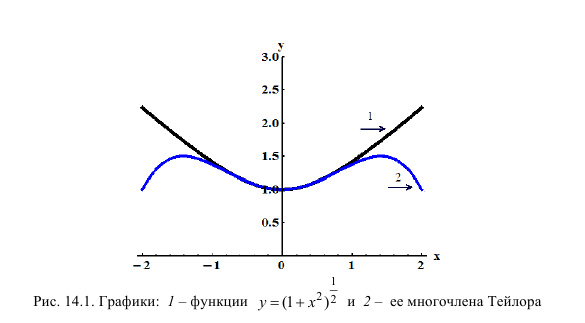
- tag{12}x-frac{x^{3}}{3!} < sin x < x-frac{x^{3}}{3!}+frac{x^5}{5!} при x > 0.
Решение.
- triangle Применяя формулу (8) при n=2 и x_0=0 к функции f(t)=sin t, получаем sin t=t-displaystylefrac{sin{xi}}{2!}t^2, откуда следует, что |displaystyle sin t-t|leqfrac{t^{2}}{2},;tinmathbb{R}.
- Если f(x)=sin x, то f(0)=f^{(2)}(0)=f^{(4)}(0)=0, f'(0)=1, f^{(3)}(0)=-1, f^{(n)}(x)=(sin x)^{(n)}=displaystylesinleft(x+nfrac{pi}{2}right). Применяя формулу (8) при n=5, x_0=0, получаем sin x=x-frac{x^{3}}{3!}+frac{x^{5}}{5!}sin(xi+5frac{pi}{2}),откуда следует правое неравенство (12), так как, очевидно, left|displaystylefrac{x^{5}}{5!}sinleft(xi+5frac{pi}{2}right)right|leqdisplaystylefrac{x^{5}}{5!} при x >0. Используя формулу (8) для f(x)=sin x при n=3, x_0=0, докажем левое неравенство (12). blacktriangle
Формула Тейлора с остаточным членом в форме Пеано.
Теорема 2.
Если существует f^{(n)}(x_0), то tag{13}f(x)=sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k}+o((x-x_{0})^{n}),qquad xrightarrow x_{0}.
Доказательство.
Из существования f^{(n)}(x_0) следует, что функция f(x) определена и имеет производные до (n-1)-го порядка включительно в delta-окрестности точки x_0. Обозначим varphi(x)=r_n(x), psi(x)=(x-x_0)^n, где функция r_n(x) определяется формулой (9). Функции varphi(x) и psi(x) удовлетворяют условиям леммы 2, если заменить номер n+1 на номер n-1 (см. равенства (10)). Используя лемму 2 и учитывая, что r_n^{(n-1)}(x_0)=0, получаем tag{14}frac{r_n(x)}{(x-x_0)^n}=frac{r_n^{(n-1)}(xi)-r_n^{n-1}(x_0)}{n!(xi-x_{0})}, где xi=xi(x) и tag{15}x_0 < xi < x < x_0+delta quad или quad x_0-delta < x < xi < x_0.
Пусть xrightarrow x_0, тогда из неравенств (15) следует, что xirightarrow
x_0, и в силу существования f^{(n)}(x_0) существует displaystylelim_{xrightarrow x_{0}}frac{r_n^{(n-1)}(x)-r_n^{(n-1)}(x_0)}{x-x_0}=displaystyle lim_{xrightarrow x_{0}}frac{r_n^{(n-1)}(xi)-r_n^{(n-1)}(x_0)}{xi-x_0}=r_n^{(n)}(x_0)=0, так как выполняются равенства (10). Таким образом, правая часть формулы (14) имеет при xrightarrow x_0 предел, равный нулю, а поэтому существует предел левой части этой формулы, также равный нулю. Это означает, что r_n(x)=o((x-x_0)^n), xrightarrow x_0, или f(x)-P_n(x)=o((x-x_0)^n), откуда следует равенство (13). bullet
Замечание 2.
Формулу (13) часто называют формулой Тейлора с остаточным членом в форме Пеано или
локальной формулой Тейлора.
Разложить функцию f(x) по формуле Тейлора в окрестности точки x_0 до o((x-x_0)^n) — значит представить ее в виде (13).
Теорема 3.
Если существует f^{(n)}(x_0) и если при xrightarrow x_0 tag{16}f(x)=a_0+a_1(x-x_0)+ldots+a_n(x-x_0)^n+o((x-x_0)^n), то tag{17}a_{k}=frac{f^{(k)}(x_0)}{k!},;k=overline{0,n}.
Доказательство.
circ По теореме 2 справедлива формула (13), и так как по условию выполняется равенство (16), то
tag{18}a_0+a_1(x-x_0)+ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\=f(x_{0})+f'(x_{0})(x-x_0)+ldots+f^{(n)}(x_{0})frac{(x-x_{0})^{n}}{n!}+o((x-x_0)^n).
Переходя к пределу при xrightarrow x_{0} в равенстве (18), получаем a_{0}=f(x_{0}). Отбросив в левой и правой частях этого равенства одинаковые слагаемые a_{0} и f(x_{0}) и разделив обе части полученного равенства на x-x_0, имеем a_1+a_2(x-x_0)+ldots+a_n(x-x_0)^{n-1}+o((x-x_0)^{n-1})=\=f'(x_0)+frac{f″(x_{0})}{2!}(x-x_0)+ldots+frac{f^{(n)}(x_{0})}{n!}(x-x_0)^{n-1}+o((x-x_0)^{n-1}).
Переходя в этом равенстве к пределу при xrightarrow x_0, находим f'(x_{0})=a_{1}. Продолжая эти рассуждения, получаем равенства (17).bullet
Замечание 3.
Теорема 3 означает, что представление в виде (16) функции, имеющей в точке x_{0} производную n-го порядка, единственно: коэффициенты разложения (16) выражаются по формулам (17).
Пример 2.
Разложить функцию displaystyle frac{1}{1-x} по формуле Тейлора в окрестности точки x_{0}=0 до o(x^{n}).
Решение.
triangle Воспользуемся равенством (1+x+ldots+x^{n})(1-x)=1-x^{n+1}, откуда displaystyle frac{1}{1-x}=1+x+ldots+x^n+r_n(x), где r_n(x)=displaystylefrac{x^{n+1}}{1-x}=o(x^{n}) при xrightarrow 0. Таким образом,
tag{19}frac{1}{1-x}=1+x+ldots+x^n+o(x^n).
Так как функция displaystyle frac{1}{1-x} бесконечно дифференцируема при xneq 1 (имеет производные любого порядка), то по теореме 3 формула (19) дает искомое разложение. blacktriangle
Разложение основных элементарных функций по формуле Тейлора.
Если x_{0}=0 и существует f^{(n)}(0), то равенство (13) принимает вид
tag{20}f(x)=sum_{k=0}^{n}frac{f^{(k)}}{k!}x^k+o(x^n), xrightarrow 0.
Формулу (20) называют формулой Маклорена.
Замечание 4.
Пусть, функция f(x) бесконечно дифференцируема на интервале (-l,l). Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции f выполняются условия f^{(2k)}(0)=0, kinmathbb{N}, а для четной функции f — условия f^{(2k-1)}(0)=0, kinmathbb{N}, так как любая непрерывная нечетная функция принимает при x=0 значение нуль.
Поэтому формулу (20) для бесконечно дифференцируемой четной функции можно записать в виде tag{21}f(x)=sum_{k=0}^{n}frac{f^{(2k)}(0)}{(2k)!}x^{2k}+o(x^{2n+2}),quad xrightarrow 0, а для нечетной функции — в виде tag{22}f(x)=sum_{k=0}^{n}frac{f^{(2k+1)}(0)}{(2k+1)!}x^{2k+1}+o(x^{2n+2}),quad xrightarrow 0.
В формуле (21) остаточный член записан в виде o(x^{(2n+1)}), а не в виде o(x^{2n}), так как для четной функции f выполняется условие f^{(2n+1)}(0)=0, и поэтому член многочлена Тейлора, который следует за слагаемым displaystylefrac{f^{(2n)}(0)}{(2n)!}x^{2n} равен нулю. Аналогично рассматривается вопрос о записи остаточного члена формулы (22).
Показательная функция.
Если f(x)=e^x, то f(0)=1 и f^{(n)}(0)=1 при любом n. Поэтому формула (20) для функции e^{x} записывается в виде
tag{23}e^{x}=1+x+frac{x^{2}}{2!}+frac{x^{3}}{3!}+ldots+frac{x^{n}}{n!}+o(x^{n}), xrightarrow 0, или e^{x}=sum_{k=0}^{n}frac{x^{k}}{k!}+o(x^{n}), xrightarrow 0.
Гиперболические функции.
Так как f(x)=sh x — нечетная функция, f^{(2k+1)}(x)=ch x, f^{(2k+1)}(0)=1 при k=0,1,2,ldots, то по формуле (22) получаем
tag{24}sh x=x+frac{x^{3}}{3!}+frac{x^5}{5!}+ldots+frac{x^{2n+1}}{(2n+1)!}+o(x^{2n+2}), xrightarrow 0, или sh x=sum_{k=0}^{n}frac{x^{2k+1}}{(2k+1)!}+o(x^{2n+2}), xrightarrow 0.
Аналогично по формуле (21) находим tag{25}ch x=1+frac{x^{2}}{2!}+frac{x^{4}}{4!}+ldots+frac{x^{2n}}{(2n)!}+o(x^{2n+1}), xrightarrow 0,
или ch x=sum_{k=0}^{n}frac{x^{2k}}{(2k)!}+o(x^{2n+1}), xrightarrow 0.
Замечание 5.
Так как sh x=displaystyle frac{e^{x}-e^{-x}}{2}, ch x=displaystyle frac{e^{x}+e^{-x}}{2}, то формулы (24) и (25) можно получить, используя равенство (23) и равенство e^{-x}=displaystylesum_{k=0}^{n}frac{(-1)^{k}x^{k}}{k!}+o(x^{n}), xrightarrow 0.
Тригонометрические функции.
Функция f(x)=sin x является нечетной, f^{(2n+1)}(x)=sin left(x+displaystyle frac{pi}{2}(2n+1)right), откуда f^{(2n+1)}(0)=sinleft(frac{pi}{2}+pi nright)=cospi n= (-1)^n.
Поэтому по формуле (22) находим tag{26} sin x=x-frac{x^{3}}{3!}+frac{x^{5}}{5!}+ldots+(-1)^nfrac{x^{2n+1}}{(2n+1)!}+o(x^{2n+2}), xrightarrow 0,
или
sin x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k+1}}{(2k+1)!}+o(x^{2n+2}),;xrightarrow 0.
Аналогично, f(x)=cos x — четная функция, f^{(2n)}(0)=displaystylecosleft(frac{pi}{2}2nright)=(-1)^{n}, и по формуле (21) получаем tag{27}cos x=1-frac{x^{2}}{2!}+frac{x^{4}}{4!}+ldots+(-1)^nfrac{x^{2n}}{(2n)!}+o(x^{2n+1}),;xrightarrow 0, или cos x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k}}{(2k)!}+o(x^{2n+1}), xrightarrow 0.
Степенная функция.
Пусть f(x)=(1+x)^{alpha}, где alphainmathbb{R}. Тогда f^{(k)}(x)=alpha(alpha-1)ldots(alpha-(k-1))(1+x)^{alpha-k}, откуда получаем f^{(k)}(0)=alpha(alpha-1)ldots(alpha-(k-1)). Обозначим tag{28} C_{alpha}^0=1, C_{alpha}^k=frac{alpha(alpha-1)ldots(alpha-(k-1))}{k!}, kinmathbb{N}
Тогда по формуле (20) получим tag{29}(1+x)^{alpha}=sum_{k=0}^{n}C_{alpha}^{k}x^k+o(x^n), xrightarrow 0.
Отметим важные частные случаи формулы (29).
tag{30}frac{1}{1-x}=1+x+x^2+ldots+x^n+o(x^n), xrightarrow 0,
или frac{1}{1-x}=sum_{k=0}^{n}x^k+o(x^n), xrightarrow 0.
Напомним, что формула (30) была получена другим способом (пример 2).
tag{31}frac{1}{1+x}=1-x+x^{2}+ldots+(-1)^{n}x^n+o(x^n), xrightarrow 0,
или frac{1}{1+x}=sum_{k=0}^{n}(-1)^{k}x^k+o(x^n), xrightarrow 0.
Логарифмическая функция.
Если f(x)=ln (1+x), то f(0)=0,
f^{(k)}(x)=frac{(-1)^{k-1}(k-1)!}{(1+x)^{k}}, f^{(k)}(0)=(-1)^{k-1}(k-1)!,
и по формуле (20) находим tag{32}ln (1+x)=x-frac{x^{2}}{2}+frac{x^{3}}{3}+ldots+frac{(-1)^{n-1}}{n}x^{n}+o(x^{n}), xrightarrow 0,
или ln(1+x)=sum_{k=1}^nfrac{(-1)^{k-1}x^{k}}{k}+o(x^n), xrightarrow 0.
Заменяя в формуле (32) x на -x получаем tag{33}ln (1-x)=-x-frac{x^{2}}{2}-frac{x^{3}}{3}-ldots-frac{x^{n}}{n}+o(x^n), xrightarrow 0,
или ln (1-x)=-sum_{k=1}^nfrac{x^{k}}{k}+o(x^n), xrightarrow 0.
Примеры разложения функций по формулам Тейлора и Маклорена.
Пример 3.
Разложить по формуле Тейлора в окрестности точки x_0=0 до o(x^n) функцию f(x), если:
- f(x)=displaystyle frac{1}{sqrt{1+x}};
- f(x)=displaystyle frac{1}{3x+2};
- f(x)=displaystyle lnfrac{x-5}{x-4};
- f(x)=(x+3)e^{-2x}.
Решение.
- triangle Применяя формулу (29) при alpha=-displaystylefrac{1}{2}, получаем frac{1}{sqrt{1+x}}=sum_{k=0}^{n}C_{-1/2}^{k}x^k+o(x^n), xrightarrow 0,
где C_{-1/2}^{k}=frac{displaystyleleft(-frac{1}{2}right)left(-frac{1}{2}-1right)ldotsleft(-frac{1}{2}-(k-1)right)}{k!}=frac{(-1)^{k}1cdot 3ldots(2k-1)}{2^{k}k!}.Обозначим (2k-1)!!=1cdot 3ldots(2k-1), тогда tag{34}frac{1}{sqrt{1+x}}=1+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!}x^k+o(x^n), xrightarrow 0.
Из формулы (34) при n=3 находим tag{35}frac{1}{sqrt{1+x}}=1-frac{1}{2}x+frac{3}{8}x^2-frac{5}{16}x^3+o(x^3), xrightarrow 0. - Так как displaystylefrac{1}{3x+2}=frac{1}{2left(1+displaystylefrac{3}{2}xright)}, то, применяя формулу (31), получаем frac{1}{3x+2}=sum_{k=0}^{n}(-1)^{k}frac{3^{k}}{2^{k+1}}x^{k}+o(x^{n}), xrightarrow 0.
- Используя равенство displaystyleoperatorname{ln}frac{x-5}{x-4}=displaystyleoperatorname{ln}frac{5}{4}+operatorname{ln}frac{1-displaystylefrac{x}{5}}{1-displaystylefrac{x}{4}} и формулу (33), находим ln frac{x-5}{x-4}=lnfrac{5}{4}+sum_{k=1}^{n}frac{x^{k}}{k}left(frac{1}{4^{k}}-frac{1}{5^{k}}right)+o(x^{n}),;xrightarrow 0.
- Так как f(x)=xe^{-2x}+3e^{-2x}, то, применяя формулу (23), получаем f(x)=xleft(displaystylesum_{k=0}^{n-1}frac{(-1)^{k}2^{k}}{k!}x^{k}+o(x^{n-1})right)+3sum_{k=0}^{n}frac{(-1)^{k}2^{k}}{k!}x^{k}+o(x^{n}), x rightarrow 0,
или
f(x)=3+sum_{k=1}^{n}frac{(-1)^{k-1}2^{k-1}}{(k-1)!}x^k+sum_{k=1}^{n}frac{3(-1)^{k}2^{k}}{k!}x^k+o(x^n), xrightarrow 0,
то есть
f(x)=3+sum_{k=1}^{n}frac{(-1)^{k-1}2^{k-1}}{k!}(k-6)x^{k}+o(x^{n}), xrightarrow 0.quadblacktriangle
Пример 4.
Разложить по формуле Маклорена до o(x^{2n+1}) функцию f(x)=cos^{4}x.
Решение.
triangle Используя равенство cos^{2}x=displaystyle frac{1+cos 2x}{2}, получаем cos^{4}x=frac{1}{4}left(1+2cos{2x}+displaystyle frac{1+cos 4x}{2}right)=frac{3}{8}+frac{1}{2}cos{2x}+ displaystylefrac{1}{8}cos4x, откуда по формуле (27) находим
cos^{4}x=1+sum_{k=1}^{n}frac{(-1)^{k}2^{2k-1}}{(2k)!}(1+2^{2k-2})x^{2k}+o(x^{2n+1}), xrightarrow 0. blacktriangle
Замечание 6.
Если существует f^{(n+1)})(0) и известно разложение функции f'(x)=sum_{k=0}^{n}b_kx^k+o(x^n),
где b_k=displaystylefrac{f^{(k+1)(0)}}{k!}, то f(x)=f(0)+sum_{k=1}^{n+1}frac{f^{(k)}(0)}{k!}x^k+o(x^{n+1})=f(0)+sum_{k=0}^{n}frac{f^{(k+1)}(0)}{(k+1)k!}x^{k+1}+o(x^{n+1}), xrightarrow 0, то есть f(x)=f(0)+sum_{k=0}^{n}frac{b_{k}}{k+1}x^{k+1}+o(x^{n+1}), xrightarrow 0.
Пример 5.
Разложить по формуле Маклорена до o(x^{2n+1}) функции:
- operatorname{arctg}x;
- operatorname{arcsin}x;
- ln (1+sqrt{1+x^2}).
Решение.
- triangle Так как (operatorname{arctg}x)’=frac{1}{1+x^2}, то, используя формулу (31) и замечание 6, получаем frac{1}{1+x^{2}}=sum_{k=0}^{n}(-1)^k{x^{2k}}+o(x^{2n+1}), xrightarrow 0,
откуда
tag{36}operatorname{arctg}x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k+1}}{2k+1}+o(x^{2n+2}), xrightarrow 0.
Из формулы (36) при n=2 находим
tag{37}operatorname{arctg}x=x-frac{x^3}{3}+frac{x^5}{5}+o(x^6).;xrightarrow 0. - Используя замечание 6, равенство (34) и формулу (operatorname{arcsin}x)’=displaystyle frac{1}{sqrt{1-x^{2}}}, получаем frac{1}{sqrt{1-x^{2}}}=1+sum_{k=1}^{n}displaystylefrac{(2k-1)!!}{2^{k}k!}x^{2k}+o(x^{2n+1}), xrightarrow 0,
откуда tag{38}operatorname{arcsin}x=x+sum_{k=1}^{n}displaystylefrac{(2k-1)!!}{2^{k}k!(2k+1)}x^{2k+1}+o(x^{2n+2}), xrightarrow 0.
Из формулы (38) при n=2 находим
tag{39}operatorname{arcsin}x=x+frac{1}{6}x^{3}+frac{3}{40}x^5+o(x^6), xrightarrow 0. - Так как (ln (1+sqrt{1+x^2}))’=frac{1}{sqrt{1+x^{2}}}, то, используя замечание 6 и разложение (34), получаем frac{1}{sqrt{1+x^{2}}}=1+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!}x^{2k}+o(x^{2n+1}), xrightarrow 0,
откуда tag{40}ln (1+sqrt{1+x^2})=x+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!(2k+1)}x^{2k+1}+o(x^{2n+2}), xrightarrow 0.Из формулы (40) при n=2 находим
tag{41}ln (1+sqrt{1+x^2})=x-frac{x^{3}}{6}+frac{3}{40}x^5+o(x^6), xrightarrow 0. blacktriangle
Пример 6.
Разложить по формуле Маклорена до o(x^6) функции:
- operatorname{tg}x;
- operatorname{th}x.
Решение.
- triangle Функция operatorname{tg}x является нечетной, и поэтому operatorname{tg}x=a_1x+a_3x^3+a_5x^5+o(x^6), xrightarrow 0, где a_1=1, так как operatorname{tg}xsim x при xrightarrow 0. Используя равенство sin x=cos xoperatorname{tg}x и разложения (26), (27), получаем
x-frac{x^3}{3!}+frac{x^5}{5!}+o(x^6)=(x+a_3x^3+a_5x^5+o(x^6))left(1-displaystylefrac{x^{2}}{2!}+frac{x^{4}}{4!}+o(x^5)right).
Приравнивая коэффициенты при x^3 и x^5, находим -displaystylefrac{1}{6}=-frac{1}{2}+a_{3}, displaystylefrac{1}{5!}=frac{1}{4!}-frac{a_{3}}{2!}+a_{5}, откуда a_3=displaystylefrac{1}{3}, a_{5}=displaystyle frac{2}{15}, и поэтому tag{42}operatorname{tg}x=x+displaystyle frac{x^{3}}{3}+displaystyle frac{2}{15}x^5+o(x^6), xrightarrow 0. - Так как operatorname{th}x — нечетная функция, то operatorname{th}x=a_1x+a_3x^3+a_5x^5+o(x^6), где a_{1}=1 (operatorname{th}xsim x при xrightarrow x). Применяя формулу sh x=ch xth x и используя разложения (24), (25), получаем x+frac{x^{3}}{3!}+frac{x^5}{5!}+o(x^{6})=(x+a_{3}x^{3}+a_{5}x^{5}+o(x^{6}))left(1+frac{x^{2}}{2!}+frac{x^{4}}{4!}+o(x^{5})right),
откуда, сравнивая коэффициенты при x^3 и x^5, находим a_{3}=-displaystyle frac{1}{3},;a_{5}=displaystyle frac{2}{15}. Следовательно,
tag{43}operatorname{th}x=x-frac{x^{3}}{3}+frac{2}{15}x^{5}+o(x^{6}). blacktriangle
Замечание 7.
Прием, использованный для нахождения разложений (42) и (43), называют методом неопределенных коэффициентов.
Замечание 8.
Разложение функции f(x) по формуле Тейлора (16) заменой x-x_{0}=t обычно сводится к разложению функции g(t)=f(x_0+t) по формуле Маклорена (20).
Пример 7.
Разложить по формуле Тейлора в окрестности точки x_0=-2 до o((x+2)^{n}) функцию f(x)=displaystyle frac{1}{x^{2}+5x}.
Решение.
triangle Так как f(x)=displaystylefrac{1}{5}left(frac{1}{x}-frac{1}{x+5}right), то, полагая x=t-2, получаем f(x)=g(t)=displaystylefrac{1}{5}left(frac{1}{t-2}-frac{1}{t+3}right)=frac{1}{5}left(-frac{1}{2left(1-frac{t}{2}right)}-frac{1}{3left(1+frac{t}{3}right)}right).
Применяя формулы (30) и (31), находим
g(t)=sum_{k=0}^{n}left(frac{(-1)^{k+1}}{5cdot 3^{k+1}}-frac{1}{5cdot 2^{k+1}}right)t^{k}+o(t^{n}), trightarrow 0, откуда f(x)=sum_{k=0}^{n}left(frac{(-1)^{k+1}}{5cdot 3^{k+1}}-frac{1}{5cdot 2^{k+1}}right)(x+2)^{k}+o((x+2)^n), xrightarrow-2.quadblacktriangle
Вычисление пределов с помощью формулы Тейлора.
Рассмотрим предел при xrightarrow 0 отношения displaystyle frac{f(x)}{g(x)}, где katex]f(0)=g(0)=0[/katex], то есть предел типа frac{0}{0}.
Будем предполагать, что f(0)=f'(0)=ldots=f^{(n-1)}(0)=0, f^{(n)}(0)neq 0.
Тогда разложение функции f по формуле Маклорена (20) имеет вид tag{44}f(x)=ax^n+o(x^n), xrightarrow 0, где aneq 0.
Аналогично, предполагая, что
g(0)=g'(0)=ldots=g^{(m-1)}(0)=0, g^{(m)}(0)neq 0.
по формуле (20) находим
tag{45}g(x)=bx^m+o(x^m), xrightarrow 0, где bneq 0.
Из равенств (44) и (45) следует, что
frac{f(x)}{g(x)}=frac{ax^n+o(x^n)}{bx^m+o(x^m)}, xrightarrow 0.
Если m=n, то displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=displaystylefrac{a}{b}. В случае, когда n > m, получаем displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=0; если же n < m, то displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=infty.
Пример 8.
Найти displaystyle lim_{xrightarrow 0}frac{operatorname{tg}x-displaystylefrac{x}{1+x^2}}{sin x-sh x}.
Решение.
triangle Используя формулы (24), (26), (31) и (42),
получаем operatorname{tg}x-frac{x}{1+x^{2}}=x+frac{x^{3}}{3}-x(1-x^2)+o(x^3)=frac{4}{3}x^3+o(x^3),
sin x-operatorname{sh}x=x-frac{x^{3}}{6}-left(x+frac{x^{3}}{6}right)+o(x^{3})=-frac{x^{3}}{3}+o(x^{3}).
Следовательно, искомый предел равен -4. blacktriangle
Пример 9.
Найти displaystyle lim_{xrightarrow 0}frac{e(1+x)^{-1/x}-1}{x}.
Решение.
triangle Воспользуемся равенством (1+x)^{-1}/{x}=e^{-(1/x)operatorname{ln}(1+x)}. По формуле (32) получаем -displaystyle frac{1}{x}operatorname{ln}(1+x)=-1+displaystyle frac{x}{2}+o(x). Используя формулу (23), находим e(1+x)^{-1/x}-1=ecdot e^{-1+x/2+o(x)}-1=е^{x/2+o(x)}-1=frac{x}{2}+o(x).
Поэтому искомый предел равен displaystyle frac{1}{2}. blacktriangle
Пример 10.
Найти
lim_{xrightarrow 0}frac{ln(x+sqrt{1+x^{2}})+displaystylefrac{1}{sqrt{1+2x}}-ch(sqrt{3}x)}{th x-xcos x}.
Решение.
triangle Пусть f(x) и g(x) — соответственно числитель и знаменатель дроби. Тогда, используя формулы (43) и (27), получаем
g(x)=x-frac{x^{3}}{3}+o(x^4)-xleft(1-frac{x^{2}}{2}+o(x^3)right)=frac{x^{3}}{6}+o(x^4).
Поэтому числитель f(x) следует разложить до o(x^3). Применяя формулы (41), (35) и (25), находим
f(x)=x-frac{x^{3}}{6}+o(x^3)+left(1-x+frac{3}{2}x^2-frac{5}{2}x^3+o(x^3)right)-\-left(1+frac{3}{2}x^2+o(x^3)right)=-frac{16}{6}x^3+o(x^3).
Следовательно, искомый предел равен -16. blacktriangle
Локальная формула Тейлора часто используется при вычислении предела при xrightarrow x_0 функции (1+f(x))^{g(x)}, где f(x)rightarrow 0 и g(x)rightarrow infty при xrightarrow x_0. Если x_0=0 и разложение функции f по формуле Маклорена имеет вид (44), а функция g(x) представляется при xrightarrow 0 в виде g(x)=frac{1}{bx^n+o(x^n)},;где;bneq 0, ninmathbb{N},
то, используя формулу 16 (см.здесь), получаем
tag{46}lim_{xrightarrow 0}(1+f(x))^{g(x)}=lim_{xrightarrow 0}left(1+ax^n+o(x^n)right)^{1/(bx^n+o(x^n))}=e^{a/b}.
Пример 11.
Найти displaystyle lim_{xrightarrow 0}(e^{operatorname{tg}x}+operatorname{ln}(1-x))^{1/(arcsin{operatorname{sh}x}-x)}.
Решение.
triangle Используя формулы (39) и (24), получаем
arcsinoperatorname{sh}x-x=arcsinleft(x+frac{x^{3}}{6}+o(x^{4})right)-x=\=x+frac{x^{3}}{6}+frac{x^{3}}{6}+o(x^3)-x=frac{x^{3}}{3}+o(x^3).
Аналогично, разложив функции e^x,;operatorname{tg}x,operatorname{ln}(1-x) по формуле Маклорена до o(x^3), находим
e^{operatorname{tg}x}+operatorname{ln}(1-x)=e^{x+x^{3}/3+o(x^4)}-x-frac{x^{2}}{2}-frac{x^{3}}{3}+o(x^3)=\=1+x+frac{x^{3}}{3}+frac{x^{2}}{2}+frac{x^{3}}{6}+o(x^{3})-x-frac{x^{2}}{2}-frac{x^{3}}{3}+o(x^{3})=1+frac{x^{3}}{6}+o(x^3).
По формуле (46) находим, что искомый предел равен e^{1/2}. blacktriangle
При вычислении предела с помощью формулы Тейлора в конечной точке x_0neq 0 можем положить t=x-x_0 и свести задачу к вычислению предела при t=0.
Неопределенности видов displaystylefrac{infty}{infty}, 0cdotinfty, infty-infty обычно приводят к пределу типа displaystyle frac{0}{0}.
Пример 12.
Найти displaystyle lim_{xrightarrow +infty}x(sqrt{x^2+2x}-2sqrt{x^2+x}+x).
Решение.
triangle Обозначим f(x)=x(sqrt{x^{2}+2x}-2sqrt{x^{2}+x}+x), тогда f(x)=x^2left(displaystylesqrt{1+frac{2}{x}}-2sqrt{1+frac{1}{x}}+1right). Полагая displaystyle frac{1}{x}=t, получаем f(x)=g(t)=displaystylefrac{1}{t^{2}}(sqrt{1+2t}-2sqrt{1+t}+1). Используя формулу (29) при alpha=displaystyle frac{1}{2}, n=2, получаем
sqrt{1+t}=1+frac{1}{2}t-frac{1}{8}t^2+o(t^2),quad trightarrow 0.
Следовательно,
g(t)=frac{1}{t^{2}}left(1+t-frac{1}{2}t^{2}-2left(1+frac{1}{2}t-frac{1}{8}t^{2}right)+o(t^{2})+1right)=\=frac{1}{t^{2}}left(-frac{1}{4}t^{2}+o(t^{2})right),;trightarrow 0,
откуда находим, что искомый предел равен -displaystyle frac{1}{4}. blacktriangle
Содержание:
Формула Тейлора и ее применение
Формула Тейлора
Теорема: Если функция
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора 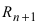
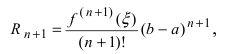
В этой формуле неизвестной является только величина 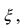
При a = 0 формула Тейлора переходит в формулу Маклoрена:
Пример:
Представить по формуле Маклорена функцию 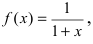
Решение:
Вычислим три первых производных заданной функции:
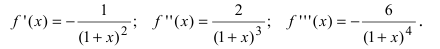
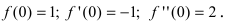
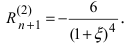
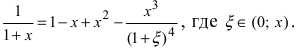
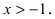
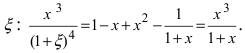
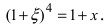
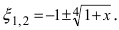
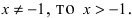
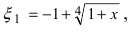
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:
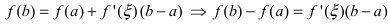
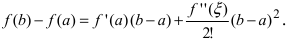
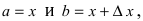
Применение формулы Тейлора
Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 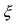
Пример:
Представить функцию 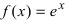
Решение:
Так как 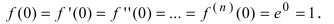
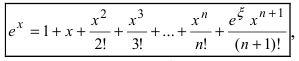
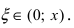
Пример:
Вычислить 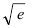
Решение:
Так как основание 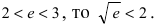
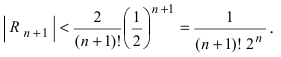
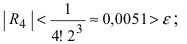
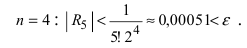
Пример:
Вычислить число е с точностью
Решение:
Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа
При n = 6 имеем
при n = 7 получаем
Итак,
Если вычислять значение числа е с точностью 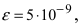
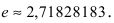
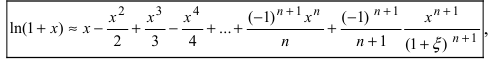
Пример:
Вычислить 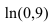
Решение:
В данном примере х = -0,1. Так как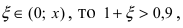
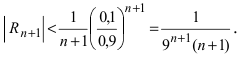
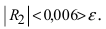
Формула тейлора
Пусть функция y=f(x) дифференцируема в точке 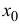
Пусть 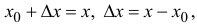
Рассмотрим многочлен
Многочлен 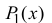
Пусть функция y=f(x) n раз дифференцируема в точке 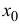
обладающий аналогичными свойствами:
Из (14.2), (14.3) следует, что
Поэтому коэффициенты 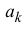
Далее
Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 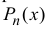
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке 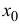
где 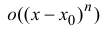
малости, чем
Формула (14.5) называется формулой Тейлора, многочлен
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности 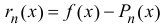
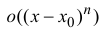
Если функция 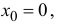
формула Маклорена.
Если функция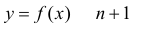
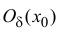
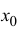
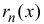
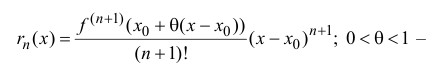
называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.
Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа:
Поэтому
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.
- Заказать решение задач по высшей математике
Пример 14.3
Разложить 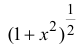
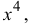
Решение
Пусть 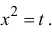
Остаточный член запишем в форме Лагранжа:
поэтому
Таким образом, 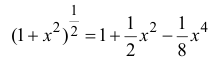
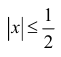
Пример 14.4
Найти
Решение
Воспользуемся разложением (14.7):
Тогда
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных