Условие задачи:
Найти предельный угол падения луча на границу раздела стекла и воды.
Задача №10.4.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(alpha_{пр}-?)
Решение задачи:
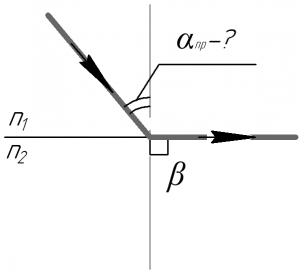
[{n_1}sin alpha_{пр} = {n_2}sin beta]
Здесь (alpha_{пр}) – предельный угол полного внутреннего отражения, (beta) – угол преломления, равный в данном случае 90°, (n_1) и (n_2) – показатели преломления сред. Показатель преломления стекла (n_1) равен 1,5, а показатель преломления воды (n_2) равен 1,33. Тогда, так как (sin beta = 1):
[{n_1}sin {alpha _{пр}} = {n_2}]
[sin {alpha _{пр}} = frac{{{n_2}}}{{{n_1}}}]
[{alpha _{пр}} = arcsin left( {frac{{{n_2}}}{{{n_1}}}} right)]
Задача решена, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[{alpha _{пр}} = arcsin left( {frac{{1,33}}{{1,5}}} right) = 62,5^circ ]
Ответ: 62,5°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.4.1 Предельный угол полного внутреннего отражения для воздуха и стекла 34°
10.4.3 Определить угол полного внутреннего отражения для алмаза, погруженного в воду
10.4.4 Предельный угол полного внутреннего отражения для льда равен 50°. Определить
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Полное внутреннее отражение (англ. total internal reflection) — это явление, при котором свет, падающий на границу двух сред из среды с большим показателем преломления под углом, превышающим предельный угол αпр , не преломляется, а полностью отражается, так что энергия падающего света отражается в первую среду.
Вам интересно, почему полное отражение электромагнитных волн зависит от различных сред и углов? А как можно вычислить угол, при которым происходит полное внутреннее отражение? Именно об этом вы узнаете далее из моей статьи.
Описание явления и формула
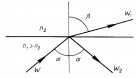
Свет, то есть электромагнитная волна в диапазоне от 380 нм до 780 нм, достигая границы сред, может претерпевать два явления: отражение и преломление (рис. 1.).
Однако иногда случается, что явление преломления не происходит. Давайте рассмотрим это подробнее. В первой среде, показатель преломления которой будет больше, чем во второй, поместим источник света под малым углом падения. Затем вы заметите, что оба явления имеют место. Теперь давайте постепенно увеличивать угол падения. В определенный момент мы достигнем ситуации, когда угол преломления будет равен 90° и свет будет «скользить» через границу сред (рис. 2.). Угол падения в этом случае называется предельным углом.
Предельный угол αпр (или критический угол) — максимальный угол падения света на границе двух сред, при котором происходит явление преломления.
Если продолжать увеличивать угол падения, то явление преломления не произойдет. Мы будем наблюдать только отражение. Это называется полным внутренним отражением. Это явление было описано в первой половине 19 века независимо друг от друга Жаком Бабинэ и Жаном-Даниэлем Колладоном.
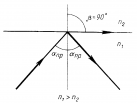
Если n1 > n2 и угол падения больше предельного угла αпр, то преломление отсутствует, т.е. происходит полное внутреннее отражение (см. рисунок 3).
Поэтому остается вопрос, каков вычислить этот предельный угол? Это максимальный угол падения, при котором мы еще можем говорить о явлении преломления. Затем, пройдя через границу сред, луч «скользит вдоль границы», и угол преломления составляет 90° (рис. 2.). Таким образом, закон преломления света принимает вид: sin ( αпр ) / sin ( 90° ) = n2 / n1 . Преобразуя приведенную выше формулу, получаем: sin ( αпр ) = sin ( 90° ) * ( n2 / n1 ) = n2 / n1 .
Предельным углом для вычисления полного отражения является угол, обратный функции синуса и отношения показателей преломления оптически менее плотной и оптически более плотной среды, то есть αпр = arcsin ( n2 / n1 ) .
Таким образом, если световая волна падает на границу двух сред таким образом, что угол падения больше arcsin ( n2 / n1 ), то мы говорим о полном внутреннем отражении света.
Но как именно можно определить, является ли среда оптически более плотной или менее плотной?
Закон преломления света можно использовать для описания изменения направления электромагнитных волн при их прохождении через различные среды. Прежде всего, необходимо дать некоторые определения.
В оптике показатель преломления n указывает на отношение длины волны λ или фазовой скорости c света в вакууме к скорости света в материале или среде ( cср ). Это определяет оптически более плотные среды и оптически менее плотные среды. Соответственно, показатель преломления без единиц измерения можно определить по следующей формуле: n = c / cср = λ / λср .
Формула закона преломления света, как известно, определяется как отношение угла падения α и угла преломленного света β. Это должно быть равно отношению показателей преломления, то есть sin α / sin β = n2 / n1 .
В случае полного внутреннего отражения угол падения или предельный угол αпр равен отношению показателя преломления оптически более плотной среды к оптически менее плотной среде.
Это означает, что если n1 > n2, то при достаточно большом угле падения α , β уже не соответствует действительному (вещественному) числу: sin β = sin α * n1/n2 > 1.
Примеры расчёта
Давайте перейдем от теории к практике и проиллюстрируем, как можно рассчитать предельный угол полного внутреннего отражения. В примере электромагнитная волна из воды попадает в воздух.
Показатель преломления воды составляет около 1,333 при 20°C, тогда как показатель преломления воздуха равен 1,000292. Из этого следует, что в данном примере вода является оптически более плотной средой, а воздух — оптически менее плотной средой, то есть nводы > nвоздуха .
Поэтому предельный угол αпр может быть рассчитан с помощью обратной функции синуса и отношения показателей преломления воздуха и воды, то есть αпр = arcsin ( 1,000292 / 1,333 ) = 48,6° .
На основе определенного предельного угла можно определить три результирующие области:
Если свет проникает через воду и попадает в оптически менее плотную среду — воздух под углом меньше 48,6°, то можно заметить, что часть света отражается, а часть преломляется в пограничном слое (см. рисунок 4).
Однако если свет падает на воздух с определенным предельным углом равным 48,6°, часть электромагнитной волны пройдет точно на границе раздела сред. Другая часть отразится (см. рисунок 5).
Если угол падения теперь больше предельного угла αпр , равного 48,6°, мы говорим о полном внутреннем отражении. В этом случае свет полностью отражается на границе раздела сред, больше не преломляется и, следовательно, больше не проникает в воздух.
Однако существуют некоторые ограничения, чтобы не нарушить общее отражение. Оптически менее плотная среда должна иметь определенную минимальную толщину. Кроме того, оптически менее плотная среда не должна быть абсорбирующей.
Коэффициент экстинкции k используется для описания ослабления электромагнитных волн, например, за счет рассеяния или поглощения. Он определяется как произведение показателя преломления n и коэффициента поглощения κ, то есть k = n * κ .
Применение
Далее рассматриваются некоторые примеры практического применения принципа полного внутреннего отражения электромагнитных волн.
Эффект полного внутреннего отражения особенно полезен для оптических волокон, таких как оптоволоконные кабели. Оптоволоконные кабели состоят из сердечника и оболочки. Сердечник из стекловолокна является оптически плотной средой, а оболочка — оптически менее плотной средой. Благодаря полному внутреннему отражению, свет внутри оптоволоконного кабеля почти полностью отражается от оболочки и остается в сердцевине.
Известный всем кабельный интернет также передается с помощью оптоволоконных кабелей. Здесь электрические сигналы преобразуются в электромагнитные импульсы с помощью электрооптических преобразователей.
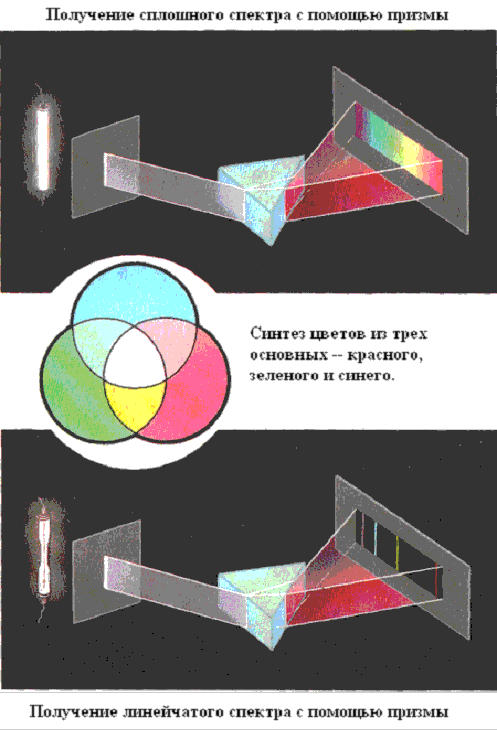
Призмы часто используются в оптике. Эти призмы обладают физическим эффектом дисперсии. Благодаря различным частотам электромагнитных волн, призмы могут быть использованы для разделения света на его спектр или спектральные цвета.
Они также используются для определения расстояния от Земли до Луны. Призма, которая служит здесь отражателем, находится на Луне. Если теперь направить лазер с Земли на эту призму, она отразит лазерный луч и отправит его обратно на Землю. Исходя из характеристики скорости света c, равной 300 000 км/с, и расчетного времени возврата t, равного примерно 2,55 с, получается, что расстояние составляет: s = c * t = 300 000 * (2,55 / 2) ≈ 382 500 км .
Другой важной областью, в которой явление полного внутреннего отражения нашло ряд применений, является медицина. Здесь в первую очередь следует отметить возможность заглянуть внутрь тела без хирургического вмешательства. Для этой цели служит устройство, состоящее из нескольких оптических волокон, объединенных вместе. Это нашло применение прежде всего в эндоскопии, которая позволяет проводить неинвазивное обследование, а также брать биопсию и проводить небольшие хирургические вмешательства.
Одно из самых популярных и известных применений этого явления — ювелирная промышленность. Он заключается в придании полированному камню соответствующей формы и покрытии его симметричными плоскостями, так что внутри камня происходит полное внутреннее отражение, и около 80% лучей преломляются. Это позволяет наблюдать характерный блеск бриллиантов
Список использованной литературы
При написании статьи использовались следующие источники информации:
- Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Учебник, Физика, 8 класс. Л.А. Исаченкова, Ю.Д. Лещинский, В.В. Дорофейчик
- Кикоин И. К., Кикоин А. К. Физика – 9, Москва, Просвещение, 1990.
Примеры решения задач
Задача 4.1. Свет переходит из стекла в
воду. Определите предельный угол падения
света на границе этих сред (
;
)
Решение. Воспользуемся законом преломления
в форме (2.8):
Для нахождения предельного угла в стекле
положим
,
,
тогда:
Отсюда следует:
Задача 4.2. Относительный показатель
преломления двух оптических сред
.Луч,
падающий на плоскую границу этих сред,
частично преломляется, частично
отражается. При каком угле падения
отраженный луч перпендикулярен лучу
преломленному?
Решение, По закону преломления
.Согласно
условию задачи
.
Поэтому
откуда следует:
Задача 4.3. В сосуд налиты две
несмешивающиеся жидкости с показателями
преломления
и
(рис. 4.2), толщина слоя каждой жидкости
– 5 см. На каком расстоянии от поверхности
жидкости кажется расположенным дно
сосуда?
Решение. Анализ рисунка 4.8 показывает,
что
Здесь Н – расстояние от верхней
поверхности до точки О’ – изображения
точки О на дне сосуда. Учитывая, что угол
мал (
),
получаем:
или
Но
,
a
.
Поэтому

Рис. 4.2 Рис. 4.3
Задача 4.4. Луч падает на поверхность
прозрачного стеклянного шара. Пройдя
сквозь стекло, он достигает поверхности
раздела стекла и воздуха. Может ли на
границе стекло – воздух при выходе луча
из шара произойти полное отражение?
Решение. Построив падающий луч, проходящий
в шар и выходящий из него, можно увидеть,
что ни при каких условиях полного
отражения не произойдет.
Задача 4.5. Под каким максимальным углом
может падать свет на плоский торец
волновода, чтобы он не выходил в оболочку?
Показатель преломления вещества жилы
,
оболочки
.
Решение. Обратимся к рисунку 4.3. Свет
испытает полное отражение на границе
жилы с оболочкой, если
,
или
.
Из закона преломления имеем
.
Но
,
т.е.
.
Следовательно,
,
или
.

Кольца Ньютона в красном и зелёном
свете. Возникновение радуги.
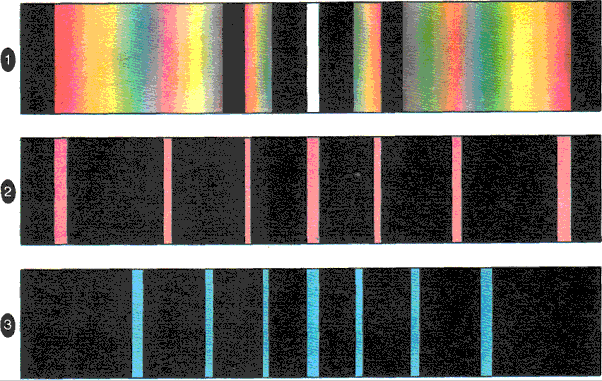
Спектральное разложение при падении
на дифракционную решетку:
-
белого света;
-
красного света;
-
синего света.

Типы спектров:
-
сплошной;
-
спектр испускания натрия;
-
спектр испускания водорода;
-
спектр испускания гелия;
-
спектр Солнца с фраунгоферовыми
линиями; -
спектр поглощения натрия;
-
спектр поглощения водорода;
-
спектр поглощения гелия.
-
Зеркала
Плоское зеркало. Построение изображения
в плоском зеркале основано на использовании
закона отражения света. Пусть над
плоским зеркалом (рис. 5.1) находится
точечный источник света S, освещающий
это зеркало. Из всего светового потока
выберем два луча 1 и 2, которые падают
на зеркало под разными углами
и
.
После отражения от зеркала эти лучи,
как видно из рисунка, расходятся.
Продолжения лучей пересекаются в точке
S’, находящейся по другую сторону зеркала
относительно источника (в Зазеркалье,
как сказала бы Алиса из книги Льюиса
Кэролла). Нашему глазу будет казаться,
что лучи 1 и 2 выходят из этой точки, как
будто там находится источник света.
Следовательно, точка S’ воспринимается
нами как изображение точечного
источника S.
Изображение, которое получается за
счет пересечения не самих лучей, а их
продолжений, называется мнимым.
Такое название связано с тем, что в
точку S’ не попадает
энергия от источника света.
Почему же мы видим мнимое изображение?
Дело в том, что хрусталик глаза и
стекловидное тело (см. раздел 6) собирают
расходящийся световой пучок на
сетчатке в точке S». Аналогично
расходящийся пучок может собрать
объектив фотоаппарата. Именно свойство
линз собирать расходящийся пучок
позволяет видеть мнимое изображение,
заглянуть в Зазеркалье. Оптика
фотоаппарата собирает расходящийся
пучок, поэтому фотоаппарат также
способен фиксировать мнимое изображение.
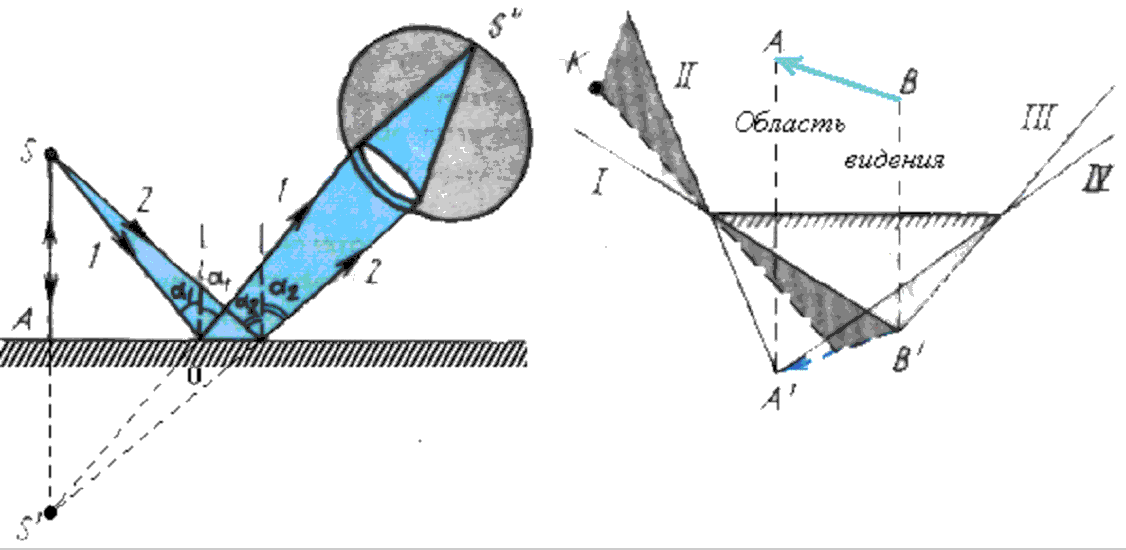
Рис. 5.1 Рис. 5.2
Совсем не обязательно строить изображение
источника или предмета в плоском
зеркале, пользуясь двумя или большим
числом лучей. Из равенства треугольников
SAО и S’AО
следует, что SA = S’A.
Значит, возможен более простой способ
построения: на перпендикуляре, опущенном
на зеркало из источника, надо отложить
отрезок S’А =SA. Так мы
найдем место мнимого изображения
S’. Здесь мы, по существу, пользуемся
симметричностью предмета и изображения
относительно зеркала.
Из практики хорошо известно, что не из
любой точки можно увидеть изображение
в зеркале. Посмотрим на рисунок 5.2, где
показано изображение предмета АВ в
зеркале. Из рисунка видно, что полностью
изображение наблюдается только из
так называемой области видения,
ограниченной прямыми II – III.
Есть еще две области I –
II и III – IV, из которых
видна только часть предмета. Например,
из точки К видна только правая часть
изображения предмета. Это – области
частичного видения. За пределами прямых
I и IV изображение не видно.
Сферическое зеркало. Если взять в
качестве отражающей поверхности часть
внешней или внутренней поверхности
зеркальной сферы, то получится
сферическое зеркало. Его основные
характеристики: главный фокус F, фокусное
расстояние f, оптический
центр, главная оптическая ось, оптическая
сила.
Различают два типа сферических зеркал:
вогнутые (у них отражающее покрытие
нанесено на внутреннюю поверхность
сферы) и выпуклые (у них отражающее
покрытие нанесено на внешнюю поверхность
сферы).
Фокусом F зеркала называется точка
на оптической оси, через которую проходит
после отражения от зеркала луч (или его
продолжение), падавший на зеркало
параллельно оптической оси. Найдем
положение фокуса вогнутого зеркала.
Для этой цели обратимся к рисунку 5.3,
a.
На зеркало падает луч KM параллельно
оптической оси ОС. В точке падения
восставим перпендикуляр к зеркалу –
им будет радиус ОМ. Воспользовавшись
законом отражения, строим луч МF, который
проходит через точку F, являющуюся
фокусом.
Очевидно, что
COM=
KMO
=
как накрест лежащие при параллельных
прямых. Но
KMO=
FMO
=
по закону отражения. Следовательно,
треугольник ОFМ является равнобедренным
и отрезок
.
Отсюда следует, что фокусное расстояние
.
Учитывая, что
,
получим окончательно:
(5.1)
Мы видим, что в сферическом зеркале
имеет место сферическая аберрация:
фокусное расстояние оказывается
различным для лучей, находящихся на
разных расстояниях от оптической оси.
Однако для параксиального пучка
условие фокусировки выполняется и
фокусное расстояние вогнутого зеркала
оказывается равным
(5.2)
Оптическая сила зеркала – это величина,
обратная фокусному расстоянию:
(5.3)
Рекомендуем читателю проверить, что
при
выражение (5.2) справедливо с точностью,
не меньшей 0,5%.
Как видно из рисунка 5.3, б, у выпуклого
зеркала фокус мнимый. Нетрудно убедиться,
что и здесь для параксиального пучка
справедливо условие (5.2). Предоставляем
читателю возможность доказать это
самостоятельно.
Фокусное расстояние выпуклого зеркала
принято считать отрицательным
числом, т.е. у выпуклого зеркала
.
Очевидно, что и оптическая сила
выпуклого зеркала – число отрицательное.
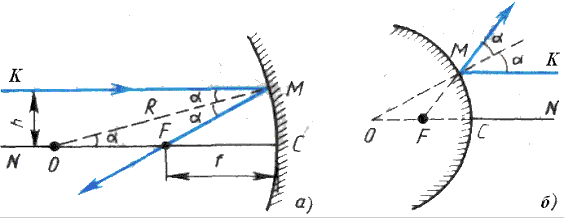
Рис. 5.3
Построение изображения в сферическом
зеркале. Для построения изображения
точки в сферическом зеркале следует
выбрать любые два луча из трех стандартных:
а) луч, проходящий через оптический
центр зеркала (центр сферы), называемый
побочной оптической осью; после отражения
от зеркала он опять проходит через
центр;
б) луч, падающий на зеркало параллельно
оптической оси; после отражения проходит
через фокус зеркала;
в) луч, проходящий через фокус зеркала,
после отражения идет параллельно
оптической оси.
Если мы строим изображение предмета,
то надо, вообще говоря, строить
изображения всех его точек. Однако в
некоторых случаях, в частности, когда
предмет – прямая линия, можно строить
изображения двух его точек. При этом
не надо забывать, что мы пользуемся
только параксиальными пучками, ширина
которых
– радиуса кривизны зеркала.
Воспользовавшись этими правилами,
построим изображения в некоторых
частных случаях (рис. 5.4, 5.5, 5.6). Как видно,
в выпуклом зеркале изображение мнимое,
прямое и уменьшенное при любом положении
предмета (см. рис. 5.4); последнее утверждение
рекомендуем проверить построением.
Мнимое, прямое, но увеличенное изображение
возникает и в вогнутом зеркале, если
предмет расположен между фокусом и
зеркалом (см. рис. 5.5).
Если же предмет расположен дальше
центра вогнутого сферического зеркала
(см. рис. 5.6), то образуется перевернутое,
уменьшенное действительное
изображение между фокусом и центром.
В самом деле, расходящийся световой
пучок, исходящий из точки А (как и из
любой другой точки), после отражения в
зеркале собирается в точке А’. Здесь
концентрируется энергия, что можно
обнаружить, поместив в это место
фотопластинку или фотопленку, на которой
получится отпечаток.

Рис. 5.4 Рис. 5.5
Пользуясь рисунком 5.6, легко сообразить,
что если предмет поместить между
фокусом и центром зеркала, то за центром
возникнет действительное увеличенное
и перевернутое изображение предмета.
Выполните это построение самостоятельно.
Рис.
5.6
Формула сферического зеркала.
Введем следующие обозначения: расстояние
от предмета до вершины зеркала ВС (см.
рис. 5.6) обозначим через d, расстояние
до изображения В’С – d’. Найдем связь
между этими величинами и фокусным
расстоянием в предположении, что размер
предмета АВ много меньше радиуса
зеркала, т. е. что все пучки параксиальные.
В этом случае AM≈BC = d, А’N≈В’С=d’, СМ≈АВ и
СN≈А’В’ подобия треугольников АВF и СNF
имеем: BF/CF=AB/A’B’, или
.
Аналогично из подобия треугольников
А’В’F и МСF имеем: СF/В’F =
CM/A’B’ = AB/A’B’, или
.
Отсюда следует:
.
После простых преобразований получим:
Разделив обе части равенства на величину
dd’f, получим окончательно:
(5.4)
Это выражение называется формулой
зеркала. При расчетах следует учесть,
что расстояния до предмета и действительного
изображения являются величинами
положительными, расстояние до мнимого
изображения – число отрицательное.
Фокусное расстояние и оптическая сила
вогнутого зеркала – величины
положительные, выпуклого – отрицательные.
-
ЛИНЗЫ
Основные параметры линзы. Линза – это
прозрачное стеклянное тело, ограниченное
двумя сферическими поверхностями с
радиусами кривизны R1 и R2∙
Одна из поверхностей линзы может
быть плоской. По форме ограничивающих
поверхностей различают шесть типов
линз: двояковыпуклая (рис. 6.1, а),
плосковыпуклая (рис. 6.1, б),
вогнуто-выпуклая (рис. 6.1, в), двояковогнутая
(рис. 6.1, г), плосковогнутая (рис. 6.1, д) и
выпукло-вогнутая (рис. 6.1, е).
Прямая, на которой лежат центры обеих
сферических поверхностей линзы,
называется главной оптической осью.
Мы будем далее рассматривать тонкие
линзы, толщина которых значительно
меньше их радиусов. У тонких линз есть
точка С, проходя через которую луч не
преломляется. Эта точка называется
оптическим центром линзы (рис. 6.2,
а, б). Прямая, проходящая через центр
линзы, называется побочной оптической
осью. Плоскость, проходящую через
центр тонкой линзы перпендикулярно
главной оптической оси, называют главной
плоскостью линзы.

Рис. 6.1 а) б) в) г) д) е)

Рис. 6.2
Если на стеклянную линзу, находящуюся
в воздухе, направить параксиальный
пучок света параллельно главной
оптической оси, то у выпуклой линзы
пучок соберется в точке F (см. рис. 6.2,
а), называемой главным фокусом.
Такие линзы относят к собирающим.
Если такой же пучок направить на вогнутую
линзу (см. рис. 6.2, б), то пучок рассеивается
так, что лучи как будто бы исходят из
точки F, которую называют мнимым
главным фокусом рассеивающей линзы.
Пучок света, направленный на собирающую
линзу параллельно побочной оптической
оси, собирается в побочном фокусе.
Все побочные фокусы лежат на фокальной
плоскости, проходящей через главный
фокус перпендикулярно главной оптической
оси. У рассеивающей линзы можно тоже
построить мнимые фокальные плоскости.
Недостатки линз. Реальным линзам
свойственны некоторые дефекты. Один
из них – сферическая аберрация, с
которой мы встречались при рассмотрении
сферического зеркала (см. раздел 5). Она
заключается в том, что выпуклая линза
лучи, отстоящие далеко от главной
оптической оси, собирает в точке
(фокусе), расположенной ближе к линзе,
чем близко прилегающие лучи (рис. 6.3,
а); у вогнутой линзы – аналогичная
картина (рис. 6.3, б).
Один из способов борьбы со сферической
аберрацией – использование только
параксиальных пучков, т. е. пучков,
близких к главной оптической оси. Для
этого линзу диафрагмируют, пропуская
через нее более узкий пучок. Но этим
уменьшается энергия пучка и освещенность
изображения. Второй способ ослабления
сферической аберрации вытекает из
того, что у собирающих и рассеивающих
линз оптическая сила имеет противоположные
знаки, и можно подобрать такую пару
линз (рис. 6.4), чтобы их аберрации
существенно компенсировались.
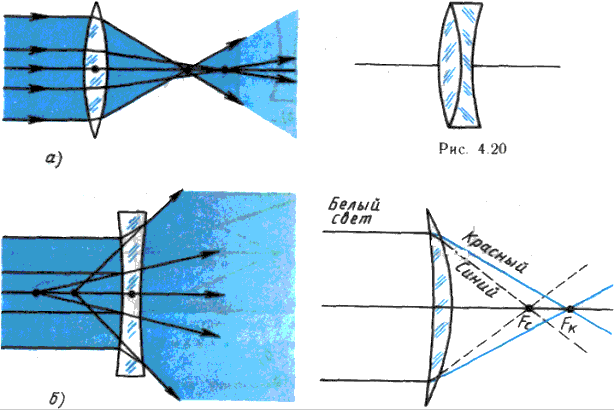
Рис. 6.3 Рис. 6.4 (вверху) и 6.5
Вторым серьезным дефектом линз является
хроматическая аберрация. Из-за дисперсии
(см. раздел 3) в линзе происходит
разложение белого света в спектр.
При этом красные лучи, преломляясь
слабее, фокусируются дальше от центра
линзы; синие и фиолетовые, преломляясь
сильнее, фокусируются ближе (рис. 6.5). В
результате хроматической аберрации
изображение в линзе оказывается
размытым и окрашенным.
Исправить хроматическую аберрацию
можно с помощью двойной линзы,
подобрав различные сорта стекла с
разной дисперсией. Линзы, в которых
устранена хроматическая аберрация,
называются ахроматами (от греч.
a(an) – не и сhrоmа – цвет). Такие линзы
используются в качестве объективов
телескопов – рефракторов, хороших
биноклей, простейших фотоаппаратов и
т. п.
Значительные аберрации возникают также
при падении на линзу лучей под большим
углом к оптической оси. Устранение этих
аберраций возможно путем подбора
системы из нескольких (до десятка) линз,
каждая из которых компенсирует недостатки
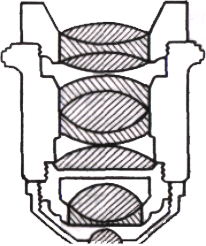
другой. На рисунке 6.6 изображен объектив
хорошего микроскопа, в котором устранены
почти все аберрации. Расчет, изготовление
и проверка таких сложных оптических
систем – весьма трудная задача, требующая
хороших знаний теории и высокой
квалификации.
Построение изображений. Пусть точка
А находится на расстоянии d от собирающей
линзы значительно дальше фокуса. Высота
предмета AB = h больше размера линзы, что
практически всегда и бывает на практике
(рис. 6.7). Из точки А выходит световой
пучок; часть его, закрашенная на рисунке,
проходит через линзу и собирается в
точке А’, которая является изображением
точки А.
Чтобы найти положение точки А’, проведем
главную плоскость линзы МN и для
построения выберем любые два из трех
стандартных (характерных) лучей:
а) луч, параллельный главной оптической
оси; после преломления он проходит
через главный фокус;
б) луч, совпадающий с побочной оптической
осью; проходит без преломления через
центр линзы;
в) луч, проходящий через главный фокус;
после преломления он идет параллельно
главной оптической оси.
П
остроив
изображение А’, опускаем перпендикуляр
на главную оптическую ось и находим
точку В’, которая является изображением
точки В. Если же предмет имеет более
сложную форму, нужно тем же способом
построить изображения основных точек,
определяющих форму предмета.
В данном случае мы получили Действительное
перевернутое уменьшенное изображение.
Очевидно, что здесь предмет и его
изображение обратимы – если в том
месте, где находится изображение,
поместить какой-то предмет, то его
изображение (увеличенное) окажется
там, где раньше располагался предмет.
Проверьте это построением.
Нетрудно убедиться, что если предмет
будет расположен между линзой и главным
фокусом, то глаз, расположенный за
линзой, увидит прямое мнимое увеличенное
изображение. Рекомендуем выполнить
Рис.6.6
это построение.
Рассеивающая линза дает прямое мнимое
уменьшенное изображение предмета (рис.
6.8).

Рис. 6.7
Формула линзы. Расстояние от тонкой
линзы до предмета d, расстояние до
изображения d’ и фокусное расстояние f
связаны формулой. Выведем ее.
Пусть двояковыпуклая линза дает
изображение высотой h’ предмета АВ,
расположенного на расстоянии BF = a от
левого фокуса линзы; изображение А’В’
расположено на расстоянии В’F’≈а’ от
правого фокуса линзы (см. рис. 6.7). Из
подобия треугольников А’В’F’ и F’СМ, а
также треугольников АВF и FСN имеем:
;
.
Определим поперечное увеличение β=h’/h,
даваемое линзой, из обоих выражений:
. (6.1)
Отсюда следует так называемая формула
Ньютона:
(6.2)
Но расстояние до предмета d = a+f, а
расстояние до изображения d’ = a’+f.
Подставляя выражения для а и а’ в формулу
Ньютона, получим:
или после приведения подобных членов:
.
Разделив обе части выражения на d’df,
получим
(6.3)
Это соотношение носит название формулы
линзы. Оно аналогично формуле зеркала
(5.4).
В формуле линзы следует учитывать знаки
входящих в нее величин. Принято считать
фокусное расстояние собирающей линзы
положительным числом, фокусное расстояние
рассеивающей линзы – отрицательным.
Расстояния от предмета до линзы и от
действительного изображения до линзы
считают положительными числами,
расстояние от линзы до мнимого изображения
– отрицательным числом.
Фокусное расстояние и оптическая
сила линзы. Опыт показывает, что
фокусное расстояние линзы зависит от
радиусов кривизны ее поверхностей, а
также показателей преломления вещества,
из которого изготовлена линза, и
окружающей ее среды. Получим выражение
для фокусного расстояния на примере
двояковыпуклой линзы. Для простоты
вывода будем считать, что обе сферические
поверхности имеют одинаковый радиус
кривизны R, а относительный
показатель преломления линзы по
отношению к окружающей среде равен
.
Все представления, которые мы использовали
в волновой теории, применимы к построению
изображений в линзах. В самом деле,
линза вырезает из всего светового
потока, даваемого источником,
определенную часть, следовательно,
действие линзы сравнимо с действием
отверстия в непрозрачном экране. Поэтому
за линзой возникают дифракционные
максимумы. В точке А’, представляющей
собой изображение точки А, находится
главный (центральный) максимум. Но это
означает, что колебания, исходящие из
точки А, пройдя через линзу, приходят
в точку А’ в одной и той же фазе.
Следовательно, хотя волны проходят в
линзе разные расстояния, оптический
путь у них один и тот же.
Пусть на двояковыпуклую линзу параллельно
главной оптической оси падает параллельный
пучок – по волновой терминологии
это плоская волна АКD (рис. 6.9). До плоскости
ВLЕ все колебания распространяются в
однородной среде с одинаковой скоростью,
так что на этой плоскости все точки
колеблются ‘в одинаковой фазе. Далее
волны будут распространяться в среде
с другим показателем преломления,
следовательно, и с другой скоростью.
Однако они должны прийти в фокус F в
одинаковой фазе, следовательно, пройти
одинаковые оптические пути.
Сравним оптические пути по лучу АВМF и
по лучу КLGF. Волна из точки В проходит
расстояние ВМ + MF= a
+ l в среде с показателем
преломления n1. Следовательно,
оптический путь

Рис. 6.9
Волна из точки L проходит расстояние
LG=2a в веществе с показателем преломления
и расстояние GF = f – a в
среде с показателем преломления
.
Следовательно, оптический путь равен
Приравняв оптические пути, получим:
,
или с учетом равенства
,
откуда
. (6.4)
Из теоремы Пифагора следует
;
с другой стороны, .
.
Поскольку линза тонкая, т. е.
,
то
;
следовательно,
.
Приравняв выражения для
,
получим:
(6.5)
Подставив значение
из соотношения (43.4), будем иметь:
Учитывая, что из-за тонкости линзы
,
получим после сокращений:
(6.6)
Величина, обратная фокусному расстоянию
линзы, называется ее оптической силой.
Для двояковыпуклой линзы с одинаковыми
радиусами кривизны оптическая сила;
(6.7)
Можно показать, что для линзы, у которой
поверхности имеют разные радиусы
кривизны (
),
справедлива формула
(6.8)
В этой формуле радиусам приписываются
определенные знаки. Если поверхность
выпуклая, то радиус кривизны считается
положительным; у вогнутой поверхности
радиус кривизны отрицательный. У плоской
поверхности радиус кривизны бесконечно
велик. Пользуясь этим правилом, убедитесь,
что у двояковыпуклой, плосковыпуклой
и вогнуто-выпуклой линз (см. рис. 6.1, а,
б, в) оптическая сила положительная; у
двояковогнутой, плосковогнутой и
выпукло-вогнутой (см. рис. 6.1, г, д, е) –
отрицательная
Единица оптической силы линзы в СИ –
диоптрия (дптр). 1 дптр – это оптическая
сила линзы с фокусным расстоянием 1
м. Чтобы получить оптическую силу линзы
в диоптриях, надо ее фокусное расстояние
выразить в метрах.
|
Полное отражение |
|
|
Если свет падает из оптически более плотной среды в оптически менее плотную, то при определенном для каждой среды угле падения, преломленный луч исчезает. Наблюдается только отражение. Это явление называется полным внутренним отражением. |
|
|
|
|
|
Угол падения, которому соответствует угол преломления 90°, называют предельным углом полного внутреннего отражения (α0). Из закона преломления следует, что при переходе света из какой-либо среды в вакуум (или воздух)
|
|
|
При переходе между двумя любыми средами: |
Предельный угол α0 для сред стекло — воздух |
|
Явление полного отражения света используется в призмах, в волоконной оптике (световодах), в водолазном деле, в ювелирной промышленности. |
|
|
Световод — стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с показателем преломления меньше чем у волокна. За счет многократного полного отражения свет может быть направлен по изогнутому пути. |
|
|
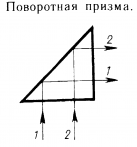
Поворотные и оборачивающие призмы применяют в перископах, биноклях, киноаппаратах, а также часто вместо зеркал. |
|
|
Если мы пытаемся из-под воды взглянуть на то, что находится в воздухе, то при определенном значении угла, под которым мы смотрим, можно увидеть отраженное от поверхности воды дно. Это важно учитывать для того, чтобы не потерять ориентировку. |
|
|
В ювелирном деле огранка камней подбирается так, чтобы на каждой грани наблюдалось полное отражение. Этим и объясняется «игра камней». |
|
|
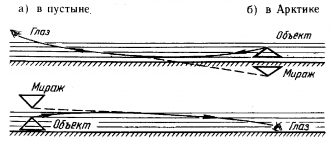
Полным внутренним отражением объясняется и явление миража. |
|