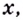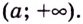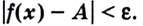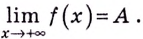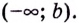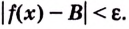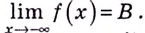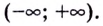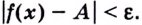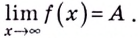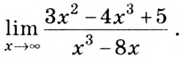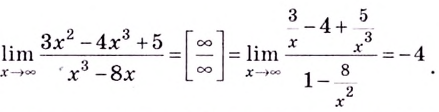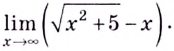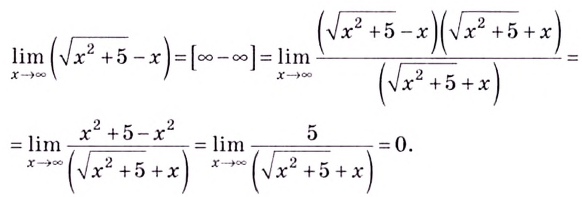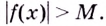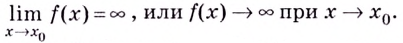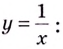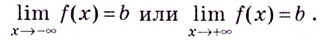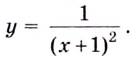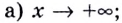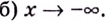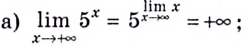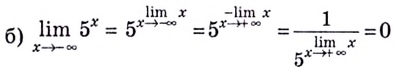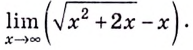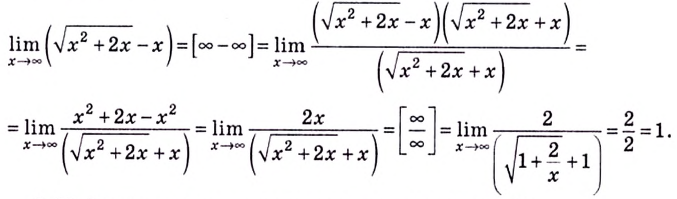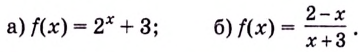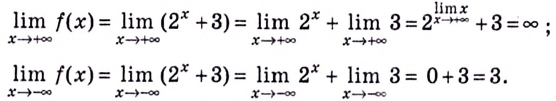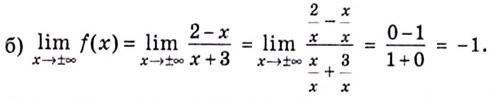Заказать задачи по любым предметам можно здесь от 10 минут
Как решать пределы с бесконечностью
Рассмотрим основные типы неопределенностей пределов на бесконечности с примерами решений:
- $ [frac{0}{0}] $
- $ [infty — infty] $
- $[frac{infty}{infty}]^{[infty]}$ и $[1 ^ infty] $
| Пример 1 |
| Вычислить предел функции, стремящейся к бесконечности $ lim limits_{x to infty} frac{x^3-4x+1}{x^3+x^2-2} $ |
| Решение |
|
Первым делом подставляем $ xto infty $ в предел, чтобы попытаться его вычислить. Вычисление не дало результата, так как появилась неопределенность. Чтобы устранить её, вынесем за скобки в числителе и знаменателе $x$ с наибольшей степенью. $$limlimits_{x to infty} frac{x^3(1 — frac{4}{x^2} + frac{1}{x^3})}{x^3(1+frac{1}{x}-frac{2}{x^3})} = limlimits_{x to infty} frac{1 — frac{4}{x^2} + frac{1}{x^3}}{1+frac{1}{x}-frac{2}{x^3}} = $$ Максимальная степень у $x^3$, поэтому вынесли именно её, а затем выполнили сокращение. Пользуясь тем, что $limlimits_{xto infty} frac{1}{x} = 0$ получаем ответ. $$ = frac{1-0+0}{1+0-0} = frac{1}{1} = 1 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ limlimits_{x to infty} frac{x^3-4x+1}{x^3+x^2-2} = 1 $$ |
| Пример 2 |
| Решить предел с бесконечностью $limlimits_{xto infty} sqrt{x^2+1}-x$ |
| Решение |
|
Так как предел стремится к бесконечности, то подставляем её в функцию под знаком предела. $$limlimits_{xto infty} sqrt{x^2+1}-x = [infty — infty] $$ Получили неопределенность. Для избавления от неё умножим и разделим функцию под знаком предела на сопряженную к ней. Она будет отличаться только одним знаком. $$limlimits_{xto infty} sqrt{x^2+1}-x = limlimits_{xto infty} frac{(sqrt{x^2+1}-x)(sqrt{x^2+1}+x)}{sqrt{x^2+1}+x} = $$ По формуле разности квадратов $ (a-b)(a+b) = a^2-b^2 $ сворачиваем числитель. А знаменатель пока не трогаем. $$ = limlimits_{xto infty} frac{x^2+1 — x^2}{sqrt{x^2+1}+x} = limlimits_{xto infty} frac{1}{sqrt{x^2+1}+x} = $$ Снова подставляем бесконечность в предел и получаем $frac{1}{infty}$, что равняется нулю. Поэтому записываем сразу ответ. $$ = limlimits_{xto infty} frac{1}{sqrt{x^2+1}+x} = frac{1}{infty} = 0 $$ |
| Ответ |
| $$limlimits_{xto infty} sqrt{x^2+1}-x = 0 $$ |
| Пример 3 |
| Решить предел на бесконечности $limlimits_{x to infty} bigg (frac{3x-4}{3x+2} bigg)^frac{x+1}{2} $ |
| Решение |
|
При подстановке $x to infty $ в предел получаем неопределенность. $$ limlimits_{x to infty} bigg (frac{3x-4}{3x+2} bigg)^frac{x+1}{2} = bigg[frac{infty}{infty}bigg]^{[infty]} $$ Для решения примера понадобится формула второго замечательного предела. $$limlimits_{xto infty} bigg(1+frac{1}{x} bigg)^x = e qquad (1) $$ Из выражения, стоящего под знаком предела вычитаем единицу, чтобы его подстроить под формулу (1). $$frac{3x-4}{3x+2} — 1 = frac{3x-4 — 3x — 2}{3x+2} = frac{-6}{3x+2} $$ Перепишем предел из условия задачи в новом виде и подставим в него $xto infty$. $$ limlimits_{xto infty} bigg (1 + frac{-6}{3x+2} bigg )^frac{x+1}{2} = [1]^infty $$ Пользуясь формулой (1) проведем вычисление лимита. В скобках перевернем дробь. $$limlimits_{xto infty} bigg (1 + frac{-6}{3x+2} bigg )^frac{x+1}{2} = limlimits_{xto infty} bigg (1 + frac{1}{frac{3x+2}{-6}} bigg )^frac{x+1}{2} = $$ По условиями формулы второго замечательного предела (1) в скобках знаменатель дроби должен быть равен степени за скобкой. Выполним преобразование степени. Для этого умножим и разделим на $frac{3x+2}{-6}$. $$ = limlimits_{xto infty} bigg (1 + frac{1}{frac{3x+2}{-6}} bigg )^{frac{3x+2}{-6} cdot frac{-6}{3x+2} cdot frac{x+1}{2}} = limlimits_{x to infty} e^{frac{-6}{3x+2} cdot frac{x+1}{2}} = $$ Остаётся сократить степень экспоненты и найти её предел. $$ = limlimits_{x to infty} e^frac{-3x-3}{3x+2} = e^{limlimits_{xto infty} frac{-3x-3}{3x+2}} = $$ Предел дроби равен отношению коэффициентов при старшей степени $x$. $$ = e^frac{-3}{3} = e^{-1} = frac{1}{e} $$ |
| Ответ |
| $$ limlimits_{x to infty} bigg (frac{3x-4}{3x+2} bigg)^frac{x+1}{2} = frac{1}{e} $$ |
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Подавляющее большинство функций, с которыми вы ознакомились ранее, определены на бесконечных промежутках. Исследуя такие функции, желательно установить их поведение для сколь угодно больших по модулю значений аргумента
Пусть функция 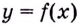
Число 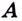
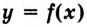
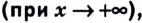
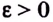
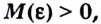
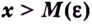
Пишут:
Пусть функция 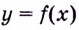
Число 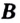
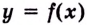
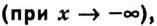
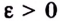
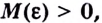
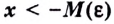
Пишут:
Пусть функция 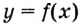
Число 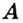
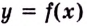
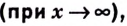
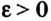
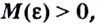
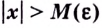
Пишут:
Геометрически это означает, что для любого 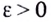
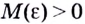
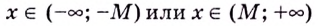
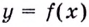
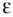
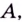
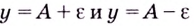
Для предела функции на бесконечности выполняются те же свойства и теоремы о пределах, что и для предела функции в точке (см. с. 102), а также те правила, которые используются при вычислении предела числовой последовательности. А именно:
1 .Для того чтобы вычислить предел дробно-рациональной функции в случае, когда при 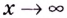
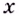
Пример:
Вычислите
Решение:
2. Для того чтобы вычислить предел функции, содержащей up рациональные выражения, в случае, когда каждый из слагаемых имеет бесконечный предел, необходимо умножить и разделить выражение, задающее функцию, на выражение, сопряжённое к нему, после этого выполнить необходимые упрощения (приведение подобных членов, сокращение и т. д.) и вычислить предел.
Пример:
Вычислите
Решение:
Исследуя функции, желательно также установить их поведение для тех значений аргумента 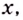
Функция 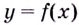
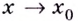
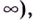
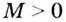
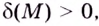
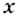
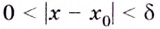
Пишут:
Понятие предела функции на бесконечности и бесконечного предела используются для нахождения асимптот.
Прямая 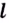
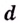
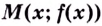
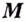
Асимптотами, например, есть оси координат для графика функции
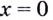
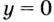
Кривая 
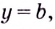
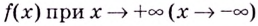
- Заказать решение задач по высшей математике
Пример:
Найдите горизонтальную асимптоту кривой
Решение:
Вычислим предел 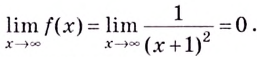
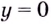
Пример:
Исследуйте поведение функции 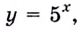
Решение:
Пример:
Вычислите
Решение:
Пример:
Найдите горизонтальные асимптоты кривой:
Решение:
а) Вычислим пределы при 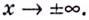
Следовательно, 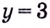
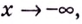
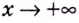
Следовательно, 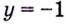
- Применение производной к исследованию функции
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Асимптоты графика функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.
- Определение предела функции
-
Решение пределов
- С заданным числом
- С бесконечностью
- С неопределенностью (икс стремится к бесконечности)
- С неопределенностью (икс стремится к конкретному числу)
Определение предела функции
Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.
Запись предела:
- предел обозначается значком lim;
- под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x, но не обязательно, например: “x→1″;
- затем справа дописывается сама функция, например:
Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):
Читается как “предел функции при икс, стремящемся к единице”.
x→1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).
Решение пределов
С заданным числом
Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x→1):
Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).
С бесконечностью
В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:
Если x→∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:
- 3 – 1 = 2
- 3 – 10 = -7
- 3 – 100 = -97
- 3 – 1000 – 997 и т.д.
Другой более сложный пример
Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.
- При x = 1, y = 12 + 3 · 1 – 6 = -2
- При x = 10, y = 102 + 3 · 10 – 6 = 124
- При x = 100, y = 1002 + 3 · 100 – 6 = 10294
Таким образом при “икс”, стремящемся к бесконечности, функция x2 + 3x – 6 неограниченно растет.
С неопределенностью (икс стремится к бесконечности)
В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.
Пример: давайте вычислим предел ниже.
Решение
Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:
Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:
1. Находим x в старшей степени для числителя (в нашем случае – это два).
2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).
3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.
4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.
С неопределенностью (икс стремится к конкретному числу)
И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.
В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.
Пример: Найдем предел функции ниже.
Решение
1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.
2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.
В нашем случаем корнями выражения в числителе (2x2 – 5x + 3 = 0) являются числа 1 и 1,5. Следовательно его можно представить в виде: 2(x-1)(x-1,5).
Знаменатель (x – 1) изначально является простым.
3. Получаем вот такой видоизмененный предел:
4. Дробь можно сократить на (x – 1):
5. Остается только подставить число 1 в выражение, получившееся под пределом: