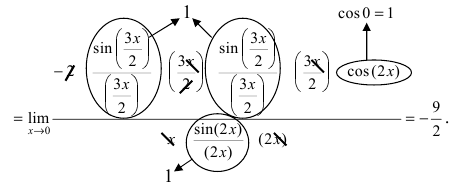
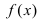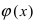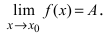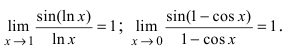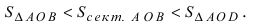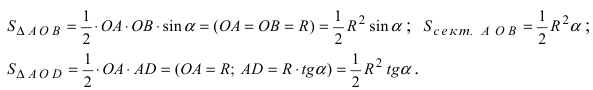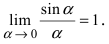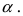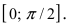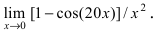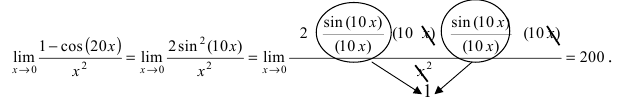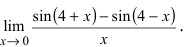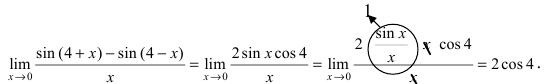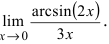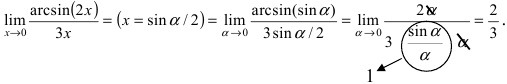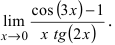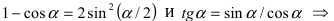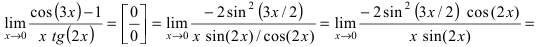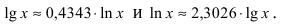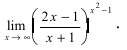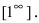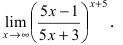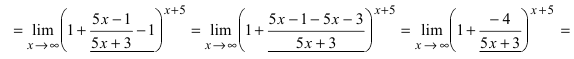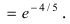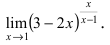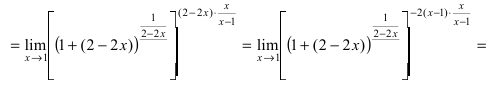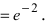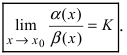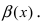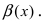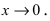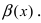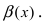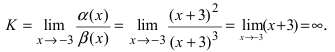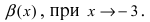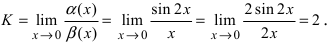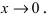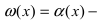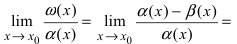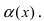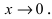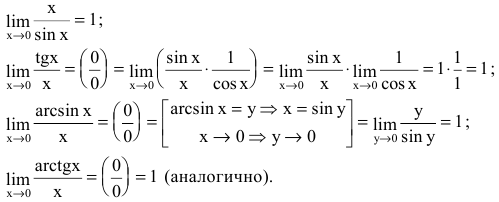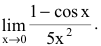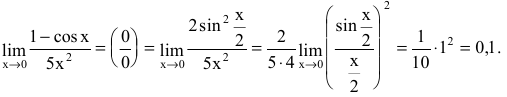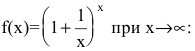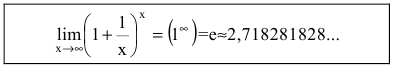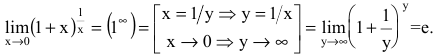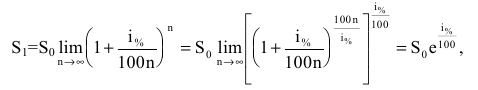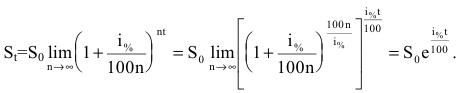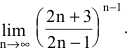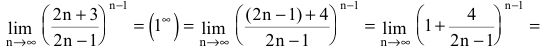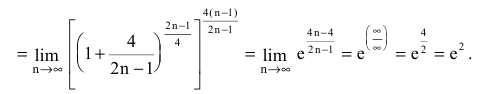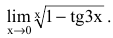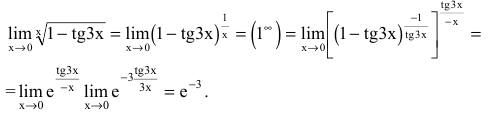Вычисление пределов степенно-показательных функций
Пусть функции
и
заданы на множестве
и функция
на нем положительна. Функция
называется степенно
— показательной.
Предположим, что
– точка сгущения множества
и существуют конечные пределы
,
,
где
.
Нужно найти
.
Воспользовавшись
тождествами
,
запишем исходное выражение в виде
.
В силу теоремы 6.1
получим
.
При заданных
значениях пределов будем иметь
.
Из проведенного
рассуждения видно, что предположение
о существовании конечных пределов
и
можно отбросить. Действительно, для
нахождения предела выражения
достаточно знать предел произведения
(конечный или бесконечный).
1) Пусть
.
Тогда
.
2) Если
,
то
.
3) Если
,
то
.
Заметим, что
произведение
может оказаться неопределенностью типа
.
Тогда и исходное выражение
представляет собой неопределенность.
Перечислим возникающие здесь
неопределенности.
1) Если
,
то вычисление предела
приводит к неопределенности типа
.
2) Если
,
то вычисление предела
приводит к неопределенности типа
.
3) Если
,
то вычисление предела
приводит к неопределенности типа
.
Во всех указанных
случаях (,
,
)
можно раскрыть неопределенность
в показателе степени, преобразуя ее к
типу
и используя соответствующие эквивалентные
бесконечно малые.
Замечание 8.3.
Приведенные выше рассуждения справедливы
и для вычисления предела степенно-показательной
функции в бесконечно удаленной точке:
.
Пример 8.2.
Вычислить
.
Решение.
Здесь
,
,
поэтому имеем неопределенность типа
.
Преобразуем выражение под знаком
предела:
.
В показателе
степени имеем неопределенность типа
.
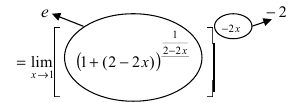
Заменой
при
на эквивалентную бесконечно малую
раскрываем ее:
.
Таким образом,
.
Замечание 8.4.
Аналогично доказывается равенство
.
Пределы
,
образуют две формы
одного и того же равенства, которое
также является замечательным
пределом
и часто служат определением числа
.
Задачи к §8
Задача
1. Вычислить

Решение.
Здесь имеем
неопределенность типа
.
Преобразуем числитель дроби к форме
произведения:

Затем
заменим бесконечно малую в точке
функцию
эквивалентной бесконечно малой
.
Тогда
получим
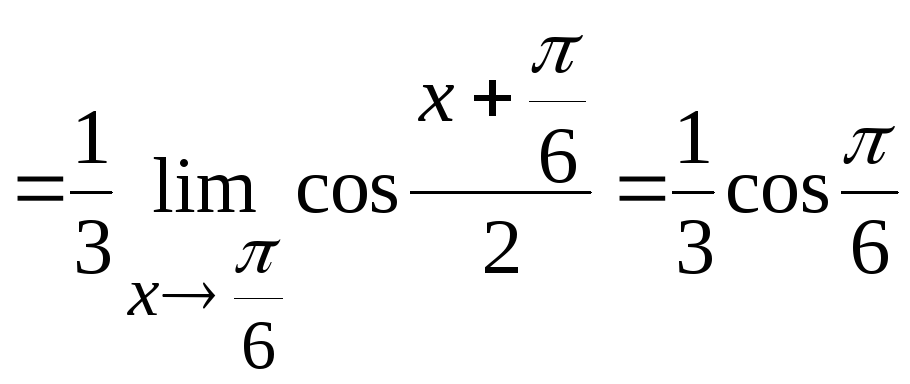
Ответ:
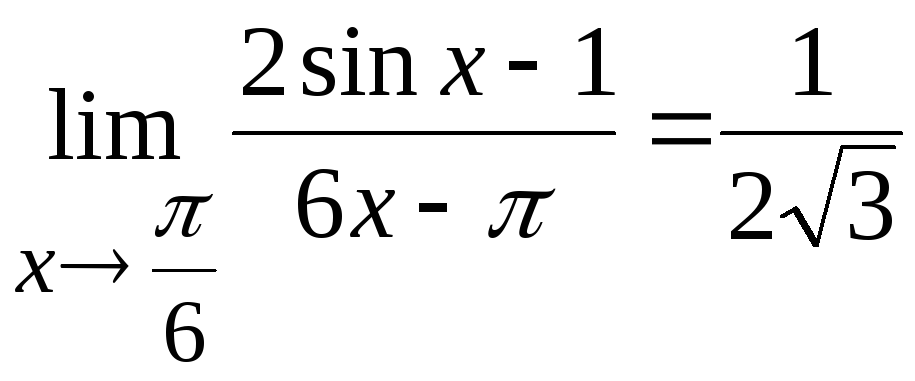
Задача
2. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Преобразуем знаменатель, воспользовавшись
свойствами логарифмической функции, и
выделим в аргументе логарифма слагаемое,
равное 1:
.
Заменим
бесконечно малую в точке
функцию
эквивалентной бесконечно малой
.
Числитель разложим на множители:
.
Тогда
получим:

Ответ:
.
Задача
3. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:
.
Затем
заменим его эквивалентной бесконечно
малой в точке
функцией
.
Функцию
в точке
тоже заменим на эквивалентную бесконечно
малую
.
Тогда
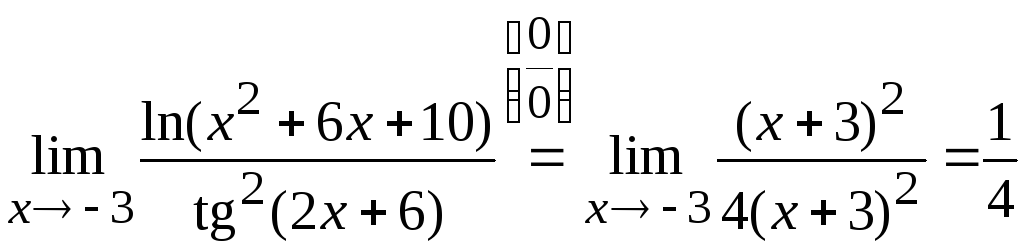
Ответ:
.
Задача
4. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:
.
Затем
заменим его эквивалентной бесконечно
малой в точке
функцией
.
Преобразуем
знаменатель:
и
заменим его на эквивалентную бесконечно
малую
.
Тогда получим
.
Ответ:
.
Задача
5. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Числитель
можно заменить эквивалентной бесконечно
малой
.
Чтобы
воспользоваться соотношением (8.4),
преобразуем знаменатель:
и
заменим его эквивалентной бесконечно
малой
.
Тогда
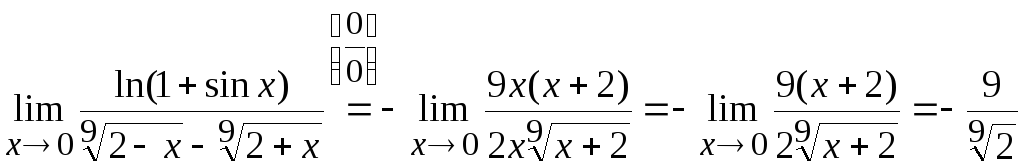
Ответ:
.
Задача
6. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к выражению
соотношение (8.3), представим его в виде:
,
и
заменим бесконечно малую функцию
эквивалентной бесконечно малой
.
Знаменатель же представим в виде:
и,
используя соотношения (8.2) и (8.8), заменим
его эквивалентной бесконечно малой
.
Учитывая проведенные выкладки и
соотношение (8.4), получим:
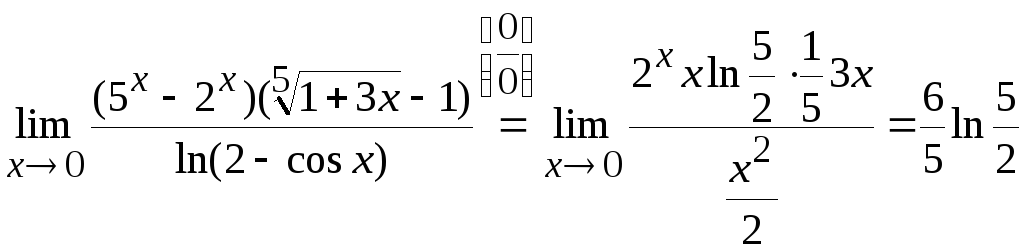
Ответ:
.
Задача
7. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7, получим
.
Ответ:
.
Задача
8. Вычислить
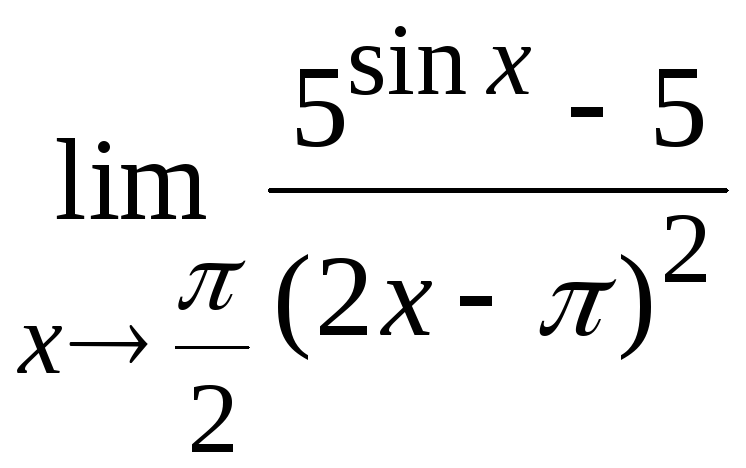
Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7 и формулы приведения для
тригонометрических функций, получим
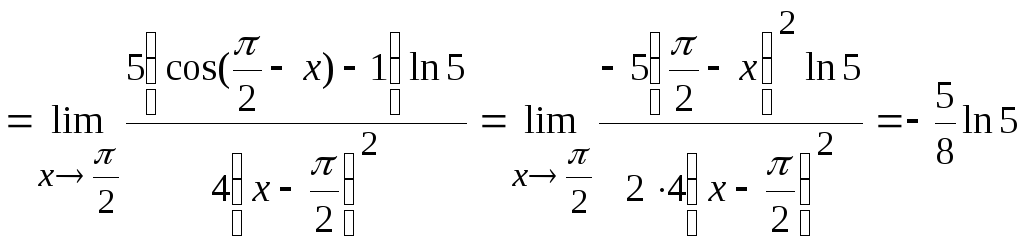
Ответ:
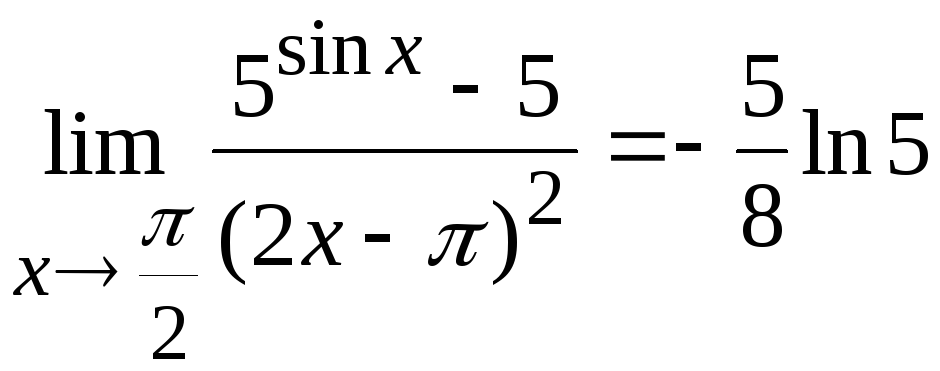
Задача
9. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к числителю соотношение
(8.2), преобразуем его следующим образом:
.
Теперь
числитель согласно соотношению (8.2)
можно заменить эквивалентной бесконечно
малой
.
Преобразуем
знаменатель
.
Заменяем,
используя соотношение (8.1),
эквивалентной бесконечно малой
.
Тогда

Ответ:
.
Задача
10. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Используя приемы, описанные выше, получим
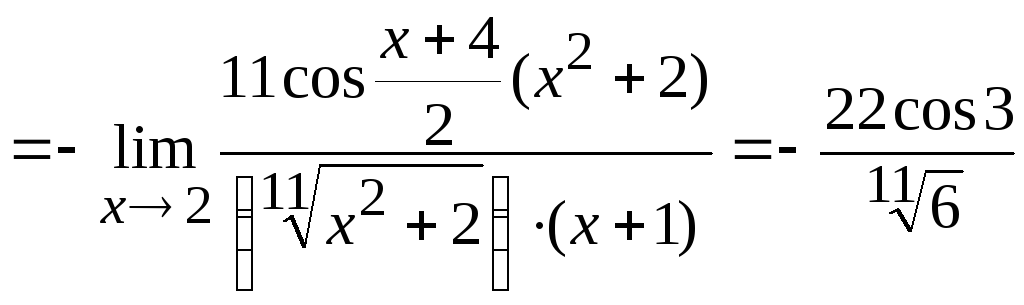
.
Ответ:
.
Задача
11. Вычислить

Решение.
Здесь имеем неопределенность типа
.
Используя теоремы 6.2 и 6.1, получим
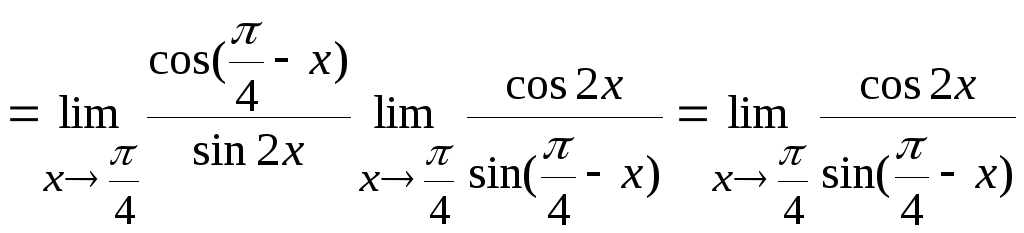
Получили
неопределенность типа
.
Преобразуем выражение с помощью формул
приведения, затем переходим к эквивалентным
бесконечно малым. В итоге получим
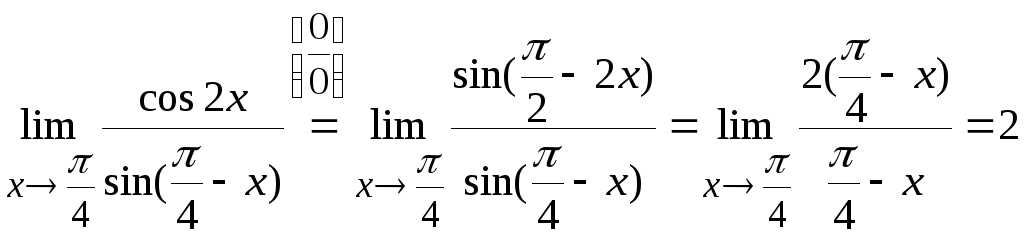
Ответ:
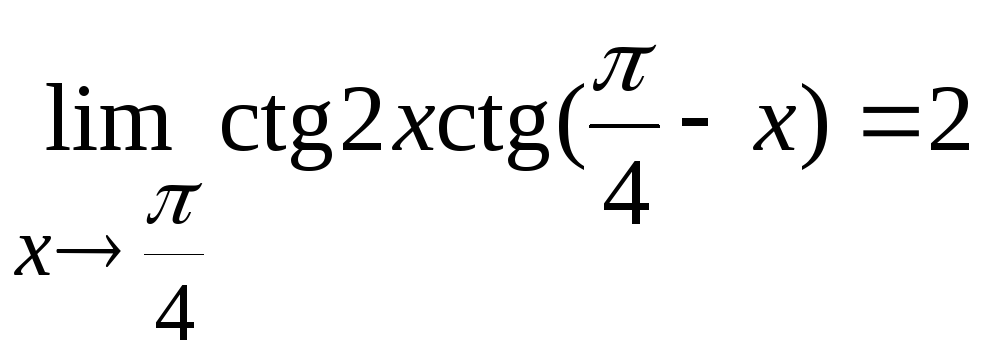
Задача
12. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Выделим
в основании степени:
.
Заметим,
что
при
.
Справедлива
цепочка равенств

Заменяя
логарифм эквивалентной бесконечно
малой согласно соотношению (8.2) и используя
замечание 6.4 для раскрытия неопределенности,
получим
.
Ответ:
.
Задача
134.
Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Введем переменную
.
Если
,
то
.
.
Выделим
в основании степени:
,
тогда
.
Заметим,
что
при
.
Заменим функцию
эквивалентной бесконечно малой
,
будем иметь
.
Используя
теорему 7.3, окончательно получим
.
Ответ:
.
Задача
14. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Поскольку
,
вычислим
сначала
.
Мы имеем дело с неопределенностью типа
.
Воспользовавшись
последовательно соотношениями (8.2) и
(8.1), будем иметь
.
Ответ:
.
Задача
15. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Воспользуемся формулой
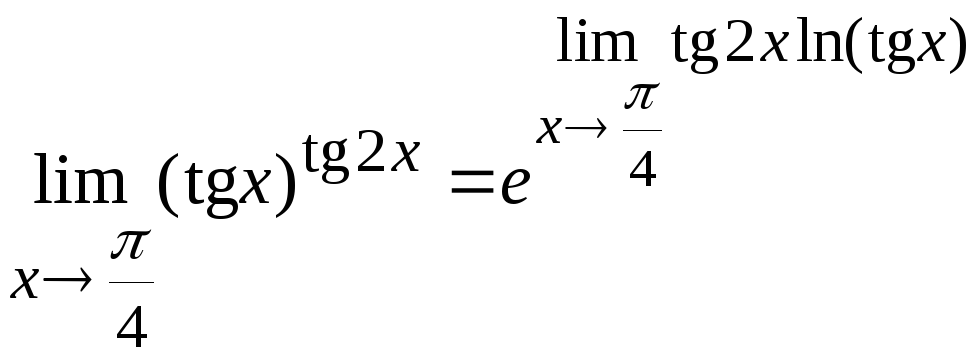
Вычислим
предел, стоящий в показателе степени.
Для этого требуется раскрыть
неопределенность типа
.
Преобразуем ее в неопределенность типа
и воспользуемся эквивалентностью
бесконечно малых:

Ответ:
.
Задача
16. Вычислить
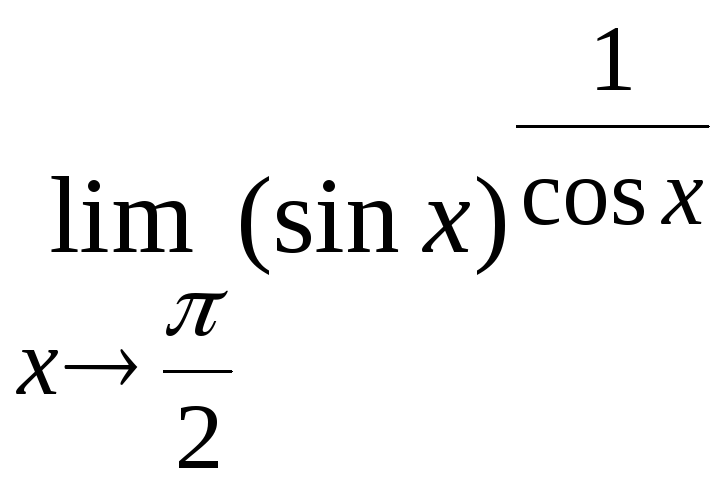
Решение.
Здесь возникает неопределенность типа
.
Преобразуем исходное предельное
выражение
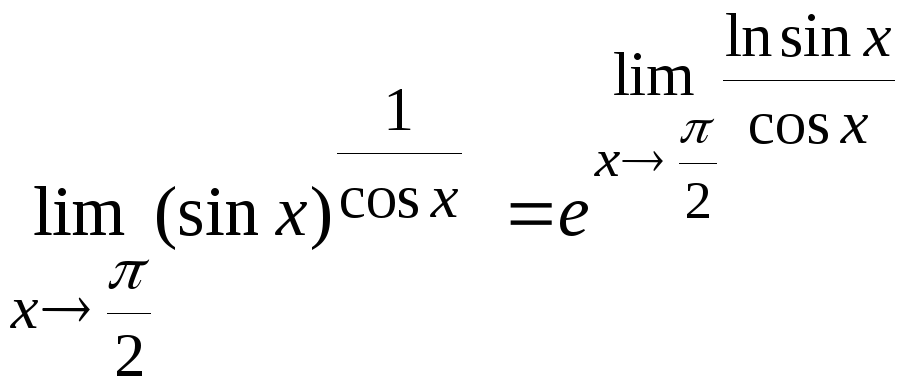
Вычислим
предел, стоящий в показателе степени.
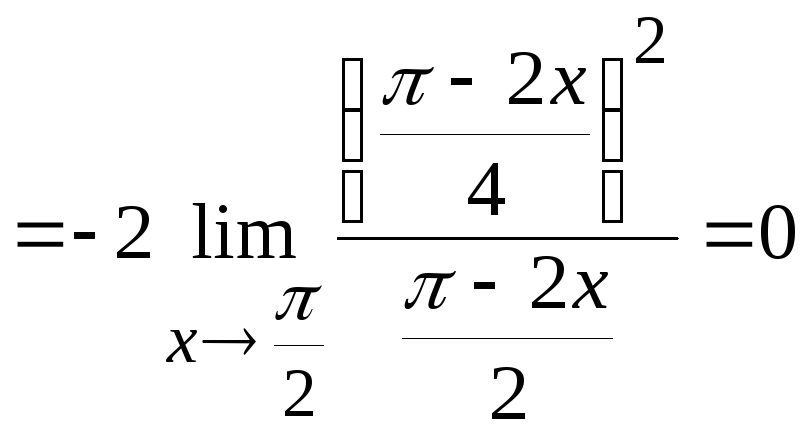
Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Продолжаем разбирать ответы к пределам функций и последовательностей. Примеров накопилось настолько много, что можно написать отдельную книгу — методичку по их вычислению.
В каждой публикации разжевываем методику вычислений до элементарных мелочей, при таких объяснениях каждый студент может без проблем решить подобные примеры.
Однако дальше от студентов поступают новые заказы с просьбой найти предел.
Порой нужно помочь с простыми функциями, что составляет впечатление что студенты имеют худшую подготовку, чем ученики в 11 классе, которые изучают эту тему.
Пример 11. Вычислить предел последовательности:
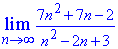
Решение: Подстановка большого номера в последовательность дает особенность вида бесконечность разделить на бесконечность. Для ее раскрытия в числителе и знаменателе дроби выделяем слагаемое, что вносит наибольший вклад. В скобках останутся константы + слагаемые, которые стремятся к нулю.
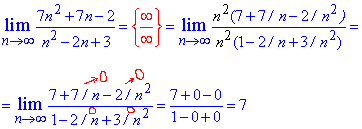
На общий множитель упрощаем, а константы дают значение предела последовательности.
Пример 12. Найти предел последовательности:
Решение: В предельном переходе имеем неопределенность вида бесконечность минус бесконечность. Функция представлена разницей корней. Чтобы избавиться от неопределенности, умножим и поделим разницу на сумму корней (сопряженное выражение). В результате придем к неопределенности бесконечность разделить на бесконечность. Чтобы ее раскрыть выносим множитель, что вносит наибольший вклад из числителя и знаменателя и сокращаем на него. Все что останется и будет пределом последовательности
Пример 13. Найти предел функции
Решение: При переменной стремящейся к нулю имеем неопределенность {0/0}. Для ее раскрытия разницу корней умножим и разделим на сопряженное выражение, чтобы в числителе образовать разность квадратов. В знаменателе имеем полином, который содержит особенность, поэтому разложим его на простые множители. После упрощений получим зависимость, предел которой легко находим методом подстановки
Пример 14. Вычислить предел
Решение: Переменная стремится к нулю, а функция задана долей синуса и тангенса в квадрате. В таких случаях нужно преобразовать выражение, чтобы в нем можно было легко выделить первый замечательный предел и его следствие. Для компенсации изменений в числитель и знаменатель записываем соответствующие константы. Далее переходим к произведению известных границ, вклад от каждой из которых равен единице.
Пример 15. Определить предел функции
Решение: При переменной стремящейся к нулю получим неопределенность вида единица в степени бесконечность. Для ее раскрытия выразим в степени множитель, который обратно пропорционален sin(4x).
Таким образом получим второй замечательный предел – экспоненту, а все что останется в показателе, даст степень экспоненты. Но здесь имеем долю sin(4x)/tan(3x), поэтому переходим к лимиту в показателе, а сам показатель сводим к первому замечательному пределу его следствии.
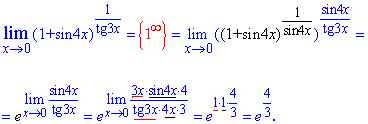
Из последнего «лимита» можно вывести простую формулу, которая может быть рассмотрена как следствие первого замечательного предела. Лимит доли тангенса к синусу (или наоборот) ровен доле их аргументов.
Пример 16. Найти предел последовательности:
Решение: Для раскрытия особенности вида бесконечность разделить на бесконечность необходимо три раза применить правило Лопиталя. Другая схема заключается в вынесении из числителя и знаменателя наибольшего множителя, и сокращении на него. В результате останутся константы и бесконечно малые функции. Последние стремятся к нулю, поэтому лимит последовательности равен
Пример 17. Вычислить предел последовательности:
Решение: Таких лимитов в предыдущих публикациях вычислено немало и суть раскрытия подобных неопределенностей заключается в умножении на сопряженное выражение – сумму корней. На это же выражение следует разделить функцию, чтобы не изменить значение лимита. В результате в числителе дроби получим разность квадратов и таким образом избавляемся от иррациональности, а предел выражения получим через оценку максимальных множителей.
Пример 18. Определить лимит функции
Решение: Когда переменная стремится к 3 имеем неопределенность вида {0/0}. Для раскрытия неопределенности в знаменателе дроби избавляемся от иррациональности умножением на сопряженное выражение, а в числителе полином раскладываем на простые множители. В результате и тат и там получаем выражение (х-3), на которое упрощаем.
Лимит функции, что осталась, вычисляем методом подстановки.
Пример 19. Найти предел функции
Решение: Предел функции в нуле дает особенность {0/0}. Ее не так просто раскрывать, как предыдущие.
Здесь следует свести выражение к первому и второму замечательному пределу и их следствиям.
Ln(1+x)/x в предельном переходе даст единицу, так же как и tan(x)/x и sin(x)/x.
Число 4/25 и будет лимитом функции.
Пример 20. Найти лимит
Решение: Предел функции в точке имеет неопределенность вида единица в степени бесконечность. Для ее раскрытия нужно преобразовать функцию под второй замечательный предел. Для этого и в скобках, и в показателе выделяем множитель, что вносит особенность (x-3) и делаем замену переменных t=x-3.
Далее переходим к экспоненте, и определяем лимит показательной функции.
Как Вы могли убедиться, задания на пределы не самые сложные в высшей математике.
Нужно знать не так много правил, чтобы без труда находить правильный ответ.
Пределы со степенями: показательная, степенная и показательно-степенная функции
Пределы со степенями бывают различных видов в зависимости от положения неизвестной $x$ в пределе. Рассмотрим примеры решений для следующих ситуаций:
- Показательная функция
$$limlimits_{xto a} a^{f(x)} = a^{limlimits_{xto a} f(x)} $$ - Степенная функция
$$ limlimits_{xto a} (f(x))^a = bigg(limlimits_{xto a} f(x) bigg)^a $$ - Показательно-степенная функция
$$limlimits_{xto a} bigg(f(x)bigg)^{g(x)} = limlimits_{xto a} frac{ln(f(x))}{frac{1}{g(x)}} $$
| Пример 1 |
| Найти предел показательной функции $limlimits_{xto 2} 2^{frac{x^2-4}{x-2}}$ |
| Решение |
|
Подставив точку $x=2$ в предел получим неопределенность $2^{big(frac{0}{0}big)}$. Итак, перенесем знак предела в показатель и попробуем его вычислить путем разложения числителя по формуле разности квадратов $a^2-b^2 = (a-b)(a+b)$. $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 2^{limlimits_{xto 2} frac{(x-2)(x+2)}{x-2}} = $$ Сокращаем числитель со знаменателем на $x-2$ и вычисляем предел степени. $$ =2^{limlimits_{xto 2} (x+2)} = 2^{2+2} = 2^4 = 16 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 16$$ |
| Пример 2 |
| Решить предел степенной функции $limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3$ |
| Решение |
|
Внесем знак предела внутрь скобок, а степень останется при этом снаружи. $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = bigg(limlimits_{xto 0} frac{sin x^2}{1-cos x}bigg)^3 = $$ При подстановке точки $x=0$ в предел получаем неопределенность $frac{0}{0}$. Для её устранения воспользуемся таблицей эквивалентностей пределов. $$sin x^2 sim x^2$$ $$ 1-cos x sim frac{x^2}{2}$$ Подставляем эквивалентные функции в предел и сокращаем $x$. $$ = bigg(limlimits_{xto 0} frac{x^2}{frac{x^2}{2}}bigg)^3 = bigg(limlimits_{xto 0} frac{2x^2}{x^2} bigg)^3 = 2^3 = 8$$ |
| Ответ |
| $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = 8$$ |
| Пример 3 |
| Вычислить предел показательно-степенной функции $limlimits_{xto 0} (tg x)^{sin x} $ |
| Решение |
|
Если подставим $x=0$, то получим предел ноль в степени ноль $(0^0)$. Превратим это в другую неопределенность $(frac{infty}{infty})$ с помощью третьей формулы. $$limlimits_{xto 0} (tg x)^{sin x} = limlimits_{xto 0} frac{ln (tg ;x)}{frac{1}{sin x}} = frac{infty}{infty} = $$ Используем правило Лопиталя для продолжения решения. По нему, как известно, предел отношения функций равен пределу отношения производных от этих функций. $$ = limlimits_{xto 0} frac{(ln (tg ;x))’}{(frac{1}{sin x})’} = limlimits_{xto 0} frac{frac{frac{1}{cos^2 x}}{tg ;x}}{-frac{cos x}{sin^2 x}} = $$ Преобразуем числитель в нормальный вид с помощью формулы $tg ; x = frac{sin x}{cos x}$ и выполняем все необходимые сокращения. $$ = limlimits_{xto 0} frac{frac{1}{sin x cos x}}{-frac{cos x}{sin^2 x}} = -limlimits_{xto 0} frac{sin x}{cos^2 x} = $$ Теперь подставляя точку $x=0$ возможно получить окончательный ответ. $$ = — frac{sin 0}{cos^2 x} = -frac{0}{1} = 0 $$ |
| Ответ |
| $$limlimits_{xto 0} (tg x)^{sin x} = 0$$ |
Рассмотрим два следствия из 2-го замечательного предела, с помощью которых можно найти предел показательной функции, в том числе, предел экспоненты.
Эти формулы можно применять и для случаев, когда на месте x стоит f(x), при условии, что при x→0, f(x)→0:
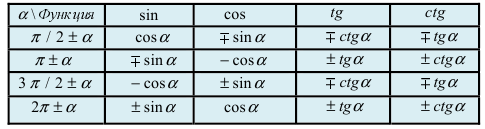
Проиллюстрируем, как найти предел показательной функции, в частности, предел экспоненты, на примерах.
Найти предел функции:
Сокращаем дробь на x. Получаем в числителе выражение вида (Ia), а значит, можем применить это следствие из 2-го замечательного предела:
Здесь мы вычли и прибавили единицу, поэтому в итоге значение выражения, стоящего в числителе, не изменилось.
Выносим общий множитель x за скобки и сокращаем на него:
В числителе получили выражения вида (Ia) и (IIа)
В числителе — выражение вида (Ia), в знаменателе — 1й замечательный предел:
Содержание:
Замечательные пределы
Сравнение бесконечно малых функций
Признак существования предела (теорема о 2-х милиционерах)
Теорема: Если значения функции
значениями функций
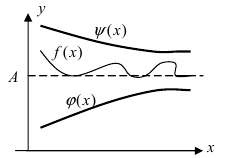
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции 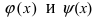
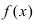
Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.
Доказательство: Пусть 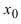
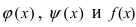
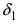
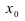
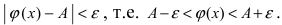
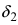
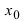
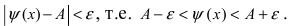
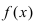
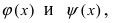
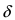
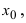
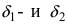
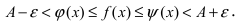
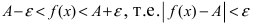
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 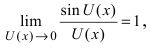
Пример:
Пределы являются первыми замечательными пределами 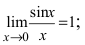
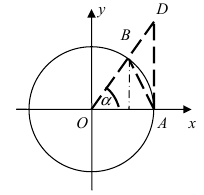
Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 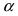
Рис. 63. Иллюстрация вывода формулы первого замечательного предела.
Из рисунка видно, что площади указанных фигу р связаны соотношением:
Вычислим эти площади
Следовательно, вышеприведенное неравенство приводится к виду 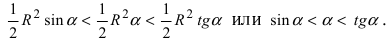
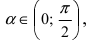
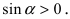
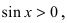
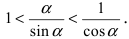
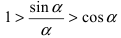
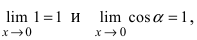
Аналогично проводится доказательство для любого значения угла
Таким образом, наличие в пределе, сводящемся к неопределенности 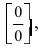
При вычислении первого замечательного предела используют следующие формулы:
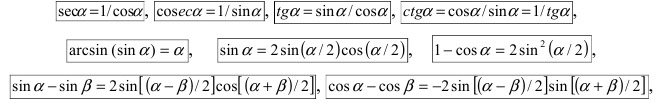
Табл. 1. Значения синуса и косинуса на интервале
Табл. 2. Формулы приведения.
Пример:
Найти
Решение:
При подстановке предельной величины переменной х имеем неопределенность 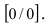
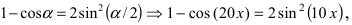
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 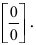
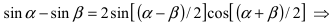
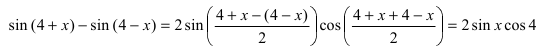
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 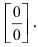
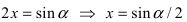
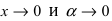
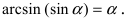
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 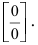
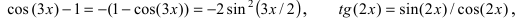
Число e и натуральные логарифмы. Второй замечательный предел
Рассмотрим логарифмическую функцию 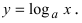
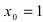
Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.
Основанием натурального логарифма является число 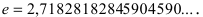
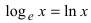
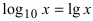
Определение: Вторым замечательным пределом называется предельное равенство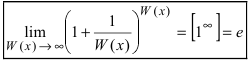
или
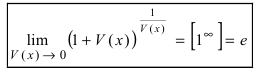
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 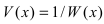
Замечание: Наличие неопределенности 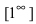
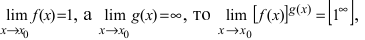
Пример:
Найти
Решение:
При подстановке предельного значения переменной х не имеем неопределенности
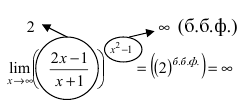
Пример:
Найти lim
Решение:
При подстановке предельного значения переменной х имеем неопределенность 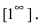
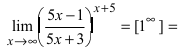
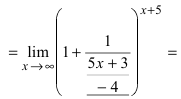
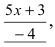
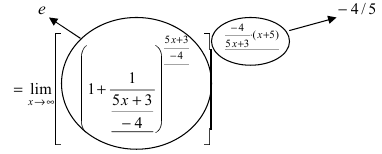
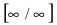
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределенность 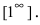
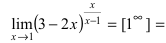
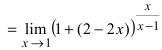
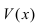
- Заказать решение задач по высшей математике
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 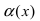
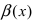
Определение: Если предел К не существует, то бесконечно малые функции 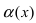
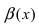
Пример:
Пусть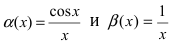
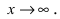
Решение:
Для доказательства вычислим предел 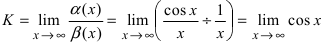
Определение: Если предел К равен нулю, то бесконечно малая функция 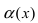
Пример:
Пусть 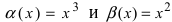
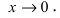
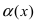
Решение:
Для доказательства вычислим предел 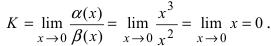
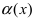
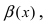
Определение: Если предел К равен 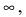
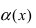
Пример:
Пусть 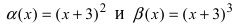
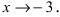
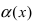
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малая функция 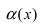
Определение: Если предел К равен конечному числу 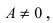
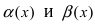
Пример:
Пусть 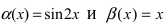
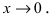
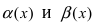
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малые функции 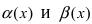
Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.
Пример:
Пусть 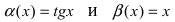
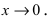
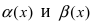
Решение:
Вычислим предел 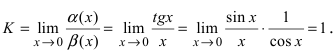

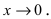
Теорема: Для того чтобы бесконечно малые функции 
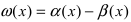

Доказательство:
1. Необходимость. Пусть бесконечно малая функция 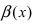
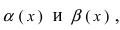
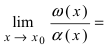
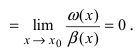
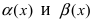
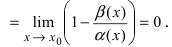
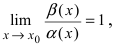
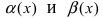
2. Достаточность. Пусть бесконечно малые функции 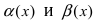
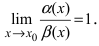
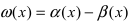
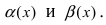
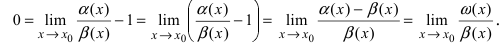
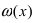
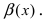
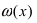
Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 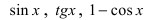
—вышмат
Замечательные пределы
Первый замечательный предел
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
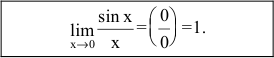
Пример №25
Найти
Решение:
Применим первый замечательный предел:
Второй замечательный предел
Числом е называется предел функции
(Для запоминания: 2<е<3; 1828 — год рождения Л.Н. Толстого) Следовательно,
Задача о непрерывном начислении процентов
Первоначальный вклад в банк составил 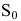
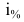
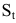
Решение:
Размер вклада будет увеличиваться ежегодно в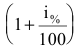
через t лет составит 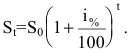
то будущая сумма составит 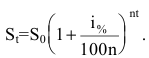
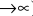
а за t лет:
Пример №26
Найти
Решение:
Т.к. 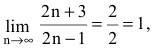
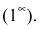
Пример №27
Найти
Решение:
Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции



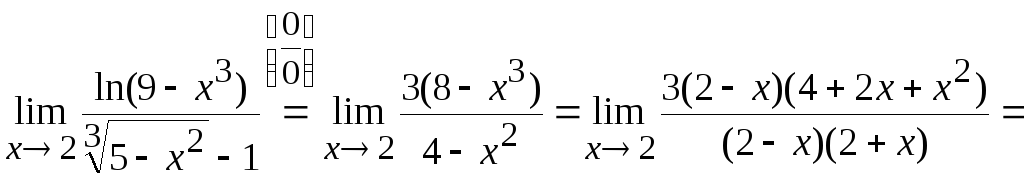
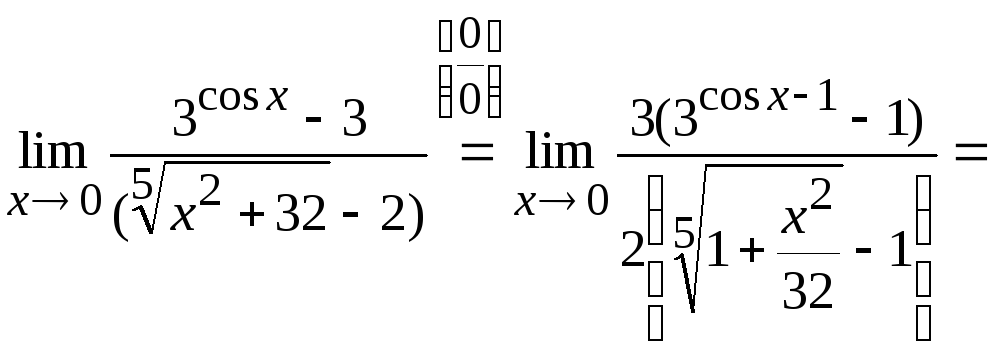
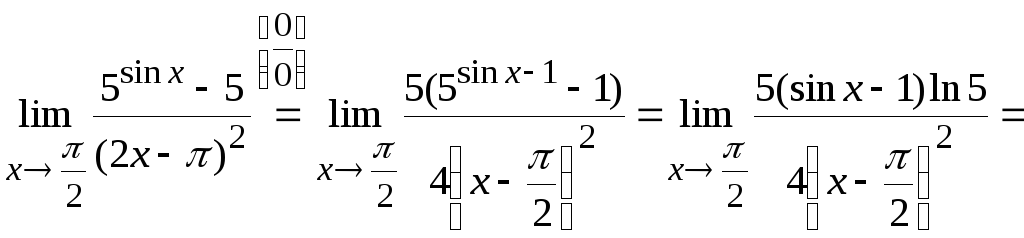




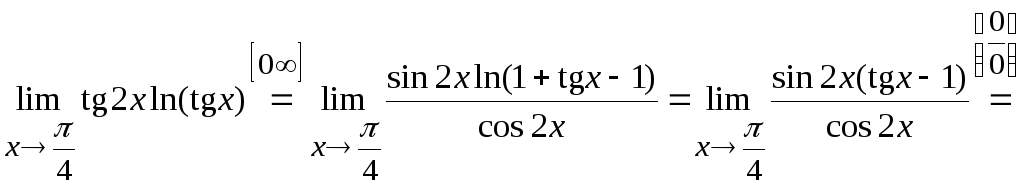
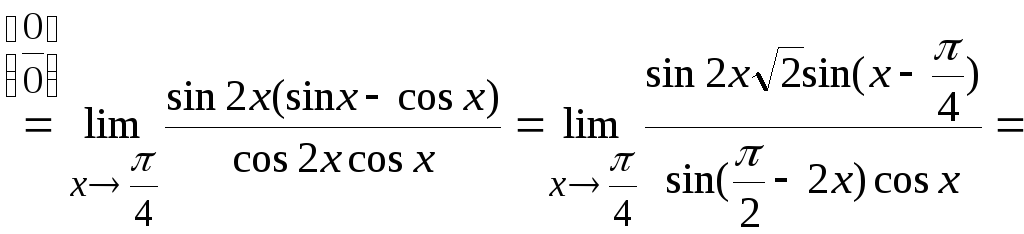

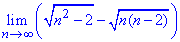
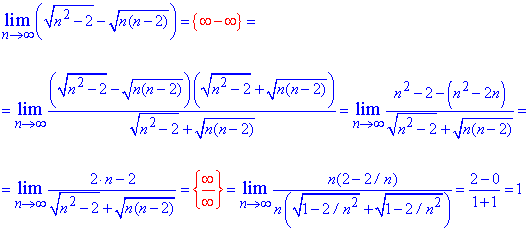
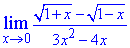
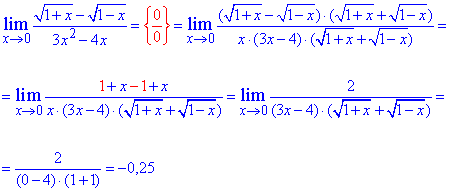
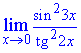
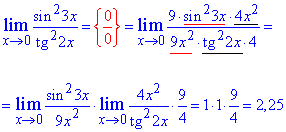
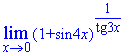
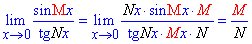
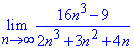
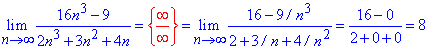
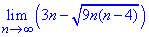
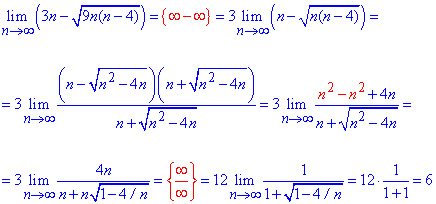
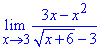
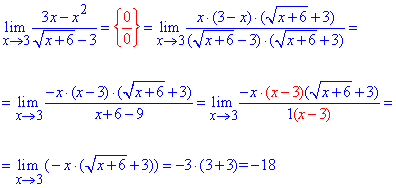
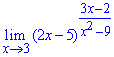
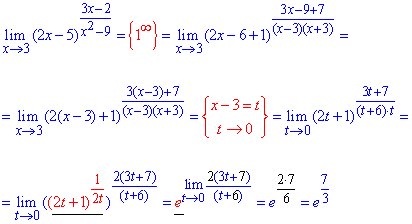
![Rendered by QuickLaTeX.com [3)mathop {lim }limits_{x to 0} frac{{{e^{10x}} - 1}}{{sin 11x}} = left[ {frac{0}{0}} right] = mathop {lim }limits_{x to 0} frac{{frac{{{e^{10x}} - 1}}{{10x}} cdot 10x}}{{frac{{sin 11x}}{{11x}} cdot 11x}} = mathop {lim }limits_{x to 0} frac{{frac{{{e^{10x}} - 1}}{{10x}} cdot 10}}{{frac{{sin 11x}}{{11x}} cdot 11}} = ]](https://www.matematika.uznateshe.ru/wp-content/ql-cache/quicklatex.com-c5ccb15465529f56363caf966e9ee4fd_l3.png)