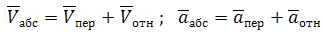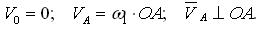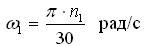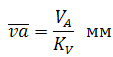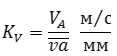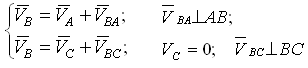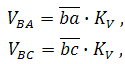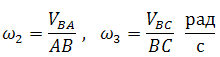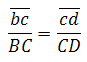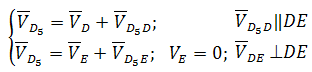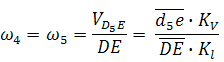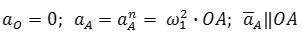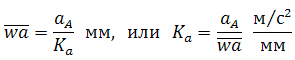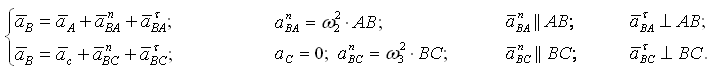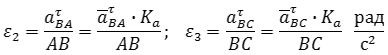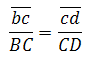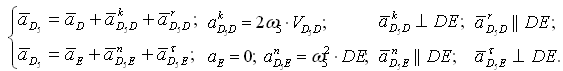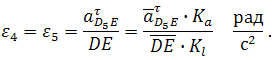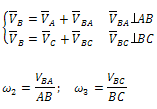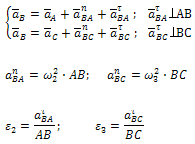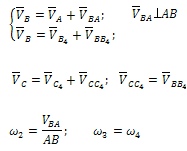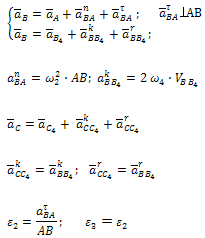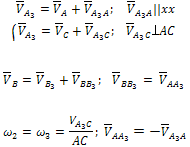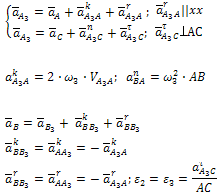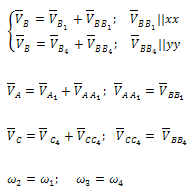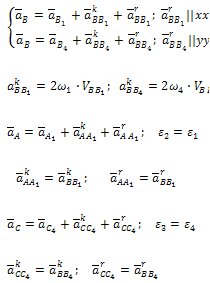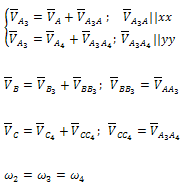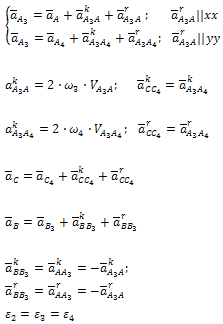Как найти полюс плана - Autoru.top - решение различных проблем

Лекция № 5

Определение скоростей и ускорений точек механизма методом планов

Наиболее
распространенным методом исследования
является графо-аналитический метод –
метод планов скоростей и ускорений.

Планом скоростей
(ускорений) называют рисунок на котором
в масштабе изображены векторы, равные
по модулю и направлению скоростям
(ускорениям) различных точек звеньев
механизма в данный момент времени.

План скоростей
(ускорений) построенный для исследуемого
положения механизма, это совокупность
нескольких планов скоростей (ускорений)
отдельных точек звеньев, у которых
полюса планов являются общей точкой-полюсом
плана скоростей (ускорений) механизма.

Планы скоростей
(ускорений) механизма могут строиться
как для каждого положения отдельно, так
и быть совмещенными.

Из теоретической
механики известно, что любое движение
точки звена может быть составлено из
переносного движения известной точки
и относительного движения, искомой
точки относительно известной

Движение звена
относительно основной системы отсчета
называется абсолютным движением.
Движение звена относительно подвижной
системы отсчета называется относительным
движением. Движение подвижной системы
отсчета относительно основной называется
переносным.

При сложном движении
тела абсолютная(ое) скорость
(ускорение)
точки равна векторной сумме переносной(го)()
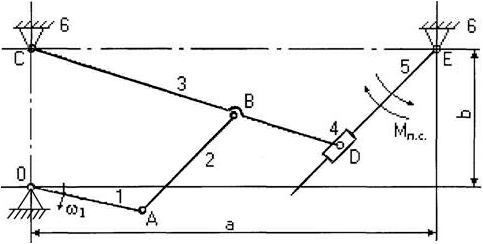
и относительной (го)скоростей (ускорений) этой точки, т.е.

(5.1)

(5.2)

где
и—
соответственно нормальное ускорение
в относительном движении, направленное
по радиусу вращения точки к центру
кривизны траектории (центру вращения)
и касательное ускорение, направленное
перпендикулярно радиусу вращения.

Планы скоростей и ускорений начального звена

Если начальное
звено механизма совершает вращательное
движение, то скорость его любой точки
например В,
определится: если задана частота вращения
n,
то
,

тогда:

где
—
скорость точкиВ,
l_АВ
– кратчайшее расстояние от оси вращения
до точки В,
—
угловая скорость звена АВ. Скорость
точкиВ
перпендикулярна
прямой АВ, (),
может быть изображена на плане скоростей
(на рис.5.1 б) как вектор,
модуль которого будет:

«рв»
=
,

где
— масштабный коэффициент скоростей.

«р»
— полюс плана скоростей; «в»
— одноименная точка на звене.

Аналогичным образом
могут быть построены скорости любых
других точек, принадлежавших этому
звену.

а)
б)
в)

Рис. Скорости
точки, ускорения и ее планы

б) – план скоростей для точки В
начального звена

в) – план ускорений для точкиВначального звена АВ.

На плане ускорений
– вектор ускорений точки В —и ее составляющие:
—
нормальное и
—
касательное.

;
II
АВ;
(масштабный
коэффициент)

;

(-угловая
скорость звена)

ускорение

Ускорение других
точек начинающего звена находятся и
строятся аналогичным образом.

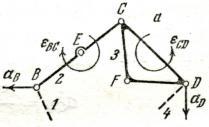
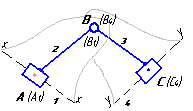
Определение скоростей и ускорений групп II класса методом планов

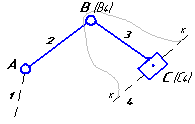
Рассмотрим группу
II
класса первого вида

Кинемат. схема II
класс 1 вид

План скоростей II
класс 1 вид

ДАНО:векторы
абсолютных скоростей точекB,
D.

векторы
скоростей точки С
относительно точек В и D.

Известны векторы
скоростей точек В и D
концевых элементов группы, которыми
звенья 2 и 3 (присоединяются), входят в
кинематические пары со звеньями 1 и 4
основного механизма, т.е. скорости
и.

Требуется определить
вектор
скорости т. С.

Движение т. С может
быть разложено на переносно-поступательное
со скоростью точки В или точки D
и относительно-вращательное вокруг
точки В или точки D.
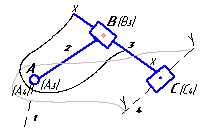
Тогда векторные уравнения для скорости

точки С будут иметь вид:

решая
совместно уравнения получаем

(5.3)

Чтобы построить
план скоростей, выбираем

Масштаб
;

Выбираем в качестве
полюса плана скоростей точку «р»,
где
,
откладываем по направлениюи векторрвкак
и
от
нее отрезки(рв)
и (рd),
представляющие собой скорости точек
и.
Проведем через т.«в»
и «d»
прямые, имеющие направление векторов
относительных скоростей
и. Пересечение прямых даст т.«с».
Точка «с»
определит конец вектора
согласно (5.3) выражается отрезком(рс),
соединяющим т. «р»
с полученной точкой «с».

Величина этой
скорости будет равна

Отрезки (вс)
и (dс)
представляют собой относительные
скорости
ив том же масштабе, т.е.

Треугольники
рвс
и рdc
– называются
планами
скоростей звеньев
№ 2 и № 3, Фигура рвсdр
– называется
планом скоростей группы ВСD,

точка «р»
— плана
называется полюсом плана скоростей.

Пользуясь планом
скоростей можно определить угловые
скорости
извеньев № 2 и № 3. Если группа ВСD
выполнена в произвольном масштабе
то

Для определения
скорости какой либо точки Е, лежащей на
оси звена ВС имеем векторное уравнение

Согласно этому
уравнению из т. «в»
плана скоростей проводим направление
вектора
относительной скорости точки. Е вокруг
точки. В. т.к. относительные скорости
любых точек, лежащих на оси ВС звена 2,ВС, то направление
совпадает с
направлением вектора скорости
,
т.е. отрезок плана скоростей(ве),
определяющий скорость
совпадает по направлению с отрезком(вс).
Величина отрезка определяется:

(1),
и

(2)

разделив уравнение
(2) на уравнение (1) получаем:

т.е. скорости
точек Е и С относительно т. «В» прямо
пропорциональны расстояниям этих точек
до т. В.

Для определения
скорости какой либо произвольной точки
F
на звене №3: также составляем уравнения:

Векторы
искоростей т.D
и C
нам известны по величине и по направлению,
а векторы
иизвестны только по направлению. ВекторотрезкуFD,
а вектор
.
Из т.d-плана
скоростей проводим прямую
FD,
а через т. «с»-
прямую
FC,
точка пересечения «f»
определяет конец вектора
полной скорости т. «F»,
отрезок «рf».

Для удобства
графического построения плана скоростей
всех звеньев группы, иногда план условно
повертывают в одном и том же направлении
на угол
.
Тогда векторы относительно скоростейибудутII
ВС и DC.

Рассматривая
плана скоростей иCFD
на звене, можно видеть, что отрезки сf,
fd,dc
на плане скоростей соответственно
к
отрезкам (CF),
(FD),(DC)
на схеме

т.е.
на
плане скоростей изображающий относительные
скоростигруппы на ее схеме и повернуты относительно
его на угол, в.
Это свойство подобия фигуры относительных
скоростей на плане скоростей фигуре
звена на схеме механизма позволяет
определять скорости любых точек этого
звена не из уравнений, а графически,
построением подобных фигур.

Для проверки
правильности графического построения
подобных фигур на схеме и на плане
скоростей: При обходе контура звена по
часовой стрелке на схеме например CDF,
должно совпадать в том же порядке на
плане скоростей: cdf

При определении
ускорений группы II
класса первого вида, известны векторы
иполных ускорений точек В иD.
Для определения ускорения а_сточки «С»,
как и для определения скорости
,точки
«С»,
рассматриваем ее движение как сложное,
состоящее из переносного со скоростями
и ускорениями т. В и D
и относительного
вращательного вокруг этих точек. Тогда
векторные уравнения для определения
ускорения точки С

(5.5)

где
инормальные
ускорения в относительном движении

и—
тангенциальные ускорения

Решая совместно
уравнения получаем

(5.6)

и
— известны

Масштаб: 1мм —
(м/с²)

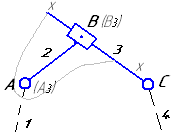
Кинемат. схема II
класс 1 вид

План ускорений II
класс 1 вид

План скоростей
предполагается построенным, т.е. известны
скорости всех звеньев, тогда. Векторы
нормальных ускорений
,в относительном движении может быть
определены:

;

Скорости
ии угловые скоростиимогут быть определены по построенному
плану скоростей, длиныl₂
и l₃
звеньев 2 и 3 определяют по схеме подставляя
в полученные равенства длины из плана
скоростей в масштабе
и со схемы,
получаем

;

(5.7)

где отрезки (вс)
и (dc)
взяты из плана скоростей.

В качестве полюса
плана выбираем точку «»
и откладываем отрезки ()
и ()-
в масштабеускорений
точек В иD.
Далее по уравнениям (5.7) вычисляем
величины ускорений
ии откладываем из точкив
и d
отрезки вn₂
и dn₃,
и представляющие в масштабе эти ускорения.
Из полученных точек n₂
и n₃
проводим прямые в направлении векторов
тангенциальных ускорений
,перпендикулярно ВС и СD.
Точка пересечения этих прямых и даст
конец вектора
полного ускорения точки С, т.е..
Построенные фигурыиносят
название планов ускорений звеньев 2 и
3, а вся фигура—
называется планом ускорений группыBCD.
Точка
—
называется началом или полюсом плана
ускорений.

Соединив точки
«в»
и «d»
плана с точкой «С»,
получим векторы полных относительных
ускорений
и.
Имеем:
=;

Модули угловых
ускорений:
;(5.8)

звеньев ВС и CD

Подставляя
соответствующие отрезки взятые из
ускорений в равенство, получаем

;

Для определения
ускорения какой-либо точки Е, лежащей
на оси звена ВС воспользуемся уравнением:

Как известно из
теоремы механики при вращательном,
плоском движении звена около некоторой
точки, ускорения всех точек звена
пропорциональны радиусом-вектором,
соединяющим исследуемые точки центром
вращения, направления этих ускорений
образуют с этими радиусами постоянный
угол
, определяемый из уравненияtg=,
где
-есть
угловое ускорение звена, а—
угловая скорость звена.

Т.к. относительное
движение звена 2 около точки В есть
движение вращательное, то, очевидно,
что относительные ускорения всех точек
звена 2 будут образовывать с радиусами-
векторами, выходящими из точки В,
постоянный угол
, удовлетворяющий соотношению

,
следовательно, направление вектора
должно
совпадать на плане ускорений с направлением
вектора,
т.е. с направлением отрезка (вс),
величина же отрезка (вl)
изображающего на плане ускорений
ускорение
,
определяется из условия пропорциональности
ускорений радиусом-вектором, т.е.

;

Для определения
ускорения точки F
жестко связанной со звеном 3, можно токже
воспользоваться правилом подобия. Для
этого строим на отрезке (сd)
плана ускорений
,
повернутый относительнона постоянный угол,
определяемый по формуле:.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

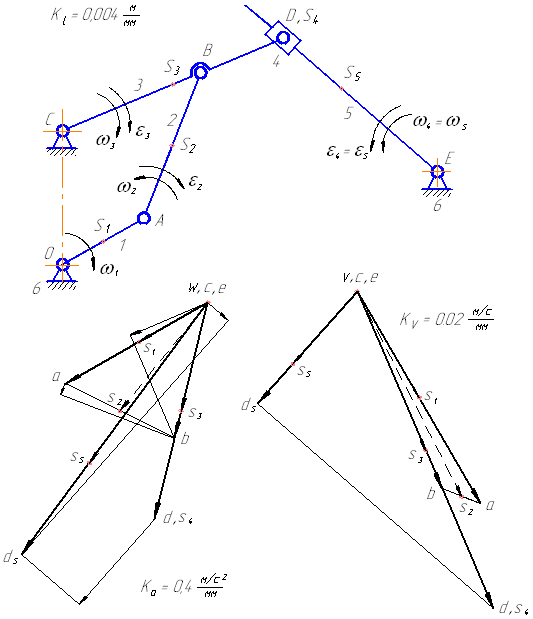
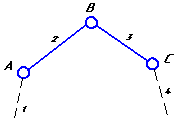
Рассмотрим порядок построения планов скоростей и ускорений точек звеньев на примере кинематического исследования плоского рычажного механизма (рисунок 1).

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:

На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.

На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.

Рисунок 1 – Кинематическая схема плоского рычажного механизма

Другие примеры решений >
Помощь с решением задач >

Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.

Начальный механизм:

Здесь

По вычисленному значению V_A выбираем масштаб плана скоростей K_V и из произвольного полюса откладываем отрезок va изображающий эту скорость:

Можно также назначать отрезок va а масштаб K_V вычислять:

Группа Ассура второго класса 1-го вида (звенья 2, 3):

Истинные значения (в м/с) относительных скоростей V_BA и V_BC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:

а зная их, можно определить и угловые скорости звеньев 2 и 3:

Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:

Группа Ассура второго класса 3-го вида (звенья 4,5) :

где D₅ — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D₅ относительно точки E можно вычислить угловую скорость звеньев 4 и 5 (ω₄=ω₅, т. к. эти звенья соединяются поступательной парой):

Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.

План ускорений строится в таком же порядке.

Начальный механизм

Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена (ω₁=соnst):

По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):

Здесь точка w – полюс плана ускорений.

Группа Ассура (звенья 2,3) второго класса 1-го вида:

После построения определяются a^τ_BA и a^τ_BC, по которым можно вычислить угловые ускорения звеньев 2 и 3:

Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:

Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма

Группа Ассура (звенья 4,5) второго класса 3-го вида:

Для определения направления a^k_D5D надо вектор V_D5D повернуть на 90° в направлении ω₅. Угловые ускорения:

При силовом расчете необходимо иметь ускорения центров масс (a_si), которые на плане ускорений определяются методом подобия.

Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.

Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.

Таблица 1 – Кинематический анализ групп Ассура II класса методом планов

Вид группы

Конфигурация
группы

Уравнения для построения планов скоростей и для определения угловых скоростей

Уравнения для построения планов ускорений и для определения угловых ускорений

Пример расчета механизма с поступательно движущимся выходным звеном >
Курсовой проект по ТММ >

Источник

Векторы ускорений асв и асс.< входящие в уравнение (4.43), известны только по направлению. Первый вектор асв перпендикулярен к направлению ВС, а второй вектор асе, параллелен оси X — X направляющей поступательной пары D. Таким образо.м, в уравнении (4.43) неизвестны только величины ускорений а св и асс,- Для их определения строим план ускорений. Для этого (рис. 4.20, б) выбираем произвольную точку л за полюс плана ускорений и откладываем от нее известные ускорения точек В [c.89]

Задача об ускорениях группы III класса стремя поводками решается аналогично задаче о скоростях. Здесь, так же как и для определения скоростей, пользуемся особой точкой S, на звене 7 (рис. 4.26, а). В качестве такой точки может быть выбрана любая из трех особых точек. Построение ускорений всех точек группы может быть выполнено следующим образом. Выбираем на плоскости произвольную точку я (рис. 4.26, в) за полюс плана ускорений и откладываем от нее отрезки л6, лс и лс1, изображающие в масштабе ц,, ускорения а , йс и Дд точек В, С uD. Ускорение as, особой точки Si определится из уравнений [c.98]

Векторное уравнение (3.5) можно изобразить в виде векторной диаграммы, которая называется планом ускорений и показана на рис. 3.5, б. Для этого из произвольной точки -л, называемой полюсом плана ускорений, отложим вектор т.а, который в масштабе изображает вектор ускорения полюса ал. Масштабный коэффициент = ол/(т а) показывает, сколько единиц ускорения содержится в одном миллиметре вектора на плане. [c.32]

Из полюса плана ускорений (рис. 4.17, в) откладываем отрезок лЬ», равный радиусу OBi кулачка на плане механизма (рис. 4.17, а) и изображающий ускорение [c.77]

Приняв некоторую точку я за полюс плана ускорений (рис. 16, в), отложим вектор, изображающий нормальное ускорение точки В в виде отрезка яп)Тогда масштабный коэффициент [c.38]

Систему уравнений (1.11) решим графически. На чертеже (рис. 1.14, в) обозначим полюс плана ускорений и выберем [c.24]

Из полюса плана ускорений в масштабе откладываем отрезок и отмечаем в полюсе точку так как ускорение точки равно нулю. Кориолисовы ускорения и равны [c.29]

Третий случаи. Если звенья / и 2 входят в высшую кинематическую пару С (рис. 101, в), то вводя заменяющее высшую пару звено, которое входит во вращательные пары, можно решить задачу на основании уравнений (4.29.) и (4.30). Чертеж (рис. 102, б, в), на котором все векторы, выражающие в некотором масштабе абсолютные скорости или в масштабе i — абсолютные ускорения точек звеньев и имеющие общее начало, называют соответственно полярным планом скоростей или планом ускорений. Точку или р , от которой откладываются указанные векторы, называют соответственно полюсом плана скоростей или полюсом плана ускорений. [c.73]

Все отрезки перечисленных нормальных и кориолисова ускорений необходимо предварительно вычислить. Полюс плана ускорений находим из построения. [c.22]

Постоянные неподвижные точки механизма (неподвижные шарниры) имеют соответствующие им точки плана ускорений расположенными в полюсе. Непостоянные неподвижные точки механизма (абсолютные мгновенные центры звеньев) имеют ускорения, не равные нулю, а поэтому соответствующие им точки плана ускорений не находятся в полюсе. Подвижные точки звеньев механизма, соответствующие полюсу плана ускорений, которые можно найти по теореме подобия, носят название мгновенных центров ускорений. В них ускорения точек звеньев в данный момент времени [c.159]

Направление его будет по кривошипу к центру вращения О. Отложим вычисленное ускорение в некотором масштабе от полюса плана ускорений в виде отрезка = да Ц АО (рис. 215). [c.166]

АО, поэтому удобно за полюс плана ускорений выбрать центр О и считать его концом всех абсолютных ускорений (фиг. 500, г) [c.358]

Из произвольной точки тс, называемой полюсом плана ускорений, в направлении вектора ад откладываем отрезок [тс а (рис. 2.16, в). [c.42]

Порядок построения плана ускорений. План ускорений следует строить рядом с планом скоростей. Вначале выбираем произвольную точку Ра, которую будем называть полюсом плана ускорений (рис. 143). [c.165]

Из полюса плана ускорений откладываем вектор Р Ь нормального ускорения точки В. Этот вектор всегда направлен по звену к центру его вращения, в данном случае от точки В к точке А (см. рис. 141). [c.166]

Подобно тому, как это имело место в задаче о скоростях, векторы абсолютных ускорений всех точек звеньев имеют своим началом точку It — полюс плана ускорений, а векторы всех относительных ускорений соединяют концы векторов абсолютных ускорений. [c.130]

Выбираем в качестве полюса плана ускорений точку % (рис. 270, б) и откладываем отрезки (пгй) и ( ), представляющие в масштабе (д.д ускорения точек В я О. Далее, пользуясь уравнениями (6.39), вычисляем величины ускорений и и откладываем из точек Ь а (I [c.168]

Для их определения строим план ускорений. Выбираем за полюс плана ускорений точку я (рис. [c.175]

Вследствие того, что тангенциальные ускорения неизвестны, положение полюса плана ускорений будем искать построением. Отложив (рис. 4.29, в) из произвольной точки чертежа последовательно отрезки Ь хЬ», Ь Ь , пропорциональные и а , и вычтя из суммы трех отрезков отрезок пропорциональный а (т. е. прибавив отрезок Ь Ь» ), через начало первого и конец последнего отрезков проведем направления, параллельные тангенциальным ускорениям а д и а , т. е. перпендикуляры соответственно к О В и О3В. Пересечение тангенциальных ускорений опре-делит положение плана полюса Ра ускорений. Построив на отрезке РаЬ треугольник, подобный О АВ, найдем конец а вектора ускорения точки А. [c.116]

Построение плана ускорений также рассмотрим для 5-го положения механизма (рис. 108, в). Принимая, что кривошип враш,ается с постоянной угловой скоростью, точка /4 кривошипа будет иметь только нормальное ускорение. Поэтому от произвольной точки л полюса плана ускорений по направлению от A , к 0 откладываем параллельно отрезок па 2, представляюш,ий собой ускорение [c.257]

Построим уравнение (3.16) в виде суммы векторов (рис. 26, б). Выбираем точку п—полюс плана ускорений. Откладываем из полюса вектор ад отрезка произвольной дли-ны ла, направленного параллельно вектору Эд. Определяем масштабный коэффициент [c.41]

Построение плана ускорений ведем в такой последовательности (рис. 24, г). Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана я откладываем отрезок (лЬ), изображающий ускорение ад, параллельно линии АВ. Длину (яй) выбираем равной (АВ) = 25 мм, т. е. строим план в масштабе кривошипа, при этом масштабы планов ускорений и их аналогов соответственно будут равны [c.46]

Соединив точку d с полюсом плана я, получаем отрезок (nd), изображающий ускорение точки D. [c.47]

Выбираем в качестве полюса плана ускорений точку я (рис. 4.18, б) и откладываем отрезки (пЪ) и (кф, представляющие в масштабе Лд ускорения точек S и D. Далее, пользуясь уравнениями (4.32), вычисляем величины ускорений а св и Лсо и откладываем из точек Ь п d отрезки Ьп ) и (diis), представляющие в масштабе fio эти ускорения. Из полученных точек 2 и з проводим прямые в направлениях векторов тангенциальных ускорений агв и a D перпендикулярно к направлениям ВС и D. Точка пересечения этих прямых и даст конец вектора ас полного ускорения точки С, т. е. [c.85]

Построенные фигуры пЬп с и пйщс носят название пшнов ускорений звеньев 2 и 3, а вся фигура пЬпп,сп- сЫ называется планом ускорений группы B D. Точка п называется началом или полюсом плана ускорений. [c.85]

Заметим, что наше построение не нарушится, если при построении заштрихованного треугольника мы возьмем вершину не в цу, а в любой точке е неподвижной плоскости. Точку е называют полюсом плана ускорений. Применение плана ускорений к определению ускорений точек фигуры покйзано в задаче № 99. [c.243]

Дл»я определения искомых величин строим план ускорений. Для этого отмечаем на чертеже точку л, которая называется полюсом плана ускорений (см. рис. 100, б). Из полюса проводим вектор пв, направленный по орту из его конца проводим вектор Исв. а через конец этого вектора — вектор i в (его длина неизвестна). После этого из полюса я проводим вектор Пс, а из его конца — вектор t . Пересечение векторов t в и t определяет точку с, в которой сходятся концы векторов t в, чосв и о>с. где чюсв есть аналог полного ускорения точки С в ее движении относительно точки В, и иВс — аналог абсолютного ускорения точки С. [c.148]

Для определения ускорений точек звена 2 воспользуемся ура-/внением (4.30). Из нротволъной точки — полюса плана ускорений (рис. i02, в) откладьтааем вектор (рЖ), представляющий собой в некотором масштабе Ца вектор ав заданного ускорения точки затем, пользу-ясь уравнением (4.31), вычисляем величину нормального ускорения й»д в относительном движении и в том же масштабе откладываем его от точки Ь» в виде отрезка Ь п параллельно СВ в направлении от тонки С к точке В. В соответствии с уравнением (4.36) из найденной точки п перпендикулярно к оси звена ВС проводим прямую в направлении вектора йсв—тангенциального ускорения в относительном движении. Лересенетие этой прямой с прямой, проведенной из полюса ра в направлении вектора ас ускорения точ-кн С, определяет конечную точку с вектора раС абсолютного ускорения точки С его величина [c.75]

Приняв некоторую точку я за полюс плана ускорений (рис. 23, а), отложим вектор, изображающий нормальное уско-рение точки В, в виде отрезка (ш ) ). Тогда масштабный коэф фициеит ускорений найдется из соотношения [c.77]

Для упрощения чертежа все ускорения строят при полюсе плана ускорений первоначального механизма, считая его общим концом всех ускорений. Пусть точки а и Ь будут началами векторов, изображающих ускорения А и в- Тогда, проводя а Ц СА отклады ваем отрезок изображающий, и проводим с пс J АС [c.389]

Из полюса плана ускорений Р проводим прямую, параллельную 5бктору скорости точки С. Эта прямая пересечет линию действия 5вктора тангенциального ускоре кия асв в точке с. В результате тересечения двух прямых получим искомые величины векторов и пс ускорений йс и асв- Истинные величины ускорений а i Ысв определяются так [c.167]

На рис. 1.24, в из полюса плана ускорений отложены в определенном масштабе направленные отрезки р к , к к и 2 2, отображающие ускорения соответственно а ,, ай 1 и а.к2кк которые известны по модулю и направлению, и из конца / 2 отрезка к ук проведена линия I — /, параллельная вектору ай 1- [c.31]

Векторы ускорений и входящие в уравнение (4.43), известны только по направлению. Первый вектор перпендикулярен к направлению ВС, а второй вектор параллелен оси х — х направляющей поступательной пары D. Таким образом, в уравнении (4.43) неизвестны только величины ускорений и. Для их определения строим план ускорений. Для этого (рис. 4.20, б) выбираем произвольную точку л за полюс плана ускорений и откладываем от нее известные ускорения точек В и С4 в виде отрезков (пЬ) и (ЛС4), изображающих в выбранном масштабе р-а ускорения fifl и ас. Далее определяем ускорения и и откладываем их в масштабе р-а в виде отрезков (Ьп) и ( k). Из точек п я k проводим прямые, имеющие направления ускорений и. Ускорение параллельно оси х — х направляющей поступательной пары D, а ускорение перпендикулярно к направлению ВС. Точка с пересечения этих двух направлений и даст конец вектора ас полного ускорения точки С. Величина полного ускорения ас точки С равна [c.93]

Выбрав в произвольной точке полюс плана ускорений (рис. 4.18), откладываем в масштабе ка ускорений отрезки РаС( и раС, пропорциональные ускорениям йлИДс- Эти отрезки определяются из равенства [c.100]

Источник

Как составить план местности?

Предположим, вам требуется составить план местности. Для этого вам понадобятся: тренога, планшет, визирная линейка и хорошо отточенный карандаш.

Ход работы

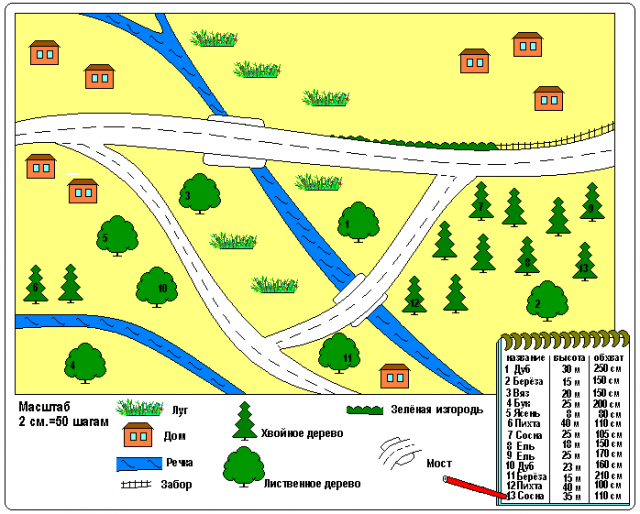
Установив треногу с планшетом на мосту через реку (отсюда мы начинаем съёмку), выберите масштаб, например 1 : 5000, и проведите стрелку «север — юг».
Затем ориентируйте планшет по сторонам горизонта. Все местные предметы нужно наносить на план условными знаками. Прежде всего на плане надо изобразить мост через реку и в центр условного знака — моста — воткнуть булавку. Это будет ваша исходная точка.
Теперь положите на планшет визирную линейку так, чтобы её край коснулся булавки. Направьте верхнее ребро линейки поочерёдно на те местные предметы, которые нужно изобразить на плане (куст, ветродвигатель, дом, колодец, дерево на берегу реки), и вычертите на планшете линии визирования на каждый объект.
Когда линии визирования на все объекты проведены, определите одним из уже известных нам способов расстояние от моста до каждого из этих объектов.
Пользуясь выбранным масштабом, отложите определённые расстояния на планшете и вычертите объекты условными знаками.
Теперь можно нанести реку. Она течёт от дерева к мосту и далее к кустарнику. После этого линии визирования можно стереть.
Дороги на плане изображаются приблизительно. Одна из них идёт от моста к дому, другая — к колодцу.
Условными знаками обозначаем луг и смешанный лес. Точка, из которой мы производили визирование на местные предметы, называется полюсом. Поэтому этот способ съёмки местности получил название полярного.

Другие способы съёмки местности

Азимутальная съёмка является более простой по сравнению с полярной. Производится она примерно так же, как и полярная, только без планшета и визирной линейки. Расположившись у моста, определите азимуты на все те объекты, которые хотите нанести на план, и измерьте расстояние до них. Всё это запишите в блокнот.

Дома на чистом листе бумаги поставьте точку полюса и от неё отложите с помощью транспортира определённые на местности азимуты и расстояния в выбранном масштабе. Местные объекты обозначьте условными знаками.

Маршрутная съёмка — это съёмка значительных по протяжённости участков местности или объектов, например реки, дороги. Её производят из нескольких точек (полюсов). Работая на одном полюсе, осуществляют съёмку видимой части местности. Затем выбирают место для следующего полюса, определяют расстояние от начального полюса до него и азимут. Далее наносят полюс на планшет и повторяют всю процедуру съёмки. И так далее.

Источник

Содержание:

Плоское движение тела
Определение скоростей точек тела
Уравнения плоского движения
Скорости точек фигуры. Мгновенный центр скоростей
Определение положения мгновенного центра скоростей
Порядок решения задач на тему: Определение скоростей точек тела
Примеры решения задач на тему: Определение скоростей точек тела
Решение задачи графоаналитическим способом
Решение задачи с помощью мгновенного центра скоростей
Определение ускорений точек тела
Ускорения точек плоской фигуры
Порядок решения задач на тему: Определение ускорений точек тела
Примеры решения задач на тему: Определение ускорений точек тела
План скоростей
Порядок решения задач на тему: План скоростей
Примеры решения задач на тему: План скоростей
План ускорений
Примеры решения задач на тему: План ускорений

Плоское движение тела — это такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Плоское движение тела

Плоскопараллельное движение (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости. Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге

Определение скоростей точек тела

Скорости точек тела пропорциональны их расстояниям до мгновенного центра скоростей, и это отношение определяет угловую скорость тела в данный момент времени: Частные случаи определения положения мгновенного центра скоростей. Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого, то точка касания Р имеет в данный момент времени скорость равную нулю, и, следовательно является мгновенным центром скоростей .

Уравнения плоского движения

Плоским называется такое движение тела, при котором траектории всех его точек лежат в плоскостях, параллельных данной неподвижной плоскости.

При таком движении все точки твердого тела, лежащих на перпендикуляре к этой плоскости, имеют одинаковые траектории, скорости и ускорения.

Плоское движение фигуры можно рассматривать как сложное (то есть, абсолютное) движение, которое включает поступательное движение вместе с произвольно выбранной точкой , что называется полюсом (переносное движение), и на вращательное движение фигуры вокруг этой точки (относительное движение).

На рис.4.1 с телом связана подвижная система координат . При движении тела начало координат и угол поворота подвижной системы координат относительно неподвижной системы со временем меняются. Таким образом, чтобы однозначно задать положение тела при плоском движении нужно задать закон движения начала подвижной системы координат (полюса ) и угол поворота подвижной системы относительно неподвижной системы координат, то есть:

Уравнения (4.1) называются уравнениями плоского движения твердого тела.

При этом, поступательная часть плоского движения описывается двумя уравнениями:

а относительная вращательная вокруг полюса — третьим уравнением:

Координаты любой точки плоской фигуры (рис.4.1), если за полюс выбрана точка и задан угол , определяются по уравнениям:

Скорости точек фигуры. Мгновенный центр скоростей

Поскольку плоское движение тела состоит из поступательного вместе с полюсом и вращательного вокруг него, то скорость любой точки тела (рис.4.2) геометрически состоит из абсолютной скорости точки , которую принято за полюс, и относительной скорости в относительном вращательном движении точки вместе с телом вокруг полюса :

Вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг полюса направлен перпендикулярно в сторону угловой скорости.

Модуль и направление абсолютной скорости находится построением соответствующего параллелограмма на векторах и (рис.4.2). Таков путь решения векторного уравнения, когда по записанному уравнению строят векторную фигуру, называется графоаналитическим.

Относительная скорость в относительном вращательном движении точки вместе с телом вокруг полюса по модулю равна:

где — угловая скорость вращения тела вокруг полюса.

Найти скорость любой точки тела можно также на основе теоремы, которая гласит:

Проекции скоростей двух точек фигуры на прямую, что соединяет эти точки, равны между собой.

Согласно этой теореме (рис.4.3) :

или

Если известна скорость точки тела, то:

При плоском движении тела в каждый момент времени существует точка тела, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей и, как правило, обозначается буквой .

Если мгновенный центр скоростей известен, то легко можно найти мгновенное распределение скоростей всех точек тела (рис.4.4).

Выберем за полюс поступательного движения мгновенный центр скоростей . Тогда для точек и тела можно записать векторные уравнения (4.3):

где — вектор абсолютной скорости полюса ;

— вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг полюса , направлен перпендикулярно ;

— вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг полюса , направлен перпендикулярно .

Поскольку скорость выбранного полюса равна нулю , то:

По модулю скорости вращения точек и вокруг полюса равны:

Разделив на получим:

Таким образом, мгновенное распределение скоростей точек тела при его плоском движении, такое же, какое было бы при его вращательном движении вокруг мгновенного центра скоростей.

Определение положения мгновенного центра скоростей

Существует несколько способов нахождения положения мгновенного центра скоростей.

Случай 1. Известна скорость одной точки тела и угловая скорость его вращения (рис.4.5).

Мгновенный центр скоростей лежит на перпендикуляре к скорости точки , на расстоянии:

Для нахождения направления перпендикуляра надо повернуть вектор относительно точки на угол в сторону угловой скорости.

Случай 2. Известны направления скоростей и двух точек и тела (рис.4.6).

Мгновенный центр скоростей должен лежать как на перпендикуляре к вектору , так и на перпендикуляре к вектору , то есть мгновенный центр скоростей лежит в точке пересечения этих перпендикуляров.

Случай 3. Скорости двух точек и тела параллельны между собой, а перпендикуляры к ним не совпадают (рис.4.7).

Говорят, что в этом случае мгновенный центр скоростей лежит на бесконечности. Угловая скорость вращения равна нулю, а скорости всех точек тела геометрически равны, то есть в данный момент времени тело выполняет поступательное движение.

Случай 4. Скорости двух точек и параллельны, направлены в одну сторону и не равны по модулю. Кроме того, и перпендикулярны отрезку (рис.4.8).

Мгновенный центр скоростей находится на продолжении отрезка той точки, скорость которой меньше. Расстояние от точки к мгновенному центру скоростей можно найти из пропорции (4.6):

Решив это уравнение относительно , получим:

Таким образом, для определения положения мгновенного центра скоростей надо знать не только направления скоростей, но и их величину.

Случай 5. Скорости двух точек и тела параллельны друг другу, перпендикулярны отрезку , но направлены в разные стороны (рис.4.9).

Мгновенный центр скоростей лежит на отрезке и делит его на части пропорциональные скоростям. Поскольку , то по формуле (4.6) можно записать:

Решив уравнение относительно , получим:

Таким образом, для нахождения положения мгновенного центра скоростей надо знать величины и направления скоростей обеих точек.

Случай 6. Тело катится без проскальзывания по неподвижной поверхности (рис.4.10).

В этом случае мгновенный центр скоростей находится в точке прикосновения тела к поверхности. Действительно, если отсутствует скольжение тела относительно поверхности, то скорости точек прикосновения тела и поверхности должны быть одинаковыми. Но скорости точки , принадлежащей неподвижной поверхности, равна нулю.

Тогда и скорость точки , которой в данный момент времени движущееся тело прикасается к неподвижной поверхности, тоже равна нулю.

Порядок решения задач на тему: Определение скоростей точек тела

а) решение графоаналитическим методом:

выбрать за полюс ту точку тела, скорость которой известна по величине и направлению или легко определяется из условий задачи;
найти точку тела, направление скорости которой известно;
пользуясь формулами плоского движения найти скорость этой точки;
определить угловую скорость тела в данный момент времени;
по известной угловой скорости и скорости полюса, пользуясь формулами плоского движения найти скорости других точек тела.

б) решение с помощью мгновенного центра скоростей:

определить положение мгновенного центра скоростей одним из известных способов;
определить значение мгновенного радиуса той точки тела, скорость которой известна, и найти угловую скорость тела;
найти скорости других точек тела.

Примеры решения задач на тему: Определение скоростей точек тела

Задача №1

Стержень (рис.4.11) длиной выполняет плоское движение. Вектор скорости точки образует угол с осью стержня и в данный момент времени равен . Вектор скорости точки в этот же момент времени образует угол с осью стержня.

Определить величину скорости точки , положение мгновенного центра скоростей, угловую скорость стержня и скорость точки , которая лежит на середине стержня.

Решение задачи графоаналитическим способом

1. Выберем за полюс точку (рис.4.11), поскольку известны направление и величина скорости этой точки.

2. Используя формулу распределения скоростей при плоском движении, запишем векторное уравнение для определения скорости точки :

где — скорость полюса точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с телом вокруг полюса .

Данное векторное уравнение можно решить построением векторного треугольника скоростей (рис.4.12). Для этого из произвольной точки плоскости надо построить правую и левую часть векторного уравнения (1).

При построении правой части уравнения (1) из точки в произвольном масштабе отложим вектор скорости , который является известным и по величине и по направлению. К вектору надо добавить вектор относительной скорости , направление которого является известным, поскольку скорость точки у ее относительном вращательном движении вокруг полюса перпендикулярна радиусу вращения, в данном случае радиус вращения — отрезок . Величина вектора неизвестна и поэтому через точку проводится только его направление (прямая рис.4.12).

Теперь из точки построим левую часть уравнения (1). Направление скорости точки является известным (по условию задачи), но неизвестна ее величина, и потому, из точки проводим линию параллельную .

Точка пересечения прямых, параллельных и , и будет решением данного векторного уравнения.

В результате построения получили замкнутый треугольник скоростей, стороны которого в выбранном масштабе определяют искомую скорость точки и относительную скорость этой же точки при ее вращении вместе с телом вокруг полюса .

В этом треугольнике известны все углы и одна сторона . С треугольника находим:

3. Определим угловую скорость вращения стержня . Поскольку , то :

4. Найдем скорость точки , лежащей посередине отрезка . Для этого запишем формулу для скорости точки относительно того же самого полюса точки :

где — скорость полюса точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с телом вокруг полюса .

Скорость имеет то же направление, что и , а по модулю равна:

Отложив от точки (рис.4.12) вектор , равный половине вектора , получим точку . Вектор, проведенный из точки начала построения (точки ) в точку изображает скорость точки .

Поскольку стороны и треугольника равны между собой и угол между ними , то треугольник равносторонний. Таким образом:

Решение задачи с помощью мгновенного центра скоростей

1. Определим положение мгновенного центра скоростей. Для этого с точек и (рис.4.13) проведем перпендикуляры к скоростям и . Пересечение этих перпендикуляров (точка ) будет мгновенным центром скоростей.

2. Определим мгновенные радиусы. Поскольку треугольник прямоугольный, то:

3. Вычислим угловую скорость вращения фигуры вокруг мгновенного центра скоростей:

4. Найдем скорости точек и :

где — мгновенный радиус точки , поскольку треугольник равносторонний ( угол между ними ), то

Если надо было бы определить только величину скорости , то можно было бы воспользоваться теоремой о равенстве проекций двух точек плоской фигуры на прямую, соединяющую эти точки:

Тогда:

Ответ:

Задача №2

Колесо радиусом катится по горизонтальной поверхности. В момент рассматриваемого времени скорость центра и угловая скорость колеса (рис.4.14).

Определить: скорости точек , и , которые лежат на концах вертикального и горизонтального диаметров.

Решение.

1. В качестве полюса выберем точку , направление и величина скорости которой известны.

2.Используя формулу распределения скоростей точек тела при плоском движении определяем скорости других точек колеса.

Для точки колеса:

где — относительная скорость точки в ее относительном вращательном движении вокруг полюса .

По модулю равна:

Скорость направлена перпендикулярно в сторону угловой скорости, то есть по направлению и будут совпадать.

Из точки (рис.4.14) строим уравнение (1): откладываем вектор , а с его конца по тому же направлению .

Тогда:

Векторное уравнение для определения скорости точки , будет иметь вид:

где — скорость точки в ее вращательном движении вокруг полюса .

Эта скорость параллельна скорости , но будет направлена в противоположную сторону и по модулю равна:

Из точки (рис.4.14) строим векторное уравнение (2): откладываем вектор , а с его конца в противоположную сторону .

Поскольку векторы коллинеарны, то:

Таким образом, скорость точки равна и направлена в противоположную сторону от . Колесо катится со скольжением по поверхности.

Составляем векторное уравнение для определения скорости точки :

где — относительная скорость точки в ее относительном вращательном движении вокруг полюса .

По модулю равна:

Скорость направлена перпендикулярно в сторону угловой скорости , то есть вертикально вниз.

Из точки (рис.4.14) строим уравнение (3): откладываем вектор , а с его конца вектор вертикально вниз. Соединив точку с концом вектора получим вектор скорости точки .

Поскольку векторы и между собой перпендикулярны, то вектор является гипотенузой прямоугольного треугольника:

Ответ:

Задача №3

Колесо радиусом катится без проскальзывания по горизонтальной поверхности со скоростью центра колеса

Определить: скорости точек , , (рис.4.15).

Решение. Решим задачу с помощью мгновенного центра скоростей.

1. Определим положение мгновенного центра скоростей. Поскольку колесо катится по неподвижной поверхности, то мгновенный центр скоростей находится в точке прикосновения колеса к неподвижной поверхности.

2. Мгновенный радиус для точки равен . Тогда с формулы (4.4) получим угловую скорость колеса:

Направлена угловая скорость по ходу часовой стрелки.

3. Определим величину и направление скоростей точек , , .

Соединим точки , , с мгновенным центром скоростей . Векторы скоростей , и будут направлены перпендикулярно мгновенным радиусам и , соответственно.

По модулю скорости будут равны:

где

Ответ:

Задачи, которые рекомендуются для самостоятельной работы: 16.2; 16.4; 16.11; 16.12 [2]

Определение ускорений точек тела

Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.

Ускорения точек плоской фигуры

Формула распределения ускорений при плоском движении тела имеет вид:

где — ускорение полюса, точки , в поступательном движении;

— относительное ускорение точки в ее вращательном движении вместе с телом вокруг полюса ;

— ускорение любой точки тела.

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения точки, которую выбрано за полюс, и ускорения точки при его вращении вместе с телом вокруг этого полюса.

Графическое определение ускорения точки выполняется следующим образом (рис.4.16):

Вычисление величины ускорения точки с помощью рассматриваемого параллелограмма затрудняет расчеты, поскольку предварительно надо определить угол между векторами и .

Учитывая, что представляет собой относительное ускорение точки в ее относительном вращательном движении вокруг полюса , то это ускорение можно разложить на относительную тангенциальную (касательную) и относительную нормальную (центростремительную) составляющие:

где

Вектор направлен перпендикулярно в сторону углового ускорения, а вектор всегда направлен от точки к выбранному полюсу (рис.4.17).

Тогда уравнение (4.10) примет вид:

Если точка , которая выбрана за полюс поступательного движения, движется не прямолинейно, то ее ускорение, в свою очередь, тоже можно разложить на тангенциальную и нормальную составляющие:

Порядок решения задач на тему: Определение ускорений точек тела

1. Выбрать точку, которая будет полюсом при записи уравнения плоского движения (как правило выбирают точку, ускорение которой известно).

2. Записать векторное уравнение распределения ускорений.

3. Спроектировать уравнение распределения ускорений на две взаимно перпендикулярные оси, одна из которых совпадает с нормальным ускорением, а вторая – с тангенциальным.

4. Определить мгновенное угловое ускорение плоской фигуры.

5. Найти искомые ускорения точек с помощью уравнения распределения ускорений.

Примеры решения задач на тему: Определение ускорений точек тела

Задача №1

Прямоугольная (рис.4.18, а) пластина движется в плоскости чертежа. Ускорение точки в данный момент времени равно и образует с прямой угол .

Ускорение точки составляет и образует угол с прямой .

Определить мгновенную угловую скорость и мгновенное угловое ускорение пластины, и ускорение точки , если

Решение.

1. Выберем за полюс точку , поскольку ее ускорение известно (задано в исходных данных).

2. Составим векторное уравнение для ускорения точки пластины:

где — относительное нормальное ускорение точки в ее вращательном движении вместе с телом вокруг точки . Вектор этого ускорения направлен от точки к точке и по модулю равен:

— относительное тангенциальное (касательное) ускорение точки в ее вращении вместе с телом вокруг точки . Направлен вектор этого ускорения перпендикулярно в сторону углового ускорения и по модулю равен .

Поскольку направление углового ускорения неизвестное, то направлением на рис. 4.18,а задаемся.

3. Спроектируем составленное уравнение (1) на оси и .

В проекции на ось получим:

В проекции на ось :

4. Из уравнения (2) получим величину нормального ускорения:

Найдем мгновенную угловую скорость фигуры:

5. Из уравнения (3) получим величину тангенциального ускорения:

Угловое ускорение фигуры:

Поскольку величина положительная, то направление тангенциального, а соответственно и углового ускорений выбрано верно.

6. Определим ускорение точки .

Для вычисления ускорения точки лучше за полюс выбрать точку , поскольку ускорение этой точки уже известно и задана сторона прямоугольника:

Направление векторов и показано на рис. 4.18,б.

Спроектируем записанное уравнение на оси и :

где

Полное ускорение точки :

Ответ:

Задача №2

Равносторонний треугольник движется в плоскости чертежа. Ускорение вершин и в данный момент времени равны и направлены вдоль сторон треугольника (рис.4.19).

Определить ускорение вершины .

Решение. Если известны ускорения двух точек плоской фигуры, например и , то задачу рекомендуется решать в следующей последовательности:

1. Рассматривая первую точку как полюс поступательного движения, записать векторное уравнение распределения ускорений при плоском движении для точки и спроектировать это уравнение на прямую , соединяющую обе точки.

2. Из уравнения проекций определить величину нормального ускорения и значение угловой скорости фигуры .

3. Спроектировать векторное уравнение распределения ускорений при плоском движении на прямую, которая перпендикулярна , и определить из уравнения проекций величину тангенциального ускорения и значение углового ускорения фигуры .

4. Если нужно, то, используя формулу распределения ускорений при плоском движении, определить ускорение любой другой точки плоской фигуры.

Решим задачу, придерживаясь приведенной последовательности.

1. Выберем за полюс точку . Для точки треугольника можно записать:

где — относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке ;

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно , направлением задаемся (рис.4.19).

Спроектируем записанное равенство (1) на прямую :

2. Откуда:

Поскольку то:

3. Спроектируем векторное уравнение на прямую, которая перпендикулярна :

Откуда:

Учитывая то, что , получим:

Поскольку величина тангенциального ускорения положительная, то его направление на рис. 4.19 выбрано верно. Отсюда следует, что угловое ускорение направлено против хода часовой стрелки.

4. Определим ускорение точки , приняв за полюс точку :

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно в сторону углового ускорение фигуры .

Учитывая, что , определим модули относительного нормального и тангенциального ускорений:

От точки (рис.4.20) отложим векторы ускорений, которые составляют правую часть уравнения (2).

Выберем систему координат , причем ось направим вдоль стороны треугольника.

Спроектируем равенство (2) на оси выбранной системы координат:

Подставляя числовые данные, получим:

Таким образом, ускорение вершины треугольника равно:

Поскольку проекция ускорения на ось равна нулю и величина проекции на ось положительная, то вектор ускорения точки будет направлен вдоль стороны треугольника от точки к точке .

Ответ:

Задача № 3

В шарнирном механизме (рис.4.21) в данный момент времени угловая скорость и угловое ускорение кривошипа равны Точка механизма движется по дуге окружности радиусом и в момент времени, что рассматривается, лежит на прямой .

Найти ускорение точки и мгновенное угловое ускорение шатуна , если

Решение. Скорость точки кривошипа, который вращается вокруг точки равен:

Направлена скорость перпендикулярно в сторону угловой скорости (рис.4.21).

Точка шатуна вращается вокруг центра и ее линейная скорость направлена перпендикулярно .

Поскольку скорости точек и шатуна параллельны, то мгновенный центр скоростей шатуна лежит в бесконечности и мгновенное движение шатуна является поступательным, то есть

Ускорение точки равно геометрической сумме нормального и тангенциального ускорений:

где

Направления ускорений и показаны на рис.4.21.

Выберем точку за полюс для шатуна . Тогда для точки шатуна:

или

где — относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке ,

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно , направлением задаемся (рис.4.22),

Свяжем с точкой прямоугольную систему координат (рис.4.22) и спроектируем уравнение (1), помня, что , на оси выбранной системы координат:

С другой стороны, при движении точки по дуге окружности радиуса , точка приобретет ускорения :

где — нормальное ускорение точки в ее вращательном движении вокруг точки направлено к центру вращения;

— тангенциальное ускорение точки в ее вращательном движении вокруг точки , направлено перпендикулярно , задаемся направлением (рис.4.22).

По величине нормальное и тангенциальное ускорения соответственно равны:

Спроектируем уравнение (4) на оси выбранной системы координат:

Подставим в (3) все рассчитанные величины:

Поскольку

то

Положительное значение величины указывает на то, что направление было выбрано верно.

Угловое ускорение тела равно:

Угловое ускорение направлено в сторону , то есть против хода часовой стрелки.

Для определения тангенциального ускорения в уравнение (2) подставим из (5):

Откуда

Поскольку величина отрицательная, то направление тангенциального ускорения выбрано не в ту сторону.

Полное ускорение точки :

Ответ:

Задачи, которые рекомендуются для самостоятельной работы: 18.12; 18.14; 18.22 [2].

План скоростей

План скоростей и план ускорений – физическое изображение векторных уравнений, связывающих скорости и ускорения точек механизма. Изображение механизма, выполненное с помощью условных обозначений (см. выше) называется структурной схемой механизма.

Определение скоростей различных точек движущейся плоской фигуры легко может быть выполнено графически с помощью построения плана скоростей.

План скоростей – это графическое изображение из единого центра (полюса) векторов абсолютных скоростей точек фигуры в фиксированный момент ее движения.

План скоростей может быть построен, если:

известная скорость одной точки плоской фигуры и направление скорости другой точки;
известная скорость одной точки плоской фигуры и мгновенная угловая скорость фигуры

Пусть известные скорости , , и , вершин прямоугольника (рис. 4.23, а). Для построения плана скоростей с произвольной точки (рис.4.23,б), которая называется полюсом плана скоростей, отложим направленные отрезки и , которые в выбранном масштабе будут изображать скорости , , и . Полученные точки и , которые называются вершинами плана скоростей, соединим между собой прямыми линиями.

Установим свойства и правила построения плана скоростей.

По уравнению распределения скоростей при плоском движении фигуры, если за полюс принять точку , то для точки получим:

где — вектор абсолютной скорости точки ;

— вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг точки , направлена перпендикулярно и по модулю равна

С другой стороны для векторов треугольника плана скоростей (рис.4.23,б) можно записать:

Учитывая, что векторы и изображают в выбранном масштабе абсолютные скорости и и, сравнивая уравнения (4.14) и (4.15), можно сделать вывод, что отрезок изображает в масштабе скорость .

Таким образом, отрезок плана скоростей направлен перпендикулярно стороне фигуры и по модулю равен:

где — масштабный коэффициент, который принят при построении плана скоростей.

Аналогично:

Отсюда мгновенная скорость вращения плоской фигуры:

Вектор согласно уравнению (4.14) направлен на плане скоростей от точки к точке . Если этот вектор перенести в точку фигуры, то можно определить направление вращения точки вокруг точки вместе с фигурой (в данном случае, по ходу часовой стрелки). Направление же мгновенной угловой скорости плоской фигуры будет совпадать с направлением ее вращения.

Из рассматриваемого вытекает:

Порядок решения задач на тему: План скоростей

1. Изображают на чертеже в выбранном масштабе плоскую фигуру и вектор скорости той точки, скорость которой известна.

2. Определяют направление скорости второй точки плоской фигуры.

3. Записывают векторное уравнение распределения скоростей при плоском движении, принимая за полюс точку, скорость которой известна, а за искомую ту точку, направление скорости которой известно.

4. Решают записанное векторное уравнение графически путем построения в выбранном масштабе плана скоростей.

5. Определяют мгновенную угловую скорость вращения плоской фигуры.

6. Определяют скорость других точек плоской фигуры.

Примеры решения задач на тему: План скоростей

Задача №1

Найти угловую скорость шатуна 2 и скорость точки ползуна 3 кривошипно-шатунного механизма (рис. 4.24), если :

Решение.

1. Согласно исходным данным в произвольном масштабе строим схему механизма (рис.4.25, а).

2. Учитывая, что кривошип 1 вращается вокруг неподвижной точки с угловой скоростью определяем скорость точки кривошипа 1 и шатуна 2:

Направлена скорость перпендикулярно в сторону угловой скорости .

3. Следующей точкой шатуна, скорость которого можно определить, является точка , поскольку она, кроме шатуна, одновременно принадлежит и ползуну 3, что движется поступательно в горизонтальных направляющих. То есть направление этой скорости известно.

Для определения скорости точки запишем уравнение распределения скоростей при плоскопараллельном движении, принимая за полюс точку , скорость которой известна:

где — относительная скорость точки в ее относительном вращательном движении вместе с шатуном 2 вокруг точки . Вектор направлен перпендикулярно ;

— абсолютная скорость точки , которая движется прямолинейно вместе с ползуном 3 в горизонтальных направляющих.

4. Решим уравнение (1) графически (рис.4.25, б). Для этого с произвольной точки (полюса плана скоростей) отложим направленный отрезок , который в определенном масштабе будет изображать вектор скорости . Через точку этого отрезка проведем линию перпендикулярно , вдоль которой от точки будет направлен вектор скорости , длина и направление которого неизвестны.

Вектор который будет на плане скоростей изображать абсолютную скорость точки , выходит из полюса параллельно к пересечению с линией в точке .

Определим направление отрезка , который на плане скоростей изображает относительную скорость . Поскольку, согласно уравнению (1), вектор надо прибавить к вектору , который на плане скоростей изображается вектором , то вектор будет направлен от точки к точке .

Полученный векторный треугольник представляет собой план скоростей для кривошипно-шатунного механизма в положении, что рассматривается. Стороны этого треугольника в определенном масштабе изображают: — абсолютную скорость точки ; — относительную скорость точки в ее относительном вращательном движении вместе с шатуном вокруг точки ; — абсолютную скорость точки .

Перенесем из плана скоростей в точку на рис.4.25, а найденные направления скоростей и .

Поскольку скорость на плане изображается вектором , а — вектором , то угол при вершине равен углу между этими двумя векторами скоростей. Если на рис.4.25, а перенести и в точку , то угол между ними будет составлять , то есть

Аналогично, равен углу между векторами и . Учитывая, что , с рис.4.25, а получим:

Таким образом, и угол при вершине тоже будет равняться , а треугольник будет равносторонним, то есть:

, или

5. Определяем мгновенную угловую скорость шатуна 2. Поскольку , то:

где , исходя из того, что треугольник (рис.4.25,а) равнобедренный.

Направление угловой скорости определяется вектором . В данном случае направлена против хода часовой стрелки.

Ответ:

Задача №2

Найти угловые скорости шатуна 2 и коромысла 3 и абсолютные скорости точек и рычажного механизма (рис.4.26), если:

Угловая скорость кривошипа 1 —

Решение.

1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.27, а).

2. Так как точка принадлежит кривошипу 1, который вращается вокруг шарнира с угловой скоростью , то:

Вектор скорости направлен перпендикулярно в сторону вращения кривошипа (рис.4.27, а).

2. Шатун 2 механизма движется плоскопараллельно. Скорость точки шатуна 2 равна скорости точки кривошипа 1. Второй точкой шатуна, направление скорости которой известно, есть точка . Точка , кроме шатуна, принадлежит и коромыслу 3, которое вращается вокруг центра . Таким образом, скорость точки направлена перпендикулярно радиусу вращения .

3. Для определения скорости точки запишем формулу распределение скоростей:

где — абсолютная скорость точки , которая направлена перпендикулярно ;

— абсолютная скорость точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с шатуном 2 вокруг полюса . Направлен вектор перпендикулярно .

4. Решаем записанное уравнение графически. Для этого из произвольной точки (полюса плана скоростей) (рис.4.27,б) проводим вектор параллельно , который в определенном масштабе будет изображать скорость точки .

Через конец вектора проводим линию перпендикулярно , вдоль которой от точки будет направлен вектор относительной скорости . Длина и направление этого вектора неизвестны.

Скорость точки направлена перпендикулярно и, по правилу, должна проходить через полюс плана скоростей. Исходя из этого, через точку проводим линию перпендикулярную коромыслу 3 к пересечению в точке с линией .

Полученный на рис. 4.27, б векторный треугольник являет собой план скоростей механизма в данном положении. В этом треугольнике вектор изображает абсолютную скорость точки , вектор направлен от полюса к точке — абсолютную скорость точки , а вектор направлен от точки к точке — относительную скорость , поскольку, согласно уравнению (2), эта скорость прибавляется к .

Перенесем направления скоростей и в точку на рис. 4.27, а.

Поскольку , а , то угол при вершине равен углу при вершине треугольника на схеме механизма (рис. 4.28), который образован путем продолжения кривошипа и коромысла к пересечению.

Таким образом

Угол при вершине будет равняться углу между продолжением прямой (рис.4.28) и прямой , поскольку сторона , а прямая . Учитывая, что , то:

Тогда угол при вершине :

Для определения сторон плана скоростей воспользуемся теоремой синусов:

Из уравнения (1) получим:

Таким образом:

5. Определим мгновенные угловые скорости шатуна 2 и коромысла 3. Поскольку , то:

Направление угловой скорости определяется направлением относительной скорости . С рис.4.27,а видно, что угловая скорость будет направлена против хода часовой стрелки.

Угловая скорость коромысла 3 равна:

где

Направление определяет скорость . Направлена угловая скорость коромысла 3 (рис.4.27,а) по ходу часовой стрелки.

6. Определить величины скоростей и можно непосредственно и путем измерения соответствующих отрезков на построенном плане скоростей.

Поскольку вектор на плане скоростей изображается отрезком , то масштабный коэффициент плана скоростей будет равен:

Скорости на плане скоростей соответствует отрезок , а скорости – .

Тогда:

7. Для определения скорости точки воспользуемся теоремой подобия.

Поскольку фигура на схеме механизма и фигура на плане скоростей должны быть подобными, то можно составить пропорцию:

В левой части пропорции (2) отношение отрезков на схеме механизма, а в правой — на плане скоростей.

Из уравнения (2) получим расстояние от точки к точке на плане скоростей:

Поскольку на схеме механизма отрезок перпендикулярен , то и на плане скоростей отрезок надо провести перпендикулярно , причем в ту сторону, чтобы обход точек , и на плане скоростей должен был быть против хода часовой стрелки, как и для точек , и на схеме механизма.

Вектор скорости точки на плане скоростей в масштабе будет изображаться вектором , а величина скорости точки равна:

Ответ:

Задача №3

В состав рычажного механизма (рис.4.29) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 вращается с угловой скоростью , а кривошип 4 с угловой скоростью .

Найти угловые скорости шатунов 2 и 3 и абсолютные скорости точек и , если: В данном положении механизма кривошип 1 расположен вертикально, а кривошип 2 – горизонтально.

Решение. Особенность этой задачи заключается в том, что определить сразу направление скорости точки невозможно. Но точка одновременно принадлежит к двум телам (шатуну и шатуну ), и для нее можно записать два векторных уравнения распределения скоростей при плоском движении (относительно точек и ), что позволяет решить задачу.

1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.30, а).

2. Так как точка принадлежит кривошипу 1, который вращается вокруг шарнира с угловой скоростью , то:

Вектор скорости направлен перпендикулярно в сторону вращения кривошипа 1 (рис.4.30, а).

Шатун 2 механизма движется плоскопараллельно. Скорость точки шатуна 2 равна скорости точки кривошипа 1.

Для определения скорости точки шатуна 2 запишем формулу распределения скоростей при плоском движении:

где — абсолютная скорость точки , величина и направление которой является неизвестным;

— абсолютная скорость точки ;

— относительная скорость точки при ее вращении вместе с шатуном 2 вокруг полюса . Направлен вектор перпендикулярно .

В уравнении (1) три неизвестных: величина и направление скорости точки ; величина скорости . Поскольку векторное уравнение

для плоскости позволяет определить только две неизвестных, то решить уравнение (1) невозможно.

3. Рассмотрим определение скорости точки шатуна 3 относительно точки .

Скорость точки кривошипа 4 равна:

Вектор скорости направлен перпендикулярно в сторону вращения кривошипа 4 (рис.4.30, а).

Учитывая, что шатун 3 механизма движется плоскопараллельно, то для определения скорости точки шатуна 3 запишем формулу распределения скоростей при плоском движении:

где — абсолютная скорость точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с шатуном 3 вокруг полюса . Направлен вектор перпендикулярно .

В записанной системе векторных уравнений (1,2) четыре неизвестных: величина и направление скорости точки ; величина скорости ; величина скорости . Поскольку из каждого уравнения можно определить две неизвестных, то записанная система является определенной и ее можно решить.

4. Решаем записанную систему векторных уравнений (1) и (2) графически. Для этого из произвольной точки построим сначала уравнение (1), а затем (2) (рис.4.30, б).

Согласно уравнению (1) из произвольной точки проводим вектор параллельно , который будет изображать скорость точки . Длину отрезка выберем .

Тогда масштабный коэффициент плана скоростей будет равен:

Теперь построим из того же самого полюса уравнение (2). Сначала отложим вектор параллельно , который в масштабе будет изображать скорость точки . Длина этого вектора соответственно равна:

Через конец вектора проводим линию перпендикулярно , вдоль которой от точки будет направлен вектор относительной скорости .

Точка пересечения прямых и , которая одновременно удовлетворяет векторным уравнением (1) и (2), и будет решением системы, а вектор который на плане скоростей изображает будет направлен от полюса к точке .

Полученный на рис. 4.30,б четырехугольник представляет собой план скоростей механизма в данном положении. В этом четырехугольнике: вектор определяет относительную скорость ; вектор — относительную скорость ; — абсолютную скорость точки .

Перенесем направления скоростей и на рис. 4.30,а и, померив длины соответствующих отрезков, определим величины этих скоростей:

5. Определим мгновенные угловые скорости шатунов.

Поскольку , то:

Направление угловой скорости определяется направлением относительной скорости . С рис.4.30, а видно, что будет направлена против хода часовой стрелки.

Аналогично, угловая скорость шатуна 3 равна:

Направление определяется относительной скоростью . Направлена угловая скорость шатуна 3 по ходу часовой стрелки.

Для определения скорости точки воспользуемся теоремой подобия. Поскольку точка на схеме механизма лежит посередине шатуна , то и на плане скоростей она должна лежать посередине отрезка .

Ответ:

План ускорений

План ускорений – построенный в определенном масштабе векторный график, характеризующие ускорения всех точек и звеньев механизма. Произвольная точка ра, из которой производится построение плана ускорений, называется полюсом плана ускорений.

Рассмотрим графический способ определения ускорений точек плоской фигуры (тела) с помощью плана ускорений.

Планом ускорений плоской фигуры является геометрическое место концов векторов ускорений любых точек фигуры, что отложены из одной произвольной точки, которую называют полюсом плана ускорений.

Построение плана ускорений основано на представлении ускорения любой точки фигуры в виде суммы трех векторов:

где — ускорение точки фигуры, которую принято за полюс поступательного движения;

— относительное нормальное (центростремительное) ускорение точки в ее относительном вращательном движении вместе с телом вокруг полюса . Направлено это ускорение от точки к точке и по модулю равно

— относительное тангенциальное (касательное) ускорение точки в ее относительном вращательном движении вместе с телом вокруг полюса . Направлено это ускорение перпендикулярно (отрезка ) в сторону углового ускорения тела и по модулю равно

Поскольку для определения величины надо знать угловую скорость плоской фигуры, то, если она не задана, предварительно надо построить план скоростей. Из плана скоростей определить относительную скорость вращения одной точки фигуры относительно второй и найти угловую скорость относительного вращательного движения (занятие 7).

Для того, чтобы уравнение (4.18) можно было решить, должно быть известно ускорение любой точки фигуры, которую выбирают за полюс поступательного движения.

Кроме того, должно быть известно:

Рассмотрим определение ускорений точек и треугольника (рис.4.31, а). Известными являются ускорение точки , направление ускорения точки и угловая скорость треугольника , то есть случай 1.

Для ускорения точки , если за полюс выбрать точку , будет справедливым векторное уравнение (4.18).

Решим уравнение (4.18) графически. Для этого (рис.4.31, б) из произвольной точки (полюса плана ускорений) построим вектор , который в масштабе будет изображать ускорение . С конца построенного вектора (точки ) построим вектор , который в том же масштабе будет изображать ускорение .

Величину ускорения определим из формулы:

а направлен этот вектор вдоль от точки к точке .

К нормальному ускорению добавим, согласно уравнению (4.18), тангенциальное ускорение . Поскольку величина этого ускорения неизвестна, то через точку (конец вектора ) проведем линию перпендикулярно , вдоль которой и будет направлен вектор .

Направление абсолютного ускорения точки известно из условия задачи. Поскольку все абсолютные ускорения точек на плане откладываются от полюса , то через полюс проведем прямую, параллельную направлению ускорения точки . Точка пересечения линий и будет решением уравнения (4.18), а вектор будет в выбранном масштабе изображать ускорение точки .

Для определения ускорения точки воспользуемся тем, что известными уже являются ускорения двух точек фигуры и (случай 2).

Запишем векторные уравнения для ускорения точки относительно полюсов и :

где и — относительные нормальные ускорения точки в ее относительном вращательном движении соответственно вокруг точек и ;

и — относительные тангенциальные ускорения точки в ее относительном вращательном движении вокруг точек и , соответственно.

Первым решаем уравнение (4.19). Поскольку ускорение точки на плане (рис.4.31, б) уже построено, то с его конца (точки ) строим вектор , который направлен от точки к точке и по модулю в масштабе равен :

Через конец вектора проводим прямую, перпендикулярную , вдоль которой будет направлено ускорение и на которой будет лежать точка конца вектора .

Следующим построим уравнение (4.20). Поскольку ускорение точки на плане уже построено, то с его конца, точки , строим вектор , который направлен от к и по модулю в масштабе равен :

Таким образом, конец вектора будет лежать на пересечении линий, вдоль которых будут направлены тангенциальные ускорения и . Вектор на плане ускорений будет в масштабе изображать абсолютное ускорение точки .

Векторы , и , выходящие из полюса плана ускорений, определяют абсолютные ускорения точек , и . Отрезки же, соединяющие концы векторов абсолютных ускорений и определяют относительные ускорения одних точек при их вращении вокруг других

Кроме абсолютных и относительных ускорений точек фигуры , определяется величина ее углового ускорения :

или или

Для определения же направления углового ускорения надо перенести в точку вектор тангенциального ускорения и направление этого вектора укажет направление углового ускорения. В данном случае, угловое ускорение направлено по ходу часовой стрелки.

Треугольник , который образовался на плане ускорений будет подобно треугольнику .

Таким образом, для плана ускорений справедливо

правило подобия: фигура, которую образуют концы векторов абсолютных ускорений точек тела на плане ускорений подобная фигуре, которую одноименные точки образуют на теле.

Примеры решения задач на тему: План ускорений

Задача №1

Найти ускорение точки ползуна 3 и угловое ускорение шатуна 2 механизма, изображенном на рис.4.24. Выходные данные: , кривошип 1 вращается равномерно

Решение. План скоростей для этого механизма был построен в задаче № 1 занятия № 7 (рис.4.25,б) и была определена угловая скорость шатуна 2

1.Построим схему механизма (рис. 4.32, а).

2. Сначала найдем ускорение точки механизме, поскольку она принадлежит кривошипу 1, который вращается вокруг точки с известной угловой скоростью.

Учитывая, что угловая скорость кривошипа постоянная то и полное ускорение будет равняться нормальному ускорению точки в ее вращательном движении вокруг :

По модулю:

Направлено ускорение от точки к точке по линии .

3. Для определения ускорения точки запишем формулу распределения ускорений при плоском движении, приняв за полюс точку , ускорение которой уже известно:

где — абсолютное ускорение точки , которое направлено по направлению движения ползуна 3 в горизонтальных направляющих;

— ускорение точки , известное по величине и по направлению;

— относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено по шатуну от точки к точке и по модулю равно:

— тангенциальное ускорение точки при ее вращении вокруг точки , направлено перпендикулярно шатуну и по модулю равно:

Поскольку направление ускорения точки известно, то уравнение (1) достаточно для определения .

4. Решим уравнение (1) графически путем построения плана ускорений.

Из произвольной точки полюса плана ускорений (рис.4.32,б) отложим вектор , который будет изображать ускорение , и который направлен параллельно линии от точки к точке . От конца этого вектора отложим вектор , что будет изображать , и который направлен параллельно от точки к точке . Через конец вектора , точку , проведем линию , перпендикулярную , вдоль которой будет направлено тангенциальное ускорение и на этой линии будет лежать точка — конец вектора абсолютного ускорения точки механизма.

Поскольку ускорение направлено по оси движения ползуна 3, то с полюса проводим горизонтальную прямую. Точка пересечения этой прямой с линией , проведенная перпендикулярно , будет концом вектора ускорения точки , а вектор будет изображать на плане ускорений .

4. Из построенного плана ускорений определим абсолютные величины ускорений и . Для этого с полюса опустим перпендикуляр на продолжение линии . Угол равен углу и составляет .

Из векторного четырехугольника (рис. 4.32, б) вытекает:

Спроектируем векторное уравнение (2) на прямую :

Учитывая, что изображает на плане ускорений , , уравнение (3) можно переписать следующим образом:

Откуда:

Теперь спроектируем уравнение (2) на прямую :

Учитывая, что на плане ускорений изображает , получим:

Откуда:

Поскольку , то:

Из полученного результата следует, что в данный момент времени шатун механизма вращается равномерно и план ускорений будет иметь вид как на рис.4.33.

Ответ:

Если построение плана ускорений выполнять с соблюдением масштаба, то ускорения характерных точек можно определить непосредственно измерением соответствующих отрезков на плане ускорений.

Задача №2

Найти абсолютное ускорение точек и на угловые ускорения шатуна 2 и коромысла 3 шарнирного механизма, схема которого изображена на рис.4.26, если: . Кривошип 1 механизма вращается с постоянной угловой скоростью

Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче № 2 занятие № 7 (рис.4.27, б) и определены мгновенные угловые скорости шатуна 2 и коромысла 3:

Решим задачу путем построения в масштабе плана ускорений.

1. Сначала в произвольном масштабе строим схему механизма (рис.4.34, а).

2.Определим ускорение точки кривошипа.

Поскольку кривошип 1 вращается вокруг неподвижной точки с постоянной угловой скоростью (то есть и соответственно ), то ускорение точки :

По модулю равно:

Направлено ускорение от точки к точке .

3.Запишем векторные уравнения для определения ускорения точки .

Точка принадлежит одновременно шатуну 2 и коромыслу 3 (случай 3). У шатуна 2 известно уже определенное ускорение точки , а в коромысла 3 ускорение точки (точка неподвижная, то есть ). Таким образом, можно записать формулы распределения ускорений для точки , взяв за полюс точку для шатуна 2 в первом уравнении и точку для коромысла 3 во втором уравнении:

где — относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке и по модулю равно:

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно и по модулю равно:

— относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке и по модулю равно:

4.Решим графически систему векторных уравнений (1,2).

Сначала построим уравнение (1). Для этого из произвольной точки полюса плана ускорений (рис.4.34,б) отложим вектор , который будет изображать ускорение . Направлен вектор параллельно линии от точки к точке . Длину этого вектора выберем . Тогда масштабный коэффициент плана ускорений будет равняться:

От конца вектора отложим вектор , который будет изображать . Направлен вектор параллельно от точки к точке , а длина этого вектора равна:

Через конец вектора проведем линию перпендикулярную , вдоль которой будет направлено тангенциальное ускорение и на этой линии будет лежать точка — конец вектора абсолютного ускорения точки механизма.

Следующим построим уравнение (2).

Поскольку , то точка будет лежать в полюсе плана ускорений.

От точки отложим вектор , который будет изображать . Направлен вектор параллельно от точки к точке , а длина этого вектора соответственно равна:

Через конец вектора проведем линию перпендикулярную , вдоль которой будет направлено тангенциальное ускорение .

Решением системы (1,2) будет точка , в которой пересекаются линии, проведенные перпендикулярно и , вдоль которых направлены соответственно тангенциальные ускорения и .

Вектор абсолютного ускорения точки на плане ускорений в масштабе будет изображаться вектором , а величина ускорения точки равна:

Величины тангенциальных ускорений и найдем путем измерения соответствующих отрезков на плане ускорений:

Поскольку и , то мгновенные угловые ускорения шатуна 2 и коромысла 3 соответственно равны:

где — длина коромысла 3, которая была определена в задаче №2 занятия №7.

Для определения направления углового ускорения перенесем мысленно в точку относительное тангенциальное ускорение . Направление указывает на то, что будет направлено по ходу часовой стрелки.

Аналогично, для определения направления в точку перенесем . Угловое ускорение будет направлено против хода часовой стрелки.

5.Для определения ускорения точки воспользуемся теоремой подобия. Для этого сначала построим прямую на плане ускорений (рис.4.34, б). Поскольку фигура на схеме механизма и фигура на плане ускорений должны быть подобными, то можно составить пропорцию:

В левой части пропорции (3) отношение отрезков на схеме механизма, а в правой — на плане ускорений.

Из уравнения (3) получим расстояние от точки к точке на плане ускорений:

Поскольку на схеме механизма отрезок перпендикулярен , то и на плане ускорений отрезок надо провести перпендикулярно , причем в ту сторону, чтобы расположение точек , и на плане ускорений было против хода часовой стрелки, как и точки , и на схеме механизма.

Ответ:

Задача №3

В состав рычажного механизма (рис.4.35) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 в настоящий момент времени вращается равномерно с угловой скоростью , а кривошип 4 – замедленно с угловой скоростью и угловым ускорением

Найти угловые ускорения шатунов 2 и 3 и абсолютные ускорения точек и , если: . В данном положении механизма кривошип 1 расположен вертикально, а кривошип 4 — горизонтально.

Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче №3 занятия №7 (рис.4.30, б) и определены мгновенные угловые скорости шатуна 2 и шатуна 3:

1. В произвольном масштабе построим схему механизма (рис. 4.36, а).

2.Сначала определим абсолютные ускорения точек и , принадлежащие соответственно кривошипам 1 и 4, угловые скорости которых известны.

Поскольку кривошип 1 вращается вокруг неподвижной точки с постоянной угловой скоростью то есть , то:

Направлено ускорение вдоль кривошипа от точки к точке .

Кривошип 4 вращается вокруг неподвижной точки с угловой скоростью и угловым ускорением . Поскольку кривошип 4 вращается замедленно, то угловое ускорение направлено противоположно угловой скорости (рис.4.35.)

Абсолютное ускорение точки кривошипа 4 представляет собой векторную сумму нормальной и тангенциальной составляющих:

Нормальная составляющая ускорения точки направлена вдоль от точки к точке и по модулю равна:

а тангенциальная — перпендикулярно в сторону углового ускорения и по модулю равна:

3. Запишем векторные уравнения для определения ускорения точки .

Точка принадлежит одновременно шатуну 2 и шатуну 3. У шатуна 2 известно ускорение точки , а у шатуна 3 — точки . Таким образом, можно записать формулы распределения ускорений для точки , взяв за полюс точку для шатуна 2 в первом уравнении и точку шатуна 3 во втором:

В уравнении (2):

— направлено вдоль от точки к точке и по модулю равно:

— направлено перпендикулярно , величина и направление этого ускорения неизвестны.

В уравнении (3):

— направлено вдоль от точки к точке и по модулю равно:

— направлено перпендикулярно , величина и направление этого ускорения неизвестны.

4. Решим графически систему векторных уравнений (2,3).

Сначала построим уравнение (2). Для этого из произвольной точки полюса плана ускорений (рис.4.36,б) отложим вектор , который будет изображать ускорение . Направлен вектор параллельно линии от точки к точке . Длину этого вектора выберем . Тогда масштабный коэффициент плана ускорений будет равняться:

Следующим построим уравнение (3).

Для построения вектора от полюса согласно уравнению (1) отложим вектор , а с его конца . Эти векторы в масштабе будут изображать ускорения и и будут направлены им параллельно (рис. 4.36, а).

Длины векторов и соответственно равны:

Абсолютное ускорение точки на плане ускорений будет изображаться вектором .

От точки отложим вектор , который будет изображать. Направлен вектор параллельно от точки к точке , а длина этого вектора равна:

Решением системы (2,3) будет точка , в которой пересекаются линии, проведенные перпендикулярно и , вдоль которых направлены соответственно тангенциальные ускорения и .

Величины тангенциальных ускорений и найдем путем измерения соответствующих отрезков на плане ускорений:

Поскольку и , то мгновенные угловые ускорение шатуна 2 и шатуна 3 соответственно равны:

Направления угловых ускорений и определяем путем перенесения мысленно в точку относительных тангенциальных ускорений и (аналогично задаче №2). Угловое ускорение направлено по ходу часовой стрелки, а — против хода часовой стрелки.

5. Для определения ускорения точки воспользуемся теоремой подобия. Поскольку точка на схеме механизма лежит посередине шатуна , то и на плане ускорений она должна лежать посередине отрезка . Вектор ускорения точки плане ускорений в масштабе будет изображаться вектором , а величина абсолютного ускорения точки равна:

Ответ:

Услуги по теоретической механике:

Заказать теоретическую механику
Помощь по теоретической механике
Заказать контрольную работу по теоретической механике

Учебные лекции:

Статика
Система сходящихся сил
Момент силы
Пара сил
Произвольная система сил
Плоская произвольная система сил
Трение
Расчет ферм
Расчет усилий в стержнях фермы
Пространственная система сил
Произвольная пространственная система сил
Плоская система сходящихся сил
Пространственная система сходящихся сил
Равновесие тела под действием пространственной системы сил
Естественный способ задания движения точки
Центр параллельных сил
Параллельные силы
Система произвольно расположенных сил
Сосредоточенные силы и распределенные нагрузки
Кинематика
Кинематика твердого тела
Движения твердого тела
Динамика материальной точки
Динамика механической системы
Динамика плоского движения твердого тела
Динамика относительного движения материальной точки
Динамика твердого тела
Кинематика простейших движений твердого тела
Общее уравнение динамики
Работа и мощность силы
Обратная задача динамики
Поступательное и вращательное движение твердого тела
Плоскопараллельное (плоское) движение твёрдого тела
Сферическое движение твёрдого тела
Движение свободного твердого тела
Сложное движение твердого тела
Сложное движение точки
Статика твердого тела
Равновесие составной конструкции
Равновесие с учетом сил трения
Центр масс
Колебания материальной точки
Относительное движение материальной точки
Статические инварианты
Дифференциальные уравнения движения точки под действием центральной силы и их анализ
Динамика системы материальных точек
Общие теоремы динамики
Теорема об изменении кинетической энергии
Теорема о конечном перемещении плоской фигуры
Потенциальное силовое поле
Метод кинетостатики
Вращения твердого тела вокруг неподвижной точки

Источник

Определение скоростей и ускорений точек механизма методом планов

Планы скоростей и ускорений начального звена

Определение скоростей и ускорений групп II класса методом планов

Начальный механизм

Как составить план местности?

Ход работы

Другие способы съёмки местности

Плоское движение тела

Определение скоростей точек тела

Уравнения плоского движения

Скорости точек фигуры. Мгновенный центр скоростей

Определение положения мгновенного центра скоростей

Порядок решения задач на тему: Определение скоростей точек тела

Примеры решения задач на тему: Определение скоростей точек тела

Решение задачи графоаналитическим способом

Решение задачи с помощью мгновенного центра скоростей

Определение ускорений точек тела

Ускорения точек плоской фигуры

Порядок решения задач на тему: Определение ускорений точек тела

Примеры решения задач на тему: Определение ускорений точек тела

План скоростей

Порядок решения задач на тему: План скоростей

Примеры решения задач на тему: План скоростей

План ускорений

Примеры решения задач на тему: План ускорений

Не пропустите также: