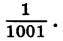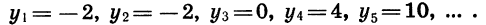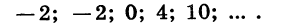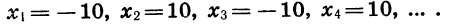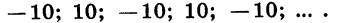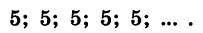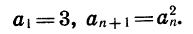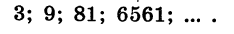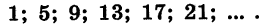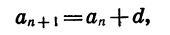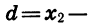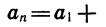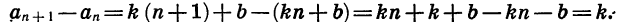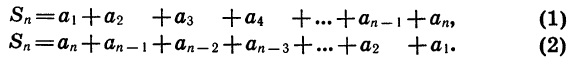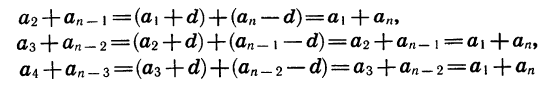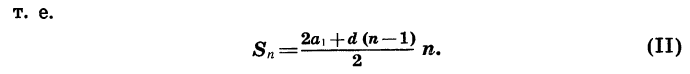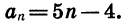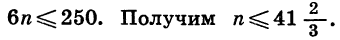Зная первый и второй члены арифметической прогрессии можно определить разность прогрессии.
d = a2 – a1 = 92 – 96 = -4.
Используем формулу n – ого члена арифметической прогрессии.
an = a1 + (n – 1) * d;
an = 96 + (n – 1) * (-4);
an = 96 – 4 * n + 4;
an = 100 – 4 * n.
Приравняем an к нулю.
100 – 4 * n = 0;
4 * n = 100;
n = 100/4 = 25.
25 – ый член арифметической прогрессии равен 0.
Если ноль это ни положительное, ни отрицательное число, то положительных чисел в прогрессии 24.
Ответ: 24 положительных числа. (25 с нулем).
14
Июл 2013
Категория: Справочные материалы
Арифметическая прогресcия. Часть 1
2013-07-14
2021-06-27

1, 3, 5, 7, 9, 11, …
Конечно, мы понимаем, что будет следовать после 11 + показать
Перед нами – как раз пример арифметической прогрессии.
Дадим определение арифметической прогрессии, после чего будем разбираться на примерах.
Арифметическая прогрессия. Формула n-го члена
Арифметическая прогрессия — числовая последовательность вида
,
то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага или разности прогрессии):
.
Любой (n-й) член прогрессии может быть вычислен по формуле:
,
где – первый член прогрессии,
– разность прогрессии.
И еще одна формула, которая способна облегчить ситуацию в отдельных случаях:
,
где ,
– разность прогрессии.
Формулы суммы n первых членов арифметической прогрессии смотрим здесь: «Арифметическая прогрессия. Часть 2»
Отправляемся в цирк
Вначале было все так понятно… вдруг какие-то Как это понимать?
Все очень просто. Возьмем еще раз наш ряд чисел 1, 3, 5, 7, 9, 11, …
Нам очень важен порядок чисел в ряду. Если мы «перетасуем» числа ряда, то закономерности, что мы обнаружили ранее, уже не будет.
Вы когда идете, например, в цирк, то вы проходите по билету, где указаны точные координаты вашей посадки. Иначе бы был бардак. Вот и мы за каждым числом в ряду закрепим место.
В нашем примере и т.д. То есть нижний индекс в записи
и означает «номер занимаемого кресла» числом в рассматриваемом ряду чисел.
Примеры
Пример 1.
{} – арифметическая прогрессия.
Найдите , если
Решение: + показать
Пример 2.
{} – арифметическая прогрессия.
Найдите первый член арифметической прогрессии, если
Решение: + показать
Пример 3.
Найдите номер члена арифметической прогрессии {}, равного
, если
Решение: + показать
Пример 4.
Найдите первый положительный член арифметической прогрессии, заданной формулой
Решение: + показать
Пример 5.
Дана арифметическая прогрессия
Найдите если
Решение: + показать
Пример 6.
Найдите значения , при которых числа
образуют арифметическую прогрессию.
Решение: + показать
Вы можете заглянуть и во вторую часть статьи «Арифметическая прогрессия. Сумма арифметической прогрессии»
Предлагаю также пройти тест по теме «Арифметическая прогрессия. Формула n-го члена».
Автор: egeMax |
комментария 2
Печать страницы
Арифметическая прогрессия — это последовательность чисел, в которой разница между двумя соседними числами — постоянна.
Пример:
Последовательность 1, 2, 3, 4,… является арифметической прогрессией с шагом(разностью) прогрессии 1.
Пример:
Последовательность 3, 5, 7, 9, 11,… является арифметической прогрессией с разностью 2.
Пример:
Последовательность 20, 10, 0, -10, -20, -30,… является арифметической прогрессией с разностью -10.
Последовательности
Будем выписывать в порядке возрастания положительные четные числа. Первое такое число равно 2, второе 4, третье 6, четвертое 8 и т. д. Получим последовательность
2; 4; 6; 8; … .
Очевидно, что на пятом месте в этой последовательности будет число 10, на десятом — число 20, на сотом — число 200. Вообще для любого натурального числа п можно указать соответствующее ему положительное четное число; оно равно 2n.
Рассмотрим еще одну последовательность. Будем выписывать в порядке убывания правильные дроби с числителем, равным 1:
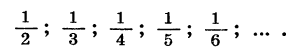
Для любого натурального числа n мы можем указать соответствующую ему дробь; она равна 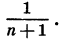
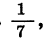
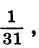
Числа, образующие последовательность, называют соответственно первым, вторым, третьим, четвертым и т. д. членами последовательности. Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена. Например, 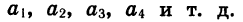
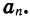
Заметим, что последовательность может содержать конечное число членов. В таком случае ее называют конечной. Например, конечной является последовательность двузначных чисел:
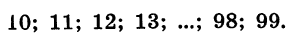
Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
Часто последовательность задают с помощью формулы n-го члена последовательности. Например, последовательность положительных четных чисел можно задать формулой 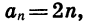
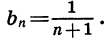
Пример:
Пусть последовательность задана формулой 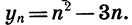
Рассматриваемая последовательность начинается так:
Пример:
Пусть последовательность задана формулой 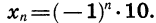
Получаем последовательность
Пример:
Формулой 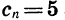
Рассмотрим еще один способ задания последовательности.
Пример:
Пусть первый член последовательности 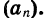
С помощью формулы 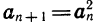
Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro — возвращаться).
Определение арифметической прогрессии
Формула n-го члена арифметической прогрессии:
Рассмотрим последовательность натуральных чисел, которые при делении на 4 дают в остатке 1:
Каждый ее член, начиная со второго, получается прибавлением к предыдущему члену числа 4. Эта последовательность является примером арифметической, прогрессии.
Определение:
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Иначе говоря, последовательность
где d — некоторое число.
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна d, т. е. при любом натуральном n верно равенство
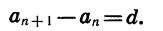
Число d называют разностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность. Приведем примеры.
Если 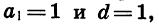
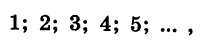
члены которой — последовательные натуральные числа.
Если 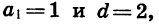
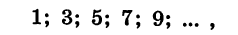
которая является последовательностью положительных нечетных чисел.
Если 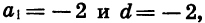
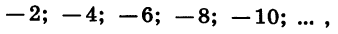
которая является последовательностью отрицательных четных чисел.
Если 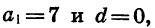
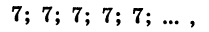
все члены которой равны между собой.
Зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т. д. члены. Однако для нахождения члена прогрессии с большим номером такой способ неудобен. Постараемся отыскать способ, требующий меньшей вычислительной работы.
По определению арифметической прогрессии
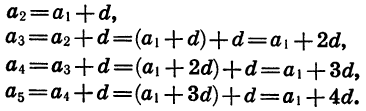
Точно так же находим, что 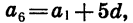
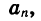
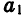
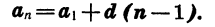
Мы получили формулу n-го члена арифметической прогрессии.
Приведем примеры решения задач с использованием этой формулы.
Пример:
Последовательность 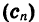
Имеем:
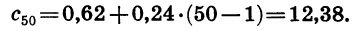
Пример:
Выясним, является ли число —122 членом арифметической прогрессии
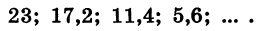
В данной арифметической прогрессии 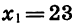
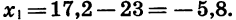
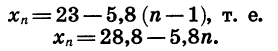
Число —122 является членом арифметической прогрессии 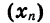
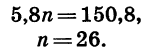
Значит, число —122 является 26-м членом данной арифметической прогрессии.
Формулу n-го члена арифметической прогрессии 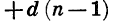
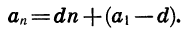
Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида
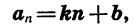
где k и b — некоторые числа.
Верно и обратное: последовательность 
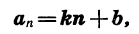
где k и b — некоторые числа, является арифметической прогрессией.
Действительно, найдем разность (n + 1)-го и n-го членов последовательности 
Значит, при любом n справедливо равенство 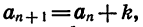

Формула суммы n первых членов арифметической прогрессии
Пусть требуется найти сумму первых ста натуральных чисел. Покажем, как можно решить эту задачу, не выполняя непосредственного сложения чисел.
Обозначим искомую сумму через S и запишем ее дважды, расположив в первом случае слагаемые в порядке возрастания, а во втором — в порядке убывания:
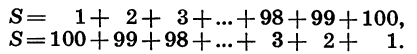
Каждая пара чисел, расположенных друг под другом, дает в сумме 101. Число таких пар равно 100. Поэтому, сложив равенства почленно, получим:
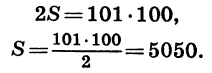
Итак,
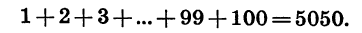
С помощью аналогичных рассуждений можно найти сумму первых членов любой арифметической прогрессии.
Обозначим сумму n первых членов арифметической прогрессии 
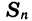
Сумма каждой пары членов прогрессии, расположенных друг под другом, равна 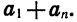
и т. д.
Число таких пар равно n. Поэтому, сложиd почленно равенства (1) и (2), получим:
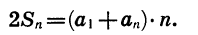
Разделив обе части последнего равенства на 2, получим формулу суммы п первых членов арифметической прогрессии:

Приведем примеры на вычисление суммы членов арифметической прогрессии.
Пример:
Найдем сумму первых тридцати членов арифметической прогрессии 4; 5,5; … .
В данной арифметической прогрессии 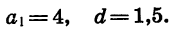
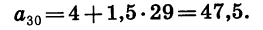
Теперь вычислим сумму первых тридцати членов:
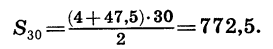
Заметим, что если заданы первый член и разность арифметической прогрессии, то удобно пользоваться формулой суммы, представленной в другом виде. Подставим в формулу (I) вместо 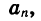
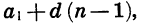
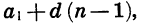
Если для решения рассмотренной задачи воспользоваться формулой (II), то вычисления будут выглядеть так:
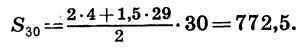
Пример:
Найдем сумму первых сорока членов последовательности 
Последовательность 
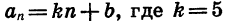
Найдем первый и сороковой члены этой арифметической прогрессии: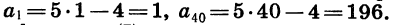
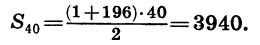
Пример:
Найдем сумму 1 + 2 + 3 + … + n, слагаемыми в которой являются все натуральные числа от 1 до n.
Применив формулу 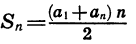
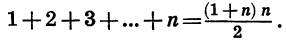
Пример:
Найдем сумму всех натуральных чисел, кратных шести и не превосходящих 250.
Натуральные числа, кратные шести, образуют арифметическую прогрессию, которую можно задать формулой 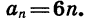
Значит, число членов прогрессии, сумму которых надо найти, равно 41. Имеем:
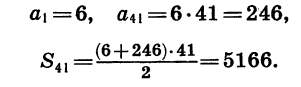
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат