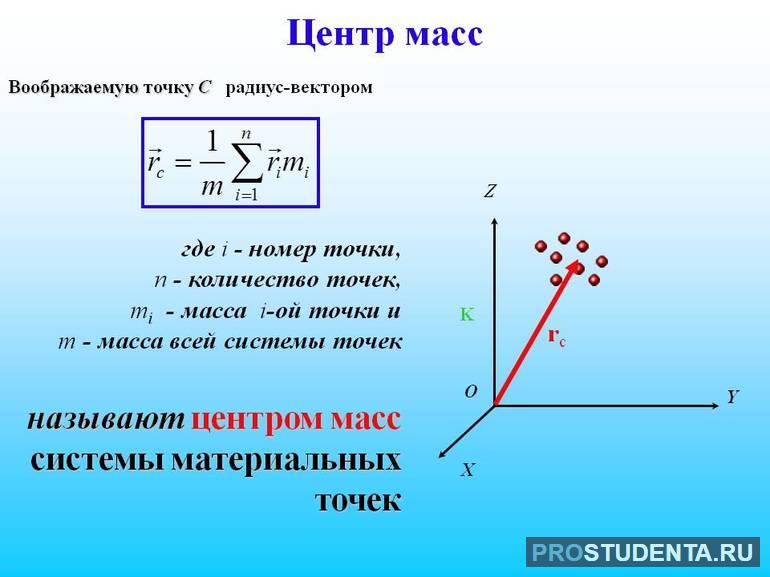
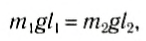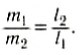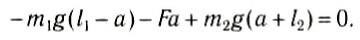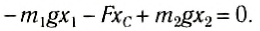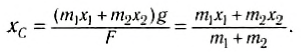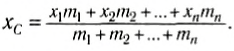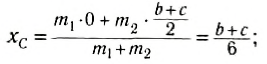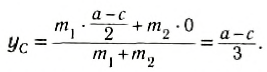Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».
Оглавление:
- Общие сведения
- Связь с центром тяжести
- Вычисление положения
- Геометрический способ определения
Общие сведения
Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.
Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.
Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:
- центра масс;
- вращения.
Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.
Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.
Связь с центром тяжести
Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.
Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.
Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.
Для примера можно привести список однородных фигур с указанием их центральной точки:
- отрезок — середина;
- параллелограмм — место пересечения диагоналей;
- треугольник — точка пересечения медиан (центроид);
- любой правильный многоугольник — центр поворотной симметрии;
- полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.
Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.
Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.
При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.
Вычисление положения
Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.
На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.
Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:
- векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
- сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.
Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.
Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.
Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.
При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.
Геометрический способ определения
Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.
Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.
Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.
Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.
Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.
Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.
Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.
Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.
Определение центра масс, теория и онлайн калькуляторы
Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Радиус-вектор и координаты центра масс
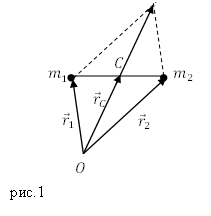
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: ${overline{r}}_1 и {overline{r}}_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором ${overline{r}}_C$ (рис.1).
Из рис.1 видно, что:
[{overline{r}}_C=frac{{overline{r}}_1+ {overline{r}}_2}{2}left(1right).]
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен ${overline{r}}_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
[{overline{r}}_C=frac{{overline{r}}_1m_1+ {overline{r}}_2m_2}{m_1+m_2}left(2right).]
Радиус -вектор ${overline{r}}_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц ${overline{r}}_1$ и ${overline{r}}_2$. Это становится очевидным, если формулу (2) представить в виде:
[{overline{r}}_C=frac{m_1}{m_1+m_2}{overline{r}}_1+frac{m_2}{m_1+m_2}{overline{r}}_2left(3right).]
Выражение (3) показывает, что радиус-вектор каждой частицы входит в ${overline{r}}_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(4right).]
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(5right).]
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Скорость центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) запишем как:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(8right),]
где $overline{P}$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Пример 2
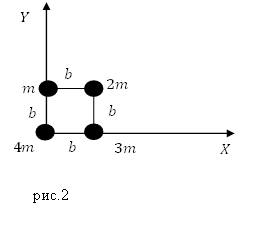
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_с=frac{sumlimits_i{Delta m_iy_i}}{m}. end{array}
right.]
Вычислим массу рассматриваемой системы точек:
[m=m+2m+3m+4m=10 m.]
Тогда абсцисса центра масс $x_{c } $равна:
[x_c=frac{0cdot 4m+3mcdot b+2mcdot b}{10m}=0,5 b.]
Ордината $y_с$:
[y_с=frac{0cdot m+mcdot b+2mcdot b}{10m}=0,3 b.]
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Пример 2
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
[frac{s_1}{s_2}=frac{m_2}{m_1}left(2.1right).]
По условию:
[s=s_1+s_2left(2.2right).]
Из уравнений (2.1) и (2.2) получаем:
[s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}.]
Ответ. $s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}$
Читать дальше: период и частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
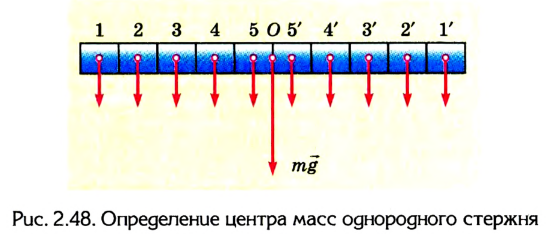
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
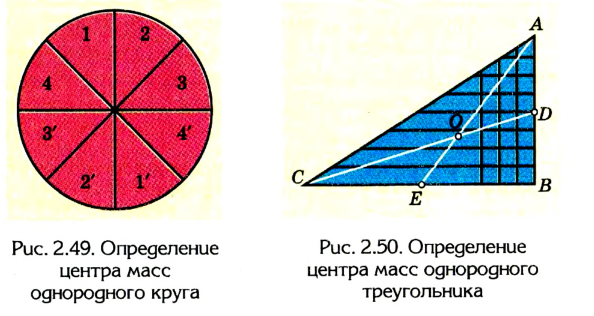
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
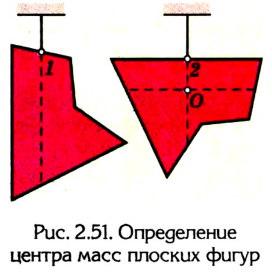
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
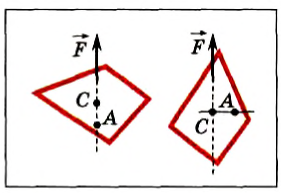
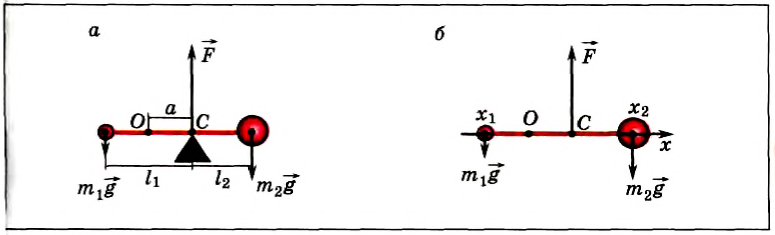
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
или
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
Отсюда
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =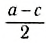
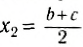
По формуле (3): .
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Сущность понятия «центр масс»
Понятие «центр масс» широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.
Определение 1
Центр масс — точка, характеризующая размещение и движение исследуемой системы как единого целого.
Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке «15 см». Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.
На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.
Нахождение координат центра масс
Определение 2
Центр масс двух тел с точечными массами $m_1$ и $m_2$ и координатами на координатной прямой $x_1$ и $x_2$ находится в точке, делящей расстояние между этими телами на отрезки с длинами обратно пропорциональными массам рассматриваемых тел.
Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.
Расстояние между точечными телами равно:
$Delta x = x_2 — x_1$
Пропорция между массами и расстояниями, согласно определению:
$frac{l_1}{l_2} = frac{m_2}{m_1}$,
«Как найти координаты центра масс» 👇
где $l_1$, $l_2$ — расстояния от соответствующих тел до центра масс.
Выразив, длины через координаты
$l_1 = x_c — x_1; l_2 = x_2 — x_c$,
центр масс можно определить как
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.
где $x_c$ — координата центра тяжести.
Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):
$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$
В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.
Замечание 1
Центр тяжести системы тел представляет собой точку, подобную центру масс, но рассчитывается не для масс, а для весов (обусловленных гравитацией сил), действующих на точечные тела, входящие в систему. Центр тяжести определяется так же, как и центр масс, если размеры системы малы в сравнении с радиусом планеты Земля. Он в большинстве случаев с достаточной для практики точностью совпадает с центром масс рассматриваемой системы.
Пример 1
Найти центр масс двух линеек, изготовленных из одинакового материала, одинаковой толщины и ширины, левые концы линеек совмещены. Длины линеек — 10 и 30 см. Толщиной линеек можно пренебречь.
Поскольку толщиной можно пренебречь, найти нужно лишь координату центра масс по оси $x$.
Разобьем мысленно систему на два отрезка. Первый — где толщина линеек складывается. Его координаты — $[0, 10]$. Второй отрезок — где длинная линейка продолжается одна. Его координаты — $[10, 30]$. Примем за единицу измерения массу одного погонного сантиметра линейки. Тогда масса второго фрагмента:
$m_2 = 30 — 10 = 20$
На каждый сантиметр первого фрагмента приходится вдвое больше массы, поскольку там сложены две линейки:
$m_1 = 10 cdot 2 = 20$
Центры масс отрезков находятся на их осях симметрии, т.е. на середине длины каждого:
$x_{c1} = frac{10}{2} = 5$;
$x_{c2} = 10 + frac{20}{2} = 20$
Подставим значения в формулу:
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$
$x_c = frac{20 cdot 5 + 20 cdot 20}{20 +20} = frac{100 + 400}{40} = 12, 5$
Ответ: центр масс находится на расстоянии 12,5 см от левого конца системы линеек.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Динамика механической системы
- Геометрия масс
- Механическая система. Центр масс механической системы
- Порядок решения задач на определение центра масс механической системы
- Примеры решения задач на тему: Определение центра масс механической системы
- Моменты инерции твердого тела относительно оси
- Моменты инерции некоторых однородных тел
- Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
- Теорема о движении центра масс механической системы
- Закон сохранения движения центра масс
- Порядок решения задач на применение теоремы о движении центра масс
- Примеры решения задач на тему: Теорема о движении центра масс механической системы
- Теорема об изменении количества движения точки и механической системы
- Импульс силы
- Теорема об изменении количества движения точки и системы
- Закон сохранения количества движения системы
- Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
- Теорема об изменении момента количества движения точки и механической системы
- Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
- Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
- Теорема об изменении кинетической энергии механической системы
- Кинетическая энергия механической системы
- Определение кинетической энергии твердого тела в различных случаях его движения
- Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
- Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика механической системы
В предыдущей главе рассматривались задачи, связанные с движением материальной точки, которая находится под действием приложенных к ней сил. Однако часто приходится встречаться с такими случаями, когда движение одной точки невозможно рассматривать изолированно от движения других материальных точек. Это заставляет нас перейти к изучению движения совокупности материальных точек, или механических систем.
В механике под механической системой материальных точек или тел имеют в виду такую их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения или движения всех других.
Совокупность тел, между которыми отсутствуют силы взаимодействия и движение которых никаким образом не связано друг с другом, механическую систему не создают. Механические системы бывают свободными и несвободными.
Система материальных точек, движение которых не ограничено никакими связями, а определяется только действующими на эти точки силами, называется системой свободных точек.
Система материальных точек, движение которых ограничивается наложенными на точки связями, называется системой несвободных точек.
Решение задач динамики механической системы базируется на теоремах динамики и некоторых принципах, которые будут рассмотрены в данной главе.
Геометрия масс
Геометрия точки масс, в просторечии известная как точки масс , является проблемой геометрии — метод решения , который применяет физический принцип центра масс к геометрическим задачам, включающим треугольники и пересекающиеся чевианы . Все задачи, которые могут быть решены с использованием геометрии материальных точек, также могут быть решены с использованием аналогичных треугольников, векторов или соотношений площадей, но многие студенты предпочитают использовать массовые точки.
Механическая система. Центр масс механической системы
В механике под механической системой подразумевают совокупность взаимодействующих между собой материальных точек или тел.
Частным случаем механической системы является абсолютно твердое тело.
Массой механической системы называется сумма масс всех точек, входящих в систему:
где 


Центром масс (центром инерции) механической системы называется точка 

где 


Декартовы координаты центра масс системы материальных точек определяются по зависимостям:
Здесь 

Для твердого тела центр масс совпадает с центром тяжести.
Порядок решения задач на определение центра масс механической системы
Решение задач, в которых необходимо определить положение центра масс и уравнение его траектории, рекомендуется проводить в следующей последовательности:
Выбрать систему координат.
Записать координаты центров тяжести каждой из масс системы, выразив их в виде функций времени:
Определить координаты центра масс системы по формулам (5.1), при этом 
Для нахождения уравнений траектории центра масс надо с последних выражений (пункт 3) исключить время.
Примеры решения задач на тему: Определение центра масс механической системы
Задача № 1
Определить положение центра масс центробежного регулятора, изображенного на рис.5.2, если вес каждого из шаров 






Решение. Система координат, относительно которой необходимо определить положение центра масс, изображена на рис.5.2.
Для определения положения центра масс системы надо определить его координаты по формулам (5.1):
где




Следовательно,
Находим координаты центров масс:
пули 
пули 
муфты 
Тогда:
поскольку
Ответ:
Задача № 2
Найти уравнение движения центра масс шарнирного параллелограмма 


Решение. Начало системы координат свяжем с шарниром 





Поскольку звенья 1,2,3 параллелограмма однородны, то центры масс их лежат посередине звеньев (точки 
Из размеров звеньев вытекает:
Определим координаты центров масс звеньев механизма как функции угла поворота 
Для определения координат центра масс шарнирного параллелограмма 
Для определения уравнения траектории центра масс (точки 

Сложим, соответственно, левые и правые части этих уравнений:
Таким образом, траекторией центра масс шарнирного параллелограмма является окружность:
с радиусом, равным 

Ответ: 
Задача № 3
Определить траекторию центра масс механизма эллипсографа (рис.5.4), который состоит из муфт 






Считать, что линейка и кривошип есть однородные стержни, а муфты — точечные массы.
Решение. Механизм состоит из 4 подвижных звеньев. Для удобства решения задачи пронумеруем звенья соответственно рис.5.4.
Система координат, относительно которой будет определяться траектория центра масс механизма показана на рисунке.
Сначала определим координаты центров масс всех звеньев механизма:
Для определения координат центра масс механизма эллипсографа воспользуемся формулой (5.1):
Следовательно, координаты центра масс эллипсографа имеют значения:
Для нахождения уравнения траектории центра масс в явном виде необходимо из этих уравнений исключить угол 


Траекторией центра масс является окружность с центром в точке 

Ответ:
Задача № 4
Определить зависимость от угла поворота кривошипа 





Решение. Выберем систему координат 



Применяя формулу (5.1), получим:
где 

С рис.5.5 находим:
Масса всей системы в данном случае равна:
Подставляя в выражения (1) и (2) значения координат центров масс тел механической системы и величину массы системы 
Ответ:
Задача № 5
Определить уравнение траектории центра масс кулисного механизма (рис.5.6), если вес кривошипа 









Будем считать, что в начальный момент ползун 
Решение. Выберем оси декартовых координат, как показано на рисунке, где положение кулисного механизма соответствует моменту времени 
Для определения положения центра масс системы 


Поскольку механическая система состоит из трех тел — кривошипа 


Индекс 1 соответствует кривошипу, индекс 2 — ползуну 
Из рисунка видно:
Подставим значения 


Исключим время 
Для этого решим оба уравнения относительно 

Возведем эти уравнения к квадрату и добавим:
Таким образом, траекторией центра масс кулисного механизма является эллипс с полуосями 
Центр эллипса лежит на оси 

Ответ: 
Моменты инерции твердого тела относительно оси
Влияние собственных свойств тела на вращательное движение значительно сложнее, чем в поступательном движении.
Также как масса тела является мерой инертности тела при его поступательном движении, так и момент инерции тела относительно данной оси является мерой инертности тела при его вращательном движении.
Как мера инертности тела момент инерции входит во все формулы вращательного движения. Не зная момента инерции тела, не умея его определить, нельзя решать задачи, которые связаны с вращательным или сложным движением тела, частью которого является вращательное движение.
Момент инерции тела (системы) относительно оси, например 

Моментом инерции тела относительно оси, например 
Если тело сплошное, то под 

где 

Этот интеграл берется по всей массе тела. Очевидно, что величина момента инерции зависит от размеров и формы тела , а также от закона распределения массы в теле.
Момент инерции измеряется в системе СИ — в 

Для тел правильной геометрической формы определение моментов инерции делается с помощью интегрального вычисления. Если тело имеет неправильную форму, то момент инерции его определяется либо приблизительно, путем разбития тела на несколько тел, которые имеют правильную геометрическую форму, либо экспериментально.
Для однородного тела, при плотности 
где интеграл берется по всему объему тела.
Для однородной материальной поверхности:
где 
Для однородной материальной линии:
где 

Для одной материальной точки, которая находится на расстоянии 
Иногда при определении момента инерции тела пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси, например 

где 
Следовательно, радиус инерции определяет расстояние от оси 

Момент инерции системы относительно начала координат равен
Моменты инерции относительно координатных осей (осевые моменты) выражаются зависимостями:
Существует простая зависимость между моментами инерции тела относительно параллельных осей, одна из которых проходит через его центр масс (теорема Гюйгенса-Штейнера).
Момент инерции тела относительно любой оси равен моменту инерции тела относительно оси, проходящей через центр масс тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями:
где 


Из выражения (5.4) вытекает, что наименьшим момент инерции тела будет относительно той оси, которая проходит через центр его масс.
Моменты инерции некоторых однородных тел
| Форма тела. | Схема тела. | Момент инерции. |
| Тонкий прямолинейный стержень |  |
 |
| -„- |  |
 |
| Круглая пластинка малой толщины |  |
 |
| Кольцо (материальная окружность) |  |
 |
| Круглый цилиндр |  |
 |
| Прямоугольный параллелепипед |  |
 |
| Полый шар со стенками малой толщины |  |
 |
| Шар |  |
 |
Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
Задача №1
Маятник, изображенный на рис. 5.7, состоит из тонкого однородного стержня длиной 


Определить момент инерции 


Решение. Маятник состоит из двух тел: стержня и диска, поэтому
где 


Момент инерции стержня равен (см. 5.5):
Момент инерции диска найдем по формуле (5.4):
где 



Итак
Пользуясь выражениями для моментов инерции стержня (2) и диска (3), найдем момент инерции маятника относительно оси 
После подстановки в выражение (4) числовых данных, получим:
Ответ:
Задача №2.
Определить момент инерции 


Решение. Для определения момента инерции стального вала относительно оси 
где 



Тогда
Ответ:
Задача № 3
Определить осевые моменты инерции 


Решение. Определим момент инерции пластинки относительно оси 


Момент инерции этой тонкой полоски относительно оси 
где 
Масса полоски равна:
где 

Тогда:
а момент инерции всей пластинки будет равен сумме моментов инерции всех полосок, на которые можно разбить пластинку:
При предельном переходе, то есть, когда
Итак,
Вычислим массу пластинки:
Таким образом
Момент инерции пластинки относительно оси 
Ответ:
Задача №4
Определить момент инерции относительно оси 


Решение. Выделим элементарный параллелепипед со сторонами основания 





Момент инерции элементарного параллелепипеда относительно оси 
где: 
Тогда,
а момент инерции всего параллелепипеда
При предельном переходе, то есть при 
Вычислим двойной интеграл:
Масса параллелепипеда:
Следовательно,
Ответ:
Задача №5
Определить момент инерции относительно оси 



Решение. Проведем на пластинке (рис.5.11) две прямые, параллельные оси 

Вычислим момент инерции относительно оси 
где 
Здесь 

Итак,
Из уравнения 
Таким образом
Момент инерции пластинки относительно оси 
Масса пластинки
где площадь пластинки
Тогда
Следовательно,
Ответ:
Задача №6
Определить для тонкого равнобедренного треугольника 



Решение. С серединой 




Для определения момента инерции треугольника относительно основания (относительно оси 


Момент инерции этой полоски относительно оси 
где 

Тогда момент инерции элементарной полоски относительно основания будет равен:
Найдем зависимость между координатой 




откуда
Подставив (2) у (1’), получим:
а момент инерции треугольника 
или
В интеграле (3) границы координаты 


Высчитаем интеграл (3):
Выразим момент инерции 


Преобразуем выражение (4):
или
Перейдем к определению момента инерции треугольника 

Поскольку у треугольника 


где 



Расчетная схема для определения момента инерции 
Выделим элементарную полоску на расстоянии 



Определим момент инерции этой полоски относительно оси 
где 
Определим зависимость между длиной полоски 




откуда
Подставив (6) у (5), получим:
Момент инерции треугольника 


или
Определим интеграл (7):
Окончательно,
Тогда, момент инерции треугольника 

Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 34.9, 34.12, 34.16 [2].
Теорема о движении центра масс механической системы
Силы, действующие на механическую систему, можно условно поделить на внешние и внутренние.
Силы, которые действуют на точки данной механической системы со стороны точек или тел, не входящих в эту систему, называются внешними.
Силы, действующие на точки механической системы со стороны точек данной системы, называются внутренними.
Внешние силы обозначаются верхним индексом 



Внутренние силы обладают следующими свойствами:
а) геометрическая сумма (главный вектор) внутренних сил равна нулю:
б) геометрическая сумма моментов (главный момент) всех внутренних сил относительно любого центра 
Теорема о движении центра масс механической системы формулируется следующим образом:
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех внешних сил, действующих на систему.
где 


Из сравнения приведенной выше формулы со вторым законом динамики, который, как известно, записан для материальной точки:
можно сделать следующий вывод:
Центр масс механической системы движется как материальная точка, в которой сосредоточено массу всей системы и к которой приложены те же внешние силы, действующие на систему.
Теорема о движении центра масс системы, если ее записать в проекциях на оси декартовой системы координат, имеет вид:
где 
Из приведенных уравнений следует, что внутренние силы непосредственно не влияют на движение центра масс. Теорема позволяет исключить из рассмотрения все ранее неизвестные внутренние силы.
Задачи динамики поступательного движения твердого тела решаются с помощью теоремы о движении центра масс системы материальных точек.
Действительно, применив эту теорему, мы определим уравнение траектории, скорость и ускорение центра тяжести твердого тела. При поступательном движении твердого тела траектории всех его точек одинаковы, одинаковы и их скорости и ускорения.
Закон сохранения движения центра масс
Из теоремы о движении центра масс вытекает несколько следствий:
а) если геометрическая сумма всех внешних сил, действующих на систему, равна нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
Пусть 


Если изначально центр масс был в покое, то он и останется в покое. Если же начальная скорость не равна нулю, то центр масс движется прямолинейно и равномерно с этой скоростью;
б) если геометрическая сумма внешних сил, действующих на систему, не равна нулю, но сумма их проекций на какую-нибудь ось (например, ось 
Если 


Если при этом равна нулю начальная скорость, то есть 

Таким образом видим, что в этом случае координата центра масс 
При 

Все эти результаты выражают законы сохранения движения центра масс системы.
Порядок решения задач на применение теоремы о движении центра масс
Рекомендуется такая последовательность решения задач:
Изобразить на рисунке все внешние силы, действующие на систему;
Выбрать систему координат;
Записать теорему о движении центра масс в векторной форме;
Спроектировать это векторное уравнение на оси координат;
Высчитать суммы проекций всех внешних сил на оси координат и подставить их в проекции уравнения движения;
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема о движении центра масс механической системы
Задача № 1
Определить главный вектор внешних сил, действующих на колесо весом 


Решение. Покажем внешние силы, которые действуют на колесо: силу тяжести 


Запишем теорему о движении центра масс в векторной форме:
Выбираем систему координат 


Поскольку 



Найдем проекцию ускорения центра масс на ось 
Итак,
Ответ:
Задача №2
Колесо весом 



Определить скорость центра масс колеса, если в начальный момент оно находилось в покое. Коэффициент трения скольжения равен 
Решение. На колесо действуют внешние силы: 




Запишем теорему о движении центра масс колеса в векторной форме:
где 
Спроектируем это уравнение на оси координат 
Во время движения колеса 

Поскольку при качении колеса со скольжением сила трения достигает своего максимального значения, то
Подставим (3) в первое из уравнений (1) и получим:
Поскольку
то
Согласно начальным условиям при 
Итак, закон изменения скорости центра масс колеса 
Ответ:
Задача №3
На однородную призму 



Определить длину 



Решение. Рассмотрим движение механической системы, состоящей из 2-х призм 



Для решения этой задачи применим теорему о движении центра масс.
На систему действуют внешние силы: тяжести 




Таким образом, все внешние силы системы вертикальны. Внутренние силы системы (давление призмы 



Введем систему координат 


Поскольку внешние силы перпендикулярны оси 
Тогда
где 
В начальный момент времени система находилась в состоянии покоя, то есть скорость центра масс 
Из этого следует, что 
Запишем выражение для определения координаты центра масс в начале движения:
где 



Выражение для определения координаты центра масс системы, когда призма 

где 



Поскольку 
или
Перепишем это уравнение следующим образом:
Найдем перемещение центров масс призм 

Присутствие слагаемого (



Подставим значение перемещений в уравнение (1):

Решим это уравнение относительно 

Ответ:
Задача №4
Три груза (рис.6.4), весом 









Решение. Изобразим все внешние силы, которые приложены к материальной системе, состоящей из пирамиды и трех грузов (рис.6.4). Внешними силами являются: 


горизонтальной плоскости. Направим ось 
Поскольку все внешние силы перпендикулярны оси 
Следовательно,
тогда
В начальный момент времени система была в состоянии покоя, то есть 
Поскольку
то
Таким образом, абсцисса центра масс системы не зависит от перемещений грузов, входящих в систему, и остается неизменной относительно неподвижной системы координат 
Запишем выражение для определения 
где 

Если груз 1 опустится на величину 









Грузы 1,2 и 3 вместе с пирамидой также переместятся влево на расстояние 
Запишем выражение для определения положения абсциссы центра масс для нового положения системы:
Поскольку 
После приведения подобных получим:
или
Окончательно
После подстановки числовых величин, получим:
Ответ:
Задача № 5
Электрический двигатель весом 
На валу электродвигателя (рис.6.5) под прямым углом закреплен одним концом однородный стержень 





Определить:
Закон горизонтального движения электродвигателя;
Угловую скорость вала электродвигателя, при которой электродвигатель будет «подскакивать» над фундаментом;
Наибольшее горизонтальное усилие 
Решение. Будем рассматривать электромотор, стержень и груз как одну механическую систему. Внешними силами, которые действуют на эту систему, являются: сила тяжести электродвигателя 




Начало неподвижной системы координат возьмем в точке 
Поскольку проекция на ось 

где 
В нашем случае 
Тогда дифференциальное уравнение движения центра масс (1) приводится к виду:
откуда
Предполагая, что в начальный момент скорость центра масс системы равна нулю, то есть, при пуске электродвигателя он был неподвижным, получим
Следовательно, 

Поскольку в начальный момент времени центр масс системы находится на оси 

При вращении стержня координаты центров масс электрического двигателя, стержня и груза 
Предположим, что в некоторый момент времени 




Поскольку все время 
где 

Тогда
откуда
и, следовательно:
Таким образом, центр электродвигателя совершает гармонические колебания вдоль оси 
и периодом
Определим угловую скорость вала, при которой электродвигатель будет «подскакивать» над фундаментом.
Для этого составим дифференциальное уравнение движения центра масс системы вдоль оси 
или
где 
Значение 
поскольку
Последнее уравнение перепишем в виде:
Возьмем из обеих частей равенства вторую производную по времени
Из уравнений (2) и (3) вытекает, что
итак,
Минимальное значение реакции фундамента будет при 
Если 
откуда
В завершение определим наибольшее горизонтальное усилие 
На рис.6.5 штрих-пунктирными линиями показаны оси болтов и горизонтальные реакции болтов 

В этом случае дифференциальное уравнение движения центра масс системы вдоль оси 
Значение 
или
Тогда
При этом уравнение (4) принимает вид:
Из последнего уравнения выходит:
Таким образом, максимальное горизонтальное усилие, действующее на болты, будет при 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 35.1; 35.6; 35.10; 35.20 [2].
Теорема об изменении количества движения точки и механической системы
Теорема об изменении количества движения (импульса) системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает количество движения с импульсом внешних сил, действующих на тела, составляющие систему.
Импульс силы
Для характеристики действия силы за некоторый промежуток времени вводится понятие импульса силы.
Если сила 

Направление импульса силы 

Единица измерения импульса в системе СИ — 

Если сила 

Импульс силы — сложная физическая величина, которая одновременно учитывает влияние модуля, направления и времени действия силы на изменение состояния движения тела.
Модуль импульса силы можно определить через его проекции на оси координат:
где 

Углы между вектором 
Теорема об изменении количества движения точки и системы
Одной из мер движения точки является количество ее движения.
Количеством движения точки называется вектор 



Понятие количества движения было введено в механику Декартом и положено в основу механики Ньютоном.
Единица измерения количества движения в системе СИ — 

Если спроектировать вектор количества движения на оси координат, то ее проекции определяются следующим образом:
Теорема об изменении количества движения точки в дифференциальной форме имеет вид:
Производная по времени от количества движения материальной точки равна геометрической сумме всех сил, действующих на эту точку.
Теорема об изменении количества движения точки в интегральной форме:
Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех сил, которые приложены к точке.
Векторному уравнению (7.1) соответствуют три уравнения в проекциях на оси координат:
Большинство практических задач решается с использованием выражения (7.2).
Количеством движения механической системы называется векторная величина 
Найти 
Замыкающая сторона векторного многоугольника будет представлять собой вектор 
Величина 

Формулу (7.3) можно записать в виде:
где 

Из этой формулы следует, что количество движения системы равно нулю, когда скорость центра масс равна нулю. Например, если тело вращается вокруг неподвижной оси, которая проходит через его центр масс, то количество движения тела равно нулю.
В случае, когда колесо катится, вектор 
Теорема об изменении количества движения системы в дифференциальной форме выразится формулой:
где 
Производная по времени от количества движения механической системы равна геометрической сумме всех действующих на точки системы внешних сил.
В проекциях на оси координат уравнение (7.5) соответствует уравнениям:
В интегральной форме теорема об изменении количества движения системы имеет вид:
где 

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, которые действуют на систему за тот же промежуток времени.
Векторному уравнению (7.7) соответствуют три уравнения в проекциях на оси координат:
Практическая ценность теоремы заключается в том, что она позволяет исключить из рассматривания неизвестные внутренние силы.
Закон сохранения количества движения системы
Выводы из теоремы об изменении количества движения системы, которые еще имеют название законов сохранения количества движения:
1. Если главный вектор внешних сил, действующих на систему, равен нулю, то вектор количества движения системы не меняется:
если
то 
2. Если сумма проекций внешних сил на какую-либо ось, например 
если
то 
Эти результаты выражают законы сохранения количества движения системы. Из них вытекает, что внутренние силы не могут изменить количество движения системы.
Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
Для материальной точки:
Изобразить на рисунке все силы, приложенные к материальной точке, то есть активные силы и реакции связей.
Выбрать систему координат.
Записать теорему об изменении количества движения точки в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Для механической системы:
Изобразить на рисунке все внешние силы.
Выбрать систему координат.
Записать теорему об изменении количества движения системы в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
Задача № 1
Железнодорожный поезд движется по горизонтальному и прямолинейному участку пути (рис.7.2). Во время торможения до полной остановки развивается сила сопротивления, равная 

Определить время 

Решение. Изобразим силы, действующие на поезд во время торможения: сила тяжести поезда 


Выберем систему координат. Поскольку движение прямолинейное и горизонтальное, достаточно рассмотреть движение по направлению оси 
Запишем теорему об изменении количества движения поезда (рассматривая его как материальную точку) в интегральной форме:
где 





Спроектируем векторное уравнение (1) на ось 
Проекции импульсов сил 




Сила сопротивления 
Скорость в конце участка торможения равна нулю, то есть
Окончательно, уравнение импульсов (2) в проекции на ось 
или
откуда
С учетом числовых значений величин 

Путь торможения определим из формулы для равнопеременного движения:
В этом случае ускорение поезда определяется из формулы:
то есть,
Тогда
Ответ:
Задача № 2
По шероховатой наклонной плоскости, которая составляет с горизонтом угол 
Определить время 



Решение. Во время движения на тело действуют сила тяжести тела 


Направим ось 
Спроектируем ровность (1) на ось 
Проекция импульса нормальной реакции 



Учитывая, что во время движения сила тяжести 

Кроме того
Итак, уравнение импульса (2) примет вид:
Вычислим силу трения:
Тогда уравнение (3) примет вид:
или
откуда
Поскольку
то
Используя полученную зависимость, сначала подсчитаем ускорение тела, а после этого — время движения.
Поскольку
то

Из формулы 

Из этой формулы находим время движения 
Ответ:
Задача № 3
На полигоне пушка, которая наклонена под углом 



Определить скорость 
Решение. В задаче рассматривается движение материальной системы, состоящей из ствола и снаряда (рис.7.4).
На систему действуют внешние силы: тяжести ствола 


Применим теорему об изменении количества движения системы:
где 




Ось 


Спроектируем уравнение (1) на ось 
Поскольку проекции сил 





Таким образом, проекция количества движения системы на ось 
В начальный момент времени (до выстрела) снаряд и ствол были неподвижны, следовательно, их количества движения равнялись нулю и
В момент вылета снаряда проекция количества движения системы на ось равна:
или
Поскольку
то
откуда

С учетом числовых значений:
Знак минус показывает, что скорость ствола направлена в сторону, противоположную скорости снаряда.
Ответ:
Задача № 4
Буксирный пароход весом 


Определить общую скорость парохода и баржи 




Решение. Для определения скорости 
На систему, которая состоит из парохода и баржи, действуют внешние силы: силы тяжести 





Внутренняя сила — натяжение буксирного каната 
Ось 
Запишем теорему об изменении количества движения данной системы в интегральной форме:
где 


Спроектируем уравнение (1) на ось 
Поскольку по условиям 

Кроме того, проекции на ось 




Подсчитаем количество движения парохода и баржи в начальный момент времени, когда скорость парохода равна 

Совместимое движение парохода и баржи происходит с одинаковой скоростью 
Поскольку
то
Отсюда имеем
Ответ:
Задача № 5
Механическая система состоит из грузов 1 и 2 массами 















Определить зависимость 
Решение. Рассмотрим механическую систему в произвольном положении (рис.7.6).
Изобразим все внешние силы, действующие на систему: силы тяжести 



Проведем координатные оси 



Определим 


Поскольку все внешние силы, действующие на систему, вертикальны, то 


где 


Определим количества движения 

где
Выразим координаты 


С рис.7.6 видно, что в произвольный момент времени абсцисса первого груза
а абсцисса второго груза
Тогда
Подставляя полученные выражения для 

Поскольку 
В соответствии с (1), выражения (2) и (4) равны, то есть:
Отсюда окончательно получим:
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 28.3; 28.7; 36.9; 36.11; 36.16 [2].
Теорема об изменении момента количества движения точки и механической системы
Наряду с количеством движения, как векторной меры поступательного движения, для вращательного движения можно ввести момент количества движения.
Для материальной точки массой 



Вектор момента количества движения прикладывается в точке 
Кинетическим моментом 
Подобно тому, как количество движения системы является характеристикой поступательного движения, кинетический момент является характеристикой вращательного движения системы.
Кинетический момент твердого тела, которое вращается относительно оси 

Производная по времени от момента количества движения точки, взятого относительно любого неподвижного центра 
Спроектировав это уравнение на оси координат, получим:
Если рассматривать движение системы, на которую действуют внешние 

Проектируя обе части уравнения на неподвижные оси 
Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки, или вращательную часть движения тела в общем случае движения свободного твердого тела.
Практическая ценность теоремы заключается еще и в том, что она позволяет при изучении движения системы исключить из рассмотрения неизвестные внутренние силы.
Из теорем об изменении кинетического момента системы (8.7)-(8.8) вытекают важные выводы:
Если сумма моментов относительно центра 

если 

Если сумма моментов всех внешних сил, действующих на систему, относительно некоторой оси, например 
если 

Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
Кинетический момент тела относительно оси вращения по уравнению (8.4) , если ось 
Следовательно,
Сумма моментов внешних сил 
Таким образом, дифференциальное уравнение вращательного движения тела имеет вид:
Из (8.9) следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение тела равно вращательному моменту
Это уравнение позволяет решать следующие задачи:
— если заданы уравнения вращения тела 

— если заданы внешние силы, приложенные к телу, начальные условия вращения 



— определить момент инерции тела 


Из уравнения 
1. Если 



2. Если 



Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
Задачи, которые относятся к этой теме, можно разделить на следующие четыре основных типа:
Вычисление кинетического момента.
Изучение движения конкретной точки механической системы, если эта точка участвует во вращательном движении системы.
Изучение вращательного движения твердого тела.
Изучение движения механической системы, в которую входят тела, совершающие как поступательные, так и вращательные движения.
Задачи первого типа могут быть решены с помощью общих формул (8.4), (8.5).
Порядок решения задач второго типа может быть следующим:
- Выбрать систему координат.
- Изобразить все внешние силы, приложенные к материальной точке; в случае произвольной точки к этим силам добавить реакции внешних связей.
- Записать в скалярной форме выражение теоремы об изменении момента количества движения точки.
- Высчитать сумму моментов сил, которые приложены к материальной точке.
- Определить количество движения материальной точки и его момент относительно осей.
- Подставить данные пунктов 4 и 5 в уравнения (8.6) теоремы об изменении момента количества движения материальной точки.
- Решить, в соответствии с условием, прямую или обратную задачу динамики точки.
При решении задач третьего типа сохранять рекомендации первых двух пунктов, а далее делать следующим образом:
- Записать дифференциальное уравнение вращательного движения тела вокруг неподвижной оси (8.9).
- Определить момент инерции твердого тела относительно неподвижной оси.
- Подсчитать сумму моментов всех внешних сил относительно оси вращения.
- Величины, полученные в п. п. 4 и 5, подставить в уравнение (8.9).
- Записать начальные условия.
- Решить уравнение п. 6 в зависимости от условия, как прямую или обратную задачу.
При решении задач четвертого типа необходимо предварительно расчленить заданную систему на отдельные твердые тела, и к каждому из них, в зависимости от характера движения, применить одну из теорем: об изменении количества движения – в случае поступательного движения тел расчлененной системы; об изменении кинетического момента – при наличии тел, которые совершают вращательные движения.
Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
Задача №1
Однородный круглый диск весом 

Определить главный момент количеств движения диска 

Решение. Главный момент количеств движения системы (кинетический момент) относительно оси вращения равен (8.6):
где 

В данном случае кинетический момент относительно оси, проходящей через центр диска 
Ответ:
Задача №2
Во время вращения барабана 1 весом 



Определить главный момент количества движения (кинетический момент) системы относительно оси 

Решение. В состав механической системы входят два твердых тела: барабан 1 и груз 2.
Следовательно, кинетический момент системы равен:
где 


Кинетический момент барабана равен (8.5):
где
тогда
Главный момент количества движения груза, который движется поступательно, определяется как момент количества движения материальной точки, то есть:
поскольку
то
Окончательно
Ответ:
Задача №3
Шарик 








Определить, через какой промежуток времени 

Решение. Ось 







Все силы указаны на рисунках, направления сил 

Запишем дифференциальное уравнение вращательного движения шарика относительно оси 
где момент инерции шарика
Поскольку момент силы тяжести 






Следовательно, дифференциальное уравнение вращательного движения имеет вид:
или
Разделим переменные и проинтегрируем:
Произвольную постоянную 

Следовательно,
Высчитаем, через какой промежуток времени 

Откуда:
Для определения числа оборотов, которые сделает стержень с шариком за промежуток времени 


Следовательно,
Разделим переменные и проинтегрируем это дифференциальное уравнение:
Произвольную постоянную 

Итак закон изменения угла поворота 
или
При 

Поскольку за 1 оборот шарик обернется на 

Ответ:
Задача №4
Для определения момента трения в цапфах, на вал насажен маховик весом 



Определить момент трения 
Решение. Направим ось 




Запишем теорему об изменении кинетического момента относительно оси вращения:
Поскольку мы рассматриваем вращение твердого тела, то
Найдем вращательный момент внешних сил относительно оси вращения 




Таким образом
Высчитаем величины, которые входят в это уравнение:
где 


Поскольку 
С учетом значений 

Ответ:
Задача №5
Однородный цилиндр (рис.8.6) радиусом 


Определить, как изменится угловая скорость 

Решение. На цилиндр действует сила тяжести 
Запишем теорему об изменении кинетического момента цилиндра:
где 

Поскольку сила 

Итак, 
где 



По теореме Гюйгенса-Штейнера
где 
Из формулы (1) получим:
Вычислим 

Следовательно,
Угловая скорость уменьшилась в три раза, поскольку в три раза увеличился момент инерции.
Ответ:
Задача №6
Молотильный барабан начинает вращаться из состояния покоя (
Определить, пренебрегая трением, частоту вращения барабана после того, как он начнет вращаться и сделает 
Решение. Для определения угловой скорости барабана воспользуемся формулой:
где 


Из (1) вытекает:

Следовательно,
Таким образом, для определения угловой скорости необходимо знать угловое ускорение 
Для определения 
где 
На барабан действуют следующие внешние нагрузки: 





С учетом действующих сил уравнение (2) будет иметь вид:
При этом 




Тогда,
Ответ:
Задача №7
Груз весом 
Определить угловое ускорение барабана 


Решение. Для определения углового ускорения 


Если применить теорему об изменении кинетического момента системы относительно оси, то натяжение каната, являющегося внутренней силой, в уравнение не войдет.
Относительно оси, которая проходит через точку 
На систему действуют следующие внешние силы: 



Силы 




Итак,
Определим кинетический момент системы относительно оси вращения 
где 

где 

поскольку
Тогда кинетический момент системы равен:
Подставим полученные результаты в уравнение (1):
Знак момента силы 

Решаем уравнение (2) и определяем угловое ускорение 
Выносим из под знака дифференциала в левой части уравнения (2) постоянные величины:
или
С учетом числовых значений угловое ускорение 
Ответ:
Теорема об изменении кинетической энергии механической системы
Теорема о кинетической энергии системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему.
Кинетическая энергия механической системы
Кинетической энергией 
Кинетической энергией 
Кинетическая энергия системы не зависит от направлений скоростей точек.
Кинетическая энергия может равняться нулю, если скорости всех точек системы равны нулю.
Кинетическая энергия системы характеризует и поступательное, и вращательное движения системы. Поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Единицей кинетической энергии в системе СИ является Джоуль (Дж).
Определение кинетической энергии твердого тела в различных случаях его движения
Поступательное движение твердого тела:
При поступательном движении твердого тела скорости всех его точек (в том числе скорость 

Кинетическая энергия твердого тела при поступательном движении равна половине произведения массы тела 
Вращательное движение твердого тела:
Скорость любой точки твердого тела, которое вращается с угловой скоростью 
где 
Тогда кинетическая энергия тела определяется согласно зависимости:
Поскольку
то
Следовательно кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Плоскопараллельное движение твердого тела:
При плоскопараллельном движении скорости всех точек тела в каждый момент времени распределены так, будто тело вращается вокруг оси, которая перпендикулярна плоскости движения и которая проходит через мгновенный центр скоростей 
В этом случае кинетическую энергию тела можно определить по формуле:
где 
Поскольку (согласно теореме Штейнера-Гюйгенса)
где 
Поскольку 
Таким образом,
в случае плоскопараллельного движения тела кинетическая энергия состоит из кинетических энергий поступательного движения вместе со скоростью центра масс и вращательного движения вокруг оси, которая проходит через центр масс перпендикулярно плоскости движения.
Теорема об изменении кинетической энергии механической системы:
Дифференциальная форма:
Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему:
Производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних и внутренних сил, действующих на систему:
Интегральная форма:
Изменение кинетической энергии механической системы при конечном перемещении ее из положения (1) в положение (2) равно сумме работ на этом перемещении всех внешних и внутренних сил, действующих на эту систему
Если механическая система неизменна, то сумма работ внутренних сил равна нулю и теорема запишется так:
Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в следующей последовательности:
а) изобразить на рисунке все внешние силы системы;
б) высчитать сумму работ всех внешних сил на перемещении точек системы;
в) вычислить кинетическую энергию системы материальных точек в начальном и конечном ее состояниях;
г ) пользуясь результатами подсчетов по пунктам б) и в) записать теорему об изменении кинетической энергии механической системы и определить искомую величину.
Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Задача № 1
Механизм эллипсографа (рис.10.1) состоит из ползунов 









Определить кинетическую энергию механизма эллипсографа, полагая, что линейка 



Решение. Заданная механическая система состоит из четырех тел: кривошипа 1 и линейки 2, ползунов 3 и 4.
Кинетическая энергия всей системы равна:
где 


Кривошип 

Тогда
Линейка 2 движется плоскопараллельно. Ее кинетическая энергия равна
где 




Для определения угловой скорости 


С другой стороны, точка 
Тогда, учитывая, что 
Момент инерции линейки относительно оси 
С учетом полученных значений 
Подсчитаем кинетическую энергию ползунов 3 и 4, которые двигаются поступательно:

Скорости точек 
Тогда
Подставляя найденные выражения (2), (4), (5) в (1), получим:
Ответ:
Задача № 2
На рисунке 10.2 изображен подъемный механизм лебедки. Груз 






где 
Определить скорость груза 




Решение. Изобразим на рисунке все внешние силы, действующие на барабан 








Запишем теорему об изменении кинетической энергии системы:
где 





Поскольку в начальный момент времени система находилась в состоянии покоя, то
В связи с тем, что трос не растягивается и при движении системы находится в натянутом состоянии, сумма работ внутренних сил системы равна нулю, следовательно
При поднятии груза 

Поскольку точки приложения сил 

Работа силы 
Работа вращательного момента в случае, когда он не меняется
где 
Поскольку в нашем случае вращательный момент меняется, то его работа определится следующим образом:
Определим угол 



Следовательно,
Таким образом,
Перейдем к подсчету кинетической энергии системы в конечном положении:
где 





Груз 
Диск 
где 

Поскольку диск 

где 
Поскольку линейная скорость обода диска равна скорости груза, угловая скорость вращения 
Итак,
Кинетическая энергия барабана 
Поскольку масса барабана 
Угловую скорость барабана высчитаем из условия равенства линейных скоростей на ободах диска и барабана:
Откуда
Таким образом
Кинетическая энергия системы в конечном положении равна
Итак, теорема об изменении кинетической энергии системы имеет вид:
Решая это уравнение относительно 


Ответ:
Задача № 3
Груз 








Определить скорость груза 

В начальный момент система находилась в состоянии покоя.
Решение. Изобразим внешние силы, которые действуют на систему: силы тяжести 




Запишем теорему об изменении кинетической энергии системы:
В начальный момент времени система находилась в покое, следовательно, 
Сумма работ внешних сил при перемещении системы в конечное положение составляет:
Работа сил 

Итак,
Работа силы 


Работу силы тяжести 











Таким образом,
Груз 


Итак,
Вычислим кинетическую энергию системы в конечном положении:
Груз 
где 

Блок 
Кинетическая энергия поступательного движения блока 
Поскольку точка 




Тогда
Таким образом,
Кинетическая энергия вращательного движения блока 
где 



Тогда
Таким образом, кинетическая энергия блока 
Блок 
то есть
Груз 


Следовательно, кинетическая энергия системы 
Таким образом, теорема об изменении кинетической энергии системы имеет вид:
Находим скорость груза 

Ответ:
Задача № 4
Прямоугольная пластинка 






Определить, сколько оборотов сделает пластинка к тому мгновению, когда ее угловая скорость станет вдвое меньше начальной?
Решение. Поскольку силы сопротивления, приложенные к пластинке, не постоянные, а зависят от скорости, то для решения задачи воспользуемся теоремой об изменении кинетической энергии системы в дифференциальной форме:
Высчитаем дифференциал кинетической энергии пластинки. Поскольку пластинка вращается вокруг неподвижной оси, то ее кинетическая энергия равна:
откуда:
где 

Перейдем к определению суммы элементарных работ внешних сил, которые действуют на пластинку. Это такие силы (рис.10.4):
— сила тяжести пластинки 
— реакции в опорах 



— сила сопротивления воздуха 
Итак,
где 



Работы реакций 


Таким образом,
Для вычета работы сил сопротивления воспользуемся формулой для работы сил, которые приложены к вращающемуся твердому телу:
где 

Чтобы определить 


и
Следовательно,
или
и

Таким образом, уравнение (1) принимает вид:
Разделим переменные и проинтегрируем:
Момент инерции пластинки составляет:
Тогда
Откуда находим:
Число оборотов 
Ответ:
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки