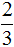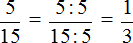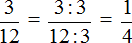When calculating half of a fraction, you are finding a fraction of a fraction. Fractions are composed of two integers, one stacked upon the other with a dash separating them. These two numbers — the top one termed the numerator and the bottom the denominator — make up a single value equal to less than one when the numerator is less than the denominator. You can halve a fraction through operations with its numerator and denominator.
Reduce the fraction to be halved to its lowest terms. To reduce or simplify the fraction, you need to eliminate the numerator and denominator’s greatest common factor, or the largest value that both share as factors. For an example, using the fraction 8/10, the factors of the numerator 8 are 1, 2, 4 and 8, and the factors of the denominator 10 are 1, 2, 5 and 10. For the numbers 8 and 10, the greatest common factor is 2. Eight divided by (8/2) equals 4 and 10/2 equals 5, so 8/10 reduced equals 4/5.
Divide the reduced fraction’s numerator by 2 if it is even. To halve 4/5, divide the numerator 4 by 2 and the final fraction is 2/5.
Multiply the reduce fraction’s denominator by 2 if the numerator is odd. As an example, the fraction 1/3 has an odd numerator. Multiply the denominator of 3 by 2 and the final fraction is 1/6.
При подсчете половины дроби вы находите дробь дроби. Фракции состоят из двух целых чисел, одно сложено на другое с чертой, разделяющей их. Эти два числа — верхнее, называемое числителем, а нижнее знаменателем — составляют единое значение, равное меньше единицы, когда числитель меньше знаменателя. Вы можете разделить дробь пополам с помощью числителя и знаменателя.
Уменьшите долю, которая будет уменьшена вдвое, до самых низких значений. Чтобы уменьшить или упростить дробь, необходимо исключить наибольший общий множитель числителя и знаменателя или наибольшее значение, которые оба имеют общие коэффициенты. Например, используя дробь 8/10, коэффициенты числителя 8 равны 1, 2, 4 и 8, а коэффициенты знаменателя 10 равны 1, 2, 5 и 10. Для чисел 8 и 10 Наибольший общий коэффициент равен 2. Восемь, деленное на (8/2), равно 4, а 10/2 равно 5, поэтому 8/10 уменьшено равно 4/5.
Разделите числитель уменьшенной дроби на 2, если он четный. Чтобы разделить пополам 4/5, разделите числитель 4 на 2, а окончательная дробь — 2/5.
Умножьте знаменатель уменьшенной дроби на 2, если числитель нечетный. Например, дробь 1/3 имеет нечетный числитель. Умножьте знаменатель 3 на 2, и конечная дробь будет 1/6.
При вычислении половины дроби вы находите дробь. Дроби состоят из двух целых чисел, расположенных друг над другом и разделяющих их тире. Эти два числа — верхнее, называемое числителем, и нижнее — знаменателем, составляют одно значение, меньшее единицы, когда числитель меньше знаменателя. Вы можете разделить дробь пополам с помощью ее числителя и знаменателя.
Уменьшите дробь, которая должна быть уменьшена вдвое, до минимального значения. Чтобы уменьшить или упростить дробь, вам нужно исключить наибольший общий множитель числителя и знаменателя или наибольшее значение, которые оба являются факторами. Например, используя дробь 8/10, множители числителя 8 равны 1, 2, 4 и 8, а множители знаменателя 10 равны 1, 2, 5 и 10. Для чисел 8 и 10 наибольший общий делитель равен 2. Восемь, разделенная на (8/2), равняется 4, а 10/2 равно 5, таким образом 8/10 уменьшенное равно 4/5.
Разделите числитель уменьшенной дроби на 2, если он четный. Чтобы разделить 4/5 пополам, разделите числитель 4 на 2, и окончательная дробь будет 2/5.
Умножьте знаменатель уменьшаемой дроби на 2, если числитель нечетный. Например, дробь 1/3 имеет нечетный числитель. Умножьте знаменатель 3 на 2, и получится 1/6.
Teachs.ru
Содержание
- Как найти дробь от числа
- Применение дробей
- Нахождение дроби от числа
- Нахождение целого числа по дроби
- Деление меньшего числа на большее
- Какую часть одно число составляет от другого
Как найти дробь от числа
Одна из простой, но интересной темы – это как найти дробь от целого (от числа).
Как найти часть от целого? У нас есть какое-то значение и нам нужно найти долю или дробь от этого значения.
К примеру, пицца весит 540 г. Сколько весит кусок пиццы, если ее разделили на 6 одинаковых кусков?
Пиццу разрезали на 6 одинаковых кусков, значит, один кусок – это 1/6 от всей пиццы.
Начертим схему: чертим отрезок, разделим его на 6 равных частей. Удобнее начертить отрезок длиной 6 или 12 см (см. статью здесь).
Если пиццу разрезали, то и весь вес надо разделить: 540:6=90 (г)
Если нужно узнать вес двух кусков, т.е. 2/6
то эти 90 взять 2 раза: 90х2= 180 (г)
В итоге, 540 : 6 х 2, или, зная правила работы с дробями — 540 х 2/6.
Видим, что для того, чтобы найти 2/6 от целой пиццы нужно просто умножить общий вес на значение этой части — 2/6.
Как-то странно. Не правда ли? И, тем не менее: чтобы найти часть, мы умножаем, а не делим. Потому что если вспомнить, что дробь, вернее, горизонтальная черта дроби — это деление. Итак:
7/8 от 24 — 24:8х7=21
3/5 от 60 – 60:5х3=45
3/4 от 12 – 12:4х3=9
7/8 от 64 – 64:8х7=56
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 70
Источник
Применение дробей
Этот урок будет интересным и познавательным. Мы научимся применять дроби для различных жизненных случаев.
Нахождение дроби от числа
Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, 
Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет 
Как вы уже догадались 

Попробуем узнать, сколько составляет 


Попробуем найти 


Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём 
Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит 
Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
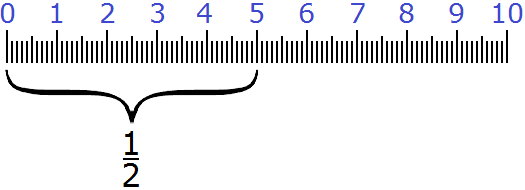
Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:
Пусть требуется найти 
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби 
Итак, делим десять сантиметров на знаменатель дроби 
Читаем вторую часть правила:
и полученный результат умножить на числитель дроби
Итак, умножаем пять сантиметров на числитель дроби 
Мы нашли 

Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.
В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби 
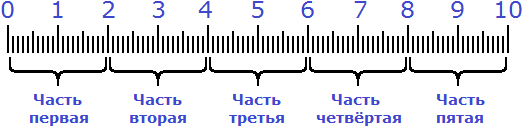
Пример 2. Найти 
Применим правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Сначала делим 10 сантиметров на знаменатель дроби
Получили два сантиметра. Этот результат нужно умножить на числитель дроби
Мы нашли 

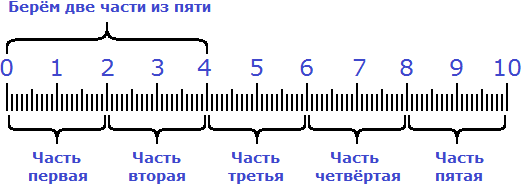
Весь процесс решения можно увидеть на следующем рисунке:
Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:
Пример 3. Найти 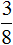
Чтобы найти 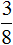
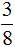
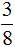
Итак, сначала делим число 56 на знаменатель дроби
Теперь умножаем полученное результат на числитель дроби
Получили ответ 21. Значит 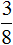
Пример 4. Найти от одного часа.
Один час это 60 минут. Задание можно понимать, как нахождение от 60 минут.
Сначала разделим 60 минут на знаменатель дроби
60 мин : 4 = 15 мин
Теперь умножим полученные 15 минут на числитель дроби
15 мин × 2 = 30 мин
Получили в ответе 30 минут. Значит от одного часа составляют тридцать минут или полчаса.
Пример 5. Найти 
Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби
100 см : 5 = 20 см
Теперь умножим полученные 20 см на числитель дроби
20 см × 4 = 80 см
Получили ответ 80 см. Значит 
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если 

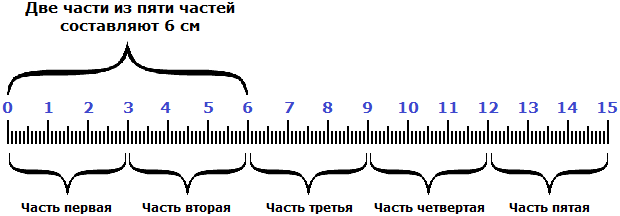
Требуется найти длину всей линейки по дроби 

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 

Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
Итак, мы нашли длину одной части. Одна часть из пяти или 
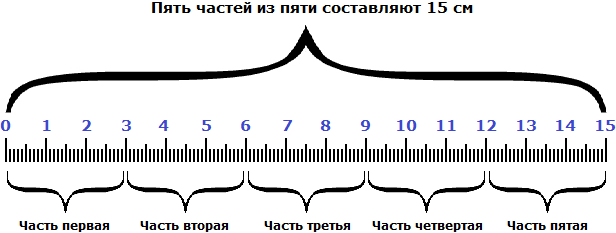
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
Знаменатель дроби 


Мы нашли 
Мы нашли 
Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти 
10 мин : 2 = 5 мин
Мы нашли 

5 мин × 3 = 15 мин
Мы нашли 
Пример 4. 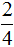
Знаменатель дроби 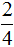
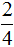
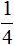
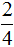
Мы нашли 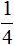
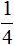
Мы нашли 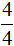
Деление меньшего числа на большее
В жизни часто возникают ситуации, когда требуется разделить меньшее число на большее. Например, представим ситуацию. Имеется трое друзей:
И требуется поровну разделить между ними два яблока. Как это сделать? Друзей трое, а яблок всего два. Мы попали в ситуацию в которой требуется разделить меньшее число на большее (два яблока на троих).
Для таких случаев предусмотрено следующее правило:
При делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Давайте применим это правило. Оно говорит, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе делитель. Делимое у нас это два яблока. Записываем в числителе число 2:
А делитель у нас это трое друзей (вспоминаем, что делитель показывает на сколько частей надо разделить делимое). Записываем тройку в знаменателе нашей дроби:
Забавно, но дробь 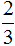
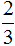
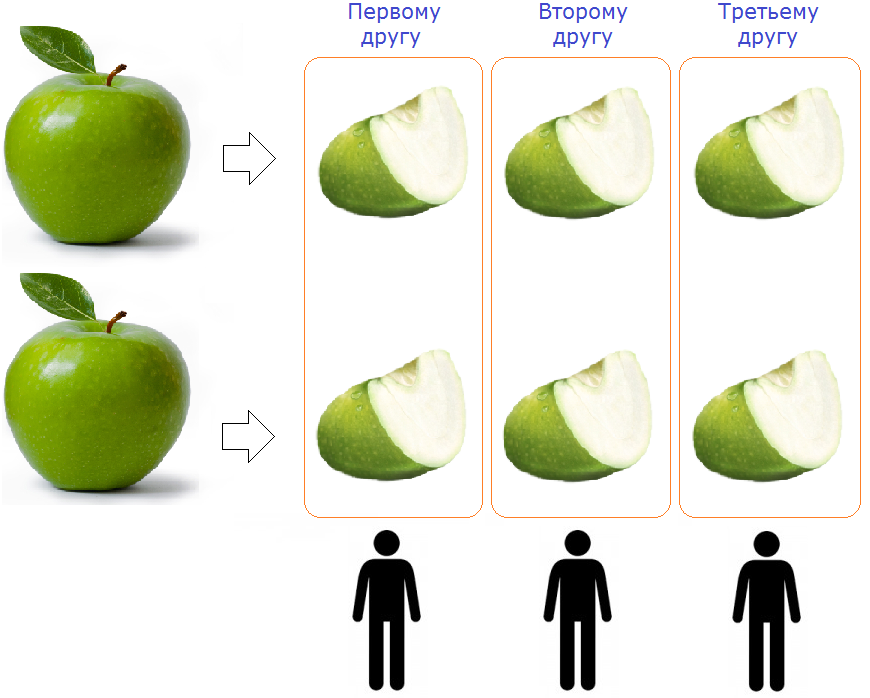
Чтобы разделить два яблока на троих, надо разрезать ножом каждое яблоко на три части и раскидать поровну эти куски между тремя друзьями:
Как видно на рисунке, каждое яблоко было разделено на три части и раскидано поровну на троих друзей. Каждому другу досталось 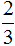
Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
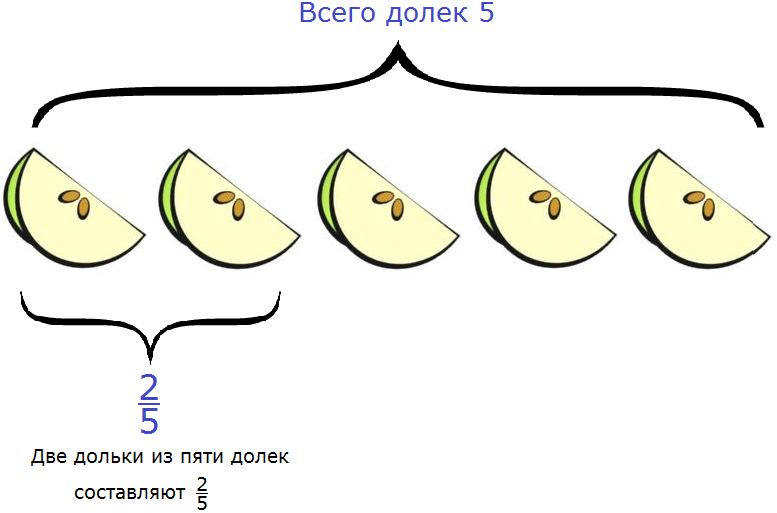
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь 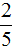
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь 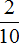
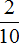
Дробь 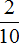
Также, эту дробь можно сократить на 2. После сокращения дроби 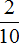
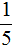
Дробь 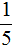
Таким образом, число 2 составляет 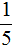
Пример 3. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь 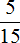
Получили аккуратную дробь 
Число 5 составляет 
Это можно даже проверить. Для этого нужно найти 
Итак, найдём 
Получили ответ 5. Значит задача была решена правильно.
Пример 4. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь 
Получили ответ 

Проверим правильно ли мы решили эту задачу. Для этого найдём 
Делим 12 на знаменатель дроби
Умножаем полученные 3 см на числитель дроби
Получили ответ 3 см. Значит задача была решена правильно.
Источник
Сегодня на уроке мы познакомимся с новым математическим понятием- доли целого (доли числа).
Эта информация доступна зарегистрированным пользователям
Научимся называть, записывать и сравнивать доли.
Вы узнаете, что такое обыкновенная дробь.
Выясним, что такое знаменатель и числитель дроби, узнаем, что они обозначают.
Эта информация доступна зарегистрированным пользователям
Рассмотрим правила чтения и записи обыкновенных дробей.
Определим, где на координатном луче располагаются дробные числа.
Не раз вы слышали такие выражения: налить треть стакана молока, отмерить пол чайной ложки соды, четверть часа, полкилограмма сахара и т.д.
Во всех предложенных фразах необходимо найти, определить, отмереть некоторую часть от целого.
Каждому человеку в своей жизни приходилось делить целое на доли, находить часть чего-либо.
Например, резать арбуз, торт, яблоко, делить мандарин, апельсин, плитку шоколадки на дольки и т.д.
Эта информация доступна зарегистрированным пользователям
Попробуем выяснить, что значит разделить на доли, что такое доля и как ее обозначают.
Представим, что на дне рождении разрезали торт на несколько равных кусков, т.е. разделили его на некоторое количество одинаковых частей.
Неразрезанный торт представлял собой целое.
Каждая равная часть, из которых состоял разрезанный торт, называется долей целого (или просто долей).
Доли- это каждая из равных частей одного целого (единицы).
Эта информация доступна зарегистрированным пользователям
Целое на доли можно разделить по-разному: можно доли сделать как большими, так и маленькими.
Допустим, две одинаковые пиццы разрезали на части (доли).
Эта информация доступна зарегистрированным пользователям
Первую пиццу разделили на четыре части, а вторую разрезали на восемь частей.
Понятно, что доли первой пиццы по размеру будут отличаться от долей второй.
Кусочки пиццы, разрезанной на четыре части, будут гораздо больше, чем кусочки пиццы, разделенной на восемь частей.
Чем больше число долей, тем меньше каждая доля.
Следовательно, чем меньше число долей, тем больше каждая доля.
При делении целого на равные части- доли, каждая доля получает свое название, которое указывает на то, какая это часть от целого, и на сколько долей разделено это целое.
Эта информация доступна зарегистрированным пользователям
Рассмотрим названия долей и каким образом эти названия образуются.
- Если единицу чего-либо (нечто целое) разделить на две доли, то каждая из них будет называться половиной.
Каждая такая часть будет равна одной второй, записывается это число так: ½ или (mathbf{frac{1}{2}}).
Эта информация доступна зарегистрированным пользователям
Число под чертой говорит на сколько равных частей разделили целое.
Число под чертой означает сколько таких частей взяли.
Половина- самая известная и часто употребляемая доля.
В жизни часто приходится находить, отмерять, отрезать и т.д. половину чего-либо.
Эта информация доступна зарегистрированным пользователям
- Если единицу (целое) разделить на три доли, то каждая из этих трех долей называется треть (третья часть).
Каждая такая часть будет равна одной третьей.
Записывается это число так: 1/3 или (mathbf{frac{1}{3}}).
Эта информация доступна зарегистрированным пользователям
- Если единицу (целое) разделить на четыре доли, то каждая из этих четырех долей называется четверть (четвертая часть).
Каждая такая часть будет равна одной четвертой.
Записывается это число так: 1/4 или (mathbf{frac{1}{4}}).
Эта информация доступна зарегистрированным пользователям
- Если единицу (целое) разделить на пять долей, то каждая из этих пяти долей называется пятой частью.
Каждая такая часть будет равна одной пятой.
Записывается это число так: 1/5 или (mathbf{frac{1}{5}}).
Эта информация доступна зарегистрированным пользователям
Если единицу (целое) разделить на n одинаковых долей, то каждая такая часть будет равна одной n-ой.
Запись 1/n или (mathbf{frac{1}{n}}) означает, что единицу разделили на n равных частей и взяли одну из них.
Эта информация доступна зарегистрированным пользователям
Для описания количества долей используют обыкновенные дроби.
Можно догадаться по смыслу, что слово «дробь» означает дробление чего-либо на части, деление, разделение.
Запись вида (mathbf{frac{m}{n}}) или m/n называют обыкновенной дробью.
Причем m и n— любые натуральные числа.
В общем говоря, математическая запись обыкновенной дроби оформляется в виде двух чисел, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).
Число, стоящее над дробной чертой («m ⁄ » или «(mathbf{frac{color{red}{m}}{}})»), называют числителем.
Числитель показывает, сколько долей взяли от целого.
Число, стоящее под дробной чертой (« ⁄ n» или «(mathbf{frac{}{color{blue}{n}}})»), называют знаменателем.
Знаменатель показывает, на сколько всего равных долей разделили целое.
Эта информация доступна зарегистрированным пользователям
Читают дроби следующим образом: сначала произносят числитель, затем- знаменатель.
При чтении обыкновенных дробей помните, что числитель дроби- количественное числительное (отвечающее на вопрос «сколько долей взято?»), например, шесть, десять, двадцать один и т.д.
Знаменатель- порядковое числительное (отвечает на вопрос: «какая?», «каких?»), например, восьмая, десятая, сотая, шестых, двадцатых и т.д.
В таком случае, если целый торт разделить на 12 частей и съесть 2 кусочка, то запись вида (mathbf{frac{2}{12}}) будет обозначать часть торта, которую съели (из 12 кусочков съели 2).
Эта информация доступна зарегистрированным пользователям
2 (количество долей, которые взяли)- числитель дроби, он располагается над дробной чертой.
12 (общее количество долей)- знаменатель дроби, стоит под дробной чертой.
Дробь (mathbf{frac{2}{12}}) читают так: «две двенадцатых».
Оставшиеся нетронутые кусочки торта найдем следующим образом:
12 — 2 = 10 кусочков торта осталось нетронутыми.
Следовательно, запись вида (mathbf{frac{10}{12}}) представляет собой часть торта, которая осталась несъеденной (из 12 кусочков 10 не съедены).
10 (количество долей, которые остались)- числитель дроби, он располагается над дробной чертой.
12 (общее количество долей)- знаменатель дроби, стоит под дробной чертой
Дробь (mathbf{frac{10}{12}}) читают так: «десять двенадцатых».
История возникновения обыкновенных дробей.
Эта информация доступна зарегистрированным пользователям
Первые упоминания дробей, согласно различным историческим исследованиям, были выявлены в глубокой древности у разных народов.
И это естественно, так как всегда существовала потребность делить целое на части, определять размеры полученных частей.
Не всегда удавалось сделать точные вычисления, выразить измеряемые величины натуральными числами, в связи с этим возникала необходимость нахождения частей целого, введения дробных величин.
Значение слова «дробь» имеет арабское происхождение, обозначает «дробить, ломать, разделять».
У разных государств древнего мира были свои представления о дробных числах, о форме их записи, о математических действиях, которые можно совершать с ними.
В Древнем Египте и Вавилоне были первые упоминания о дроби.
Эти два великих древних государства имели различный подход в представлении дробного числа.
Первой известной дробью в истории дробных чисел была «половина»- одна вторая ((mathbf{frac{1}{2}})), затем появились треть, четверть и т.д.
Эта информация доступна зарегистрированным пользователям
Обыкновенную дробь можно изобразить на координатном луче.
Известно, что любому числу координатного луча соответствует одна единственная точка.
Следовательно, любому дробному числу соответствует конкретное место на координатном луче.
Чтобы обозначить на координатном луче точку с координатой (mathbf{frac{m}{n}}), необходимо от начала координат отложить m отрезков, длина каждого такого отрезка должна составлять (mathbf{frac{1}{n}}) от единичного отрезка.
Чтобы найти число (mathbf{frac{1}{n}}), нужно единичный отрезок разделить на n равных частей.
Рассмотрим поясняющий пример.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком 1 деление = 1 единица.
Отметим на координатном луче точку А((mathbf{frac{4}{6}})).
Дробь (mathbf{frac{4}{6}}) говорит о том, что из шести долей единичного отрезка взяли четыре.
Единичный отрезок разобьем на 6 равных частей, равных (mathbf{frac{1}{6}}).
Следовательно, точка А((mathbf{frac{4}{6}})) удалена от начала координат О(0) на расстояние четырех таких отрезков.
Эта информация доступна зарегистрированным пользователям