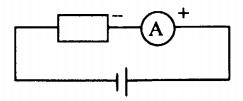
Для измерения силы тока используется амперметр. В идеале собственное сопротивление амперметра стремится к нулю, и оно никак не влияет на значение силы тока. Он включается в цепь последовательно с соблюдением полярности:
Вольтметр
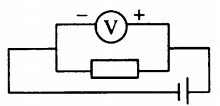
Для измерения напряжения участка цепи используется вольтметр. В идеале собственное сопротивление вольтметра стремится к бесконечности, и устройство не проводит через себя ток. Он включается в электрическую цепь параллельно участку, в котором будет измеряться напряжение, с соблюдением полярности:
Как правильно записывать показания измерительных приборов с учетом погрешности
При записи величин (с учетом погрешности) следует пользоваться формулой:
A=a±Δa
где A — измеряемая величина, a — результат измерений, Δa — погрешность измерений.
Важно!
Погрешность измерений равна половине цены деления шкалы измерительного прибора, если в задаче не указана другая величина погрешности.
Цена деления шкалы — разность значений величины, соответствующих двум соседним отметкам шкалы. Чтобы найти цену деления шкалы, нужно:
- Найти два ближайших штриха шкалы, возле которых написаны значения величин.
- Вычесть из большего значения меньшее.
- Полученное число разделить на число делений (промежутков), находящихся между ними.
Пример №1. Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.
Видно, что стрелка вольтметра встала на значении «2,0» Вольт. Она немного не дотягивает до штриха «2», но к нему она находится ближе, чем к предыдущему штриху.
Два ближайших штриха шкалы с указанными значениями имеют значения 1 и 2 В. Всего между ними 5 промежутков. Следовательно, цена деления шкалы равна: (2 – 1)/5 = 0,2 (Вольт).
Так как по условию задачи погрешность равна половине цене деления шкалы, то она равна 0,1 Вольтам. Следовательно, вольтметр показывает: 2,0 ± 0,1 В.
Задание EF18821
Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения равна цене деления вольтметра.
Ответ: (____± ____) В.
Алгоритм решения
1.Определить цену деления шкалы измерительного прибора.
2.Определить погрешность измерений.
3.Определить показания прибора.
4.Записать показания прибора с учетом погрешности измерений.
Решение
Так как два ближайших штриха, обозначенными числовыми значениями, показывают 1 и 2 Вольта, а между ними 5 делений, то цена деления шкалы равна:
2−15=0,2 (В)
Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка вольтметра стоит в трех делениях от штриха, обозначенном цифрой «1». 3 деления по 0,2 Вольта равны 0,6 Вольтам. Следовательно, вольтметр показывает 1,6 В. С учетом погрешности: V = 1,6 ± 0,2 В.
Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».
Ответ: 1,60,2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18883
Определите показания амперметра (см. рисунок), если погрешность прямого измерения силы тока равна цене деления амперметра.
Ответ: ( ____± ____) А.
Алгоритм решения
1.Определить цену деления шкалы измерительного прибора.
2.Определить погрешность измерений.
3.Определить показания прибора.
4.Записать показания прибора с учетом погрешности измерений.
Решение
Так как два ближайших штриха, обозначенными числовыми значениями, показывают 0 и 0,2 Ампера, а между ними 10 делений, то цена деления шкалы равна:
0,2−010=0,02 (А)
Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка амперметра стоит на штрихе, обозначенном числом «0,2». Следовательно, амперметр показывает 0,2 А. Так как при измерении учитываются сотые доли Амперов, правильно результат измерения записывается так: I = 0,20 А. С учетом погрешности: I = 0,20 ± 0,02 А.
Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».
Ответ: 0,200,02
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19038
Ответ: ( ____±____ ) В.
Алгоритм решения
1.Определить цену деления шкалы измерительного прибора.
2.Определить погрешность измерений.
3.Определить показания прибора.
4.Записать показания прибора с учетом погрешности измерений.
Решение
Так как два ближайших штриха, обозначенными числовыми значениями, показывают 2 и 4 Вольта, а между ними 10 делений, то цена деления шкалы равна:
4−210=0,2 (В)
Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка вольтметра стоит в пяти делениях от штриха, обозначенном цифрой «2». 5 делени1 по 0,2 Вольта равны 1 Вольту. Следовательно, вольтметр показывает 3 В. Так как при измерении учитываются сотые доли Вольтов, правильно результат измерения записывается так: U = 3 В.С учетом погрешности: U = 3,0 ± 0,2 В.
Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».
Ответ: 3,00,2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.4k
Как определить цену деления амперметра и вольтметра?
Если на шкале 100 делений, а переключатель пределов измерения стоит на 1000, то цена одного деления = 1000 / 100 = 10 единиц измерения. Если переключатель пределов стоит на 100, то цена деления соответственно 1 ед. Если переключатель на 10, то цена равна 0,1 единицы и т. д.
Внимательно посмотреть на шкалу и вспомнить арифметику.
берешь 2 цифры на нем написаные, 5 и 10 к примеру. вычитаешь из большего меньшее (10-5) и делишь на количество промежутков между делениями.
Например. 0 l l l l 5 l l l l 10 — цена деления 1 (10-5/5)
Погрешности измерений, представление результатов эксперимента
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin triangle=frac= frac>=0,5 text end Инструментальная погрешность: begin d=frac=frac=0,25 text end Истинное значение: (L_0=4 text) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text $$ Относительная погрешность: $$ delta=fraccdot 100text=6,25textapprox 6,3text $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin triangle=frac= frac>=0,1 text end Инструментальная погрешность: begin d=frac=frac=0,05 text end Истинное значение: (L_0=4,15 text) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text $$ Относительная погрешность: $$ delta=fraccdot 100textapprox 1,2text $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin m_0=frac=fracapprox 100,4 text end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end Находим среднее абсолютное отклонение: begin triangle_=frac=frac=0,5 text end Мы видим, что полученное значение (triangle_) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin triangle m=maxleft; dright>=maxleft\ text end Записываем результат: begin m=m_0pmtriangle m\ m=(100,4pm 0,5) text end Относительная погрешность (с двумя значащими цифрами): begin delta_m=fraccdot 100textapprox 0,050text end
п.6. Представление результатов эксперимента
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
- относительная погрешность их произведения равна сумме относительных погрешностей
- относительная погрешность их частного также равна сумме относительных погрешностей
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
- относительная погрешность произвольной натуральной степени (a^n) равна
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac), мл |
| 1 | 20 | 40 | 4 | (frac=4) |
| 2 | 100 | 200 | 4 | (frac=20) |
| 3 | 15 | 30 | 4 | (frac=3) |
| 4 | 200 | 400 | 4 | (frac=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac), мл |
Относительная погрешность (delta_V=fraccdot 100text) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text, x_2=(4,0pm 0,03) text $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin delta_1=fraccdot 100text=2,5text\ delta_2=fraccdot 100text=0,75text end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac=5 (text), triangle v_2=frac=0,5 (text) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text, v_2=(72pm 0,5) text $$ Скорость сближения равна сумме скоростей: $$ v_0=v_+v_, v_0=54+72=125 text $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text $$ Относительная погрешность: $$ delta_v=fraccdot 100textapprox 4,4text $$ Ответ: (v=(126,0pm 5,5) text, delta_vapprox 4,4text)
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac=0,05 text)
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text, b=(60,10pm 0,05) text $$ Относительные погрешности (не забываем про правила округления): begin delta_1=fraccdot 100textapprox 0,0554textapprox uparrow 0,056text\ delta_2=fraccdot 100textapprox 0,0832textapprox uparrow 0,084text end Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text+0,084text=0,140text=0,14text $$ Абсолютная погрешность: begin triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text^2\ S=(5421,0pm 7,6) text^2 end Ответ: (S=(5421,0pm 7,6) text^2, delta_Sapprox 0,14text)
Шкала измерительного прибора, цена деления шкалы
Стрелочные измерительные приборы: вольтметры, амперметры, омметры и т. д., — обладают шкалами.
Шкала — плоская или цилиндрическая поверхность, относительно которой движется стрелка, на которой нанесены деления.
Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка. Давайте же разберемся, что это за шкалы, и как ими пользоваться, чтобы ничего не напутать.
Для начала отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.
Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет наверняка условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.
Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.
Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.
Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.
У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.
Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.
В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.
Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.
На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.
В этой таблице приведены расшифровки основных обозначений, которые можно встретить на шкалах. Надеемся, что эта краткая статья поможет вам научиться правильно проводить измерения при помощи стрелочных измерительных приборов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Чайковский филиал ПГТУ
Лабораторная
работа №2
Определение
основных
показателей погрешности вольтметра
Для студентов специальности 230100
«Информатика» и
специализации 552800 «Автоматизация и
управление»
Подготовил профессор Лисовский А.Ф.
Чайковский 2006
Цель работы — ознакомление с принципом
действия и устройством приборов для
измерения напряжений и токов, исследование
их основных метрологических характеристик.
Общие сведения. Метод и средства
для измерения напряжения.
При измерении напряжения и тока используют
прямые и косвенные способы.
Прямые измерения основаны на
сравнении измеряемой величина с мерой
этой величины или на непосредственной
оценке измеряемой величины по отчетному
устройству измерительного прибора.
Косвенные измерения основаны
на прямых измерениях другой величины,
функционально связанной с измеряемой
величиной.
Основные метрологические характеристики
приборов для измерения напряжения:
диапазон измерения напряжения, погрешность
измерения, чувствительность или цена
деления.
Диапазон измерений представляет
собой область значений напряжения,
измеряемых прибором с нормированной
погрешностью.
Для многопредельных приборов диапазон
измерений указывают на каждом пределе
с различной нормированной погрешностью.
Переключение пределов измерений
производится вручную или автоматически.
Способность приборов работать при
сигналах, превышающих предел измерения,
называют их перегрузочной способностью.
Перегрузочная способность современных
цифровых вольтметров достигает 300%.
Различают полный и рабочий диапазоны
измерений. Полный диапазон определяют
по формуле
(1)
где
и
максимальное и минимальное значения
измеряемого напряжения.
Если эти максимальное и минимальное
значения измеряемого напряжения
определяются с заранее установленными
погрешностями, то обычно используют
понятие рабочего диапазона
(2)
который обычно меньше полного диапазона.
Погрешность измерений является
основной метрологической характеристикой
прибора. Различают абсолютную,
относительную и приведенную погрешности
приборов.
Абсолютная погрешность
определяется разностью между показанием
прибора Uпр
и истинным значением измеряемого
напряжения Uиcт:
=Uпр
—Uист
(3)
Абсолютная погрешность, взятая с обратным
знаком, называется поправкой П=-.
Относительная погрешность
определяется отношением абсолютной
погрешности
к истинному значению измеряемого
напряжения Uист и выражается
в процентах
(4)
Относительная погрешность зависит от
значения измеряемого напряжения и с
уменьшением напряжения увеличивается.
Приведенная погрешность
определяется отношением абсолютной
погрешности к некоторому нормирующему
значению Uнорм
напряжения и выражается в процентах
(5)
В качестве нормирующего напряжения
принимают предельное значение шкалы
приборов с односторонней шкалой или
сумму предельных значений шкалы для
приборов с двухсторонней шкалой.
Приведенная погрешность не зависит от
значения измеряемого напряжения.
Программа работы:
— показать
величины полного
и рабочего диапазона измерений изучаемого
прибора;
-определить
основную погрешности прибора;
— найти вариации показаний и поправки
к показаниям прибора;
— установить чувствительность и цену
деления прибора.
Порядок выполнения работы.
1. Определение основной погрешности,
вариации показаний, поправки прибора
выполняется по схеме, изображенной на
рис. 1. В качестве поверяемого прибора
используется вольтметр типа МПЛ-46, а
образцовым служит цифровой вольтметр
типа В2-23.
2.
2. Перед проведением измерений провести
следующие действия:
— прибор В2-23 включить в сеть и выждать
10…15 мин:
— произвести установку нуля и калибровку
вольтметра В2-23 в соответствии с
инструкцией по пользованию прибором;
— выполнить установку нуля вольтметра
МПЛ-46, пользуясь корректором.
3. Для выполнения работы поверяемый
вольтметр МПЛ-46 установить на диапазон
15 В и измерить напряжение на всех
оцифрованных делениях шкалы, изменяя
входное напряжение регулируемого
источника ТЕС-13.
Измерение напряжения на каждом
оцифрованном делении шкалы МПЛ-46
производят дважды:
-один раз при возрастании напряжения
(показание образцового вольтметра
U’обр);
— второй раз при убывание напряжения
(показание образцового вольтметра
U’’обр). При этом на образцовом
вольтметре В2-23 необходимо выбрать
поддиапазон, обеспечивающий не менее
трех значащих цифр.
Результаты измерений по показаниям
поверяемого прибора и образцового
вольтметра занести в форму 1.
4. . По данным измерений рассчитать все
остальные метрологические характеристики
поверяемого прибора.
Занести результаты расчетов в форму 1.
|
Измеряемые величины |
Харак- терис-тики |
№№ измерений |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||
|
Показания |
Uпр ,В |
|||||||||||||||
|
Uобр,В |
||||||||||||||||
|
Показания образцового |
U’пр ,В |
|||||||||||||||
|
U’’обр ,В |
||||||||||||||||
|
Действительное значение напряжения |
Uср ,В |
|||||||||||||||
|
Погрешность |
|
|||||||||||||||
|
|
||||||||||||||||
|
|
||||||||||||||||
|
Поправка |
П, В |
|||||||||||||||
|
Вариация показаний |
|
|||||||||||||||
|
|
Форма 1.
Действительные значения на оцифрованных
делениях шкалы поверяемого вольтметра
как среднее значение двух измерений
Uср=(U’обр+U’’обр)/2.
Расчет погрешности измерений
выполнить по формулам:
Абсолютная
погрешность
U=Uпов—Uср,
Относительная
погрешность
=(
U/
Uпов)*100%,
Приведенная
погрешность
п=(
U/
Uном) *100%, где Uном=15
В – номинальное значение поверяемого
напряжения.
Вариацию показаний вольтметра определить
по формулам:
Абсолютное значение
вариации
U=U’обр—U’’обр,
Приведенное
значение вариации
в=(
Uобр/
Uном)*100%,
Поправку вольтметра
вычислить по формуле П=-U.
Использование
табличных значений поправки позволяет
существенно уменьшить погрешность
измерения напряжения поверяемым
вольтметром. Вводя поправку в результат
измерения, получим действительное
значение напряжения U=Uпов—U=Uпов+П.
Из полученных значений
п
и
в
необходимо выбрать наибольшее и сравнить
их с классом точности Кu поверяемого
вольтметра. Если
п
макс и
в
макс окажутся больше Кu, то
поверяемый вольтметр нельзя использовать
с указанным классом точности.
5. Представить отчет по выполненной
лабораторной работе.
5
Соседние файлы в папке разное
- #
- #
- #
- #
Механика — квантовая физика, методы научного познания
В. З. Шапиро
В задании 22 ЕГЭ по физике проверяется, как вы применяете знание физики в практической деятельности и повседневной жизни. В задании дается изображение какого-либо школьного физического прибора, по которому надо определить показания с учетом погрешности измерения.
Что необходимо знать и уметь?
- Вычислять цену деления измерительного прибора. Для этого надо найти два ближайших штриха, обозначенных числами, из большего вычесть меньшее и поделить на число делений.
- Определить границы измерения для приборов, имеющих две шкалы измерения, например, вольтметра, амперметра, барометра. Соответственно, надо выбрать необходимую шкалу для определения показаний прибора.
- Определить погрешность измерения в соответствии с ее описанием в условии. Погрешность измерения может быть равна цене деления или половине цены деления измерительного прибора. Расчет в соответствии с условием задачи.
- В некоторых задачах погрешности измерений могут быть приведены в условии для разных шкал. При выборе определенной шкалы измерений выбирается соответствующая ей погрешность.
- Запись ответа в бланк с учетом требований: каждая цифра и запятая в отдельной клеточке. Если погрешность указана до десятых (или сотых), то показания прибора точно также должны быть указаны до десятых (или сотых).
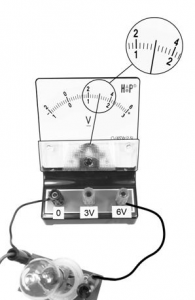
- Чему равна сила тока в лампочке (см. рисунок), если погрешность прямого измерения силы тока амперметром на пределе измерения 3 А равна 0,15 А, а на пределе измерения 0,6 А равна 0,03 А?
Ответ: ( ± ) А.
Согласно рисунку, амперметр подключен к зажимам 0 и 0,6 А. Поэтому определять показания необходимо по нижней шкале. Цена деления этой шкалы равна (0,4 — 0,2):5 = 0,02 (А). Показания амперметра равны 0,28 А. Для выбранной шкалы погрешность измерений указана в условии задачи. Она равна 0,03 А.
Ответ: (0,28 ± 0,03) А.
В бланк надо записать ответ в следующем виде:
| 0 | , | 2 | 8 | 0 | , | 0 | 3 |
Секрет решения. Задание является достаточно простым, но требует внимательного чтения условия. Если в задаче приводится в качестве измерительного прибора термометр со шкалой, проградуированной в градусах Цельсия, а ответ требуется дать по шкале Кельвина, то надо учесть, что погрешности по этим двум шкалам одинаковые. Добавление к погрешности +273 является грубой ошибкой.
+273 требуется только для перевода температуры из шкалы Цельсия в шкалу Кельвина.
2. Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?
Ответ: ( ± ) Н.
Цена деления динамометра определяется следующим расчетом:
(1,5 – 1) : 5 = 0,1 (Н).
Показания динамометра равны 1,1 Н.
Погрешность измерения, согласно условию задачи, равна цене деления, т.е. 0,1 Н.
Ответ: (1,1 ± 0,1) Н.
В бланк надо записать ответ в следующем виде:
| 1 | , | 1 | 0 | , | 1 |
Секрет решения. Задание достаточно простое, но требует внимательного проведения простых расчетов. Главное – правильная запись в бланк ответов №1 показаний динамометра с учетом погрешности измерений.
- Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.
Ответ: ( ___________ ± ___________) В.
Цена деления вольтметра определяется следующим расчетом:
(2 – 1) : 5 = 0,2 (Н).
Показания вольтметра равны 2 В.
Погрешность измерения, согласно условию задачи, составляет половину цены деления, т.е. 0,1 В.
Ответ: (2,0 ± 0,1) В.
| 2 | , | 0 | 0 | , | 1 |
Секрет решения. В этой задаче надо обратить внимание на то, что погрешность измерений равна половине цены деления. При заполнении бланка ответов №1 показания вольтметра необходимо указать с учетом десятичной записи числа (2,0).
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 22 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})