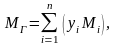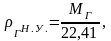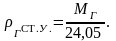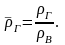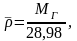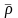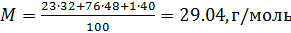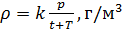Density is referred to as the ratio of the mass per unit of volume of a substance under specific conditions of pressure and temperature. Mathematically, it can be defined as mass divided by volume. It is generally represented by “ρ” or “D”. The density of a substance varies depending on its pressure and temperature. For example, the density of an ideal gas can be doubled as the pressure doubles or by halving its absolute temperature. That means the density of gas always increases as the pressure increases and decreases as the temperature increases. We can determine the molar mass of a substance if we know its density. Generally, the density of a substance is different for different materials. At standard conditions for temperature and pressure, osmium and iridium are the densest known elements.
Density (ρ) = m/V
Where “m” is the mass, and “V” is the volume.
The SI unit of density of a substance is kilogram per cubic meter (kg/m3). Some other units of measurement of density are kilogram per liter (kg/L), gram per milliliter (g/mL), tonne per cubic meter (t/m3), etc.
Density of Gas Formula
The formula to determine the density of a gas is given as follows:
Density of a gas (ρ) = PM/RT
Where,
“P” is the pressure of the gas,
“M” is the molar mass (g/mol),
“R” is the universal gas constant (R = 0.082 L⋅ atm⋅ K−1⋅ mol−1), and
“T” is the temperature of the gas (K)
Derivation For the Density of Gas formula
The density of a gas is equal to the total mass of the gas to the total volume of the gas. To determine the molar mass of a gas, we have to consider the ideal gas equation.
From the ideal gas equation, we have
PV = nRT …………(1)
where,
“P” is the pressure of the gas,
“V” is the volume of the gas
“n” is the number of moles
“R” is the universal gas constant (R = 0.082 L⋅ atm⋅ K−1⋅ mol−1), and
“T” is the temperature of the gasWe know that, number of moles (n) = m/M
where,
“m” is the mass of the gas,
“M” is the molecular mass of the gas.Now, substitute n = m/M in equation (1).
Thus, PV = mRT/M
P = mRT/MV ……….(2)
we know that density (ρ) = m/V. So, substitute the value of ρ in equation (2).
Thus, we get
P = ρ RT/M
ρ = PM/RT
Thus, the ideal gas density formula is ρ = PM/RT.
Solved Examples on Gas Density
Example 1: What will be the density of a gas at 37 °C and a pressure of 5 atm and a molar mass of 84 g/mol?
Solution:
Given data:
Molar mass (M) = 84 g/mol
The pressure of the gas (P) =5 atm
The temperature of the gas (T) = 37 °C = 310 K
Universal gas constant (R) = 0.082 L⋅atm⋅K−1⋅mol−1
From the ideal gas density formula, we have
ρ = MP/RT
ρ = (84 × 5)/ (0.082 × 310)
ρ = 420/25.42 g/L
ρ = 16.522 g/L
Hence, the density of a gas is 16.522 g/L.
Example 2: Determine the density of a gas at 27 °C at a pressure of 7 atm and a molar mass of 54 g/mol. (R = 0.082 L⋅atm⋅K−1⋅mol−1)
Solution:
Given data:
Molar mass (M) = 54 g/mol
The pressure of the gas (P) =7 atm
The temperature of the gas (T) = 27 °C = 300 K
Universal gas constant (R) = 0.082 L⋅atm⋅K−1⋅mol−1
From the ideal gas density formula, we have
ρ= MP/RT
ρ= (54 × 7)/ (0.082 × 300)
ρ= 378/24.6 g/L
ρ= 15.37 g/L
Hence, the density of a gas is 15.37 g/L.
Example 3: Determine the density of carbon monoxide at 40 °C and a pressure of 730 Torr. (R = 0.082 L⋅atm⋅K−1⋅mol−1)
Solution:
Given data:
Molar mass of carbon monoxide (M) = 28 g/mol
Pressure (P) =730 Torr = 730/760 atm = 0.9605 atm
Temperature (T) = 40 °C = 313 K
Universal gas constant (R) = 0.082 L⋅atm⋅K−1⋅mol−1
From the ideal gas density formula, we have
ρ= MP/RT
ρ= (28 × 0.9605)/ (0.082 × 313)
ρ= 26.894/25.666 g/L
ρ= 1.0478 g/L
Hence, the density of carbon monoxide at 40 °C and a pressure of 730 Torr is 1.0478 g/L.
Example 4: If the density of a gas is 9.35 g/L at STP, then determine its density at 30 °C and a pressure of 700 mmHg.
Solution:
Given data:
The density of a gas (ρ1) = 9.35 g/L
We know that at STP pressure is equal to 0.987 atm and temperature is equal to 273.15 K.
So, P1 = 0.987 atm
T1 = 273.15 K
Let the density of the gas at 30 °C and pressure of 700mmHg be ρ2.
P2 = 700mmHg = 700 × 0.00131579 atm = 0.9210 atm
T2 = 30 °C = 303K
From the ideal gas density formula, we have
ρ= MP/RT
As we are calculating the density of the same gas at different conditions, the mass of the gas remains the same.
ρ ∝ P/T
ρ1/ρ2 = (P1/T1)/ (P2/T2)
9.35/ρ2 = (0.987/273.15)/ (0.9210/303)
9.35/ρ2 = (0.987 × 303)/ (0.9210 × 273.15)
9.35/ρ2 = (299.061/251.57)
ρ2 = (9.35 × 251.57)/299.061
ρ2 = 7.865 g/L
Hence, the density of the gas at 30 °C and pressure of 700mmHg is 7.865 g/L.
Example 5: What is the density of nitric oxide (NO) at a temperature of 51 °C and a pressure of 6 bar? (R = 0.082 L⋅atm⋅K−1⋅mol−1)
Solution:
Given data:
Density (ρ) = 3.42 g/L
Temperature (T) = 51 + 273 = 324 K
Pressure (P)= 6 bar = 6 × 0.9869 atm = 5.9215 atm
The molar mass of nitric oxide = 30 g/mol
Universal gas constant (R) = 0.082 L⋅atm⋅K−1⋅mol−1
From the ideal gas density formula, we have
ρ= MP/RT
ρ= (30 × 5.9215)/ (0.082 × 324)
ρ= 177.645/26.568 g/L
ρ= 6.686 g/L
Hence, the density of nitric oxide at 51 °C and a pressure of 6 bar is 6.686 g/L.
FAQs on Gas Density
Question 1: Define the density of the gas.
Answer:
Density is referred to as the ratio of the mass per unit of volume of a substance under specific conditions of pressure and temperature. Mathematically, it can be defined as mass divided by volume. It is generally represented by “ρ” or “D”.
Density (ρ) = m/V
Where “m” is the mass, and “V” is the volume.
Question 2: What is the effect of pressure and temperature on the density of gas?
Answer:
The density of a substance varies depending on its pressure and temperature. For example, the density of an ideal gas can be doubled as the pressure doubles or by halving its absolute temperature. That means the density of gas always increases as the pressure increases and decreases as the temperature increases.
Question 3: What is meant by an ideal gas? Write down the ideal gas density formula.
Answer:
The gas that strictly follows Boyle’s law, Charles’ law, and Avogadro’s law is known as an ideal gas. It is a hypothetical gas that is proposed to simplify the calculations. Many real gases behave qualitatively like an ideal gas under various conditions of temperature and pressure, where the gas molecules act as the ideal particles.
Ideal gas density formula
ρ = PM/RT
Where “P” is the pressure of the gas,
“M” is the molar mass (g/mol),
“R” is the universal gas constant (R = 0.082 L⋅ atm⋅ K−1⋅ mol−1), and
“T” is the temperature of the gas (K)
Question 4: What are units of measurement of density?
Answer:
The SI unit of density of a substance is kilogram per cubic meter (kg/m3). Some other units of measurement of density are kilogram per liter (kg/L), gram per milliliter (g/mL), tonne per cubic meter (t/m3), etc.
В этой статье мы коснемся нескольких краеугольных понятий в химии, без которых совершенно невозможно
решение задач. Старайтесь понять смысл физических величин, чтобы усвоить эту тему.
Я постараюсь приводить как можно больше примеров по ходу этой статьи, в ходе изучения вы увидите множество примеров
по данной теме.

Относительная атомная масса — Ar
Представляет собой массу атома, выраженную в атомных единицах массы. Относительные атомные массы указаны в периодической
таблице Д.И. Менделеева. Так, один атом водорода имеет атомную массу = 1, кислород = 16, кальций = 40.
Относительная молекулярная масса — Mr
Относительная молекулярная масса складывается из суммы относительных атомных масс всех атомов, входящих в состав вещества.
В качестве примера найдем относительные молекулярные массы кислорода, воды, перманганата калия и медного купороса:
Mr (O2) = (2 × Ar(O)) = 2 × 16 = 32
Mr (H2O) = (2 × Ar(H)) + Ar(O) = (2 × 1) + 16 = 18
Mr (KMnO4) = Ar(K) + Ar(Mn) + (4 × Ar(O)) = 39 + 55 + (4 * 16) = 158
Mr (CuSO4*5H2O) = Ar(Cu) + Ar(S) + (4 × Ar(O)) + (5 × ((Ar(H) × 2) +
Ar(O))) = 64 + 32 + (4 × 16) + (5 × ((1 × 2) + 16)) = 160 + 5 * 18 = 250
Моль и число Авогадро
Моль — единица количества вещества (в системе единиц СИ), определяемая как количество вещества, содержащее столько же структурных единиц
этого вещества (молекул, атомов, ионов) сколько содержится в 12 г изотопа 12C, т.е. 6 × 1023.
Число Авогадро (постоянная Авогадро, NA) — число частиц (молекул, атомов, ионов) содержащихся в одном моле любого вещества.

Больше всего мне хотелось бы, чтобы вы поняли физический смысл изученных понятий. Моль — международная единица количества вещества, которая
показывает, сколько атомов, молекул или ионов содержится в определенной массе или конкретном объеме вещества. Один моль любого вещества
содержит 6.02 × 1023 атомов/молекул/ионов — вот самое важное, что сейчас нужно понять.
Иногда в задачах бывает дано число Авогадро, и от вас требуется найти, какое вам дали количество вещества (моль). Количество вещества в химии
обозначается N, ν (по греч. читается «ню»).
Рассчитаем по формуле: ν = N/NA количество вещества 3.01 × 1023 молекул воды и 12.04 × 1023 атомов углерода.
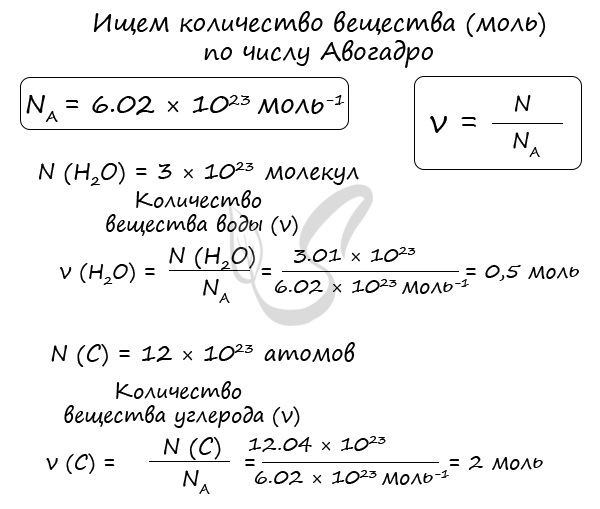
Мы нашли количества вещества (моль) воды и углерода. Сейчас это может показаться очень абстрактным, но, иногда не зная, как найти
количество вещества, используя число Авогадро, решение задачи по химии становится невозможным.
Молярная масса — M
Молярная масса — масса одного моля вещества, выражается в «г/моль» (грамм/моль). Численно совпадает с изученной нами ранее
относительной молекулярной массой.
Рассчитаем молярные массы CaCO3, HCl и N2
M (CaCO3) = Ar(Ca) + Ar(C) + (3 × Ar(O)) = 40 + 12 + (3 × 16) = 100 г/моль
M (HCl) = Ar(H) + Ar(Cl) = 1 + 35.5 = 36.5 г/моль
M (N2) = Ar(N) × 2 = 14 × 2 = 28 г/моль
Полученные знания не должны быть отрывочны, из них следует создать цельную систему. Обратите внимание: только что мы рассчитали
молярные массы — массы одного моля вещества. Вспомните про число Авогадро.
Получается, что, несмотря на одинаковое число молекул в 1 моле (1 моль любого вещества содержит 6.02 × 1023 молекул),
молекулярные массы отличаются. Так, 6.02 × 1023 молекул N2 весят 28 грамм, а такое же количество молекул
HCl — 36.5 грамм.
Это связано с тем, что, хоть количество молекул одинаково — 6.02 × 1023, в их состав входят разные атомы, поэтому и
массы получаются разные.

Часто в задачах бывает дана масса, а от вас требуется рассчитать количество вещества, чтобы перейти к другому веществу в реакции.
Сейчас мы определим количество вещества (моль) 70 грамм N2, 50 грамм CaCO3, 109.5 грамм HCl. Их молярные
массы были найдены нам уже чуть раньше, что ускорит ход решения.

ν (CaCO3) = m(CaCO3) : M(CaCO3) = 50 г. : 100 г/моль = 0.5 моль
ν (HCl) = m(HCl) : M(HCl) = 109.5 г. : 36.5 г/моль = 3 моль
Иногда в задачах может быть дано число молекул, а вам требуется рассчитать массу, которую они занимают. Здесь нужно использовать
количество вещества (моль) как посредника, который поможет решить поставленную задачу.
Предположим нам дали 15.05 × 1023 молекул азота, 3.01 × 1023 молекул CaCO3 и 18.06 × 1023 молекул
HCl. Требуется найти массу, которую составляет указанное число молекул. Мы несколько изменим известную формулу, которая поможет нам связать
моль и число Авогадро.

Теперь вы всесторонне посвящены в тему. Надеюсь, что вы поняли, как связаны молярная масса, число Авогадро и количество вещества.
Практика — лучший учитель. Найдите самостоятельно подобные значения для оставшихся CaCO3 и HCl.
Молярный объем
Молярный объем — объем, занимаемый одним молем вещества. Примерно одинаков для всех газов при стандартной температуре
и давлении составляет 22.4 л/моль. Он обозначается как — VM.
Подключим к нашей системе еще одно понятие. Предлагаю найти количество вещества, количество молекул и массу газа объемом
33.6 литра. Поскольку показательно молярного объема при н.у. — константа (22.4 л/моль), то совершенно неважно, какой газ мы
возьмем: хлор, азот или сероводород.
Запомните, что 1 моль любого газа занимает объем 22.4 литра. Итак, приступим к решению задачи. Поскольку какой-то газ
все же надо выбрать, выберем хлор — Cl2.


Моль (количество вещества) — самое гибкое из всех понятий в химии. Количество вещества позволяет вам перейти и к
числу Авогадро, и к массе, и к объему. Если вы усвоили это, то главная задача данной статьи — выполнена 

Относительная плотность и газы — D
Относительной плотностью газа называют отношение молярных масс (плотностей) двух газов. Она показывает, во сколько раз одно вещество
легче/тяжелее другого. D = M (1 вещества) / M (2 вещества).
В задачах бывает дано неизвестное вещество, однако известна его плотность по водороду, азоту, кислороду или
воздуху. Для того чтобы найти молярную массу вещества, следует умножить значение плотности на молярную массу
газа, по которому дана плотность.
Запомните, что молярная масса воздуха = 29 г/моль. Лучше объяснить, что такое плотность и с чем ее едят на примере.
Нам нужно найти молярную массу неизвестного вещества, плотность которого по воздуху 2.5

Предлагаю самостоятельно решить следующую задачку (ниже вы найдете решение): «Плотность неизвестного вещества по
кислороду 3.5, найдите молярную массу неизвестного вещества»

Относительная плотность и водный раствор — ρ
Пишу об этом из-за исключительной важности в решении
сложных задач, высокого уровня, где особенно часто упоминается плотность. Обозначается греческой буквой ρ.
Плотность является отражением зависимости массы от вещества, равна отношению массы вещества к единице его объема. Единицы
измерения плотности: г/мл, г/см3, кг/м3 и т.д.
Для примера решим задачку. Объем серной кислоты составляет 200 мл, плотность 1.34 г/мл. Найдите массу раствора. Чтобы не
запутаться в единицах измерения поступайте с ними как с самыми обычными числами: сокращайте при делении и умножении — так
вы точно не запутаетесь.

Иногда перед вами может стоять обратная задача, когда известна масса раствора, плотность и вы должны найти объем. Опять-таки,
если вы будете следовать моему правилу и относится к обозначенным условным единицам «как к числам», то не запутаетесь.
В ходе ваших действий «грамм» и «грамм» должны сократиться, а значит, в таком случае мы будем делить массу на плотность. В противном случае
вы бы получили граммы в квадрате 
К примеру, даны масса раствора HCl — 150 грамм и плотность 1.76 г/мл. Нужно найти объем раствора.

Массовая доля — ω
Массовой долей называют отношение массы растворенного вещества к массе раствора. Важно заметить, что в понятие раствора входит
как растворитель, так и само растворенное вещество.
Массовая доля вычисляется по формуле ω (вещества) = m (вещества) / m (раствора). Полученное число будет показывать массовую долю
в долях от единицы, если хотите получить в процентах — его нужно умножить на 100%. Продемонстрирую это на примере.

Решим несколько иную задачу и найдем массу чистой уксусной кислоты в широко известной уксусной эссенции.
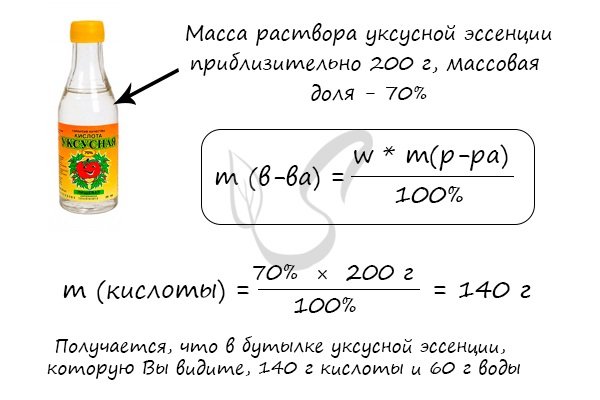
© Беллевич Юрий Сергеевич 2018-2023
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.
Одним из важных
параметров газа является его молекулярная
масса,
которая определяется путем суммирования
масс атомов, входящих в молекулу.
Молекулярная масса
углеводородного газа, представляющего
собою смесь компонентов, при известном
объёмном составе, рассчитывается по
формуле:
(2.6)
где yi
– объёмная
доля i—
го компонента в газовой смеси;
Mi
– молекулярная
масса i—
го компонента;
n
– число компонентов в смеси газов.
Под плотностью
углеводородного газа понимают его
массу, заключенную в 1 м3
при определенных условиях (нормальных
или стандартных), в системе СИ измеряется
в кг/м3.
г
= m/V.
(2.7)
Под нормальными
условиями понимают условия, при которых
давление Р = 0,1 МПа, а температура Т = 273
К (0С);
под стандартными условиями – Р = 0,1 МПа,
Т = 293 К (20С).
Для всех газов
объем 1 киломоля постоянен и равен при
нормальных условиях – 22,41 м3,
при стандартных условиях – 24,05 м3.
Зная молекулярную массу газа, плотность
газа при нормальных условиях можно
вычислить по формуле:
(2.8)
при стандартных
условиях – по формуле:
(2.9)
На практике часто
пользуются относительной
плотностью газа,
равной отношению плотности газа к
плотности воздуха при определенных
условиях:
(2.10)
При расчетах
следует помнить, что плотность воздуха
при нормальных условиях
составляет
вн.у.
= 1,293
кг/м3,
при стандартных
вст.у.
= 1,205
кг/м3.
Зная молекулярную
массу газа МГ,
относительную плотность газа можно
также рассчитать по формуле:
(2.11)
где 28,98 –
молекулярная масса воздуха.
Задача 2.2. Даны
составы газов типичных газовых,
газоконденсатных и нефтяных месторождений.
Рассчитать молекулярную массу Мi
каждого компонента, входящего в состав
газа, молекулярную массу газа Мг,
плотность газа при нормальных (гн.у.)
и стандартных
условиях (гст.у.),
а также относительную плотность по
воздуху
г
(при нормальных
и стандартных условиях). Определить тип
газа (природный, попутный или газ
газоконденсатного месторождения).
Исходные данные для расчетов приведены
в таблицах 2.2 и 2.3.
Таблица 2.2 –
Компонентный состав газа
|
Вариант |
Месторождение |
Компонентный |
|||||||
|
СН4 |
С2Н6 |
С3Н8 |
С4Н10 |
С5Н12 и выше |
СО2 |
N2 |
H2S |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
Самотлорское |
53,40 |
7,20 |
15,1 |
8,30 |
6,30 |
0,10 |
9,60 |
— |
|
2 |
Уренгойское |
98,84 |
0,10 |
0,03 |
0,02 |
0,01 |
0,30 |
1,70 |
— |
|
3 |
Оренбургское |
84,00 |
5,00 |
1,60 |
0,70 |
1,80 |
1,10 |
4,20 |
1,60 |
|
4 |
Шатлыкское |
95,60 |
2,00 |
0,34 |
0,10 |
0,05 |
1,15 |
0,76 |
— |
|
5 |
Астраханское |
58,80 |
1,88 |
0,60 |
0,23 |
0,12 |
11,0 |
1,37 |
26,0 |
|
6 |
Ромашкинское |
37,30 |
20,70 |
18,9 |
9,50 |
4,80 |
— |
8,80 |
— |
|
7 |
Туймазинское |
39,47 |
16,83 |
6,58 |
2,80 |
1,10 |
— |
31,62 |
1,60 |
|
8 |
Южно-Первомайское |
55,18 |
13,67 |
8,09 |
1,02 |
20,20 |
0,30 |
1,54 |
— |
|
9 |
Бавлинское |
35,00 |
20,70 |
19,9 |
9,80 |
5,80 |
0,40 |
8,40 |
— |
|
10 |
ПО Пермьнефть |
38,70 |
22,60 |
10,7 |
2,70 |
0,70 |
0,50 |
23,8 |
0,30 |
|
11 |
Коробковское |
81,50 |
8,00 |
4,00 |
2,30 |
0,50 |
0,50 |
3,20 |
— |
|
12 |
ПО Самаранефть |
58,00 |
17,20 |
7,40 |
2,10 |
0,50 |
0,80 |
13,50 |
0,50 |
|
13 |
Ямбургское |
89,67 |
4,39 |
1,64 |
0,74 |
2,36 |
0,94 |
0,26 |
— |
|
14 |
ПО Грознефть |
76,70 |
13,20 |
5,40 |
2,50 |
2,20 |
— |
— |
— |
|
15 |
Медвежье |
98,78 |
0,10 |
0,02 |
— |
— |
0,10 |
1,00 |
— |
|
16 |
Вуктыльское |
74,80 |
8,70 |
3,90 |
1,80 |
6,4 |
0,10 |
4,30 |
— |
|
17 |
Тенгизское |
42,23 |
8,47 |
5,21 |
3,34 |
21,18 |
2,60 |
0,77 |
16,2 |
|
18 |
Карачаганакское |
72,99 |
6,22 |
2,59 |
1,50 |
7,55 |
5,35 |
0,57 |
3,23 |
|
19 |
Калужское |
88,18 |
2,94 |
2,31 |
2,48 |
3,59 |
0,50 |
— |
— |
|
20 |
Узеньское |
50,10 |
20,10 |
16,8 |
7,70 |
3,00 |
— |
2,30 |
— |
|
21 |
Талинское |
44,88 |
7,38 |
3,85 |
1,39 |
42,50 |
— |
— |
— |
|
22 |
Марковское |
45,46 |
11,23 |
5,55 |
4,13 |
33,12 |
— |
0,51 |
— |
|
23 |
Уренгойское |
82,27 |
6,56 |
3,24 |
1,49 |
5,62 |
0,50 |
0,32 |
— |
|
24 |
Северо-Соленинское |
89,52 |
4,15 |
1,82 |
0,48 |
2,58 |
0,49 |
0,96 |
— |
|
25 |
Совхозное ПХГ |
84,85 |
5,77 |
2,33 |
0,75 |
0,35 |
0,95 |
5,00 |
— |
|
26 |
Дмитриевское |
35,88 |
2,82 |
1,69 |
2,17 |
56,12 |
0,33 |
0,99 |
— |
|
27 |
Северо-Ставропольское |
92,80 |
2,80 |
0,90 |
0,40 |
0,10 |
0,50 |
2,50 |
— |
|
28 |
Александровское |
85,10 |
1,93 |
6,74 |
3,38 |
0,28 |
2,57 |
— |
— |
|
29 |
Радаевское |
32,70 |
13,40 |
15,2 |
4,90 |
2,60 |
27,8 |
3,20 |
— |
|
30 |
Ново-Дмитриевское |
64,76 |
9,68 |
10,8 |
7,02 |
6,01 |
0,81 |
0,91 |
— |
Таблица 2.3 – Атомные
массы компонентов
|
Компонент |
Водород |
Углерод |
Кислород |
Сера |
Азот |
|
Атомная масса |
1,008 |
12,011 |
15,999 |
32,064 |
14,007 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Введение
Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].
Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.
К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.
В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.
Математическая модель определения плотности газа
Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:
1. Уравнение Менделеева-Клапейрона:
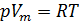
где:


R — универсальная газовая постоянная,
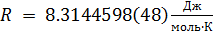
T — абсолютная температура, T=273.16 К.
2. Два измеряемых параметра:
p – давление газа, Па
t – температура газа, °С.
Известно, что молярный объём 
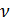
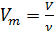
Также известно, что
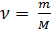
где: m – масса газа, M – молярная масса газа.
Учитывая (2) и (3) перепишем (1) в виде:
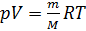
Как известно, плотность вещества

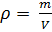
Из (4) и (5) выведем уравнение для плотности газа

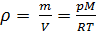
и введём обозначение параметра
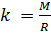
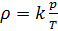
Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.
Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.
Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:
Молярные массы этих веществ воздуха будут соответственно равны:
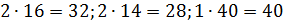
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:
Теперь, зная значение константы
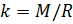

Приведение плотности газа к нормальным, стандартным условиям
Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].
Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.
Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 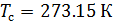
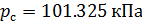
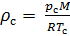
Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для 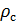
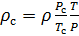
Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура 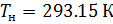
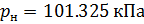

В уравнениях (10) и (11) используем значения параметров воздуха 
Реализация измерительного канала давления и температуры
Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.
Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).
Для этого, на аппаратном уровне, нам понадобятся компоненты:
- Arduino (Uno, …) – используем как программатор;
- микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
- кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
- тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
- BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
- преобразователь интерфейсов TTL/USB;
- расходные материалы – провода, припой, монтажная плата, и др.
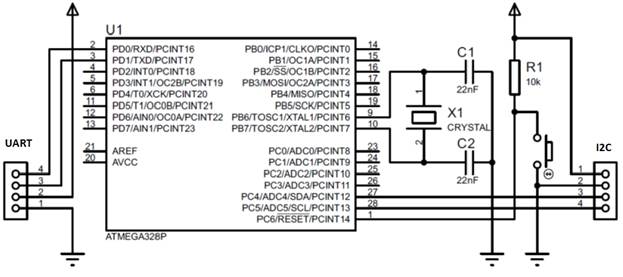
Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры
Теперь рассмотрим этапы осуществления нашей задачи.
1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.
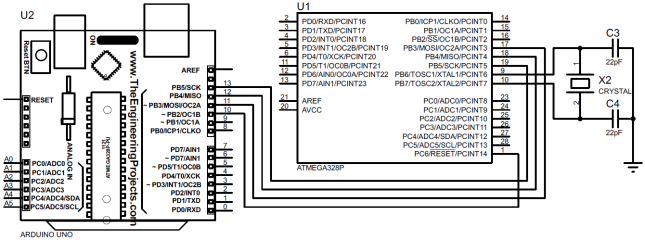
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.
Рис. 2 – Схема подключения микроконтроллера к программатору
3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.
Рис. 3 Система измерения давления и температуры
Листинг 1 — Программа опроса измерительного преобразователя давления и температуры
#include <SFE_BMP180.h>
SFE_BMP180 pressure;
double T,P;
void setup()
{
Serial.begin(9600);
pressure.begin();
}
void loop()
{
P = getPressure();
Serial.println(P+0.5, 2);
Serial.println(T+0.54, 2);
delay(1000);
}
double getPressure(){
char status;
status = pressure.startTemperature();
if (status != 0){
delay(status); // ожидание замера температуры
status = pressure.getTemperature(T);
if (status != 0){
status = pressure.startPressure(3);
if (status != 0){
delay(status); // ожидание замера давления
status = pressure.getPressure(P,T);
if (status != 0){
return(P);
}
}
}
}
}
Программа Python для фильтрации по каналам температуры и давления, и получение результатов
Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.
Листинг 2 – Определение плотности газа по результатам измерения давления и температуры
import numpy as np
import matplotlib.pyplot as plt
import serial
from drawnow import drawnow
import datetime, time
from pykalman import KalmanFilter
#вводим матрицу перехода и матрицу наблюдений
transition_matrix = [[1, 1, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 0, 0, 1]]
observation_matrix = [[1, 0, 0, 0],
[0, 0, 1, 0]]
#вводим и инициируем матрицу измерений
initial_state_mean = [101000,
0,
28,
0]
#параметры уравнения состояния идеального газа:
#универсальная газовая постоянная R, [Дж/(моль*К)]
R = 8.314459848
#молярная масса воздуха M, [г/моль]
M = 29.04
#коэффициент k = M/R, [г/(Дж*К)]
k = M / R
#абсолютная температура, [K]
K = 273.16
#стандартное (нормальное) давление, [Па]
Pn = 101325
#определяем количество измерений
# общее количество измерений
str_m = input("введите количество измерений: ")
m = eval(str_m)
# количество элементов выборки
mw = 16
#настроить параметры последовательного порта
ser = serial.Serial()
ser.baudrate = 9600
port_num = input("введите номер последовательного порта: ")
ser.port = 'COM' + port_num
ser
#открыть последовательный порт
try:
ser.open()
ser.is_open
print("соединились с: " + ser.portstr)
except serial.SerialException:
print("нет соединения с портом: " + ser.portstr)
raise SystemExit(1)
#определяем списки
l1 = [] # для значений 1-го параметра
l2 = [] # для значений 2-го параметра
t1 = [] # для моментов времени
lw1 = [] # для значений выборки 1-го параметра
lw2 = [] # для значений выборки 2-го параметра
n = [] # для значений моментов времени
nw = [] # для значений выборки моментов времени
l1K = [] # для фильтрованных значений 1-го параметра
l2K = [] # для фильтрованных значений 2-го параметра
ro = [] # для плотности газовой среды
#подготовить файлы на диске для записи
filename = 'count.txt'
in_file = open(filename,"r")
count = in_file.read()
count_v = eval(count) + 1
in_file.close()
in_file = open(filename,"w")
count = str(count_v)
in_file.write(count)
in_file.close()
filename = count + '_' + filename
out_file = open(filename,"w")
#вывод информации для оператора на консоль
print("nпараметры:n")
print("n - момент времени, с;")
print("P - давление, Па;")
print("Pf - отфильтрованное значение P, Па;")
print("T - температура, град. С;")
print("Tf - отфильтрованное значение T, град. С;")
print("ro - плотность воздуха, г/м^3;")
print("nизмеряемые значения величин параметровn")
print('{0}{1}{2}{3}{4}{5}n'.format('n'.rjust(3),'P'.rjust(10),'Pf'.rjust(10),
'T'.rjust(10),'Tf'.rjust(10),'ro'.rjust(10)))
#считываение данных из последовательного порта
#накопление списков
#формирование текущей выборки
i = 0
while i < m:
n.append(i)
nw.append(n[i])
if i >= mw:
nw.pop(0)
ser.flushInput() #flush input buffer, discarding all its contents
line1 = ser.readline().decode('utf-8')[:-1]
line2 = ser.readline().decode('utf-8')[:-1]
t1.append(time.time())
if line1:
l = eval(line1)
#l = np.random.normal(l,100.0)
l1.append(l)
lw1.append(l1[i])
if i >= mw:
lw1.pop(0)
if line2:
l = eval(line2)
#l = np.random.normal(l,1.5)
l2.append(l)
lw2.append(l2[i])
if i >= mw:
lw2.pop(0)
#-------------------------
initial_state_mean = [l1[i],0,l2[i],0]
kf1 = KalmanFilter(transition_matrices = transition_matrix,
observation_matrices = observation_matrix,
initial_state_mean = initial_state_mean)
if i == 0:
measurements = np.array( [ [l1[i], l2[i]],
[initial_state_mean[0], initial_state_mean[2]] ] )
measurements = np.array( [ [l1[i], l2[i]],
[l1[i-1], l2[i-1]] ] )
kf1 = kf1.em(measurements, n_iter=2)
(smoothed_state_means, smoothed_state_covariances) = kf1.smooth(measurements)
l1K.append(smoothed_state_means[0, 0])
l2K.append(smoothed_state_means[0, 2])
#плотность воздуха в рабочих условиях
#ro.append( k * l1K[i]/( l2K[i] + K) )
#плотность воздуха, приведенная к стандартным условиям
ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/K/l1K[i]) )
#плотность воздуха, приведенная к нормальным условиям
#ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/(K+20)/l1K[i]) )
print('{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}'.
format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i]))
i += 1
ser.close()
time_tm = t1[m - 1] - t1[0]
print("nпродолжительность времени измерений: {0:.3f}, c".format(time_tm))
Ts = time_tm / (m - 1)
print("nпериод опроса датчика: {0:.6f}, c".format(Ts))
#запись таблицы в файл
print("nтаблица находится в файле {}n".format(filename))
for i in np.arange(0,len(n),1):
out_file.write('{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}n'.
format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i]))
#закрыть файл с таблицей
out_file.close()
now = datetime.datetime.now() #получаем дату и время
#выводим графики
plt.figure('давление')
plt.plot( n, l1, "b-", n, l1K, "r-")
plt.ylabel(r'$давление, Па$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.figure('температура')
plt.plot( n, l2, "b-", n, l2K, "r-")
plt.ylabel(r'$температура, degree С$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
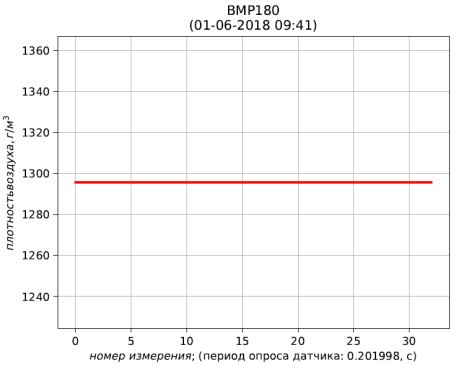
plt.figure('плотность воздуха')
plt.plot( n, ro, "r-")
plt.ylabel(r'$плотность воздуха, г/м^3$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.show()
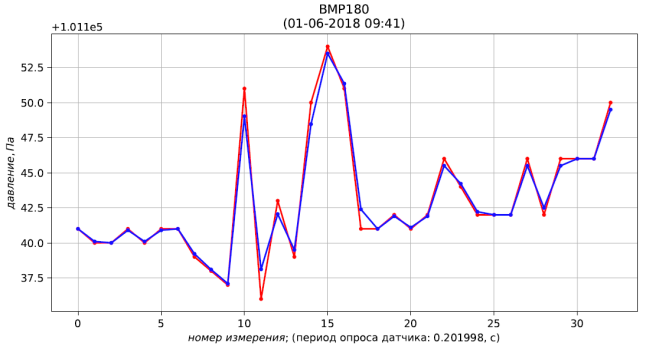
Результаты расчёта представлены листингом и рис. 4, 5, 6.
Интерфейс пользователя и таблица результатов расчёта
введите количество измерений: 33
введите номер последовательного порта: 6
соединились с: COM6
параметры:
n - момент времени, с;
P - давление, Па;
Pf - отфильтрованное значение P, Па;
T - температура, град. С;
Tf - отфильтрованное значение T, град. С;
ro - плотность воздуха, г/м^3;
измеряемые значения величин параметров
n P Pf T Tf ro
0 101141.000 101141.000 28.120 28.120 1295.574
1 101140.000 101140.099 28.190 28.183 1295.574
2 101140.000 101140.000 28.130 28.136 1295.574
3 101141.000 101140.901 28.100 28.103 1295.574
4 101140.000 101140.099 28.100 28.100 1295.574
5 101141.000 101140.901 28.110 28.109 1295.574
6 101141.000 101141.000 28.100 28.101 1295.574
7 101139.000 101139.217 28.100 28.100 1295.574
8 101138.000 101138.099 28.090 28.091 1295.574
9 101137.000 101137.099 28.100 28.099 1295.574
10 101151.000 101149.028 28.100 28.100 1295.574
11 101136.000 101138.117 28.110 28.109 1295.574
12 101143.000 101142.052 28.110 28.110 1295.574
13 101139.000 101139.500 28.100 28.101 1295.574
14 101150.000 101148.463 28.110 28.109 1295.574
15 101154.000 101153.500 28.120 28.119 1295.574
16 101151.000 101151.354 28.110 28.111 1295.574
17 101141.000 101142.391 28.130 28.127 1295.574
18 101141.000 101141.000 28.120 28.121 1295.574
19 101142.000 101141.901 28.110 28.111 1295.574
20 101141.000 101141.099 28.120 28.119 1295.574
21 101142.000 101141.901 28.110 28.111 1295.574
22 101146.000 101145.500 28.120 28.119 1295.574
23 101144.000 101144.217 28.130 28.129 1295.574
24 101142.000 101142.217 28.130 28.130 1295.574
25 101142.000 101142.000 28.140 28.139 1295.574
26 101142.000 101142.000 28.130 28.131 1295.574
27 101146.000 101145.500 28.150 28.147 1295.574
28 101142.000 101142.500 28.190 28.185 1295.574
29 101146.000 101145.500 28.230 28.225 1295.574
30 101146.000 101146.000 28.230 28.230 1295.574
31 101146.000 101146.000 28.220 28.221 1295.574
32 101150.000 101149.500 28.210 28.211 1295.574
продолжительность времени измерений: 6.464, c
период опроса датчика: 0.201998, c
таблица находится в файле 68_count.txt
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления
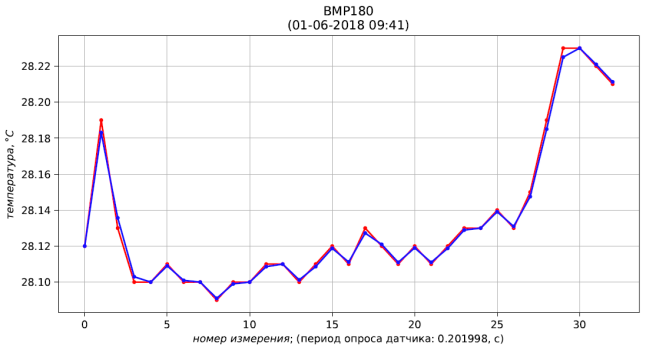
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)
Выводы
Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.
Ссылки на источники информации
- ГОСТ 8.586.5-2005. URL
- ГОСТ Р 8.740 – 2011. URL
- Ideal gas law. URL
- Standard conditions for temperature and pressure. URL
Как вам известно, вещества могут находиться в твёрдом, жидком и газообразном состоянии. Молекулы жидкости и твёрдого вещества располагаются близко друг к другу. Это возможно благодаря тому, что молекулы притягиваются друг к другу. То есть существуют силы, которые удерживают молекулы жидкости или твёрдого вещества вместе. Из курса химии 8-го класса вы знаете, что эти силы называются силами межмолекулярного взаимодействия. Молекулы газов находятся на значительно большем расстоянии друг от друга, чем в случае жидкостей и твёрдых веществ. На таком расстоянии молекулы практически не взаимодействуют друг с другом. Поэтому, чтобы превратить жидкость или твёрдое вещество в газ, необходимо преодолеть силы межмолекулярного взаимодействия, отдалив молекулы друг от друга.
Переход в газообразное состояние осуществляется в результате нагревания веществ, находящихся в твёрдом или жидком состоянии (кипение жидкостей, возгонка твёрдых веществ).
Так как расстояние между молекулами газов значительно больше размеров самих молекул, то объём, который занимает газ, — это, по существу, объём свободного пространства между хаотически движущимися молекулами газа. Величина этого пространства определяется условиями, при которых находится газ, т. е. температурой и давлением. Эта величина примерно одинакова для всех газов. При этом объёмом, занимаемым самими молекулами, можно пренебречь. Отсюда следует закон Авогадро — в равных объёмах различных газов при одинаковых условиях содержится одинаковое число молекул.

Авогадро (1776—1856)
Интересно знать
Из курса химии 8-го класса вы уже знакомы с постоянной Авогадро, равной 6,02 ∙ 1023 моль–1, которая показывает, сколько частиц содержится в одном моле вещества. Эта величина названа в честь выдающегося итальянского учёного Амедео Авогадро, внёсшего значительный вклад в развитие молекулярной физики, электрохимии и других областей естествознания. На основании исследования соотношения объёмов реагирующих и образующихся газов, таких как водород и хлор, кислород и азот, Авогадро впервые предположил, что молекулы азота, кислорода, водорода и хлора состоят из двух атомов. Это предположение, сначала долго не находившее понимания у учёных того времени, впоследствии блестяще подтвердилось.
Из закона Авогадро вытекают два основных следствия.
Первое следствие. Один моль любого газа при одинаковых условиях занимает одинаковый объём. Этот объём называется молярным объёмом газа (Vm), и измеряется в дм3/моль. Молярный объём газа равен отношению объёма газа к его количеству:
.
Величина Vm зависит от температуры и давления. Например, при нагревании газы расширяются. Значит, при нагревании увеличивается молярный объём газа. В связи с этим сравнение характеристик различных газовых смесей необходимо осуществлять при одинаковых условиях — температуре и давлении. В качестве эталона таких условий приняты нормальные условия (н. у.): температура таяния льда (0 °С или 273,15 K) и атмосферное давление (101,3 кПа). При нормальных условиях Vm = 22,4 дм3/моль.
Таким образом, из закона Авогадро следует, что 22,4 дм3 любого газа при нормальных условиях содержат 6,02 ∙ 1023 молекул.
Второе следствие. Плотности газов относятся между собой как молярные массы газов.
Это видно из следующих соображений. Пусть имеется две порции различных газов. Рассчитаем их плотности:
газ 1: 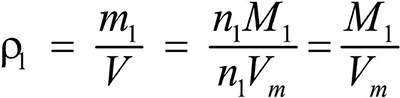
газ 2: 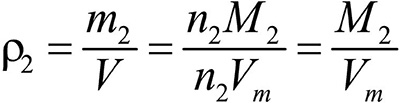
Разделив плотность первого газа на плотность второго, получим: 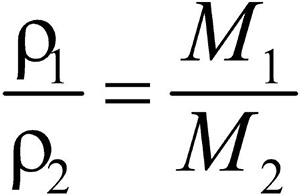
Отношение плотностей газов, равное отношению молярных масс, называется относительной плотностью одного газа по другому (D). D — величина безразмерная.
Зная D и молярную массу одного газа, легко найти молярную массу другого газа:
Пример 1. Относительная плотность газа по водороду равна 8. Определите молярную массу газа.
М(Х) = М(Н2) ∙ D = 2 ∙ 8 = 16 г/моль.
Газ с такой молярной массой — метан СH4.
Пример 2. Относительная плотность некоторого газообразного углеводорода по воздуху равна 2. Определите молярную массу углеводорода.
Средняя молярная масса воздуха равна 29 г/моль;
М(Х) = М(возд.) ∙ D = 29 ∙ 2 = 58 г/моль.
Углеводород с такой молярной массой — бутан С4Н10.
Следует отметить, что газы с молярной массой меньше 29 легче воздуха, больше 29 — тяжелее.
В расчётных задачах могут быть даны относительные плотности неизвестного газа по азоту, кислороду и другим газам. В этом случае для нахождения молярной массы неизвестного газа необходимо умножить относительную плотность на молярную массу соответственно азота (28 г/моль), кислорода (32 г/моль) и т. д.
Закон Авогадро широко применяется в химических расчётах. Поскольку для газов объёмы пропорциональны количествам (моль) веществ, то коэффициенты в уравнении реакции между газообразными веществами, отражающие количественное соотношение реагирующих веществ, пропорциональны объёмам взаимодействующих газов. Очевидно, что объёмы должны быть измерены при одинаковых условиях.
Пример 3. Какой объём кислорода потребуется для сжигания 2 дм3 пропана? Объёмы измерены при н. у.
Уравнение реакции горения пропана:
С3Н8 + 5О2 3СО2 + 4Н2О
Из закона Авогадро следует, что равные объёмы различных газов содержат одинаковое количество (моль) веществ. Пусть объём пропана равен 1 дм3. Тогда, согласно приведённому уравнению, для сжигания 1 дм3 пропана потребуется 5 дм3 кислорода. Следовательно, для сжигания 2 дм3 пропана потребуется:
1 дм3 С3Н8 — 5 дм3 O2,
2 дм3 С3Н8 — 10 дм3 О2
Ответ: V(О2) = 10 дм3.
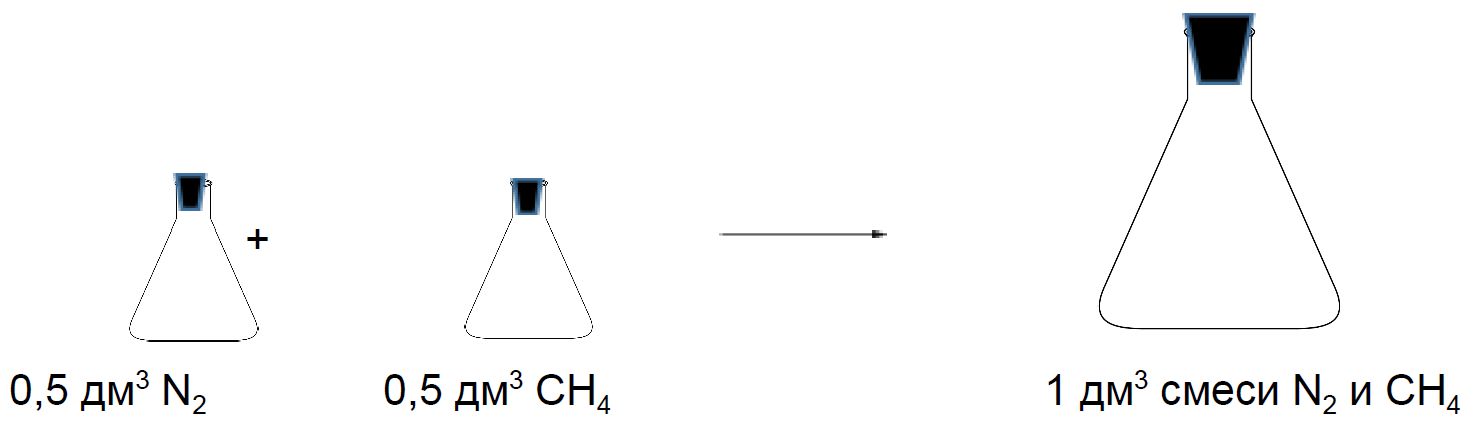
Смеси газов
Рассмотрим две колбы объёмом 0,5 дм3. Одна колба заполнена азотом, а другая метаном. Давление и температура в колбах одинаковые. Если смешать содержимое этих колб, то полученная смесь займёт при таких же условиях объём 1 дм3.
Состав смеси газов часто выражают в объёмных долях. Объёмная доля газа обозначается греческой буквой φ (фи) и равна отношению объёма данного газа к объёму смеси. Рассчитаем объёмную долю азота в полученной выше смеси газов:
φ = = 0,5, или 50 %.
Пример 4. В результате пропускания 150 дм3 (н. у.) воздуха через избыток известковой воды выпало 0,201 г осадка. Найдите объёмную долю (%) углекислого газа в данном образце воздуха.
Уравнение реакции взаимодействия углекислого газа с известковой водой:
СО2 + Са(ОН)2 = СаСО3 + Н2О
Найдём количество (моль) карбоната кальция, выпавшего в осадок (M(CaCO3) = 100 г/моль):
n(СаСО3) = 0,201/100 = 0,00201 моль.
По уравнению реакции:
n(СаСО3) = n(СО2).
Рассчитаем объёмную долю углекислого газа в воздухе:
V(CO2) = 0,00201 ∙ 22,4 = 0,045 дм3;
φ(СО2) = 0,045/150 = 0,0003, или 0,03 %.
Ответ: φ(СО2) = 0,03 %.
Пример 5. Объём смеси водорода с хлором составляет 50 см3. После взаимодействия газов осталось 10 см3 хлора. Найдите состав исходной смеси в объёмных долях. Все объёмы измерены при н. у.
Уравнение реакции взаимодействия водорода с хлором:
H2 + Cl2 2HCl
Поскольку после взаимодействия осталось 10 см3 хлора, то 40 см3 исходной смеси прореагировало. Хлор и водород реагируют между собой в равных объёмных отношениях. Исходя из этих соображений, в реакцию вступили по 20 см3 хлора и водорода. Поскольку осталось 10 см3 хлора, то в первоначальной смеси было 20 см3 водорода и 30 см3 хлора.
Рассчитаем объёмные доли газов в исходной смеси:
φ(H2) = 20/50 = 0,4, или 40 %;
φ(Cl2) = 30/50 = 0,6, или 60 %.
Ответ: φ(H2) = 40 %; φ(Cl2) = 60 %.
Согласно закону Авогадро, в равных объёмах различных газов при одинаковых условиях содержится одинаковое количество молекул.
Один моль любого газа при нормальных условиях (температура таяния льда, атмосферное давление) занимает объём
22,4 дм3. Эта величина называется молярным объёмом газа (Vm).
Плотности газов, измеренные при одинаковых условиях, относятся между собой как их молярные массы. Это отношение называется относительной плотностью одного газа по другому газу.
Газы, имеющие молярную массу более 29 г/моль, тяжелее воздуха, а менее 29 г/моль — легче воздуха.
Объёмная доля газа в смеси равна отношению объёма данного газа к общему объёму смеси.