Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
|
Рис. 6.1. |
Рис. 6.2. |
Рис. 6.3 |
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
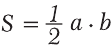
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R2, (6.4) .
Значение числа 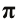
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
|
Рис. 6.4. |
Рис. 6.5. |
|
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR2 · h (6.7)
Объем шара (рис. 6.6)
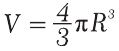
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
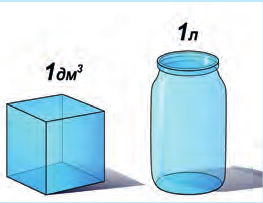
Куб с ребром 1 м имеет объем 1 м3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см3. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
Рис. 6.7. Один литр – это 1дм3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м3 = 1 000 л | 1 м3 = 1 000 000 см3 |
| 1 л = 1 дм3 | 1 л = 1000 см3 |
| 1 дм3 = 1 000 см3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
- Заказать решение задач по физике
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.
Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см3)
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R2.
- Объем шара равен
.
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
- Точность измерений и погрешности
2 h}
Тип конуса
прямойусеченный
Найти объем через
высоту и радиусвысоту и площадь основания
Высота (h)
ммсмдммкмдюймы (in)футы (ft)
Радиус (R)
ммсмдммкмдюймы (in)футы (ft)
Результат в
кубические миллиметры (мм³)кубические сантиметры (см³)кубические дециметры (дм³)кубические метры (м³)кубические километры (км³)микролитры (мкл)миллилитры (мл)сентилитры (cl)децилитры (dl)декалитрылитры (л)столовая ложка (15мл)десертная ложка (10мл)чайная ложка (5мл)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Конус — это трехмерная фигура, в основании которой лежит круг. Чтобы найти объем конуса достаточно знать два параметра — высоту (h) и радиус основания (r).
2
Чтобы вычислить периметр квадрата, умножьте длину одной из его сторон на 4. Следующая формула вычисляет периметр квадрата, сторона которого находится в ячейке с именем сторона:
=сторона*4
Площадь и периметр прямоугольника
Площадь прямоугольника рассчитывается путем умножения его высоты на основание. Следующая формула возвращает площадь прямоугольника, используя ячейки с именами высота и основание:
=высота*основание
Периметр прямоугольника можно вычислить путем сложения его удвоенной высоты и удвоенного основания. Следующая формула возвращает площадь прямоугольника, используя ячейки с именами высота и основание:
=(высота*2)+(основание*2)
Площадь круга и длина окружности
Площадь круга рассчитывается как произведение квадрата радиуса на величину π. Следующая формула возвращает площадь круга. Ячейка с именем
радиус содержит радиус окружности. 2)
2)
Радиус окружности равен половине ее диаметра.
Чтобы вычислить длину окружности, необходимо умножить диаметр окружности на величину π. Следующая формула рассчитывает длину окружности, используя ячейку с именем диаметр.
=диаметр*ПИ()
Диаметр окружности равен радиусу окружности, умноженному на 2.
Площадь трапеции
Для вычисления площади трапеции необходимо сложить две параллельные стороны, умножить их сумму на высоту и разделить на 2. Следующая формула вычисляет площадь трапеции, используя ячейки с именами сторона1, сторона2 и высота:
=((сторона1+сторона2)*высота)/2
Площадь треугольника
Площадь треугольника представляет собой сумму основания и высоты треугольника, деленную на два. Следующая формула рассчитывает площадь треугольника, используя ячейки с именами
основание и высота:
=(основание*высота)/2
Площадь поверхности и объем шара
Чтобы вычислить площадь поверхности шара, нужно умножить квадрат радиуса на число π, а затем полученное произведение умножить на 4. 2)*высота)
2)*высота)
Объем пирамиды
Чтобы вычислить объем пирамиды, необходимо определить площадь ее основания, а затем умножить ее на высоту и разделить на 3. Представленная ниже формула вычисляет объем пирамиды, используя для расчетов ячейки с именами ширина (ширина основания), длина (длина основания) и высота (высота пирамиды).
=(ширина*длина*высота)/3
В начало
Полезное
Автор СергейОпубликовано 25.02.201725.02.2017Рубрики Использование функций в формулах
Как рассчитать площадь поверхности по объему
••• Bychykhin_Olexandr/iStock/GettyImages
Обновлено 13 марта 2018 г. , цилиндры, прямоугольные призмы или конусы. Для задач такого типа важно знать формулы как для площади поверхности, так и для объема этих фигур. Это также помогает понять, каковы определения площади поверхности и объема. Площадь поверхности — это общая площадь всех открытых поверхностей данной трехмерной фигуры или объекта. Объем — это количество места, занимаемое этой фигурой. Вы можете легко рассчитать площадь поверхности по объему, применяя правильные формулы. 92) = 4?(1,50X1,50) равно 9? квадратных футов
Площадь поверхности — это общая площадь всех открытых поверхностей данной трехмерной фигуры или объекта. Объем — это количество места, занимаемое этой фигурой. Вы можете легко рассчитать площадь поверхности по объему, применяя правильные формулы. 92) = 4?(1,50X1,50) равно 9? квадратных футов
Подставляя значение pi= ?= 3,14 в ответ 9? квадратных футов, вы обнаружите, что площадь поверхности составляет 28,26 квадратных футов. Чтобы решить эти типы задач, вам нужно знать формулы как для площади поверхности, так и для объема.
-
Калькулятор T1-83 Plus использовался для нахождения кубического корня в шаге 6. Используя этот калькулятор, чтобы найти решение, вы должны сначала нажать функциональную клавишу «MATH», а затем найти функциональную клавишу для кубических корней. Поскольку могут быть различия в использовании других моделей калькуляторов, ознакомьтесь с инструкциями по вычислению кубических корней в руководствах пользователя.
Связанные статьи
Ссылки
- Math.
 com
com - MATH3.org
- Алгебра Лаборатория
Советы
- А. этот калькулятор, чтобы найти решение, вы должны сначала нажать функциональную клавишу «MATH», а затем найти функциональную клавишу для кубических корней. Поскольку могут быть различия в использовании других моделей калькуляторов, ознакомьтесь с инструкциями по вычислению кубических корней в руководствах пользователя.
Длина, площадь и объем | геометрия
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- В этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и многое другое. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
Дано:
V (кубический метр) — объем некоторого бассейна;
h (метр) — глубина этого бассейна.
Требуется определить s (квадратный метр) — площадь дна бассейна.
Так как в условии задачи не указано, считаем, что бассейн имеет геометрическую форму прямоугольного параллелепипеда. Тогда, чтобы определить площадь дна бассейна, необходимо воспользоваться следующей формулой:
V = s * h, отсюда находим, что:
s = V / h.
Ответ: зная объем и глубину бассейна, его площадь можно определить по формуле s = V / h.
In geometry, students must often calculate surface areas and volumes of different geometric shapes such as spheres, cylinders, rectangular prisms or cones. For these types of problems, it is important to know the formulas for both surface area and volume of these figures. It also helps to understand what the definitions of surface area and volume are. Surface area is the total area of all exposed surfaces of a given three-dimensional figure or object. Volume is the amount of space occupied by this figure. You can easily calculate surface area from volume by applying the right formulas.
-
A T1-83 Plus calculator was used to find the cubic root in Step 6. Using this calculator to find a solution, you must press the “MATH” function key first and then find the function key for cubic roots. Since there may be differences in the use of other calculator models, check the user manuals for instructions on calculating cubic roots.
Solve surface area problem of any geometric figure when given its volume by knowing the formulas. For instance, the formula for surface area of a sphere is given by SA= 4?(r^2), while its volume (V) is equal to (4/3)?(r^3) where «r» is the radius of the sphere. Note that most formulas for surface area and volume for various figures are available online (see the Resources).
Use the formulas in Step 1 to calculate the surface area for a sphere with a volume of 4.5? cubic feet where ? (pi) is approximately 3.14.
Find the radius of the sphere by substituting 4.5? ft^3 for V in the formula in Step 1 to get: V=4.5? cubic feet.= (4/3)?(r^3)
Multiply each side of the equation by 3 and the equation becomes: 13.5 ? cubic feet =4?(r^3)
Divide both sides of the equation by 4? in Step 4 to solve for the radius of the sphere. To get: (13.5? cubic feet)/(4?) =(4? )(r^3)/ (4?), which then becomes: 3.38 cubic feet= (r^3)
Use the calculator to find the cubic root of 3.38 and subsequently the value of the radius “r” in feet. Find the function key designated for cubic roots, press this key and then enter the value 3.38. You find that the radius is 1.50 ft. You can also use an online calculator for this calculation (see the Resources).
Substitute 1.50 ft. in the formula for SA= 4?(r^2) found in Step 1. To find: SA = 4?(1.50^2) = 4?(1.50X1.50) is equal to 9? square ft.
Substituting the value for pi= ?= 3.14 in the answer 9? square ft., you find that the surface area is 28.26 square ft. To solve these types of problems, you need to know the formulas for both surface area and volume.
Tips
Найди верный ответ на вопрос ✅ «Как найти площадь, если известен объём и плотность материала? …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы

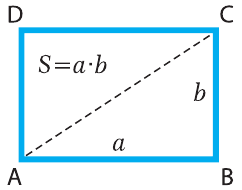
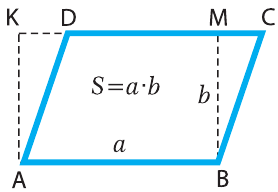
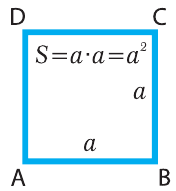
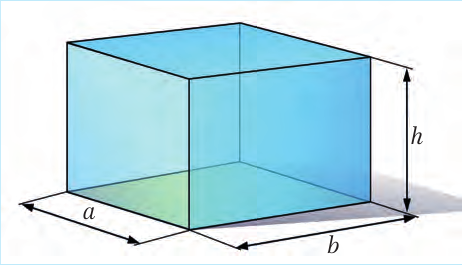
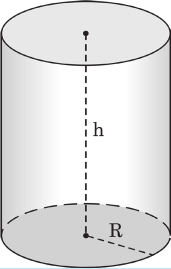
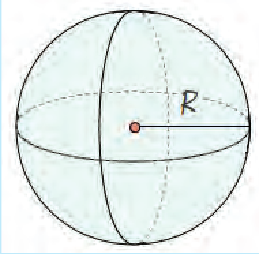 Рис. 6.6.
Рис. 6.6.