Как найти площадь сферы 6 класс - Autoru.top - решение различных проблем

Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.

Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?

Важно!

Шар — это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.

Примеры шара в жизни: арбуз и стальной шарик.

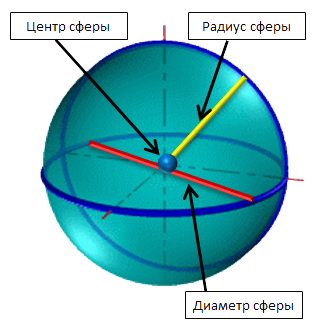
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.

Важно!

Сфера — поверхность шара. У сферы можно найти площадь поверхности.

Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.

Как найти площадь сферы

Запомните!

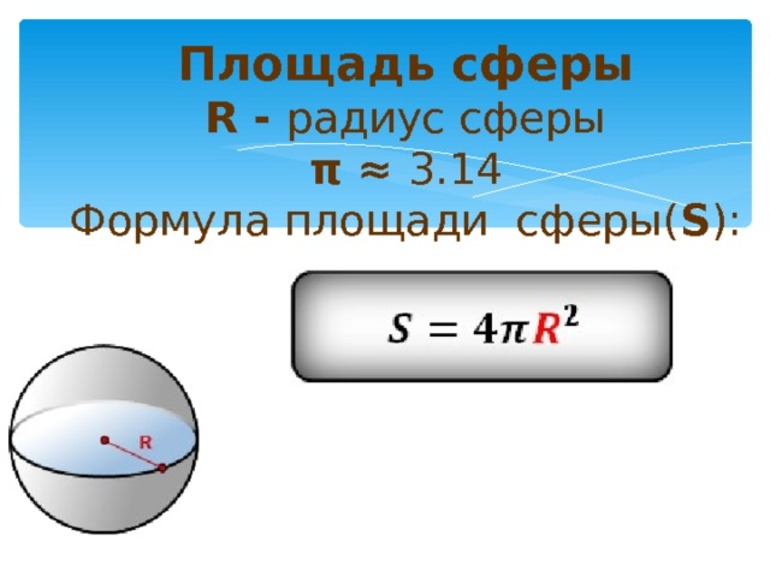
Формула площади сферы:
S = 4πR²

Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.

S = 4π R² =
4πR · R;

Закрепим полученные знания и решим задачу на площадь сферы.

Зубарева 6 класс. Номер 692(а)

Условие задачи:

Вычислите площадь сферы, если её радиус равен
1 м. (возьмите π как
3)

Вспомнив, как выделить целую часть
и перемножить дроби,
воспользуемся формулой площади сферы:

S = 4 · πR² =
4 · 3 ·

(1 ) ² =

4 · ·

() ² =

4 · ·

= =

=
45
м²

Как найти объем шара

Запомните!

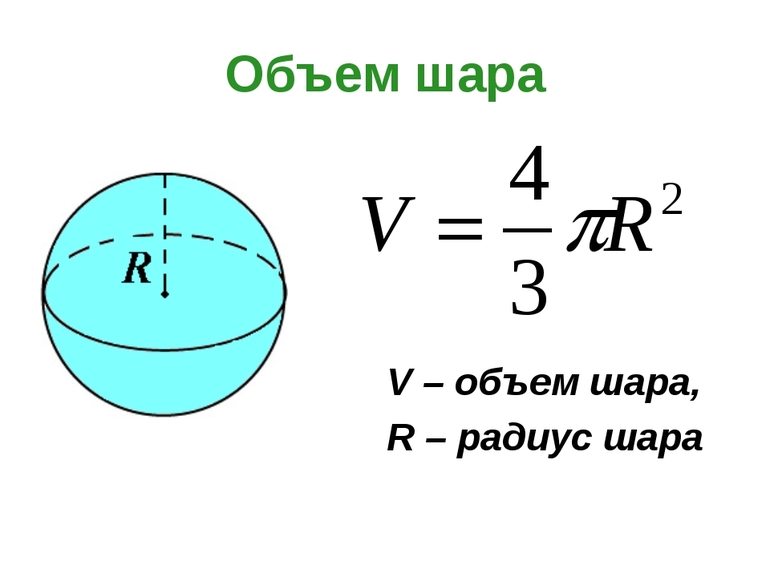
Формула объема шара:
V = πR³

Зная определение степени,
можно записать формулу объема шара следующим образом.

V =
π R³ =

π R · R · R;

Для отработки полученных знаний решим задачу на объем шара.

Зубарева 6 класс. Номер 691(а)

Условие задачи:

Вычислите радиус шара, если его объем равен
4 м³ (возьмите π как
3)

Выразим из формулы объема шара радиус.

V =
π R³
π R³
= V
π R³

=
R³

=

Подставим в формулу известные нам значения. Число π
возьмем как задано в задании «3».

R³

= (3 ·

4) /

(4 · 3)

Чтобы не запутаться, отдельно рассчитаем
числитель дроби.

3 ·
4 =

3 ·
=

Теперь снова подставим полученное значение в нашу формулу:

R³

=
/ (4 · 3)

=

/ (4 · )

=

/ () =

=

· () =

= =

=

= 1
R³ = 1
R = 1 м

Важно!

Уважаемые родители!

При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.

В 6 классе при решении такой задачи используйте метод перебора.

Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

14 февраля 2019 в 22:59

Руслан Магомедов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Руслан Магомедов
Профиль
Благодарили: 0

Сообщений: 1

Рассчитайте объем чашки высотой 7 см с диаметром 6,5 с

0
Спасибо thanks
Ответить

Источник

Рис. (1). Футбольный мяч

Шар — это геометрическое тело.

Предметы, имеющие форму шара, окружают нас очень часто.

Форму шара имеет мяч (футбольный, теннисный, баскетбольный).

Представление о шаре дают арбуз, апельсин, горошина.

Шарообразна и наша планета Земля.

Шар характеризует длина радиуса и диаметра.

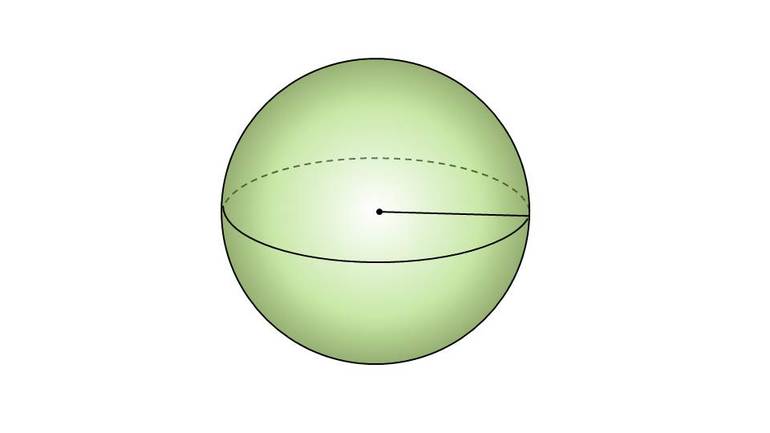
Рис. (2). Шар

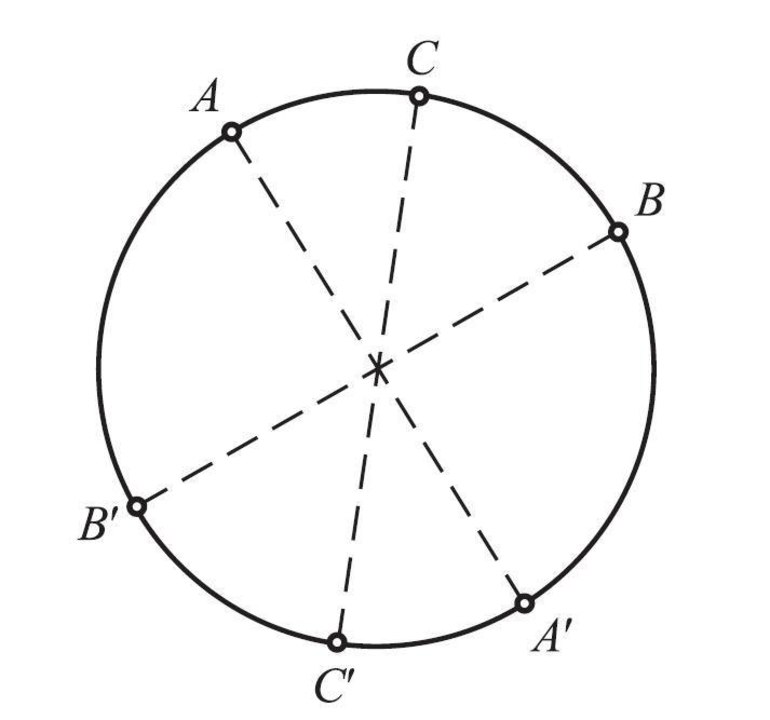
Перед нами изображение шара с центром в точке (O). Все точки поверхности шара находятся на одинаковом расстоянии от его центра.

Это означает, что если мы выберем на поверхности три любые точки, например, точку (A), точку (B) и точку (C), соединим их с центром шара, то полученные отрезки будут равны ((OA = OB = OC)).

Такие отрезки называют радиусами.

(OA) — радиус шара, (OB) — радиус шара и (OC) — также радиус шара.

Так как центр шара можно соединить с бесконечно многими точками на поверхности шара, то можно провести бесконечно много радиусов.

Радиус шара — это отрезок, который соединяет точку поверхности шара и его центр.

На чертеже отрезок (AB) соединяет две точки поверхности шара и проходит через его центр.

Отрезок (AB) — это диаметр шара. Заметим, что отрезок (AB) состоит из двух отрезков (OA) и (OB).

Эти отрезки являются радиусами шара.

Поэтому диаметр шара в два раза больше его радиуса.

Диаметром шара называется отрезок, соединяющий две точки поверхности шара и проходящий через его центр.

Есть название и для поверхности шара. Её называют сферой.

Для шара можно вычислить объём по формуле:

Для сферы можно вычислить поверхность по формуле:

Источники:

Рис. 1. Футбольный мяч. Указание авторства не требуется, 2021.06.03, бесплатно для коммерческого использования,, https://pixabay.com/images/id-157930/
Рис. 2. Шар. © Якласс

Источник

Площадь сферы. Объём шара.
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас слышал про эту знаменитую спортивную игру. Всем известно, что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть людей скажут, что форму шара, а часть, что формы сферы. Так кто же из них прав? И в чем разница между сферой и шаром?

Шар — это пространственное тело. Внутри шар чем-либо заполнен. Поэтому у шара можно найти объем.

Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.

Сфера — поверхность шара. У сферы можно найти площадь поверхности.

Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный теннис.

Как найти площадь сферы

Формула площади сферы: S = 4πR²

Для того, чтобы найти площадь сферы, необходимо вспомнить, что такое степень числа. Зная определение степени, можно записать формулу площади сферы следующим образом.
S = 4π R² = 4π R • R;

Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
• Вычислите площадь сферы, если её радиус равен 3 м

Воспользуемся формулой площади сферы:
S = 4 • πR² = 4 • 3,14 • 3 • 3=113,04 м²

Как найти объем шара
Формула объема шара: V = 4

πR³
3

Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)

Условие задачи:
• Вычислите радиус шара, если его объем равен 4 м³
Выразим из формулы объема шара радиус.

• R³ = 3V
4 π
Подставим в формулу известные нам значения. Число «Пи» возьмем как 3,14.

3 • 4 =1
4 • 3, 14
Теперь снова подставим полученное значение в нашу формулу:
• R³ = 1
• R = 1 см

Уважаемые родители!

При окончательном расчете радиуса не надо заставлять ребенка считать кубический корень. Учащиеся 6-го класса еще не проходили и не знают определение корней в математике.

В 6 классе при решении такой задачи используйте метод перебора.

Спросите ученика, какое число, если его умножить 3 раза на самого себя даст единицу.

Источник

Важные измерения

Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.

Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:

S = 4 * 3,14 * 10²;
S мяча равна ≈ 1256 см².

Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.

Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.

Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).

Терминология и сферическая геометрия

Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).

Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).

Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.

Одиннадцать свойств

В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:

Точки на сфере находятся на одинаковом расстоянии от одной фиксированной, называемой центром. Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
Контуры и плоские участки сферы являются кругами. Это однозначное свойство, которое определяет шар.
Сфера имеет постоянную ширину и обхват. Ширина поверхности — это расстояние между парами параллельных касательных плоскостей. Множество других замкнутых выпуклых поверхностей имеют постоянную ширину, например, тело Мейснера. Обхват поверхности — это окружность границы её ортогональной проекции на плоскость. Каждое из этих свойств подразумевает другое.
Все точки сферы омбилические. В любой точке поверхности вектор нормали расположен под прямым углом к ней, поскольку шар — это линии, выходящие из его центра. Пересечение плоскости, которая содержит нормаль с поверхностью, сформирует кривую — нормальное сечение. Любая замкнутая поверхность будет иметь как минимум четыре точки, называемых омбилическими. Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
У шара нет центра поверхности. Например, два центра, соответствующие минимальной и максимальной секционной кривизне, называются фокальными точками, а совокупность всех таких точек образует одноимённую поверхность. И только у шара она преобразуется в единую точку.
Все геодезические сферы являются замкнутыми кривыми. Для этой фигуры они большие круги. Многие другие поверхности разделяют это свойство.
Имеет наименьшую площадь при наибольшем объёме. Это определяет шар однозначно. Например, мыльный пузырь: его окружает фиксированный объём, поверхностное натяжение минимизирует площадь его поверхности для такого объёма. Конечно, пузырь не будет идеальным шаром, поскольку внешние силы, такие как гравитация, будут искажать его форму.
Сфера — единственная вложенная поверхность, у которой нет границы или сингулярностей с постоянной положительной средней кривизной.
Сфера имеет наименьшую общую среднюю кривизну среди всех выпуклых тел с заданной площадью поверхности.
Шар имеет постоянную гауссову кривизну. Это внутреннее свойство, которое определяется путём измерения длины и углов и не зависит от того, как поверхность встроена в пространство.

Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.

Так называлась работа, опубликованная античным математиком Архимедом. Она вышла в двух томах в 225 году до н. э. Он был первым, кто сделал полный и подробный трактат по основам вычисления площади поверхности сферы, объёма шара и аналогичных значений для таких элементов, как цилиндр. Результатами его деятельности пользуются до сих пор.

Архимед особенно гордился формулой объёма шара, где он доказал, что эта величина составляет две трети объёма описанного цилиндра. Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.

Аргумент, который Архимед использовал для доказательства формулы V шара, был довольно сложным и сильно вовлечён в его геометрию. Поэтому во многих современных учебниках используется упрощённая версия, основанная на концепции предела, которого, конечно, не было в античные времена. Великий математик создавал в сфере усечённый конус путём построения и вращения геометрических фигур, и только после этого он определил объём.

Сейчас кажется, что он специально выбирал такие оригинальные методы. Однако это был всего лишь лучший из тех, которые были ему доступны в греческой математике. Его основные работы были вновь открыты в XX веке. Например, Метод механических теорем, как он назывался в трактате автора.

Источник

Download Article

The surface area of a sphere is the number of square units (cm², square inches, square feet — whatever your measurement) that are covering the outside of a spherical object.^[1] Discovered by the Greek philosopher and mathematician Aristotle thousands of years ago, the equation is relatively simple, even if its origins are not. To find the surface area of a sphere, use the formula (4πr²), where r = the radius of the circle.

1
Know the parts of the equation, Surface Area = 4πr². This nearly ancient formula is still the easiest way to determine the surface area of a sphere.^[2] Using almost any calculator, you can plug in the radius to get the surface area of your sphere.
- r, or «radius: The radius is the distance from the center of the sphere to the edge of that sphere.
- π, or «pi:» This incredible number (equalling roughly 3.14) represents the ratio between a circle’s circumference and diameter, and is useful in all equations with circles and spheres. It is commonly shortened as π = 3.1416, but there are an infinite number of decimals.^[3]
- 4: For somewhat complex reasons, the surface area of a sphere is always 4 times as large as the area of a circle with the same radius.
2
Find the radius of the sphere. Sometimes your problem will supply you the radius, and other times you will have to find it yourself. If you are given the diameter of a circle, simply divide the diameter by 2 to get the radius.^[4] For example, a sphere of diameter 10 inches has a radius of 5 inches.
- Advanced Tip:If you only know the volume of a sphere, you need to do a little more work to get the radius. Divide the volume by 4π, then multiply that answer by 3. Finally, take the cube root of this answer.^[5]
Advertisement
3

Square the radius by multiplying it by itself. You can either do this by manually multiplying (5² = 5 * 5 = 25) or by using your calculator’s «square» function (sometimes labeled as «x²«).^[6]
4
Multiply this result by 4. While you can multiply either 4 or pi first, it is generally easier to start with 4 since there are no decimals to multiply yet.^[7]
- If our radius is 5, like above, you would be left with 4 * 25 * π, or 100π.
5
Multiply the results by pi (π). If your problem says «exact value», write the symbol π after your number and call it done. Otherwise, use the approximation π=3.14 or your calculator’s π button.^[8]
- 100 * π = 100 * 3.14
- 100π = 314
6
Remember to add you units to the final answer. Is your sphere’s surface area 314 inches big, or 314 miles (505 km) big? The units need to be written as «units²,» because this denotes area, otherwise known as «square units».^[9]
- The full answer to the sphere in the pictures is: Surface Area = 314 units².
- The units you use are always the same ones used to measure the radius. If the radius is in meters, the answer will be in meters.
- Advanced Tip: We square the units because area measures how many flat squares we could fit on the surface of the sphere. Say we measure the practice problem in inches. This means on a sphere where r=5, we could fit 314 squares on the surface of the sphere if the sides of every square are 1 inch long.
7
Practice with an example. If the radius of a sphere is 7 centimeters, what is the surface area of that sphere?
- 4πr²
- r = 7
- 4 * π * 7²
- 49 * 4 * π
- 196π
- Answer: Surface Area = 615.75 centimeters², or 615.75 square centimeters.
8
Understand surface area. The surface area of a sphere is the area covering the outside of the sphere — think of it as the rubber covering a kickball or the surface of the earth. Because it is curved, it is much harder to measure the surface area of a sphere than a box, so we need an equation to determine the area.^[10]
- Rotating a circle around its axis (the center point) will produce a sphere. Think of spinning a coin on the table and how it appears to form a sphere. While it won’t be explained here, this is where our equation comes from.
- Advanced Tip: Spheres have a smaller surface area per volume than any other shape — that means it can hold more things in a smaller area than any other shape.

Add New Question

Question

How do I find the volume of a sphere?

Volume = (4/3) π r³.
Question

What is the circumference of a sphere?

Pi multiplied by the diameter.
Question

How do I find the area of half a sphere?

Divide total area by 2.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

If your radius includes a square root, like 3 √ 5, remember to square coefficient squares and the radical. (3 √ 5)² becomes 9×5 which gives 45.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To find the surface area of a sphere, use the equation 4πr2, where r stands for the radius, which you will multiply by itself to square it. Then, multiply the squared radius by 4. For example, if the radius is 5, it would be 25 times 4, which equals 100. If the problem calls for an exact answer, then leave the answer as 100π. If the answer doesn’t need to be exact, multiply by 3.14 to get the surface area. Be sure to label your answer as the appropriate units squared. If you want to learn how to find the radius of a sphere, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 330,673 times.

Did this article help you?

Источник

Как найти площадь сферы

Зубарева 6 класс. Номер 692(а)

Как найти объем шара

Зубарева 6 класс. Номер 691(а)

Ваши комментарии

Важные измерения

Терминология и сферическая геометрия

Одиннадцать свойств

Video

References

About This Article

Did this article help you?

Не пропустите также: