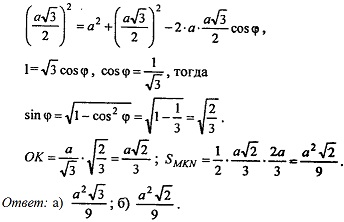я могу помочь с этим заданием
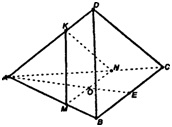
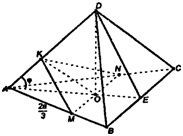
а) Пусть т. О — центр грани АВС. Построим МК || DB, MN || ВС. пл .MKN — искомое сечение.
Пусть ребро тетраэдра равно а. Тогда
Т.к. ΔADB — равносторонний, а КМ || DB, то ΔАМК — также равносторонний, АМ=КМ=
(углы с соответственно параллельными и одинаково направленными сторонами):
б) Построим отрезок в пл. ADO. Т.к. пл.
то
Т.к. и
то
Значит, ΔKMN — искомое сечение,
ΔAMN — равносторонний, MN = AM =
Из ΔADE по теореме косинусов имеем:
DE2 = AD2 + АЕ2 — 2 ∙ AD ∙ АЕ ∙ cos φ,
Найдите площадь и периметр сечения, параллельного плоскости основания тетраэдра, ребро которого равно 10см.
На этой странице находится вопрос Найдите площадь и периметр сечения, параллельного плоскости основания тетраэдра, ребро которого равно 10см?, относящийся к категории
Математика. По уровню сложности данный вопрос соответствует знаниям
учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Математика. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
Зря вы готовый ответ показали. 
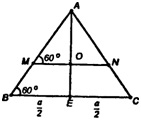
На рисунке справа показана ситуация для грани ABC. Но ситуация, из соображений симметрии, аналогична для граней ADB и ADC. Уже на показанном на рисунке треугольнике ABC видно, что из-за параллельности стороны искомого треугольника и стороны CB тетраэдра, если не ошибаюсь, по теореме Фалеса, этот отрезок (красный на рисунке) пересекает AB точно посередине, т.е. AT=TB.
Пусть со стороной AC он пересекается в точке H, при этом AH=HC по условию. Из подобия треугольников ABC и ATH (по общему углу при вершине A и двум прилежащим пропорциональным сторонам) следует, что BC/TH=AB/AT, т.е. a/TH=2 => TH=a/2.
Как уже был сказано, то же выполняется аналогичным образом и для двух других граней тетраэдра, так что красно-жёлтый треугольник (со стороной TH) — равносторонний. Проведём в нём высоту h. Она будет медианой, и будет разбивать красно-жёлтый треугольник на два прямоугольных (с катетами h и ТН/2=a/4, а гипотенузой равной TH=a/2). По теореме Пифагора h^2 = (a/2)^2-(a/4)^2 => h = a*sqrt(1/4-1/16) = a*sqrt(3)/4.
По высоте h и стороне a/2 уже можно посчитать площадь как S = h*(a/2)/2 = (a^2)*sqrt(3)/16. Что и требовалось.