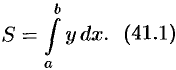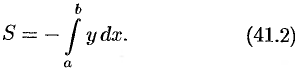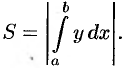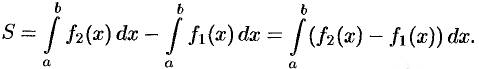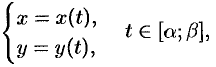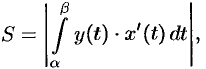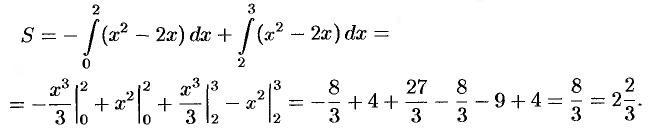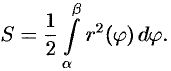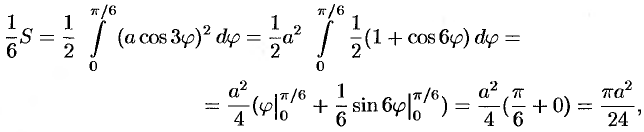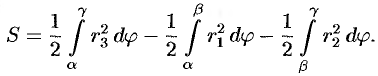Ответ: 8π
Пошаговое объяснение: r=4sin (3ф) это уравнение 3-х лепестковой розы в полярной системе координат.
Максимальное значение r=4, min r=0.
Период функции Sin (3ф)= 2π/3 Разделим на3 равные части лучами [0; 2π] в полярной системе координат, выполним рисунок (прилагается). Найдём площадь S₁ половины лепестка розы, а затем умножим на 6. Пределы интегрирования от 0 до π/6 ( у знака интеграла плохо видно)
S₁= 1/2·∫₀ⁿ⁾⁶(4sin(3ф))²dф= 1/2·∫₀ⁿ⁾⁶ 16sin²(3ф)dф=8·∫₀ⁿ⁾⁶sin²(3ф)dф=
4·∫₀ⁿ⁾⁶(1-сos(6ф)dф= 4·∫₀ⁿ⁾⁶dф — 4/6 ·∫₀ⁿ⁾⁶сos(6ф)d(6ф)=
=(4ф-sin(6ф))|₀ⁿ⁽⁶=2π/3 — sin(π)-0+0=2π/3
Значит S=6·S₁=6·(2π/3)=8π
Приложения:
1. Вставьте и объясните окончание прилагательных: ранн ___ (какое?) утро, певчие птицы, пахучие ( ?) масло, рычащ_____ ( ?) львица, в погожие ( ?) деньки, дальн__ ( ?)дорога, на син_____ ( ?) птицу, бескрайнее ( ?) поле, на последн______ ( ?) электричку, ранн______ ( ?) пташка, могуч______ ( ?) богатырь, мешающ______ся ( ?) стол, с сыпуч______ ( ?) крупой, к робк _____ ( ?) человеку, по виноградн______( ?) кусту, через ветвист______ ( ?) дерево.
2. Объяснить окончание существительных: по ботаникЕ (1 скл, по земле или Д.п.), о волнениИ ( на –ИЕ).
в сопротивлени__ ( ) на верхушк__ ( )
к лодк__ ( ) на территори__ ( )
при молчани__ ( ) у тропинк__ ( )
по чашк __ ( ) по тропинк ___ ( )
без матер___ ( ) на лекци__ ( )
в колокольчик__ ( ) на кочк__ ( )
Вычисление площадей плоских фигур
Прямоугольные координаты
Как уже было установлено (см. «геометрический смысл определенного интеграла»), площадь криволинейной трапеции, расположенной «выше» оси абсцисс (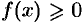
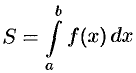
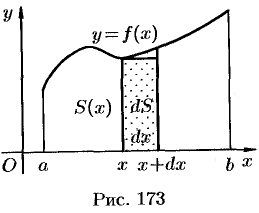
), равна соответствующему определенному интегралу:
или 
Формула (41.1) получена путем применения схемы I — метода сумм. Обоснуем формулу (41.1), используя схему II. Пусть криволинейная трапеция ограничена линиями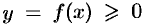 
, 
, 
, 
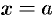
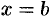
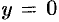
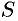
(см. рис. 173). Для нахождения площади 
этой трапеции проделаем следующие операции:
1. Возьмем произвольное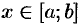 
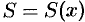
и будем считать, что 
.
2. Дадим аргументу 
приращение 
. Функция получит приращение 
, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).
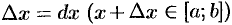
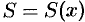
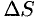
Дифференциал площади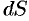 
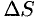
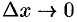
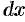
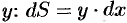
есть главная часть приращения при 
, и, очевидно, он равен площади прямоугольника с основанием 
и высотой 
.
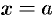
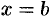
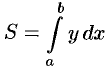
3. Интегрируя полученное равенство в пределах от до , получаем 
.
Отметим, что если криволинейная трапеция расположена «ниже» оси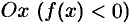 
, то ее площадь может быть найдена по формуле
Формулы (41.1) и (41.2) можно объединить в одну:
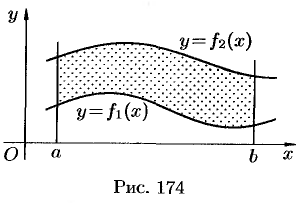
Площадь фигуры, ограниченной кривыми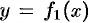 
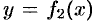
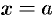
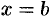
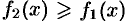
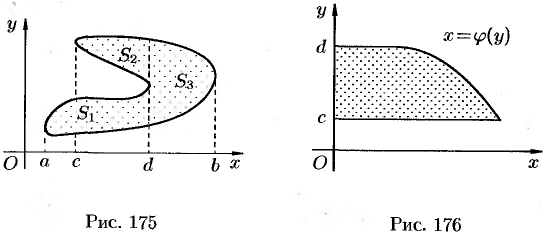
и 
, прямыми и (при условии 
) (см. рис. 174), можно найти по формуле
Если плоская фигура имеет «сложную» форму (см. рис. 175), то прямыми, параллельными оси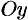 
, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.
Если криволинейная трапеция ограничена прямыми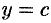 
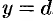
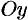
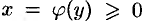
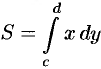
и 
, осью 
и непрерывной кривой 
(см. рис. 176), то ее площадь находится по формуле 
.
И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически
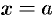
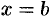
прямыми и и осью 
, то площадь ее находится по формуле
где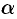 
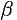
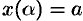
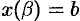
и 
определяются из равенств 
и 
.
Пример №41.1.
Найти площадь фигуры, ограниченной осью и графиком функции 
при 
.
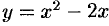
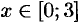
Решение:
Фигура имеет вид, изображенный на рисунке 177. Находим ее площадь :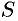
Дополнительный пример №41.2.
Полярные координаты
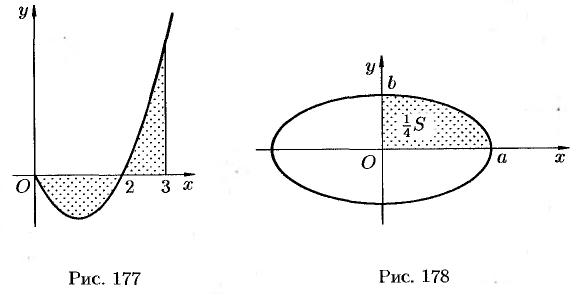
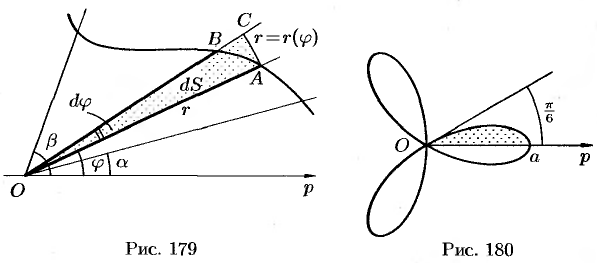
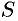
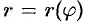
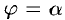
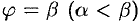
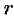
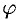
Найдем площадь криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией 
и двумя лучами 
и 
, где 
и 
— полярные координаты (см. рис. 179). Для решения задачи используем схему II — метод дифференциала.
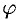
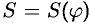
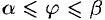
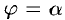
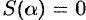
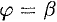
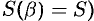
1. Будем считать часть искомой площади S как функцию угла , т. е. 
, где 
(если , то 
, если 
, то 
.
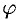
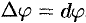
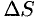
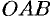
2. Если текущий полярный угол получит приращение 
, то приращение площади равно площади «элементарного криволинейного сектора» 
.
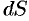
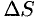
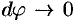
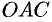
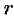
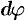
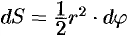
Дифференциал представляет собой главную часть приращения при 
и равен площади кругового сектора 
(на рисунке она заштрихована) радиуса с центральным углом 
. Поэтому 
.
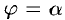
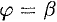
3. Интегрируя полученное равенство в пределах от до , получим искомую площадь
Пример №41.3.
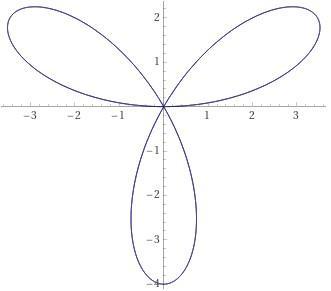
Найти площадь фигуры, ограниченной «трехлепестковой розой»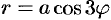 
(см. рис. 180).
Решение:
Найдем сначала площадь половины одного лепестка «розы», т. е.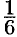 
часть всей площади фигуры:
т. е.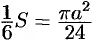 
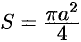
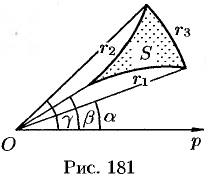
. Следовательно, 
.
Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке 181, имеем:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
