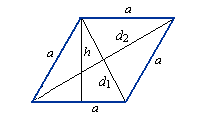
Ромб — это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор площади ромба
Если стороны ромба образуют прямой угол, то получим квадрат.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
aa — сторона;
hh — высота, опущенная на сторону aa.
Решим простой пример.
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.
Решение
a=5a=5
h=2h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)
Ответ: 10 см. кв.
Формула площади ромба через диагонали
Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.
S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2
d1,d2d_1, d_2 — диагонали ромба.
Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.
Решение
d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1
Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)
Ответ: 49 см. кв.
Формула площади ромба через две стороны и угол между ними
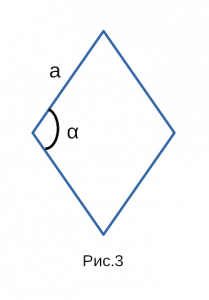
S=a2⋅sin(α)S=a^2cdotsin(alpha)
aa — сторона ромба;
αalpha — любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
a=10a=10
α=30∘alpha=30^{circ}
По формуле получаем:
S=a2⋅sin(α)=100⋅sin(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба по радиусу вписанной окружности и углу
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.
Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности — 4 (см.).
Решение
r=4r=4
α=60∘alpha=60^{circ}
S=4⋅r2sin(α)=4⋅16sin(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)
Ответ: 73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S=2⋅a⋅rS=2cdot acdot r
aa —сторона ромба;
rr — радиус вписанной окружности в ромб.
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
a=5a=5
r=4r=4
S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)
Ответ: 40 см. кв.
Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!
Тест на тему “Площадь ромба”
Содержание:
- Формулы площади ромба:
- Формула периметра ромба:
Ромб — это четырёхугольник, у которого все стороны равны.
Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали
взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.
Формулы площади ромба:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади ромба выражается числом заключающихся в него квадратных единиц.
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
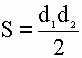
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула периметра ромба:
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
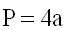
P — периметр ромба
a — длина стороны ромба
Остались вопросы?
Здесь вы найдете ответы.
Что понимается под высотой ромба?
Высота ромба представляет собой перпендикуляр, который опущен из одного из
его углов на сторону, противоположную данному углу.
Высота ромба, опущенная из одного его угла, делит противолежащую сторону
пополам. Как найти величины углов этого ромба?
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и
используя теорему, которая является обратной теореме о 30-градусном угле,
можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно
найти неизвестную величину третьего угла треугольника:
BAH=180-30-90=60 градусов.
Так, угол АВС равен:
ABC=180-60=120 градусов.
Как найти высоту ромба, если единственной величиной, которая известна,
является длина одной его стороны?
Известна формула площади (S) ромба, которая представляет собой
произведение длины его стороны (а) на высоту (h), проведенную к ней:
S = a*h.
Есть возможность выразить высоту из приведенной выше формулы. Она будет
равна отношению площади ромба к длине его стороны:
h = S/a.
Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?
Площадь (S) треугольника с прямым углом рассчитывается путем деления
пополам произведения длин его катетов. В данном случае она будет равна:
SΔ = 4*3/2 = 6 см.кв.
Площадь ромба определяется умножением длины его стороны на высоту,
проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба
равна площади прямоугольного треугольника (6 см.кв.), то:
S = 5*x = 6 см.кв.
Отсюда можно найти значение х:
х = 6/5 = 1,2 см.
Ответ: высота ромба составляет 1,2 см.
Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8
см.?
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:
с = √(9+16) = √25 = 5 см.
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное
пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба,
в которой длина его стороны (а) умножается на высоту(h):
S = a*h
Из данной формулы выражаем высоту:
h = S/a = 24/5 = 4,8 см.
Ответ: Высота ромба составляет 4,8 см.
Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина
стороны – а?
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) –
известные величинами. В этом случае для определения неизвестной высоты
следует пользоваться приведенной ниже формулой:
h = (d1 * d2)/a
Площадь ромба составляет 60 см.кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по
следующей формуле:
Р = а+а+а+а
В данном случае периметр ромба равен 48 см., это значит, что:
а+а+а+а = 48 см.
Находим значение а:
а = 48/4 = 12 см.
Площадь ромба (S) является произведением длины его стороны (а) и высоты
(h), проведенной к этой стороне:
S = а*h
В задании сказано, что площадь ромба – 60 см.кв. Значит:
а*h=60
Находим неизвестную высоту:
h=60/а=60/12=5 см.
Ответ: Высота ромба – 5 см.
Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а
периметр – 32 см.?
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его
сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую
длину. Из этого следует, что длина одной стороны будет равна ¼ части его
периметра:
а = Р/4 = 32/4 = 8 см.
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на
высоту (h), проведенную к ней:
S = а* h
В конкретном случае:
48 = 8* h
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
H = 48/8 = 6 см.
Ответ: Высота ромба составляет 6 см.
Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52
см. Как найти высоту ромба в данном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых
равны. Это значит:
Р = 4*а
По условию задачи:
52 = 4*а
Следовательно:
а = 52/13 = 13 см.
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина
второй его диагонали будет выглядеть как 24х. Отношение их длин можно
записать в следующем виде:
10х:24х=10:24
Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую
степень, равна длине гипотенузы, которая также возведена в квадрат:
с2 = а2 + b2
Для данной задачи это равенство записывается так:
(5х)²+(12х)²=13²
Отсюда видно, что:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина
второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
S = d₁*d₂/2 или a·h
Из этого можно составить следующее уравнение:
d₁*d₂=2a*h
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Какая формула используется с целью вычисления высоты ромба?
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты. Есть возожность высчитать высоту ромба при помощи различных
параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В
этом случае высота ромба будет равна отношению его площади к длине высоты:
h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также
его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся
между смежными сторонами, то для расчета высоты ромба используется
следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.
В каком виде записываются формулы, используемые для определения площади
ромба?
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a —
сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины.
Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь
ромба?
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Р/4 = 8 см.
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь
можем определить длину высоты:
h = 8-1,7 = 6,3 см.
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее
опущена:
8 * 6,3 = 50,4 см².кв.
Ответ: S = 50,4 см. кв.
Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10
см. Как найти площадь ромба?
Если длины диагоналей фигуры относятся как 4/3, то их половины будут
относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Отсюда:
25d²=100
d =2,
Значит:
d¹/2 = 4d = 8 см.
d²/2 = 3d = 6 см.
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Как записывается формула расчета площади ромба через длины его диагоналей d1
и d2?
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур,
основанием которых является одна диагональ, а вторая диагональ ромба
представляет собой сумму длин высот этих фигур. Диагонали ромба при
пересечении образуют угол в 90 градусов. На основании этого можно найти
площадь ромба следующим образом:
S = ½ d1*d2.
Как записать формулу вычисления площади ромба через диагонали?
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а
затем разделить полученное число на два:
S = ½ d1*d2.
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а
вторая – 4 см. Тогда его площадь будет равна:
S=1/2*5*4=10 см. кв.
Как выглядит формула для определения площади ромба?
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и
высоту (h). Формула записывается так:
S=a*h.
См. также: Программа для расчета периметра ромба.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Площадь ромба равна произведению
высоты на основание.
Формула площади ромба через параллелограмм:
( S = ah )
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Диагонали ромба являются биссектрисами его углов, кроме этого,
пересекаются под углом 90 градусов.
Формулировка площади ромба через две диагонали:
Площадь ромба равна половине произведения
одной диагонали на другую.
Формула площади ромба через две диагонали:
( S = frac{1}2d_1 d_2 )
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Площадь ромба равна произведению квадрата стороны
на синус угла прилежащего к этой стороне.
Формула площади ромба через синус и сторону в квадрате:
( S = a^2sinalpha )
a — сторона; sin α — синус угла;
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
|
Как найти площадь ромба если известны диагонали ? Это еще школьный материал, все подобные задачи решали на уроках геометрии. Что же такое ромб. Это 4-х угольная фигура с 4-мя сторонами, у которой противоположные стороны параллельны друг другу и по длине одинаковые. Ромб очень похож на квадрат. Если нам известны диагонали, то формула вычисления площади фигуры следующая: S=d1*d2/2, в формуле d1,d2 — это диагонали фигуры. модератор выбрал этот ответ лучшим Alexsandr82 6 лет назад Чтобы найти площадь ромба если известны обе его диагонали нужно просто их перемножить изатем разделить на два. Сложнее бывает если известна только одна диагональ, а вторую нужно найти, зная один из углов ромба или известен радиус вписанной окружности и один из углов ромба. В таких случаях сначала ищем неизвестную диагональ, а затем находим площать ромба. Формула рассчета диагоналей если известны угол и вторая диагональ: d1 = d2*tg(b/2) d2 = d1*tg(a/2) Где d1 — большая диагональ, d2 — малая, а — меньший угол ромба, b — больший угол. Формула для рассчета диагоналей ромба если известен один угол и радиус вписанной окружности: d1 = 2r/sin(a/2) d2 = 2r/sin(b/2) Зная обе диагонали мы можем рассчитать площадь ромба. Думаю, что эту формулу можно легко вывести самой. Достаточно представить себе ромб и провести некоторые дополнительные построения, чтобы сделать из ромба более простую фигуру. А именно легко заметить, что диагонали ромба разбивают его на четыре одинаковых прямоугольных треугольника. Если каждый такой треугольник, удвоить, отразить относительно гипотенузы, то есть стороны ромба, то вместо ромба мы получим прямоугольник. То есть мы на диагоналях ромба строим прямоугольник, у которого параллельные стороны равны соответствующей диагонали. А площадь прямоугольника равна а*b или в нашем случае d*d. Но этот прямоугольник в два раза больше нашего ромба, а следовательно формула площади ромба примет вид S=d*d/2. Ксарфакс 6 лет назад Если известны диагонали ромба a и b, то можно легко найти его площадь. Она будет равна: S(ромба) = 0,5*a*b, то есть половина произведения диагоналей. Доказательство Диагонали ромба разбивают его на 4 равных прямоугольных треугольника. Катеты каждого из них равны половине диагоналей: 0,5a и 0,5b. Площадь прямоугольного треугольника равна половине произведения катетов. Соответственно, площадь ромба равна 4 площадям одного треугольника, который был образован пересечением диагоналей. S(ромба) = 4*(0,5a*0,5b*0,5) = 4*0,125*a*b = 0,5a*b. Что и требовалось доказать. Пример Диагональ a = 4 см. Диагональ b = 8 см. S(ромба) = 0,5*4*8 см. = 16 см. Алиса в Стране 5 лет назад Очень даже просто. Существует очень простая специальная математическая формула для этого случая, которую дети изучают в школах: d1 х d2 / 2, где d1 и d2 — это диагонали ромба. Звучит это так: чтобы найти площадь ромба нужно перемножить его диагонали и поделить это произведение на два. Таня Ляпаева 8 лет назад Хм…У ромба стороны противоположны, он же и параллелограмм. Если нам известны диагонали, то можно вычесть площадь из этой фигуры. Пусть диагонали b1 и b2, тогда Площадь (S) = b1*b2/b2. Мы просто перемножаем эти диагонали и делаем все по формуле. Юлия1578 9 лет назад Задача очень простая. Нужно только логически поразмыслить и вспомнить одну простую математическую формулу. Чтобы вычислить искомую площадь ромба, зная параметры диагонали, выполняем всего два арифметических действия:
Артём Денисов 7 лет назад Если известны только параметры диагоналей, то чтобы отыскать площадь самой фигуры, следует перемножить сами диагонали ((S) = d1*d2/d2). Где S — площадь, а d1 и d2 — диагонали. Именно таким образом и находится площадь ромба, когда известны лишь диагонали этой фигуры. Внутри ромба имеется четыре прямоугольных треугольника. площадь одного треугольника равна: S= d1xd2/8, поскольку в ромбе таких треугольников четыре, площадь ромба будет равняться: Sр= d1xd2/8×4= d1xd2/2 т.е. половине произведения его диагоналей. Стрымбрым 8 лет назад Ромбом называют параллелограмм, у которого все стороны равны между собой. Частный случай ромба — квадрат (ромб с прямыми углами). А чтобы определить площадь ромба, требуется перемножить его диагонали и разделить пополам. иришенька 8 лет назад Сделать это совсем несложно. Итак, если известны диагонали то их нужно просто перемножить, а затем разделить на 2. Думаю, теперь вы без труда сможете определить площадь ромба, зная только его диагонали. Знаете ответ? |
Онлайн калькулятор площади ромба может вычислить плошадь семью различными методами.
Сделав расчет на этом калькуляторе площади ромба Вы сможете получить детальное пошаговое решение с ответом. Также Вы сможете понять алгоритм нахождения площади ромба различными методами.Тем самым Вы усвоите пройденный материал и закрепите полученные знания.
Ромбом называется параллелограмм, у которого все стороны равны.
Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
Свойства ромба.
1) Противоположные стороны ромба равны.
2) Противоположные углы ромба равны.
3) Диагонали ромба точкой пересечения делятся пополам.
4) Сумма углов, прилежащих к одной стороне ромба, равна 180 °.
5) Диагонали ромба взаимно перпендикулярны.
6) Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).
7) Диагонали делят ромб на четыре равных прямоугольных треугольника.
Скачать все формулы нахождения площади ромба в формате Word