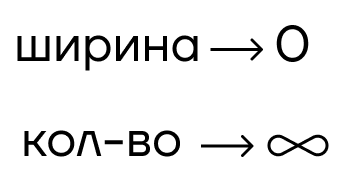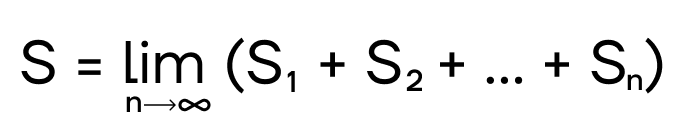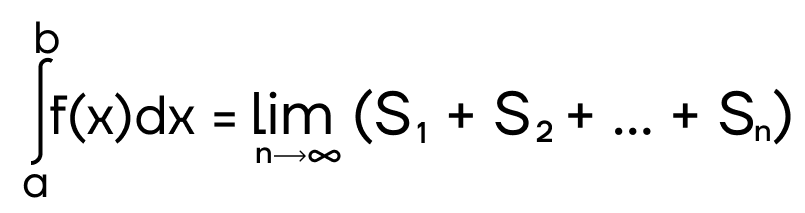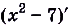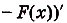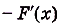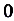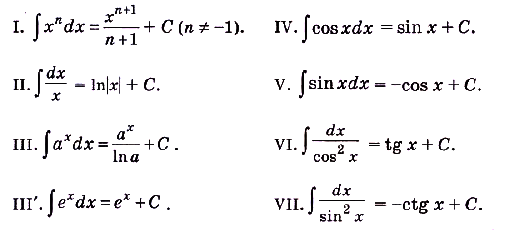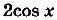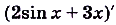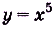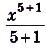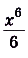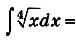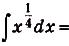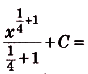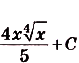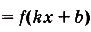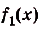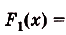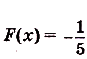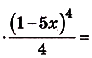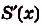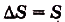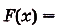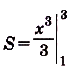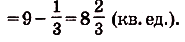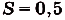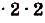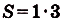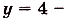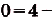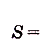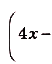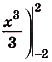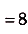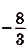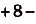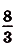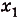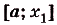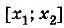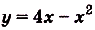СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
26 мая
Как заработать +20–30 баллов на ЕГЭ благодаря разборам ЕГЭ с Дальнего Востока
24 мая
Обновлённая панель инструментов
22 мая
Беседы Решу ЕГЭ по подготовке к ЕГЭ
11 мая
Решение досрочных ЕГЭ по всем предметам
5 мая
Обновленный поиск заданий по ключевым словам
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Поиск
?
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 9 1–9
Добавить в вариант
Тип 7 № 323079
i
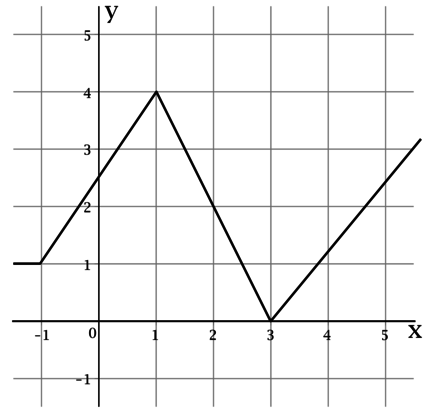
На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Видеокурс
·
Помощь
Тип 7 № 323080
i
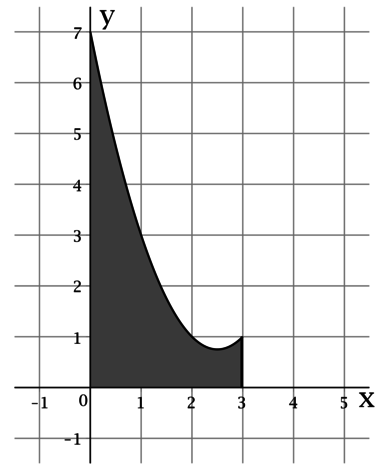
На рисунке изображён график некоторой функции y = f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
3 комментария
·
Видеокурс
·
Помощь
Тип 7 № 323283
i
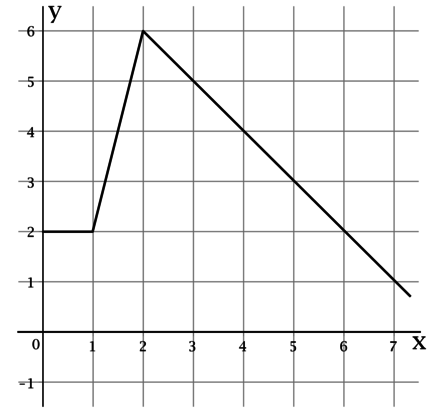
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323373
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323375
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323379
i
На рисунке изображён график функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323383
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323475
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323477
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Всего: 9 1–9
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
На этой странице вы узнаете:
- Как связаны Ньютон и Лейбниц?
- Почему площадь криволинейной трапеции считается через интеграл?
Интеграл
В топ-5 страшилок по математике неизменно входит интеграл. Так ли он ужасен на самом деле?
Если объяснять простыми словами, интеграл — это площадь фигуры под графиком функции. Например, в геометрии есть формулы, чтобы посчитать площадь прямоугольника или треугольника, а если нужно посчитать площадь фигуры с кривой стороной, заданной функцией, поможет интеграл.
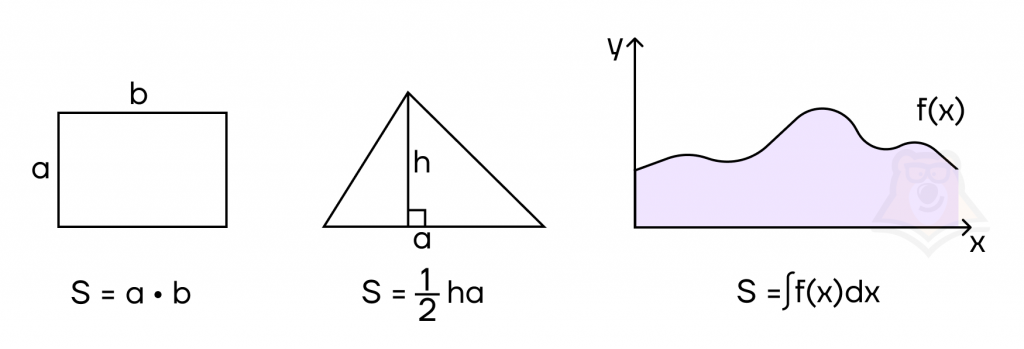
Если у функции y = f(x) есть первообразная y = F(x), тогда множество значений первообразных у = F(x) + С называют неопределенным интегралом функции y = f(x)
Записывается это следующим образом:
(int f(x)dx = F(x) + C)
Какие бывают интегралы?
Интегралы бывают неопределенные и определенные.
Рассмотрим определенный интеграл. У такого интеграла в отличие от неопределенного есть предел интегрирования, то есть определённый отрезок.
Определенный интеграл функции на отрезке [a; b] – это приращение первообразных
Записывается это следующим образом:
(intlimits_a^b f(x)dx = F(b) — F(a))
Для данного интеграла пределом является отрезок от a до b
И Ньютон, и Лейбниц, бесспорно, являются великими учеными. Как и у обычных людей, у них бывают споры. Именно такой спор и послужил названию одной из формул в математике в честь этих двух замечательных ученых. Формула Ньютона-Лейбница используется для вычисления определенного интеграла. Она была выведена Ньютоном и Лейбницем независимо друг от друга. Есть мнение, что Ньютон свою версию создал раньше Лейбница, но опубликовал позже, из-за этого и случился спор, который завершился только после смерти обоих ученых.
Формула Ньютона-Лейбница
Если функция f(x) непрерывна на промежутке [a; b], то
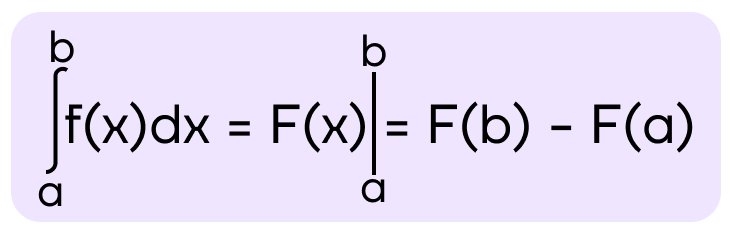
где F(x) – первообразная для функции f(x),
a – нижний предел интегрирования,
b – верхний предел интегрирования
Данная формула применяется для вычисления определенного интеграла
Пример вычисления определенного интеграла по формуле Ньютона – Лейбница:
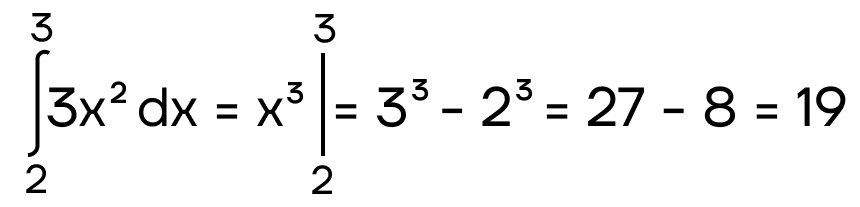
Интеграл для нахождения площади фигуры
Представим, что нам нужно посчитать расстояние, пройденное автомобилем с непостоянной скоростью в промежуток времени [a; b].
Нарисуем график.
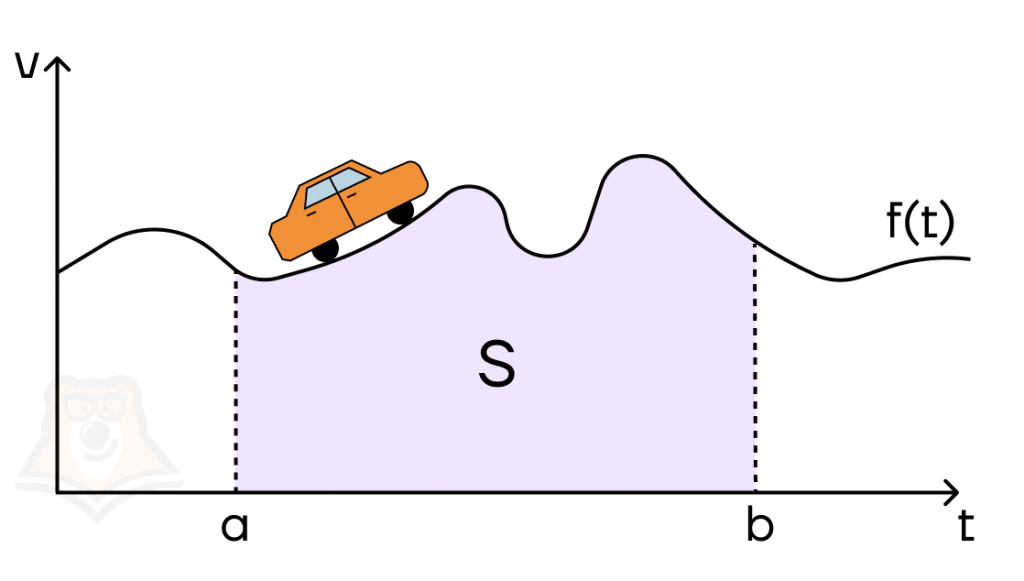
Скорость автомобиля V изменяется с течением времени, как f(t). Тогда, чтобы её найти, нам нужно посчитать площадь фигуры, ограниченной графиком функции f(t) на отрезке [a; b]. Такой фигурой будет являться криволинейная трапеция, а посчитать площадь можно с помощью интеграла. Далее мы подробно разберем, как это сделать.
Криволинейная трапеция – это фигура на плоскости, ограниченная графиком непрерывной функции на определенном отрезке, прямыми линиями и осью абсцисс.
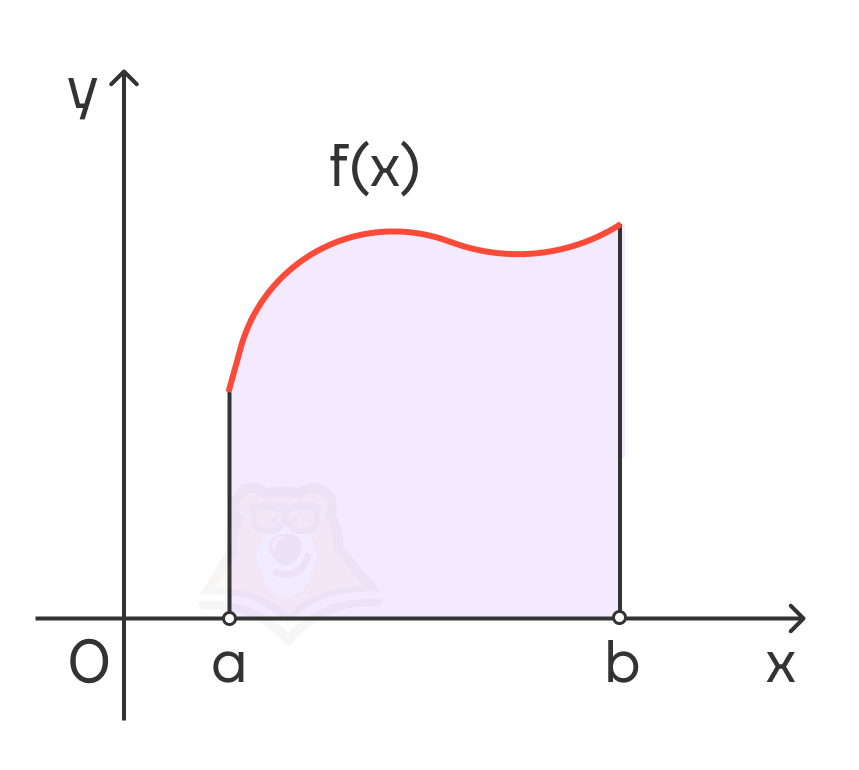
На данном рисунке фигура ограничена y = f(x), x = a, x = b, y = 0
Как найти площадь фигуры, используя интеграл?
Площадь такой фигуры, расположенной над осью абсцисс, можно посчитать, вычислив определённый интеграл по уже известной формуле Ньютона-Лейбница.
(S = intlimits_a^b f(x)dx)
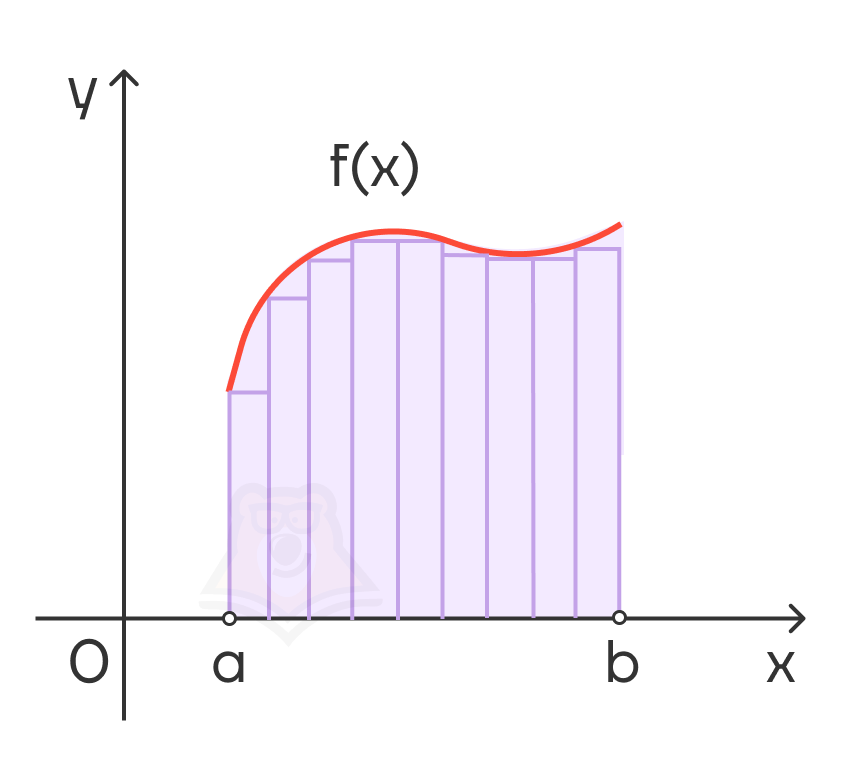
Чтобы понять это, разобьем фигуру на конечное число узких прямоугольных столбцов.
Найдем общую площадь, умножив высоту каждого столбика на его ширину и сложив все полученные значения, такая площадь будет приблизительной.
Если разделить данную фигуру на большее количество столбиков, только уже меньших по ширине, получим более точное значение. Повторять такое действие можно до бесконечности, следовательно, ширина будет стремиться к нулю, а количество прямоугольников — к бесконечности.
Сумму такого количества прямоугольников запишем в виде предела при количестве прямоугольников, стремящемся к бесконечности.
При таких условиях рассматриваемая сумма площадей сходится к пределу, описываемому следующим образом
, и равна какому-то числу.
А если фигура расположена под осью абсцисс, для вычисления площади фигуры нужно добавить минус к изначальной формуле.
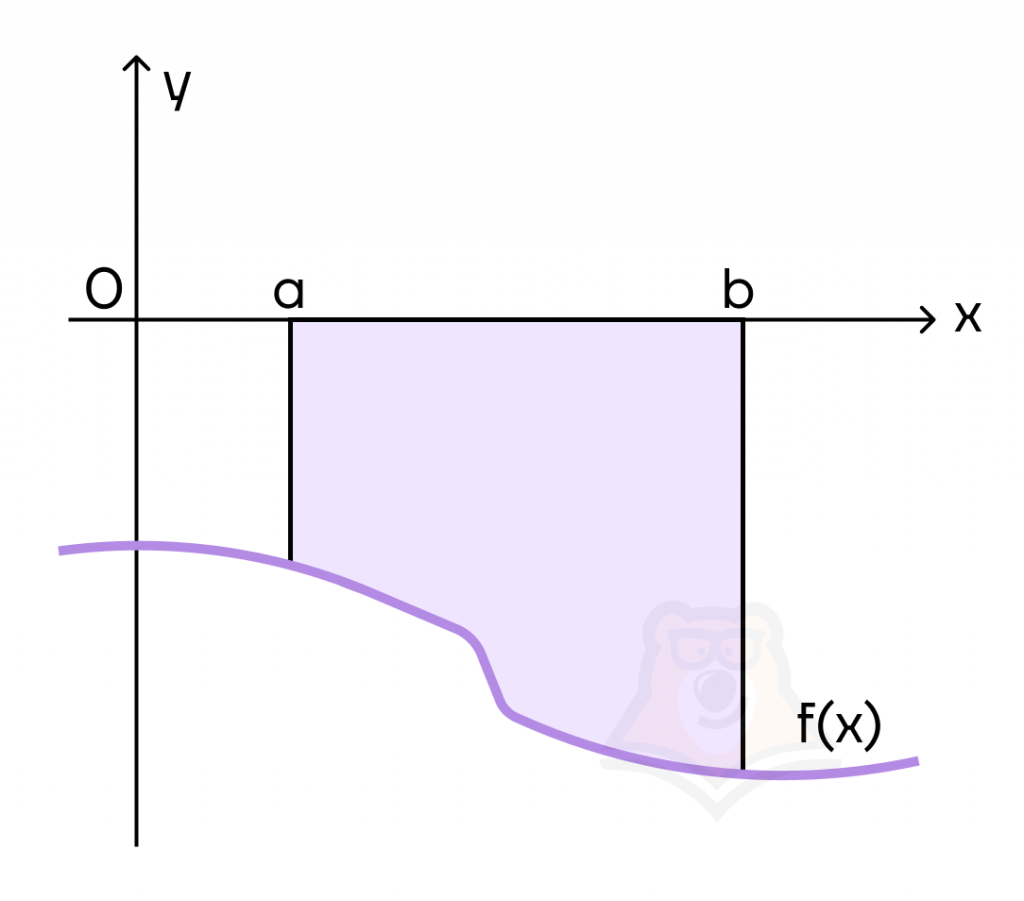
(S = -intlimits_a^b f(x)dx)
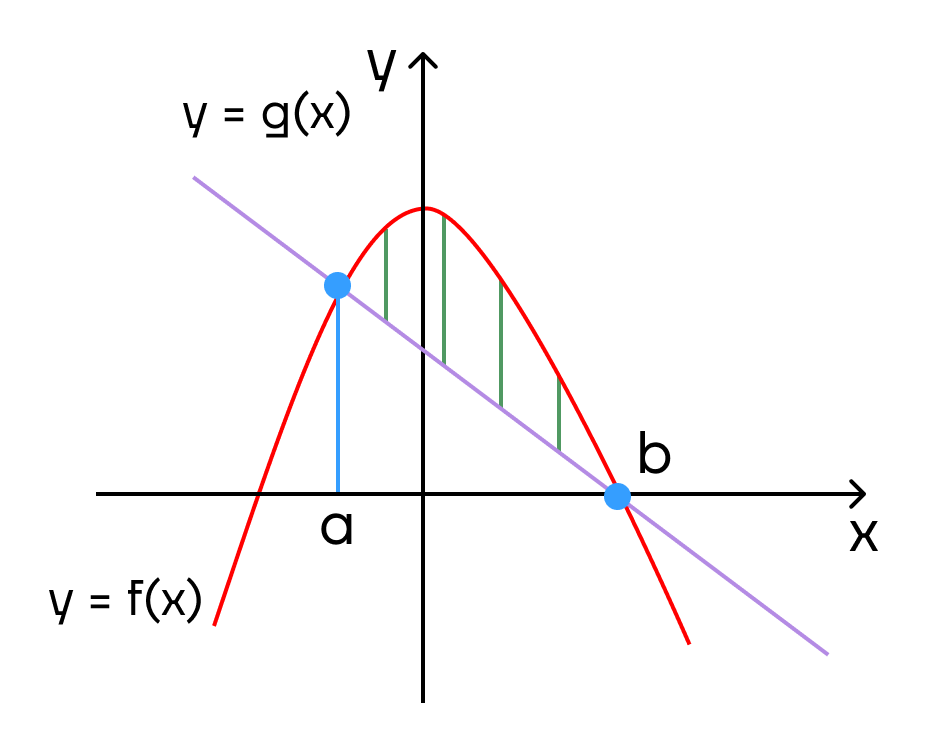
Если нужно найти площадь фигуры, ограниченной двумя функциями f(x) и g(x), то сначала данные функции приравниваются, так находится предел, а далее определяется функция, которая находится выше, и записывается формула
(S = intlimits_a^b (f(x) — g(x))dx)
где f(x) – функция находящаяся выше
g(x) – функция находящаяся ниже
a и b – границы предела
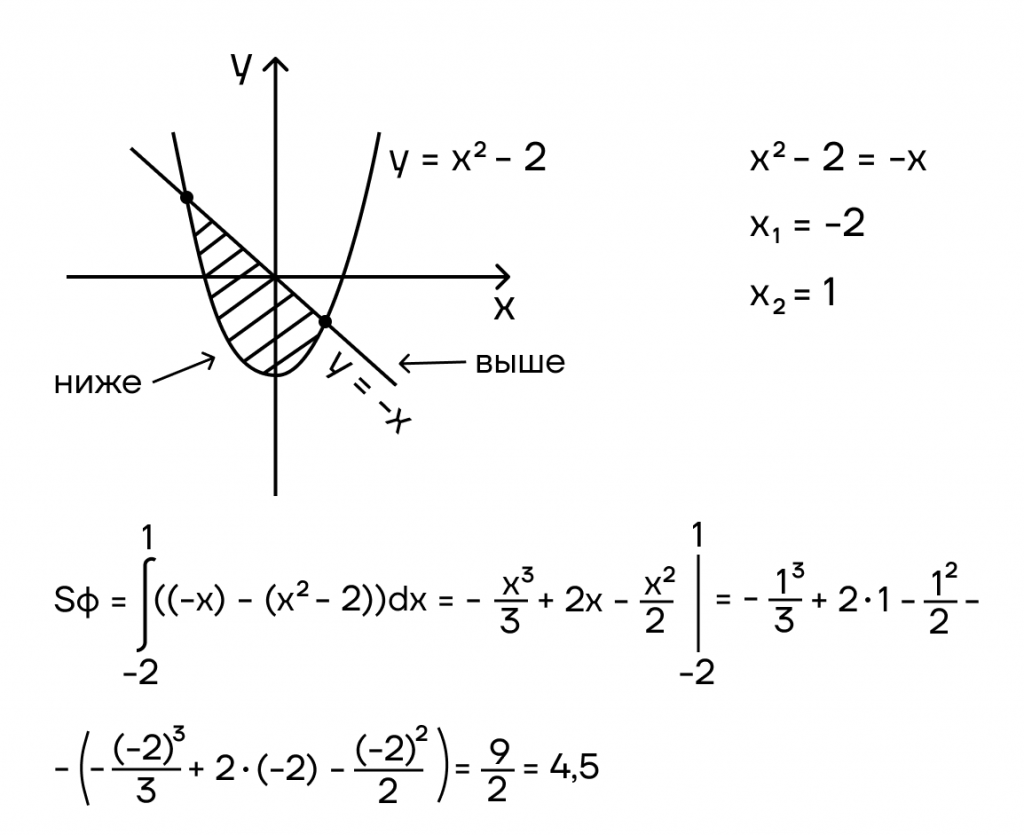
Пример:
Найти площадь фигуры ограниченной функциями y=x2 — 2 и y = -x
Фактчек
- Интеграл — это площадь фигуры, находящейся под графиком функции.
- Неопределённый интеграл функции fx : (int f(x)dx = F(x) + C)
- Определенный интеграл функции fx на отрезке [a; b] : (intlimits_a^b f(x)dx = F(b) — F(a))
- Формула Ньютона-Лейбница (intlimits_a^b f(x)dx = F(x) |_a^b = F(b) — F(a))
- Формула для нахождения криволинейной трапеции над осью х
(S = intlimits_a^b f(x)dx) - Формула для нахождения криволинейной трапеции под осью х
(S = -intlimits_a^b f(x)dx) - Формула для нахождения площади фигуры, ограниченной двумя функциями
(S = intlimits_a^b (f(x) — g(x))dx), где
f(x) – функция находящаяся выше
g(x) – функция находящаяся ниже
Проверь себя
Задание 1.
Найдите значение интеграла (intlimits_1^5 3dx)
- 3
- 5
- 12
- 14
Задание 2.
Вычислите площадь фигуры ограниченной (y = sin x, x = 0, x = frac{pi}{2})
- 1
- 0
- 1,5
- 2
Задание 3.
Вычислите площадь фигуры ограниченной y = 2x2 — 5, x = -1, x = 1
- 9
- (8frac{2}{3})
- (frac{20}{3})
- 8
Задание 4.
Вычислите площадь фигуры ограниченной y = x2 — 3 и y = -2x2 + 9
- 32
- 18
- 24
- 2
Ответы: 1. – 3; 2. – 1; 3. – 2; 4. – 1
Решение:
Площадь под графиком функции f(x) на отрезке [a; b] равна разности первообразных:
S = F(b) — F(a)
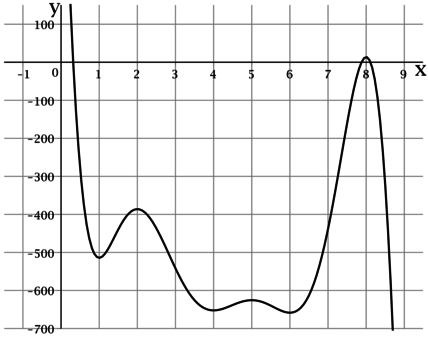
Нам необходимо найти площадь закрашенной фигуры на отрезке [-8; -6], то есть a = -8; b = -6. Значит S = F(-6) — F(-8).
Найдем F(-8):
F(-8) = (-8)3 + 21⋅(-8)2 +151⋅(-8) — 1
F(-8) = — 512 + 21⋅64 — 151⋅8 — 1
F(-8) = — 512 + 1344 — 1208 — 1
F(-8) = — 513 + 136
F(-8) = -377
Найдем F(-6):
F(-6) = (-6)3 + 21⋅(-6)2 +151⋅(-6) — 1
F(-6) = — 216 + 21⋅36 — 151⋅6 — 1
F(-6) = — 216 + 756 — 906 — 1
F(-6) = — 217 — 150
F(-6) = -367
Тогда площадь закрашенной фигуры равна:
S = F(-6) — F(-8) = -367 — (-377) = -367 + 377 = 10
Ответ: 10
Тема 7.
Взаимосвязь функции и ее производной
7
.
08
Первообразная и площадь под кривой
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
взаимосвязь функции и ее производной
Решаем задачи
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой на
интервале Пользуясь рисунком, определите количество решений уравнения
на отрезке
Показать ответ и решение
Так как — одна из первообразных функции
то
Производная равна нулю в точках, в которых касательная к графику функции
расположена горизонтально.
Таких точек на отрезке ровно 6.
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале Определите по рисунку количество решений уравнения
на отрезке
Показать ответ и решение
По определению первообразной Тогда имеем:
Отсюда получаем
Показать ответ и решение
По определению первообразной Тогда имеем:
Отсюда получаем
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале Определите по рисунку количество решений уравнения
на отрезке
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале Определите по рисунку количество решений уравнения
на отрезке
На рисунке изображён график некоторой функции Функция
— одна из первообразных
функции Найдите площадь закрашенной фигуры.
Показать ответ и решение
Нам нужно найти площади под графиком функции на отрезке
Такая площадь равна интегралу
По
формуле Ньютона-Лейбница имеем:
На рисунке изображён график функции Пользуясь рисунком, вычислите
где
— одна из
первообразных функции
Показать ответ и решение
По формуле Ньютона-Лейбница имеем:
Заметим, что такой интеграл равен площади под графиком функции на отрезке
Значит, нам
нужно найти площадь выделенной фигуры, состоящей из прямоугольного треугольника и двух прямоугольников:
Тогда имеем:
На рисунке изображён график функции Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
На рисунке изображён график функции Вычислите по рисунку
где
— одна из первообразных
функции
На рисунке изображён график функции Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
На рисунке изображён график функции Вычислите по рисунку
где
— одна из первообразных
функции
На рисунке изображён график функции — одной из первообразных
функции определённой на интервале
Найдите количество решений
уравнения на отрезке
Показать ответ и решение
По определение первообразной то есть решением уравнения
будут точки экстремума функции
которые помечены на графике.
Получим семь точек.
Ранее вы ознакомились с операцией дифференцирования: нахождения производной по данной функции. Не менее важна и обратная ей операция — интегрирование: нахождение функции по её производной.
Пусть дано функцию 
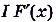
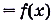

Функция F(x) называется первообразной функции 

Например, на всей числовой оси (т. е. на R] функция F(x) = 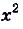
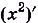
Функция F(x) 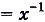

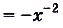
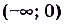
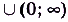
Одна ли функция 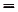
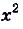
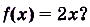
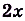
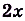
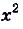

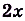
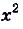

Существуют ли другие функции, отличные от 
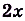
Теорема. (Основное свойство первообразных.) Каждая первообразная для функции 

Доказательство 1. Пусть


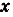


По правилу нахождения производной суммы
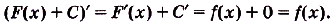
Этим доказано» что какая бы ни была постоянная С, если 


Пусть 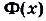

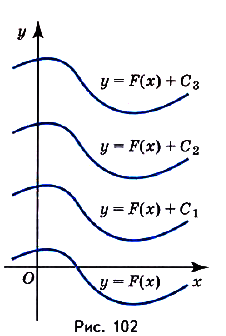





Как видим, функция 

Такое свойство имеет только определённая на

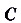

Этим доказано, что если 







Каждая первообразная рассматривается на некотором промежутке. Если же для краткости его не указывают, то имеют в виду промежуток максимально возможной длины. В частности, если функция 
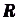

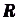
Операцию нахождения производной данной функции называют дифференцированием. Обратная ей операция — нахождение первообразной — называется интегрированием.
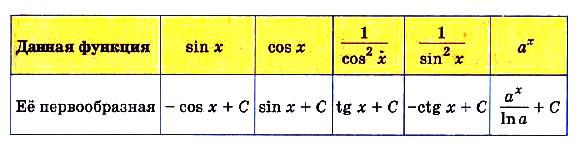
Используя формулы дифференцирования (с. 218), составим таблицу первообразных. Советуем запомнить её.

Обосновать эту таблицу можно дифференцированием функции из её второй строки. Пользуясь таблицей, можно сразу писать, что, например, для функции 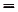
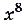

Множество всех первообразных функции 
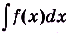
Выражение «проинтегрировать функцию

То есть, если 

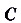

Слово интеграл в переводе с латинского языка означает целый. Почему его так назвали, вы поймёте, когда ознакомитесь с определённым интегралом (см. с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении 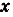
Таблицу первообразных, с помощью символа неопредёлен-ного интеграла можно записать так:
Примеры с решением
Пример №1
Докажите, что функция 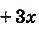
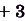
Доказательство.
Имеем 

Пример №2
Найдите первообразную для функции : а) 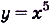
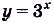
Решение:
Воспользуемся таблицей первообразных.
а) Первообразной для функции 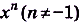
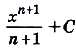
Для функции 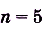

б) Первообразной для функции 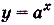
Для функции 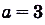

Пример №3
Найдите для функции 
Решение:
Пользуясь таблицей, найдём общий вид первообразных: 

Следовательно, 
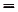
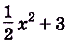
Ответ.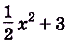
Пример №4
Проинтегрируйте функцию 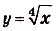
Решение:
Нахождение первообразных
Выведем несколько правил, подобных правилам дифференцирования, которые облегчают нахождение первообразных.
I. Если
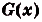

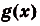

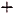
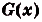

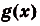
Действительно, если 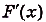

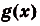
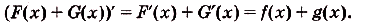
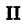


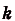
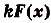
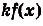
Ведь 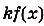


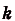
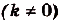
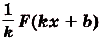
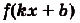
»
Ведь
Пример №5
Найдите первообразную для функции:
а) 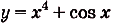
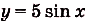
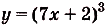
Решение:
а) Для функций 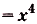
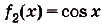
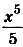
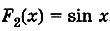
Поэтому для суммы данных функций общий вид первообразных
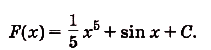
б) По правилу II: 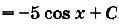
в) Одной из первообразных для функции 
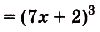
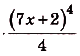
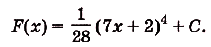
К нахождению первообразных сводятся прежде всего задачи, обратные тем, которые решаются с помощью производной. Рассмотрим пример..
Если известен закон прямолинейного движения тела 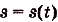
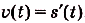
Задача №1.
Точка движется прямолинейно с переменной скоростью 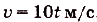
Решение:
Искомый закон движения выражается такой функцией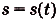
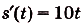
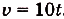
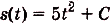
Ответ. Искомый закон движения точки 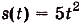
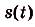
Примеры других применений первообразной рассмотрим в следующих параграфах.
С помощью неопределённого интеграла правила интегрирования записываются так:
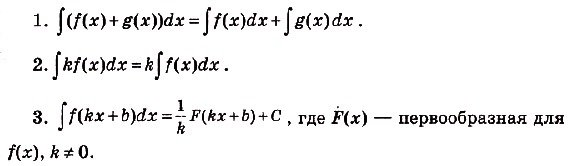
Пример №6
Найдите одну из первообразных для функции:
а)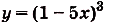
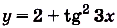
Решение:
а) Для функции 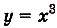
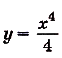
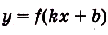
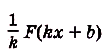
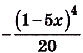
б) преобразуем сначала формулу, задающую функцию:
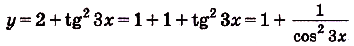
Тогда 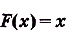
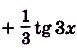
Пример №7
Тело движется прямолинейно с ускорением 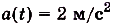
Определите скорость данного движения как функцию от времени f, если в момент t = 0 она равнялась 3 м/с.
Решение:
Ускорение — производная скорости. Поэтому если 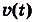
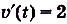
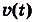
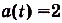
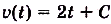
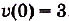
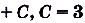
Ответ. 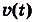
Первообразная и площадь криволинейной трапеции
Пусть на координатной плоскости задан график непрерывной функции 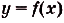
Криволинейную трапецию называют также под графиком функции 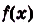
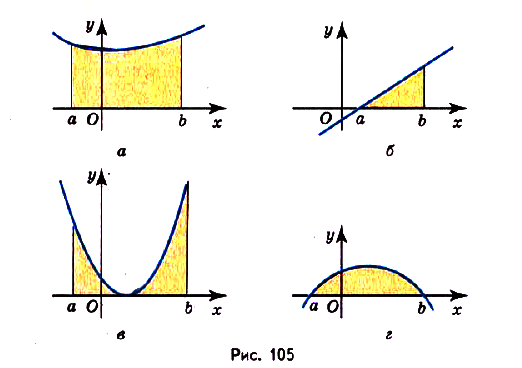
Несколько криволинейных трапеций изображено на (рис. 105).
Каждая криволинейная трапеция имеет определённую площадь (это доказано в строгих курсах математического анализа). Эти площади можно находить с помощью первообразных.
Теорема. Площадь криволинейной трапеции, образованной графиком функции 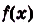
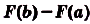


Доказательство. Рассмотрим произвольную криволинейную трапецию, образованную графиком функции 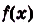
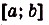
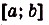
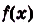
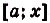
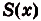
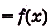
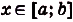
Дадим переменной х приращение 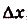
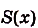
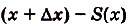

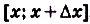
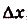
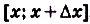
Следовательно, 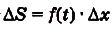
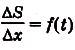
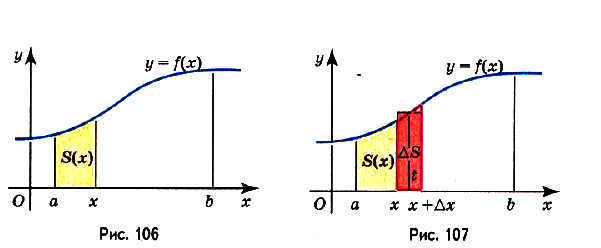
Если 
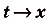
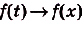
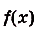

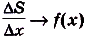
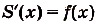
Как видим, функция S(x) — первообразная для 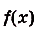
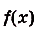
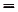
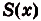
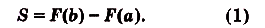
Значение выражения F(b) — F(a) вычисляют часто, поэтому для удобства его записывают ещё и так:.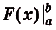

Задача №2.
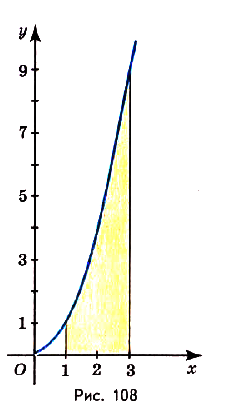
Найдите площадь криволинейной трапеции, образованной графиком функции 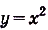
Решение:
На (рис) 108 изображена фигура, площадь которой нужно найти. Для функции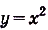
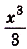
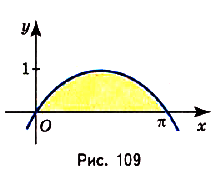
Задача №3.
Найдите площадь фигуры, ограниченной одной аркой синусоиды и осью абсцисс (риc. 109).
Решение:
Надо найти площадь криволинейной трапеции, образованной графиком функции 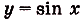
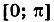
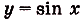
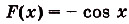
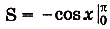
Пользуясь термином «криволинейная трапеция следует иметь в виду, что «криволинейная трапеция» не всегда является трапецией (риc. 109) и не всегда она криволинейная(риc. 105, б). А вообще она — не геометрическая фигура в научном понимании. Любое движение отображает каждую фигуру на равную ей фигуру такого же вида. А если «криволинейную трапецию *, например, изображенную на (рис 108), повернуть на 90°, она отображается на фигуру, которая не является криволинейной трапецией. Поэтому вместо «криволинейная трапеция» говорят и пишут «подграфик функции».
Задача №4.
Найдите площадь криволинейной трапеции, образованной графиком функции у = х на [0; 2].
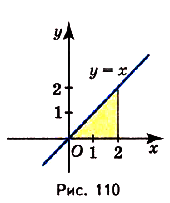
Решение:
Данная криволинейная трапеция — прямоугольный треугольник с катетами 2 и 2 (риc. 110). Его площадь 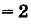
Ответ. 2кв. ед.
Задача №5.
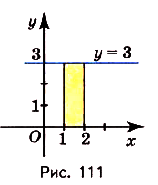
Найдите площадь криволинейной трапеции, образованной графиком функции у -3 на [1,2].
Заданная криволинейная трапеция — прямоугольник с измерениями 1 и 3 (риc. 111). Его площадь 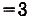
Ответ. 3 кв. ед.
Задача №6.
Найдите площадь фигуры, ограниченной графиком функции 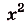
Решение:
Найдем абсциссы точек пересечения графика данной функции с осью Ох. В этих точках ордината функции равна нулю: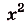
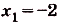
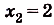
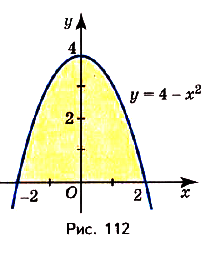
графиком функции 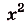
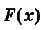
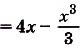
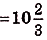
Ответ. 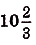
Определённый интеграл
Рассмотрим другой подход к определению площади криволинейной трапеции.
Пусть дана криволинейная трапеция, образованная графиком функции f(x) на [a;b] (рис. 117). Разобьём отрезок [а; Ь] точками 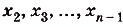
Построим на первом из этих отрезков прямоугольник высотой 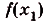
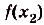
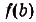
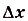
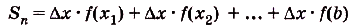
Суммы такого вида называют интегральными суммами функции f(x) на [а; Ь]. Полученную интегральную сумму можно считать приближённым значением площади S криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]. При этом если 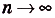
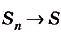
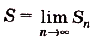
He только задача о нахождении площади криволинейной трапеции, но и много других важных прикладных задач приводят к вычислению пределов подобных интегральных сумм. Поэтому для такого понятия введено специальное название и обозначение.
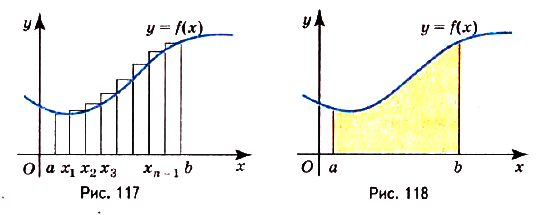
Предел интегральной суммы 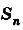
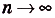
Его обозначают символом 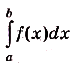
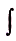
Следовательно, площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь], равна 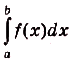
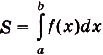
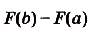
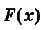
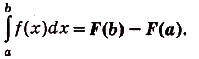
Это — формула Ньютона—Лейбница, основная формула математического анализа. Она даёт возможность решать много разных интересных и содержательных задач — абстрактных и прикладных, в частности — и очень важных. Решали такие задачи сотни математиков еще задолго до создания математического анализа. Но для каждой задачи раньше они находили отдельный оригинальный способ решения. Найдя и обосновав формулу Ньютона—Лейбница, учёные получили общий и очень эффективный способ решения таких задач. Не случайно открытие формулы Ньютона—Лейбница специалисты считают самым важным открытием XVII века.Рационализировать вычисления определённых интегралов часто помогает такое их с в о й с т в о:
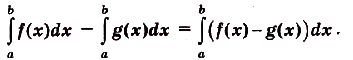
Справедливость этой формулы вытекает из следующих преобразований:
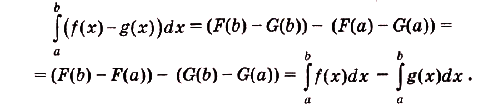
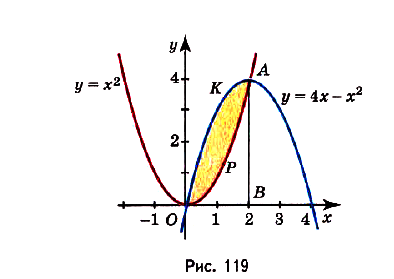
Задача №7.
Найдите площадь фигуры, ограниченной графиками функций 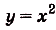
Решение:
Построим графики данных функций (рис. 119). Надо найти площадь закрашенной фигуры. Она равна разности площадей фигур ОВАК и ОВАР. Границы интегрирования — абсциссы точек О и А, в которых пересекаются графики функций, т. е. значения х удовлетворяющие системе уравнений 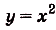
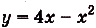
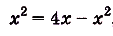
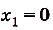
Следовательно, искомая площадь
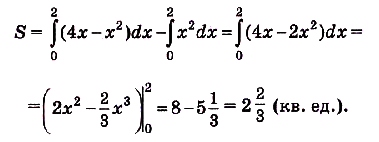
Ответ. 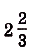
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся: