Антенна собирает энергию падающего на нее потока мощности электромагнитного излучения. A — геометрическая площадь, Ae — эффективная площадь, E — электрическое поле, H — магнитное поле Иллюстрация для калькулятора
Калькулятор позволяет определить эффективную площадь антенны Ae для заданной частоты f или длины волны λ и коэффициента усиления антенны G. Этот и другие калькуляторы на TranslatorsCafe.com пригодятся не только инженерам и студентам технических специальностей, но и всем, кто хочет изучить технический английский, так как все они есть и в английской версии.
Пример: Рассчитать эффективную площадь антенны радиотелескопа РТ-70 в Крыму: коэффициент усиления его антенны 69,5 дБи или 9000000, рабочая частота 5,0 ГГц (или длина волны 6 см).
Входные данные
Частота
f
или Длина волны
λ
Коэффициент усиления антенны, линейный
G
или Коэффициент усиления антенны, dBd
G дБ
или Коэффициент усиления антенны, dBi
G дБ
Поделиться ссылкой на этот калькулятор, включая входные параметры
Выходные данные
Эффективная площадь антенны
Ae м²
Для расчета введите величины в соответствующие поля, выберите единицы и нажмите на кнопку Рассчитать.
Эффективная площадь антенны представляет собой площадь эквивалентной плоской антенны с равномерным амплитудно-фазовым распределением и максимальным коэффициентом направленного действия (КНД), равным КНД рассматриваемой антенны. С этой площади антенна, направленная на источник сигнала, поглощает энергию падающего электромагнитного излучения. Для удобства объяснения рассмотрим эффективную площадь приемной антенны. Поглощенная антенной мощность P определяется как
P = Pd A
Здесь Pd —плотность потока мощности (удельная мощность на единицу поверхности) падающей электромагнитной энергии и A — площадь раскрыва (геометрическая площадь) антенны. Коэффициент усиления антенны G прямо пропорционален геометрической площади антенны A. Его можно увеличить путем фокусирования излучения только в одном направлении с одновременным уменьшением излучения во всех остальных направлениях. Поэтому чем ýже ширина пучка, тем выше коэффициент усиления антенны. Соотношение между коэффициентом усиления антенны и ее площадью выражается формулой, в которую также входит КПД антенны:
или
Здесь λ — длина волны и η — КПД антенны, который всегда меньше единицы:
Здесь Ae — эффективная площадь (апертура) антенны, которая определяется как физическая площадь антенны, умноженная на КПД антенны. Если КПД антенны равен 1 (или 100%), это означает, что вся энергия, подаваемая передатчиком в передающую антенну излучается в пространство. Если же это приемная антенна, то при единичном КПД вся энергия, принимаемая антенной, попадает в приемник. Однако на практике часть энергии всегда теряется в форме тепловой энергии, которая расходуется на разогрев элементов конструкции антенны и фидера.
Заменяя произведение площади на КПД Aη на эффективную площадь Ae, получаем:
или
Эта формула и используется в данном калькуляторе. Из нее видно, что для заданной эффективной площади антенны ее коэффициент усиления возрастает с квадратом длины волны или при постоянной длине волны коэффициент усиления антенны прямо пропорционален ее эффективной площади. Отметим, что для апертурных антенн, таких как рупорные или параболические, эффективная площадь связана с геометрической площадью и всегда меньше этой площади. Однако, для проволочных антенн (например, симметричных и несимметричных вибраторов, антенн типа «волновой канал»), эффективная площадь обычно значительно (иногда в десятки раз) больше физической площади антенны.
Радиотелескоп РТ-70 в 2 км от пос. Молочное (Сакский район, Крым, Россия). Эффективная площадь его антенны составляет только 67% от геометрической площади антенны.
Коэффициент усиления (КУ) антенны по мощности G, называемый обычно просто коэффициентом усиления, представляет собой отношение мощности излучения направленной антенны к мощности, излучаемой идеальной ненаправленной антенной, причем ко входам обеих антенн подводится одинаковая мощность. Коэффициент усиления — величина безразмерная, но чаще она выражается в децибелах (дБ, отношение по мощности) или изотропных децибелах (дБи, dBi, также отношение по мощности). Изотропный децибел характеризует коэффициент усиления антенны по сравнению с идеальной изотропной антенной, равномерно излучающей энергию во всех направлениях.
Например, определим эффективную площадь российского телескопа РТ-70, который находится в Крыму неподалеку от Евпатории.
Эффективная площадь (апертура) антенны типа «волновой канал». Отметим, что, в отличие от любой параболической антенны, эффективная площадь которой всегда меньше ее физической площади, эффективная площадь антенны «волновой канал» всегда значительно больше физических размеров антенны. Эллипс эффективной площади расположен перпендикулярно траверсе. Отметим также, что чем выше коэффициент усиления антенны, тем больше ее эффективная площадь. Антенна с большим числом элементов и более длинной траверсой имеет больший КУ и бóльшую эффективную площадь.
Коэффициент усиления антенны G = 69,5 дБи или 9 000 000.
Диаметр антенны d = 70 м.
Рабочая частота f = 5,0 ГГц (6 см).
Геометрическая площадь антенны A = πD²/4 = π70²/4 = 3848 м². В то же время, ее эффективная площадь равна
Как мы видим, эффективная площадь составляет только 67% от геометрической площади антенны.
Теперь рассчитаем эффективную площадь 5-элементной антенны типа «волновой канал» (также называемой по именам японских изобретателей антенна Яги-Уда, антенна Уда-Яги или просто антенна Яги), работающей на частоте 500 МГц и имеющей коэффициент усиления 40 дБи, который соответствует безразмерному коэффициенту усиления 10. Длина активного элемента несколько меньше половины длины волны 0,5λ = 30 см, где λ = 60 см — длина волны.
Диаметр круга площадью 0,28 кв. м определяется как
Эта телевизионная антенна состоит из двух антенн: антенны дециметрового диапазона типа «волновой канал» с 18 директорами и уголковым рефлектором с КУ=14 дБи (справа) и логопериодической антенны с V-образными элементами метрового диапазона (слева)
То есть, для активного элемента длиной около 0.5λ = 30 см мы получаем круг диаметром 60 см (точнее, эллипс).
1.Импульсные сигналы
Для
вычисления эффективной отражающей
площади поверхностных целей необходимо
найти площадь Sп поверхности
земли в пределах разрешаемого объема.
Облучаемая
импульсным сигналом площадь в общем
случае зависит от длины разрешаемого
объёма по дальности, ширины диаграммы
направленности антенны в горизонтальной
и вертикальной плоскостях.
Для
обычных импульсных сигналов длина
разрешаемого объёма по дальности
равна сИ/2.
При малых углах визирования цели (рис.3.6)
разрешаемая площадь равна
|
|
(3.46) |
Так
как обычно угол мал,
то
|
|
(3.47) |
Другой
предельный случай получается при больших
углах наклона и
узкой диаграмме направленности.
Разрешаемая площадь при этом не зависит
от длительности импульса и равна
|
|
(3.48) |
При
расчётах необходимо выбирать меньшую
из величин, определяемых по формулам
(3.46) и (3.48).
В
случае применения в РЛС других более
сложных сигналов вычисление Sп выполняется
аналогичным образом. Находится в каждом
случае длина разрешаемого объёма как
функция параметров сигнала.
Рис.3.6.
Определение эффективной отражающей
площади поверхностной цели при малых
углах наклона луча .
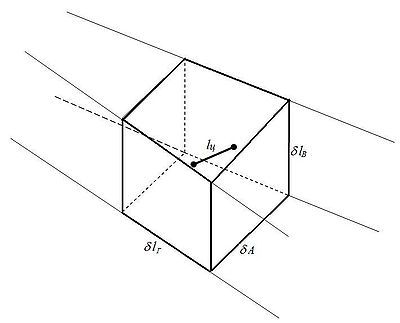
2.Непрерывное излучение
Рассмотрим
в качестве примера вычисление
площади Sп для
РЛС непрерывного излучения с доплеровской
селекцией сигналов. На рис.3.7показан
участок поверхности земли, облучаемый
лучом антенны. В пределах этого участка
различные точки создают отражённые
сигналы с различными доплеровскими
частотами. Так как в РЛС обычно применяется
фильтр с полосой fф для
выделения сигналов, то через фильтр
проёдут только доплеровские частоты в
пределах от FД1 до FД1+fф.
Следовательно, в РЛС применяются только
сигналы, отражённые от узкой полоски
земли, которая на рис.3.7 заштрихована.
Определим размеры этой полоски.
Доплеровская
частота сигнала, отражённого от ближнего
к РЛС участка полоски, равна
|
|
(3.49) |
где Vc – скорость
полёта.
Соответственно
для дальнего участка полоски имеем
|
|
(3.50) |
Рис.3.7. К
определению эффективной отражающей
площади поверхностной цели для РЛС с
доплеровской селекцией сигналов.
Разность
частот Доплера тогда равна
|
|
(3.51) |
Из
рис.3.7 видно,
что
|
|
(3.52) |
Левая
часть формулы (3.51) равна fф.
Правую часть преобразуем с учётом
соотношений (3.52). В результате формула
(3.51) принимает вид
|
|
(3.53) |
Определим
ширину полоски D.
Как следует на рис.3.7,
она равна
|
|
(3.54) |
Подставляя
произведение синусов из (3.53), получаем
для ширины отражающей полоски равенство
|
|
(3.55) |
Азимутальный
размер полоски l равен
|
|
(3.56) |
Окончательно
площадь отражающей полоски находим в
виде
|
|
(3.57) |
Из
формулы (3.57) следует, что площадь полоски
зависит от ширины полосы пропускания
применяемого в РЛС фильтра доплеровских
частотfф,
от угла 0 и
наклонной дальности D.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2020-05-31
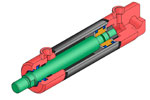
Эффективная площадь гидроцилиндра
Эффективная площадь гидроцилиндра — это площадь поверхности поршня, как которую воздействует давление жидкости. Она не всегда определяется только диаметром поршня, так как присоединенный к поршню шток изолирует часть площади, значит эффективная площадь в этом случае будет меньше.
Эффективная площадь поршня
На рисунке показан гидравлический цилиндр двухстороннего действия.
В том случае, если жидкость будет поступать в поршневую полость, давление будет действовать на всю площадь поршня. Получается, что эффективную площадь в этом случае можно вычислить по формуле:
Аэф. п = πD2 /4
В данном случае эффективная площадь гидроцилиндра равна площади поршня.
Эффективная площадь со стороны штоковой полости
Если жидкость поступает в штоковую полость, то давление будет действовать на кольцевую поверхность, образованную наружными диаметрами поршня и штока.
Эффективная площадь, в этом случае будет равна площади кольца:
Аэф. ш = πD 2 /4 — πd2 /4 = π/4(D2-d2)
У гидроцилиндра с двухсторонним штоком, в обоих полостях эффективные площади будут кольцевыми, а их размеры будут зависеть от диаметров поршня и штоков.
Эффективная площадь пневмоцилиндра
В пневмоцилиндре на поршень воздействует не жидкость, а сжатый воздух. Его давление также будет воздействовать на некоторую поверхность поршня, определяется эффективная площадь пневматического цилиндра точно также,как и гидравлического.
Читайте также:
Все новости
Пример диаграммы ЭПР ()
Эффективная площадь рассеяния (в некоторых учебниках — Эффективная поверхность рассеяния) в радиолокации — площадь некоторой фиктивной поверхности, являющейся идеальным изотропным отражателем, и, будучи помещённым в точку расположения цели нормально по направлению облучения, создаёт в точке расположения РЛС ту же плотность потока мощности, что и реальная цель.
Величина имеет размерность площади и измеряется обычно в квадратных метрах.
ЭПР конкретного объекта зависит от его формы, размеров, материала из которого он изготовлен, а также от его ориентации по отношению к приёмнику и передатчику.
Содержание
- 1 Расчёт ЭПР
- 2 Физический смысл ЭПР
- 3 ЭПР распространённых точечных целей
- 3.1 Выпуклой поверхности
- 3.1.1 Плоской пластины
- 3.2 Шара
- 3.3 Уголкового отражателя
- 3.3.1 Треугольный
- 3.3.2 Четырёхугольный
- 3.3.3 Применение уголковых отражателей
- 3.4 Дипольного отражателя
- 3.5 ЭПР сложных целей (реальных объектов)
- 3.1 Выпуклой поверхности
- 4 ЭПР сосредоточенной цели
- 4.1 Диаграмма обратного рассеяния
- 5 Определение ЭПО распределённых целей
- 5.1 Условие распределённости цели
- 5.2 Удельное ЭПР
- 6 Примечания
- 7 Ссылки
Расчёт ЭПР
Если отражённая от цели мощность — это произведение ЭПР на плотность потока мощности
|
(1) |
где:
— отношение потока мощности отражённой волны к потоку мощности падающей,
где:
— плотность потока мощности отражённой от цели волны данной поляризации в точке расположения РЛС.
|
(2) |
где:
— расстояние от РЛС до цели;
Интегрируя поток мощности по всей поверхности сферы получаем полную мощность отражённой волны:
S — поверхность сферы.
Подставляя выражение (2) в (1) получаем ЭПР цели:
|
(3) |
где:
площадь сферы с радиусом дистанции до цели.
|
(4) |
где:
Что бы определить ЭПР цели надо определить напряжённость поля в точке расположения РЛС и направление отражённой волны.
Мощность на входе приёмника:
|
(5) |
— Эффективная площадь антенны.
Можно определить поток мощности падающей волны через излучённую мощность и КНД антенны.
|
(6) |
Подставляя (6) и (2) в (5) можем рассчитать мощность на входе приёмника РЛС:
|
|
(7) |
|
(8) |
где:
Если считать, что ![~P = frac{U_m^2}{2}Bigr|_{R=1[Ohm]}](https://dic.academic.ru/pictures/wiki/files/100/d6e01557fa9ba35376d8e9e897888882.png)
|
|
(9) |
Таким образом…
Физический смысл ЭПР
ЭПР имеет размерность площади [м2], но не является геометрической площадью(!), а является энергетической характеристикой, то есть определяет величину мощности принимаемого сигнала.
Аналитически ЭПР можно рассчитать только для простых целей. Для сложных целей ЭПР измеряется практически на специализированных полигонах, или в безэховых камерах.
ЭПР цели не зависит ни от интенсивности излучаемой волны, ни от расстояния между станцией и целью. Любое увеличение ρ1 ведёт к пропорциональному увеличению ρ2 и их отношение в формуле не изменяется. При изменении расстояния между РЛС и целью отношение ρ2 / ρ1 меняется обратно пропорционально R2 и величина ЭПР при этом остается неизменной.
ЭПР распространённых точечных целей
Для большинства точечных целей сведения о ЭПР можно найти в справочниках по радиолокации
Выпуклой поверхности
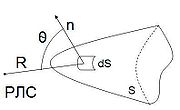
Поле от всей поверхности S определяется интегралом 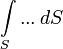
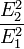
|
(10) |
где k — волновое число.
1) Если объект небольших размеров, то 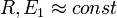
Тогда:
Плоской пластины
Плоская поверхность — частный случай криволинейной выпуклой поверхности.
|
|
(15) |
Если плоскость с площадью 1 м2, а длина волны 10 см (30 ГГц), то
Шара
Для шара 1-ой зоной Френеля будет зона, ограниченная экватором.
|
|
(16) |
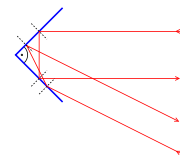
Уголкового отражателя
Принцип действия уголкового отражателя
Уголковый отражатель представляет собой три перпендикулярно расположенных поверхности. В отличии от пластины уголковый отражатель даёт хорошее отражение в широком диапазоне углов.
Треугольный
Если используется уголковый отражатель с треугольными гранями, то ЭПР
|
(17) |
где a — размер ребра.
Четырёхугольный
Если уголковый отражатель составлен из граней четырёхугольной формы, то ЭПР
|
(18) |
Применение уголковых отражателей
Уголковые отражатели применяются
- в качестве ложных целей
- как радио-контрасные ориентиры
- при проведении экспериментов сильного направленного излучения
Дипольного отражателя
Дипольные отражатели используются для создания пассивных помех работе РЛС.
Величина ЭПР дипольного отражателя зависит в общем случае от ракурса наблюдения, однако, ЭПР по всем ракурсам:
Дипольные тражатели используются для маскировки воздушных целей и рельефа местности, а так же как пассивные радиолокациионные маяки.
Сектор отражения дипольного отражателя составляет ~70°
ЭПР сложных целей (реальных объектов)
ЭПР сложных реальных объектов измеряются на специальных установках, или полигонах, где достежимы условия дальней зоны облучения.
| # | Тип цели | σц [м2] |
|---|---|---|
| 1 | Авиация | |
| 1.1 | Самолёт истребитель | 3-5 |
| 1.2 | Фронтовой бомбардировщик | 7-10 |
| 1.3 | Тяжёлый бомбардировщик | 13-20 |
| 1.3.1 | Бомбардировщик В-52 | 40 |
| 1.4 | Транспортный самолёт | 40-70 |
| 1.5 | «Стелс» | 0,0001..0,01 |
| 1.5.1 | Бомбардировщик, изготовленный по технологии «Стелс» B-2B[1] | 0,75 |
| 1.5.2 | Многоцелевой истребитель F-22 | 0,1-0,08 |
| 2 | Суда | |
| 2.1 | Подводная лодка в надводном положении | 30-150 |
| 2.2 | Рубка подводной лодки в надводном положении | 1-2 |
| 2.3 | Малые суда (до 200 тонн) | 50-200 |
| 2.4 | Средние корабли (1000..10000 тонн) | (3-10)2 |
| 2.5 | Большие корабли (больше 10000 тонн) | > 102 |
| 2.6 | Крейсер | ~12 000 — 14 000 |
| 3 | Наземные цели | |
| 3.1 | Автомобиль | 1-3 |
| 4 | Малые воздушные цели | |
| 4.1 | Крылатая ракета | 0,1-0,3 |
| 5 | Прочие цели | |
| 5.1 | Человек | 0,8-1 |
| 5.2 | Птица в полёте | ~0,8 |
ЭПР сосредоточенной цели
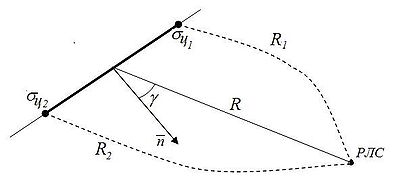
Двуточечная цель в разрешающем объёме локатора
Двуточечной целью будем называть пару целей, находящуюся в одном объёме разрешения РЛС. Используя формулу (4) можем найти амплитуды полей отражённой волны:
Временные задержки можно расчитать:
Отсюда:
К расчёту ЭПР двуточечной цели
тогда:
|
|
(23) |
Следовательно,
|
|
(26) |
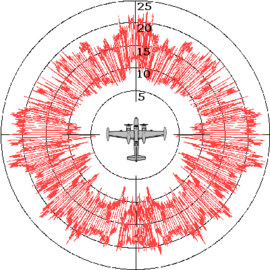
Диаграмма обратного рассеяния
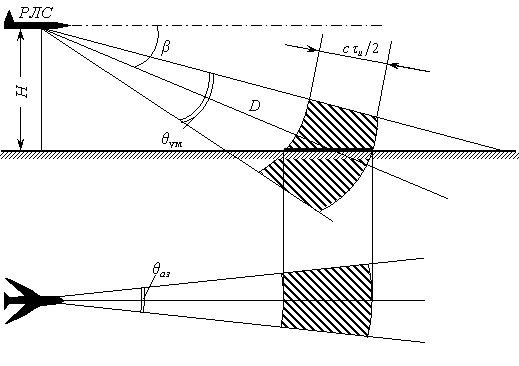
Зависимость ЭПР от угла отражения 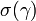
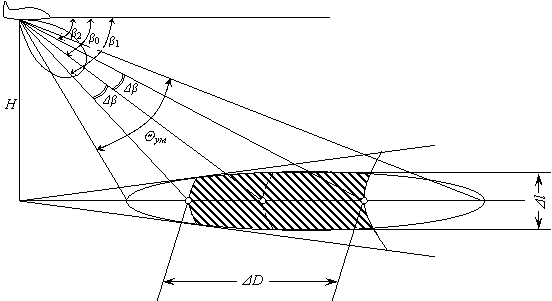
Пусть 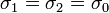
Реаьные объекты имеют несколько колеблящихся точек.
, а значит
.
Тогда суммарное поле:
— определяется, как изменение фазовых структур отражённой волны.
Фазовый фронт отражённой волны отличается от сферического.
Определение ЭПО распределённых целей
Распределённая цель — цель, размеры которой выходят за пределы разрешающего объёма РЛС
Условие распределённости цели
Нарушение любого из условий вводит цель в класс распределённых
Здесь:
Тоесть, линейные размеры цели должны полностью находиться внутри элемента разрешения РЛС.
Если это не так, то в этом случае ЭПР цели будет суммой ЭПР каждого элементарного участка цели:
.
Если распределённый объект состоит из изотропных однотипных отражателей с одинаковыми свойствами, то общее ЭПР можно найти, как произведение ЭПР на число отражателей:
Но число элементов такой цели обычно неизвестна!
Удельное ЭПР
В этом случае целесообразно ввести удельное ЭПР (σуд) — это ЭПР единичной площади (dS), или единичного объёма (dV) распределённой цели.
Здесь:
S и V целиком определяются размерами ширины диаграммы направленности и элементом разрешения по дальности, тоесть параметрами излучёного сигнала.
Примечания
- ↑ С некоторых ракурсов облучения и для некоторых длин волн
Ссылки
Что такое ЭПР — заметка в блоге dxdt.ru
Wikimedia Foundation.
2010.
Поток вектора Умова — Пойнтинга передающей антенны на расстоянии r от нее определяется по формуле $$begin{equation}p=p_{н}G=Gfrac{P_{изл}}{4pi{r^2}}end{equation}tag{2.142}$$
Перехватываемая антенной мощность зависит от такого параметра, как площадь апертуры (раскрыва) антенны. Для того чтобы лучше уяснить себе этот термин, представим приемную антенну в виде рупорной антенны, на которую падает плоская волна (рис. 2.57). Если бы эта антенна могла поглощать всю мощность, падающую на ее раскрыв (апертуру), то мощность, принятая антенной, была бы равна $$begin{equation}P=pAend{equation}tag{2.143} $$
Падающая на раскрыв антенны электромагнитная волна возбуждает в антенне с входным сопротивлением ZA=RА+iХА электродвижущую силу V. Часть принятой антенной мощности передается к приемнику, имеющему входное сопротивление Z0=R0+iX0 (рис. 2.58). Тогда ток, который проходит в приемник, подключенный к антенне, $$begin{equation}I_A=frac{V}{Z_0+Z_A}end{equation}tag{2.144}$$ а мощность, выделяемая в приемнике, $$begin{equation}P_0=I_A^2R_0=frac{V^2R_0}{left(R_A+R_0right)^2+left(X_A+X_0right)^2} end{equation}tag{2.145}$$
Достаточно просто показать, что максимальная мощность, выделяемая в приемнике, соответствует условию согласования сопротивлений, согласно которому RA=R0 и —ХA=Х0.
Введем понятие эффективной площади раскрыва, под которой будем понимать отношение мощности, попадающей в приемник Р0, к плотности мощности р, падающей на раскрыв антенны: $$begin{equation}A_{эфф}=frac{P_0}{p}end{equation}tag{2.146}$$
Для антенны без потерь (Rп=0) согласно формуле (2.136) RA=Rизл. Тогда при полном согласовании, т. е. при R0=Rизл получаем формулу для максимального значения эффективной площади раскрыва $$begin{equation}A_{эфф;max}=frac{V^2}{4pR_{изл}}=frac{I_A^2R_0}{p}end{equation}tag{2.147}$$
В табл. 2.4 приведены значения Aэфф max для некоторых типов антенн.
Для реальных антенн значение Aэфф max всегда меньше физической площади раскрыва антенны. Для оценки эффективной площади раскрыва антенны вводят понятие коэффициента использования поверхности раскрыва, равного отношению эффективной площади раскрыва антенны к физической площади раскрыва: $$begin{equation}K_{и.п.}=frac{A_{эфф}}{A_{ф}}end{equation}tag{2.148}$$
Максимальное значение коэффициента использования поверхности раскрыва достигает (для идеальных антенн) значения Kип=1. Для весьма хороших антенн значение коэффициента использования поверхности достигает значений 0,7 … 0,8.
Ток IA в антенне с сопротивлением излучения RA является источником переизлученной волны с мощностью $$begin{equation}P_{рас}=I_A^2R_Aend{equation}tag{2.149}$$
Отношение мощности, переизлученной антенной, к плотности мощности, падающей на раскрыв антенны р, определяет площадь переизлучения (апертуру рассеяния) Aрас: $$begin{equation}A_{рас}=frac{P_{рас}}{p}=frac{V^2R_A}{left(R_A+R_0right)^2+left(X_A+X_0right)^2}end{equation}tag{2.150}$$
Для короткозамкнутой антенны, полностью согласованной с падающим полем, Aрас = Aэфф max. При рассогласовании антенны $$begin{equation}alpha_{рас}=frac{A_{рас}}{A_{эфф;max}}end{equation}tag{2.151}$$ причем αрас ≤ 1.
Если сопротивление потерь Rп> 0, то часть энергии выделяется в антенне в виде тепловой энергии. Можно ввести понятие площади потерь $$begin{equation}A_{п}=frac{I_A^2R_п}{p}end{equation}tag{2.152}$$
Теперь суммарная апертура $$begin{equation}A_{sum}=A_{эфф}+A_{рас}+A_{п}=frac{I_A^2}{pleft(R_0+R_{изл}+R_{п}right)}end{equation}tag{2.153}$$
На рис. 2.59 приведены графики зависимости отдельных составляющих Ап и суммарной апертуры AΣ от отношения сопротивлений R0/Rизл.
Существует класс апертурных антенн. К таким антеннам относятся параболические антенны (здесь апертура — раскрыв зеркала), рупорные антенны (апертура — раскрыв рупора) и др.
Единицей измерения площади раскрыва может быть или квадратный метр, или λ2.
Коэффициент использования поверхности раскрыва определяется по формуле (2.148).
Для класса апертурных антенн Kи п < 1, но для некоторых типов антенн значение этой величины может и превышать 1. К последним относятся антенны поверхностной волны и большинство проволочных антенн.
Взаимосвязь между эффективной площадью раскрыва Aэфф, коэффициентом направленного действия D и длиной войны λ записывается в виде соотношения $$begin{equation}A_{эфф}=frac{lambda^2D}{4pi}end{equation}tag{2.154}$$
На рис. 2.60 приведены графики зависимости Aэфф(D, λ). Взаимосвязь между Aэфф и шириной диаграммы направленности в двух Плоскостях αE и αH можно установить, используя формулу (2.128).
Приемная антенна, поглощающая мощность электромагнитного поля при падении на нее электромагнитной волны, является своеобразным экраном для радиоволн. На рис. 2.61 схематично показано распределение поля за приемной антенной.
Из рисунка видно, что сразу за приемной антенной напряженность электромагнитного поля уменьшается.
Для полуволнового диполя эффективная площадь раскрыва представляет собой эллипс (рис. 2.62) с большой осью AE = 3λ/4 и малой осью AH = λ/4.
Для антенн поверхностной волны, например антенны Уда — Яги, взаимосвязь между линейными размерами эффективного раскрыва и ширинами диаграммы направленности антенны в двух основных плоскостях αE и αH устанавливаются соотношениями $$begin{equation}A_E=2sqrt{frac{A_{эфф}alpha_E}{pialpha_H}}end{equation}tag{2.155}$$ $$begin{equation}A_H=2sqrt{frac{A_{эфф}alpha_H}{pialpha_E}}end{equation}tag{2.156}$$
Если две или более элементарные антенны расположены вблизи друг от друга (например, одна над другой, рис. 2.63), то для уменьшения потерь усиления результирующей антенной системы необходимо, чтобы эффективные площади раскрыва парциальных элементов антенны не перекрывались. Наиболее целесообразно в этом случае располагать элементы антенной системы таким образом, чтобы края парциальных эффективных площадей раскрыва соприкасались друг с другом.
Для решетки излучателей поперечного излучения (рис. 2.64) линейные размеры эффективной площади раскрыва одного элемента вычисляются по формулам $$begin{equation}A_E=sqrt{frac{A_{эфф}alpha_E}{alpha_H}}end{equation}tag{2.157а}$$ $$begin{equation}A_H=sqrt{frac{A_{эфф}alpha_H}{alpha_E}}end{equation}tag{2.157б}$$
Сравнение формул (2.156) и (2.157) показывает, что в последнем случае линейные размеры эффективной площади раскрыва приблизительно на 12% меньше, чем при использовании этих же элементов в антеннах продольного излучения. Рассмотрим несколько примеров.
Пример 1. На зажимах приемной антенны, выполненной в виде полуволнового диполя, принимающего радиоизлучение с длиной волны λ = 2 м и нагруженного на сопротивление R0 = Rизл = 73 Ом, наведено напряжение UA = 0,1 мВ. Необходимо ‘рассчитать мощность излучения станции, расположенной на расстоянии r = 100 км от приемной антенны, при условии, что в качестве передающей антенны используется полуволновый диполь, а обе антенны ориентированы друг на друга максимумами диаграмм направленности.
1. Электродвижущая сила на выходе приемной антенны V = 2UA = 2·0,1·10-3 = 2·10-4 В.
2. Эффективная площадь раскрыва для полуволнового диполя (см. табл. 2.4) Aэфф = 0,13λ2 = 0,13·22 = 0,52 м2.
3. Плотность мощности в месте расположения приемной антенны p = V2/4AэффRизл = (2·10-4)2/4·0,52·73 = 2,63·10-10 Вт/м2.
4. Мощность излучения передающей антенны Pизл = 4πr2p/G = 4π(100·103)2·2,63·10-10/1,64 = 20,1 Вт.
Пример 2. Ширины диаграммы направленности антенны Уда-Яги, работающей на волне длиной λ = 2 м, равны αE = 25° и αH = 35°. Эта антенна нагружена на согласованное сопротивление R0 = 75 Ом. Плотность мощности электромагнитного поля, падающего на антенну, р=2,63·10-10 Вт/м2. Требуется определить напряжение на выходных клеммах данной антенны.
1. Используя номограмму, приведенную на рис. 2.54, по заданным значениям αE = 25° и αH = 35° определим усиление антенны G = 15,l дБ.
2. Используя графики, приведенные на рис. 2.60, по известным значениям G = 15,l дБ и α = 2 м определим Aэфф = 16,5 м2.
3. Используя формулу (2.147), определим ЭДС: $$V=sqrt{4pR_{изл}A_{эфф}}=sqrt{4cdot{2,63cdot{10^{-10}}cdot{73}cdot{16,5}}}=1,12 мВ$$
4. Напряжение на выходных клеммах антенны UA =V/2 = 0,56 мВ.
Пример 3. Необходимо рассчитать расстояние Н между этажами двухэтажной антенны типа Уда — Яги, при котором реализуется диаграмма направленности с шириной αE = 250 и αH = =35°, а усиление антенны максимально.
1. Используя графики, приведенные на рис. 2.60, по заданным значениям αE и αH, определим эффективную площадь раскрыва Aэфф = 4,5λ2.
2. Используя формулу (2.156), найдем: $$H=A_H=2sqrt{frac{A_{эфф}alpha_H}{alpha_E}}=sqrt{frac{4,3lambda^2{35}}{25}}=2,8lambda$$
3. При расстоянии между этажами двухэтажной антенны Н = 2,8λ получаем максимальное значение коэффициента усиления, которое, как нам уже известно, реализуется при условии, что края эффективных площадей раскрыва обоих элементов антенны соприкасаются друг с другом.
4. Для длины волны λ = 2 м искомое расстояние Н = 5,6 м.
Отметим, что двойное увеличение апертуры антенны приводит к двукратному росту усиления (+3 дБ).
Для расчета радиолиний связи вводится понятие множителя ослабления δ: $$begin{equation}delta=frac{P_A}{P_{изл}}=frac{A_{эфф.пр}A_{эфф.пер}}{lambda^2{r^2}}end{equation}tag{2.158}$$ где PA — мощность, принятая приемной антенной, имеющей эффективную площадь раскрыва Aэфф пр; Pизл — мощность, излученная передающей антенной, имеющей эффективную площадь раскрыва Aэфф пер; r — расстояние между передающей и приемной антеннами, м; λ — длина волны, м.
Формула (2.158) получена в предположении, что антенны не имеют потерь, ориентированы относительно друг друга наилучшим образом, а также при условии, что расстояние между ними $$begin{equation}rgeqfrac{2d^2}{lambda}end{equation}tag{2.159}$$ где d — наибольший линейный размер антенны; λ — длина волны.
В том случае, когда радиоволна распространяется вблизи поверхности земли, может возникнуть, кроме прямой волны, и отраженная волна. Результатом взаимодействия этих двух волн является изменение величины δ, рассчитанной по формуле (2.158). Реальное значение множителя ослабления δР изменяется в пределах 0 < δр < 4δ.
Продолжим рассмотрение примеров.
Пример 4. Мощность излучения передающей полуволновой дипольной антенны Pизл = 20,1 Вт. Необходимо рассчитать мощность, выделяемую в согласованной нагрузке приемной антенны при R0 = 73 Ом и условии, что Aэфф пер = 16,5 м2, Aэфф пр = 0,13 м2 и λ = 2 м.
1. Используя формулу (2.158), найдем $$P_A=P_{изл}frac{A_{эфф.пер}A_{эфф.пр}}{lambda^2{r^2}}=20,1frac{0,13cdot{2^2}cdot{16,5}}{2^2left(10^5right)^2}=43cdot{10^{-10}} Вт$$
2. Напряжение на выходных клеммах антенны $$U=sqrt{P_{A}R_{0}}=sqrt{43cdot{10^{-10}}cdot{73}}=0,53cdot{10^{-3}} В$$.
Обратим внимание читателя на тот факт, что иногда мощность выражается в децибелах, при этом уровень 0 дБ соответствует мощности в 1 Вт.
Пример 5.
Если Ризл = 20,1 Вт или Ризл = 10·lg 20,1 = +13 дБ/Вт, то РA = = 43·10-10 Вт или РA = 10·lg 43·10-10 = —83,6 дБ/Вт.












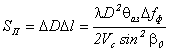





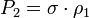 ,
,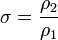 — отношение потока мощности отражённой волны к потоку мощности падающей,
— отношение потока мощности отражённой волны к потоку мощности падающей,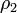 — плотность потока мощности отражённой от цели волны данной поляризации в точке расположения РЛС.
— плотность потока мощности отражённой от цели волны данной поляризации в точке расположения РЛС.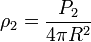 ,
,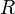 — расстояние от РЛС до цели;
— расстояние от РЛС до цели;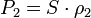
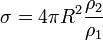 ,
,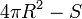 площадь сферы с радиусом дистанции до цели.
площадь сферы с радиусом дистанции до цели.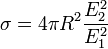 ,
,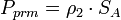 ,
,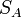 — Эффективная площадь антенны.
— Эффективная площадь антенны.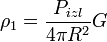 ,
,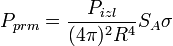
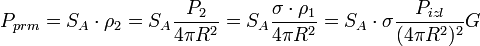
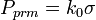 ,
,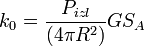
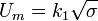
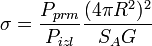
![sigma[db] = 10lgfrac{sigma}{sigma_0}](https://dic.academic.ru/pictures/wiki/files/56/866568dc4f07382be711720add416ee6.png)
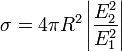
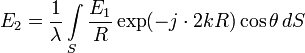 ,
,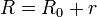
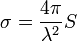
![sigma = frac{4piapprox 12}{10^210^{-4}}approx 1200[m^2]](https://dic.academic.ru/pictures/wiki/files/57/9ba8d6afdb5727090c3e40994be4f974.png)
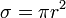
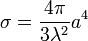 ,
,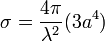 ,
,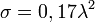
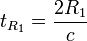
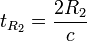
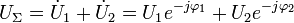
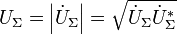
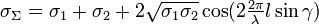
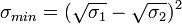
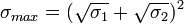
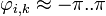 , а значит
, а значит 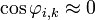 .
.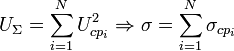
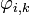 — определяется, как изменение фазовых структур отражённой волны.
— определяется, как изменение фазовых структур отражённой волны.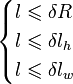
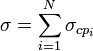 .
.