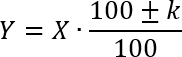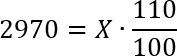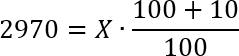Простейшие формулы помогут узнать, выгодны ли скидки, и не нарушить пропорцию классного рецепта.
1. Как посчитать проценты, разделив число на 100
Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.
Пример 1
Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.
Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.
Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.
Умножьте 4,58 на 7, и вы получите 32,06 рубля.
Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.
Пример 2
Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.
Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.
Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.
100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.
2. Как посчитать проценты, разделив число на 10
Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.
Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.
Пример
Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.
В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.
Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.
Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.
В любом случае такими крупными числами оперировать довольно просто.
3. Как посчитать проценты, составив пропорцию
Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:
сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.
Или можно записать её так: a : b = c : d.
Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.
Пример 1
Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.
Сначала вычисляем процентную долю оставшегося шоколада.
90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.
Х = 70 × 100 / 90 = 77,7%.
Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:
200 г : 100% = Х : 77,7%, где Х — нужное количество масла.
Х = 77,7 × 200 / 100 = 155,4.
Следовательно, в тесто нужно положить примерно 155 г масла.
Пример 2
Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.
Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.
Составьте пропорцию: 1 499 : 100 = Х : 87.
Х = 87 × 1 499 / 100.
Заплатите 1 304,13 рубля и носите блузку с удовольствием.
4. Как посчитать проценты с помощью соотношений
В некоторых случаях можно воспользоваться простыми дробями. Например, 10% — это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.
- 20% — 1/5, то есть нужно делить число на 5;
- 25% — 1/4;
- 50% — 1/2;
- 12,5% — 1/8;
- 75% — это 3/4. Значит, придётся разделить число на 4 и умножить на 3.
Пример
Вы нашли брюки за 2 400 рублей со скидкой 25%, но у вас в кошельке только 2 000 рублей. Чтобы узнать, хватит ли денег на обновку, проведите серию несложных вычислений:
100% — 25% = 75% — стоимость брюк в процентах от первоначальной цены после применения скидки.
2 400 / 4 × 3 = 1 800. Именно столько рублей стоят брюки.
5. Как посчитать проценты с помощью калькулятора
Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.
- Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
- Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
- Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.
6. Как посчитать проценты с помощью онлайн-сервисов
Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах.
Planetcalc
На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.
Planetcalc→
Калькулятор — справочный портал
Ещё один сервис с калькуляторами на любой вкус.
Калькулятор — справочный портал→
Allcalc
Каталог онлайн-калькуляторов, 60 из которых предназначены для подсчёта финансов. Можно вычислить налоги и пени, размер субсидии на ЖКУ и многое другое.
Allcalc→
Читайте также 📑
- ТЕСТ: Умеете ли вы считать в уме?
- Математические игры — отличная разминка для мозга
- 11 книг, которые прокачают математическое мышление
- Как выучить таблицу умножения легко и быстро
Формула простого процента: как найти исходное значение
13 ноября 2013
В этом коротком видеоуроке мы научимся решать задачи на проценты с помощью специальной формулы, которая так и называется: формула простого процента. Давайте оформим эту формулу в виде теоремы.
Теорема о простом проценте. Предположим, что есть некая исходная величина x, которая затем меняется на k%, и получается новая величина y. Тогда все три числа связаны формулой:
Плюс или минус перед коэффициентом k ставится в зависимости от условия задачи. Если по условию величина x возрастает, то перед k стоит плюс. Если же величина уменьшается, то перед коэффициентом k стоит минус.
Несмотря на кажущуюся мудреность этой формулы, многие задачи с ее помощью решаются очень быстро и красиво. Давайте попробуем.
Задача. Цена на товар была повышена на 10% и составила 2970 рублей. Сколько рублей стоил товар до повышения цены?
Чтобы решить эту задачу с помощью формулы простых процентов, нам необходимы три числа: исходное значение x, проценты k и итоговое значение y. Из всех трех чисел нам известны проценты k = 10 и итоговое значение y = 2970. Обратите внимание: 2970 — это именно итоговая цена, т.е. y. Потому что по условию задачи исходная цена на товар неизвестна (ее как раз требуется найти). Но затем она была повышена, и только тогда составила 2970 рублей.
Итак, нам нужно найти x, т.е. исходное значение. Что ж, подставляем наши числа в формулу и получаем:
Складываем числа в числителе и получаем:
Сокращаем по одному нулю в числителе и знаменателе, а затем умножаем обе части уравнения на 10. Получим:
11x = 29 700
Чтобы найти x из этого простейшего линейного уравнения, нужно разделить обе стороны на 11:
x = 29 700 : 11 = 2700
Как видите, это довольно большие числа, поэтому в уме такие вычисления не провести. В случае, если такая задача встретится вам на ЕГЭ, придется делить уголком. При этом все разделилось без остатка, и мы получили значение x:
x = 2700
Именно столько стоил товар до повышения цены. И именно это число нам требовалось найти по условию задачи. Поэтому все: задача решена. Причем решена не «напролом», а с помощью формулы простого процента — быстро, красиво и наглядно.
Разумеется, эту задачу можно было решать по-другому. Например, через пропорции. Или экзотическим методом коэффициентов. Но будет гораздо лучше и надежнее, если у вас на вооружении будет несколько приемов для решения любой задачи на проценты. Так что обязательно попрактикуйтесь в использовании данной формулы.
А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Смотрите также:
- Процент: неизвестно начальное значение (метод пропорции)
- Формула простого процента: неизвестно конечное значение
- Решение ЕГЭ-2011: вариант 1, часть B
- Метод коэффициентов, часть 1
- Деление многочленов уголком
- Сфера, вписанная в куб
Enter the current sale price and the percent off of the original price to calculate the original price of a good. This calculate can also determine the sale price or percentage off given the original price and other variable.
- All Price Calculators
- Discount Factor Calculator
- Double Discount Calculator
- Triple Discount Calculator
- Price Variance Calculator (VMP)
Original Price Formula
The following equation is used to calculate the original price of a good on discount.
- Where OP is the original price ($)
- SP is the current sale price ($)
- PO is the total percent off
To calculate the original price of an item, divide the sale price by the value of 1 minus the value of the percentage off divided by 100.
Original Price Definition
An original price is defined as the original price an object is sold at before a discount is applied.
Original Price Example
The following is an example of how to calculate the original price of a discounted item.
- First, determine the sale price. This is usually the price found on the sticker. For this example, we will say 50$ is the sale price.
- Next, determine the percent off. For this example, we will assume a discounted rate of 25%.
- Finally, enter these values into the formula above. This yields an original price of 66.67$.
FAQ
What is a percent off?
A percent off, also known as a discount, is a reduction in the price of an item that makes the good “on-sale”.
What is a normal percent off?
Anything above 25% off is considered a great deal. Be wary of businesses increasing their price, then claiming a large discount that only gets it back to the original price before it was increased.

Сколько выйдет % из ?
Результат:
Ответ ={Процентыболее 100}раз Всего.
какой это процент ?
Результат:
Ответ ={Частьв сумме}умножить на 100.
является % которого??
Результат:
Ответ ={Частьв процентах}умножить на 100.
На сколько процентов увеличилось/уменьшилось и ?
Результат:
Ответ ={Конечное значение-Начальное значение превышающее начальное значение} умноженное на 100
Вы ищете способ легко производить вычисления с использованием процентов? Если это так, то калькулятор процентов — это именно то, что вам нужно! Этот удобный инструмент позволяет легко вычислить, на сколько процентов одно число отличается от другого, какое число соответствует определенному проценту от другого числа, а также сложить или вычесть проценты из числа.
Калькулятор разработан специально для расчета процентов и предлагает множество других функциональных возможностей, когда дело доходит до работы с процентами. Он состоит из четырех различных калькуляторов, которые адаптированы к вашим потребностям в вычислениях. При каждом вычислении результат округляется до требуемых знаков после запятой для дополнительного уровня точности и удобства. Так зачем же ждать? Получите в свои руки калькулятор процентов уже сегодня и сделайте эти процентные вычисления проще, чем когда-либо прежде!
Проценты
Наш простой процентный калькулятор рассчитывает ежемесячные платежи по кредиту только с процентами. Просто укажите процентную ставку, и вы узнаете, сколько стоит этот кредит.
Разница между «просто» процентами и платежом по ипотеке проста: с помощью ипотечного калькулятора каждый месяц вы выплачиваете часть основного долга, а остаток по кредиту становится все меньше и меньше. С помощью калькулятора простых процентов выплачиваются только проценты. Сумма кредита остается неизменной навсегда. Со временем ничего не меняется.
Простые проценты могут быть использованы как при взятии взаймы, так и при одалживании денег. В первом случае проценты добавляются к отдельной стопке денег каждый месяц (и не облагаются дополнительными процентами в следующем месяце).
Если вы хотите рассчитать процентную ставку, вы можете легко использовать наш Калькулятор процентной ставки как для кредитов, так и для депозитов.
Что такое процент?
Процент — одно из наиболее часто используемых слов в финансах. Студенты-экономисты знакомятся с этим термином уже на первых лекциях. Финансовые консультанты, финансовые служащие, биржевые маклеры, банкиры, инвестиционные менеджеры и другие финансовые эксперты используют этот термин сотни раз в своей повседневной деятельности. Итак, в начале этой статьи мы попытаемся ответить на вопрос «Что такое процент?». Позже вы найдете ответы на следующие вопросы:
- Что такое простые проценты?
- В чем разница между простыми процентами и сложными процентами?
- Какова формула уравнения простых процентов и как найти значение простых процентов?
- Каковы реальные примеры кредита под простые проценты?
В следующих разделах мы также покажем вам несколько примеров простого расчета процентов. Но всему свое время. Начнем с определения проценты.
Как правило, проценты — это стоимость займа денег. Это цена, которую заемщик платит кредитору за использование его денег. Процент обычно выражается в процентах (%) от первоначальной суммы (основной суммы, остатка).
Проценты могут быть как простыми, так и сложными. Простые проценты основаны на первоначальной сумме, а сложные проценты основаны на исходной сумме и процентах, которые накапливаются на нее в каждом периоде.
Определение процентной ставки
В финансах процентная ставка определяется как сумма, которую кредитор взимает с заемщика за использование активов. Таким образом, можно сказать, что для заемщика процентная ставка — это стоимость долга, а для кредитора — норма прибыли.
Обратите внимание, что если вы делаете депозит в банке (например, кладете деньги на свой сберегательный счет), с финансовой точки зрения это означает, что вы даете деньги в долг банку. В таком случае процентная ставка отражает вашу прибыль.
Процентная ставка обычно выражается в процентах от основной суммы (непогашенной ссуды или стоимости депозита). Обычно он предоставляется ежегодно. В этом случае это называется годовой процентной доходностью (APY) или эффективной годовой ставкой (EAR).
Простые и сложные проценты
Простые проценты используются для оценки процентов, полученных или выплаченных на определенный остаток (первоначальную сумму) в течение определенного периода. Простые проценты не учитывают эффект начисления сложных процентов. Начисление процентов означает начисление процентов на проценты. Другими словами, при начислении сложных процентов вы зарабатываете проценты не только на основную сумму, но и на проценты, полученные за предыдущие периоды. Это важная информация, поскольку она означает, что простые проценты могут занижать сумму процентов, полученных или выплаченных за рассматриваемый период.
Если вы хотите предположить, что проценты за предыдущие периоды влияют на первоначальную сумму, вы должны применить сложные проценты. Подробную информацию о сложных процентах вы найдете в нашем калькуляторе сложных процентов. Здесь мы упомянем только его самое основное определение, в котором говорится, что сложные проценты — это проценты, начисленные на первоначальную основную сумму, а также проценты, накопленные в течение последовательных периодов.
Обратите внимание, что, поскольку простые проценты рассчитываются только на исходную сумму, их гораздо проще определить, чем сложные проценты. Однако с нашими калькуляторами вы не почувствуете разницы.
Определение простых процентов и формула простых процентов
Согласно общепринятому определению, простые проценты — это проценты, которые выплачиваются или начисляются на первоначальную сумму кредита или сумму депозита. Формула простых процентов:
проценты = сумма * процентная_ставка
Знаете ли вы, что термин простые проценты был впервые использован в 1798 году? (В том же году слова «проценты» и «оборотный капитал» впервые появились и в английском языке).
Как рассчитать простые проценты?
Вам интересно, как рассчитать простые проценты? Вот пример, который должен помочь вам понять это.
Предположим, вы положили на свой сберегательный счет 1000 рублей. Это так называемая исходная сумма. (Обратите внимание, что вы также можете рассматривать эти 1000 рублей как первоначальную стоимость вашего кредита с простыми процентами).
- Прежде всего, возьмите процентную ставку и разделите ее на сто. 5% = 0,05.
- Затем умножьте исходную сумму на процентную ставку. 1000 рублей * 0,05 = 50 рублей. Вот и все. Вы только что рассчитали свой годовой процент!
- Чтобы получить ежемесячный процент, разделите это значение на количество месяцев в году (12). 50 рублей / 12 = 4,17 рублей. Таким образом, ваш ежемесячный процент составляет 4,17 рубля. Если первоначальные 1 000 рублей – это депозит, это будет ваша ежемесячная прибыль. Если эти 1000 рублей является кредитом, это значение представляет собой ваши ежемесячные платежи.
Теперь попробуем произвести дальнейшие расчеты.
Если вы хотите рассчитать сумму процентов, выплаченных за определенный период, все, что вам нужно сделать, это умножить ежемесячные проценты на соответствующее количество месяцев или лет.
Например, вы можете рассчитать общую сумму процентов, которую вы получите в течение следующих двух с половиной лет. Для этого вам нужно умножить 4,17 рублей на 30 (2 года = 24 месяца, полгода = 6 месяцев). 4,17 * 30 = 120,83 рубля.
Очевидно, что все вышеперечисленные расчеты можно сделать быстро и безболезненно с помощью нашего умного калькулятора. При тестировании этого инструмента не забудьте попробовать расширенный режим.
Пример простых процентов на практике
Вы унаследовали 1 000 000 рублей и намерены использовать их для получения стабильного дохода — вы не хотите ни тратить их, ни инвестировать. Вы кладете их на банковский счет с процентной ставкой 5% годовых. Каждый год вы получаете 50 000 рублей (5 % от 1 миллиона рублей). Каждый месяц вы будете получать 4 166,67 рублей (1/12 от 50 000 рублей). Неважно, сколько времени пройдет, у вас все еще будет 1 миллион рублей на этом счете.
Альтернатива — сложные проценты
Но что, если бы вы оставили эти дополнительные деньги на счете? Тогда эти проценты будут продолжать работать на вас, и каждый месяц остаток на счете будет увеличиваться (и все это станет инвестицией. Для простоты предположим, что проценты начисляются ежегодно (начисляются один раз в год).
- в конце первого года у вас будет 1 050 000 рублей (1 миллион рублей плюс 5%).
- в конце второго года у вас будет 1 102 500 рублей (1 050 000 рублей плюс 5 %).
- 3-й год — 1 157 625 рублей.
- 10-й год — 1 628 894,63 рублей.
- 50-й год — 11 467 399,79 рублей.
- 100-й год – 131 501 257,85 рублей.
Вот это уже кое-что, не так ли? Вы не будете получать свои 4166 рублей каждый месяц, но через 100 лет у вас будет в 131 раз больше в банке.
Реальные примеры займов под простые проценты
Что ж, не все получат в наследство 1 000 000 рублей (хотя мы искренне вам этого желаем). Однако это не значит, что в повседневной жизни вы не встретите простого интереса. Типичными примерами использования простых процентов являются
-
автокредиты,
-
кредитные линии (например, кредитные карты),
-
скидки при досрочном погашении.
-
Предположим, вы берете автокредит под простые проценты. Если автомобиль стоит 5000 долларов, а у вас нет сбережений, для его финансирования вам потребуется занять 5000 долларов. Это основная сумма автокредита. Зная, что годовая процентная ставка составляет 3% и кредит должен быть погашен в течение одного года, вы можете рассчитать простые проценты по этому кредиту следующим образом:
$5,000 * 3% = $150
В итоге вам нужно будет вернуть основную сумму плюс проценты. Так:
$5,000 + $150 = $5,150
- Предположим, что у вас есть кредитная карта с лимитом в 2500 рублей и процентной ставкой 15% без начисления сложных процентов*. В предыдущем месяце вы купили товаров на 1800 рублей, а в начале этого месяца заплатили только минимальную сумму, которая составляла 100 рублей. Это означает, что у вас осталось 1700 рублей на балансе. Проценты, которые будут начисляться на вашу кредитную карту в этом месяце, составляют:
$1,700 * 15% / 12 = $21.25
Однако имейте в виду, что кредитные карты обычно имеют сложные процентные ставки. Простые проценты по кредитным картам в наше время — это нечто экстраординарное (Ну, попробуйте догадаться, почему…)
- Скидки на досрочные платежи используются в основном в бизнесе. Продавец может предложить скидку своему подрядчику, чтобы побудить его оплатить счет наличными или досрочно. Например, выставитель счета на 30 000 долларов может предложить скидку 0,2% при оплате в течение недели после покупки. Это означает, что сумма скидки составляет:
$30,000 * 0,2% = $60
Итак, покупателю придется заплатить:
$30,000 - $60 = $29,940
Можете ли вы рассчитать годовую процентную ставку этой скидки? Попробуйте сделать это самостоятельно и проверьте результат на нашем удобном калькуляторе.
Простая процентная ставка и бессрочный срок
Чтобы объяснить, что такое бессрочная рента, мы должны начать с термина рента. В наиболее интуитивном смысле аннуитет — это серия платежей, которые производятся в течение определенного периода через равные промежутки времени. Бессрочная рента — это особый вид ренты, которая не имеет конца. Другими словами, мы могли бы сказать, что бессрочный платеж — это поток платежей, который продолжается вечно (неопределенно долго).
Предполагая, что платежи начинаются в конце первого периода, ежемесячный платеж на бессрочный период рассчитывается по следующей формуле:
ежемесячный платеж = основная сумма * процентная_ставка
Обратите внимание, что приведенная выше формула не случайно очень похожа на формулу простых процентов, представленную в разделе «Определение простых процентов и формула простых процентов» (проценты = сумма * процентная_ставка). По сути, мы вычисляем одно и то же значение, только имена переменных изменились.
Вам интересно, какова стоимость основной суммы, которая гарантирует, что вам больше не придется работать? Предположим, что для этого вам нужен годовой доход, равный 100 000 долларов. Мы также должны предположить, что процентная ставка составляет 4% и постоянна во времени. Таким образом:
100 000 долларов США = основная сумма * 4%
Так:
основная сумма = 100 000 долларов США / 4% = 2 500 000 долларов США
Хм… довольно много, не так ли?
К сожалению, даже если бы у вас была такая сумма, в настоящее время существует всего несколько финансовых продуктов, основанных на концепции бессрочных сделок. Однако в прошлом их выпускали многие финансовые учреждения (страховые компании и банки) и даже правительства. Например, так называемые консоли были выпущены британским правительством и окончательно погашены в 2015 году.
Дальнейшие расчеты процентной ставки
Теперь вы знаете, что такое простые проценты и как их рассчитать. Так что самое время познакомиться с более сложными понятиями финансовой математики.
Несомненно, термин, который больше всего ассоциируется с простыми процентами, — это сложные проценты. Мы уже описывали эту идею в одном из предыдущих разделов. Но знаете ли вы, что расчеты, основанные на сложных процентах, могут использоваться для расчета будущей стоимости ваших инвестиций или сбережений? Все, что вам нужно сделать, это использовать один из наших калькуляторов. В начале мы предлагаем попробовать калькулятор будущей стоимости, калькулятор инвестиций и калькулятор сбережений.
Вам также может быть интересно, как сравнить несколько предложений банковского депозита (или кредита), если они имеют разные сроки начисления процентов и разные процентные ставки. Для этого вам необходимо рассчитать годовую процентную доходность, также известную как эффективная годовая ставка (EAR). Это значение говорит вам, какова процентная ставка на годовой основе, и, таким образом, помогает вам принять наилучшее (то есть наиболее разумное) финансовое решение. Мы считаем, что наиболее удобный способ сделать это — использовать наш калькулятор. Однако вы также можете сделать это самостоятельно. Если вы не знаете, как это сделать, прочитайте описание калькулятора APY, где все подробно объясняется.
Еще одна интересная вещь, которую вы можете сделать, углубившись в расчет процентов, — это вычислить, сколько времени потребуется, чтобы увеличить ваши инвестиции на n%. Вам интересно, сколько времени вам нужно, чтобы удвоить ваши первоначальные инвестиции? Утроить? Мы предлагаем вам использовать наш умный калькулятор правила.
В этом уроке мы узнаем, как найти первоначальную цену, учитывая цену продажи и процентную скидку.
Правила поиска первоначальной цены с учетом цены продажи и процентной скидки
Сначала рассмотрим неизвестную первоначальную цену как « х ».
Тогда рассмотрим ставку дисконта.
Чтобы найти фактическую скидку, умножьте ставку дисконта на исходную сумму « х ».
Чтобы найти продажную цену, вычтите фактическую скидку из первоначальной суммы « х » и сравните ее с данной продажной ценой.
Решите уравнение и найдите исходную сумму « х ».
Письменный стол продается со скидкой 36%. Цена продажи составляет $ 496. Какова была его первоначальная цена?
Шаг 1:
Пусть первоначальная цена будет = х
Дисконтная ставка = 36%
Шаг 2:
Скидка = 36% от х = 0,36 х х = 0,36 х
Цена продажи = Первоначальная цена – Скидка = x – 0.36 x = 0.64 x
Шаг 3:
Цена продажи = $ 496 = 0,64 х
Решение для х
x = $ frac {496} {0.64} = $ 775
Итак, первоначальная цена = 775 $
Если Play Station была куплена за 558 долларов США со скидкой 10%, какова была первоначальная цена Play Station?
Шаг 1:
Пусть первоначальная цена будет = х
Дисконтная ставка = 10%
Шаг 2:
Скидка = 10% от х = 0,10 × х = 0,1 х
Цена продажи = Первоначальная цена – Скидка = х – 0,1 х = 0,9 х
Шаг 3:
Цена продажи = $ 558 = 0,9 х
Решение для х
x = $ frac {558} {0.9} = $ 620
Итак, первоначальная цена = 620 $