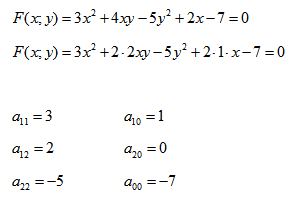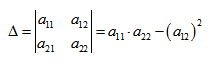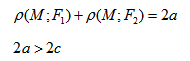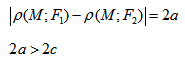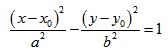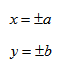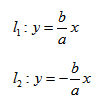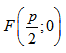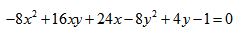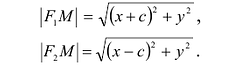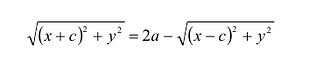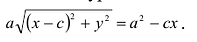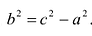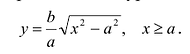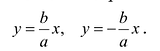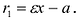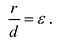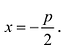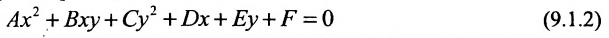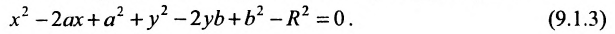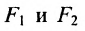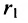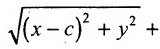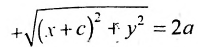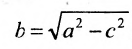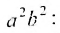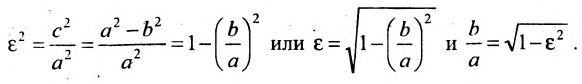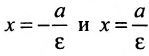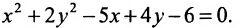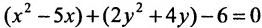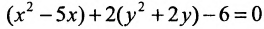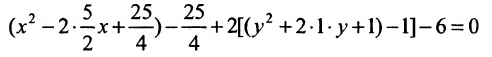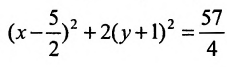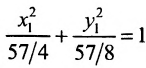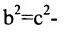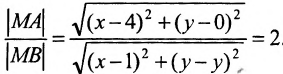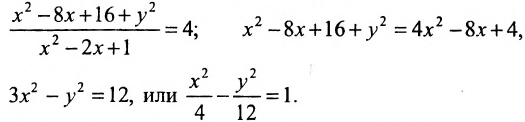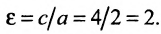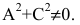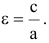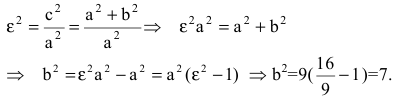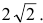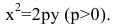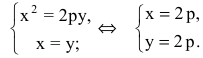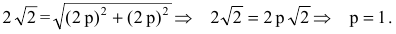|
|
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.или можно встретить следующую форму записи: К кривым второго порядка относятся окружность, эллипс, гипербола и парабола. |
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ < 0, кривая второго порядка гиперболического типа.
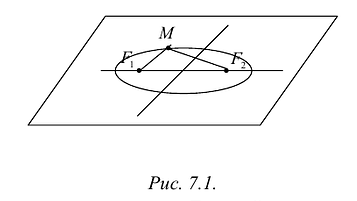
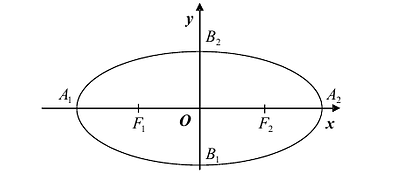
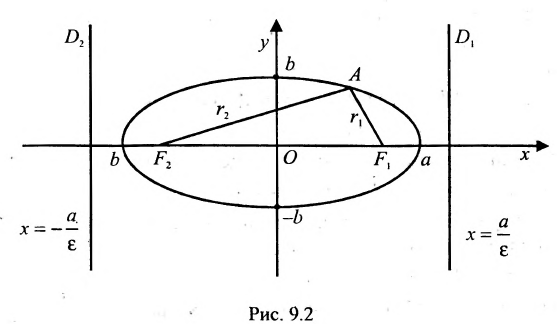
Эллипс — множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 есть величина постоянная, большая расстояния между этими точками.
F1 и F2 — фокусы.
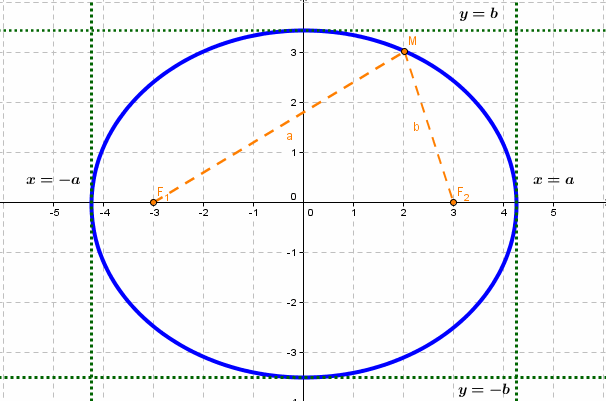 |
с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус. |
Каноническое уравнение эллипса с центром симметрии в начале координат:
2а — большая ось эллипса, 2b — малая ось эллипса.
а — большая полуось эллипса, b — малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
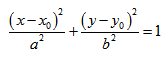
Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
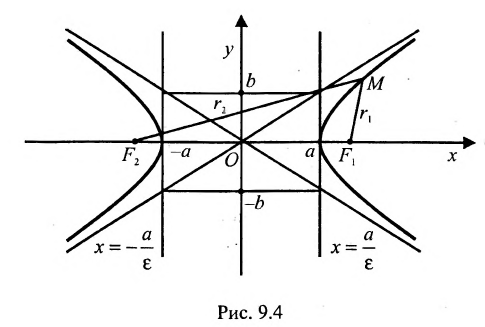
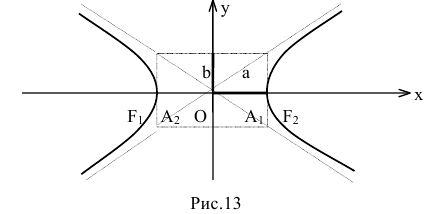
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
F1 и F2 — фокусы.
 |
с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус. А1(-а;0), А2(а;0) — вершины. |
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:

x — действительная ось, y — мнимая ось.
а — действительная полуось, b — мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 — правая директриса, f2 — левая директриса.
Уравнения директрис:
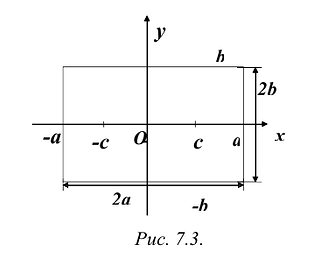
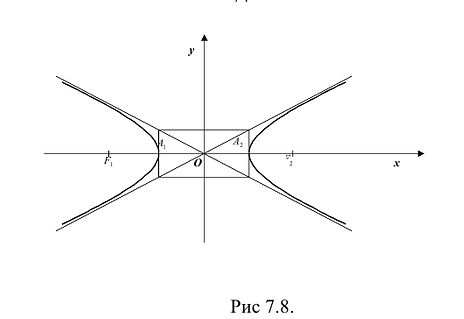
Порядок построения гиперболы:
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А1(-а;0), А2(а;0).
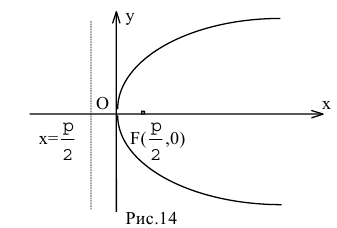
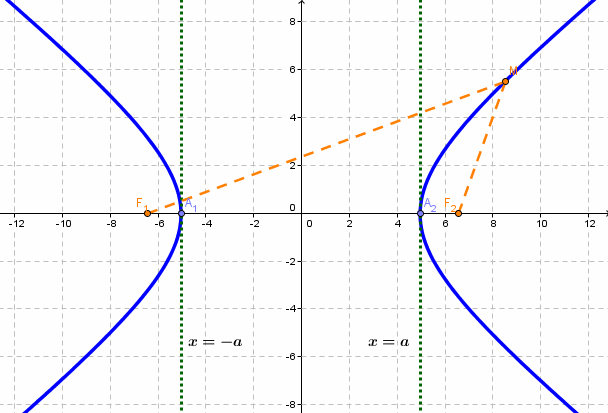
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
 |
р — фокальное расстояние Фокус параболы: Директриса параболы: |
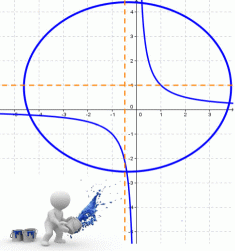
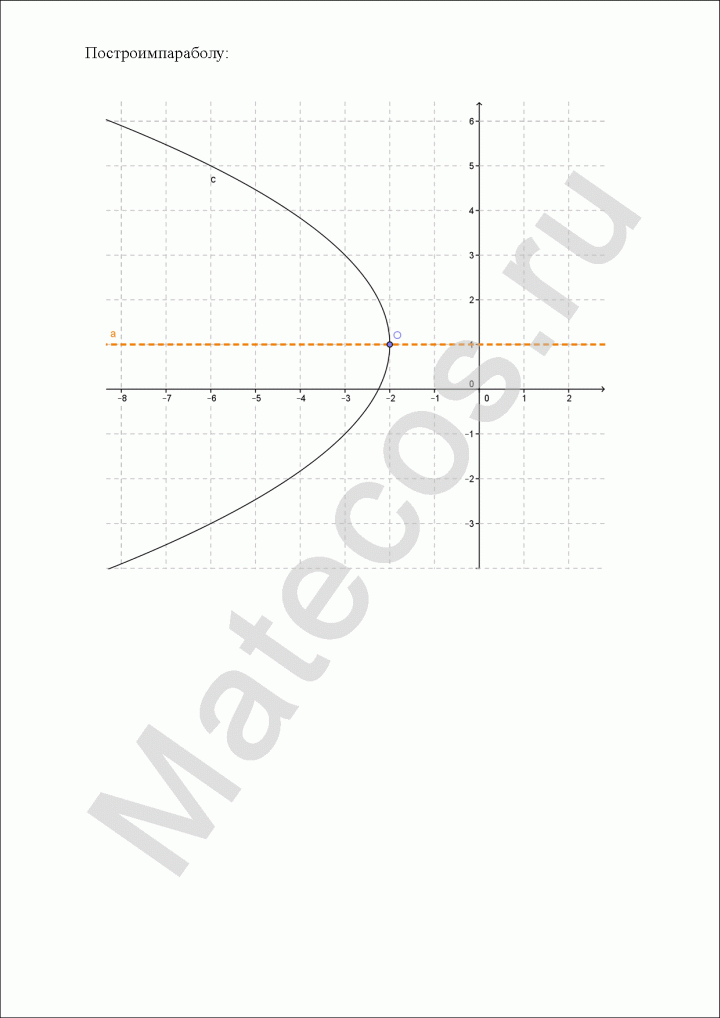
Пример по теме кривые второго порядка №1
Привести к каноническому виду и построить график кривой второго порядка.

Пример по теме кривые второго порядка №2
По виду уравнения определить тип кривой и нарисовать ее в декартовой системе координат:
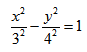
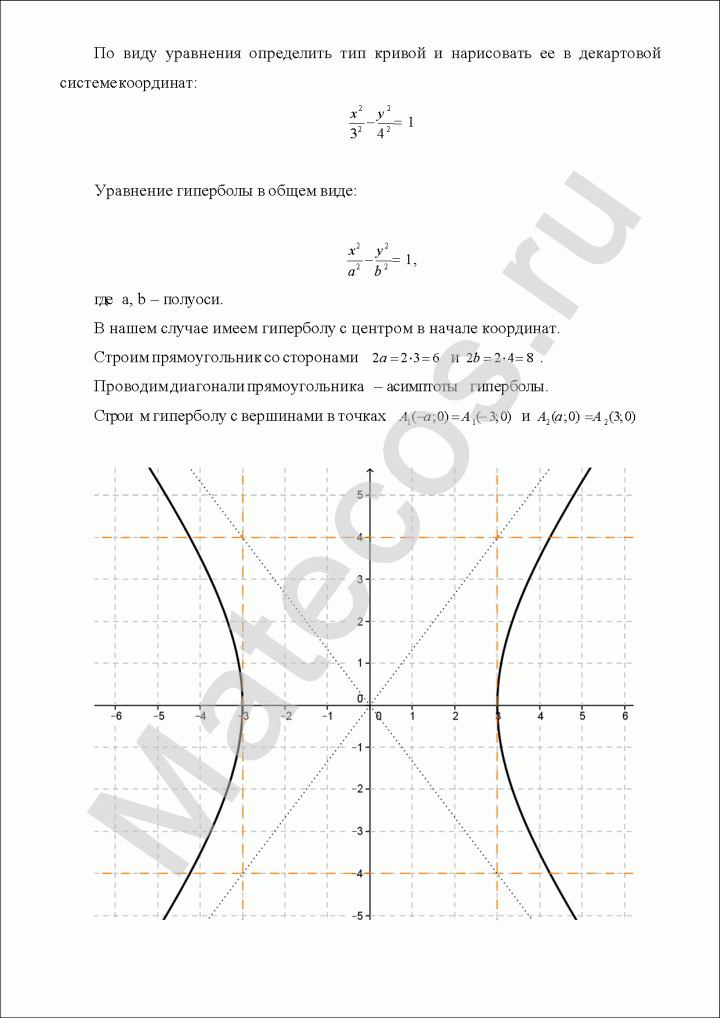
Пример по теме кривые второго порядка №3
Построить кривую второго порядка:
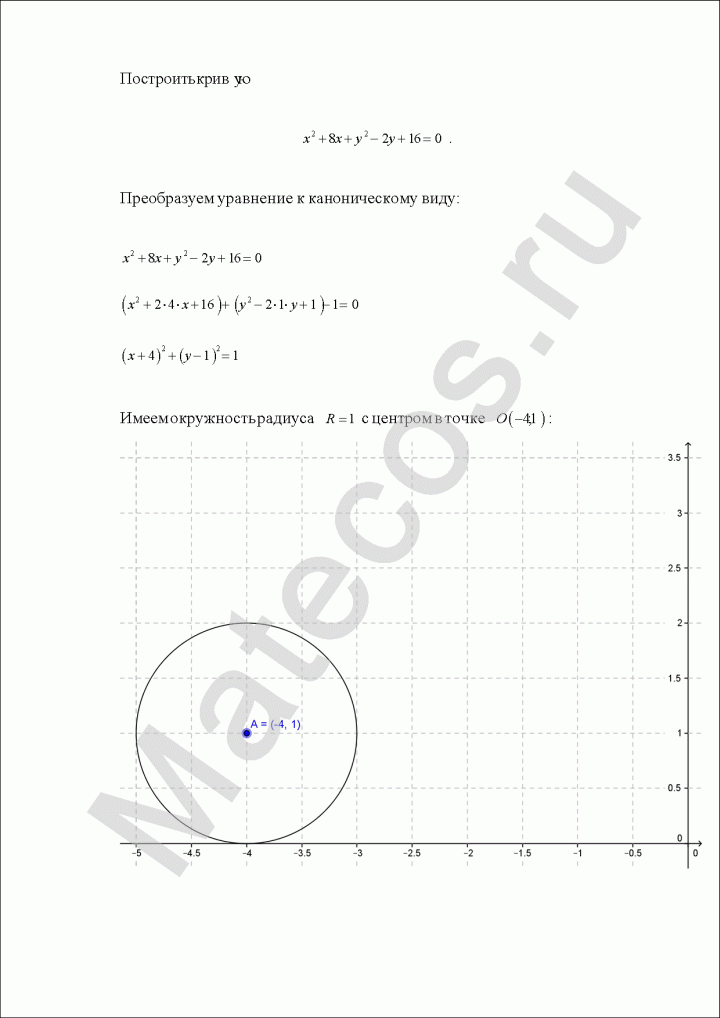
Пример по теме кривые второго порядка №4
Построить кривую второго порядка:
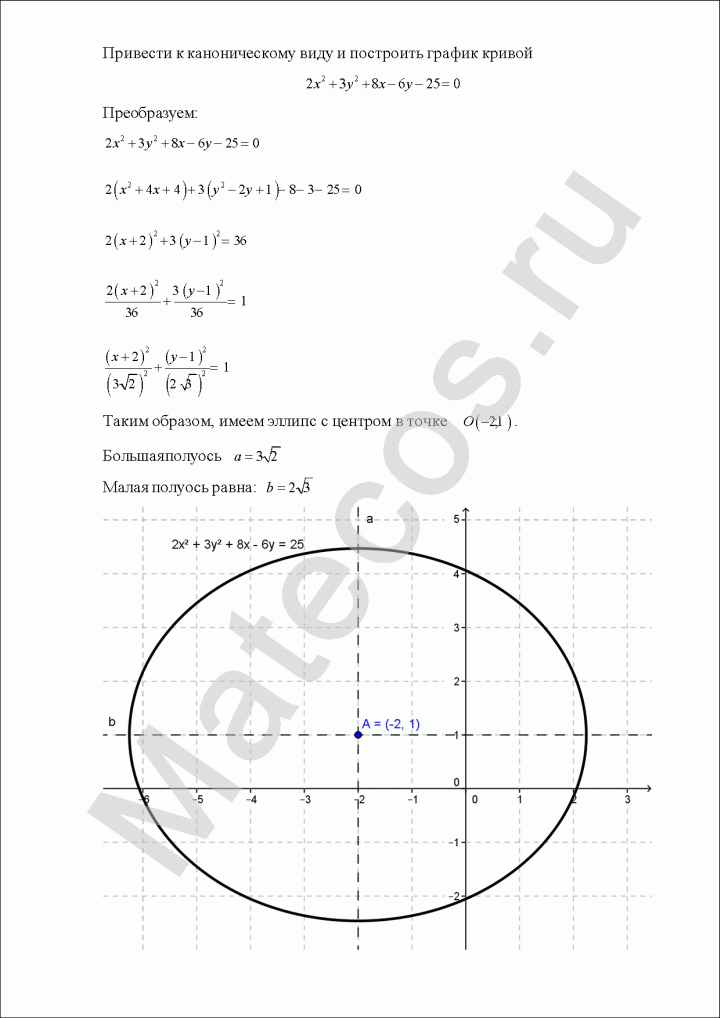
Пример по теме кривые второго порядка №5
Провести заданное уравнение линии второго порядка к каноническому виду и построить ее:

Пример по теме кривые второго порядка №6
Определить центр и радиус окружности:
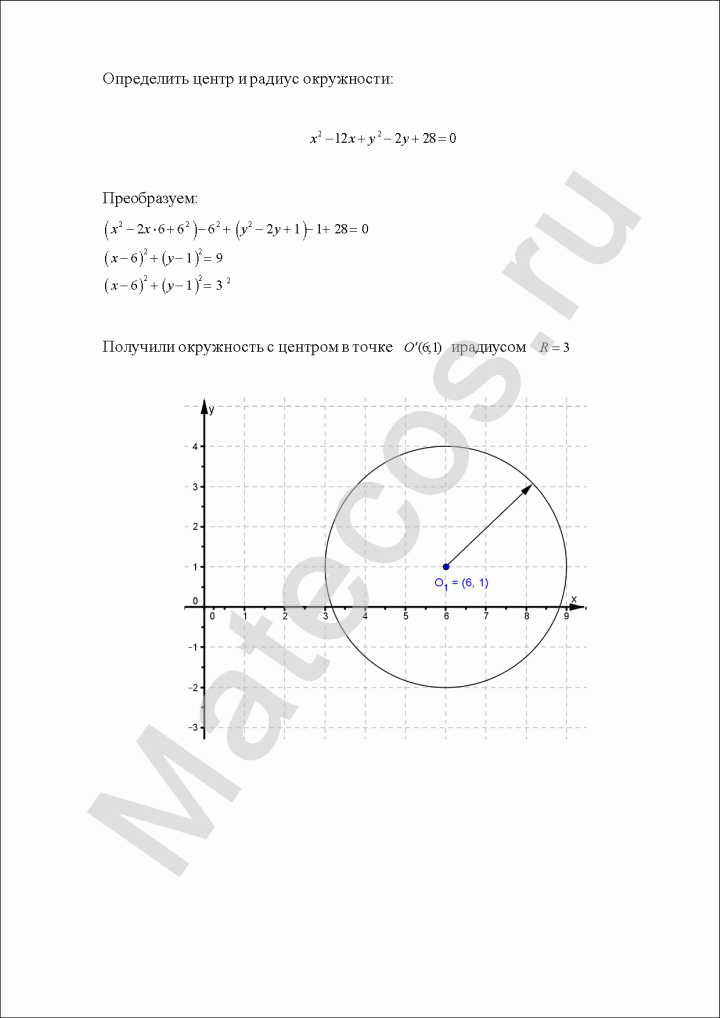
Пример по теме кривые второго порядка №7
Определить центр и полуоси эллипса:
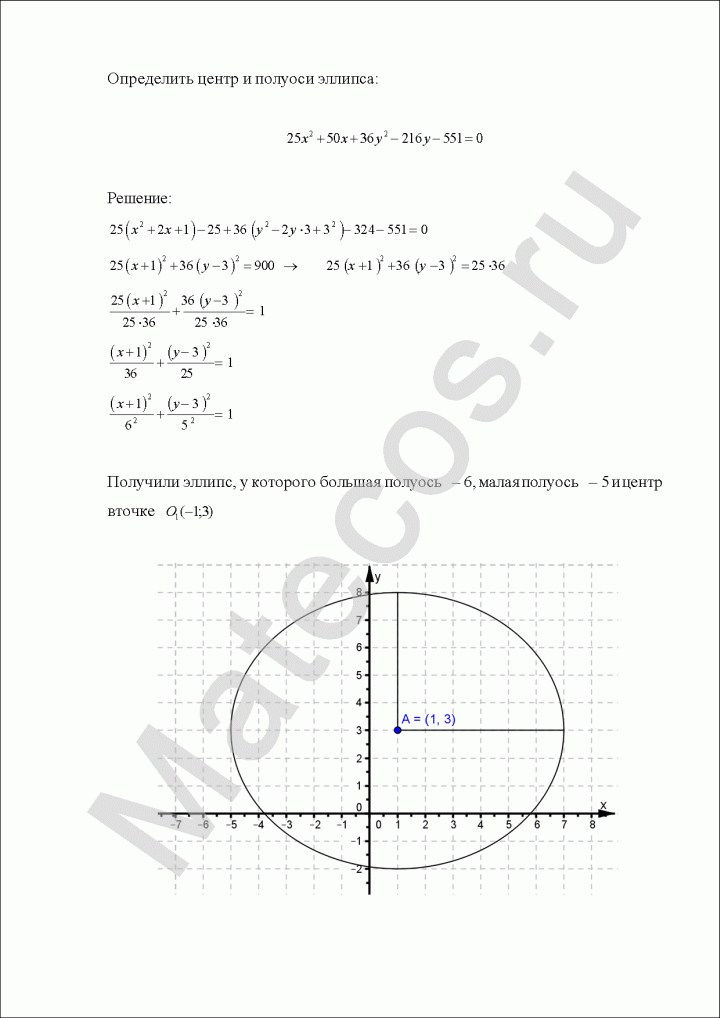
Пример по теме кривые второго порядка №8
Определить центр, полуоси и асимптоты гиперболы:
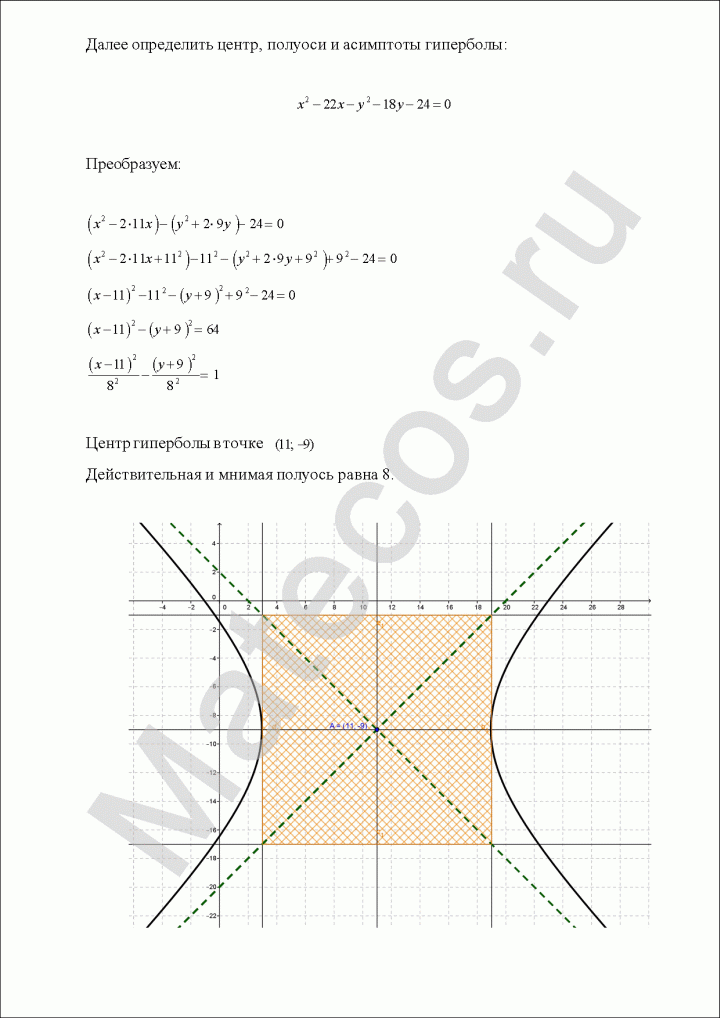
Пример по теме кривые второго порядка №9
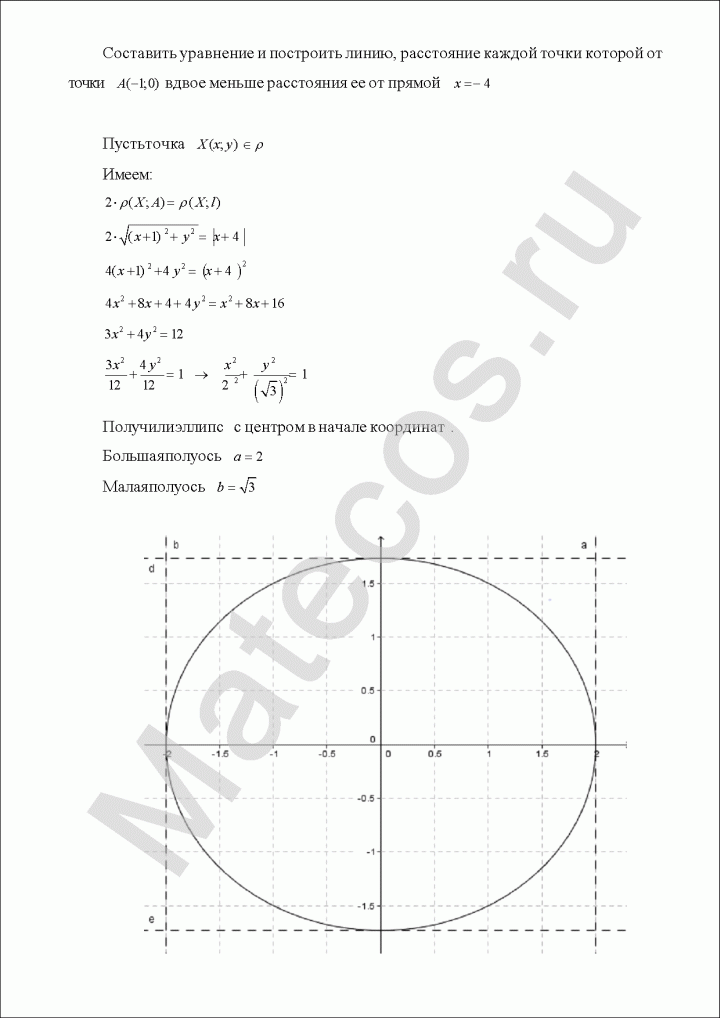
Составить уравнение и построить линию, расстояние каждой точки которой от точки A(-1;0) вдвое меньше расстояния ее от прямой x=-4
Пример по теме кривые второго порядка №10
Определить тип кривой второго порядка:
Пример по теме кривые второго порядка №11
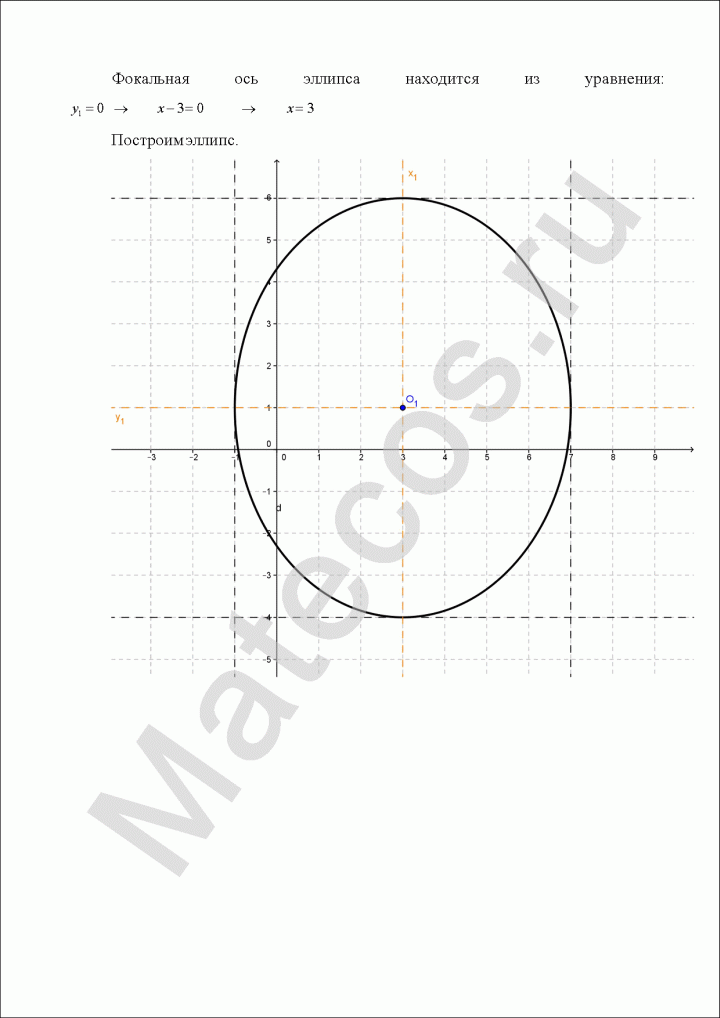
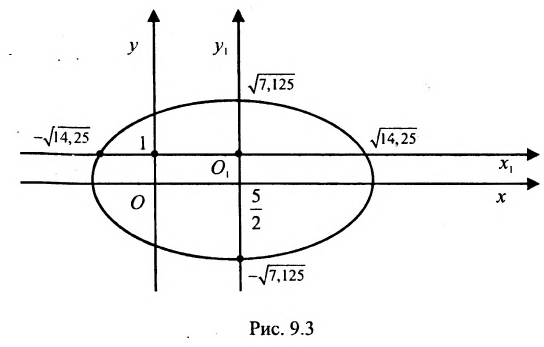
Дана кривая:
Докажите, что эта кривая – эллипс.
Найдите координаты центра симметрии.
Найдите его большую и малую полуоси.
Запишите уравнение фокальной оси.
Постройте данную кривую.
Пример по теме кривые второго порядка №12
Дана кривая:
Доказать, что данная кривая – парабола.
Найти координаты вершины параболы.
Найдите значение ее параметра.
Запишите уравнение оси симметрии параболы.
Постройте данную параболу.
Пример по теме кривые второго порядка №13
Дана кривая:
Докажите, что кривая – гипербола.
Найдите координаты центра симметрии гиперболы.
Найдите действительную и мнимую полуоси гиперболы.
Запишите уравнение фокальной оси гиперболы.
Найдите данную гиперболу.
Пример по теме кривые второго порядка №14
Все графике в этой статье были построены в Geogebra.Подробно о построении графиков функции быстрым и удобным способом читать тут:
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках 
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы 
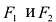
Пусть М(х,у) — произвольная точка эллипса, тогда:
Подставляя сюда значения 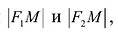
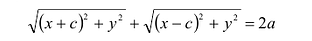
Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим
его:
Возведя обе части уравнения в квадрат и приведя подобные члены, получим:
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 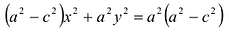
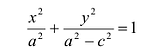
Положительную величину 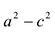
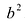
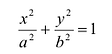
Оно называется каноническим уравнение эллипса.
Координаты точек эллипса ограничены неравенствами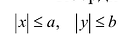
Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки 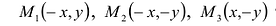
Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:
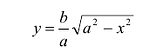
При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.
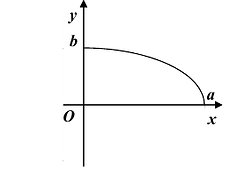
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).
Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии — точка О — центром эллипса. Точки 
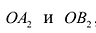
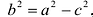
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 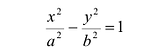
Уравнение (7.6) называется каноническим уравнением гиперболы.
Из уравнения (7.6) видно, что 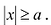
Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
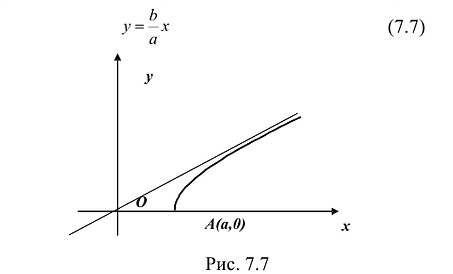
График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 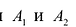
Эксцентриситетом гиперболы называется число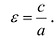
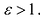
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами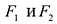
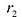
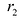
Для правой — ветви 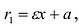
Для левой — ветви
Прямые 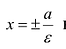
Парабола
Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой 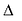
Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе 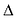
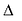
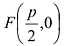
В выбранной системе координат уравнение параболы имеет вид:
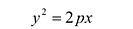
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти 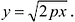
При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10).
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.
Исследование на плоскости уравнения второй степени
Рассмотрим уравнение:
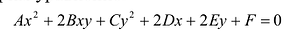
где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) — уравнение второй степени относительно х и у.
Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол
Старые координаты х, у выражаются через новые координаты 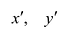
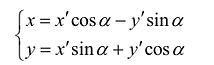
Подставив выражения для х и у в уравнение (8), получим: 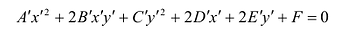
Это уравнение в системе координат 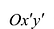
Если в уравнении (7.9) 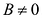
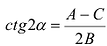
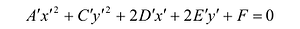
Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:
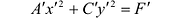
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:
Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.
Кривые второго порядка в высшей математике
Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.
Окружность
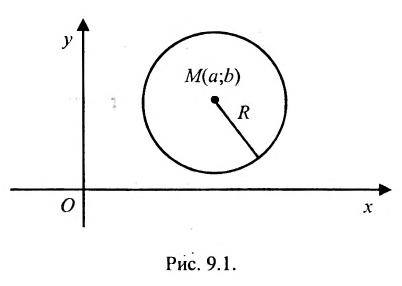
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки — центра окружности.
Если точка 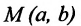
или
Найдём условия, при которых общее уравнение второй степени с двумя переменными
определяет окружность. Раскрыв скобки в (9.1.1), получим
Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,
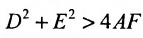
Эллипс
Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.
Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами 
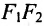
Если точка А — произвольная точка эллипса с координатами (х, у), то
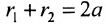
где 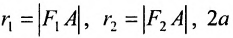
расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 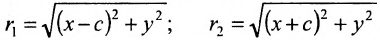
и 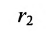
Обе части этого уравнения возведем в квад-Упростив и обозначив
получим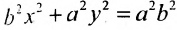
Уравнение (9.2.2) называется каноническим уравнением эллипса, где а — большая полуось, b — малая полуось.
Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет 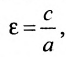
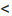
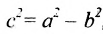
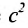
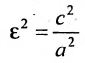
Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше 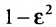
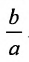
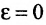
Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 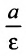
Пример:
Исследовать, какая линия определяется уравнением
Решение:
Сгруппируем члены, содержащие одну и туже переменную, получим
Из второй скобки вынесем коэффициент при 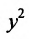
В каждой из скобок выделим полный квадрат
или
Произведём замену: 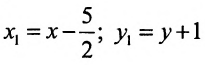
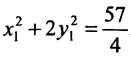
Разделив обе части этого уравнения на 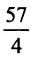
Заданное уравнение определяет эллипс с полуосями 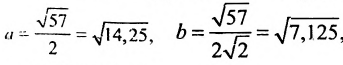
Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку 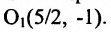
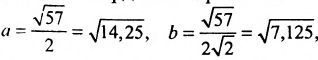
Гипербола
Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению).
Пусть М- произвольная точка гиперболы с фокусами 
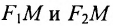
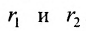
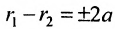
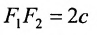
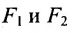
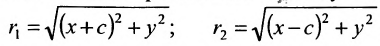
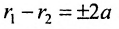
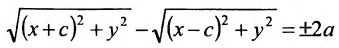
Возведя в квадрат обе части этого уравнения и обозначая 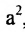
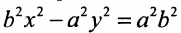
Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 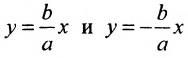
Уравнение вида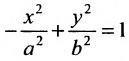
Форму гиперболы характеризует её эксцентриситет 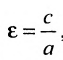
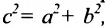
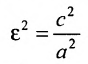
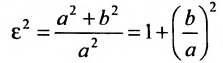
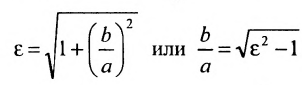
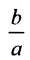
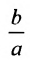
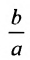
Прямые, заданные уравнениями 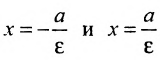
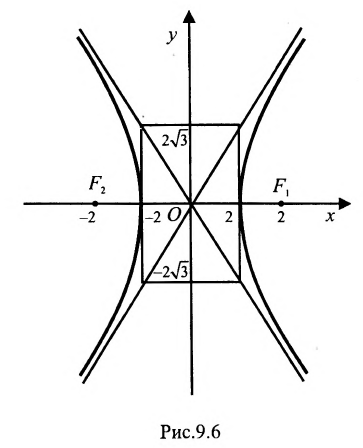
Пример:
Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.
Решение:
В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) — произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи 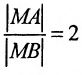
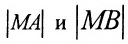
Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:
Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая 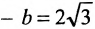
Определим фокусы гиперболы. Для гиперболы выполняется равенство 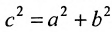
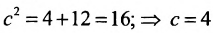
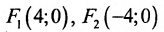
А(4, 0) является правым фокусом гиперболы.
Эксцентриситет полученной гиперболы равен
Подставив значения а и b в уравнения асимптот 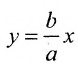
у =—получим уравнения асимптот гиперболы: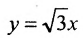
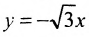
Для построения гиперболы строим основной прямоугольник с полуосями 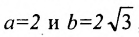
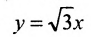
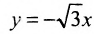
- Заказать решение задач по высшей математике
Парабола
Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).
Обозначим фокус параболы — F, расстояние от фокуса до директрисы — р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть 

Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию



Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.
Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и
Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.
Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению
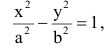
Число а называют действительной полуосью гиперболы, число
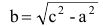
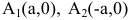
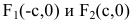
Координатные оси являются осями симметрии гиперболы, а начало координат — ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.
Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 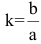
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси:
Эксцентриситет гиперболы изменяется от единицы до бесконечности 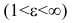
Замечание. Каноническое уравнение 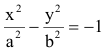
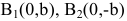
Пример:
Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.
Решение:
Каноническое уравнение гиперболы имеет вид
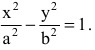
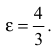
Следовательно, уравнение искомой гиперболы:
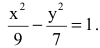
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 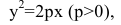
Точка O(0,0) называется вершиной параболы, число р — параметром параболы, 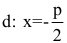
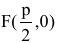
Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид 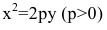
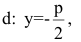
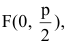
Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:
Пример:
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной
Решение:
Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:
Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений
Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной 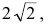
По теореме Пифагора
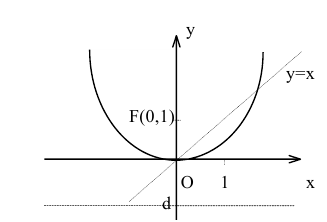
Тогда искомое уравнение параболы
Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).
Задача решена.
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Числовые множества
- Вектор — определение и основные понятия
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
Примеры решений: кривые второго порядка
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.
См. также: Решения по аналитической геометрии на плоскости,
Решения задач с квадратичными формами
Полезная страница? Сохрани или расскажи друзьям
Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.
$$9x^2-4y^2-90x-8y+185=0.$$
Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.
$$6x^2+2sqrt{5}xy+2y^2=21.$$
Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.
$$3x^2-6y^2-12x-108y-492=0.$$
Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.
$$9x^2+25y^2-18x-100y-116=0.$$
Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.
Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.
Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt{2/5}$. Привести это уравнение к каноническому виду и определить тип кривой.
Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.
Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.
Не получаются задачи? Решим быстро и подробно!
Содержание:
- Кривые второго порядка и их нахождение и решение
- Окружность
- Эллипс
- Гипербола
- Парабола
- Общее уравнение второго порядка с двумя переменными
- Кривые второго порядка
- Окружность и его уравнения
- Эллипс и его уравнения
- Гипербола и ее уравнение
- Асимптоты гиперболы
- Парабола и ее уравнение
- Линии второго порядка. Общее уравнение линии второго порядка
- Окружность и ее уравнение
- Каноническое уравнение эллипса. Эксцентриситет
- Каноническое уравнение гиперболы. Асимптоты. Эксцентриситет
- Каноническое уравнение параболы
- Кривые линии второго порядка
- Круг
- Эллипс
- Гипербола
- Парабола
- Общее уравнение кривой второго порядка: типы кривых
- Канонические уравнения окружности и эллипса
- Каноническое уравнение гиперболы. Асимптоты гиперболы
- Парабола. Каноническое уравнение
- Возведение общего уравнения кривой второго порядка к каноническому виду
- Квадратичные формы. Применение к превращению уравнений кривой 2-го порядка
Кривые второго порядка и их нахождение и решение
Кривые, которые получаются при пересечении круговой конической поверхности плоскостью называются конечными поверхностями или кониками. К ним относятся такие кривые как окружность, эллипс, гипербола, парабола.
Действительно:
— Если плоскость пересекает коническую поверхность перпендикулярно оси вращения, то в пересечении образуется окружность, если плоскость проходит через вершину конуса, то в пересечении образуется точка, то есть вырожденная окружность (рис. 1).
— Если плоскость пересекает только одну часть конической поверхности и не параллельна ни одной образующей, тогда в пересечении будет эллипс (рис. 2).
— Если плоскость пересекает одну часть конической поверхности и параллельна одной образующей, тогда в пересечении будет парабола (рис. 3а), если плоскость проходит через вершину и одну из образующих, тогда в пересечении будет прямая, то есть вырожденная парабола (рис. 3б).
— Если плоскость пересекает две части конической поверхности и параллельна оси конической поверхности, то в пересечении будет гипербола (рис. 4а), если секущая плоскость проходит через вершину конуса и пересекает две его части, то в пересечении будет пара прямых, которые пересекаются, то есть вырожденная гипербола (рис. 4б).
Рассмотрим каждую из этих кривых.
Окружность
Окружностью называется множество точек плоскости, равноудалённых от данной точки, которая называется центром. Если точка С — цент окружности, R — её радиус, М — произвольная точка окружности, то по определению окружности
Данное равенство является уравнением окружности радиуса R с центром в точке С.
Пусть на плоскости задана прямоугольная декартовая система координат (рис. 5) и точка 

Данное уравнение называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке
Например, уравнение
является уравнением окружности радиуса R=5, с центром в точке (1; -3).
Если центр окружности совпадает с началом координат, то уравнение окружности принимает вид:
Данное уравнение называют каноническим уравнением окружности.
Пример 1. Составить уравнение окружности радиуса R=9 с центром в точке C(3; -6).
Решение:
Подставив значения координат точки С и значение радиуса в уравнение окружности, получаем 
Пример 2. Доказать, что уравнение 
Решение:
Преобразуем левую часть заданного уравнения
Это уравнение является уравнением окружности с центром в точке (-2; 1), радиус окружности равен 3.
Эллипс
Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же самой плоскости постоянна и больше чем расстояние между этими точками.
Такие точки называются фокусами эллипса, а расстояние между ними фокальным расстоянием. Покажем, как, исходя из определения эллипса, можно разбить эллиптическую клумбу. Забьём в землю два колышка (рис. 6) потом нитку свяжем в кольцо и натянем это кольцо на оба колышка. Натянув нитку третьим колышком, чертим эллипс. Изменив расстояние между колышками и длину нитки, получаем эллипсы разных размеров и форм.
Обозначим фокусы эллипса буквами 



Заметим, что по определению эллипса 



Это уравнение является уравнением окружности радиуса 

Выберем систему координат так, чтобы ось абсцисс проходила через фокусы эллипса, ось ординат через середину отрезка 
Тогда фокусами будут точки 
подставляя найденные значения 
Сведём данное уравнение до простейшего вида. Для этого перенесём второе слагаемое в правую часть и возведём обе части в квадрат
после упрощений получаем
Возведя обе части в квадрат получаем
по определению эллипса 



Разделив обе части равенства на 
Это уравнение называется каноническим уравнением эллипса.
Если 

что вычисляет уравнение окружности.
Пример 1. Составить каноническое уравнение эллипса, который проходит через точку М(5;0), если фокальное расстояние равно 6.
Решение:
Поскольку фокальное расстояние равняется 6, то с=3. Запишем уравнение эллипса
По условию задачи точка М(5; 0) принадлежит эллипсу, следовательно
отсюда 
Следовательно, искомым уравнением эллипса является уравнение
Пример 2. Доказать, что уравнение 
Решение:
Разделив обе части уравнений на 3600, получаем
это является уравнением эллипса.
Из уравнение 




Исследуем эллипс по его уравнению.
1. Эллипс не проходит через начало системы координат, так как координаты точки О(0; 0) не удовлетворяют уравнение.
2. Эллипс пересекает каждую из осе координат в двух точках.
Чтобы вычислить координаты точек пересечения эллипса с осью Ох, необходимо решить уравнение 
Следовательно, точками пересечения эллипса с осью Ох будут
Аналогично находим точки пересечения с осью Оу:
Точки А, В, С, D называют вершинами эллипса.
Отрезок АВ называется большой осью эллипса, отрезок ВD — малой осью. Фокусы эллипса 





3. Эллипс имеет две взаимно перпендикулярные оси симметрии, а также центр симметрии.
Это легко показать, так как неизвестные в уравнение входят только во второй степени. Центр симметрии эллипса называется центром эллипса.
4. Эллипс можно получить равномерным сжиманием окружности.
Рассмотрим окружность радиуса 

Тогда 








Следовательно, 
Таким образом, эллипс можно достать с окружности равномерным сжатием до оси Ох, при котором, ордината точек уменьшается в том самом соотношении 







Поскольку 

Пример. Дано два эллипса 
Решение:
Перепишем уравнение эллипсов в виде 





Гипербола
Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний к двум данным точкам плоскости постоянный и меньший чем расстояние между этими точками.
Такие точки называются фокусами гиперболы, а расстояние между ними — фокальным расстоянием.
Обозначим фокусы гиперболы буквами 
Если М — произвольная точка гиперболы (рис. 10), то по определению гиперболы модуль разности 

Отметим, что по определениям гиперболы 
Данное равенство является уравнением гиперболы. Выберем систему координат так, чтобы ось абсцисс проходила через фокус гиперболы; ось ординат проходила через середину отрезка 

Пусть 

Подставляя значения 

Это уравнение является гиперболой в выбранной системе координат. Его можно привести к более простому виду.
Пусть 
Возведём обе части уравнения в квадрат
По определению гиперболы 



Разделив почленно на 
Если 
и также, как при 
Уравнение 
Пример 1. Записать каноническое уравнение гиперболы, которая проходит через точку 
Решение. Поскольку 
По условию точка принадлежит гиперболе, следовательно:
Из второго уравнения получим соотношение для вычисления
Решим систему:
найдём 
Пример 2. Доказать, что уравнение
является уравнением гиперболы. Найти координаты фокусов.
Решение: Разделив обе части уравнения на 580, получим
Это является уравнением гиперболы, для которой 


Исследуем гиперболу по её уравнениям.
Рассмотрим гиперболу, заданную в некоторой прямоугольной декартовой системе координат своим каноническим уравнением
Приведём такие свойства гиперболы:
1. Гипербола не имеет общих точек с осью Оу, а ось Ох пересекает в двух точках.
Чтобы вычислить координаты точек пересечения гиперболы с осью Оу, необходимо решить совместно их уравнения
Подставляя х=0 в уравнение гиперболы, получим 
Чтобы вычислить координаты точек пересечения с осью Ох, необходимо решить совместно их уравнения
Точка пересечения гиперболы с осью Ох должна иметь ординату у=0 и, кроме того, должна принадлежать гиперболе. Подставив у=0 в уравнение гиперболы, получим
Следовательно, точками пересечения гиперболы с осью Ох будут точки 

Отрезок АВ называется действительной осью гиперболы. Длина отрезка АВ, очевидно, равна 

2. Гипербола имеет две взаимно перпендикулярные оси симметрии.
В уравнение переменные х и у входят только во второй степени. Таким образом, если координаты точки N(x; y) удовлетворяют уравнение, то это же уравнение будут удовлетворять и координаты точек 
Легко увидеть, что точка 
3. Гипербола имеет центр симметрии.
Если координаты точки N(x; y) удовлетворяют уравнение гиперболы, то это же уравнение удовлетворяют и координаты 
Центр симметрии гиперболы называется центром гиперболы.
4. Гипербола пересекается с прямой 

Чтобы вычислить координаты точек пересечения гиперболы и прямой у=kх, необходимо решить систему уравнений
При 



При 

Таким образом, каждая прямая, которая проходит через начало координат с угловым коэффициентом, модуль которой меньше чем 

Поскольку гипербола симметрична относительно осей координат, то достаточно выучить её формулу в первом квадранте координатной плоскости. По формулам
имеем, что из возрастания k от 
Как уже видели (рис. 11), ветка гиперболы размещена выше от асимптоты 


Как и в случаи эллипса, для характеристики формулы гиперболы целесообразно пользоваться не соотношением 

Соотношение полуфокусного расстояния с к действительной полуоси 
Поскольку для гиперболы 

Выразим эксцентриситет гиперболы через соотношение 
то есть:
Согласно формуле, меньшим значением соотношения 
Гипербола называется равносторонней (или равнобокой), если длины её полуосей равны между собой. Поскольку для равносторонней гиперболы 
Асимптотами равносторонней гиперболы являются прямые у=х и у= -х. Следовательно, асимптоты равносторонней гиперболы взаимно перпендикулярны.
Эксцентриситет равносторонней гиперболы:
Пример 3. Даны фокусы гиперболы 

Решение.
Записав уравнение асимптоты в виде 
Из условия задачи вытекает, что с=10. Поэтому 
Подставив 
откуда 

Парабола
Параболой называется множество точек на плоскости, для каждой из которых расстояние до данной точки равно расстоянию до данной прямой, которая не проходит через данную точку.
Такая точка называется фокусом параболы, а прямая — директрисой (направляющей). Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается как р.
Выберем систему координат таким образом, чтобы ось Ох была проведена через фокус F перпендикулярно к директрисе. Точка пересечения оси абсцисс с директрисой обозначим D (рис. 12), за начало координат О возьмём середину отрезка DF, за положительное направление оси Ох — направление луча OF/
В этой системе координат фокус F имеет координаты 
Пусть М(х; у) — любая искомая точка искомого множества. Опустим из точки М перпендикуляр на директрису, и пусть N — основа этого перпендикуляра. Тогда |MN| является расстоянием от точки М до директрисы и, следовательно,
Это уравнение является уравнением параболы в выбранной системе координат. Его можно упростить. В следствии того, что обе части уравнения неотъемлемые, то уравнение
равносильно предыдущему уравнению. В результате преобразований получим уравнение
Оно называется каноническим уравнением параболы.
Приведём такие свойства параболы:
1. Парабола имеет ось симметрии.
Переменная у входит в уравнение только во второй степени. Поэтому, если координаты точки М1(х; у) удовлетворяют уравнение параболы, то и его координаты N2 (х; -у) будут удовлетворять его. Точка N1 симметрична точке N2 относительно оси Ох. Следовательно, ось Ох является симметрией параболы. Ось симметрии параболы называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Вершина параболы находится в начале координат.
2. Парабола расположена в полуплоскости
Правда, поскольку параметр р положительный, то уравнения могут удовлетворять только точки с неотрицательными абсциссами, то есть точки полуплоскости
3. Парабола является объединением графиков функций
Чтобы убедиться в этом, достаточно решить уравнение относительно переменной у.
Пример 1. Световой луч у=-2 падает на зеркало, осевым сечением которого является парабола у2=24х (рис. 14). Найти уравнение прямой, которой принадлежит отражённый луч.
Решение.
Если падающий луч параллельный главной оптической оси параболического зеркала, то отражённый луч проходит через его фокус. В этом случаи ось параболического зеркала совпадает с осью Ох. Прямая у=-2 параллельна оси абсцисс, и поэтому отражённый луч пройдёт через фокус параболы у2=24х. Поскольку 2р=24, то есть 
Чтобы найти точки падения светового луча, необходимо решить систему уравнений
Решив эту систему, найдём точку падения луча 
Отражённый луч принадлежит прямой, которая проходит через точки 

Запишем уравнение этой прямой
Отсюда получим
Если фокус параболы расположенный левее оси Оу (рис. 15), то есть имеет координаты 
Если фокус параболы лежит на оси Оу (рис. 16), то есть имеет координаты 
Если фокус параболы лежит правее оси Оу (рис. 17), то есть имеет координаты 
Общее уравнение второго порядка с двумя переменными
Общее уравнение второго порядка с двумя переменными имеет вид
Рассмотренные ранее канонические уравнения прямых являются частными случаями данного уравнения.
1. 
и, соответственно, будет уравнением окружности.
2. 
и, соответственно, будет уравнением эллипса.
3. 
и, соответственно, будет уравнением гиперболы.
4. 
и, соответственно, будет уравнением параболы.
Кривые второго порядка
Кривыми второго порядка называются линии, уравнения которых являются уравнениями второй степени относительно бегущих координат. Общий вид уравнения кривой второго порядка
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0. (2.109)
К кривым второго порядка относятся круг, эллипс, гипербола и парабола.
Окружность и его уравнения
Определение 1. Окружностью называется множество точек плоскости, равноудаленных от заданной точки, называется центром окружности.
Рис. 50.
Пусть центр окружности находится в произвольной точке С (a, b) (рис. 50). Выходя из определения 1, расстояние произвольной точки M (x, y) плоскости к центру C (a, b) — величина постоянная и равна r. По формуле (2.3) имеем 
(x – a) 2 + (y – b) 2 = r 2. (2.110)
Выясним условия, при которых общее уравнение второй степени с двумя переменными (2.109) является уравнением окружности. В этом уравнении А, В и С не равны нулю одновременно, т .е. A2 + B2 + C2 ≠ 0. Когда в уравнении (2.110) раскрываем скобки, то получим
x2 + y2 – 2ax – 2by + (a2 + b2 – r2) = 0. (2.111)
Чтобы уравнения (2.109) и (2.111) представляли одну и ту же линию, нужно, чтобы коэффициент B = 0, а все остальные пропорциональны, в частности

Ax2 + Ay2 + Dx + Ey + F = 0. (2.112)
Уравнение (2.112) называется общим уравнением окружности.
Обе части уравнения (2.112) поделим на A ≠ 0 и дополним члены, содержащие x и y, до полных квадратов. Получим

Сравнивая (2.113) с уравнением окружности (2.110), можно сделать вывод, что уравнение (2.109) является уравнением окружности при следующих трех условиях:
1) A = C, 2) B = 0, 3) D2 + E2 – 4AE > 0.
При выполнении этих условий для окружности (2.113) центр находится в точке 
Пример 1. Привести общее уравнение окружности x2 + y2 – 6x + 4y – 3 = 0 к нормальному виду.
Решение. Сгруппируем члены с x и y и дополним их до полного квадрата, тогда получим
(x2 – 6 x + 9) – 9 + (y2 + 4 y + 4) – 4 – 3 = 0, или (x – 3) 2 + (y + 2) 2 = 16. Координаты центра окружности a = 3, b = 2, а радиус окружности r = 4.
Пример 2 (экономического характера). Два предприятия, расстояние между которыми 80 км, производят некоторую продукцию, причем фабрично-заводская цена продукции на обоих предприятиях одинакова и равна p. Пусть транспортные расходы на перевозку единицы продукции от компании A до потребителя составляет 10 руб./км, а от компании B составляет 6 руб./км. Как будет размещен рынок сбыта, если расходы потребителей должны быть одинаковыми?
Рис. 51.
Решение. Оси координат проведем через середину отрезка AB. Предположим, что потребитель находится в точке M (x, y); введем обозначения AM = s1, BM = s2 (рис. 51). Расходы потребителя на покупку единицы изделия у компании A составляют
p + s1⋅ 10, а у предприятия B — p + s2⋅ 6. Расходы потребителей одинаковые, если p + s1⋅ 10 = p + s2⋅ 6, или 10 s1 = 6 s2, 5 s1 = 3 s2.
Из рис. 51 видно, что 
Аналогично 

Для потребителя расходы на покупку продукции одинаковые, если 
(x + 85)2 + y2 = 5625. Это нормальное уравнение окружности, центр которой находится на оси абсцисс с абсциссой «–85», а радиус окружности r = 75.
Для потребителей, которые находятся на этой окружности, расходы на покупку изделия одинаковы. Для потребителей, которые находятся за окружностью, расходы на покупку продукции меньше на предприятии B, а для потребителей, которые находятся внутри окружности — на предприятии A. Значит, рынок будет распределен следующим образом:
а) потребители, которые находятся внутри окружности, будут приобретать данные изделия на предприятии А;
б) для потребителей, находящихся на окружности, все равно, на каком предприятии будут производиться закупки;
в) потребители, которые находятся снаружи окружности, будут закупать изделия на предприятии В.
Эллипс и его уравнения
Определение 2. Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.
Исходя из определения 2, выведем уравнение эллипса. Пусть заданы две точки, которые называются фокусами, F1 и F2, расстояние между которыми обозначим через 2с (фокальное расстояние) (рис.52). Через фокусы проведем прямую, которую возьмем за ось абсцисс, а за ось ординат возьмем прямую, перпендикулярную оси OX, проходящую через середину отрезка F1F2 (точка О).
Поскольку расстояние между фокусами приняли за 2с, то координаты фокусов будут соответственно F1 (c, 0) и F2 (–c, 0).
Рис. 52.
Пусть M (x, y) произвольная точка эллипса. Отрезки F1M и F2M, соединяющие точку эллипса с его фокусами, называют локальными радиус-векторами этой точки и обозначают r1 и r2 . Тогда r1 + r2 является величиной постоянной по определению, обозначим ее через 2а:
r1 + r2 = 2а (2.114)
(2а > 2с, потому что в треугольнике F1MF2 сумма двух сторон больше третьей). Покажем, какому уравнению удовлетворяют координаты точки M (x, y).
Найдем r1 и r2:


Возведя обе части (2.115) и (2.116) в квадрат и отнимая, получим

Расписав разность квадратов в (2.117) и учитывая (2.114), получим

Рассмотрим систему из уравнений (2.114) и (2.118):

Из этой системы находим


Подставим (2.121) в (2.116), получим


Обозначим a2 – c2 = b2 (2.123)
и тогда (2.122) перепишем после простых преобразований в виде

Уравнение (2.124) является каноническим уравнением эллипса. Это уравнение второй степени, значит, эллипс — кривая второго порядка. Уравнение (2.124) содержит x и y в четных степенях, значит, кривая, определяемая этим уравнением, симметрична относительно осей Оx и Оy. Оси симметрии эллипса называют его осями. Точку О называют центром эллипса. Из уравнения (2.124) найдем y:

Так как у, который находится в первом квадранте, является положительным, то

Из равенства (2.126) видно, если x = 0, то y = b и при возрастании x от нуля до a, y убывает от b к нулю.
В первом квадранте часть эллипса — это дуга A1B1. Если провести зеркальное отражение этой дуги относительно осей координат, то мы получим весь эллипс (рис. 52).
Если в уравнении (2.124) y = 0, то x = ± a, a если x = 0, то y = ± b. Значит вершинами эллипса есть точки A1 (a, 0), A2 (–a, 0), B1 (0, b), B2 (0, –b). Отрезок A2 A1 = 2a, а отрезок B2 B1 = 2b. Эти
отрезки соответственно называются большой и малой осями эллипса. Соответственно, a и b — большая и малая полуоси эллипса.
Определение 3. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси.
Обозначим эксцентриситет через ε, то тогда

Если a = b (ε = 0), то эллипс превращается в окружность. Подставим (2.127) в (2.120) и (2.121), тогда получим
r1 = a – εx, (2.128)
r2 = a + εx. (2.129)
Эти формулы используются при решении задач.
Пример 3. Составить каноническое уравнение эллипса, зная, что большая ось 2a = 10, а эксцентриситет ε = 0,8.
Решение. Из уравнения (2.127) найдем c. Зная, что a = 5, c = a ⋅ ε = 5 ⋅ 0,8 = 4. А теперь найдем b из равенства (2.123):
b2 = a2 – c2 = 52 – 42 = 25 – 16 = 9, b = 3.
Подставляя a = 5, b = 3 в уравнение (2.124), получим 
Гипербола и ее уравнение
Определение 4. Гиперболой называется множество точек плоскости, абсолютное значение разницы расстояний которых от двух заданных точек, называемых фокусами, есть величина постоянная.
Основываясь на определении 4, выведем каноническое уравнение гиперболы. Пусть заданы две точки F1 и F2 , являющиеся фокусами гиперболы. Обозначим расстояние между ними через 2c, а абсолютную величину разности расстояний точки гиперболы от точек F1 и F2 обозначим через 2a (a > 0). За ось абсцисс возьмем прямую, проходящую через фокусы, а за ось ординат возьмем прямую, перпендикулярную оси абсцисс и проходящую через середину отрезка F2F1 (рис. 58), то есть через точку О. Поскольку F2F1 = 2с, то координатами фокусов будут соответственно F1 (c; 0) и F2(–c; 0), а фокальные радиусы соответственно r1 = F1M, r2 = F2M, 
Рис. 58.
Пользуясь формулой расстояния между двумя точками и определением 4, имеем уравнение гиперболы:

Запишем это уравнение в таком виде:


Возведя в квадрат обе части этого уравнения, получим:
или после упрощения 
x2 (c2 – a2) – a2 y2 = a2 (c2 – a2). (2.132)
Разделив обе части уравнения (2.132) на a2 (c2 – a2), получим:

Покажем, что c2 – a2 > 0 (c > a). Поскольку в любом треугольнике разность двух сторон меньше трех, то

c2 – a2 = b2. (2.134)
Подставляя (2.134) в (2.133), получим каноническое уравнение гиперболы

Уравнение (2.135) является уравнением второй степени, значит гипербола является кривой второго порядка. Исследуем форму гиперболы по ее уравнению (2.135). Поскольку уравнение содержит x и y только в четных степенях, то гипербола симметрична относительно обеих осей координат.
Найдя y и x из уравнения (2.135), получим


Из уравнения (2.136) можно сделать следующие выводы:
а) значения у мнимые, если | х | < a , значит гипербола не пересекает оси Оу и не имеет точек, находящихся в полосе, ограниченной прямыми х = ± a;
б) когда x = ± a, y = 0, значит гипербола пересекает ось абсцисс в двух точках A1 (a, 0) и A2 (–a, 0), которые называются вершинами гиперболы;
в) для каждого | x | > a, ордината y имеет два значения, которые отличаются только знаком, отсюда следует, что гипербола симметрична относительно оси Оx.
Уравнение (2.137) показывает, что гипербола симметрична и относительно оси Оy.
При неограниченном росте абсциссы x ордината также неограниченно растет. Поскольку гипербола находится вне полосы, ограниченной прямыми x = ± a, то гипербола состоит из двух отдельных веток (рис. 59).
Отрезок A2 A1 называется действительной осью гиперболы, а точки A1 (a, 0) и A2 (–a, 0) —вершинами гиперболы. Отрезок B1B2, соединяющий точки В1 (0, b) и В2 (0, –b), называется мнимой осью гиперболы. Точки F1 (c, 0) и F2 (–c, 0) называются фокусами гиперболы.
Рис. 59.
Гипербола, которая определяется уравнением 

Если действительная и мнимая оси равны, то гипербола называется равносторонней, а ее уравнение будет x2 — y2 = a2.
Степень сжатия гиперболы характеризуется ее эксцентриситетом.
Определение 5. Эксцентриситетом гиперболы называется отношение расстояния между фокусами 2с к длине ее действительной оси 2a, то есть

Так как для гиперболы с > a, то ε > 1.
Примечание. Для гиперболы легко показать как связаны r1 и r2 с ε, а именно




Формулы (2.139) и (2.140) получаются аналогично как и для эллипса.
Предоставим читателю самостоятельно убедиться в справедливости формул (2.139) и (2.140).
Асимптоты гиперболы
Определение 6. Прямая l называется асимптотой кривой (k), если расстояние d = MN от точки M кривой до точки N прямой l стремится к нулю при неограниченном удаленные точки M от начала координат вдоль кривой (k) в том или ином направлении (рис. 60).
Рис. 60.
Покажем, что прямая 
Найдем разницу между ординатами (Y-y) точек N и M, которые имеют одну и ту же абсциссу 
Теперь умножим и разделим правую часть этого равенства на 

Отсюда видно, что при неограниченном увеличении абсциссы x разница (Y-y) неограниченно уменьшается. Таким образом, точка гиперболы ограниченно удаляясь по ветке гиперболы, неограниченно приближается к асимптоте 


Пример 4. Составить уравнение гиперболы, если известно, что она проходит через точку M1 (10; 5) и имеет асимптоты 

Решение. Из условия задачи получаем, что 

Из первого уравнения находим 

Отсюда 
Итак, искомое уравнение гиперболы будет
Парабола и ее уравнение
Определение 7. Параболой называется множество точек плоскости, одинаково удаленных от заданной точки, называемой фокусом, и от заданной прямой, называемой директрисой.
Исходя из определения 7, выведем уравнение параболы. Пусть прямая AB является директрисой параболы, а точка F является ее фокусом (рис. 61).
Рис. 61.
Проведем через точку F прямую, перпендикулярную директрисе AB, и возьмем эту прямую за ось абсцисс, а за ось ординат возьмем прямую, перпендикулярную оси абсцисс и проходящую через точку O, середину отрезка CF. Длину отрезка CF обозначим через p (p > 0). Координаты фокуса будут 

Пусть точка M (x, y) является произвольной точкой параболы. Опустим из точки M перпендикуляр на директрису AB в точке D и соединим точку M с фокусом F. Тогда
по определению 7 имеем, что DM = MF. Точка D имеет координаты 

Это и будет уравнение параболы относительно выбранной системы координат. Возведя обе части данного уравнения в квадрат и упростив, получим
y2 = 2 px. (2.142)
Уравнение (2.142) и является каноническим уравнением параболы. Как видно из уравнения (2.142), парабола является линией второго порядка, и все ее точки размещены справа от оси Оy. Парабола проходит через начало координат. Решив уравнение (2.142) относительно y, получим

Так как p > 0, то y будет действительной величиной только тогда, когда x положительные, а когда p < 0, то парабола определена для x ≤ 0.
Из (2.143) видно, что каждому значению x соответствует два знания y, которые равны по абсолютной величине, но противоположны по знаку.
Значит ось Оx является осью симметрии для параболы. Точку O (0,0) называют вершиной параболы.
Если x неограниченно растет, то и y неограниченно растет. Величина р называется параметром параболы и при увеличении р парабола расширяется, то есть ее точки будут удаляться от оси Ох.
Если уравнение параболы имеет вид y2 = –2px, то вершина параболы находится в начале координат, осью симметрии является ось абсцисс, но парабола размещена слева от оси Oy (рис. 62), а директриса такой параболы будет размещена справа от оси ординат, а фокус 
Если директриса параболы параллельна оси абсцисс, а фокус находится на оси ординат, то уравнение параболы имеет вид: x2 = ± 2py. (2.144)

Рис. 62. Рис. 63.
Парабола (2.144) изображена на рис. 63. Эта парабола симметрична относительно оси Oy и размещена над осью абсцисс, если в уравнении взять знак (+), и под осью абсцисс, если взять знак (-).
Если в уравнении (2.144) обозначить 
Пример 5. Фермы, поддерживающие железнодорожный мост длиной 112 м, имеют вид параболы, которая задается уравнением y = ax2. Найти уравнение соответствующей параболы, если наибольшая высота мостовой арки составляет 44 м.
Решение. Возьмем за начало координат вершину фермы. Тогда симметричные точки в основании фермы будут иметь координаты (-56; -44) и (56; -44). Подставляя любую пару координат в уравнение y = ax2, получим — 44 = a ⋅ 3136. Отсюда

Таким образом, мостовая ферма имеет вид параболы 
Линии второго порядка. Общее уравнение линии второго порядка
Напомним, что линия второго порядка — это множество точек, координаты которых удовлетворяют уравнениям вида

где коэффициенты a,b,c,d,e,f— действительные числа, причем хотя бы одно из чисел a,b,c отлично от нуля, то есть 







Линии второго порядка называют также коническими сечениями, так как их можно получить пересечением кругового конуса с плоскостью. Окружность образуется как линия пересечения плоскости, перпендикулярной к оси конуса и не проходящей через его вершину (рис. 1, а); эллипс — линия пересечения плоскости, пересекающей все образующие конуса, не перпендикулярная к оси конуса и не проходящая через его вершину (рис. 1, б); если пересечь двуполостной конус плоскостью, параллельной двум образующим, то получим гиперболу (рис. 1, в), а одной образующей — параболу (рис. 1, г).
Кривые второго порядка — важная составляющая окружающего мира.
1. Планеты Солнечной системы движутся по эллипсам, имеющим общий фокус, в котором расположено Солнце.
2. Если в фокусе параболы разместить источник света, то лучи, отразившись от параболы, пойдут параллельно ее оси. На этом свойстве основывается конструкция прожектора.
3. Движение материальной точки под действием центрального поля силы тяготения осуществляется по одной из линий второго порядка.
Окружность и ее уравнение
Окружностью называют множество точек плоскости (рис. 2), находящихся на одинаковом расстоянии 


Если в уравнении (2) раскрыть скобки, то получим общее уравнение окружности

где А = -2а , В = -2b, С = 

Уравнение окружности имеет следующие свойства.
1°. Коэффициенты 

2°. В уравнении отсутствует член с произведением 
Если центр окружности расположен в начале координат, то а =b = 0 и уравнение (2) имеет вид

Уравнение (4) называется каноническим уравнением окружности.
Пример №7
Найти центр и радиус окружности 
Решение:
Сгруппируем произведения с переменной 

Поэтому, точка (-2; 3) — центр окружности, a 
Каноническое уравнение эллипса. Эксцентриситет
Возьмем на плоскости две точки 












Каноническим уравнением эллипса называется равенство

где

Отметим некоторые свойства эллипса.
1°. Эллипс симметричен относительно осей 


2°. Эллипс пересекает оси координат в точках 





3°. Если а = b , то уравнение (5) принимает вид 
Мера отклонения эллипса от окружности характеризуется величиной 

причем 


Итак, если 


4°. Пусть 








Пример №8
Составить каноническое уравнение эллипса, фокусы которого расположены на оси 
Решение:
Поскольку 2с = 14, то с = 7. Из формул (7) и (6) получим а = 9 и 
Каноническое уравнение гиперболы. Асимптоты. Эксцентриситет
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Обозначим через 









1°. Гипербола симметрична относительно осей 

2°. Удаляясь в бесконечность, переменная точка 

Такие прямые называются асимптотами гиперболы.
Оси симметрии называются осями гиперболы, а точка пересечения осей — ее центром. Ось 







При построении гиперболы (9) удобно сначала построить ее основной прямоугольник (рис. 4), провести прямые, проходящие через противоположные вершины этого прямоугольника, — асимптоты гиперболы и определить вершины 


также определяет гиперболу, которая называется сопряженной гиперболе (9). Гипербола (12) показана на рис. 4 штриховой линией. Вершины этой гиперболы находятся в точках 

3°. Эксцентриситет гиперболы определяется как отношение половины фокального расстояния к длине ее действительной полуоси:

Поскольку с > а, то 
Поэтому эксцентриситет гиперболы характеризует ее форму: чем больше эксцентриситет, тем больше отношение 



4°. Прямые .

Пример №9
Составить каноническое уравнение гиперболы, фокусы которой расположены на оси 

Решение:
Поскольку 2а = 6, то а= 3. Из формул (10) и (13) находим, что b = 4. Искомое уравнение имеет вид
Каноническое уравнение параболы
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой, и не проходит через фокус.
Пусть заданы фокус 








Каноническое уравнение параболы имеет вид

Ось симметрии параболы называется ее осью; точка пересечения оси с параболой — вершиной параболы; число, равное расстоянию от фокуса до директрисы, — параметром параболы. Осью параболы, заданной уравнением (14), является ось 

Замечание. Используя свойство 4° эллипса и гиперболы и определение параболы, можно дать такое общее определение кривой второго порядка (кроме окружности): множество точек, для которых отношение 



Пример №10
В параболу 
Решение:
Пусть точка А(






Рис. 6 Иллюстрация к примеру 4.
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
Другие темы которые вам помогут понять высшую математику:
Кривые линии второго порядка
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.
Круг
Кругом называется геометрическое место точек плоскости, которые равноудалены от одной и той же точки этой плоскости (рис. 2.13).
Уравнение круга с центром 


Круг — уравнение второго порядка. Общее уравнение кривой второго порядка: 


Эллипс
Эллипсом называется геометрическое место точек, сумма расстояний которых к двум фиксированным точкам, что называются фокусами, является постоянными и равны 
Координаты фокусов эллипса 





Отрезки 
Эксцентриситет эллипса
Расстояние 


Две прямые, которые параллельны к малой оси эллипса и находятся от нее на расстоянии 

Уравнение эллипса с осями, что параллельные координатными осям, имеет вид:
где 
Гипербола
Гиперболой называют геометрическое место точек, для каждой их которых абсолютное значение разницы расстояний от двух заданный точек, что называется фокусами, является величина постоянная и равна 
Координаты фокусов гиперболы 

Точки пересечения гиперболы с осью абсцисс 

Точки 

Эксцентриситет гиперболы
Расстояние 


по условию, что точка 
Две прямые, которые параллельны мнимой оси гиперболы и находятся от нее на расстоянии 
Прямые, которые обозначаются уравнением:
называются асимптотами гиперболы.
Две гиперболы, что заданы уравнениями:
называются спряженными. Они имеют общие асимптоты.
Если оси гиперболы равны, то есть 
Ее асимптотами служат биссектрисы координатных углов.
Если за оси координат принять асимптоты равносторонней гиперболы, то ее уравнение получит вид: 
Парабола
Параболой называется геометрическое место точек равноудаленных от заданной точки — фокуса и заданной прямой — директрисы (рис. 2.16).
Каноничное уравнение параболы имеет вид:
где 
Координаты фокуса 

Фокальный радиус 
Эксцентриситет параболы считается равным единице, то есть
Если осью симметрии параболы служит ось ординат (рис. 2.17), то уравнение параболы имеет вид:
Уравнение директрисы в этом случае:
Уравнение параболы с осью симметрии =, которая параллельна одной из координатных осей, имеет вид:
или
где 
Примеры решения задач:
Задача 2.51.
Сложить уравнение круга с центром в точке 
Решение. В уравнении (2.16) 


Задача 2.52
Обозначить центр и радиус угла, которое задано уравнением:
Решение. Как в заданном уравнении коэффициент при 


Выделим полный квадрат:
Левая часть заданного уравнения запишем так:
откуда:
Уравнивая полученное уравнение с уравнением (2.16) приходим к выводу, что это уравнение обозначает круг, центр которого имеет координаты
Задача 2.53
Сложить уравнение круга, что проходит через точки 

Решение. Каноническое уравнение круга:
Так как круг проходит через точки 

если центр круга находится на прямой 
решим систему уравнений:
отнимем от первого уравнения второе.
Получим систему:
Получим:
подставим полученное значение 

Таким образом, координаты центра круга:
Чтобы обозначить 
Следует, уравнение круга:
Задача 2.54
Сложим уравнение круга, что проходит через три заданные точки: 
Решение. Искомое уравнение имеет вид 
Подставим по очереди в искомое уравнение координаты заданных точек, получим три уравнения для определения 
От первого уравнения отнимем второе, а потом от первого уравнения отнимем третье. Получим систему двух уравнений с двумя неизвестными:
Откуда.
Для нахождения 

искомое уравнение круга имеет вид:
Задача 2.55
Найти длину осей, координаты фокусов и эксцентриситет эллипса
Решение. Приведем эти уравнения к каноничному виду (2.17):
Разделив обе части заданного уравнения на 144, получим:
отсюда получим, что 





Координаты фокусов будут: 

эксцентриситет эллипса
Задача 2.56
Большая ось эллипса равно 8, а расстояние между директрисами равно 16. Найти уравнение эллипса. Чему равен его эксцентриситет?
Решение. Для нахождения уравнения эллипса необходимо найти его полуоси 

Полуось 


Таким образом,
Получим уравнение эллипса:
Эксцентриситет эллипса будет
Задача 2.57
Сложить уравнение гиперболы, фокусы которого находятся на оси абсцисс, симметрично началу координат, если задана точка 
Решение. Для нахождения уравнения гиперболы 




Уравнение асимптот 

Получили систему уравнений:
Подставим полученные значения параметров в каноничное уравнение гиперболы:
Таким образом, получим искомое уравнение гиперболы:
Задача 2.58
Найти каноническое уравнение гиперболы, если угол между ее асимптотами равно 

Решение. Каноничное уравнение гиперболы имеет вид:
Уравнение асимптот 


Так как угол между асимптотами равен 
Отсюда,
По условию задачи 


Решим систему уравнений:
Получим уравнение:
Задача 2.59
Вычислить длину стороны правильного треугольника, который вписан в параболу 
Решение. Треугольник 
По условию задачи 





Следует, точка 
Эта точка лежит на параболе, ее координаты удовлетворяют уравнению параболы. Отсюда:
тогда,
Длина сторон треугольника
Общее уравнение кривой второго порядка: типы кривых
Кривой второго порядка называется линия, которая описывается уравнением
где 



Уравнение (8.1) называют общим уравнением линии 2-го порядка. При определенных условиях относительно значений коэффициентов при переменных и свободного члена оно описывает одну из четырех, знакомых со школы, кривых: круг, эллипс, гиперболу, параболу.
Однако может случиться, что не существует точек 

Кроме того, имеют место случаи вырождения кривых 2-го порядка в прямые или точку. К примеру:



Известно, что в зависимости от знака величины 
1) эллиптический, если 


2) гиперболический, если 
3) параболический, если 
Канонические уравнения окружности и эллипса
Круг — это множество точек плоскости, расстояние от которых до одной фиксированной точки, называется центром, является величиной постоянной. Расстояние от центра круга до любой точки называют радиусом круга.
Каноническое уравнение окружности (7.2) было получено в примере к главе 7:
Если в уравнении (8.2) раскрыть скобки, получим общее уравнение кривой 2-го порядка при 

которое называется общим уравнением круга.
Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух фиксированных точек (фокусов) является величиной постоянной. Пусть точка 


равна 
Рис. 8.1
Тогда согласно определению эллипса имеет место соотношение: 
или
Далее избавляемся от иррациональности поднесением к квадрату обеих частей (8.4) и упрощаем:
или
Уравнение (8.5) называют каноническим уравнением эллипса.
Поскольку 


Анализируя уравнение (8.5), делаем выводы:
1) точки эллипса не выходят за пределы прямоугольника, который описывается неровностями: 

Рис. 8.2
2) эллипс является симметричным относительно осей координат, поскольку уравнение содержит только квадраты текущих координат 

3) кривая пересекает координатные оси в точках — вершинах эллипса — с абсциссами 









Форма эллипса относительно оси 



С помощью соотношения 



Каноническое уравнение окружности 



Если эксцентриситет эллипса 




Известно, что планеты и кометы движутся по орбитам, имеющих форму эллипса. Орбиты планет близки к кругам, а орбиты комет — до вытянутых эллипсов (эксцентриситет орбиты Земли и кометы Галлея равны соответственно 0,02 и 0,97).
Прямые 
Расстояния от произвольной точки эллипса до его фокусов называют локальными радиусами эллипса (рис. 8.1):
Фокальные радиусы связаны соотношением 
Замечания. Каноническое уравнение эллипса можно получить, выбирая фокусы на оси 

Найдем уравнение эллипса 

Поскольку точка 
чи 

Следовательно, уравнение эллипса имеет вид:
Каноническое уравнение гиперболы. Асимптоты гиперболы
Гиперболой называется множество точек плоскости, модуль разности расстояний которых до двух фиксированных точек, называемых фокусами, есть величиной постоянной, отличной от нуля.
Выберем оси координат таким образом, чтобы фокусы гиперболы 


Воспользуемся рисунком 8.1, на котором теперь 

или
Выполняем преобразования, аналогичные тем, которые осуществлялись при выводе уравнения эллипса:
или
Уравнение (8.9) называется каноническим уравнением гиперболы.
Поскольку 


Анализ полученного уравнения позволяет прийти к выводам:
1) точки гиперболы выходят (кроме двух) за пределы вертикальной полосы, которая описывается неравенством: 

2) гипербола симметрична относительно осей координат, поскольку ее уравнение содержит только квадраты переменных 

3) кривая пересекает ось 










Рис. 8.3
Прямоугольник со сторонами 

Асимптотой гиперболы называется прямая, расстояние до которой от точек гиперболы стремится к нулю при неограниченном росте абсциссы 
Асимптоты гиперболы описываются уравнениями прямых:
на которых лежат диагонали основного прямоугольника гиперболы.
Пусть 


Поделим и умножим правую часть (8.11) на выражение, сопряженный к выражению под знаком модуля, то есть на выражение 
При неограниченном росте 
Аналогично можно показать, что прямая 
Согласно определению асимптот гиперболы ее геометрическое изображение начинают с построения основного прямоугольника и его диагоналей.
Части графика кривой при 

Как и для эллипса, форму гиперболы характеризует отношение фокусного расстояния 

Прямые 
Расстояния от произвольной точки гиперболы до ее фокусов называют фокальными радиусами гиперболы:
Фокальные радиусы связаны соотношением 



Примечание:
1) каноническое уравнение гиперболы в случае расположения ее фокусов на оси 
тогда действительной осью гиперболы является 

Кривые, описываемые уравнениями (8.9) и (8.14), называются взаимно сопряженными гиперболами;
2) если в уравнениях (8.9) и (8.14) 

Кривые, описываемые уравнениями (8.15), называются равносторонними гиперболами.
Пусть задано общее уравнение гиперболы: 
Найдем ее параметры и определим координаты вершин.
Запишем уравнение гиперболы в канонической форме:
Отсюда имеем:


Парабола. Каноническое уравнение
Параболой называется множество точек плоскости, равноудаленных от фиксированной точки (фокуса) и фиксированной прямой (директрисы).
Выберем на плоскости систему координат 






Рис. 8.4
Пусть 

или
Уравнение (8.16) называется каноническим уравнением параболы.
Число 
Анализ уравнения (8.16) позволяет прийти к выводам:
1) парабола симметрична относительно оси 

уравнения в второй степени; ось симметрии (



2) при росте 





Парабола с фокусом в точке 

Рис. 8.5
Задачи на составление канонических уравнений параболы сводятся к отысканию только одной величины — параметра
Составим каноническое уравнение параболы, проходящей через точку 

Поскольку точка 



Уравнение 





Задача вывода уравнений кривых 2-го порядка усложняется, если центр центральных кривых лежит не в начале координат и (или) оси симметрии не является координатными осями; а для нецентральных кривых — если фокус не лежит на координатной оси и (или) директриса не ортогональная одной из осей координат.
Для установления положение на плоскости кривых 2-го порядка, которые описываются общим уравнением, путем параллельного переноса и (или) поворота исходной системы координат переходят к такой системе координат, в которой общее уравнение приобретает каноническому виду.
Возведение общего уравнения кривой второго порядка к каноническому виду
Выберем на плоскости две системы координат, тогда координаты той же точки в этих системах будут разными.
Задача преобразования координат заключается в том, чтобы найти связь между координатами точек в двух системах координат, одну из которых назовем выходной, вторую — новой. Любую новую систему координат 






Рис. 8.6
Параллельный перенос. Выберем на плоскости произвольную точку 







Рис. 8.7
Введем в рассмотрение радиусы-векторы
Вектор 


Соотношения (8.17) называются формулами параллельного переноса.
Поворот осей координат. Установим связь между координатами произвольной точки 





Рис. 8.8
Обозначим через 






Найдем проекции вектора 


Соотношение (8.18) называют формулами поворота осей координат.
Если осуществляется параллельный перенос и поворот осей координат, то исходные координаты 

Найдем уравнение равносторонней гиперболы 

По формуле (8.18) выражаем текущие координаты точек исходной системы через текущие координаты новой системы:
Подставляем выражения для 


Рассмотрим применение формул параллельного переноса и поворота осей координат до сведения общего уравнения кривой 2-го порядка к каноническому виду.
1. Сведение к каноническому виду общего уравнения, не содержит произведения переменных
Преобразование уравнения (8.20) в уравнение каноническому виду осуществляется с помощью параллельного переноса системы координат, которому предшествует выделение полных квадратов по обоим переменным.
Пусть задано общее уравнение кривой: 
а) устанавливаем тип заданной кривой 

б) группируем в левой части уравнения члены с переменными 

в) вводим новые координаты: 
Итак, заданная кривая 2-го порядка является гиперболой с полуосями: 
2. Возведение общего уравнения кривой к каноническому виду.
Преобразование этого уравнения в уравнение каноническому виду осуществляется в два этапа:
1-й этап. С помощью поворота осей координат сводим общее уравнение к уравнению (8.20), которое не содержит произведения переменных. Соответствующий угол поворота осей 
откуда по формулам тригонометрии имеем:
где знак выбирается в зависимости от того, в какой четверти находится угол 
По формуле (8.18) выражаем текущие координаты точек исходной системы через текущие координаты новой системы:
что дает возможность получить уравнения относительно переменных 

2-й этап. С помощью параллельного переноса осей координат превращаем уравнение, которое было получено на первом этапе, на уравнение канонического виду.
Замечания. Преобразование общего уравнения кривой 2-го порядка можно начинать с параллельного переноса осей с целью избавиться членов, содержащих переменные в первой степени. В этом случае получают квадратичную форму, которую приводят к каноническому виду известными методами, например, методами Лагранжа, Якоби, Сильвестра. Кроме того применяют аппарат приведения матрицы коэффициентов квадратичной формы к диагональному виду с помощью собственных чисел и собственных векторов этой матрицы. Данные методы являются достаточно громоздкими и выходят за рамки данного учебника.
Приведем еще один пример применения параллельного переноса осей.
Проведем исследование кривой 2-го порядка, заданной общим уравнением:
Это уравнение можно представить в виде дробно линейной функции:
Поделим числитель на знаменатель дроби (8.24), то есть выделяем целую часть дроби, а именно:
Обозначим:
Уравнение (8.25) в новой системе координат приобретает следующий вид:
Следовательно, графиком дробно-линейной функции является гипербола с асимптотами, параллельными осям координат, и центром симметрии в точке
Квадратичные формы. Применение к превращению уравнений кривой 2-го порядка
Пусть 

где 
Квадратичная форма 

Квадратичная форма 
Матрица 


Теорема 8.1 (о матричной записи квадратичной формы). Любую квадратичную форму можно представить в матричном виде как произведение двух линейных преобразований, первое из которых тождественно 

Доказательство. С помощью тождественных алгебраических преобразований получаем:
Теорема обобщается на квадратичные формы относительно любого конечного числа переменных:
При 

Теорема 8.2 (о сведении симметричной квадратичной формы к каноническому виду). Если вектор переменных 


где 


Доказательство. Подставим в матричный запись квадратичной формы вместо 



После перехода к ортонормированному базису с учетом свойств: 
Если по теореме 8.2 сводить к каноническому виду уравнение кривых второго порядка, то в зависимости от того, каким будет определитель матрицы квадратичной формы 



Покажем справедливость третьего соотношения:
Пусть, 
Найдем собственные числа:
В новом (ортонормированном) базисе уравнением кривой будет квадрат только одной переменной, а значит соответствующая линия является кривой параболического типа.
Аналогично доводятся другие случаи, когда каноническая форма (8.29) содержит слагаемые соответствии с одинаковыми или разными знаками.
Для использования квадратичных форм с целью упрощения уравнений кривых второго порядка коэффициенты при переменных обозначают строчными буквами с индексами:
Сведем к канонической форме общее уравнение кривой
где
В данном уравнении 

а) 
решаем систему двух линейных уравнений:
определяя таким образом начало новой координатной системы 
В системе 

которое в левой части содержит квадратичную форму относительно переменных
Находим собственные числа матрицы этой квадратичной формы:
Поскольку 
Определяем собственные векторы, принадлежащие каждому собственному числу:
Векторы 


Переходим от полученного базиса к ортонормированному:
в котором каноническая форма заданного уравнения имеет вид:



Следовательно, имеем случай вырождения кривой в точку.

то есть кривой является эллипс с параметрами
Замечания. Для кривых параболического типа упрощения уравнения начинают, как правило, с поворота осей координат.
В заключение отметим, что существуют величины, составленные из коэффициентов уравнения (и свободного члена), которые не изменяются при переходе от одной прямоугольной декартовой системы координат к другой такой же системы. Эти величины называются инвариантами кривой второго порядка. К ним относятся:
1) сумма коэффициентов при квадратах координат:
2) определитель, образованный из коэффициентов при старших членах:
3) определитель, составленный из параметров уравнения:
По значениям инвариантов, возведенными в табл. 8.1, устанавливают не только тип кривой, но и возможные случаи ее вырождения.
Инварианты кривой второго порядка и распознавания за ними типа кривой Таблица 8.1
Установим, вырожденная ли линия второго порядка, заданная уравнением:
Вычисляем инварианты кривой и анализируем результаты:
Согласно табл. 8.1 кривая гиперболического типа, распадается на две прямые, пересекающиеся:
Лекции:
- Линейные дифференциальные уравнения
- Теорема Муавра Лапласа
- Вычислить двойной интеграл
- Формула Ньютона-Лейбница
- Найти первую и вторую производные функции
- Признаки сходимости рядов
- Цилиндр
- Условный экстремум
- Коэффициент вариации
- Функция плотности распределения