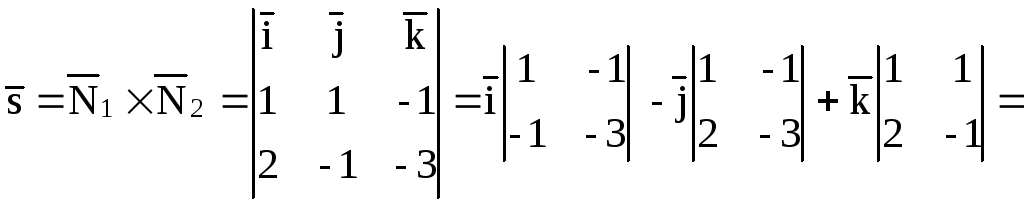Как найти параметрическое уравнение прямой в пространстве - Autoru.top

3.1. Канонические
уравнения прямой.

Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

(см. рис.18).Обозначим через
вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторыколлинеарны, следовательно, их
соответствующие координаты пропорциональны:

(3.3.1)

Эти уравнения
называются каноническими
уравнениями прямой.

Пример: Написать
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору

Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:

Это канонические
уравнения прямой.

Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.

3.2.
Параметрические
уравнения прямой.

Пусть прямая
задана каноническими уравнениями

Обозначим тогдаВеличина t
называется параметром и может принимать
любые значения:
.

Выразим x,
y
и z
через t
:

(3.2.1)

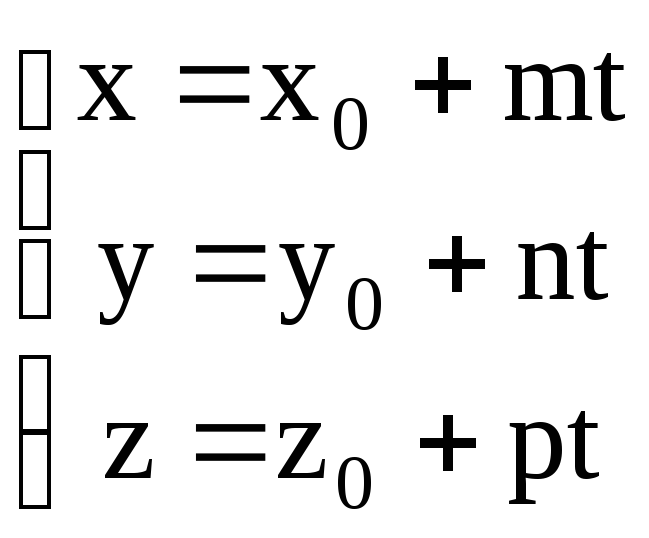
Полученные уравнения
называются параметрическими
уравнениями прямой.

Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору

Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:

Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):

Итак,
— параметрические уравнения данной
прямой.

Ответ:

Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).

Решение:
Вектор является направляющим
вектором искомой прямой.

Найдем вектор .

= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

— это искомые
параметрические уравнения прямой.

3.3. Уравнения
прямой, проходящей через две заданные
точки.

Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Векторможно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
находим
по формулам (3.1.1):).

(3.3.1)

Пример 1.
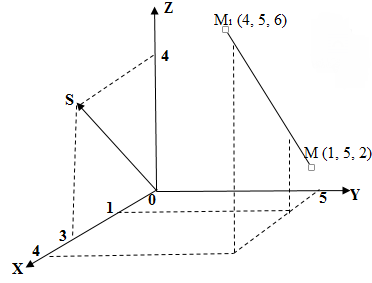
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

Применяем
формулу (3.3.1)

Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

— это параметрические
уравнения прямой.

Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

По формулам
(3.3.1) получим:

Это канонические
уравнения.

Переходим к
параметрическим уравнениям:

— параметрические
уравнения.

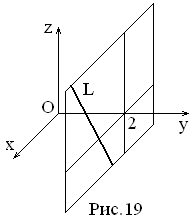
Полученная прямая
параллельна оси oz
(см. рис.21).

3.4. Прямая как
линия пересечения двух плоскостей.

Пусть в
пространстве даны две плоскости

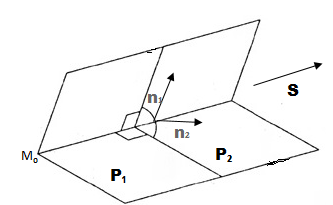
Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:

Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий векторКоординаты точкиполучим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть

Пример 1.
Составить
канонические уравнения прямой

Решение: Пусть
z
= 0. Решим систему

Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.

Итак, точка
лежит на искомой прямой.

Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:

Уравнения прямой
находим по формулам (3.1.1):

Ответ: .

Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).

Пример 2.
Составить канонические и параметрические
уравнения прямой

Решение:
Пусть y
= 0. Тогда система примет вид:

Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку

Для нахождения
второй точки положим x
= 0. Будем иметь:

То есть

Далее применяем
формулы (3.3.1):

Получили канонические
уравнения прямой.

Составим
параметрические уравнения прямой:

Ответ:

; .

3.5. Взаимное
расположение двух прямых в пространстве.

Пусть прямые
заданы уравнениями:

;: .

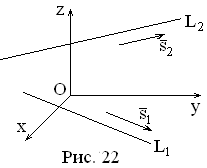
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот уголнаходим по формуле из векторной алгебры:

или

(3.5.1)

Если прямые перпендикулярны
(),то
Следовательно,

(3.5.2)

Это условие
перпендикулярности двух прямых в
пространстве.

Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть

(3.5.3)

Это условие
параллельности двух прямых в пространстве.

Пример 1. Найти
угол между прямыми:

а).
и

б). и

Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий векторвторой прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему

Затем найдем их векторное произведение:

(см. пример 1
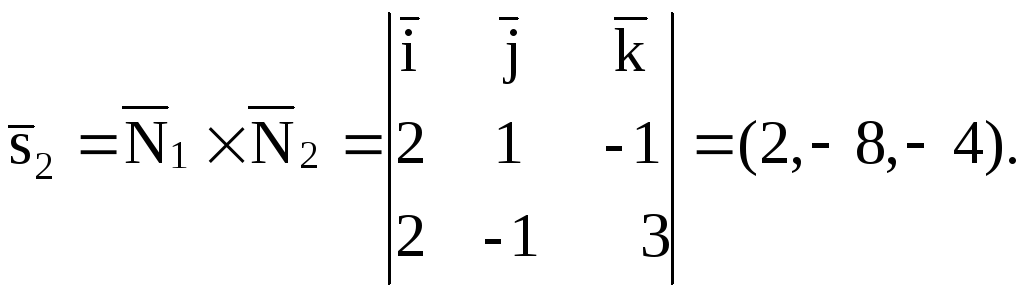
пункта 3.4).

По формуле (3.5.1)
получим:

Следовательно,

б). Запишем
направляющие векторы данных прямых:
Векторыколлинеарны, так как их соответствующие
координаты пропорциональны:

Значит прямые
параллельны (),
то есть

Ответ: а).
б).

Пример 2. Доказать
перпендикулярность прямых:

Решение:
Запишем направляющий вектор первой
прямой

Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:

Вычислим их векторное произведение:

(См. пример 1пункта 3.4).

Применим условие
перпендикулярности прямых (3.5.2):

Условие выполнено;
следовательно, прямые перпендикулярны
().

Соседние файлы в предмете Математика

#
#
#
#
#
#
#
#
#
03.03.20154.96 Кб8Содержание OneNote.onetoc2
#

Источник

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

каноническое уравнение,
параметрическое уравнение,
общее уравнение прямой,
уравнение прямой с угловым коэффициентом,
уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Каноническое уравнение прямой на плоскости

{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}

x_a и y_a — координаты первой точки A,

x_b и y_b — координаты второй точки B

Параметрическое уравнение прямой на плоскости

{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}

x_a, y_a — координаты точки, лежащей на прямой,

{l;m} — координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Каноническое уравнение прямой в пространстве

{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}

x_a, y_a и z_a — координаты первой точки A,

x_b, y_b и z_b — координаты второй точки B

Параметрическое уравнение прямой в пространстве

{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }

x_a, y_a и z_a — координаты точки, лежащей на прямой,

{l;m;n} — координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Пример нахождения уравнения прямой, проходящей через две точки

Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).

Каноническое уравнение прямой

Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}

Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}

Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}

Уравнение прямой с угловым коэффициентом

Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}

Параметрическое уравнение прямой

Параметрическое уравнение прямой имеет вид:

{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }

где {x_a, y_b} — координаты точки, лежащей на прямой, {{l;m}} — координаты направляющего вектора прямой, t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.

Найдем координаты направляющего вектора:

overline{AB} = {x_b — x_a; y_b — y_a} = {3-1; 8-2} = {2; 6}

Получаем параметрическое уравнение:

begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}

Используем калькулятор для проверки полученного ответа.

Источник

Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.

Параметрическое и каноническое уравнение прямой в пространстве
Уравнение прямой в пространстве, которая проходит через две заданные точки
Общее уравнение прямой – переход к каноническому уравнению
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Примеры решения задач

Параметрическое и каноническое уравнение прямой в пространстве

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку $M_{1} (x_{1}, y_{1}, z_{1})$ параллельно направляющему вектору .

Пусть, – произвольная точка прямой, тогда векторы $overline{M_{1}M} = (x - x_{1}, y - y_{1}, z - z_{1})$ и коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

${x - x_{1}over{l}} = {y - y_{1}over{m}} = {z - z_{1}over{p}}$

(1)

это и есть канонические уравнения прямой.

Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:

$left{ begin{aligned} x = lt + x_{0}\ y = mt + y_{0}\ z = pt + z_{0} end{aligned}$

(2)

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки $M_{1}(x_{1}, y_{1}z_{1}$ и $M_{2}(x_{2}, y_{2}, z_{2})$ можно не только геометрично провести линию, но и сложить её уравнения.

За направляющий вектор возьмём $overline{S} = overline{M_{1}M} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1})$ , тогда по формуле (1) у нас получается:

${x - x_{1}over{x_{2} - x_{1}}} = {y - y_{1}over{y_{2} - y_{1}}} = {z - z_{1}over{z_{2} - z_{1}}}$

(3)

уравнение прямой в пространстве, которые проходят через две заданные точки.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Общее уравнение прямой – переход к каноническому уравнению

Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

Пусть известны их уравнения:

$left{begin{aligned}A_{1}x + B_{1}y + C_{1}z + D_{1} = 0\A_{2}x + B_{2}y + C{2}z + D_{2} = 0 end{aligned}$

(4)

Тогда система (4) называется общим уравнением прямой.

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку $M_{0}$ этой прямой.

Точку $M_{0}$ находим, как один из решений системы (4). Например, положив в (4) находим $x_{0}, y_{0}$ , тогда и точку $M_{0} (x_{0}, y_{0}, 0)$ . Направляющий вектор , который параллелен к каждой из плоскостей $P_{1}$ и $P_{2}$ и перпендикулярен к их нормальным векторам $overline{n_{1}} = (A_{1}, B_{1}, C_{1})$ и $overline{n_{2}} = (A_{2}, B_{2}, C_{2})$ , то есть $overline{S}perp{overline{n_{1}}}$ , $overline{S}perp{overline{n_{2}}}$ . (см. рис. 1). Поэтому вектор можно найти при помощи векторного произведения $overline{n_{1}}$ и $overline{n_{2}}$

= $overline{n}_{1}$ x $overline{n}_{2}$ = $begin{vmatrix} overline{i}&overline{j}&overline{k}\ A_{1}&B_{1}&C_{1}\ A_{2}&B_{2}&C_{2} end{vmatrix}$

Найдены координаты $M_{0}$ и подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

$left{begin{aligned} 2x + 7y - z - 4 = 0\ 4x - 9y - 2z - 8 = 0 end{aligned}$

Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём $x = 2, z = 0, M_{0} (2, 0, 0)$ . Нормальные векторы $overline{n_{1}} = (2, 7, -1)$ и $overline{n_{2}} = (4, -9, -2)$ . Тогда направляющий вектор

Рис. 1

$overline{S} = overline{n}_{1}$ x $overline{n}_{2}$ = $begin{vmatrix} overline{i}&overline{j}&overline{k}\ 2&7&-1\ 4&-9&-2 end{vmatrix} = -23overline{i} - 0overline{j} - 46overline{k}$ ,

и канонические уравнения станут:

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми :

${x - x_{1}over{l_{1}}} = {y - y_{1}over{m_{1}}} = {z - z_{1}over{p_{1}}}$ и ${x - x_{2}over{l_{2}}} = {y - y_{2}over{m_{2}}} = {z - z_{2}over{p_{2}}}$

равен углу между их направляющими векторами $overline{S_{1}} = (l_{1}, m_{1}, p_{1})$ и $overline{S_{2}} = (l_{2}, m_{2}, p_{2})$ , поэтому

${cosvarphi = cos(overline{S}_{1}}, overline{S}_{2}})$ = ${l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2}}over{sqrt{l_{1}^2 + m_{1}^2 + p_{1}^2}} * {sqrt{l_{2}^2 + m_{2}^2 + p_{2}^2}}$

(5)

Условия параллельности и перпендикулярности прямых соответственно запишутся:

${l_{1}over{l_{2}}} = {m_{1}over{m_{2}}} = {p_{1}over{p_{2}}}$ и $l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2} = 0$ .

(6)

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

Задача

При точке и направляющем векторе необходимо:

составить каноническое уравнение прямой;
построить эту прямую.

Решение

1) По формуле (1) запишем каноническое уравнение прямой :

= .

2) Рассмотрим два способа построения прямой .

Первый способ

В системе координат строим вектор и точку и проводим через точку прямую параллельную вектору .

Второй способ

По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:

$left{begin{aligned} x = 3t + 1\ y = 0 * t + 5\ z = 4t + 2 end{aligned} right$

На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой . Так при находим координаты $M_{1}(4, 5, 6)$ . Через две точки и $M_{1}$ проводим прямую .

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

Задача

Найти острый угол между прямыми:

(7)

Решение

По формуле (7) получаем:

= ${6 * (-2) + (-2)(-1) + 3 * (-2)}over{sqrt{6^2 + (-2)^2 + 3^2} * sqrt{(-2)^2 + (-1)^2 + (-2)^2}$ = =

Так как , тогда угол тупой, , а острый угол .

Ответ

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

Задача

Составить уравнение прямой , которая проходит через точку и параллельна прямой .

Решение

От параметрического уравнения переходим к каноническому При условии параллельности прямых $overline{S}||overline{S_{1}}$ то есть направляющим вектором новой прямой может служить известный вектор и по формуле (1) у нас получается:

Ответ

Источник

Уравнения прямых в пространстве

Уравнение прямой как линии пересечения двух плоскостей

Пусть в координатном пространстве Oxyz (в прямоугольной системе координат) две плоскости заданы общими уравнениями

$begin{aligned}rho_{1}colon & ,A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0;\[2pt] rho_{2}colon & ,A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0,end{aligned}$

в которых коэффициенты при неизвестных непропорциональны, т.е. $operatorname{rang}!begin{pmatrix}A_{1}&B_{1}&C_{1}\A_{2}&B_{2}&C_{2}end{pmatrix}=2$ . Это условие означает, что плоскости $rho_{1}$ и $rho_{2}$ пересекаются (см. условие (4.25)), поскольку их нормали $vec{n}_{1}=A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k}$ и $vec{n}_{2}=A_{2}vec{i}+B_{2}vec{j}+C_{2}vec{k}$ неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений

$begin{cases} A_{1}cdot x+D_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+D_{2}cdot y+C_{2}cdot z+D_{2}=0. end{cases}$

(4.31)

Система (4.31) называется общим уравнением прямой в пространстве.

Общее уравнение прямой в пространстве как пересечение двух плоскостей

Пример 4.13. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту треугольника.

Решение. Прямая является линией пересечения двух плоскостей: плоскости $rho_{1}$ , треугольника ABC и плоскости $rho_{2}$ , проходящей через точку перпендикулярно вектору overrightarrow{BC} (рис.4.26). По формуле (4.21) составим уравнение плоскости $rho_{1},$ проходящей через три точки A,,B,,C:

$begin{vmatrix}x-1&y-2&z-3\3-1&0-2&2-3\7-1&4-2&6-3end{vmatrix}= begin{vmatrix} x-1&y-2&z-3\ 2&-2&-1\ 6&2&3 end{vmatrix}=0 quad Leftrightarrow quad x+3y-4z+5=0.$

По формуле (4.14) составим уравнение плоскости $rho_{2}$ , проходящей через точку перпендикулярно вектору overrightarrow{BC}=(7-3)vec{i}+(4-0)vec{j}+(6-2)vec{k}=4vec{i}+4vec{j}+4vec{k}:

4cdot(x-1)+4cdot(y-2)+4cdot(z-3)=0 quad Leftrightarrow quad x+y+z-6=0.

Следовательно, общее уравнение (4.31) прямой имеет вид $begin{cases}x+3y-4z+5=0,\x+y+z-6=0.end{cases}$

Параметрическое уравнение прямой в пространстве

Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.

Пусть в координатном пространстве Oxyz заданы точка $M_{0}(x_{0}, y_{0}, z_{0})$ и ненулевой вектор vec{p}= avec{i}+ bvec{j}+ cvec{k} (рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору vec{p} и проходящей через точку $M_{0}(x_{0},y_{0},z_{0})$ .

Выберем на прямой произвольную точку $M_{0}(x,y,z)$ . Обозначим vec{r}=overrightarrow{OM}, $vec{r}_{0}=overrightarrow{OM_{0}}$ — радиус-векторы точек M(x,y,z) и $M_{0}(x_{0},y_{0},z_{0})$ (рис.4.28).

Параметрическое уравнение прямой в пространстве и направляющий вектор прямой

Точка принадлежит заданной прямой тогда и только тогда, когда векторы $overrightarrow{M_{0}M}$ и vec{p} коллинеарны. Запишем условие коллинеарности: $overrightarrow{M_{0}M}=tvec{p}$ , где — некоторое действительное число (параметр). Учитывая, что $overrightarrow{M_{0}M}=vec{r}-vec{r}_{0}$ , получим векторное параметрическое уравнение прямой в пространстве:

$vec{r}=vec{r}_{0}+tcdotvec{p}, quad tinmathbb{R},,$

(4.32)

где vec{p} — направляющий вектор прямой, а $vec{r}_{0}$ — радиус-вектор заданной точки $M_{0}(x_{0},y_{0},z_{0})$ принадлежащей прямой.

Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве

$begin{cases}x=x_{0}+acdot t,\y=y_{0}+bcdot t,\z=z_{0}+ccdot t,end{cases}tinmathbb{R},,$

(4.33)

где a,b,c — координаты направляющего вектора vec{p} прямой. Параметр в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина пропорциональна расстоянию от заданной точки $M_{0}(x_{0}, y_{0}, z_{0})$ до точки $M(x,y,z)equiv M(x_{0}+at,y_{0}+bt,z_{0}+ct)$ . Физический смысл параметра в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки по прямой. При t=0 точка M(x,y,z) совпадает с заданной точкой $M_{0}$ . При возрастании параметра движение происходит в направлении направляющего вектора.

Каноническое уравнение прямой в пространстве

Выразим параметр из каждого уравнения системы (4.33): $t=frac{x-x_{0}}{a},, t=frac{y-y_{0}}{b},, t=frac{z-z_{0}}{c}$ , а затем исключим этот параметр:

$frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}, quad a^2+b^2+c^2ne0.$

(4.34)

Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты a,b,c не равны нулю одновременно, так как это координаты направляющего вектора прямой.

Замечания 4.6.

1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:

а) каноническое уравнение $frac{x-x_{0}}{0}=frac{y-y_{0}}{0}=frac{z-z_{0}}{c}$ — это уравнение $begin{cases}x=x_{0},\y=y_{0}end{cases}$ прямой, параллельной оси аппликат (рис.4.29,а);

б) каноническое уравнение $frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{0}$ — это уравнение $begin{cases}z=z_{0},\dfrac{x-x_{0}}{a}=dfrac{y-y_{0}}{b}end{cases}$ прямой, параллельной координатной плоскости Oxy (рис.4.29,б).

Прямые в пространстве, параллельные координатным плоскостям

2. Направляющий вектор vec{p} прямой определяется неоднозначно. Например, любой ненулевой вектор lambdacdotvec{p} , где lambdainmathbb{R} , также является направляющим вектором для той же прямой.

Переход от общего уравнение к каноническому

3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:

1) найти любое решение $(x_{0},y_{0},z_{0})$ системы $begin{cases} A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0, end{cases}$ определяя тем самым координаты точки $M_{0}(x_{0},y_{0},z_{0})$ , принадлежащей прямой;

2) найти направляющий вектор vec{p} прямой как векторное произведение нормалей $vec{n}_{1}=A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k},$ $vec{n}_{2}= A_{2}vec{i}+ B_{2}vec{j}+ C_{2}vec{k},$ заданных плоскостей:

$vec{p}= begin{bmatrix}vec{n}_{1},vec{n}_{2}end{bmatrix}= acdotvec{i}+ bcdotvec{j}+ ccdotvec{k}= begin{vmatrix} vec{i}&vec{j}&vec{k}\ A_{1}&B_{1}&C_{1}\ A_{2}&B_{2}&C_{2} end{vmatrix}.$

3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.

4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы

$left{!begin{aligned}frac{x-x_{0}}{a}&=frac{y-y_{0}}{b},,\frac{y-y_{0}}{b}&=frac{z-z_{0}}{c},,end{aligned}right.$ и привести подобные члены.

5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):

$frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}=t quad Leftrightarrow quad begin{cases}x=x_{0}+acdot t,\y=y_{0}+bcdot t,\z=z_{0}+ccdot t,end{cases} tinmathbb{R},.$

6. Если в каноническом уравнении (4.34) прямой фиксировать координаты $x_{0},y_{0},z_{0}$ точки $M_{0}$ , а коэффициентам a,b,c придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке $M_{0}(x_{0},y_{0},z_{0})$ , т.е. совокупность всех прямых, проходящих через точку $M_{0}$ .

7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.

Пример 4.14. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис. 4.30). Требуется:

В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1,2,3), B(3,0,2), C(7,4,6) треугольника

а) составить каноническое уравнение прямой, содержащей высоту треугольника;

б) составить общее уравнение прямой, содержащей биссектрису треугольника.

Решение. а) Общее уравнение прямой получено в примере 4.13: $begin{cases}x+3cdot y-4cdot z+5=0,\x+y+z-6=0.end{cases}$ Перейдем от общего уравнения к каноническому.

1) Найдем любое решение $(x_{0},y_{0},z_{0})$ системы, например, $x_{0}=1,$ $y_{0}=2,$ $z_{0}=3$ (это координаты точки A(1;2;3) ).

2) Найдем направляющий вектор vec{p} прямой как векторное произведение нормалей $vec{n}_{1}=vec{i}+3vec{j}-4vec{k},$ $vec{n}_{2}=vec{i}+vec{j}+vec{k}$ заданных плоскостей

$vec{p}= begin{bmatrix}vec{n}_{1},vec{n}_{2}end{bmatrix}= begin{vmatrix} vec{i}&vec{j}&vec{k}\ 1&3&-4\ 1&1&1 end{vmatrix}= 7cdotvec{i}-5cdotvec{j}-2cdotvec{k},.$

3) Запишем каноническое уравнение (4.34): $frac{x-1}{7}=frac{y-2}{-5}=frac{z-3}{-2}$ .

б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор vec{l} этой прямой. Учитывая, что диагональ ромба является биссектрисой, vec{l}=vec{b}+vec{c} , где vec{b} и vec{c} — единичные векторы, одинаково направленные с векторами overrightarrow{AB} и overrightarrow{AC} соответственно. Находим

$begin{gathered}overrightarrow{AB}= 2cdotvec{i}-2cdotvec{j}-1cdotvec{k}, quad begin{vmatrix}overrightarrow{AB}end{vmatrix}=3, quad vec{b}= frac{overrightarrow{AB}}{begin{vmatrix} overrightarrow{AB}end{vmatrix}}= frac{2}{3}cdot vec{i}-frac{2}{3} cdotvec{j}-frac{1}{3}cdot vec{k},;\[3pt] overrightarrow{AC}= 6cdot vec{i}+ 2cdotvec{j}+3cdotvec{k}, quad begin{vmatrix} overrightarrow{AC} end{vmatrix}=7, quad vec{c}= frac{overrightarrow{AC}}{begin{vmatrix} overrightarrow{AC}end{vmatrix}}= frac{6}{7}cdotvec{i}+ frac{2}{7}cdotvec{j}+ frac{3}{7}cdotvec{k},;\[3pt] vec{l}=vec{a}+vec{c}= left(frac{2}{3}cdotvec{i}-frac{2}{3}cdotvec{j}-frac{1}{3}cdotvec{k}right)+ left(frac{6}{7}cdotvec{i}+frac{2}{7}cdotvec{j}+frac{3}{7}cdotvec{k}right)= frac{32}{21}cdotvec{i}-frac{8}{21}cdotvec{j}+frac{2}{21}cdotvec{k},. end{gathered}$

Составляем каноническое уравнение прямой $ALcolon,frac{x-1}{32/21}=frac{y-2}{-8/21}=frac{z-3}{2/21}$ .

Записывая двойное равенство в виде системы, получаем общее уравнение прямой AL:

$left{!begin{aligned}frac{x-1}{32/21}&=frac{y-2}{-8/21},\ frac{y-2}{-8/21}&=frac{z-3}{2/21},end{aligned}right. quad Leftrightarrow quad begin{cases}x+4cdot y-9=0,\ y+4cdot z-14=0.end{cases}$

Расстояние от точки до прямой, заданной каноническим уравнением

Расстояние от точки до прямой в пространстве

Найдем расстояние от точки $M_{1}(x_{1},y_{1},z_{1})$ до прямой , заданной каноническим уравнением (рис.4.31)):

$lcolon, frac{x-x_{0}}{a}= frac{y-y_{0}}{b}= frac{z-z_{0}}{c},.$

Искомое расстояние равно высоте параллелограмма, построенного на векторах

vec{p}=avec{i}+bvec{j}+cvec{k} и $vec{m}=overrightarrow{M_{0}M_{1}}=(x_{1}-x_{0})vec{i}+(y_{1}-y_{0})vec{j}+(z_{1}-z_{0})vec{k}$ , то есть.

$d=frac{begin{vmatrix}begin{bmatrix}vec{m},vec{p}end{bmatrix}end{vmatrix}}{begin{vmatrix}vec{p}end{vmatrix}}= frac{sqrt{begin{vmatrix}x_{1}-x_{0}&y_{1}-y_{0}\a&bend{vmatrix}^2+ begin{vmatrix}y_{1}-y_{0}&z_{1}-z_{0}\b&cend{vmatrix}^2+ begin{vmatrix}x_{1}-x_{0}&z_{1}-z_{0}\a&cend{vmatrix}^2}}{sqrt{a^2+b^2+c^2}},.$

(4.35)

Уравнение прямой, проходящей через две заданные точки

Уравнение прямой в пространстве, проходящей через две заданные точки

Пусть в координатном пространстве Oxyz заданы две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ . Требуется составить уравнение прямой, проходящей через заданные точки.

Как показано в разд., точка M(x,y,z) принадлежит прямой $M_{0}M_{1}$ тогда и только тогда, когда ее радиус-вектор overrightarrow{OM} удовлетворяет условию (рис.4.32): $overrightarrow{OM}= (1-t)cdot overrightarrow{OM_{0}}+ tcdotoverrightarrow{OM_{1}}$ , где — некоторое действительное число (параметр). Это уравнение, а также его координатную форму

$begin{pmatrix}x\y\zend{pmatrix}= (1-t)cdot!begin{pmatrix}x_{0}\y_{0}\z_{0}end{pmatrix}+tcdot!begin{pmatrix}x_{1}\y_{1}\z_{1}end{pmatrix}! quad Leftrightarrow quad !begin{cases} x=(1-t)cdot x_{0}+tcdot x_{1},\ y=(1-t)cdot y_{0}+tcdot y_{1},\ z=(1-t)cdot z_{0}+tcdot z_{1}.end{cases} tinmathbb{R}$

(4.36)

будем называть аффинным уравнением прямой, проходящей через две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ .

Выражая параметр из каждого уравнения системы (4.36), получаем: $frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}}=frac{z-z_{0}}{z_{1}-z_{0}}=t$ . Исключая параметр , приходим к уравнению прямой, проходящей через две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ :

$frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}}=frac{z-z_{0}}{z_{1}-z_{0}},.$

(4.37)

Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора vec{p}=avec{i}+bvec{j}+cvec{k} вектор $overrightarrow{M_{0}M_{1}}=(x_{1}-x_{0})vec{i}+(y_{1}-y_{0})vec{j}+(z_{1}-z_{0})vec{k},$ т.е. подставляя $a=x_{1}-x_{0},$ $b=y_{1}-y_{0},$ $c=z_{1}-z_{0}.$

Треугольник в пространстве по координатам вершин, его высота и медиана

Пример 4.15. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис.4.33). Требуется:

а) составить уравнение прямой ;

б) составить уравнение прямой, содержащей медиану треугольника;

в) найти высоту h=|AH| треугольника, опущенную на сторону .

Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки B(3;0;2), C(7;4;6):

$frac{x-3}{7-3}=frac{y-0}{4-0}=frac{z-2}{6-2}~ Leftrightarrow~ frac{x-3}{1}=frac{y}{1}=frac{z-2}{1},.$

б) Находим координаты середины стороны BCcolon M(5;2;4) . Составляем уравнение (4.37) прямой AM:

$frac{x-1}{5-1}=frac{y-2}{2-2}=frac{z-3}{4-3}~ Leftrightarrow~ frac{x-1}{4}=frac{y-2}{0}=frac{z-3}{1},.$

в) Искомую высоту находим по формуле (4.35), полагая vec{m}=overrightarrow{BA}=-2vec{i}+2vec{j}+vec{k} и vec{p}=vec{i}+vec{j}+vec{k}:

$h=|AH|=frac{begin{vmatrix}begin{bmatrix}vec{m},vec{p}end{bmatrix}end{vmatrix}}{begin{vmatrix}vec{p}end{vmatrix}}= frac{sqrt{begin{vmatrix}-2&2\1&1end{vmatrix}^2+begin{vmatrix}2&1\1&1end{vmatrix}^2+begin{vmatrix}-2&1\1&1end{vmatrix}^2}}{sqrt{1^2+1^2+1^2}}=frac{sqrt{16+1+9}}{sqrt{3}}= sqrt{frac{26}{3}},.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

(схема 27)

Пусть задан
вектор , параллельный заданной прямой l (без учета направления) и точка M₀, лежащая на данной прямой. Таким образом, прямая l
однозначно определяется в пространстве точкой M₀(x₀;y₀;z₀) и вектором , называемым для l направляющим.
Обозначим
и определим его
с точностью до коллинеарности (рис. 2.21).

Пусть точка M(x;y;z) – текущая точка прямой l,
тогда текущий вектор прямой имеет координаты . Значит, векторы и коллинеарны. По
следствию из теоремы 2.5 данное условие
можно записать в виде:

– (2.43)

канонические уравнения прямой в
пространстве. Равенство нулю одного из знаменателей означает обращение
в нуль соответствующего числителя.

Пусть прямая l проходит через две точки,
одна из которых – уже введенная в
рассмотрение точка M₀(x₀;y₀;z₀). Другую точку обозначим M₁(x₁;y₁;z₁). Тогда в качестве направляющего вектора прямой можно взять вектор . При этом уравнения (2.43) принимают вид:

– (2.44)

уравнения прямой в пространстве, проходящей
через две заданные точки.

Все
соотношения (2.43) равны между собой, следовательно, может быть введен
коэффициент пропорциональности t,
называемый параметром прямой:

– параметрические уравнения прямой. (2.45)

Можно записать
частный случай уравнений (2.45) для плоскости: . Они представляют собой параметрические уравнения
прямой линии на плоскости. Проводя аналогичные рассуждения, в качестве
направляющего вектора прямой на плоскости можно взять вектор , параллельный прямой (без учета направления), а точку
M₀(x₀;y₀) – в качестве произвольной точки
прямой. Заметим, что канонические уравнения (2.4) прямой на плоскости
представляют собой частный случай уравнений (2.44).

Чтобы задать прямую l в пространстве в общем виде
надо рассмотреть её как линию пересечения двух
плоскостей, которые обозначим через α
и β, и зададим уравнениями соответственно: . Это
означает, что прямая задается системой, состоящей из уравнений плоскостей α и β:

(2.46)

–
общее уравнение прямой в пространстве.
Здесь (в противном случае плоскости параллельны
или совпадают).

Поставим
задачу – привести общее уравнение (2.46) прямой к ее каноническим уравнениям (2.43). Решение
состоит из трех этапов.

1. Отыскание точки M₀(x₀;y₀;z₀), лежащей на данной прямой.

Координаты
точки M₀ должны удовлетворять системе (2.46), так как
точка принадлежит обеим плоскостям α и β.

Ранг
системы (2.46) равен 2, сама система является совместной неопределенной.
Объявим базисными переменными, например, x и y,
тогда z – свободная переменная. Придадим ей конкретное
значение z=z₀. Система примет вид: при условии, что главный определитель . Так как надо знать только одну точку прямой (одно решение системы (2.46)), то
достаточно найти одно ее частное решение.
Для простоты вычислений можно придать свободной переменной нулевое значение, то есть z₀=0. После этого определенную систему уравнений решают известными методами. Решение
системы x=x₀; y=y₀
в совокупности со значением свободной переменной представляет собой координаты
искомой точки M₀(x₀;y₀;z₀).

2. Рассмотрим нахождение направляющего вектора прямой. Так как перпендикулярен нормальным векторам и плоскостей α и β,
то его можно найти по теореме 2.5 как векторное произведение указанных
векторов:

. (2.47)

3. Найденную точку M₀ и вектор подставляем в
уравнение (2.43). Таким образом, задача о приведении общего уравнения прямой к
каноническому виду решена.

Пример 2.16.
Привести общее уравнение прямой в
пространстве к
каноническому виду.

Решение. Найдем точку M₀(x₀;y₀;z₀), принадлежащую данной прямой. Достаточно найти одно
частное решение заданной системы, например, при z₀=0. Решение будет представлять собой координаты точки M₀: