Отношением двух отрезков называется отношение их длин.
Рассмотрим два отрезка (AB) и (VN), где отрезок (AB) в (2) раза больше второго отрезка.
Отношение отрезков (AB) и (VN) равно (2 : 1):
Можно также сказать, что отношение отрезков (VN) и (AB) равно (1 : 2):
В этом примере отрезок (AR) равен трём единицам, а (VZ) равен двум единицам.
Отношение отрезков (AR) и (VZ) равно (3 : 2):
ARVZ=32
или
Если отношение отрезков (a) и (b) равно отношению отрезков (c) и (d), т. е.
ab=cd
,
то эти отрезки называются пропорциональными.
Сравниваем данные ранее отрезки, они не пропорциональны, т. к.
ABVN≠ARVZ
.
Рассмотрим данные рисунки:

Сравним отношения отрезков
ABVNиAHVT
.
ABVN=21иAHVT=4221=21
.
Значит,
ABVN=AHVT
— эти пары отрезков пропорциональны.
Чтобы записать отношение отрезков, необходимы два отрезка. Чтобы найти пропорциональные отрезки, необходимы две пары отрезков.
При сравнении двух значений какой-то величины часто
возникает вопрос:
во сколько раз одно значение больше другого? или
какую часть по отношению к другому оно составляет?
Например, во сколько раз заяц пробежит быстрее
некоторое расстояние, чем это же расстояние проползёт улитка? Или какую часть
всех деревьев леса составляют берёзы?
Вы знаете, что ответ в таких случаях дается в виде
частного двух чисел, которое называют отношением. Отношение показывает,
во сколько раз первое число больше второго, или какую часть первое число
составляет от второго.
Отношением отрезков и
называется
отношение их длин, т. е. (или
).
Отрезки и
пропорциональны
отрезкам и
,
если .
Например, отрезки AB
и
A1B1
равны соответственно 3 сантиметра и 5 сантиметров; а отрезки CD
и C1D1
– соответственно сантиметра
и 7,5 сантиметра.
;
.
Отрезки и
пропорциональны
отрезкам и
.
Следует отметить, что понятие пропорциональности
справедливо и для большего количества отрезков. Например, отрезки AB,
CD и EF
пропорциональны отрезкам A1B1;
C1D1
и E1F1,
если справедливо равенство: .
А теперь давайте посмотрим на рисунок.
Так, матрёшки имеют одинаковую форму, но разные
размеры. То же самое можем сказать про футбольный и теннисный мячи, про
одинаковые фотографии разных размеров.
В геометрии фигуры одинаковой формы называют
подобными. Любые два квадрата и любые два круга являются подобными.
А какие два треугольника называют подобными? Возьмём
два треугольника ABC
и A1B1C1,
у которых угол А равен углу A1,
угол B равен углу B1,
а угол C равен углу C1.
Тогда стороны AB
и A1B1,
BC и B1C1,
AC и A1C1
называются сходственными. И если эти сходственные стороны
пропорциональны ,
то треугольники ABC
и
A1B1C1
являются подобными. Подобие треугольников обозначается следующим образом
Сформулируем определение: подобными называются
треугольники, у которых углы соответственно равны, а сходственные стороны
пропорциональны.
Отношение сходственных сторон называют коэффициентом
подобия. Если стороны треугольника ABC
в два раза больше сторон треугольника A1B1C1,
то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.
Подобие треугольников можно установить, проверив
только некоторые из равенств:
,
т. е.
И позднее мы с вами познакомимся с тремя признаками
подобия треугольников.
Решим несколько задач.
Задача. Найдите
отношение отрезков и
,
если их длины соответственно равны см
и см.
Изменится ли это отношение, если длины отрезков выразить в миллиметрах?
Решение.
см
мм,
см
мм.
.
Ответ: ;
не
изменится.
Задача. Пропорциональны
ли отрезки и
,
соответственно равные см
и см,
отрезкам и
,
соответственно равным см
и см?
Решение.
;
;
.
Ответ: пропорциональны.
Задача. В подобных
треугольниках и
стороны
и
,
и
являются
сходственными. Найдите стороны треугольника ,
если см,
см,
см,
а отношение сторон .
Решение.
то есть
(см).
(см).
(см).
Ответ: см,
см,
см.
Итак, на уроке мы узнали, что отношением отрезков и
называется
отношение их длин, т. е. (или
);
что отрезки и
пропорциональны
отрезкам и
,
если .
Также мы выяснили, что подобными называются
треугольники, у которых углы соответственно равны, а сходственные стороны
пропорциональны.
|
Вспомним общие термины: Отрезок — часть прямой, которая ограничена 2 точками. Отношение — результат деления одной величины на другую. Соответственно, можно понять, что отношением двух отрезков называется результат деления одного отрезка на другой. Благодаря отношению отрезков, во сколько раз один отрезок больше/меньше другого. Здесь нужно оговориться, что эти отрезки должны иметь длины в одних и тех же единицах измерения, например, сантиметрах. В ином случае, отношение найти не получится и оно не будет иметь смысла. Нужно будет перевести длины в одинаковые единицы измерения. Пример Отрезок AB = 5 см. Отрезок CD = 20 мм. Переведём миллиметры в сантиметры: 20 мм = 2 см. Теперь можно найти отношение: AB/CD = 5/2 = 2,5. Значит, отрезок AB больше отрезка CD в 2,5 раз. автор вопроса выбрал этот ответ лучшим Galina7v7 7 лет назад Отношением двух отрезков в геометрии считается отношение их длин ,выраженных в той или иной метрической мере .То есть дан отрезок АВ = 5,7 см и отрезок ВС =10 см , то отношением отрезков АВ и ВС считается выражение : АВ : ВС = 5,7 см : 10 см = 0 ,57. В геометрии есть замечательная теорема Фалеса , позволяющая разделить любой отрезок в нужном отношении. Пусть дан отрезок АС .Требуется разделить его в отношении 2 : 3. Для решения откладываем отрезок АС.Из точки А проводим произвольно второй луч АД ,получили угол ДАС.На стороне угла ДА откладываем 5 = (2+3 ) равных отрезка,небольших ,но соразмерных с чертежом.АД1 = Д1Д2 = Д2Д3 =..Д4Д5.Точку Д5 соединяем с т.С.и проводим параллельные отрезки Д5С , Д4С4 ,…и так далее.Видим , что и исходный отрезок АС делится на 5 равных частей.Затем берем 2 части и остаётся 3 части , то есть отрезок разделили В ОТНОШЕНИИ 2: 3. Само слово отношение определяет, как соотнести два предложенных отрезка. если вы слышите найти отношение, значит обязательно надо разделить одну величину на другую. Проще и красивее делить меньшую на большую -тогда всегда получается правильная дробь. Отношением длин двух отрезком тогда будет дробь у которой в числителе окажется длина одного отрезка, а в знаменателе — второго. При этом возможны два варианта ответа, которые можно рассмотреть на примере. Общий случай — длины не делятся без остатка. Например даны отрезки длиной 5 и 7 сантиметров. Их отношением будет дробь 5/7. Второй случай, частный. Длины отрезков делятся друг на друга. Пример 3 и 6. Тогда их отношением будет дробь 3/6 или 1/2 — происходит сокращение. natasha lykova 8 лет назад Отношением двух отрезков называется отношение тех чисел, которые выражают длины этих отрезков при условии, что отрезки измерены единицами одного наименования. В арифметике отношением одного числа к другому называется частное от деления первого числа на второе, поэтому можно сказать, что отношением одного отрезка к другому является частное от деления длины первого отрезка на длину второго, если длины отрезков выражены в единицах одного наименования. Если даны два отрезка АВ = 6 см и СD = 4 см, то отношение отрезка АВ к отрезку СD равно АВ/СД=6/4=1,5. В этом случае делимое (АВ) называется предыдущим членом отношения, делитель (СD) — последующим членом отношения, а частное (1,5) — отношением. Знаете ответ? |
Отношением двух отрезков называется отношение их длин.
Рассмотрим два отрезка (AB) и (VN), где отрезок (AB) в (2) раза больше второго отрезка.
Отношение отрезков (AB) и (VN) равно (2 : 1):
Можно также сказать, что отношение отрезков (VN) и (AB) равно (1 : 2):
В этом примере отрезок (AR) равен трём единицам, а (VZ) равен двум единицам.
Отношение отрезков (AR) и (VZ) равно (3 : 2):
ARVZ=32
или
Если отношение отрезков (a) и (b) равно отношению отрезков (c) и (d), т. е.
ab=cd
,
то эти отрезки называются пропорциональными.
Сравниваем данные ранее отрезки, они не пропорциональны, т. к.
ABVN≠ARVZ
.
Рассмотрим данные рисунки:

Сравним отношения отрезков
ABVNиAHVT
.
ABVN=21иAHVT=4221=21
.
Значит,
ABVN=AHVT
— эти пары отрезков пропорциональны.
Чтобы записать отношение отрезков, необходимы два отрезка. Чтобы найти пропорциональные отрезки, необходимы две пары отрезков.
Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.
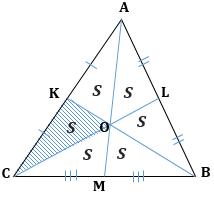
ОТНОШЕНИЯ ОТРЕЗКОВ:
1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.
2. Средняя линия треугольника равна половине основания: $MN = frac{1}{2}BC$
3. Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна ее половине $CM = frac{1}{2}AB$
4. Диагонали параллелограмма точкой пересечения делятся пополам.
|
Произвольный параллелограмм или ромб: АО = ОС, BO = OD |
Прямоугольник или квадрат: АО = ОС = BO = OD |
ОТНОШЕНИЯ ПЛОЩАДЕЙ:
1. Медиана разбивает треугольник на два равновеликих (по площади) треугольника: $S_{ACM} = S_{AMB} = S$
2. Треугольник делится тремя медианами на шесть равновеликих треугольников:
$S_{AKO} = S_{ALO} = S_{CKO} = S_{CMO} = S_{BMO} = S_{BLO} = S$
3. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна $frac{3}{4}S$
$S_{AKC(LMB)} = frac{3}{4}S_{ABC}$
ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:
|
Лемма 1 |
Площади подобных фигур относятся как квадрат коэффициента подобия. $S_{ABC} sim S_{EKF} \ displaystylefrac{S_{ABC}}{S_{EKF}} = (frac{AC}{EF})^2 = k^2$ |
|
Лемма 2 |
Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания. $displaystylefrac{S_{ABC}}{S_{ABE}} = frac{frac{1}{2}BH cdot AC}{frac{1}{2}BH cdot AE} = frac{AC}{AE} \ \ displaystylefrac{S_{EBC}}{S_{ABE}} = frac{frac{1}{2}BH cdot EC}{frac{1}{2}BH cdot AE} = frac{EC}{AE}$ |
|
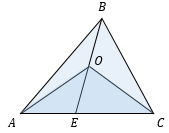
Лемма 3 |
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE. $displaystylefrac{S_{ABC}}{S_{AOC}} = frac{BE}{OE}$ |
|
Лемма 4 |
Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу. $displaystylefrac{S_{ABC}}{S_{EBF}} = frac{frac{1}{2}AB cdot BCcdotsinangle{B}}{frac{1}{2}EB cdot BFcdotsinangle{B}} = frac{ABcdot BC}{EBcdot BF}$ |
|
Продолжение леммы 4: |
Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В. $sinangle{FBE} = sin(180^{circ} — angle{ABC}) = sinangle{ABC} \ \ displaystylefrac{S_{ABC}}{S_{EBF}} = frac{frac{1}{2}AB cdot BCcdotsinangle{ABC}}{frac{1}{2}EB cdot BFcdotsinangle{FBE}} = frac{ABcdot BC}{EBcdot BF} $ |