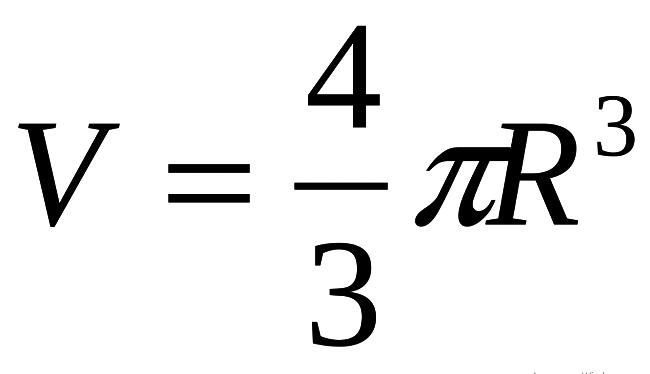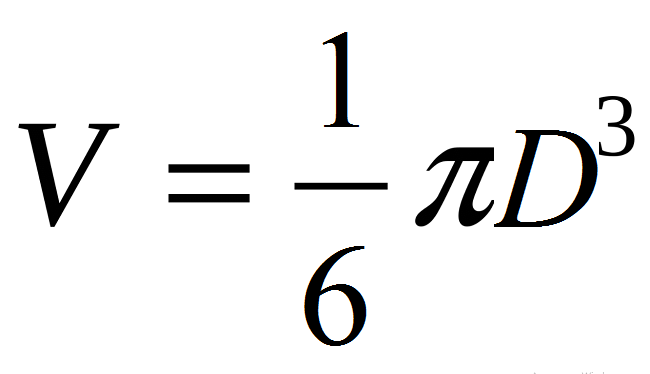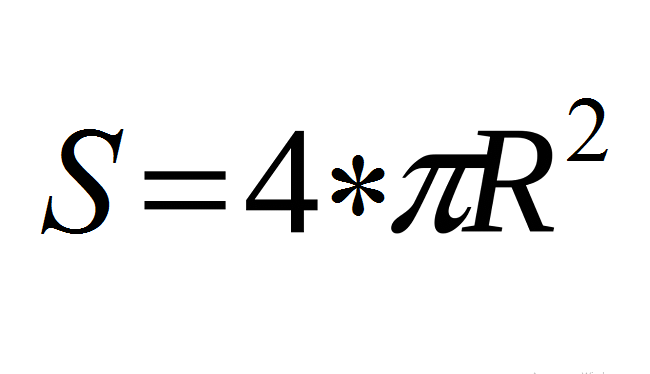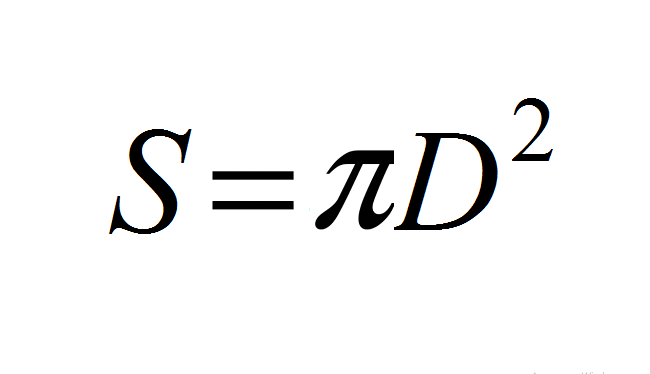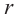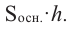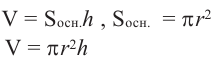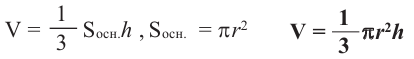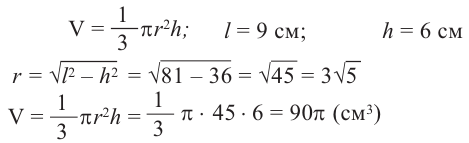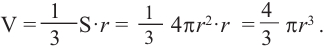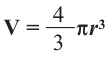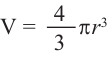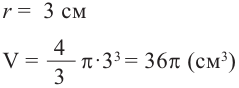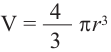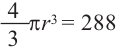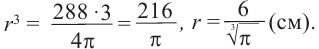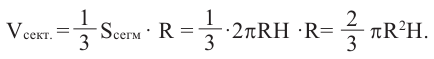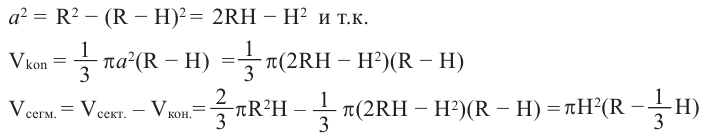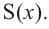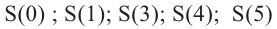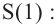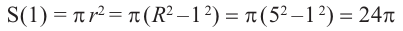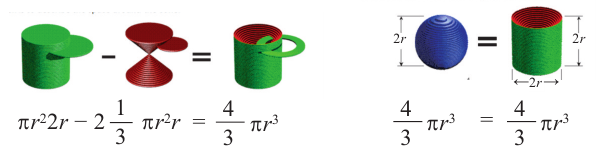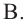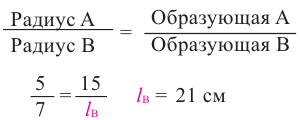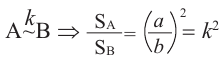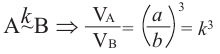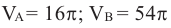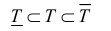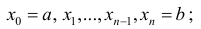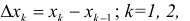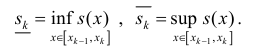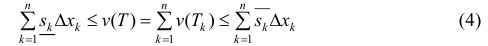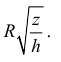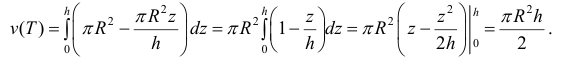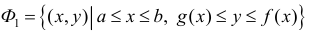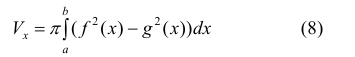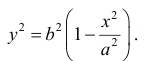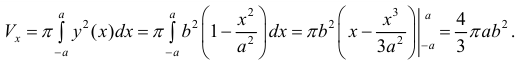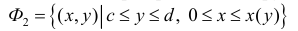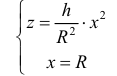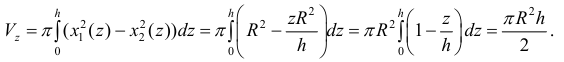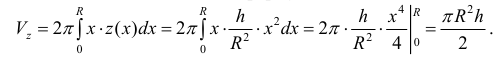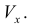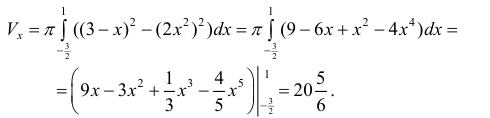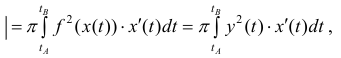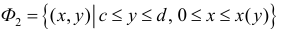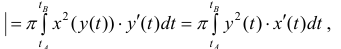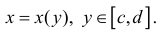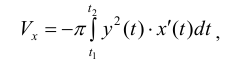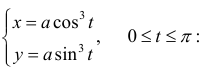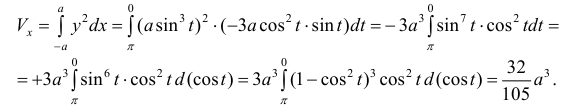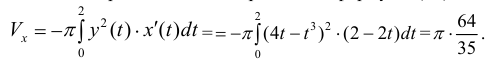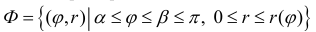Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Статья будет полезна школьникам и будущим абитуриентам, которые готовятся к сдаче ЕГЭ.
Содержание
- Формула объема шара через радиус: значение
- Формула объема шара через диаметр: значение
- Примеры вычисления объема шара, через радиус и диаметр шара: описание
- Формула полной поверхности шара, сферы через радиус: значение
- Формула полной поверхности шара, сферы через диаметр: значение
- Примеры вычисления площади поверхности, сферы шара, через радиус и диаметр шара: описание
- Как найти объем шара через площадь поверхности шара, сферы: пример решения задачи
- Видео: ЕГЭ математика. Объем и площадь поверхности тел вращения.
Формула объема шара через радиус: значение
Объем шара V вычисляется по формуле (см. ниже), где R — радиус шара, число «пи» — π — математическая константа, ≈ 3,14.
Данная формула является базовой!
Формула объема шара через диаметр: значение
- Воспользуйтесь базовой формулой: V=4/3*π*R³.
- Радиус R — это ½ диаметра D или R=D/2.
- Отсюда: V=4/3*π*R³ → V=(4π/3)*(D/2)³ → V=(4π/3)*(D³/8)→ V= πD³/6.
Или
Примеры вычисления объема шара, через радиус и диаметр шара: описание
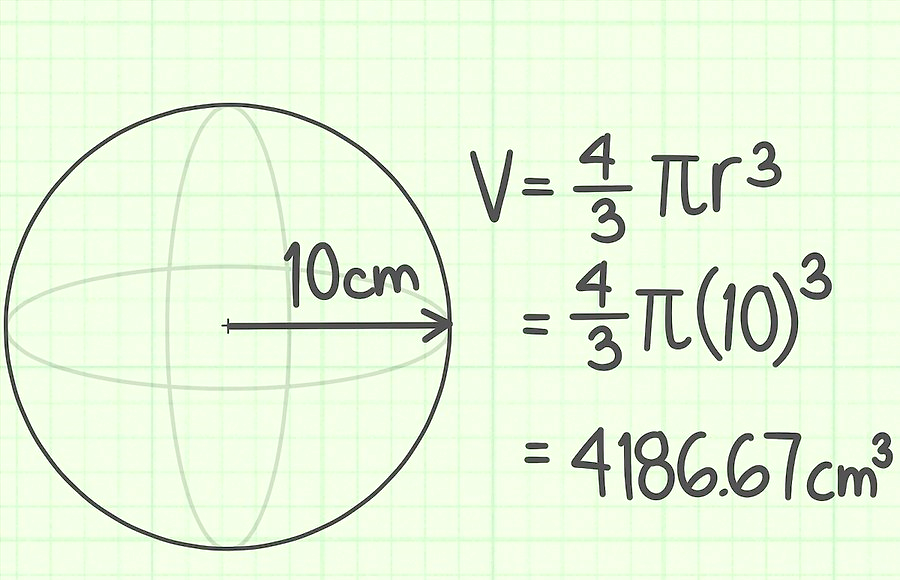
Задача 1.
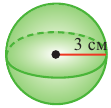
Радиус шара равен 10 см. Найди его объем.
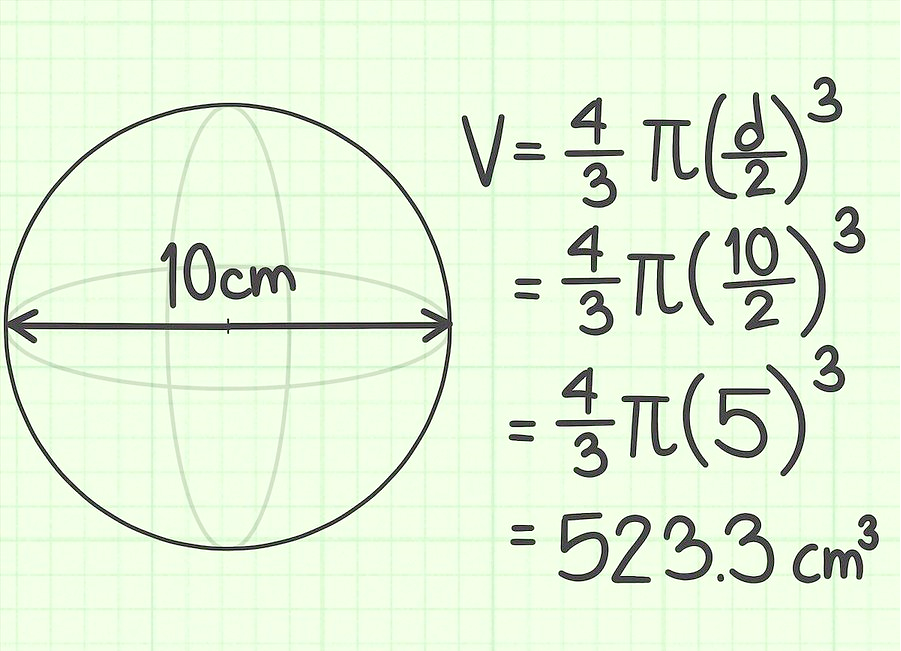
Задача 2.
Диаметр шара равен 10 см. Найди его объем.
Задача 3.
Соотношение диаметра Луны и диаметра Земли 1:4. Во сколько раз объем Земли больше объема Луны?
Решение:
Ответ: в 64 раза.
Важно: существует множество онлайн калькуляторов, позволяющих быстро найти заданную величину. Например, сервис Webmath.
Формула полной поверхности шара, сферы через радиус: значение
Площадь поверхности сферы/шара S вычисляется по формуле (см. ниже), где R — радиус шара, число «пи» — π — математическая константа, ≈ 3,14.
Данная формула является базовой!
Формула полной поверхности шара, сферы через диаметр: значение
- Воспользуйтесь базовой формулой: S = 4*π*R².
- Радиус R — это ½ диаметра D или R=D/2.
- Отсюда: S=4*π*R² → S=4*π*(D/2)² → S=(4π)*(D²/4)→ S = (4πD²)/4 → S = πD².
Или
Примеры вычисления площади поверхности, сферы шара, через радиус и диаметр шара: описание
Задача 4.
Задача 5.
Задача 6.
Как найти объем шара через площадь поверхности шара, сферы: пример решения задачи
Задача 7.
Задача 8.
Видео: ЕГЭ математика. Объем и площадь поверхности тел вращения.
From Wikipedia, the free encyclopedia
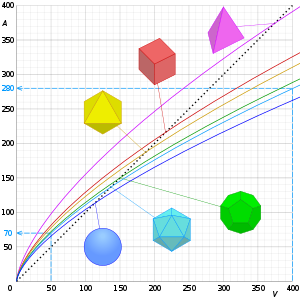
Graphs of surface area, A against volume, V of the Platonic solids and a sphere, showing that the surface area decreases for rounder shapes, and the surface-area-to-volume ratio decreases with increasing volume. Their intercepts with the dashed lines show that when the volume increases 8 (2³) times, the surface area increases 4 (2²) times.
The surface-area-to-volume ratio (surface-to-volume ratio, denoted as sa/vol, SA/V or SA:V, is the amount of surface area per unit volume of an object or collection of objects.
SA:V is an important concept in science and engineering. It is used to explain the relation between structure and function in processes occurring through the surface and the volume. Good examples for such processes are processes governed by the heat equation,[1] that is, diffusion and heat transfer by thermal conduction.[2] SA:V is used to explain the diffusion of small molecules, like oxygen and carbon dioxide between air, blood and cells,[3] water loss by animals,[4] bacterial morphogenesis,[5] organism’s thermoregulation,[6] design of artificial bone tissue,[7] artificial lungs [8] and many more biological and biotechnological structures. For more examples see Glazier.[9]
The relation between SA:V and diffusion or heat conduction rate is explained from flux and surface perspective, focusing on the surface of a body as the place where diffusion, or heat conduction, takes place, i.e., the larger the SA:V there is more surface area per unit volume through which material can diffuse, therefore, the diffusion or heat conduction, will be faster. Similar explanation appears in the literature: «Small size implies a large ratio of surface area to volume, thereby helping to maximize the uptake of nutrients across the plasma membrane»,[10] and elsewhere.[9][11][12]
For a given volume, the object with the smallest surface area (and therefore with the smallest SA:V) is a ball, a consequence of the isoperimetric inequality in 3 dimensions. By contrast, objects with acute-angled spikes will have very large surface area for a given volume.
SA:V for balls and n-balls[edit]
A ball is a three-dimensional object, being the solid version of a sphere. (In geometry, the term sphere properly refers only to the surface, so a sphere thus lacks volume in this context.) Balls exist in any dimension and are generically called n-balls, where n is the number of dimensions.
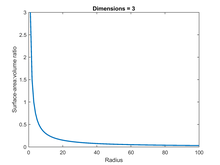
Plot of the surface-area:volume ratio (SA:V) for a 3-dimensional ball, showing the ratio decline inversely as the radius of the ball increases.
For an ordinary three-dimensional ball, the SA:V can be calculated using the standard equations for the surface and volume, which are, respectively, 

The same reasoning can be generalized to n-balls using the general equations for volume and surface area, which are:
volume = 

Plot of surface-area:volume ratio (SA:V) for n-balls as a function of the number of dimensions and of radius size. Note the linear scaling as a function of dimensionality and the inverse scaling as a function of radius.
So the ratio reduces to 
Dimension[edit]
The surface-area-to-volume ratio has physical dimension L−1 (inverse length) and is therefore expressed in units of inverse distance. As an example, a cube with sides of length 1 cm will have a surface area of 6 cm2 and a volume of 1 cm3. The surface to volume ratio for this cube is thus
.
For a given shape, SA:V is inversely proportional to size. A cube 2 cm on a side has a ratio of 3 cm−1, half that of a cube 1 cm on a side. Conversely, preserving SA:V as size increases requires changing to a less compact shape.
Physical chemistry[edit]
Materials with high surface area to volume ratio (e.g. very small diameter, very porous, or otherwise not compact) react at much faster rates than monolithic materials, because more surface is available to react. An example is grain dust: while grain is not typically flammable, grain dust is explosive. Finely ground salt dissolves much more quickly than coarse salt.
A high surface area to volume ratio provides a strong «driving force» to speed up thermodynamic processes that minimize free energy.
Biology[edit]
The ratio between the surface area and volume of cells and organisms has an enormous impact on their biology, including their physiology and behavior. For example, many aquatic microorganisms have increased surface area to increase their drag in the water. This reduces their rate of sink and allows them to remain near the surface with less energy expenditure.[citation needed]
An increased surface area to volume ratio also means increased exposure to the environment. The finely-branched appendages of filter feeders such as krill provide a large surface area to sift the water for food.[13]
Individual organs like the lung have numerous internal branchings that increase the surface area; in the case of the lung, the large surface supports gas exchange, bringing oxygen into the blood and releasing carbon dioxide from the blood.[14][15] Similarly, the small intestine has a finely wrinkled internal surface, allowing the body to absorb nutrients efficiently.[16]
Cells can achieve a high surface area to volume ratio with an elaborately convoluted surface, like the microvilli lining the small intestine.[17]
Increased surface area can also lead to biological problems. More contact with the environment through the surface of a cell or an organ (relative to its volume) increases loss of water and dissolved substances. High surface area to volume ratios also present problems of temperature control in unfavorable environments.[citation needed]
The surface to volume ratios of organisms of different sizes also leads to some biological rules such as Allen’s rule, Bergmann’s rule[18][19][20] and gigantothermy.[21]
Fire spread[edit]
In the context of wildfires, the ratio of the surface area of a solid fuel to its volume is an important measurement. Fire spread behavior is frequently correlated to the surface-area-to-volume ratio of the fuel (e.g. leaves and branches). The higher its value, the faster a particle responds to changes in environmental conditions, such as temperature or moisture. Higher values are also correlated to shorter fuel ignition times, and hence faster fire spread rates.
Planetary cooling[edit]
A body of icy or rocky material in outer space may, if it can build and retain sufficient heat, develop a differentiated interior and alter its surface through volcanic or tectonic activity. The length of time through which a planetary body can maintain surface-altering activity depends on how well it retains heat, and this is governed by its surface area-to-volume ratio. For Vesta (r=263 km), the ratio is so high that astronomers were surprised to find that it did differentiate and have brief volcanic activity. The moon, Mercury and Mars have radii in the low thousands of kilometers; all three retained heat well enough to be thoroughly differentiated although after a billion years or so they became too cool to show anything more than very localized and infrequent volcanic activity. As of April 2019, however, NASA has announced the detection of a «marsquake» measured on April 6, 2019, by NASA’s InSight lander.[22] Venus and Earth (r>6,000 km) have sufficiently low surface area-to-volume ratios (roughly half that of Mars and much lower than all other known rocky bodies) so that their heat loss is minimal.[23]
Mathematical examples[edit]
| Shape | Characteristic length 
|
Surface area | Volume | SA/V ratio | SA/V ratio for unit volume |
|
|---|---|---|---|---|---|---|
| Tetrahedron | 
|
edge | 
|

|

|
7.21 |
| Cube | 
|
edge | 
|

|

|
6 |
| Octahedron | 
|
edge | 
|

|

|
5.72 |
| Dodecahedron | 
|
edge | 
|

|

|
5.31 |
| Capsule | 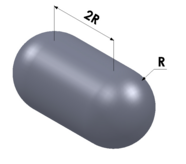
|
radius (R) | 
|

|

|
5.251 |
| Icosahedron | 
|
edge | 
|

|

|
5.148 |
| Sphere | 
|
radius | 
|

|

|
4.83598 |
| Side of cube |
Side2 | Area of a single face |
6 × side2 | Area of entire cube (6 faces) |
Side3 | Volume | Ratio of surface area to volume |
|---|---|---|---|---|---|---|---|
| 2 | 2×2 | 4 | 6×2×2 | 24 | 2×2×2 | 8 | 3:1 |
| 4 | 4×4 | 16 | 6×4×4 | 96 | 4×4×4 | 64 | 3:2 |
| 6 | 6×6 | 36 | 6×6×6 | 216 | 6×6×6 | 216 | 3:3 |
| 8 | 8×8 | 64 | 6×8×8 | 384 | 8×8×8 | 512 | 3:4 |
| 12 | 12×12 | 144 | 6×12×12 | 864 | 12×12×12 | 1,728 | 3:6 |
| 20 | 20×20 | 400 | 6×20×20 | 2,400 | 20×20×20 | 8,000 | 3:10 |
| 50 | 50×50 | 2,500 | 6×50×50 | 15,000 | 50×50×50 | 125,000 | 3:25 |
| 1,000 | 1,000×1,000 | 1,000,000 | 6×1,000×1,000 | 6,000,000 | 1,000×1,000×1,000 | 1,000,000,000 | 3:500 |
See also[edit]
- Compactness measure of a shape
- Dust explosion
- Square–cube law
- Specific surface area
References[edit]
- Schmidt-Nielsen, Knut (1984). Scaling: Why is Animal Size so Important?. New York, NY: Cambridge University Press. ISBN 978-0-521-26657-4. OCLC 10697247.
- Vogel, Steven (1988). Life’s Devices: The Physical World of Animals and Plants. Princeton, NJ: Princeton University Press. ISBN 978-0-691-08504-3. OCLC 18070616.
- Specific
- ^ Planinšič, Gorazd; Vollmer, Michael (February 20, 2008). «The surface-to-volume ratio in thermal physics: from cheese cube physics to animal metabolism». European Journal of Physics. 29 (2): 369–384. Bibcode:2008EJPh…29..369P. doi:10.1088/0143-0807/29/2/017. S2CID 55488270. Retrieved 9 July 2021.
- ^ Planinšič, Gorazd (2008). «The surface-to-volume ratio in thermal physics: from cheese cube physics to animal metabolism». European Journal of Physics European Physical Society, Find Out More. 29 (2): 369–384. Bibcode:2008EJPh…29..369P. doi:10.1088/0143-0807/29/2/017. S2CID 55488270.
- ^ Williams, Peter; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (2005). Gray’s Anatomy (39 ed.). Churchill Livingstone. pp. 1278–1282.
- ^ Jeremy M., Howard; Hannah-Beth, Griffis; Westendorf, Rachel; Williams, Jason B. (2019). «The influence of size and abiotic factors on cutaneous water loss». Advances in Physiology Education. 44 (3): 387–393. doi:10.1152/advan.00152.2019. PMID 32628526.
- ^ Harris, Leigh K.; Theriot, Julie A. (2018). «Surface Area to Volume Ratio: A Natural Variable for Bacterial Morphogenesis». Trends in Microbiology. 26 (10): 815–832. doi:10.1016/j.tim.2018.04.008. PMC 6150810. PMID 29843923.
- ^ Louw, Gideon N. (1993). Physiological Animal Ecology. Longman Pub Group.
- ^ Nguyen, Thanh Danh; Olufemi E., Kadri; Vassilios I., Sikavitsas; Voronov, Roman S. (2019). «Scaffolds with a High Surface Area-to-Volume Ratio and Cultured Under Fast Flow Perfusion Result in Optimal O2 Delivery to the Cells in Artificial Bone Tissues». Applied Sciences. 9 (11): 2381. doi:10.3390/app9112381.
- ^ J. K, Lee; H. H., Kung; L. F., Mockros (2008). «Microchannel Technologies for Artificial Lungs: (1) Theory». ASAIO Journal. 54 (4): 372–382. doi:10.1097/MAT.0b013e31817ed9e1. PMID 18645354. S2CID 19505655.
- ^ a b Glazier, Douglas S. (2010). «A unifying explanation for diverse metabolic scaling in animals and plants». Biological Reviews. 85 (1): 111–138. doi:10.1111/j.1469-185X.2009.00095.x. PMID 19895606. S2CID 28572410.
- ^ Alberts, Bruce (2002). «The Diversity of Genomes and the Tree of Life». Molecular Biology of the Cell, 4th edition. New York: Garland Science. ISBN 0-8153-3218-1. ISBN 0-8153-4072-9.
- ^ Adam, John (2020-01-01). «What’s Your Sphericity Index? Rationalizing Surface Area and Volume». Virginia Mathematics Teacher. 46 (2).
- ^ Okie, Jordan G. (March 2013). «General models for the spectra of surface area scaling strategies of cells and organisms: fractality, geometric dissimilitude, and internalization». The American Naturalist. 181 (3): 421–439. doi:10.1086/669150. ISSN 1537-5323. PMID 23448890. S2CID 23434720.
- ^ Kils, U.: Swimming and feeding of Antarctic Krill, Euphausia superba — some outstanding energetics and dynamics — some unique morphological details. In Berichte zur Polarforschung, Alfred Wegener Institute for Polar and Marine Research, Special Issue 4 (1983): «On the biology of Krill Euphausia superba«, Proceedings of the Seminar and Report of Krill Ecology Group, Editor S. B. Schnack, 130-155 and title page image.
- ^ Tortora, Gerard J.; Anagnostakos, Nicholas P. (1987). Principles of anatomy and physiology (Fifth ed.). New York: Harper & Row, Publishers. pp. 556–582. ISBN 978-0-06-350729-6.
- ^ Williams, Peter L; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (1989). Gray’s Anatomy (Thirty-seventh ed.). Edinburgh: Churchill Livingstone. pp. 1278–1282. ISBN 0443-041776.
- ^ Romer, Alfred Sherwood; Parsons, Thomas S. (1977). The Vertebrate Body. Philadelphia, PA: Holt-Saunders International. pp. 349–353. ISBN 978-0-03-910284-5.
- ^ Krause J. William (July 2005). Krause’s Essential Human Histology for Medical Students. Universal-Publishers. pp. 37–. ISBN 978-1-58112-468-2. Retrieved 25 November 2010.
- ^ Meiri, S.; Dayan, T. (2003-03-20). «On the validity of Bergmann’s rule». Journal of Biogeography. 30 (3): 331–351. doi:10.1046/j.1365-2699.2003.00837.x. S2CID 11954818.
- ^ Ashton, Kyle G.; Tracy, Mark C.; Queiroz, Alan de (October 2000). «Is Bergmann’s Rule Valid for Mammals?». The American Naturalist. 156 (4): 390–415. doi:10.1086/303400. JSTOR 10.1086/303400. PMID 29592141. S2CID 205983729.
- ^ Millien, Virginie; Lyons, S. Kathleen; Olson, Link; et al. (May 23, 2006). «Ecotypic variation in the context of global climate change: Revisiting the rules». Ecology Letters. 9 (7): 853–869. doi:10.1111/j.1461-0248.2006.00928.x. PMID 16796576.
- ^ Fitzpatrick, Katie (2005). «Gigantothermy». Davidson College. Archived from the original on 2012-06-30. Retrieved 2011-12-21.
- ^ «Marsquake! NASA’s InSight Lander Feels Its 1st Red Planet Tremor». Space.com. 23 April 2019.
- ^ «Archived copy» (PDF). Archived from the original (PDF) on 2018-06-13. Retrieved 2018-08-22.
{{cite web}}: CS1 maint: archived copy as title (link)
External links[edit]
- Sizes of Organisms: The Surface Area:Volume Ratio Archived 2017-08-14 at the Wayback Machine
- National Wildfire Coordinating Group: Surface Area to Volume Ratio
- Previous link not working, references are in this document, PDF
Further reading[edit]
- On Being the Right Size, J.B.S. Haldane Archived 2011-08-22 at the Wayback Machine
Получи верный ответ на вопрос 🏆 «Площадь поверхности первого шара относится к площади поверхности второго шара как 5:3. Найдите отношение объема первого шара к объему …» по предмету 📕 Математика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » Математика » Площадь поверхности первого шара относится к площади поверхности второго шара как 5:3. Найдите отношение объема первого шара к объему второго шара.
Содержание:
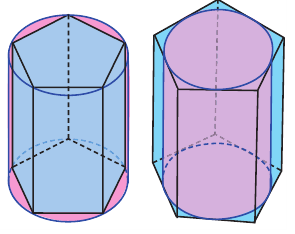
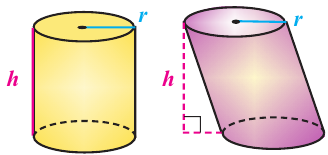
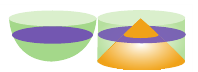
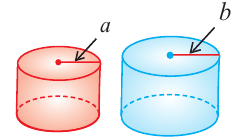
Говоря об объеме, имеют ввиду вместимость пространственной фигуры. Как вы думаете, емкость какого из цилиндров на рисунке больше?
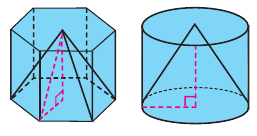
Призмой, вписанной (описанной) в цилиндр, называется призма, основания которой вписаны (описаны) в основания цилиндра.
Объем цилиндра
Пусть в цилиндр с радиусом
При бесконечном возрастании 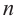
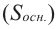
Объем цилиндра равен произведению площади основания на высоту.
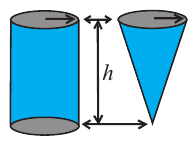
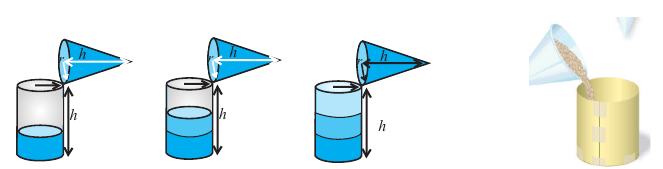
Практическая работа. Какая связь существует между объемами призмы и пирамиды, если они имеют одинаковые высоты и основания? Можно ли эту связь применить для объемов цилиндра и конуса?
Сделайте из картона модели сосудов в виде конуса и цилиндра, радиусы оснований и высоты которых одинаковы. Заполните цилиндрический сосуд при помощи сосуда в виде конуса (песком, рисом, и т. п.).
Сколько таких сосудов понадобится, чтобы заполнить цилиндрический сосуд? Верно ли утверждение, что цилиндрический сосуд можно заполнить тремя полными сосудами в виде конуса?
Обобщите соответствующую информацию о вычислении объема призмы, цилиндра, пирамиды и конуса, записав ответ в закрашенные ячейки.
Объем призмы и цилиндра:
Объем = площадь основания
Объем пирамиды и конуса:
Объем = 
основание и высоту.
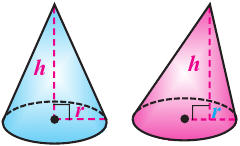
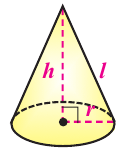
Объем конуса
Объем конуса равен произведению одной третьей площади основания на высоту.
Пример №1
Образующая конуса 9 см, высота 6 см. Найдите объем конуса.
Решение:
Объем шара и его частей
Практическая работа.
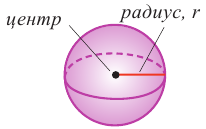
1. Возьмите мяч. Определите его диаметр.
2. Изобразите на бумаге развертку цилиндра, диаметр и высота которого равны диаметру шару.
3. Вырежьте и сверните полученную развертку в цилиндр без верхней крышки. Скрепите развертку при помощи клейкой ленты. Разделите высоту цилиндра на 3 равные части и сделайте соответствующие разметки.
4. Обверните мяч фольгой или плотным материалом и сделайте мешок сферической формы. Наполните его песком.
5. Пересыпьте песок в цилиндр. Какая часть цилиндра заполнится?
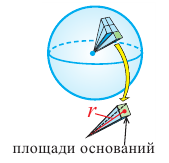
Если разделить поверхность шара сеткой из вертикальных и горизонтальных линий и маленький «прямоугольный» кусочек сферы соединить с центром шара, то можно представить, что шар состоит из множества «маленьких пирамид».
Объем шара можно выразить через сумму объемов «маленьких пирамид» 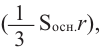
Сумма площадей оснований «маленьких пирамид» будет равна площади поверхности шара. Учитывая, что площадь поверхности шара равна 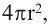
Объем шара:
Объем шара равен произведению 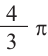
Пример №2
Найдите: а) объем шара радиуса 3 см
b) радиус шара объемом 288
Решение:
а)
b)
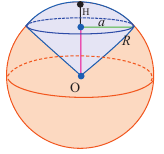
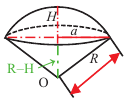
Сектор шара и сегмент шара
Шаровой сектор — это часть шара, ограниченная конической поверхностью с вершиной в центре шара. Шаровой сектор-объеденение конуса и шарового сегмента.
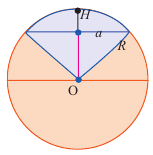
Так как шаровой сектор можно рассмотреть как предел суммы объемов маленьких пирамид, вершины которых находятся в центре шара, а основания касаются его поверхности, то
Здесь 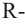
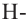
С другой стороны,
Проектная работа.
Отношение между объемами цилиндра, конуса и шара, которое получил Архимед.
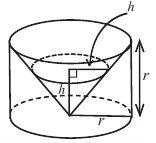
Архимед нашел формулу для нахождения объема шара, исследовав связь между объемом цилиндра, описанного вокруг шара радиуса и объемом конуса, вписанного в данный цилиндр. Попробуйте и вы выполнить это исследование.
Если 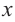
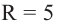
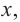
a) Вычислите следующие значения функции
Для примера найдено значение
b) Представьте свои суждения о значениях 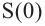
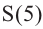
c) Запишите общую формулу для определения площади сечения, расположенного на расстоянии 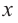
d) Свяжите формулу, полученную в пункте 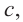
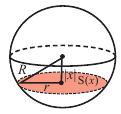
e) Чтобы понять умозаключения Архимеда, вернемся к начальному рисунку.
При «извлечении» конуса из цилиндра в поперечном сечении получаем кольца, параллельные основанию.
На одном и том же уровне поперечное сечение шара является кругом. Из подобия треугольников можно доказать, что площадь кольца каждого слоя равна 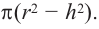
Объемы подобных фигур
Отношения соответствующих линейных размеров подобных пространствнных фигур должны быть равны.
По заданным соответствующим размерам подобных пространственных фигур можно найти неизвестные размеры.
Пример №3
Конусы 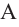
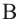
Решение: Запишем отношение линейных размеров: Радиус А Образующая А
Известно, что отношение площадей поверхностей двух подобных пространственных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия:
Объемы подобных пространственных фигур
Отношение объемов подобных пространственных фигур 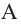
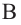
Пример №4
Отношение боковых поверхностей двух подобных цилиндров равно 4:9. Зная, что разность объемов равна 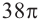
Решение: по условию 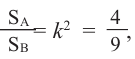
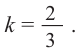
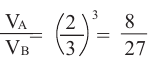
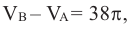
Объемы тел в высшей математике
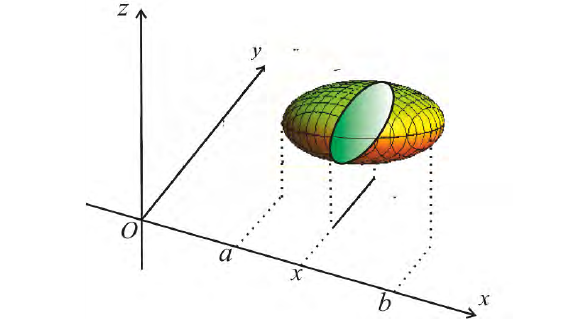
Под телом Т будем подразумевать ограниченное множество в пространстве.
Будем рассматривать тела, имеющие внутренние точки и границу, которая также принадлежит телу (замкнутые тела), причем такие, что любые две внутренние
точки можно соединить непрерывной линией, проходящей внутри тела.
Определение 1. Рассмотрим тело 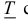
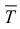
Пусть 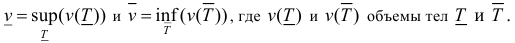
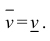
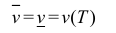
Замечание. Для кубируемости тела Т необходимо и достаточно, чтобы 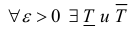
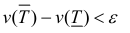
Пусть для кубируемого тела Т известны площади s=s(x) его сечения плоскостями перпендикулярными оси Ох, проходящими через точки (х, 0, 0),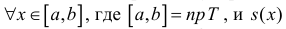
Разобьем отрезок [ a b ] на n частичных отрезков точками 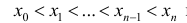
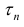
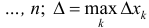
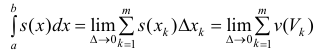
Где 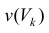
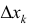
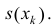
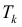
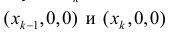
Так как Т – кубируемо, то 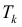
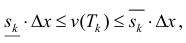
Тогда
∀n ∈ N, или
Где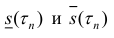
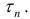
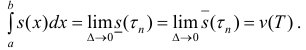
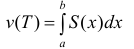
Замечание. Нужно заметить, что неравенство (4), которое использовалось для вывода формулы (6), выполняется, когда любые два рассматриваемые сечения
тела Т при проекции на плоскость yOz полностью содержатся одно в другом.
Однако формула (6) верна и в общем случае. Для этого достаточно потребовать,
чтобы тело Т было кубируемым и функция s (x) – непрерывной.
Пример №5
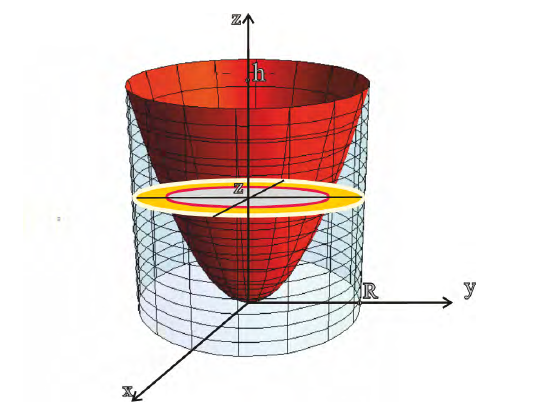
Найти объем тела ограниченного поверхностями 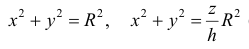
Решение.
Из системы уравнений 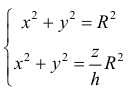
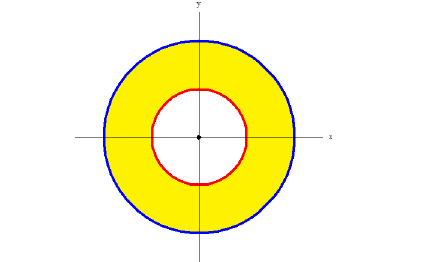
В сечении тела плоскостью проходящей через точку (0, 0, z) перпендикулярно оси Оz получается кольцо
Радиус внешней окружности равен R, радиус внутренней равен
Поэтому по формуле (6):
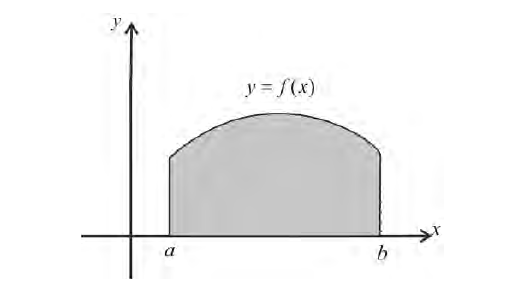
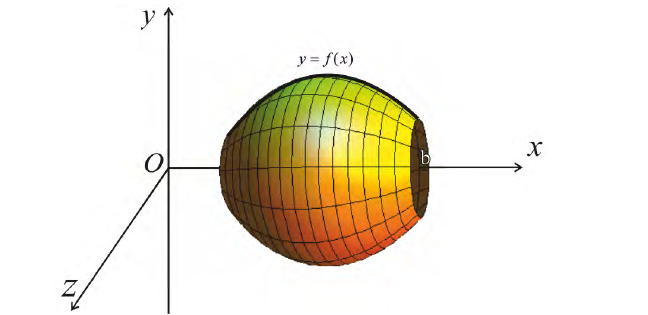
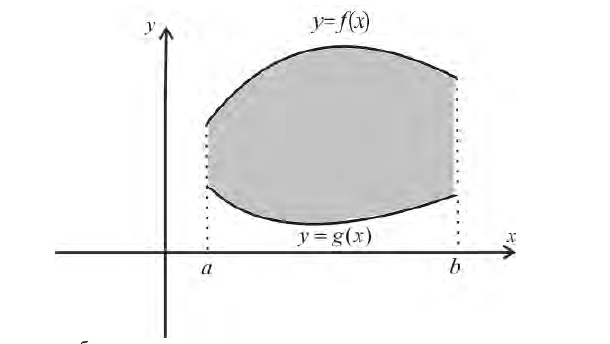
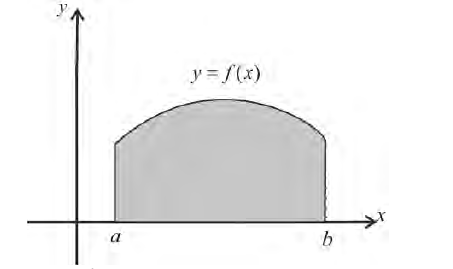
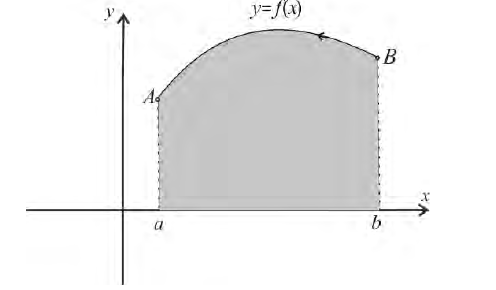
Формулу (6) удобно применять к телам вращения. Пусть y=f(x) – непрерывна на отрезке 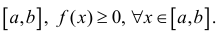
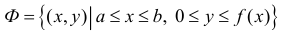
вокруг оси Ох. Получим тело:
Тогда сечением полученного тела плоскостью проходящей через точку (х,0,0) и перпендикулярной оси Ох будет круг радиуса 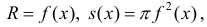
Где y=f(x).
Аналогично, если 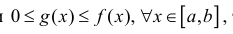
Получим тело, объем которого
Пример №6
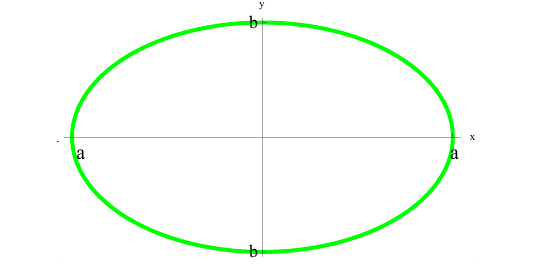
Рассмотрим фигуру Φ ограниченную эллипсом 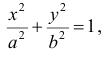
Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Φ .
Решение.
По формуле (7):
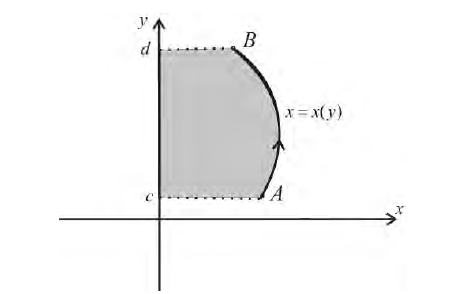
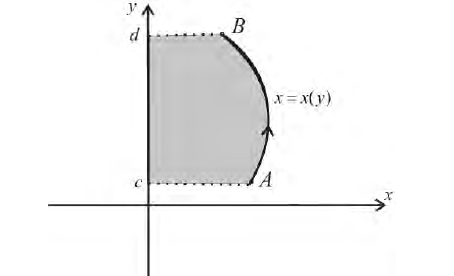
Пусть функция x=x(y) – непрерывна при 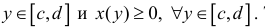
Получим тело, объем которого 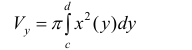
Если же вращать вокруг оси Оу трапецию 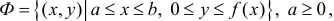
то 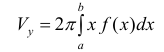
Пример №7
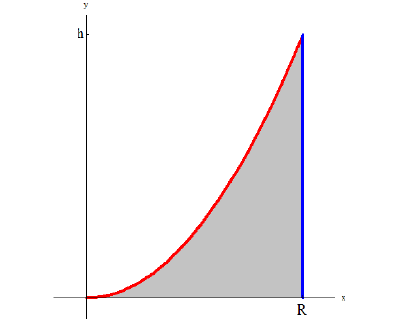
Рассмотрим тело Т из примера 1. Оно получается, если вращать вокруг оси Oz фигуру, ограниченную линиями:
Из первого уравнения найдем 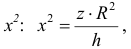
Пример №8
Объем 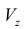
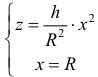
Пример №9
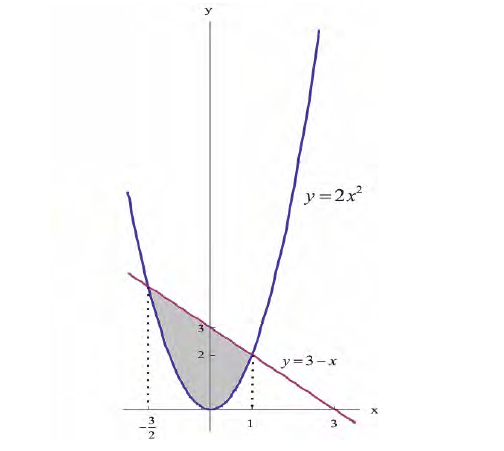
Фигура Ф ограничена линиями 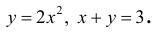
Решение.
Абсциссы точек пересечения: 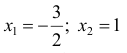
Замечание. Для непрерывной функции 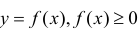
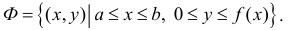
Пусть 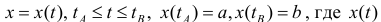
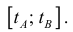
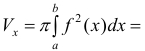
Где 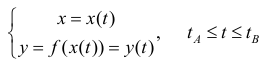
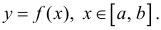
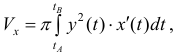
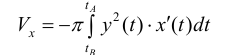
(кривая обходится так, чтобы область Ф оставалась слева).
Аналогично, для непрерывной функции 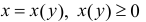
Пусть 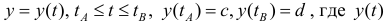
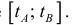
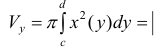
Где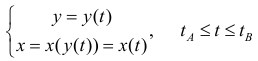
Таким образом 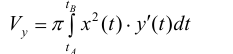
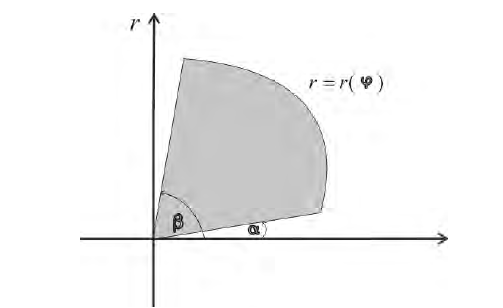
Рассмотрим область ,ограниченную простой замкнутой кривой
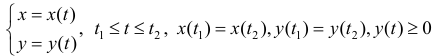

(кривая обходится так, чтобы область оставалась слева).
Аналогично ,для области ограниченной простой замкнутой кривой
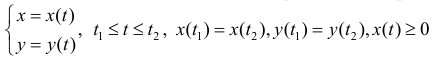
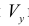
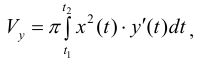
Пример №10
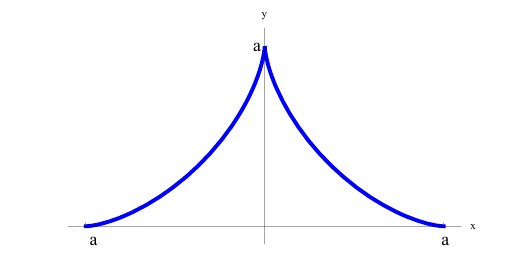
Дана астроида
Найдем 
Решение.
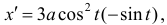
Пример №11
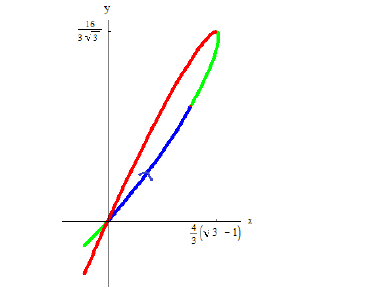
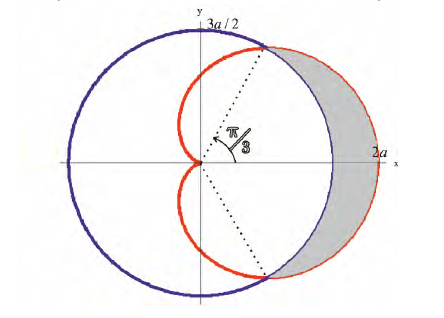
Петля кривой 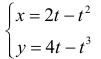

Решение.
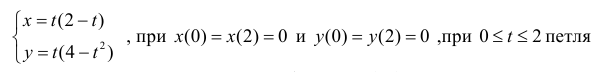
Пусть 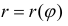
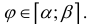
Тогда объем тела при вращении фигуры ϕ вокруг полярной оси равен
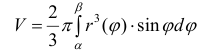
Пример №12
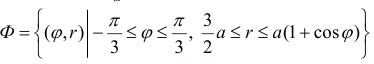
Найдем 
Решение.
По формуле (14):
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры — виды, изображения, свойства
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар