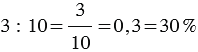|
Как найти отношение сторон прямоугольника?Помоги себе сам 4 года назад
Эта задачка для семиклассника. Но мы ведь с Вами учились дольше!
Задачу решить просто даже для семиклассника. Сначала нужно произвести анализ условия и определить алгоритм достижения цели. Нужно найти соотношение сторон. Но соотношение должно быть выражено в числовых величинах. Для этого нужно узнать размеры сторон АВ и ВС. Известно количество равных прямоугольников, из которых состоит прямоугольник ABCD. Известно, что в прямоугольнике противоположные стороны равны между собой. Еще у нас есть число 7, которое будет частью ответа. Думаю, что решение понятно. Успехов! Кстати, задача решается, как говорят, в уме, числового ответа не даю, потому что нужно понять и получить знания для решения подобных задач.
в избранное
ссылка
отблагодарить Вл50 Ответ выдали, но на чертеже нет обозначений сторон малых прямоугольников. Поэтому обойдемся без иксов и игреков. ВС = AD
Гэндальф 4 года назад Обозначим короткую сторону маленького прямоугольника «х», а длинную его сторону «у». Тогда АВ = х + у, ВС = 4х, а АД = 3у. Но так как ВС=АД, то 4х = 3у. Отсюда находим х = 3у/4. Подставим этот икс в полученное выше уравнение АВ = х + у, получим АВ = 3у/4 + у = 7у/4. Теперь находим соотношение искомое АВ/ВС. АВ = 7у/4, ВС = 3у. Поэтому соотношение будет АВ/ВС = 7у/4 / 3у. Делим одну дробь на другую, сокращаем игреки и получаем, что соотношение равно 7/12. комментировать
в избранное
ссылка
отблагодарить
Евгений трохов 4 года назад Рассмотрим стороны ВС и АД .Так вот,если принять длинную сторону маленького прямоугольника за 1, то другая меньшая сторона будет равна 3/4.Теперь найдём соотношение АВ/ВС=(1+3/4)/(4*(3/4)=7/12.Можно и по другому.У нас ВС=АД.Тогда АВ/ВС=АВ/АД=(1+(3/4))/3=7/12.Ответ-7/12 комментировать
в избранное
ссылка
отблагодарить
габбас 4 года назад Обозначим стороны маленького прямоугольника через х и у. Тогда АВ = х+у, ВС = 4*у. По рисунку видно, что 4*у = 3*х, то есть х = (4*у)/3. Получим АВ = (4*у)/3 +у = (7*у)/3. Значит искомое отношение АВ:ВС = (7*у)/3 : 4*у = 7/12. Ответ: 7:12.
в избранное
ссылка
отблагодарить Вл50 Нужно решить без X и Y.
SIlm В седьмом классе не знают решение задачи подстановкой неизвестного?
Видно, что соотношение стороне маленьких прямоугольников составляет 3/4, а тогда соотношение сторон большого прямоугольника составит (3+4)/(3+3+3+3), или 7/12 комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Rectangles have four sides, and generally the adjacent sides are not equal. Knowing the measurements of the two sides allows you to create a ratio of the rectangle. This tells you how much bigger one side is compared to the other side. This is used in basic geometry and helps students understand properties of a rectangle. If you know the ratio of a rectangle and know the measurement of one side, you can calculate the adjacent side.
-
Rectangles with the same length-to-width ratios are considered similar.
Measure your rectangle’s sides. For example, assume your rectangle has a side of 8 inches and another of 4 inches.
Set up a ratio where your large side is on top of the fraction and the smaller side is on the bottom of the fraction. In the example, 8 inches / 4 inches.
Divide the ratio, then set the bottom number to one. In the example, 8 divided by 4 equals 2. So your ratio is 2 to 1.
Tips
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
Кроме этого:
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
или
Из равенства (1) найдем d:
Пример 1. Стороны прямоугольника равны 
. Найти диагональ прямоугольника.
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:
Ответ: 
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
Подставляя (3) в (2), получим:
Пример 2. Стороны прямоугольника равны 
. Найти радиус окружности, описанной вокруг прямоугольника.
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:
Ответ: 
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:
Ответ: 
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
Из формулы (7) найдем ( small b ) и подставим в (6):
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул:
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
Действительно.
Тогда
Имеем ( small sqrt{D} <2d ,) ( small P > 2d .) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна 
, а периметр равен 
. Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):
Подставляя значения и 
в первую формулу (12), получим:
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и 
в формулу, получим:
Ответ: 
, 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Прямоугольники имеют четыре стороны, и, как правило, смежные стороны не равны. Знание измерений двух сторон позволяет создать соотношение прямоугольника. Это говорит вам, насколько больше одна сторона по сравнению с другой стороной. Это используется в базовой геометрии и помогает студентам понять свойства прямоугольника. Если вы знаете соотношение прямоугольников и знаете размеры одной стороны, вы можете рассчитать соседнюю сторону.
-
Прямоугольники с одинаковым отношением длины к ширине считаются одинаковыми.
Измерьте стороны вашего прямоугольника. Например, предположим, что у вашего прямоугольника есть сторона 8 дюймов, а другая — 4 дюйма.
Установите соотношение, где ваша большая сторона находится сверху фракции, а меньшая — снизу фракции. В примере 8 дюймов / 4 дюйма.
Разделите соотношение, затем установите нижнее число на единицу. В этом примере 8, деленное на 4, равно 2. Таким образом, ваше соотношение составляет 2 к 1.
подсказки
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 
и 
— члены отношения; число — предыдущий член отношения; — последующий член отношения.
Например:
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
— отношение числа 
к числу 
;
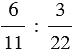
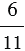
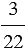
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .
Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и 
.
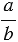
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
.
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
.
Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.
На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Например:
Пусть на карте задан масштаб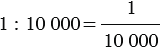 
, то есть карта сделана в масштабе одна десятитысячная.
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 
длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:
5 : = 1 : 10 000;
Решаем данное уравнение:
= 5
10 000;
= 50 000;
50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:
: 9,5 = 1 : 10 000;
Решаем данное уравнение:
= 9,5 : 10 000;
= 0,00095;
0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 646,
Мерзляк, Полонский, Якир, Учебник
Номер 650,
Мерзляк, Полонский, Якир, Учебник
Номер 685,
Мерзляк, Полонский, Якир, Учебник
Номер 741,
Мерзляк, Полонский, Якир, Учебник
Номер 1167,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 773,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 845,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 863,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1313,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 146,
Мерзляк, Полонский, Якир, Учебник
Номер 149,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 405,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 426,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 303,
Мерзляк, Полонский, Якир, Учебник