Как найти отклонение частицы

В предыдущем ответе не учёл то обстоятельство, что угол между вектором скорости частицы и вектором магнитной индукции всё время меняется при отклонении частицы, поэтому нельзя пренебрегать синусом угла между ними..

Итак, разложим вектор скорости частицы на две координатные оси: одна вдоль вектора магнитной индукции (У), другая (х) — вдоль вдоль начальной траектории частицы, эти координатные оси взаимно перпендикулярны..

Скорость вдоль х неизменна и её можно найти из энергетического соотношения:

mv^2/2=qU

Откуда v(х)=sqrt(2qU/m)

Путь, пройденный вдоль оси у равен: L=v(x)t

Или t=L/v(x)

Скорость вдоль у перед влётом в магнитное поле равна нулю и определяется всецело силой Лоренца:

F=qvB sin(alpha)

Путь, пройденный вдоль оси у равен:

S=(F/m)(t^2)=(qvB/m) sin(alpha)(t^2)=(qvB/m) sin(alpha)(mL)/(2qU/m)

Таким образом получается поперечное смещение:

S=sqrt(q/(2mU))B(L)^2 sin (alpha)

Отношение поперечного смещения к продольному есть тангенс искомого угла:

tg(alpha)=S/L=sqrt(q/(2mU))B L sin (alpha)

Далее учитываем, что tg(a)=sin(a)/cos(a)

cos(alpha)= 1/(sqrt(q/(2mU))B L)

или окончательно:

alpha= arccos(1/(sqrt(q/(2mU))B L))

подставляем значения

m=1,67×10^(-27)кг

q=1,6×10^(-19)Кл

B=50×10^(-3)Тл

U=1200В

L=0,1м

Это продолжение разговора о неравенствах Белла. Начало здесь: Введение

Часть 1. Что такое спин?

Физические эксперименты всегда подразумевают измерение каких-либо величин. В экспериментах по схеме Белла мы «будем измерять» спин элементарных частиц, поэтому нам следует разобраться, что же это за штука такая.

В классической механике есть такая величина: момент импульса. Так же, как и просто импульс, момент импульса характеризует количество движения. Разница вот в чём: импульс характеризует поступательное движение тела в определённой системе отсчёта, а момент импульса — вращательное движение тела вокруг определённой оси вращения.

Вы знаете, конечно, что импульс определяется как произведение массы тела на его линейную скорость. А момент импульса определяется как произведение момента инерции тела на его угловую скорость, ту, которая измеряется в оборотах в секунду. Что такое момент инерции — я тут объяснять не буду, для нашей задачи это несущественно. Зато очень существенно вот что: момент импульса является величиной векторной, то есть, характеризуется не только абсолютным значением, но и направлением, которое всегда совпадает с направлением оси вращения. Тут вы можете спросить: но ведь у оси вращения два направления. Например, куда направлен вектор момента импульса вращающейся юлы-волчка, вверх или вниз? Отвечу: принято определять направление вектора момента импульса по «правилу буравчика». При вращении тела этот вектор направлен туда, куда вкручивался бы штопор, вращай мы его также. Так что, если юла раскручена по часовой стрелке, то считается, что вектор момента импульса направлен вниз. А если против часовой — тогда вверх.

Момент импульса, как и импульс, подчиняется закону сохранения. То есть, если вращающееся тело не взаимодействует ни с какими другими телами, его момент импульса остаётся неизменным, что бы там не происходило внутри самого тела. Даже если тело самопроизвольно развалится на несколько частей, то суммарный момент импульса всех осколков будет равен моменту импульса развалившегося тела. Причём, момент импульса не меняется не только по абсолютной величине, но и по направлению. Это можно наблюдать на примере той же юлы: пока она достаточно быстро крутится, её ось вращения направления не меняет. Повторяю: если тело ни с чем не взаимодействует, то его момент импульса сохраняется. Но если на тело воздействовать извне, то его момент импульса изменить можно, как по абсолютной величине (мы можем притормозить или раскрутить юлу), так и по направлению (если толкнуть вращающуюся юлу, её ось начнёт раскачиваться).

Спин элементарной частицы – это её момент импульса. Можно считать, что частица – это шарик, который вращается вокруг собственной оси, как, например, наша планета. Такое представление, вообще-то, довольно примитивно, но для нашей задачи сгодится. Надо только понимать, что спин, в отличие от классического момента импульса – величина квантовая, и поэтому обладает некоторыми специфическими особенностями, которые мы ниже рассмотрим.
Момент импульса тела может быть любым как по направлению, так и по абсолютной величине. Спин частицы по абсолютной величине изменяться не может: для каждого конкретного типа частиц значение спина — это «константа», так же как электрический заряд, например. С этим значением спина частица рождается, с ним же и умирает. А вот «направление» спина частицы изменить можно, например, подействовав на частицу магнитным полем. Стало быть, «измерять» мы будем именно направление спина.

Ну что же, перейдём к «практической» части. Нет, это ещё не «белловские» эксперименты, пока мы просто «поставим» несколько простых опытов, чтобы лучше понять свойства спина и поупражняться с его измерением.
Для измерения спина частиц используют устройство, которое называется «прибор Штерна-Герлаха», по фамилиям его изобретателей. Дальше мы будем называть это устройство сокращено: «ПШГ». Кратко рассмотрим принцип действия прибора.

Элементарная частица имеет электрический заряд и вращается, а значит, она представляет собой маленький магнит. Другими словами, если у частицы есть спин, значит, у неё есть и магнитные свойства, или, говоря более научно – магнитный момент (на всякий случай отмечу, что магнитным моментом обладают и частицы с нулевым зарядом, например, нейтроны, но механизм этого явления мы тут рассматривать не будем). Вот этот-то магнитный момент вращающейся частицы и использует ПШГ. Устройство ПШГ, а также прочее оборудование, необходимое для опытов, показаны на рисунке 1.1.

Собственно, сам ПШГ состоит из двух магнитов. Верхний и нижний магниты имеют различную форму, благодаря чему магнитное поле в промежутке между ними неравномерно. Также на рисунке изображены источник частиц, (надо же их откуда-то брать?) и экран, который регистрирует точку попадания частицы. Например, в качестве экрана может использоваться фотопластинка: попавшая в неё частица «засвечивает» точку попадания.

Для наших дальнейших опытов решающее значение будет иметь ориентация самого прибора, а также спинов частиц в
пространстве. Поэтому на рисунке показана система координат XYZ. Ориентацию ПШГ мы будем показывать толстой серой стрелкой. В данном случае прибор ориентирован вдоль положительного направления оси Z. Направление векторов спинов (для компактности будем говорить просто «направление спинов») частиц будем показывать тонкой черной стрелкой. На рисунке спин «красной» частицы направлен вверх, в направлении +Z, а спин «синей» частицы направлен вниз, в направлении –Z .

Итак, источник выпускает частицу в направлении оси X. Затем частица попадает в ПШГ и проходит через зазор между магнитами. Если частица не обладает спином, то магнитное поле на неё никак не влияет, она движется по прямой и попадает в центр экрана – его мы приняли за начало координат. Траектория такой частицы показана на рисунке зелёной линией. На самом деле мы тут будем «работать» только с частицами, обладающими ненулевым спином, так что зелёную траекторию я нарисовал чисто для того, чтобы обозначить центр экрана.

Если спин направлен вверх, то неравномерное магнитное поле в зазоре отклоняет частицу вверх (красная траектория). Если спин направлен вниз, то частица отклоняется вниз (синяя траектория). Таким образом, наблюдая на экране точку попадания частицы, мы определяем, как был направлен её спин – вверх или вниз.

Мы рассмотрели случаи, когда спин частицы направлен вдоль оси Z. То есть, направление спина совпадает с ориентацией прибора или строго противоположно ей. Но ведь спин частицы может быть ориентирован в пространстве как угодно. Возникает вопрос: а что же будет с частицей, если её спин и ориентация ПШГ не совпадают? Тут классическая физика и квантовая механика дают разные ответы.

Если рассматривать ситуацию чисто «классически», и представлять себе частицу как вращающийся заряженный шарик, то ответ будет такой: отклонение частицы пропорционально проекции её спина на направление ориентации прибора (в нашем случае это то же самое, что ось Z). То есть, максимальное отклонение точки попадания от центра экрана будет у тех частиц, у которых спин направлен параллельно оси Z (Рисунок 1.2-a, точка «Zmax»). Разумеется, если спин параллелен оси Z, но направлен в противоположную сторону, то частица попадёт в точку «–Zmax».

Если спин частицы направлен под углом к оси Z, частица должна попасть в точку где-то между -Zmax и Zmax (Рисунок 1.2-b). Если же спин частицы ориентирован перпендикулярно оси Z, например, вдоль оси Y? то частица вообще не должна отклоняться от центра (Рисунок 1.2-c).

Ось X на рисунке 1.2 и на следующих не показана, чтобы не загромождать. Можете считать, что она направлена от нас прямо вглубь рисунка. Места попадания частиц в регистрирующий экран показаны красной звёздочкой. Направление спина показано так, как мы условились раньше: тонкой чёрной стрелкой.

Квантовая механика предсказывает совершенно другой результат: все частицы будут отклоняться на максимально возможное расстояние и попадать только в одну из двух точек, причём, линия, походящая через эти две точки и центр экрана, будет параллельна ориентации прибора. В нашем случае, когда ПШГ ориентирован параллельно оси Z, это будут точки либо «Zmax», либо «–Zmax». В этом, собственно, и заключается «квантовость». Если в «классике» мы можем намерять любое отклонение, а значит и направление момента импульса, то в квантовой механике направление спина «квантуется»: есть только два возможных результата измерения.

Тут, чтобы вас не запутать на будущее, я должен оговорить вот что: на самом деле два результата измерения мы получим только на частицах с так называемым «полуцелым» спином. К таким частицам относятся, в частности, электроны, протоны, нейтроны и некоторые другие. Для прочих частиц возможны три результата, четыре, пять и так далее, но в любом случае число возможных результатов будет конечным. Чтобы не делать в дальнейшем таких оговорок, давайте определимся: мы будем в наших экспериментах работать только с протонами.

Итак, классическая физика и квантовая механика предсказывают разные результаты опытов с протонами. Ну что же, вооружившись банальностью «опыт – критерий истины» приступим к экспериментальной проверке.

Установка для опыта у нас уже есть, она показана на рисунке 1.1. Только там у нас был «источник частиц», теперь это будет источник конкретно протонов.

Предполагаем, что источник выпускает протоны со случайно ориентированным спином. Значит, если права классическая физика, то протоны должны попадать в экран со случайным отклонением по оси Z в диапазоне от «–Zmax» до «Zmax». Тогда, если мы выпустим достаточно много протонов, то картинка на экране должна будет выглядеть так, как показано на рисунке 1.3-a. То есть, будет сплошная полоса попаданий.

Ну а если права квантовая механика, то после серии «выстрелов» на экране будет картинка как на рисунке 1.3-b: только два варианта попаданий. Причём, попадания распределятся примерно пополам: половина вверх, половина вниз.

В реальности такой эксперимент даёт картинку в полном соответствии с предсказаниями квантовой механики, как на рисунке 1.3-b. Это один из тех экспериментов, о которых я говорил во введении: с точки зрения классической физики его результаты объяснить не удаётся, а квантовая механика объясняет их «на раз».

Сторонники классического подхода тут могут «уцепиться за соломинку»: мол, мы предположили, что спин протонов, испускаемых источником, ориентирован случайно, а вдруг это не так? Возможно, источник выпускает протоны, ориентированные только вертикально, вдоль оси Z. В таком случае «классический» расчёт даст такую же картину распределения попаданий, как и квантовый (рисунок 1.3-b).

Хорошо, мы это можем легко проверить. Повернём ПШГ на некоторый угол вокруг оси X и проделаем опять длинную серию «выстрелов». Если версия «классиков» верна, то мы увидим на экране картинку типа 1.4-a. Ну а если всё же правда на «квантовой» стороне, то картинка будет как 1.4-b.

Я пока не буду объяснять, почему классический (a) и квантовый (b) расчёты дадут при такой ориентации прибора именно эти картины распределения попаданий. Если вам непонятно, то предлагаю тут притормозить и разобраться самостоятельно. Вся необходимая для этого информация изложена выше и даже выделена жирным курсивом. Также вам помогут, надеюсь, дополнительные построения, нарисованные пунктирными линиями.

Разобрались? Отлично, тогда едем дальше. Проделав эксперимент с «повёрнутым» ПШГ (на рисунке 1.4 он повёрнут вокруг оси X на 60 градусов вправо), убеждаемся, что результаты опыта совпадают с квантовыми предсказаниями: половина (приблизительно) протонов попадает в точку A1, половина – в точку A2. Для верности можем провести эксперименты с разными углами поворота ПШГ и убедиться: результат всегда таков, как предсказывает квантовая механика. Заодно мы убедимся в том, что наше предположение о случайной ориентации спинов на входе прибора было правильным.

Итак, констатируем важный вывод, на который мы будем ссылаться в дальнейших рассуждениях:

Утверждение 1.1.

Для порядка отмечу, что в нашем случае измерительным прибором является устройство, включающее ПШГ и
регистрирующий экран. Однако, утверждение 1.1. верно и для любого другого устройства, измеряющего направление спина. Но мы будем и дальше пользоваться прибором Штерна-Герлаха. Только вот, в свете утверждения 1.1., регистрирующий экран нам больше не нужен. Поскольку из ПШГ все протоны выходят только по одной из двух возможных траекторий, мы можем вместо экрана поставить на каждой траектории детектор протонов. Теперь схема эксперимента, показанного на рисунке 1.1, будет выглядеть так, как на рисунке 1.5-a.

Детекторы обозначены как D+ (плюс – детектор) и D- (минус – детектор). В плюс – детектор будут попадать все протоны, направление спина которых совпадает с ориентацией прибора. В минус – детектор попадут все протоны с противоположной прибору ориентацией.

Разумеется, если мы теперь захотим покрутить ПШГ вокруг «линии выстрела», показанной на рисунке зелёным пунктиром, то мы должны будем соответствующим образом переместить и детекторы, иначе все «выстрелы» уйдут в «молоко». Чтобы не мучится с определением нового положения детекторов, мы можем просто объединить ПШГ и детекторы в единую конструкцию и вращать её всю целиком так, как нам требуется. Дальше при описании опытов я буду эту измерительную конструкцию изображать так, как показано на рисунке 1.5-b.

Пожалуй, на сегодня достаточно информации. Если что-то в рассказе непонятно, велкам, задавайте вопросы.

Продолжение тут.

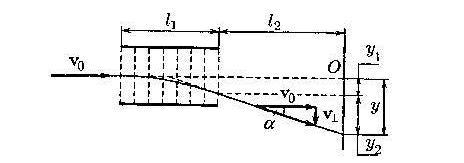
Отклонение движущихся заряженных частиц электрическим и магнитным полями

1).
Рассмотрим
узкий пучок одинаковых заряженных
частиц, попадающий в отсутствии полей
на перпендикулярный ему экран в точке
О. Определим смещение следа пучка,
вызываемое перпендикулярным пучку
электрическим полем, действующим на
пути длиной l₁
при расстоянии от границы области, в
которой имеется поле, до экрана l₂
.

Пусть первоначальная
скорость частиц равна
.
Войдя в область поля каждая частица
будет двигаться с постоянным по модулю
и направлению ускорением

.

Движение под
действием поля продолжается в течение
времени
.
За это время частицы сместятся на
расстояние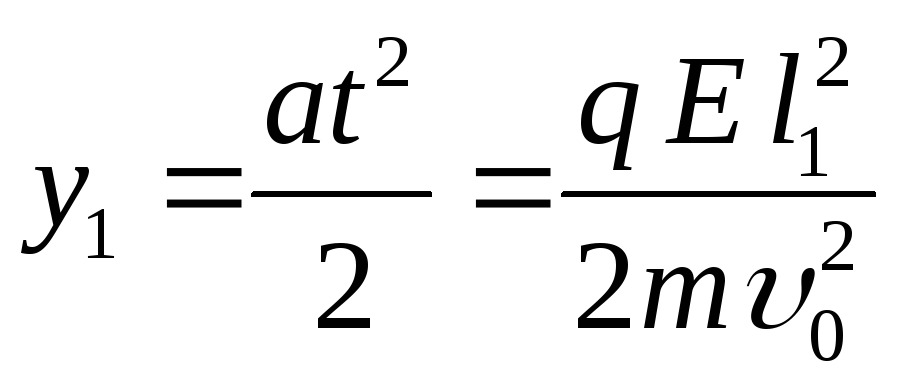и приобретут, перпендикулярную ксоставляющую скорости.

В дальнейшем
частицы летят прямолинейно в направлении,
которое образует с вектором
угол, определяемый соотношением .

Смещение
.

Общее смещение
пучка
или.

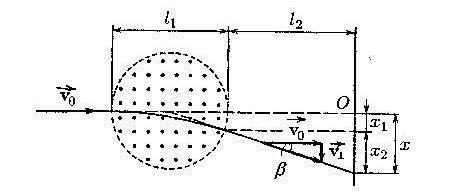
2).
Рассмотрим
узкий пучок одинаковых заряженных
частиц, имеющих скорость
,
проходящих на путиl₁
участок
с однородным магнитным полем, вектор
индукции которого перпендикулярен
скорости частиц. Определим смещение х
пучка на экране, отстоящем на расстоянии
l₂
от границы участка с магнитным полем
.

Под действием
поля каждая частица получит постоянное
по модулю ускорение

.

Ограничиваясь
случаем, когда отклонение пучка полем
невелико, можно считать, что ускорение

почти постоянно по направлению и.
Тогда для расчёта смещения можно
воспользоваться формулой, полученной
для предыдущего случая, заменив в ней
ускорениезначением:

.

Угол, на который
отклонится пучок магнитным полем
определяют соотношением

.

Получаем окончательно

.

Ускорители заряженных частиц

Для лабораторных
исследований в области ядерной физики,
а также для промышленных установок и
электроракетных двигателей нашли
применения направленные пучки заряженных
частиц (электронов, протонов, ионов
разных элементов), обладающих кинетической
энергией от нескольких сотен эВ до
десятков ГэВ.

По форме траектории
ускоряемых частиц все ускорители можно
разделить на две основные группы:
линейные ускорители и циклические
ускорители. В первых траектории частиц
близки к прямым линиям, во вторых – к
окружностям или раскручивающимся
спиралям.

Энергия частиц
увеличивается при их движении в
электрическом
поле ускорителя.

В
электростатическом линейном ускорителе
заряженная частица проходит через
ускоряющее электрическое поле однократно.
Если
заряд частицы, аипотенциалы поля в начальной и конечной
точках траектории в поле, то энергия,
приобретаемая частицей в ускорителе,
равна.
Здесь можно получить энергии не
превышающие 15 МэВ.

Значительно
большие энергии (до 22 ГэВ) можно сообщать
заряженным частицам в линейных
резонансных ускорителях,
в которых переменное электрическое
поле сверхвысокой частоты изменяется
синхронно с движением ускоряемых частиц.

Циклотрон
состоит из двух металлических дуантов

М и
N,
представляющих собой две половины
невысокой тонкостенной цилиндрической
коробки разделённые узкой щелью.

Дуанты заключены в плоскую замкнутую
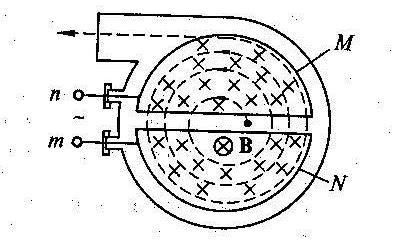
камеруА,
помещённую между полюсами сильного
электромагнита. Вектор
направлен перпендикулярно плоскости
чертежа.

Дуанты с помощью
электродов т
и
п
присоединены к полюсам электрического
генератора, создающего в щели между
ними переменное электрическое поле.
Ускорение частиц возможно только в
том случае, если движение частицы и
изменение электрического поля в зазоре
будут происходить строго синхронно.

В циклотроне
магнитное поле постоянно, а напряжённость
электрического поля в зазоре изменяется
во времени по гармоническому закону
с постоянным периодом.

В синхрофазотроне
изменяются и частота ускоряющего
напряжения, создаваемого генератором
напряжения меняющейся частоты, и индукция
магнитного поля. Ускоряемые частицы
движутся не по спирали, а по кольцу. По
мере увеличения скорости частиц индукция
магнитного поля растёт так, чтобы радиус
окружности, по которой движутся частицы
оставался постоянным. При этом период
обращения изменяется как из-за скорости

так и из-за магнитной индукции.

Большой
адронный коллайдер
– ускоритель адронов (частиц, состоящих
из кварков) на встречных пучках,
предназначенный для разгона протонов
и тяжёлых ионов
в противоположных направлениях
и изучения продуктов их соударений.

Коллайдер построен
на границе Швейцарии и Франции. Длина
основного кольца ускорителя составляет
26 659 м.

Скорость частиц
в БАК на встречных пучках близка к
скорости света в вакууме. На первом
этапе низкоэнергетичные линейные
ускорители производят инжекцию протонов
и ионов свинца в синхротрон, где они
приобретают энергию в 28 ГэВ. После
этого ускорение частиц продолжается в
суперсинхрофазотроне, где энергия
частиц достигает 450 ГэВ. Затем пучок
направляют в основное кольцо и в точках
столкновения шесть детекторов фиксируют
происходящие события.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Следы частиц на наших снимках — либо дуги большого радиуса, если это тяжелые частицы, либо спирали в случае электронов и позитронов. Искривление траектории возникает под действием магнитного поля. На заряженную частицу в магнитном поле действует сила Лоренца, направленная перпендикулярно как скорости частицы , так и вектору индукции магнитного поля . Если частица влетает в магнитное поле перпендикулярно полю, то она движется по окружности, если же она влетает под углом — то по винтовой линии. На разноименно заряженные частицы, движущиеся в одном направлении, действуют противоположно направленные силы — именно поэтому следы электронов и позитронов расходятся в разные стороны.

Запишем второй закон Ньютона для частицы с зарядом Ze и массой m, движущуюся по окружности в магнитном поле с индукцией В. Причем сделаем это в такой форме, которая пригодна как для медленных, так и для быстрых частиц, в том числе и для ультрарелятивистских, скорость которых близка к скорости света:

Если частица движется по окружности радиусом R со скоростью , то ее импульс , оставаясь постоянным по модулю, поворачивается с угловой скоростью

При этом изменение импульса за время равно

Тогда второй закон Ньютона принимает вид

.

(Если частица движется медленно, то , и в левой части последнего равенства появляется произведение массы на центростремительное ускорение. Для релятивистских и ультрарелятивистских частиц это не так.) Подставляя сюда , получаем формулу, выражающую импульс частицы через радиус окружности:

.

Специалисты, работающие на ускорителях, любят выражать не импульс, а произведение импульса на скорость света, т.е. величину рс, имеющую размерность энергии. Разделив на заряд электрона, мы выразим эту величину в электрон-вольтах. Кроме того, физики привыкли измерять магнитную индукцию не в теслах, а в гауссах (1 Гс = 10-4 Тл). Учтя все это, получим рабочую формулу, которая используется при обсчетах траекторий частиц:

где измеряется в сантиметрах.

Отметим, что величина удобна еще и тем, что через нее простым образом выражается энергия частицы. В частности, для медленных частиц

где — энергия покоя (в случае электрона она равна 0,51 МэВ). А для ультрарелятивистских частиц, энергия которых гораздо больше энергии покоя,

Число капель на следе — мера скорости частицы

Когда заряженная частица движется в пузырьковой камере, она растрачивает свою энергию на возбуждение атомов или молекул жидкости. Если переданная энергия достаточно велика, электрон может быть выбит из атома — произойдет образование иона и свободного электрона. Энергия, потерянная частицей на единице пути, т.е. величина , зависит от скорости частицы: чем скорость меньше, тем больше времени частица взаимодействует с электроном. Величина оказывается обратно пропорциональной квадрату скорости частицы. В первом приближении можно считать, что

(*)

где — отношение скорости частицы к скорости света, — некоторая постоянная, зависящая от свойств среды, в которой тормозится частица (дальше мы оценим эту величину для жидкого водорода). Таким образом, получается, что быстрая частица () ионизирует слабее всего. Соответственно, тонкие следы в камере принадлежат быстрым (релятивистским) частицам, а жирные следы из слипшихся капель образованы медленными частицами. На рисунке 3 ясно видно, что частицы основного пучка, пронизывающие камеру снизу вверх, — быстрые частицы (для р-мезона с энергией 1 ГэВ, например, ). Скорость же протона, возникшего при 0-распаде, мала, и поэтому протон оставляет плотный след.

Итак, мы видим, что по следам в пузырьковой камере можно измерить импульс частицы и ее скорость. А зная скорость и импульс, можно определить массу частицы.