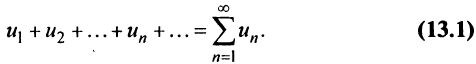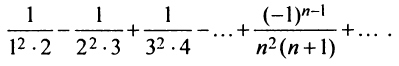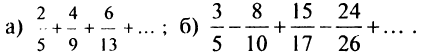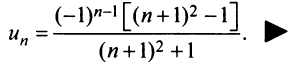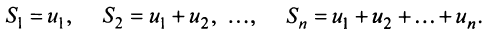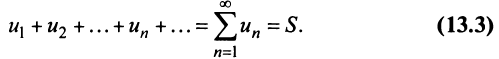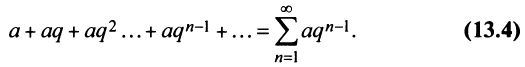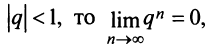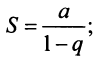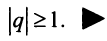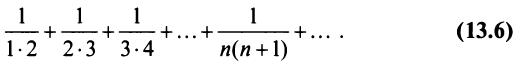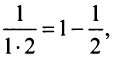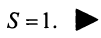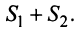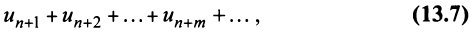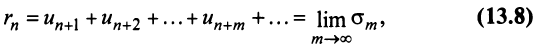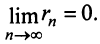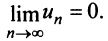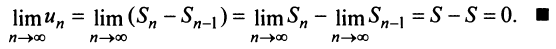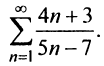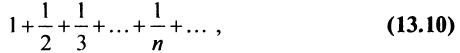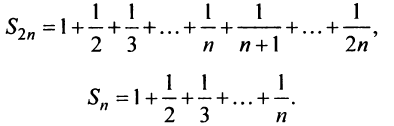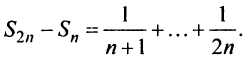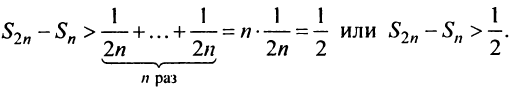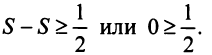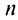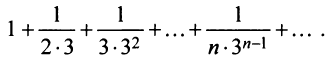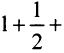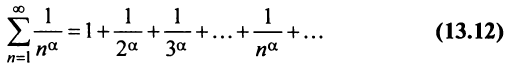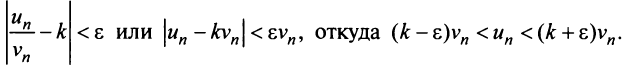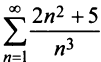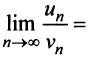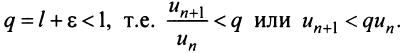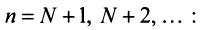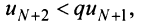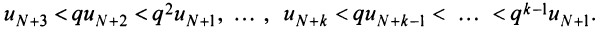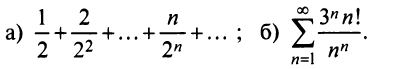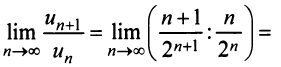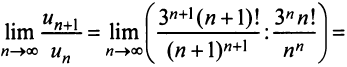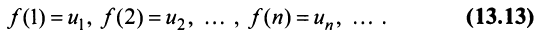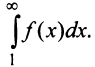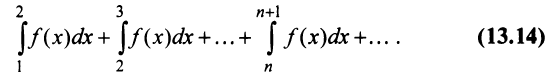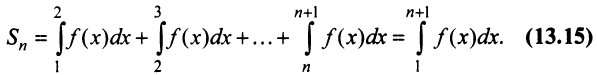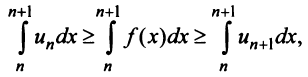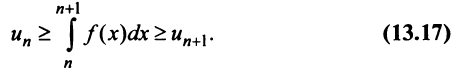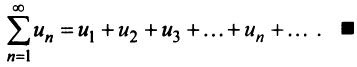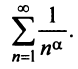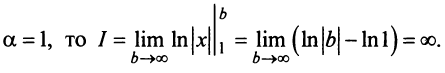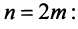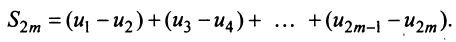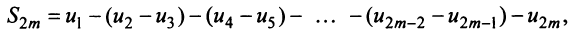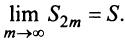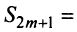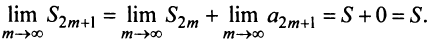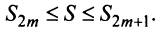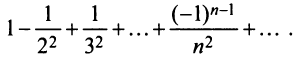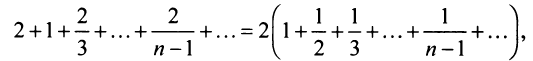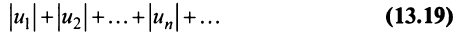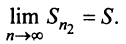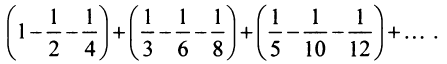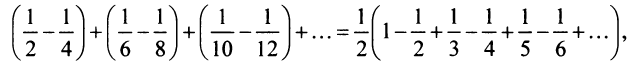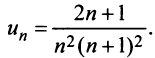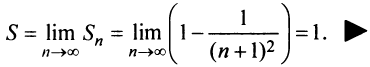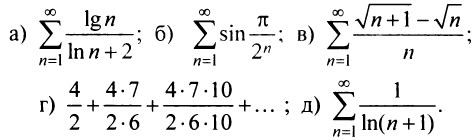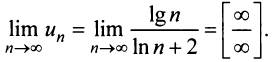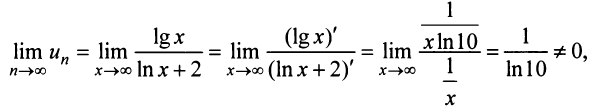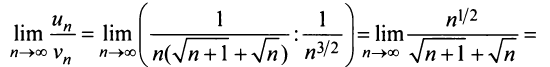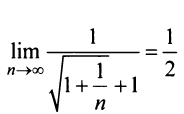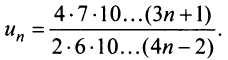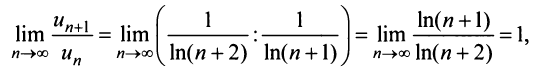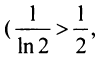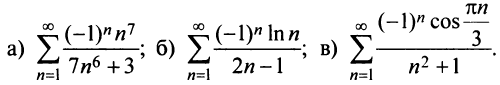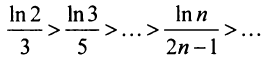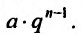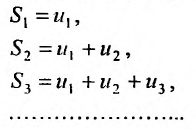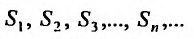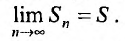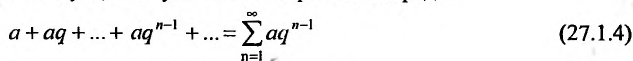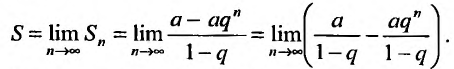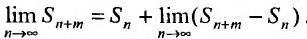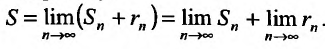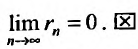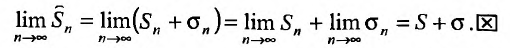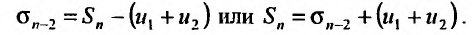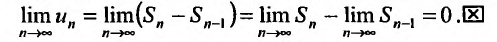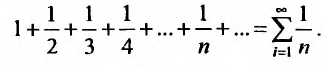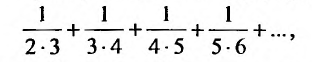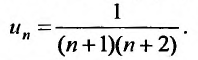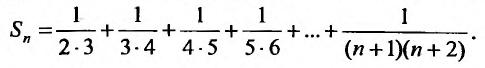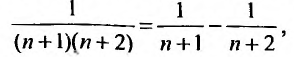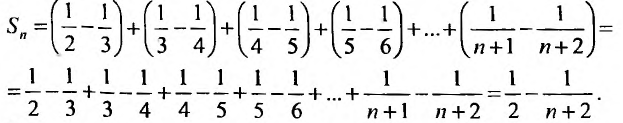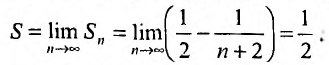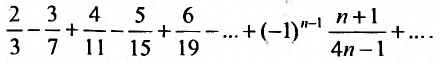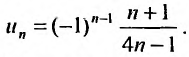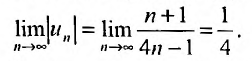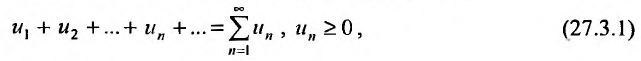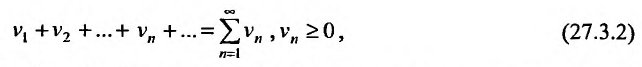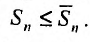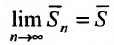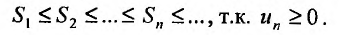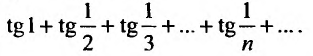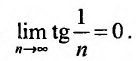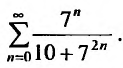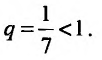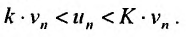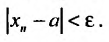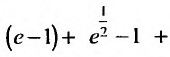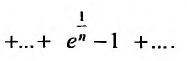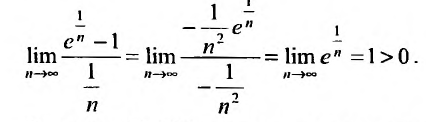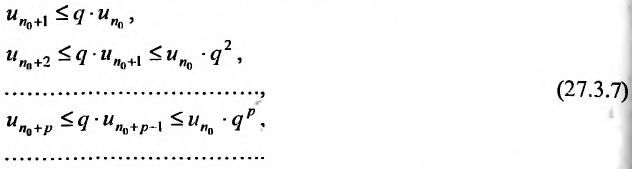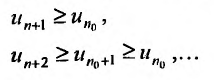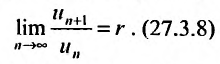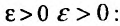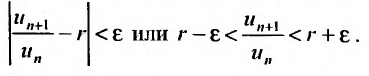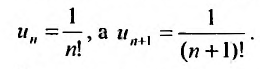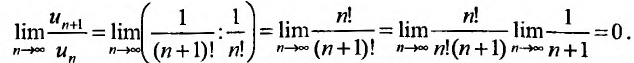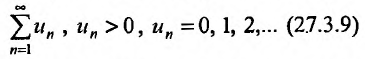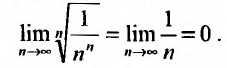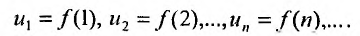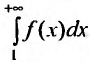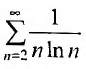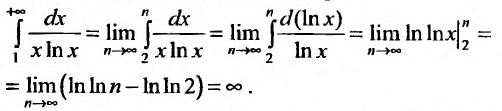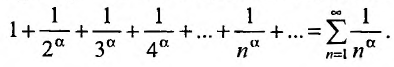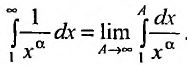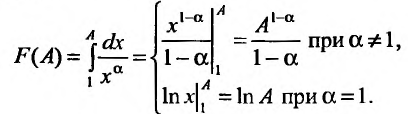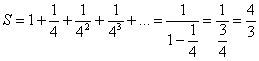Заказать задачи по любым предметам можно здесь от 10 минут
Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ — это общий член ряда. $n$ — это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ — первый член прогрессии, а $q$ — основание. В данном случае сумма равна $S = frac{1}{1 — frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |
Содержание:
Числовые ряды:
При решении ряда математических задач, в том числе и в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых решается в теории рядов.
Основные понятия. Сходимость ряда
Определение. Числовым рядом называется бесконечная последовательность чисел
Числа 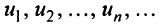
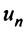
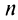
Ряд (13.1) считается заданным, если известен его общий член 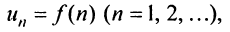
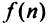
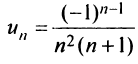
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение.
Пример:
Найти в простейшей форме общий член ряда:
Решение:
Нетрудно убедиться, что для ряда а) общий член 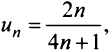
Рассмотрим суммы конечного числа членов ряда:
Сумма п первых членов ряда 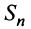
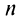
Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.
Число 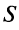
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
Пример:
Исследовать сходимость геометрического ряда, т.е. ряда, составленного из членов геометрической профессии
Решение:
Необходимо установить, при каких значениях знаменателя профессии 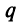
Из школьного курса алгебры известно, что сумма 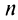
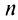
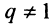
Возможно несколько случаев:
1) если
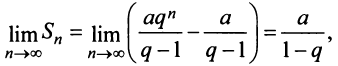
2) если 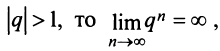
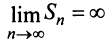
3) если 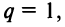
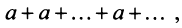
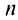
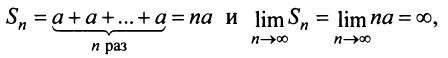
4) если 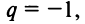
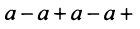
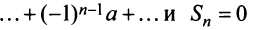
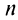
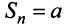
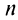
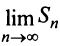
Таким образом, геометрический ряд сходится к сумме 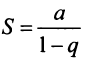
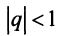
Пример:
Найти сумму ряда
Решение:
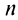
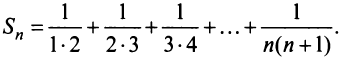
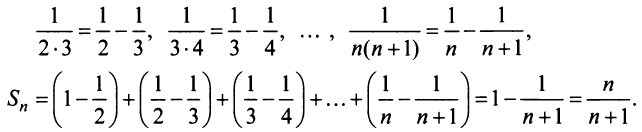
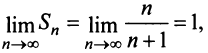
Свойства сходящихся рядов. 1. Если ряд 
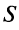
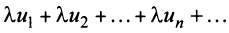
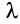
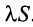
2. Если ряды 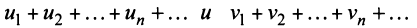
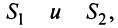
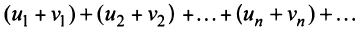
Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.
3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
Пусть в сходящемся ряде (13.1) отброшены 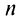
имеющий частичную сумму 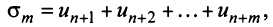
Очевидно, что 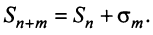
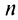
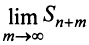
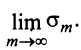
Ряд (13.7), полученный из данного отбрасыванием его первых 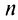
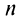
Если сумму 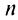
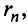
то сумму ряда (13.1) можно представить в виде
В результате мы подошли к свойству 4.
4. Для того чтобы ряд (13.1) сходился, необходимо и достаточно, чтобы при 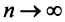
Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций (см. § 6.3).
Установить сходимость (расходимость) ряда путем определения 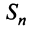
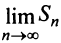
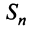
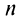
Необходимый признак сходимости. Гармонический ряд
Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 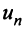
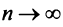

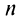
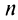
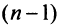
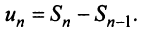
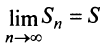
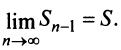
Пример №1
Проверить выполнение необходимого признака для ряда (13.6).
Решение:
Выше было доказано, что ряд (13.6) сходится, и действительно 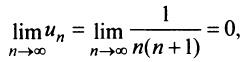
Следствие. Если предел общего члена ряда (13.1) при 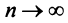
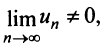
Предположим противное, т.е. ряд (13.1) сходится. Но в этом случае из приведенной выше теоремы следует 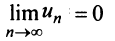
Пример №2
Исследовать сходимость ряда
Решение:
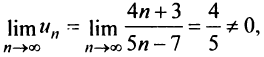
Замечание. Следует подчеркнуть, что рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если 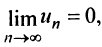
В качестве примера рассмотрим ряд
называемый гармоническим.
Необходимый признак сходимости выполнен: 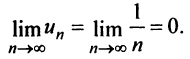

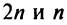
Найдем разность
Заменяя в сумме каждое слагаемое наименьшим, равным 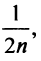
Предположим противное, т.е. что гармонический ряд сходится, тогда 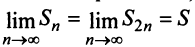
Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится. ■
В следующих двух параграфах рассмотрим достаточные признаки сходимости.
Ряды с положительными членами
Теорема (признак сравнения). Пусть даны два ряда с положительными членами: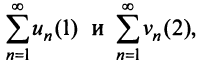
Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.

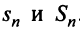
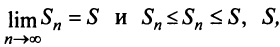
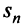
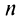
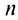
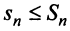
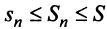
Следовательно, на основании признака существования предела (см. § 6.5) последовательность 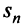
б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходится и ряд 1, что противоречит предположению; т.е. ряд 2 расходится. ■
Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие (13.11) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами 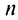
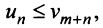
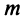
Пример №3
Исследовать сходимость ряда
Решение:
Сравним данный ряд со сходящимся геометрическим рядом 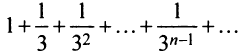
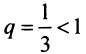
Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 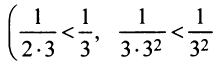
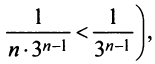
Пример №4
Исследовать сходимость ряда
Решение:
Сравним данный ряд с гармоническим 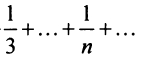
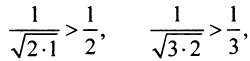
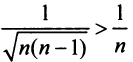
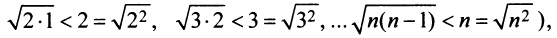
сходится при 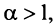
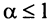
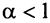
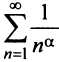
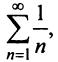
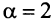
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (13.11), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п.). В ряде случаев более простым оказывается предельный признак сравнения.
Теорема (предельный признак сравнения)
Теорема (предельный признак сравнения). Если 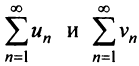
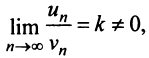

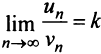
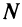
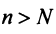
Если ряд 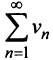
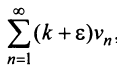
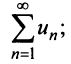
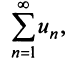
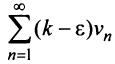
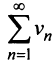
Пример №5
Исследовать сходимость ряда
Решение:
Сравним данный ряд с расходящимся гармоническим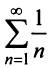
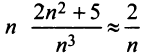
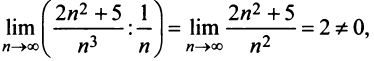
Весьма удобным на практике является признак Даламбера.
Теорема (признак Даламбера)
Теорема (признак Даламбера). Пусть для ряда 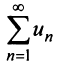
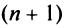
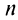
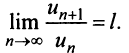
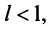
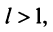
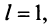
Из определения предела последовательности следует, что для любого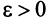
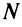
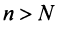
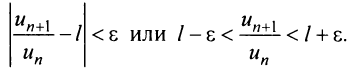
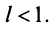
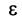
Последнее неравенство будет выполняться для всех 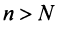
Получили, что члены ряда 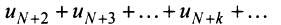
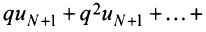
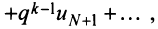
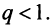
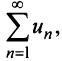
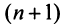
2) Пусть 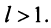
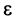
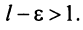
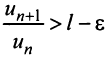
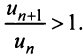
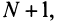
Пример №6
Исследовать сходимость рядов:
Решение:
а) Так как 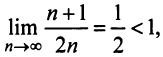
б) Так как
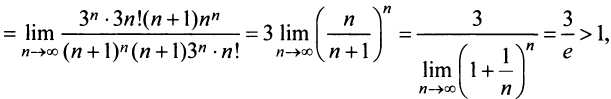
Замечание 1. Если 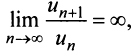
Замечание 2. Если 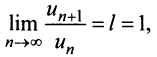
Теорема (интегральный признак сходимости)
Теорема (интегральный признак сходимости). Пусть дан ряд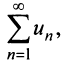

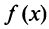
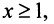
Тогда для сходимости ряда 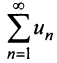
Рассмотрим ряд
Его 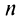
Сходимость ряда (13.14) означает существование предела последовательности его частичных сумм (13.15), т.е. сходимость несобственного интеграла 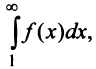
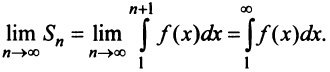
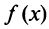
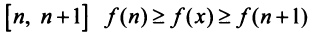
Интегрируя (13.16) на отрезке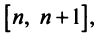
откуда
Если ряд 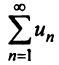
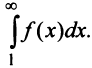
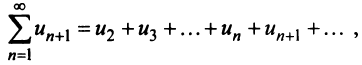
Пример №7
Исследовать сходимость обобщенного гармонического ряда
Решение:
Пусть 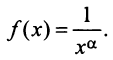
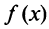
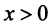
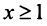
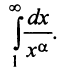
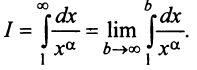
Если 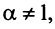
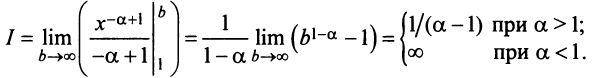
Ряды с членами произвольного знака
Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 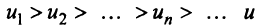
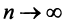
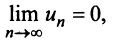
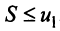
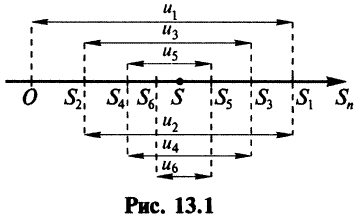
Рассмотрим последовательность частичных сумм четного числа членов при
Эта последовательность возрастающая (так как с ростом 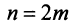
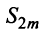
откуда следует, что 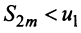
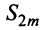
Попутно заметим, что, переходя к пределу в неравенстве 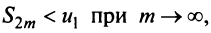
Теперь рассмотрим последовательность частичных сумм нечетного числа членов при 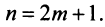
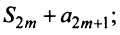
Итак, при любом 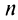
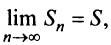
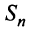
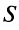
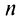
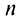
Из рис. 13.1 вытекает еще одна оценка для суммы 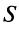
Пример №8
Исследовать сходимость ряда
Решение:
Так как члены знакочередующегося ряда убывают по абсолютной величине 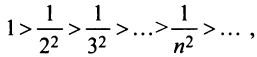
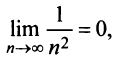
Замечание. В теореме Лейбница существенно не только условие 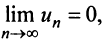
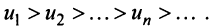
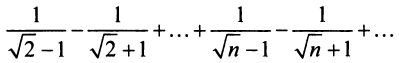
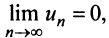
т.е. «удвоенного» гармонического ряда.
Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.
По формуле (13.9) сумму сходящегося ряда можно представить как сумму 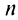
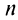
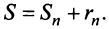
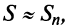
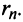
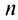
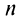
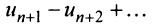
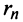
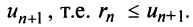
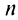
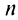
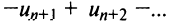
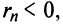
Пример №9
Какое число членов ряда 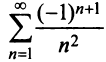
Решение:
По условию 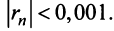
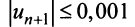
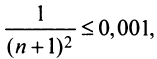
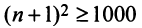
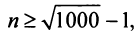
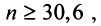
Знакопеременные ряды. Пусть 
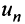
Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда (13.1)
сходится, то сходится и данный ряд.
Обозначим 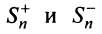
Тогда частичная сумма данного ряда 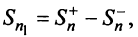
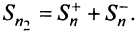
Последовательности 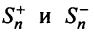
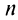
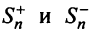
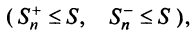
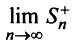
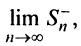
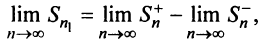
Следует отметить, что обратное утверждение неверно. Ряд (13.19) может расходиться, а ряд (13.1) сходиться. Например, ряд 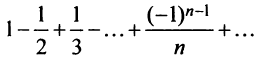
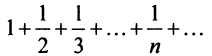
Поэтому введем следующие определения.
Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Таким образом, рассмотренный выше ряд 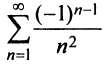
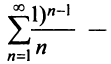
Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.
Условно сходящиеся ряды такими свойствами не обладают.
Возьмем, например, ряд 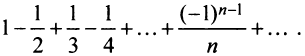
Перепишем ряд в виде:
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.
Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
Пример №10
Найти сумму ряда 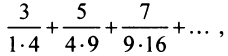
Решение:
Очевидно, что общий член ряда
Представим сумму 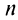
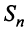
Пример №11
Исследовать сходимость ряда:
Решение:
а) Проверим выполнение необходимого признака сходимости, найдя предел общего члена:
Для вычисления предела отношения двух бесконечно больших функций натурального аргумента правило Лопиталя непосредственно применять нельзя, ибо для таких функций не определено понятие производной. Поэтому применяя теорему о «погружении» дискретного аргумента 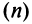
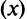
следовательно, ряд расходится.
б) Очевидно, что задан ряд с положительными членами, так как 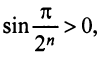
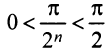
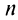
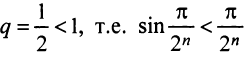
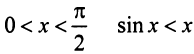
в) Представим общий член ряда в виде
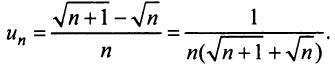
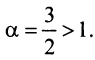
есть конечное число, не равное нулю, то данный ряд, так же как и «эталонный», сходится.
г) Применим признак Даламбера, заметив, что общий член ряда 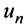
Тогда 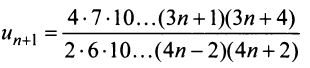
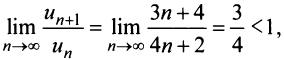
д) Применим признак Даламбера:
т.е. вопрос о сходимости ряда остается открытым. Проверим выполнение необходимого признака (с этого можно было начать исследование): 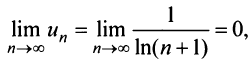
Применим признак сравнения в более простой предельной форме. Сравним данный ряд, например, с гармоническим.
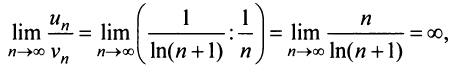
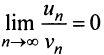
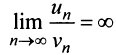
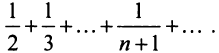
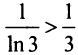
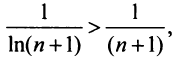
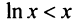
Пример №12
Исследовать сходимость ряда:
Решение:
а) Предел общего члена ряда 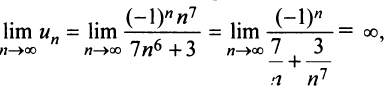
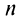
б) Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине —
и предел общего члена 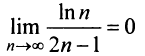
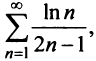
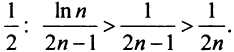
в) Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося ряда (13.12) при 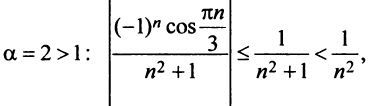
Определение ряда и его сходимость
Пусть
бесконечная последовательность чисел.
Определение 27.1.1. Выражение
называется числовым рядом, а элементы последовательности 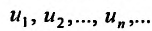
Поскольку выражение (27.1.2) рассматривается как единое целое, то для задания ряда необходимо задать каждый его член 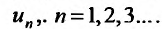
Припишем теперь определенный смысл выражению (27.1.2), т.е. введем определение.
Определение 27.1.2. Сумма n первых членов ряда (27.1.2) 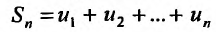
Ясно, что первая, вторая, третья и т.д. частичные суммы ряда
составляют бесконечную последовательность:
Определение 27.1.3. Ряд (27.1.2) называется сходящимся, если последовательность 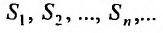
Значение S этого предела называется суммой ряда (27.1.2). Ряд (27.1.2) называется расходящимся, если последовательность его частичных сумм предела не имеет (например, если члены последовательности возрастают по модулю неограниченно).
Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов.
В принципе можно доказывать сходимость или расходимость каждого ряда, а также вычислять сумму сходящегося ряда, опираясь непосредственно на определения сходимости и суммы. Для этого в каждом случае составляется аналитическое выражение для n- ой частичной суммы ряда и находится предел этого выражения при возрастании n.
Пример:
Для ряда 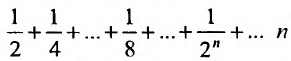
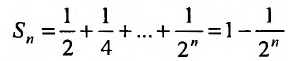
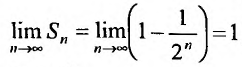
Пример:
Последовательность вида
называется геометрической прогрессией, где а — первый член, а
q — её знаменатель; выражение 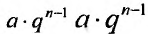
Числовой ряд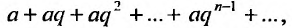
Если в прогрессии (27.1.3) имеется только конечное число членов, то прогрессия называется конечной; в противном случае, если за каждым членом прогрессии следует ещё хотя бы один член, то прогрессия называется бесконечной.
В случае конечной прогрессии 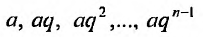
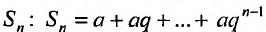
Известно, что при 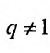
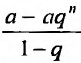
называется предел её частичных сумм 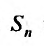
Так как а и q от n не зависят, то последнюю формулу представим в виде:
Если 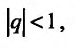
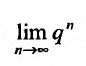
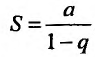
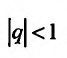
но, сходится и ряд (27.1.4). Если же 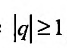
Итак, мы привели примеры, в которых исследование сходимости рядов проводили, применяя определение 27.1.3., т.е. вычисляли частичные суммы и находили предел их последовательностей. Ясно, что в общем случае, составление аналитического выражения для n- ой частичной суммы трудный вопрос. Кроме того, при исследовании рядов нередко значения сумм не представляют интереса, т.к. нужно определить только сходится ряд или нет. Поэтому представляют интерес методы анализа рядов, когда не требуется вычислять суммы рядов. Далее перейдем к изложению таких методов.
Свойства сходящихся рядов
Пусть дан ряд
Определение 27.2.1. Ряд 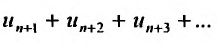
Очевидно, m- я частичная суммаn -го остатка ряда равна разности 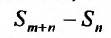
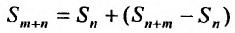
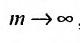
Предел слева есть сумма исходного ряда, а предел справа-сумма 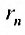
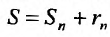
Теорема 27.2.1. Если ряд (27.2.1) сходится, то сумма его n-го остатка с ростом n стремится к нулю.
Доказательство. Выше показано, что 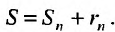
Но для сходящегося ряда 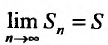
Рассмотрим теперь свойства сходящихся рядов, которые позволяют действовать с ними, как с конечными суммами.
Теорема 27.2.2. Если ряд
имеет сумму S, то ряд
полученный из предыдущего умножением всех членов на одно и тоже число a, имеет сумму aS.
Доказательство. Обозначим последовательность частичных сумм ряда (27.2.2) 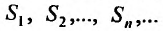
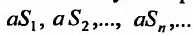
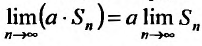
(27.2.2) сходится, то 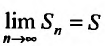
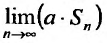
Теорема 27.2.3. Если ряды
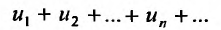
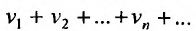
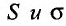
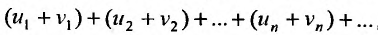
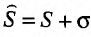
Доказательство. Пусть 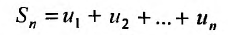
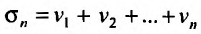
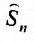
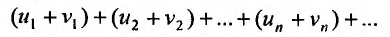
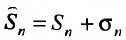
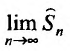
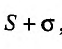
Следствие. Разность двух сходящихся рядов-ряд сходящийся.
Теорема 27.2.4. Свойства сходимости или расходимости ря-,ki не нарушается, если в ряде исключить или приписать к нему любое конечное число членов.
Доказательство. Пусть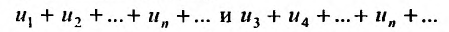
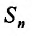
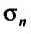
Из этого равенства следует, что, если 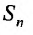
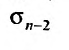
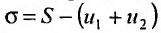
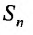
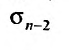
Теорема 27.2.5. (Необходимое условие сходимости ряда). Если ряд 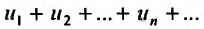
Доказательство. Пусть ряд 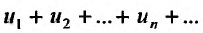
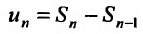
Отметим, что условие (27.2.4) не является достаточным, т.е. общий член может стремиться к нулю, но ряд все же может быть расходящимся. Но если общий член ряда не стремится к нулю, то ряд будет расходящийся.
- Заказать решение задач по высшей математике
Пример №13
Исследуем на сходимость гармонический ряд
Решение:
Вначале находим предел общего члена: 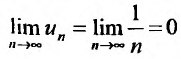
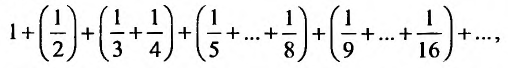
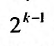
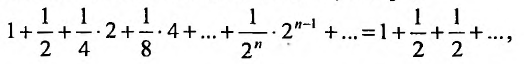
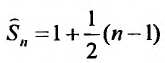
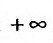
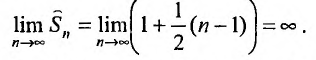
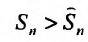
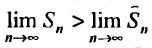
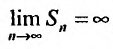
Пример №14
Найти формулу для общего члена ряда
считая, что каждый его последующий член определяется по тому же закону, по которому образованы записанные члены, и найти ею сумму.
Решение:
Каждый член данного ряда представляет собой дробь, числитель которой равен 1, а знаменатель равен произведению двух последовательных натуральных чисел 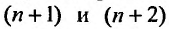
Для вычисления суммы ряда составим n -ую частичную сумму:
Представим выражение для общего члена в виде разности:
тогда
Переходя к пределу, получаем сумму ряда:
Пример №15
Исследовать сходимость ряда
Решение:
Общий член ряда определяется формулой
Вычислим предел модуля общего члена:
Так как предел общего члена не стремится к нулю, то ряд расходится.
Признаки сходимости числовых знакоположительных рядов
Рассмотрим числовые ряды с положительными членами. Существует много приёмов, называемых признаками сходимости, позволяющих установить сходимость или расходимость числовых рядов Так мы познакомились с методом исследования сходимости ряда на основании выяснения имеет ли предел последовательность частичных сумм. Стремление к нулю члена ряда по мерс роста его номера также является признаком сходимости, хотя только необходимым. Ниже мы приведём ряд достаточных признаков сходимости.
Признаки сравнения
Теорема 27.3.1. (I признак сравнения). Пусть
и
два ряда, причём члены первого ряда, начиная с некоторого номера k , не превосходят соответствующих членов второго
Тогда из сходимости ряда (27.3.2) следует сходимость ряда (27.3.1), а из расходимости ряда (27.3.1) следует расходимость ряда (27.3.2).
Доказательство. Так как исключение конечного числа членов ряда не влияет на его сходимость (теорема 27.2.4.), то достаточно доказать теорему для случая когда неравенства (27.3.3) выполняются для k = 1.
Пусть 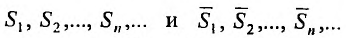
Пусть ряд (27.3.2) сходится. Тогда сходится соответствующая последовательность частичных сумм ряда (27.3.2), т.е.
Поскольку выполняются неравенства (27.3.3), то члены последовательности частичных сумм ряда (27.3.1) удовлетворяют неравенству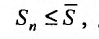
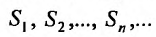
Поэтому, в силу признака Больцано-Всйсрштраса, последовательность частичных сумм ряда (27.3.1) сходится. По определению 27.1.3, сходится и ряд (27.3.1).
Пусть теперь ряд (27.3.1) расходится. Это значит, что его частичные суммы неограниченно возрастают. Но тогда, в силу неравенств (27.3.3), неограниченно возрастают и частичные суммы ряда (27.3.2), что означает, что этот ряд расходится.
Пример №16
Пусть дан ряд
Исследуем его сходимость.
Решение:
Необходимый признак выполняется, т.е.
Для исследования сходимости заданного ряда применим 1 признак
сравнения (теорему 27.3.1). Сравним заданный ряд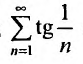
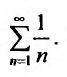
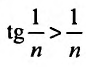
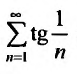
Пример №17
Исследовать сходимость ряда
Решение:
Очевидно, что предел общего члена при возрастании т стремится к нулю.
Сравним данный ряд, общий член которого 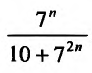
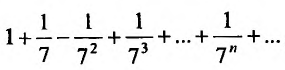
Поскольку 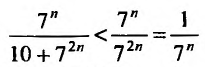
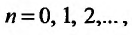
Теорема 27.3.2. (II признак сравнения). Если для рядов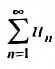
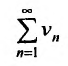
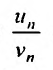
то ряды 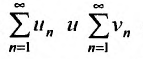
Доказательство. Предельное соотношение (27.3.4), в силу определения 
выполняется неравенство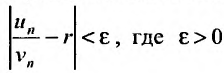
Обозначив 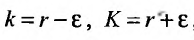
Предположим, что ряд 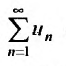
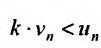
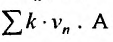
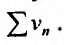
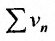
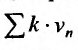
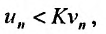
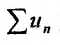
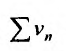
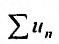
Последовательность 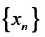
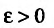
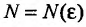
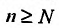
Пример №18
Исследовать сходимость ряда
Решение:
Очевидно, что 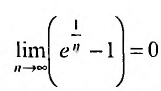
Теорема 27.3.2 выполняется, поэтому из расходимости гармонического ряда 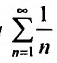
Признаки Д’Аламбсра и Коши
Иногда вместо признаков сравнения оказываются полезными некоторые специальные признаки сходимости ряда. Отметим среди них признаки Д’Аламбсра и Коши, непосредственно получающиеся из признаков сравнения, если в качестве ряда сравнения взять соответствующим образом выбранную геометрическую прогрессию.
Теорема 27.3.3. (признак Д’Аламбера). Если для ряда
с положительными членами существует такой номер 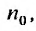
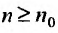
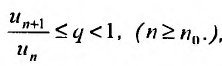
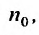
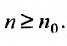
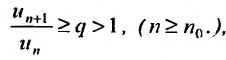
Доказательство. Пусть 0 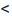
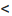
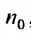
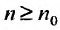
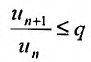
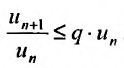
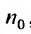
Ряд 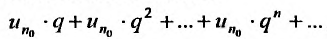
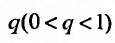
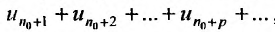
т.к. на сходимость ряда не влияет исключение конечного числа е^ членов.
Если же существует такое 
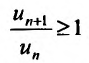
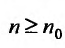
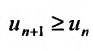
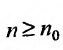
Так как по предположению 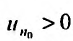
Следствие 1. Пусть существует предел отношения последующего члена ряда (27.3.6) к предыдущему равный r :
Тогда, если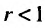
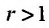
Доказательство. Воспользовавшись определением предела, для фиксированного 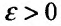
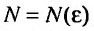
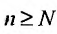
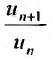
Рассмотрим правую часть двойного неравенства: 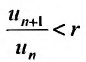
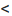
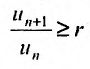
Пример №19
Рассмотрим ряд 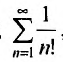
Решение:
Выпишем вначале значения
Затем вычислим предел отношения последующего члена ряда к предыдущему:
Так как этот предел меньше 1, то, в силу следствия 1, данный ряд сходится.
Заметим, что при исследовании сходимости ряда обычно (как правило, но не всегда) применяют следствие 1 из теоремы 27.3.3.
Теорема 27.3.4. (признак Kouiu). Если для ряда
с положительными членами, начиная с некоторого номера 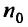
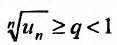
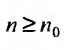
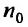
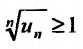
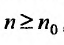
Доказательство. Пусть существует такой номер 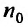
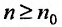
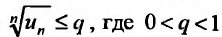
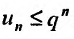
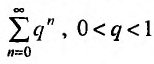
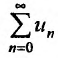
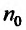
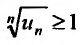
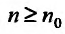
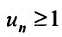
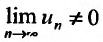
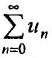
Следствие 2. Пусть существует предел корня n -ой степени из n-го члена ряда (27.3.9):
Тогда, если 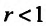
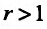
Доказательство. Из определения предела следует, что для фиксированного 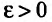
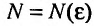
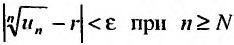
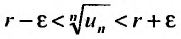
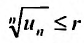
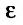
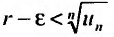
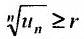
Пример №20
Рассмотрим ряд 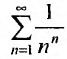
Решение:
Выпишем значение n-го члена ряда 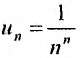
Так как этот предел меньше 1, то, согласно следствию 2, ряд сходится.
Замечание. Если пределы (27.3.8) и (27.3.10) равны 1, то для исследования сходимости ряда (27.3.9) нужно применять другие признаки, с которыми можно ознакомиться в [3].
Интегральный признак сходимости
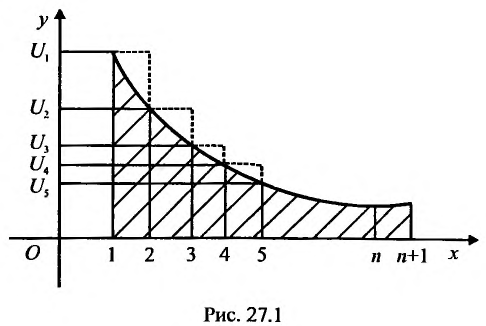
Рассмотрим признак, достоинство которого состоит в исключительно высокой его чувствительности. Этим признаком проводится исследование сходимости там, где сформулированные признаки Д’Аламбсра и Коши «не работают».
Каждый член числового ряда 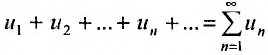
Эта функция определена пока только для целых положительных значений аргумента. Поэтому, доопределив значение функции f для всех нецелых значений аргумента, больших единицы, мы сможем, говорить о функции f(x), принимающей значения для любого 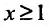
члены которого положительны и не возрастают 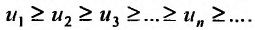
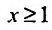
расходится интеграл
Доказательство. Пусть члены ряда (27.3.11) удовлетворяют условиям теоремы. Изобразим их графически, откладывая по оси Ох независимую переменную, а по оси Оу — соответствующие значения 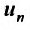
При таком графическом изображении сумма n первых членов ряда 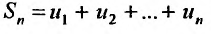
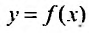
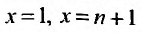
С другой стороны, криволинейная трапеция содержит сумму площадей вписанных прямоугольников, которая равна 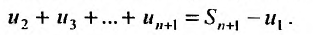
Из (27.3.12) и (27.3.13) следует неравенство:
Предположим, что несобственный интеграл 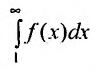
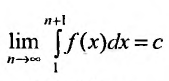
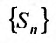
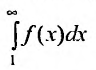
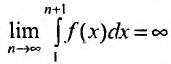
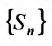
Пример №21
Исследовать сходимость ряда
Решение:
Применим интегральный признак. Рассмотрим функцию 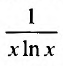
Так как несобственный интеграл расходится, то расходится и ряд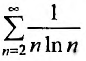
Замечание. Исследовать сходимость данного ряда при помощи следствий 1 и 2 не представляется возможным, так как соответствующие пределы равны 1.
Пример №22
Исследовать сходимость ряда Дирихле
Решение:
Если 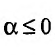
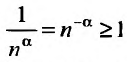
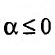
Пусть а > 0, тогда необходимый признак, очевидно, выполняется. Применим интегральный признак Коши. Введем функцию
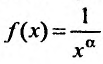
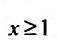
Вычислим определенный интеграл, записанный под знаком предела:
Если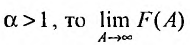
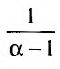
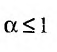
Таким образом, при a>1 несобственный интеграл 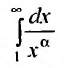
- Знакопеременные ряды
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
Числовой
ряд, сходимость, сумма. Основные свойства
сходящихся
рядов. Признаки сходимости числовых
рядов.
Повторить:
1. понятие числовой последовательности;
2.
арифметическую и геометрическую
прогрессии;
3.
технику вычисления пределов;
4.
факториал;
5.
сходимость несобственного интеграла.
§1. Основные определения
Пусть дана
последовательность
,
где индексы 1,2,3…п
показывают место членов последовательности.
Определение.
Сумма членов бесконечной числовой
последовательности
называется
рядом.
(1)
При
этом числа
будем называть членами
ряда, а un
– общим
членом ряда.
Если
—
числа, то ряд называют числовым.
Если
—
функции, то ряд называют функциональным.
Определение.
Суммы
,
n
= 1, 2, …
называются
частными
(частичными) суммами ряда.
Таким образом, возможно рассматривать
последовательности частичных сумм ряда
S1,
S2,
… ,Sn,
…
Пример 1
Записать первые
три члена ряда
На практике довольно часто требуется
записать несколько членов ряда.
Сначала
,
тогда:
Затем
,
тогда:
Потом
,
тогда:
Процесс можно
продолжить до бесконечности, но по
условию требовалось написать первые
три члена ряда, поэтому записываем
ответ:
Пример 2.
Записать первые
три члена ряда
подставляем
в общий член ряда
сначала
,
потом
и
.
В итоге:
Ответ оставляем
в таком виде, полученные
члены ряда лучше не упрощать,
то есть не
выполнять
действия:
,
,
.
Ответ оставим в
виде
Пример 3.
Записать сумму в
свёрнутом виде с общим членом ряда
Здесь
нет какого-то четкого алгоритма решения,
закономерность
нужно просто увидеть.
В
данном случае:
Пример 4.
Записать
сумму в свёрнутом виде с общим членом
ряда
Пример 5.
Записать первые
три члена ряда
Одной из
ключевых задач теории числовых рядов
является исследование
ряда на сходимость.
При этом возможны два случая:
Определение.
Ряд
называется сходящимся,
если
сходится
последовательность его частных сумм.
Сумма
сходящегося
ряда – предел
последовательности его частных
сумм.
(2)
Определение.
Если последовательность частных сумм
ряда расходится, т.е.
не имеет предела,
или имеет бесконечный предел, то ряд
называется
расходящимся
и ему не ставят в соответствие
никакой суммы.
-
Хороший
пример расходящегося числового ряда
встретился в начале лекции:
.
Здесь
совершенно очевидно, что каждый следующий
член ряда – больше, чем предыдущий,
поэтому
и,
значит, ряд расходится. Чуть ниже мы
рассмотрим более строгий математический
критерий для данного примера.
-
В качестве примера
сходящегося числового ряда можно
привести
бесконечно убывающую
геометрическую прогрессию, известную
нам со школы:
.
Сумму членов бесконечно убывающей
геометрической прогрессии можно найти
по формуле:
,
где
–
первый член прогрессии,
–
основание прогрессии. В данном случае:
,
.
Таким образом:
.
Получено конечное число, значит, ряд
сходится,
что и требовалось доказать.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #