Основание параллелограмма — это сторона, к которой можно
провести перпендикуляр из точки, лежащей на противоположной стороне.
У каждого параллелограмма только два основания. От любой
точки, лежащей на основании параллелограмма, можно провести
перпендикуляр только к одной точке на противоположной стороне.
Так, как у параллелограмма два основания, соответственно
перпендикуляры, которые проведены из любого основания,
оканчиваются на противоположном основании.
В параллелограмме все перпендикуляры,
имеют начало и конец на двух основаниях.
Площадь параллелограмма рассчитывается через
основание параллелограмма (a) и его высоту (h):
[ S = ah ]
Основания у параллелограмма параллельны
друг другу и не имеют общих точек.
Если отрезок можно провести из вершины параллелограмма
к его основанию, под углом 90 градусов, то этот отрезок разделит
параллелограмм на две геометрические фигуры — треугольник
и прямоугольную трапецию. Два отрезка уже разделят параллелограмм
на два треугольника и прямоугольник между ними.
Каждое основание параллелограмма имеет две общие точки с
двумя сторонами, которые не являются основаниями.
Как найти основание параллелограмма? Основание легко
найти, зная формулу площади параллелограмма. Исходя из
этой формулы, формула основания следующая:
[ a = frac{S}{h} ]
a — основание
S — площадь
h — высота
Углы, которые прилежат к любому из оснований,
составляют в сумме 180 градусов.
Опубликована отличная статья про признаки параллелограмма.
Вы здесь
-
Основание и высота параллелограмма
Свойства
Подтемы
Смотрите также
Опубликовано 3 года назад по предмету
Геометрия
от азалия78
-
Ответ
Ответ дан
marmadraИз формулы площади параллелограма:
S=a*h
Можно выразить основание а следующим образом:
а=S/h-
Ответ
Ответ дан
азалия78как разделить 34см² на 8,5см
-
Самые новые вопросы
Математика — 3 года назад
Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x — 5,21 = 9,54
Информатика — 3 года назад
Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.
География — 3 года назад
Почему япония — лидер по выплавке стали?
Математика — 3 года назад
Чему равно: 1*(умножить)х? 0*х?
Русский язык — 3 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Параллелограмм
- Высота
- Площадь
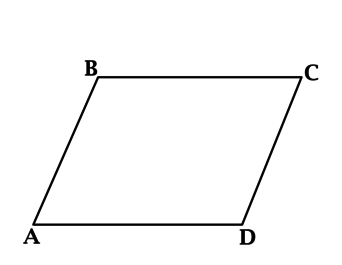
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником, а прямоугольник, у которого все стороны равны, называется квадратом.
Все параллелограммы обладают следующими свойствами:
- противоположные стороны равны:
AB = CD и BC = DA;
- противолежащие углы равны:
∠ABC = ∠CDA и ∠DAB = ∠BCD;
- сумма углов, прилежащих к одной стороне, равна 180°:
∠ABC + ∠BCD = 180°,
∠BCD + ∠CDA = 180°,
∠CDA + ∠DAB = 180°,
∠DAB + ∠ABC = 180°;
- в точке пересечения диагонали делятся пополам:
AO = OC и BO = OD;
- каждая диагональ делит параллелограмм на два равных треугольника:
ΔABC = ΔCDA и ΔABD = ΔBCD;
- точка пересечения диагоналей — это центр симметрии параллелограмма:
Точка O — это центр симметрии.
Высота
Нижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, — высотой.
AD — это основание параллелограмма, h — высота.
Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.
Площадь
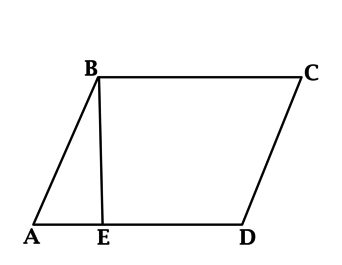
Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD:
Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ΔABE и ΔDCF. Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE, прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF. Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.
Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:
площадь ABCD = AD · BE.
Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту.
Общая формула площади параллелограмма:
S = ah,
где S — это площадь параллелограмма, a — основание, h — высота.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
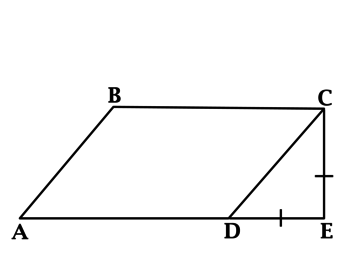
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды