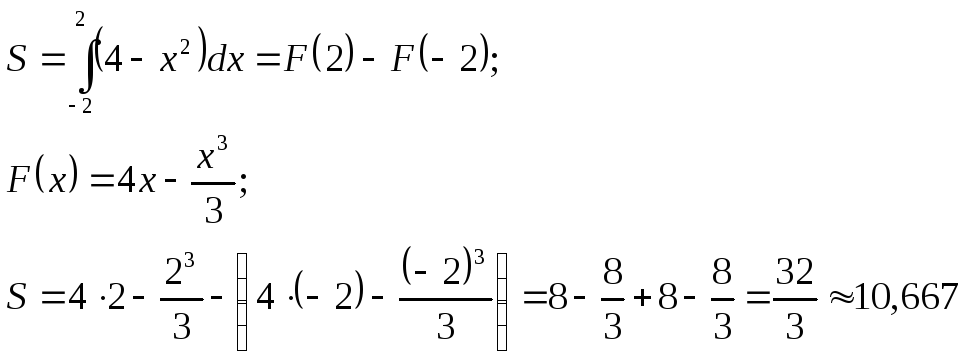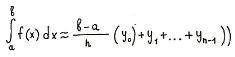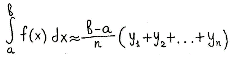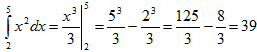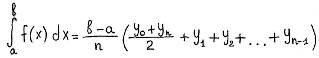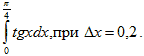7
Лекция 7
Вычисление
определённых интегралов
Для функции вида
y=f(x)
значением
интеграла в пределах [a,
b]
при условии, что на этом интервале
f(x)>0,
является
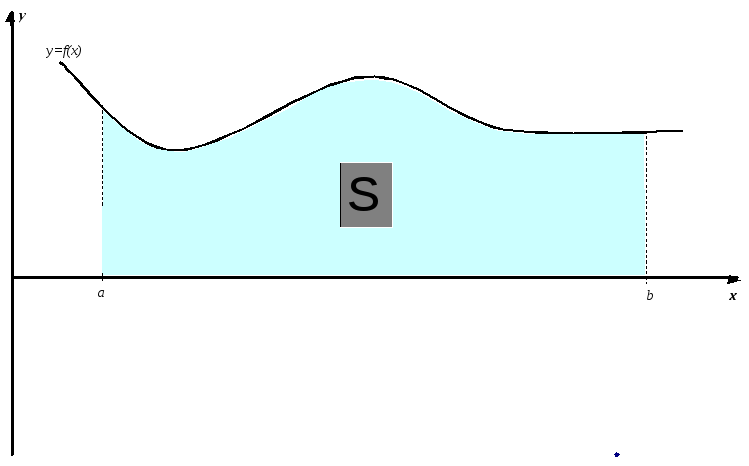
площадь под кривой f(x),
ограниченная вертикальными прямыми
x=a
и x=b
(рис. 1).
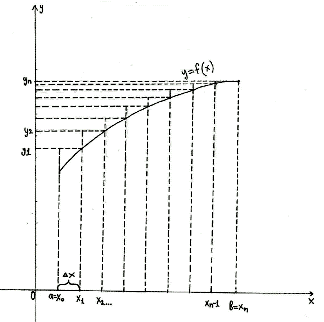
Рис. 1. Графическая
интерпретация определённого интеграла.
Все численные
методы решения задач, связанных с
вычислением определённых интегралов,
основаны на графической интерпретации
данной задачи. Иными словами, вычислить
определённый интеграл одним из численных
методов, значит найти площадь под кривой,
образованной подынтегральной функцией,
в заданных пределах интегрирования.
Общеизвестно, что
аналитически определённый интеграл
вычисляется с использованием первообразных:
. (1)
Однако первообразные
известны или достаточно легко выводятся
для простых функций. Для функционалов
со сложными структурами приходится
прибегать к численным методам.
Среди методов
численного интегрирования рассмотрим
методы прямоугольников, трапеций и
парабол (Симпсона).
Метод прямоугольников,
как и все другие методы, основан на
разбиении исходного интервала
интегрирования [a,
b]
на равные, малые по величине подынтервалы,
на которых рассчитывается площадь
простейшей геометрической фигуры, в
данном случае – прямоугольника.
Шаг интегрирования
(ширина подынтервала) (x)
напрямую
зависит от количества подынтервалов
(n):
. (2)
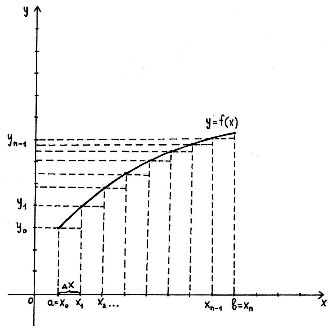
Графическая
иллюстрация метода прямоугольников
представлена на рис. 2.
Рис. 2. Графическая
иллюстрация метода прямоугольников.
Алгоритм метода
прямоугольников следующий.
-
Выбирается шаг
интегрирования (количество подынтервалов). -
По соотношению
(3) рассчитывается сумма площадей на
всех подынтервалах:
, (3)
где
здесь и
далее
.
Задание 1.
Для функции вида
вычислить определённый интеграл в
пределах [–2;
2] двумя
способами: аналитически и методом
прямоугольников при n=8.
Рассчитать погрешности численного
метода.
Аналитическое
решение:
Численное решение
представлено в табл. 1.
Таблица 1
Вычисление определённого интеграла методом прямоугольников
-
xi
f(xi)
f(xi)x
–2,0
0,00
0,000
–1,5
1,75
0,875
–1,0
3,00
1,500
–0,5
3,75
1,875
0,0
4,00
2,000
0,5
3,75
1,875
1,0
3,00
1,500
1,5
1,75
0,875
f(xi)x
10,5
Абсолютная
погрешность метода: |10,500–10,667|=0,167.
Относительная
погрешность:
.
Очевидно, что чем
меньше шаг интегрирования, тем меньшую
погрешность даёт метод. Однако в данной
постановке погрешность всё равно будет
достаточно высокой. Для уменьшения
ошибки можно модифицировать метод
прямоугольников.
Модификация
метода прямоугольников
заключается в том, что высота прямоугольника
на каждом участке интегрирования
определяется не значением функции в
крайней точке участка, а значением
функции, вычисленном в середине
подынтервала (рис. 3).
Рис. 3. Графическая
иллюстрация модификации метода
прямоугольников.
В этом случае в
алгоритме формула (3) изменяется:
. (4)
Задание 2.
Для функции вида
вычислить определённый интеграл в
пределах [–2;
2]
модифицированным методом прямоугольников.
Рассчитать погрешности данного метода.
Численное решение
представлено в табл. 2.
Таблица 2
Вычисление определённого интеграла модифицированным методом прямоугольников
-
xi+0,5x
f(xi+0,5x)
f(xi+0,5x)x
–1,75
0,9375
0,46875
–1,25
2,4375
1,21875
–0,75
3,4375
1,71875
–0,25
3,9375
1,96875
0,25
3,9375
1,96875
0,75
3,4375
1,71875
1,25
2,4375
1,21875
1,75
0,9375
0,46875
f(xi+0,5x)x
10,75
Абсолютная
погрешность метода: |10,750–10,667|=0,083.
Относительная
погрешность:
.
В методе
трапеций,
как следует из названия, формой каждого
участка под заданной кривой является
не прямоугольник, а трапеция (рис. 4).
Соответственно, и площадь каждого
участка вычисляется по формуле площади
трапеции.
Формула для
вычисления определённого интеграла
выглядит следующим образом:
. (5)
Задание 3.
Для функции вида
вычислить определённый интеграл в
пределах [–2;
2] методом
трапеций. Рассчитать погрешности данного
метода.
Численное решение
представлено в табл. 3.
Таблица 3
Учебно-воспитательные задачи:
- Дидактическая цель. Познакомить учащихся с методами
приближённого вычисления определённого интеграла. - Воспитательная цель. Тема данного занятия имеет большое
практическое и воспитательное значение. Наиболее просто к идее численного
интегрирования можно подойти, опираясь на определение определённого
интеграла как предела интегральных сумм. Например, если взять какое-либо
достаточно мелкое разбиение отрезка [a; b] и построить для
него интегральную сумму, то её значение можно приближённо принять за
значение соответствующего интеграла. При этом важно быстро и правильно
производить вычисления с привлечением вычислительной техники.
Основные знания и умения. Иметь понятие о приближённых методах
вычисления определённого интеграла по формулам прямоугольников и трапеций.
Обеспечение занятия
- Раздаточный материал. Карточки-задания для самостоятельной работы.
- ТСО. Мультипроектор, ПК, ноутбуки.
- Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод
прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора). - Вычислительные средства: ПК, микрокалькуляторы.
- Методические рекомендации
Вид занятия. Интегрированное практическое.
Мотивация познавательной деятельности учащихся. Очень часто приходится
вычислять определённые интегралы, для которых невозможно найти первообразную. В
этом случае применяют приближённые методы вычисления определённых интегралов.
Иногда приближённый метод применяют и для “берущихся” интегралов, если
вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого
вычисления интеграла заключается в том, что кривая
заменяется
новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой
можно использовать ту или иную приближённую формулу интегрирования.
Последовательность занятия.
- Формула прямоугольников.
- Формула трапеций.
- Решение упражнений.
План занятия
- Повторение опорных знаний учащихся.
Повторить с учащимися: основные формулы интегрирования, сущность изученных
методов интегрирования, геометрический смысл определённого интеграла.
- Выполнение практической работы.
Решение многих технических задач сводится к вычислению определённых
интегралов, точное выражение которых сложно, требует длительных вычислений и не
всегда оправдано практически. Здесь бывает вполне достаточно их приближённого
значения.
Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение
которой неизвестно. В этом случае можно заменить данную линию более простой,
уравнение которой известно. Площадь полученной таким образом криволинейной
трапеции принимается за приближённое значение искомого интеграла.
Простейшим приближённым методом является метод прямоугольников. Геометрически
идея способа вычисления определённого интеграла по формуле прямоугольников
состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой
площадей прямоугольников, одна сторона которых равна
, а друга —
.
Если суммировать площади прямоугольников, которые показывают площадь
криволинейной трапеции с недостатком [Рисунок1], то получим формулу:
[Рисунок1]
то получим формулу:
Если с избытком
[Рисунок2],
то
Значения у0, у1,…, уn находят из
равенств ,
к
=
0, 1…,
n
.Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.
Итак, чтобы найти приближённое значение интеграла
, нужно:
- разделить отрезок интегрирования [a, b] на n равных частей
точками х0=а,
х1, х2,…, х
n
-1,
х
n
=
b
; - вычислить значения подынтегральной функции
в
точках деления, т.е. найтиу
0
=
f (x0),
у
1
=
f (x1),
у
2
=
f (x2),
у
n
-1
=
f (xn-1),
у
n
=
f (xn)
; - воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
Пример 1. Вычислить по формуле прямоугольников
. Найти
абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных
частей. Тогда а
=
0,
b =
3
,
х
k = a + k
х
х0 = 2 + 0
= 2
х1 = 2 + 1
= 2,5
х2 = 2 + 2
=3
х3 = 2 + 3
= 3
х4 = 2 + 4
= 4
х5 = 2 + 5
= 4,5
f (x0) = 22 = 4
f
(x
1
)
= 2
,5
2
=
6,25
f
(x
2
)
=
32
=
9
f
(x
3
)
=
3,52
=
12,25
f
(x
4
)
=
42
=
16
f
(x
5
)
=
4,52
=
20,25.
| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
По формуле (1):
Для того, чтобы вычислить относительную погрешность вычислений, надо найти
точное значение интеграла:
Вычисления проходили долго и мы получили довольно-таки грубое округление.
Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться
техническими возможностями компьютера.
Для нахождения определённого интеграла методом прямоугольников необходимо
ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в
диапазоне х
[2
;5
]
с заданным шагом
х = 0,1.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (2). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (2,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А32, до значения х=5). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2 и с клавиатуры ввести формулу =А2^2 (при английской
раскладке клавиатуры). Нажимаем клавишу Enter. В ячейке В2 появляется
4. Теперь необходимо скопировать функцию из ячейки В2.
Автозаполнением копируем эту формулу в диапазон В2:В32.
В результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В33 может быть найдено приближённое значение интеграла.
Для этого в ячейку В33 вводим формулу = 0,1*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции (f(x)).
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция — функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В31. Нажимаем кнопку ОК. В
ячейке В33 появляется приближённое значение искомого интеграла с недостатком
(37,955) .
Сравнивая полученное приближённое значение с истинным значением интеграла (39),
можно видеть, что ошибка приближения метода прямоугольников в данном случае
равна
=
|39 — 37
,
955| = 1
,045
Пример 2. Используя метод прямоугольников, вычислить
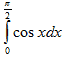
заданным шагом х =
0,05.
Решение:
- Для нахождения определённого интеграла значения подынтегральной функции
f(x) должны быть введены в рабочую таблицу Excel в диапазоне
с
заданным шагомх
= 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница
интегрирования (0). В ячейку А3 вводится второе значение аргумента –
левая граница диапазона плюс шаг построения (0,05). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=1,55). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2. Здесь должно оказаться значение косинуса, соответствующее
значению аргумента в ячейке А2. Для получения значения косинуса
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку
Вставка функции (
f
х
)
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция — функцию COS.
Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя
указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле
вправо, чтобы открыть столбец данных (А). Указываем значение
аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В
ячейке В2 появляется 1. Теперь необходимо скопировать функцию из
ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В
результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла.
Для этого в ячейку В34 вводим формулу = 0,05*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции(
(
f
х
))
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция — функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В32. Нажимаем кнопку ОК. В
ячейке В34 появляется приближённое значение искомого интеграла с избытком (1,024056).
Сравнивая полученное приближённое значение с истинным значением интеграла
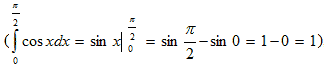
видеть, что ошибка приближения метода прямоугольников в данном случае равна
Метод трапеций обычно даёт более точное значение интеграла, чем метод
прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций
и приближённое значение определённого интеграла находится как сумма площадей
трапеций
[Рисунок3]
Пример 3. Методом трапеций найти
с шагом
х = 0,1.
Решение.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (0). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (0,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=3,1). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение (в примере синуса). Для этого табличный курсор
необходимо установить в ячейку В2. Здесь должно оказаться значение синуса,
соответствующее значению аргумента в ячейке А2. Для получения значения
синуса воспользуемся специальной функцией: нажимаем на панели инструментов
кнопку Вставка функции f(x). В появившемся диалоговом окне
Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические.
Справа в поле Функция — функцию SIN. Нажимаем кнопку ОК.
Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле
окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец
данных (А). Указываем значение аргумента синуса щелчком мыши на
ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту
формулу в диапазон В2:В33. В результате должна быть получена таблица данных
для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла
по методу трапеций. Для этого в ячейку В34 вводим формулу =
0,1*((В2+В33)/2+, затем вызываем Мастер функций (нажатием на панели
инструментов кнопки Вставка функции (f(x)). В появившемся
диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем
Математические. Справа в поле Функция — функцию Сумм. Нажимаем кнопку ОК.
Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон
суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке
В34 появляется приближённое значение искомого интеграла с недостатком (1,997)
.
Сравнивая полученное приближённое значение с истинным значением интеграла
можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.
- Решение упражнений.
- Вычислить
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить
разделив отрезок [0;4] на 40 равных частей. - Вычислить
разделив отрезок [0;8] на 40 равных частей. - Вычислить
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рассмотрим задачу, в которой требуется вычислить определённый интеграл $int^b_a f(x)dx$, при этом функция $f(x)$ является непрерывной на промежутке $left[a;bright]$. Обычно, если существует возможность, интегралы вычисляются через нахождение первообразной, но так как это не всегда возможно, прибегают к использованию приближённых методов.
К наиболее часто используемым приближённым методам относят:
- Метод прямоугольников;
- Метод трапеций;
- Метод Симпсона или иначе метод парабол.
В данной статье мы подробно расcмотрим метод прямоугольников.
Сущность метода прямоугольников
Рассмотрим нахождение определённого интеграла от функции $f(x)$ с точки зрения геометрии. Интеграл $int^b_a f(x)dx$ в данном случае есть не что иное, как площадь фигуры, ограниченной сверху графиком $f(x)$, по бокам прямыми $x=a$ и $x=b$, а снизу осью абсцисс.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽

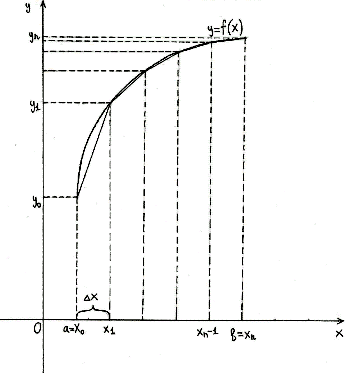
Рисунок 1. Метод средних прямоугольников
Для того чтобы найти площадь всей фигуры, можно воспользоваться определением интеграла и разбить всю фигуру на равные сегменты одной и той же длины. Точки на оси абсцисс, которые будут разбивать фигуру, обозначим как $x_i$. Нулевая точка при разбиении $x_0=a$, а конечная точка $x_n=b$. Для того чтобы вычислить длину одного сегмента, воспользуемся формулой:
$Δx_i=frac{b-a}{n}$
В методе средних прямоугольников каждый сегмент заменяется на прямоугольник, за высоту которого принимается ордината середины отрезка. Получается, что площадь одного такого прямоугольника равна $S_i= frac{b-a}{n} cdot f(ξ_i)$, а площадь всей фигуры будет равна:
«Метод прямоугольников» 👇
$int^b_a f(x)dx=frac{b-a}{n}cdot (f( ξ_0)+f( ξ_1)+…+f( ξ_{n-1})$, где $x_i≤ ξ_i≤x_{i+1}$
Эта формула позволяет не вычислять напрямую площадь искомой фигуры, ограниченной кривой линией, а заменить её приблизительной площадью ступенчатой фигуры, состоящей из прямоугольников.
При использовании метода средних прямоугольников так как $ξ_i=frac{x_i+x_{i+1}}{2}=x_{i+frac{1}{2}}$, тогда $f( ξ_i)=f(x_{i+frac{1}{2}})$ обозначим как $y_{i+ frac{1}{2}}$,
и формула примет вид:
Определение 1
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_{frac{1}{2}} + y_{frac{3}{2}} + y_{n- frac{1}{2}}left(1right)$
Эта формула называется формулой средних прямоугольников.
Методы левых и правых прямоугольников
Данные методы отличаются от метода средних прямоугольников тем, что здесь в качестве ординаты для элементарного прямоугольника выбирается либо крайнее левое значение функции $f(x)$ (и тогда метод называется методом левых прямоугольников), либо крайнее правое, и тогда метод носит название метода правых прямоугольников.
Определение 2
Формула для применения метода левых прямоугольников выглядит так:
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_0 + y_1 + y_{n- 1})left(2right)$
Определение 3
Формула для метода правых прямоугольников:
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_1 + y_2 + y_n)left(3right)$
Формулы $(1), (2), (3)$ иначе также называются квадратурными составными формулами.
Погрешность метода прямоугольников
Для того чтобы оценить общую погрешность метода прямоугольников, необходимо рассмотреть каждый из элементарных сегментов кривой по отдельности. Общая погрешность в таком случае представляет собой сумму погрешностей всех погрешностей сегментов.
Итак, рассмотрим, чему равна погрешность на одном сегменте.
Площадь одного сегмента вычисляется по приближённой формуле:
$int^{x_i}_{x_{i-1}} f(x)dx≈f(x_{i-1}+frac{x_i-x_{i-1}}{2}) cdot (x_i-x_{i-1})left(4right)$
Погрешность будем определять по разнице со значением первообразной, вычисленной с помощью формулы Ньютона-Лейбница:
$δ_i= int^{x_i}_{x_{i-1}} f(x)dx — f(x_{i-1}+frac{x_{i}-x_{i-1}}{2}) cdot (x_i-x_{i-1})left(5right)$
Так как в левой части равенства $x_{i}-x_{i-1}$ есть не что иное как $int^x{i}_{x_{i-1}}dx$ — длина элементарного отрезка, его можно заменить на $dx$. Перепишем правую часть равенства $(4)$, используя это:
$f(x_{i-1}+frac{x_i-x_{i-1}}{2}) cdot (x_i-x_{i-1})=int^{x_i}_{x_{i-1}} f(x_{i-1}+ frac{x_{i}-x_{i-1}}{2})dx$
$δ_i=int^{x_i}_{x_{i-1}} f(x)dx — int^{x_i}_{x_{i-1}} f(x_{i-1}+ frac{x_{i}-x_{i-1}}{2})dx =int^{x_i}_{x_{i-1}}(f(x)-f(x_{i-1}+ frac{x_i-x_{i-1}}{2})dx left(6right)$
Допуская, что фунцкия $f(x)$ дважды дифференцируема в точке $x=x_{i}-x_{i-1}$ и вокруг неё, разложим её в бесконечную сумму степенных функций, используя ряды Тейлора и формулу Лагранжа:
$f(x)=f(x_{i-1}+frac{Δx}{2})+f’(x_{i-1}+frac{Δx}{2}) cdot (x-(x_{i-1}+frac{Δx}{2}))+f’’(ε_i) cdot frac{(x-(x_{i-1}+frac{Δx}{2}))^2}{2}$
Применим полученное для подстановки:
$f(x)-f(x_{i-1}+ frac{Δx}{2})=f’(x_{i-1}+frac{Δx}{2}) cdot(x-(x_{i-1} + frac{Δx}{2}))+f’’(ε_i) cdot frac{(x-(x_{i-1}+frac{Δx}{2}))^2}{2}left(7right)$
Проинтегрируем $(7)$:
$int^{x_{i}}_{x_{i-1}}(f(x)-f(x_{i-1}+ frac{Δx}{2})dx= int^{x_{i}}_{x_{i-1}}f’(x_{i-1}+frac{Δx}{2}) cdot(x-(x_{i-1}+frac{ Δx}{2}))dx+ int^{x_{i}}_{x_{i-1}} f’’(ε_i) cdot frac{x-(x_{i-1}+ frac{Δx}{2}))^2}{2}dx$
В конечном итоге для элементарного сегмента $left[x_{i-1};x_iright]$ имеем:
$δ_i=int^x{i}_{x_{i-1}} (f(x)-f(x_{i-1}+frac{Δx}{2}))=frac{f’’(ε_i) cdot h^3}{24}$ и наконец,
$|δ_i|≤max_{xin left[x_{i-1};x_iright]}|f’’(x)| cdot frac{h^3}{24}.$
Для всей же фигуры погрешность полученной площади составит:
$δ_i=sum^n_{i=1}int^{x_i}_{x_{i-1}}(f(x)-f(x_{i-1}+frac{Δx}{2}))dx$
и в конечном виде:
Определение 4
$|δ_i|≤max_{xin left[a;bright]}|f’’(x)| cdot frac{(b-a)^3}{24n^2}$
Данная формула используется для получения погрешности при использовании формулы для средних прямоугольников.
Формула для погрешности методов правых и левых прямоугольников выводится аналогичным способом и имеет следующий вид:
Определение 5
$|δ_i|≤max_{xin left[a;bright]}|f’(x)| cdot frac{(b-a)^2}{2n}$
Погрешность, полученная с использованием метода правых или левых прямоугольников для вычисления интегралов больше, чем погрешность при использовании метода средних прямоугольников. Поэтому более предпочтительным для приближённого интегрирования является именно метод средних прямоугольников.
Пример 1
Вычислить интеграл $int_1^2 frac{dx}{x}=ln2$ с точностью до $0, 001$ используя формулу средних прямоугольников.
Разобьём нашу функцию на 10 равных сегментов.
В начале оценим погрешность вычисления:
$|δ_n|≤max_{xin left[a;bright]}|(frac{1}{x})’| cdot frac{(2-1)^3}{24 cdot 10^2}$
В данном случае погрешность меньше либо равна:
$|δ_n|≤0.000042$, следовательно, в данном случае для разбиения можно использовать 10 сегментов.
Разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=frac{2-1}{10}=0,1$ и вычислим значение подынтегральной функции $y(x)=frac{1}{x}$ в середине каждого отрезка:
$x_frac{1}{2}=1,05; y_frac{1}{2}=0,9524;$
$x_frac{3}{2}=1,15; y_frac{3}{2}=0,8696;$
$x_frac{5}{2}=1,25; y_frac{5}{2}=0,8;$
$x_frac{7}{2}=1,35; y_frac{7}{2}=0,7407;$
$x_frac{9}{2}=1,45; y_frac{9}{2}=0,6897;$
$x_frac{11}{2}=1,55; y_frac{11}{2}=0,6452;$
$x_frac{13}{2}=1,65; y_frac{13}{2}=0,6061;$
$x_frac{15}{2}=1,75; y_frac{15}{2}=0,5714;$
$x_frac{17}{2}=1,85; y_frac{17}{2}=0,5405;$
$x_frac{19}{2}=1,95; y_frac{19}{2}=0,5128;$
Сумма всех вычисленных значений функции $f(x)$ составит $6.9284$, а само значение составит:
$int_1^2 frac{dx}{x}=frac{6,9284}{10}=0.69284$ — что отвечает требуемому условию о погрешности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме