Как найти опред интеграл - Autoru.top - решение различных проблем

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие «интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

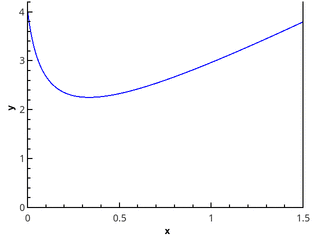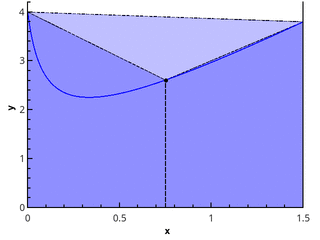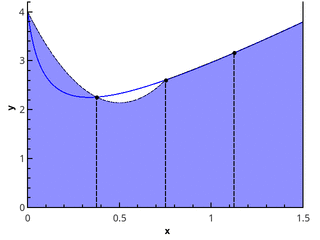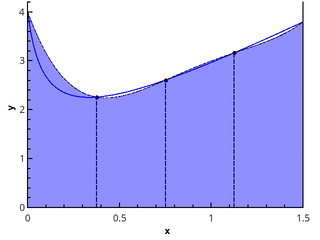
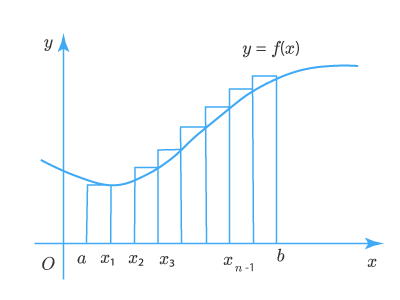
В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

«Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Производная от интеграла равна подынтегральной функции:

Константу можно выносить из-под знака интеграла:

Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

Линейность:

Знак интеграла изменяется, если поменять местами пределы интегрирования:

При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Содержание:

Определённый интеграл
Геометрическое содержание определённого интеграла
Основные свойства определённого интеграла
Непосредственное вычисление определённого интеграла
Вычисление определённого интеграла методом подстановки
Вычисления определённого интеграла частями
Приближённые методы вычисления определённых интегралов
Практическое применение определённого интеграла
Вычисление площадей плоских фигур
Объём тела вращения
Путь, пройденный точкой
Сила давления жидкости
Несобственные интегралы
История определенного интеграла
Определенный интеграл в математике
Геометрический смысл интеграла
Понятие определенного интеграла
Задачи, приводящие к понятию определенного интеграла
Задача о нахождении площади криволинейной трапеции
Задача об определении пройденного пути материальной точки
Задача о нахождении объема продукции
Основные свойства определенного интеграла
Связь между определенным и неопределенным интегралами
Формула Ньютона-Лейбница
Методы вычисления определенного интеграла
Непосредственное определенное интегрирование
Вычисление интеграла методом подстановки
Интегрирования по частям в определенном интеграле
Длина дуги плоской кривой
Вычисление площади геометрической фигуры
Вычисление объемов тел по известным площадям поперечных сечений
Вычисление объема тела вращения
Приближенное вычисление определенных интегралов
Формула прямоугольников
Формула трапеций
Формула Симпсона

Определённый интеграл

Определенный интеграл – это число, а именно величина площади криволинейной трапеции. Неопределенный интеграл – это функция (точнее, семейство функций), которая является первообразной для интегрируемой функции.

Понятие определённого интеграла:

Пусть функция f(х) определена на промежутке Считаем для удобства, что функция f(х) на указанном промежутке неотъемлемая и Разобьём этот отрезок на n частей точками На каждом из отрезков возьмём произвольную точку и вычислим сумму:

где Эта сумма называется интегральной суммой функции f(х) на отрезке

Геометрически (рис. 1) каждое слагаемое интегральной суммы равно площади прямоугольника с основанием и высотой , а вся сумма равна площади фигуры, которую получили соединением всех указанных выше прямоугольников.

Очевидно, при всех возможных разбиениях отрезка на части получим разные интегральные суммы, а значит и разные ступенчатые фигуры.

Будем увеличивать число точек разбиения так, чтобы длина наибольшего отрезка стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, независимым ни от способа, которым выбираются точки деления ни от того, как выбираются промежуточные точки

Это предел и называют определённым интегралом для функции f(х) на отрезке

Определённым интегралом для функции f(х) на отрезке называется предел, к которому стремится интегральная сумма при стремлении к нулю длины большего частичного промежутка. Он обозначается и читается «интеграл от до b от функции f(х) по dx», или сокращённо «интеграл от до b от f(х)dx».

По определению

Число называется нижней границей интегрирования; число b — верхней границей; отрезок — отрезком интегрирования.

Отметим, что любая непрерывная на промежутке функция f(х) имеет определённый интеграл на этом отрезке.

Геометрическое содержание определённого интеграла

Если интегрированная на отрезке функция f(х) неотъемлемая, то определённый интеграл численно равен площади S криволинейной трапеции ABb (рис. 1).

Уточним, что криволинейную трапецией называют фигуру, ограниченную графиком непрерывной функции у=f(х), где , прямыми х=, х=b и осью ОХ.

Следовательно, геометрическое содержание определённого интеграла — это площадь криволинейной трапеции.

Рассмотрим криволинейную трапецию CHKD (см. рис. 2), в которой абсцисса точки С равна х, а точки . График функции у=f(х) пересекает ось OY в точке А. Тогда площадь криволинейной трапеции CHKD равна разности площади криволинейных трапеций OAKD и OAHC.

Поскольку площадь криволинейной трапеции ОАНС зависит от х, то её можно изобразить символом S(х). Аналогично, площадь криволинейной трапеции CHKD является функцией от и её можно обозначить . Поэтому площадь криволинейной трапеции CHKD равна разности и S(х) и обозначается символом

Построим два прямоугольника CHED и CMKD. Площадь первого равна Поскольку площадь криволинейной трапеции CHKD не меньшая площадь прямоугольника CHED и не большая площади прямоугольника CMKD, то можно записать неравенство:

Разделим обе части этого неравенства на и найдём пределы выражений при

Вспомним, что и учитывая непрерывность функции f(х),

получим:

отсюда

то есть производная площади криволинейной трапеции равна функции, которая задаёт верхнюю границу трапеции.

Таким образом, площадь криволинейной трапеции является одной из первичных функций, которая задаёт верхнюю границу трапеции, и может быть вычислена с помощью интегрирования.

Последнее равенство верно для всех х с промежутка . Подставим вместо х число . Получим . Но S()=0, ведь криволинейная трапеция преобразуется в отрезок, поэтому Таким образом,

При х=b получим выражение для вычисления площади криволинейной трапеции

Полученное выражение для вычисления S является приростом первичной F(х) на . Поскольку первичные отличаются только на постоянную, то очевидно, что все они будут иметь одинаковый прирост на промежутке . Отсюда выходит ещё одно определение определённого интеграла:

определённым интегралом называют прирост произвольной первичной при изменении аргумента от до b.

Данное определение записывают в виде формулы Ньютона-Лейбница:

где F(х) — первичная для функции f(х).

Основные свойства определённого интеграла

Все ниже приведённые свойства сформулированы в предположении, что данные функции интегрированы на определённых промежутках.

1. Определённый интеграл с одинаковыми границами интегрирования равен нулю:

2. При перестановке границ интегрирования определённый интеграл меняет знак на противоположный:

3. Отрезок интегрирования можно разбивать на части:

где

4. Постоянный множитель можно вынести за знак определённого интеграла:

5. Определённый интеграл от алгебраической суммы конечного числа функции равен алгебраической сумме определённых интегралов от функции, сто доказываются:

Доказательство свойств базируется на формуле ньютона-Лейбница. Как пример, докажем свойство 3:

что и требовалось доказать.

Данное свойство легко иллюстрировать графически (рис. 3).

или

На рис. 3 легко увидеть справедливость утверждения теоремы о среднем.

Теорема. Если функция f(х) непрерывна на промежутке , то существует точка с которая принадлежит данному промежутку, такая, что

То есть, площадь криволинейной трапеции равна площади прямоугольника со сторонами f(с) и (b — ).

Непосредственное вычисление определённого интеграла

Для вычисления определённого интеграла при условии существования первичной пользоваться формулой Ньютона-Лейбница:

По этой формуле виден порядок вычисления определённого интеграла:

1) найти неопределённый интеграл от данной функции;

2) в полученную первичную подставить на место аргумента сначала в верхнюю, а потом нижнюю границу интеграла;

3) найти прирост первично, то есть вычислить интеграл.

Пример 1: Вычислить интеграл:

Решение: Использовав указанные правила, вычислим данный определённый интеграл:

Ответ:

Пример: Вычислить интеграл:

Решение: Используем определение степени с дробным отрицательным показателем и вычислить определённый интеграл:

Ответ:

Пример 3: Вычислить интеграл:

Решение: Интеграл от разности функций заменим разностью интегралов от каждой функции.

Ответ:

Пример 4: Вычислить интеграл:

Решение: Используем определения степени с дробным показателем, правило деления суммы на число и вычислить определённый интеграл от суммы:

Ответ:

Вычисление определённого интеграла методом подстановки

Вычисление определённого интеграла методом подстановки выполняется в такой последовательности:

1) ввести новую переменную;

2) найти дифференциал новой переменной;

3) найти новые границы определённого интеграла;

4) всё подынтегральное выражение выразить через новую переменную;

5) вычислить полученный интеграл.

Пример 5. Вычислить интеграл:

Решение: Сделаем замену тогда

Вычислим границы интегрирования для переменной t.

При х=0 получаем t_н=8-0=8, при х=7 получим t_b=8-7=1.

Выразим подынтегральное выражение через t и dt и перейдём к новым границам, получим:

Пример 6. Вычислить интеграл:

Решение: Будем считать, что х³+2=t, тогда . Определим границу интегрирования для переменной t. При х=1, получим при х=2 получим

Выразим подынтегральное выражение через t и dt, затем перейдём к новым пределам, получим:

Ответ:

Пример 7. Вычислить интеграл:

Решение: Пусть тогда

Вычислим границы интегрирования для переменной t:

Выразим подынтегральное выражение через t и dt, и перейдём к новым пределам, получим:

Ответ:

Пример 8. Вычислить интеграл:

Решение: Сначала преобразуем подынтегральное выражение:

Вычислим интеграл от разности функций, заменив его разностью определённых интегралов от каждой функции:

Ответ:

Вычисления определённого интеграла частями

Если функции и их производные непрерывны на промежутке , то формула интегрирования для определённого интеграла имеет вид:

Пример 9. Вычислить интеграл:

Решение:

Ответ:

Пример 10. Вычислить интеграл:

Решение:

Ответ:

Приближённые методы вычисления определённых интегралов

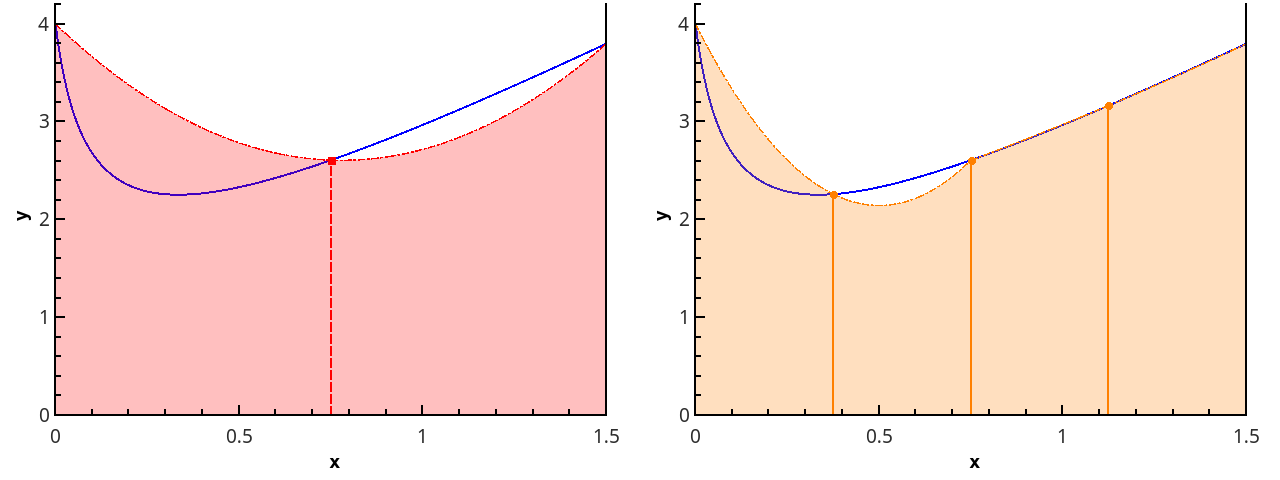
В тех случаях, когда вычислить определённый интеграл по формуле Ньютона-Лейбница невозможно или сложно, используют методы приближённого интегрирования. Все они основываются на простых геометрических построениях. Очевидно, что при достаточно малом отрезке площадь S криволинейной трапеции приближённо равна площади прямоугольника («левого» прямоугольника рис. 4а, и «правого» прямоугольника рис. 4б), трапеции (рис. 5) или параболы (рис. 6).

Запишем следующие приближённые равенства:

Чтобы добиться большей точности при нахождении площади S, промежуток от разбивают на n равных частей (рис. 7) (при приближении параболами промежуток разбивают на 2n частей).

Если для каждой из маленьких дуг использовать предыдущие приближения, то для всей площади S получим приближённое значение представленное в виде суммы площадей криволинейных трапеций:

Первые две формулы носят названия формул «левых» и «правых» прямоугольников соответственно, третья — формулы трапеции, а последняя — формулы Симпсона.

Пример 11. Вычислить по формулам прямоугольников и трапеций при n=10.

Решение: Разделим отрезок [0; 1] на (n=10) заданное количество частей. Тогда составим таблицу значений подынтегральной функции в точках разбиения.

По формуле «левых» прямоугольников имеем:

По формуле «правых» прямоугольников имеем:

По формуле трапеции получим:

Для достижения большей точности число разбиений отрезка необходимо увеличить, например взять n=20.

Практическое применение определённого интеграла

С помощью определённого интеграла можно решать задачи физики, механики и т. д., которые тяжело или невозможно решить методами элементарной математики. Так, понятия определённого интервала используют при решении задач на вычисление площади фигур, работы переменной силы, давления на вертикальную поверхность, пути, пройденного телом и ряда других. Рассмотрим некоторые из них.

Вычисление площадей плоских фигур

Если фигура Ф является криволинейной трапецией, то её площадь S_ф согласно геометрическому содержанию определённого интеграла равна:

Если фигура Ф не является криволинейной трапецией, то вычисления её площади сводится к одному из следующих случаев:

а) кривая у=f(х)<0 на ,

в этом случаи площадь можно вычислить по формуле:

б) если f(х)=

в этом случаи для нахождения площади фигуры находят точку с, как абсциссу точки перегиба графиков функций а площадь вычисляют по формуле:

в) если фигура ограничена двумя кривыми у=f₁(х) и у=f₂(х), (),

в этом случаи площадь S_ф находят по формуле:

Пример 12. Вычислить площадь фигуры, ограниченную гиперболой ху=1, осью ОХ и прямыми х=1; х=е (рис. 11).

Решение: Использовав формулу вычисления площади криволинейной трапеции, получаем:

Ответ: S=1 кв. ед.

Пример 13. Вычислить площадь фигуры ограниченной линиями у=х² и у²=х (рис. 12).

Решение: найдём пределы интегрирования, то есть абсциссы точек перегиба графиков функций у=х² и у²=х. Для этого решим систему:

Вычисление площади фигуры сводится к случаю в) поэтому

Ответ: S_ф = 1/3 кв. ед.

Пример 14. Вычислить площадь фигуры ограниченной параболами у=4-х²; у=х²-2х (рис. 13).

Решение: Найдём границы интегрирования, то есть абсциссы точек перегиба графиков функций у=4-х²и у=х²-2х. Для этого решим систему:

Искомую площадь вычисляем по формуле

Ответ: S=9 кв. ед.

Объём тела вращения

Объём тела, образованного вращением вокруг оси ОХ криволинейной трапеции , ограниченной непрерывной кривой у=f(х), (где ), отрезком оси ОХ и отрезками прямых и (рис. 14), вычисляется по формуле:

Пример 15. Вычислить объём шара радиусом R (рис. 15).

Решение: Шар образован вращением вокруг оси ОХ круга, ограниченного кругом х²+у²=R² с центром в начале координат и радиусом R.

Учитывая симметрию круга относительно оси ординат, сначала найдём половину искомого объёма:

Ответ: (куб. ед.).

Путь, пройденный точкой

Если точка движется прямолинейно и её скорость является известной функцией времени, то путь, который прошла точка за промежуток времени , вычисляется по формуле:

Пример 16. Тело движется прямолинейно со скоростью Найти путь, пройденный телом за 10 с.

Решение: Используя формулу находим:

Ответ: S = 250 (м).

Пример 17. Скорость тела, которое движется прямолинейно равна Вычислить путь, который прошло тело от начала движения до остановки.

Решение: В момент остановки скорость тела равна нулю, то есть

Следовательно, тело остановится через 4 с.

Путь, который прошло тело за это время, вычисляем по формуле:

Ответ:

Работа силы.

Если переменная силы F=F(x) действует в направлении оси ОХ, то работа силы на отрезке вычисляется по формуле:

Пример 18. Вычислить работу силы, которая необходима при сжимании пружины на 0,08 м., если для сжимания её на 1 см., необходима сила 10Н.

Решение: Согласно закона Гука, сила F, которая растягивает или сжимает пружину на х метров, равна F=kх, где k — коэффициент пропорциональности.

Следовательно, 10=k*0.01, то есть k=1000, отсюда F=kx=1000x.

Искомую работу находим по формуле:

Ответ: А= 3,2 (Дж).

Пример 19. Сила 196,2Н растягивает пружины на 18 см. Какую работу она выполняет?

Решение: Согласно закона Гука F=kx, отсюда F = 1090х. Находим искомую работу:

Ответ: А=17,7 (Дж).

Пример 20. Для сжатия пружины на 3 см. необходимо выполнить работу в 16 Дж. На какую длину можно сжать пружину, выполнив работу в 144 Дж.?

Решение: Согласно закона Гука, F=kx; тогда

Ответ: Пружину можно сжать на 9 см.

Сила давления жидкости

Сила давления Р жидкости плотностью р на вертикальную пластину, погружённую в жидкость, вычисляется по формуле:

Где ускорение свободного падения, S — площадь пластинки, а глубина погружения пластинки меняется от a до b.

Пример 21. Вычислить силу давления воды на одну из стенок аквариума, длиною 30 см. и высотою 20 см.

Решение: Стенка аквариума имеет форму прямоугольника, поэтому S=0,3х, где . Плотность воды равна 1000 кг/м³. Тогда сила давления воды на стенку аквариума, вычисляется по формуле:

Ответ: Р=58,86 (Н).

Пример 22. Вычислить силу давления бензина на стенки цилиндрического бака высотой 3 м. и радиусом 1 м.

Решение: Площадь поверхности стенки цилиндрического бака , где . Плотность бензина — 800 кг/м³. Тогда сила давления бензина на стенки бака будет:

Ответ: Р= 2,2*10⁵ (Н).

Пример 23. Вычислить давление воды на погружённую в неё вертикальную треугольную пластину, с основанием 6 м. и высотой 2 м., считая, что вершина треугольника лежит на поверхности воды, а основание параллельно ей (рис. 16).

Решение: Пусть NM — ширина пластины на уровне BE=х. Из схожих треугольников ABC и MBN, находим

Использовав формулу получаем:

Ответ: Р = 78480 (Н).

Несобственные интегралы

Интегралы с бесконечными границами интегрирования или от функций, которые имеют бесконечный разрыв называют несобственными.

Несобственные интегралы с бесконечными границами интегрирования определяют следующим образом:

где с — произвольное действительное число.

Несобственные интегралы от функций с бесконечными разрывами также вычисляют через предельный переход.

Если функция разрывная на одном конце отрезка интегрирования, например, в точке х=b, то

если же функция f(х) имеет безграничный разрыв в точке х=с, где и непрерывна во всех других точках этого промежутка, то

Если приведённые выше пределы существуют для конкретного интеграла, то его называют сходящимся, если же предела не существует — расходящимся.

Поскольку вычисление пределов — трудоёмкая работа, то иногда для вычисления схожести несобственного интеграла можно воспользоваться признаком схожести:

Признак схожести: Пусть Тогда, если сходящийся, то и будет сходящимся.

Геометрически, в прямоугольной системе координат, несобственный интеграл — это площадь криволинейной трапеции с бесконечной основой либо «незакрытой» сверху.

Пример 1: Вычислить интеграл

Решение: Это несобственный интеграл с верхней границей равной . Согласно определения

Следовательно, интеграл сходящийся.

Пример 2: Вычислить интеграл

Решение: Это несобственный интеграл, так как функция неопределённая в точке х=0 и . Согласно определениям

Вычислим частями:

Ответ:

История определенного интеграла

Интегральный расчет получен в результате определения площади и объема. Эмпирически обнаруженные правила измерения площади и объема некоторых простейших фигур были известны древним восточным ученым. Уже в 2000 году до нашей эры. Египтяне и вавилоняне, в частности, знали правила расчета площади круга и расчета объема усеченной пирамиды на основе квадрата. Древнегреческая наука значительно продвинула расчет площади и объема различных фигур. Особенно значительный вклад внес Архимед. Архимед обнаружил множество человеческих территорий и значительное количество объемов тела, основываясь на идее, что плоская фигура состоит из бесчисленных прямых линий, а геометрическое тело состоит из бесчисленных параллельных плоских частей.

Архимед (287-212 до н.э.) — древнегреческий математик, физик, астроном и изобретатель. Родился в Сиракуз (Сицилия) и жил во времена Первой и Второй Поенских войн. Архимед является автором многих технических изобретений. Ирригационные машины с нулевой точкой, подъемные механизмы (винты Архимеда), рычажные системы, блоки для подъема тяжелых предметов, военные метательные машины. Его метательная машина заставила римлян отказаться от попыток совершить набег на город и заставить их пойти на осаду.

Математические исследования Архимеда намного опередили свое время и были правильно оценены только в эпоху исчисления. Архимед вычислил площадь эллипса, параболы и осколков из сегментов и нашел площадь поверхности и шара, сегмент шара и сферы, а также объем различных вращающихся тел и их сегментов. Он также относится к понятию центра тяжести тела, находит положение центра тяжести различных людей и тел и дает математический вывод закона биений. Архимед, как сообщается, находит решение проблемы определения количества золота и серебра в короне жертвоприношения короля Сиракузы Иерона во время омовения и крика «Эврика!» Его величайшим достижением в астрономии было создание планетария — полой вращающейся сферы, которая могла наблюдать Солнце и пять планет, фазы Луны, а также движение Солнца и лунное затмение.

Архимед был убит римским солдатом во время захвата Сиракузы. Согласно легенде, он сталкивался со словами «Не трогай мою фотографию». На могиле Архимеда был установлен памятник с изображением шара и цилиндра вокруг него. Надпись показала, что эти объемы тела i, i называются двумя.

Систематическое развитие подобные представления получили значительно позже — лишь в веке.

Теорема Архимеда о том, что площадь круга равна площади треугольника с основанием, равным окружности, и высотой, равной радиусу, I. Площадь круга состоит из бесконечного числа треугольников, которые в совокупности равны одинаковой высоте, радиусу и треугольнику, основание которого равно сумме всех оснований, окружности.

Кеплер (Kepler) Йохан (1571-1630) — немецкий астроном и математик. Родился в Вайль-дер-Штадт (Вюртемберг, Германия). Обрабатывая наблюдения датского астронома Г. Врага, он установил три закона движения планет. Он изложил теорию солнечных и лунных затмений, их причины и методы прогнозирования. Изобрел самый легкий телескоп. Это до сих пор называют его именем. Он нашел 92 вращающихся тела как оригинальный метод интеграции.

Используя такие рассуждения, Кеплер нашел объем многих новых революционных тел. Закон Кеплера, известный в астрономии, также был фактически получен с использованием приближенного интегрирования.

Удивительно остроумный трюк Архимеда. Но Кеплер и другие ученые не были строгими, и, самое главное, в принципе, они обладали свойством геометрического преобразования.

Кавальер и, Торричелли, Ферма, Паскаль и другие ученые века еще больше приблизились к современным представлениям об интеграле. Барроу установил связь между задачей о разыскании площади и задачей о разыскании касательной. А И. Ньютон и Г. Лейбниц независимо друг от друга в 70-х годах века отделили эту связь от упомянутых частных геометрических задач и создали алгоритмы дифференциального и интегрального исчислений.

И. Ньютон открыл взаимность операций дифференциации и интеграции. Он отметил, что все задачи нового анализа сводятся к двум взаимно противоположным задачам, которые можно сформулировать с точки зрения механики: 1) Использование известного пути к скорости в определенный момент 2) определите путь, пройденный в конкретное время по известной скорости движения. В данном случае «время» понималось просто как общее обсуждение всех переменных. Он также вводит понятие дифференциации. И. Ньютон намечает программу построения анализа на основе учения о пределе, не давая впрочем формального определения этого понятия, получившего глубокое развитие в математике века.

Г. Лейбниц использует нотацию для выражения определенных различных способов вычисления площадей и получения касательных в единую систему взаимосвязанных аналитических концепций и для бесконечного отслеживания действий определенных алгоритмов. Это может быть выполнено. Кроме того, различие в основном понималось как небольшая разница между двумя смежными значениями величины (поэтому символ -первая буква латинского слова (дифференция) — разница и отношение производной к производной) кривой считалась многоугольником с бесконечно большой бесконечно малой стороной, касательной в виде прямой линии, следующей за одной из таких сторон. Г. Лейбниц ввел понятие интегрирования как сумму бесконечного числа производных. Следовательно, Г. Основной концепцией анализа Лейбница была дифференциация как дифференциал и интеграция как сумма.

Дальнейшее развитие методы интегрирования получили в и веках. В веке в работах Л. Эйлера были найдены практически все известные в настоящее время приемы интегрирования в элементарных функциях. В веке О. Коши он аналитически доказал существование интегралов от непрерывных функций, реконструированных производных и интегральных вычислений и построил концепцию пределов функций в качестве основы для них.

Дальнейшее обобщение концепции интеграции связано с немецким ученым Б. Риманом и французским ученым А. Лебегом.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Определенный интеграл в математике

Пусть на отрезке задана функция Проделаем следующие 5 операций над отрезком и функцией

1. Раздробим отрезок на частей при помощи точек где

Для единообразия обозначений положим еще Наибольшую из разностей где мы обозначим через . Эта величина, характеризующая, насколько мелко раздроблен отрезок

называется рангом произведенного дробления.

2. На каждом отрезке выберем по точке и вычислим значение нашей функции в этой точке.

3. Умножим на длину отрезка

4. Сложим все полученные произведения, т. е. составим сумму

Эта сумма носит название интегральной суммы или суммы Римана (по имени немецкого математика 19-го века, изучавшего такие суммы).

5. Будем измельчать произведенное дробление, заставляя стремиться к нулю. Во многих случаях при этом измельчении сумма Римана будет стремиться к некоторому конечному пределу не зависящему ни от способа, каким выбираются точки деления ни от того, как выбираются промежуточные точки

Этот предел

и называется определенным интегралом от функции по промежутку Он обозначается символом

Числа называются соответственно нижним и верхним пределами интегрирования, а отрезок — промежутком интегрирования. Таким образом Определенный интеграл есть конечный предел суммы Римана при стремлении к нулю ранга дробления, порождающего эту сумму

Так как определенный интеграл есть предел некоторой переменной величины, а вовсе не всякая переменная имеет предел, то не у всякой функции существует определенный интеграл. Однако справедлива важная

Теорема. Если функция непрерывна на отрезке то интеграл

существует.

Эту теорему мы примем без доказательства. В дальнейшем будут рассматриваться, главным образом, функции непрерывные, хотя справедлива и более общая

Теорема. Интеграл существует, если кусочно непрерывна.

Понятие .кусочно непрерывной* функции легко разъяснить на простом примере. Пусть функция задана и непрерывна на а функция на Тогда функция совпадающая с при и при (чему равно безразлично), как бы состоит из двух непрерывных кусков (рис. 199). Такая функция и называется .кусочно непрерывной*. Она может состоять и из нескольких непрерывных кусков. Все же, если не будет оговорено противное, подынтегральные функции будут предполагаться непрерывными.

Возможно вам будут полезны данные страницы:

Геометрический смысл интеграла

Пусть — положительная непрерывная функция, заданная на отрезке

Заметим, что дробление, т. е. набор точек деления не полностью определяет сумму Для задания нужно указать еще промежуточные

точки

Рассмотрим (рис. 200) фигуру, ограниченную снизу осью сверху линией (т. е. графиком нашей функции), а с боков прямыми Если бы линия

была прямой, то наша фигура представила бы собой обыкновенную трапецию. В общем же случае эта фигура называется криволинейной трапецией.

Найдем площадь этой криволинейной трапеции. Для этого разложим отрезок на малых отрезков точками

Если через точки деления провести прямые то они разрежут нашу криволинейную трапецию (рис. 201) на узких полосок. Каждую из этих полосок можно приближенно принять за прямоугольник. В самом деле, если бы функция в пределах отрезка была постоянной, то полоска, имеющая своим основанием этот отрезок, и в самом деле была бы прямоугольником. В действительности не будет постоянной на но благодаря своей

непрерывности эта функция не успевает заметно измениться на если только этот отрезок весьма мал. Иными словами, почти постоянна на отрезках когда эти отрезки малы, а это и значит, что упомянутые полоски почти являются прямоугольниками (один такой прямоугольник заштрихован на рис. 201). Принимая за значение на всем ее значение в какой-нибудь точке этого отрезка (выбор этой точки безразличен, поскольку речь все равно идет о приближенном подсчете, а все точки отрезка равноправны), получаем, что высотой прямоугольника, за который мы принимаем нашу полоску, будет

Поскольку длина основания этого прямоугольника, очевидно, равна то площадь одной полоски приближенно равна произведению Отсюда для интересующей нас площади всей криволинейной трапеции получается приближенное равенство

Из самого вывода ясно, что точность этого равенства тем выше, чем меньше отрезки т. е. чем меньше ранг дробления Но тогда точное значение площади будет пределом написанной суммы при

Поскольку, однако, сумма (8) является суммой Римана, то по самому

определению ее пределом при

служит интеграл

Таким образом мы приходим к формуле

Читая ее справа налево, выясняем

Геометрический смысл интеграла.

Если

непрерывна и положительна на то интеграл равен площади криволинейной трапеции, ограниченной линиями

Интеграция может быть использована для поиска областей, объемов, центральных точек и многих полезных вещей. Но это часто используется, чтобы найти область под графиком функции

Примеры с решением

Пример 1:

Найти

Решение:

Фигура, ограниченная линиями (рис. 202), есть обыкновенная трапеция. Ее площадь равна полусумме оснований, умноженной на высоту:

откуда

Пример 2:

Найти

Решение:

Линия есть расположенная выше половина окружности Та часть линии, которая получается при изменении лежит в 1-м координатном угле. Отсюда ясно, что фигура, ограниченная линиями является (рис. 203) четвертью круга с центром в начале координат и радиусом Площадь этой фигуры равна откуда

Сейчас мы еще не научились вычислять определенные интегралы, я в этих примерах нам пришлось прибегнуть к помощи геометрии. В дальнейшем, наоборот, с помощью интегрального исчисления мы сможем вычислять площади различных криволинейных фигур *).

Два простейших свойства интеграла. Когда мы занимались неопределенными интегралами, то отмечали, что

Таким образом, в записи подынтегральной функции и в записи результата интегрирования независимая переменная обозначалась одной и той же буквой. Стало быть, обозначение этой независимой переменной, которую называют переменной интегрирования, оказывалось существенным .

Это становится ясным, если мы вспомним хотя бы, как вычисляетсяинтеграл Ведь его надо записать сначала в виде а затем в виде Значит, Таким образом, нам совсем не безразлично, написать ли (что верно) или (что уже неверно!).

I. Обозначение переменной интегрирования в определенном интеграле никакой роли не играет

Читатель сразу поймет это, если задаст себе вопрос: который из двух интегралов

Больше? Ясно, что они одинаковы! Более отчетливо мы разберемся в этом, если заметим, что для вычисления любого из интегралов мы должны разбить отрезок [3, 5] на мелкие части, в каждой части выбрать по точке и вычислить в ней значение подынтегральной функции (а она в обоих интегралах одна и та же: удвоенный куб аргумента, сложенный с самим аргументом) и т. д. Иными словами все вычисления в обоих случаях будут тождественными. Также обстоит дело и в более общем случае интегралов чем и доказано формулированное свойство чем и доказано формулированное свойство I определенного интеграла.

Переходя к другому важному его свойству, заметим, что в выражении

мы предполагали Что же следует понимать под символом

На этот вопрос легко ответить, если вспомнить геометрический смысл интеграла. В нашем случае боковые стороны криволинейной трапеции сливаются в одну прямую и трапеция вырождается в прямолинейный отрезок (рис. 204). Площадь этого отрезка равна нулю, а потому и

т.е.

Определенный интеграл с совпадающими пределами интегрирования равен нулю.

Например,

Понятие определенного интеграла

Рассмотрим непрерывную функцию не принимающую отрицательных значений, так что график ее целиком лежит выше оси в некоторых точках. Пусть такие числа, что функция определена при Кривая и прямые ограничивают некоторую область плоскости, называемую областью под кривой от

или криволинейной трапецией.

Если требуется вычислить площадь криволинейной трапеции, то можно, например, покрыть плоскость сетью мелких квадратов и сосчитать число квадратов, лежащих внутри нашей области (рис. 12.1). Это не дает еще всей площади, поскольку некоторые из квадратов лежат частично внутри, а частично вне рассматриваемой области. Но если сделать сеть достаточно густой. то можно вычислить с любой степенью точности.

Можно вычислить площадь криволинейной трапеции и с помощью тонких прямоугольников. Лейбниц считал, что криволинейная трапеция составлена из бесконечно тонких прямоугольников (рис. 12.2). Каждый такой прямоугольник поднимается над точкой интервала он имеет высоту и бесконечно

Малую ширину площадь ого равна, следовательно, Общая же площадь есть сумма всех таких площадей.

Напомним, Лейбниц писал Символ означал у него сумму. Этот символ происходит от удлинения буквы

(первой буква слова Summa). Погаже ученик Лейбница Иоган Вернул-ли предложил отличат!» «целостную сумму бесконечно малых» от обычной суммы и предложил знак именовать интегралом от латинского слова integrals (целостный). Фурье усовершенствовал обозначение Лейбница, предложив явно указывать начальное и конечное значения

Рассуждения математиков XIX века носили нестрогий характер. Термин бесконечно малая величина не был достаточно строго определен, что приводило к противоречиям. Строгое определение основано на понятии предела и интегральной суммы. Оно вобрало в себя качественный смысл определения Лейбница и устранило нечеткость формулировок.

Пусть функция неотрицательна на Разобьем отрезок на промежутков точками

На каждом отрезке разбиения выберем точку и положим

Тогда произведение равно площади прямоугольника ,-со сторонами

Сумма площадей всех таких прямоугольников равна сумме вида

Эта сумма представляет площадь ступенчатой фигуры. Чем уже ступеньки, тем ближе площадь ступенчатой фигуры к площади криволинейной трапеции (рис. 12.2). Естественно ожидать, что при неограниченном возрастании числа промежутков, так что наибольшая из их длин стремится к нулю, сумма стремится к площади криволинейной трапеции

Введем теперь точное определение. Пусть на отрезке задана функция (теперь уже не обязательно неотрицательная). Разобьем отрезок на промежутков точками

На каждом отрезке разбиения выберем точку и положим

Сумму вида

назовем интегральной суммой для функции Очевидно, что интегральная сумма зависит от способа разбиения отрезка точками так и от выбора точек на каждом из промежутков разбиения Обозначим через максимальную из длин отрезков где

Определение. Пусть предел интегральной суммы

при стремлении к нулю существует, конечен и не зависит от способа выбора точек Тогда этот предел называется определенным интегралом от функции на и обозначается

а сама функция называется интегрируемой на отрезке т.е.

Эта запись читается: «интеграл от а до бэ эф от икс дэ икс». При этом число называется нижним пределом, число его верхним пределом («пределы интегрирования» не имеют ничего общего с термином «предел функции»); функция подынтегральной функцией, выражение подынтегральным выражением, а задача о нахождение интегрированием функции на отрезке

Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия. Неопределенный интеграл представляет функцию (а точнее семейство функций), а определенный интеграл — это число.

Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования, т. е.

Верхний предел может быть больше или меньше нижнего

В первом случае

Во втором случае

Поэтому по определению полагают

Понятие определенного интеграла распространяют и на случай интеграл с равными пределами считается равным нулю:

Это соглашение оправдано тем, что интегральная сумма стремится к нулю при сближении

Очевидно, если функция интегрируема на отрезке то она и ограничена на этом отрезке. В самом деле, если не ограничена на отрезке то она не ограничена на некотором отрезке За счет выбора точки

интегральную сумму можно сделать сколь угодно большой, а такая интегральная сумма не имеет конечного предела, что противоречит определению, согласно которому предел интегральной суммы существует и конечен.

Покажем на примере функции Дирихле, что обратное утверждение неверно: существует ограниченная функция, не являющаяся интегрируемой. Напомним, что функция Дирихле равна единице в рациональных точках и нулю — в иррациональных. На любом отрезке эта функция ограничена, но не является интегрируемой на нем. Действительно, если в каждом отрезке выбрать рациональную точку то интегральная сумма

Если выбрать иррациональную точку то и

Таким образом, с одной стороны а, с другой стороны

Поэтому предел интегральных сумм не существует и функция Дирихле не является интегрируемой.

Отметим без доказательств, что справедливы следующие утверждения:

1. Если функция интегрируема на отрезке то она интегрируема на любом отрезке содержащимся в

2. Если функция непрерывна на отрезке то она интегрируема на этом отрезке.

3. Если функция имеет на отрезке конечное число точек разрыва первого рода, то она интегрируема на

Пример 3:

Вычислить

Решение. Запишем выражение для интегральной суммы, предполагая, что все отрезки разбиения имеют одинаковую длину равную где число отрезков разбиения, причем для каждого из отрезков , разбиения точка совпадает с правым концом этого отрезка, т.е где (В силу интегрируемости функции выбор такого «специального» способа разбиения отрезка интегрирования на части и точек , на отрезках разбиения не повлияет на искомый предел интегральной суммы.) Тогда

Известно, что сумма квадратов чисел натурального ряда равна

Следовательно,

Анализ приведенного примера показывает, что успешное решение поставленной задачи оказалось возможным благодаря тому, что интегральную сумму удалось привести к виду, удобному для нахождения предела. Однако такая возможность существует далеко не всегда, поэтому долгое время задача интегрирования конкретных функций оставалась задачей чрезвычайно сложной.

Пример 4:

Вычислить:

Решение:

а) Произвольная первообразная для функции имеет вид Для нахождения интеграла 3 по формуле Ньютона—Лейбница возьмем такую первообразную, у которой (см. замечание выше). Тогда

что совпадает, конечно, с результатом, полученным в примере 11.1.

б) Первообразную подынтегральной функции найдем, используя формулу (10.9). Применяя формулу Ньютона—Лейбница, получаем При нахождении интеграла из примера 11.26 было использовано свойство приращения первообразной

где- некоторое число.

Заметим,что введеное ранее определение (11.2) и его следствие (11.3) согласованы с формулой Ньютона-Лейбница. Действительно,

Таким образом, и при применении формулы Ньютона-Лейбница несущественно, какой из пределов интегрирования больше: верхний или нижний.

Пример 5:

Вычислить

Решение:

Положим Тогда

Если то

Следовательно

Рассмотрим теперь, как выполняется интегрирование по частям в определенном интеграле.

Задачи, приводящие к понятию определенного интеграла

Пусть неотъемлемая функция определена и непрерывна на отрезке где и — конечные числа.

Задача о нахождении площади криволинейной трапеции

Пусть плоская фигура ограничена графиком функции осью вертикальными прямыми (рис. 23.1). Эта геометрическая фигура называется криволинейной трапецией для функции на отрезке

Рис. 23.1

Необходимо определить ее площадь.
Для решения задачи выполним следующее:

1) разобьем отрезок произвольно образом на частей точками:

2) выберем на каждом из частичных отрезков произвольную точку

Длину частичного отрезка обозначим через

3) вычислим значение функции в точках и составим сумму произведений этих значений с длинами частичных отрезков:

Сумма называется интегральной суммой для функции на отрезке Геометрический смысл этой суммы очевиден — это сумма площадей прямоугольников с основами и высотами

4) найдем границу при условии, что и наибольшая (максимальная) длина частных отрезков стремится к нулю.

Если существует конечный предел интегральной суммы при условии, что при то ее принимают за числовое значение площади криволинейной трапеции для на

Задача об определении пройденного пути материальной точки

Задача об определении пройденного пути материальной точки за промежуток времени от до Пусть скорость прямолинейного движения материальной точки задана как функция времени Необходимо найти путь, который пройдет точка за промежуток времени от до

Если скорость не изменяется в течение времени, то есть — постоянная величина, то путь пройденный точкой за промежуток времени вычисляется по формуле

При переменной скорости совершаем те же действия, что и в предыдущей задаче:

1) разобьем отрезок в частичных промежутков времени точками:

2) выберем на каждом из частичных отрезков времени произвольную точку

3) вычислим значения скорости в точке то есть на каждом отрезке времени и определим путь пройденный точкой за промежуток времени как произведение тогда весь путь, пройденный за время приближенно определяется интегральной суммой для функции на отрезке

4) найдем границу интегральной суммы при и при

Если существует конечный предел интегральной суммы (при условии — при ), то ее и принимают за числовое значение пути пройденного материальной точкой за промежуток времени

Задача о нахождении объема продукции

Пусть функция описывает зависимость производительности труда некоторого производства от времени Необходимо найти объем продукции произведенной за промежуток времени

Если производительность не меняется в течение времени, то есть — постоянная величина, то объем продукции произведенной за промежуток времени вычисляется по формуле При переменной производительности труда, используя приближенную равенство где которая будет тем более точной, чем меньше будет выполним следующие действия:

1) разобьем отрезок на промежутки времени точками:

2) выберем на каждом из отрезков произвольную точку

3) вычислим производительность труда в каждой точке то есть для каждого промежутка времени; определим объем продукции произведенной за время как произведение если на каждом промежутке времени считать производительность труда постоянной величиной; тогда полный объем продукции приближенно определяется как интегральная сумма для функции на отрезке

4) найдем границу если стремится к нулю и и получим объем продукции, произведенной за промежуток времени

Следует отметить, что при решении этих трех различных задач, были выполнены одни и те же действия, и мы пришли к одному и тому же итоге — возникает необходимость определить границу интегральной суммы.

Если существует конечный предел интегральной суммы для функции на отрезке найденная при условии, что при неограниченном возрастании числа точек разбиения которая не зависит ни от способа разбиения отрезка на части, ни от выбора точек то эта граница называется определенным интегралом функции на отрезке и обозначается Следовательно,

где — пределы интегрирования ( — нижняя, — верхняя)

— подынтегральная функция;

— дифференциал переменной интегрирования;

— подынтегральное выражение.

Теорема 23.1 (о существовании определенного интеграла). Если функция непрерывна на отрезке или ограничена на нем и имеет конечное число точек разрыва первого рода, то существует конечное предел интегральной суммы, и она не зависит ни от способа разбиения отрезка на части, ни от выбора точек внутри них для составления интегральной суммы, то есть существует определенный интеграл от функции

Теорема существования определенного интеграла примем без доказательства.
Соответственно, функция для которой на отрезке существует определенный интеграл, называется интегрируемой на этом отрезке.

Вернемся к первой из рассмотренных задач и приведем геометрический смысл определенного интеграла: если функция неотъемлемая на конечном отрезке где то определенный интеграл

численно равна площади криволинейной трапеции, ограниченной кривой отрезком и прямыми и

Основные свойства определенного интеграла

Поскольку по определению определенный интеграл является границей интегральной суммы, то доказательства его свойств базируется на свойствах границ с привлечением, для наглядности и лучшего понимания, геометрического содержания определенного интеграла.

1 (о интеграл с равными пределами интегрирования). Для любой интегрируемой функции определенный интеграл с равными пределами интегрирования равен нулю:

ведь криволинейная трапеция вырождается в вертикальный отрезок.

2 (об изменении знака). Если функция интегрируема на то имеет место формула

то есть, если поменять местами пределы интегрирования, то определенный интеграл изменит свой знак на противоположный.

Действительно, в интегральной сумме приросты меняют знак на противоположный.

3 (о стабильном множителе). Если функция интегрируема на то постоянный множитель можно выносить за знак определенного интеграла:

поскольку как общий множитель слагаемых интегральной суммы можно вынести за знак суммы и, соответственно, за знак границы.

4 (о определенном интеграле от суммы функций). Если функции и интегрируемые на то интеграл от их суммы или разности равна соответственно сумме или разности интегралов от этих функций:

Справедливость (23.11) следует из того, что интегральную сумму левой части равенства можно представить в виде алгебраической суммы двух интегральных сумм:

а по свойству границы суммы функций и получаем (23.11).

Свойство распространяется на любое конечное число слагаемых.

5 (о аддитивности). Если отрезок интегрирования разбит на две части, то определенный интеграл на равна сумме интегралов на этих частях:

так как по геометрическим содержанием таком разбивке соответствуют две криволинейные трапеции, сумма площадей которых равна площади выходной трапеции.
Свойство распространяется на любое конечное число частей разбиения.

6 (о переходе к определенному интегралу в неровностях). Если на отрезке интегрирования значения функций и связанные неравенством то такой же, по знаку, неравенством связаны определенные интегралы от этих функций :

Действительно, при одном и том же разбиении отрезка на части слагаемые интегральной суммы для и будут связаны тем же знаком неравенства, и те же функции, а предельный переход не изменит знака неравенства.

7 (о границах значений определенного интеграла). Если и — наибольшее и наименьшее значения функции то есть и то

Если функция определена и непрерывна на отрезке то среди ее значений на этом отрезке существуют меньше и больше то есть (рис. 23.2). Тогда (23.14) можно рассматривать как следствие свойства (23.13), а именно:

при этом

тогда

и свойство доказано.

Если доводить это свойство по геометрическим содержанием определенного интеграла (рис. 23.2), то площадь криволинейной трапеции, которая соответствует определенному интегралу, не может быть меньше (больше) за площадь прямоугольника с основанием высота которого, соответственно, наименьшим (крупнейшим ) значением функции на

Рис. 23.2

8 (теорема о среднем). Если функция непрерывна на отрезке то на нем найдется такая точка что:

Таких точек на промежутке может быть несколько.
Отношение определенного интеграла от функции на отрезке к длине отрезка интегрирования называется средним значением функции:

С геометрической точки зрения теорема о среднем (рис. 23.3) означает, что площадь под кривой на отрезке интегрирования равна площади прямоугольника с высотой и основой

Рис. 23.3

Связь между определенным и неопределенным интегралами

Если функция интегрируема на отрезке то она интегрируема и на отрезке где Интеграл от такой функции также является функцией от и называется интегралом с переменным верхним пределом интегрирования. Обозначим его через

В этом выражении переменная интегрирования обозначена буквой чтобы отличить ее от верхней границы интегрирования. Численно функция равна площади криволинейной трапеции, основой которой является промежуток

Теорема 23.2. Если функция непрерывна на отрезке то в каждой точке производная от функции по переменным верхним пределом равна подынтегральной функции от верхней границы интегрирования, то есть:

Доказательство. Для доказательства этой теоремы применим определение производной.
По условию функция непрерывна на отрезке поэтому она непрерывна и на любом отрезке Предоставим аргумента прирост тогда и функция также получит некоторый прирост

Последний интеграл было получено с помощью свойства 5 определенного интеграла. Поскольку

то применяя на отрезке теорему о среднем (23.15), получим:

где

Переходя к пределу при а также ввиду того, что при этом и получим:

Равенство значит, что функция является первоначальной для функции на отрезке Следовательно, с теоремы 23.2 следует важное следствие: для всякой непрерывной на отрезке функции существуют первобытные на этом отрезке, одной из которых является определенный интеграл с переменным верхним пределом. Поэтому согласно определению неопределенного интеграла в семье первичных имеем:

Формула (23.19) описывает связь между определенным и неопределенным интегралами: неопределенный интеграл является суммой определенного интеграла с переменным верхним пределом и произвольной действительной постоянной.

Формула Ньютона-Лейбница

Теорема 23.3 (основная формула интегрального исчисления). Если функция интегрируема на отрезке то определенный интеграл от является разницей значений любой из ее первоначальных функций в точках и

Формула (23.20) для вычисления определенного интеграла называется формулой Ньютона-Лейбница

Доказательство основывается на соотношении (23.19), которое позволяет любую первоначальную функции на отрезке записать так: . Последнее равенство будет справедливой при соответствующем выборе постоянной для всех значений

Подставляя вместо поочередно и получаем (23.20):

Отметим, что поскольку все первоначальные отличаются друг от друга только константой, то разница не зависит от выбора

Для обозначения прироста первоначальной на отрезке вводят символ двойной подстановки который удобно использовать при решении примеров:

Заметим, что именно формула Ньютона-Лейбница отображает тесная связь между неопределенным и определенным интегралами. По этой формуле вычисления определенного интеграла сводится к двум шагов:

1) нахождение одной из первоначальных для на (по сути это нахождение неопределенного интеграла)
2) вычисление значений первоначальной в точках, соответствующих границам интегрирования и определение разницы между ее значениями на верхней и нижней границах.

Вычислим определенный интеграл:

Обычно шаги 1), 2) осуществляют одной цепочкой:

Методы вычисления определенного интеграла

При вычислении определённых интегралов используются методы непосредственного интегрирования, замены переменной (подста-. новки) и интегрирования по частям. Непосредственное интегрирование предполагает сведение данного интеграла с помощью алгебраических и арифметических преобразований к формулам таблицы основных интегралов и использование формулы Ньютона-Лейбница.

Непосредственное определенное интегрирование

Поскольку вычисления определенного интеграла по формуле Ньютона-Лейбница предполагает сначала взятия неопределенного интеграла, а затем выполнение арифметических действий, то это означает, что принципиальных различий в методах нахождения неопределенного и вычисления определенного интегралов нет, следовательно, непосредственное вычисление определенного интеграла предусматривает непосредственное неопределенное интегрирование (нахождение одной из первоначальных).

Вычислим интеграл

Вычисление интеграла методом подстановки

Напомним, что существует два типа подстановок, которые используются при интегрировании с применением новой переменной: и

Пусть для определенности при вычислении интеграла проведения подстановку

Теорема 23.4 (о замене переменной в определенном интеграле). если:
1) функция и ее производная непрерывные на отрезке [, α β];
2) значение в точках и такие, что и
3) составлена функция непрерывна на то

то сравнивая результаты интегрирования по переменным и получаем справедливость (23.22).

Подстановка в случае существования обратной к функции сводится к рассматриваемой:

Отметим, что при вычислении определенного интеграла методом подстановки нет необходимости возвращаться к исходной переменной, вместо этого нужно находить пределы интегрирования по новой переменной.

Вычислим определенные интегралы:

Интегрирования по частям в определенном интеграле

Рассмотрим случай, когда при вычислении определенного интеграла нахождения первоначальной требует применения интегрирования по частям.

Теорема 23.5 (формула интегрирования по частям для определенного интеграла). Если в определенном интеграле подынтегральное выражение представлен в виде произведения где и — дифференцируемы на отрезке функции, то выполняется соотношение:

Доказательство. Поскольку

то

Применяя к левой части последнего равенства формулу Ньютона-Лейбница, а также учитывая, что а v d ¢ x d = v, получим

отсюда окончательно имеем:

Теорема доказана.

Соотношение (23.23) называется формулой интегрирования по частям в определенном интеграле.

Если пределы интегрирования симметричны относительно нуля, то для упрощения вычислений целесообразно учитывать четности и нечетности подынтегральной функции.

Так, если — четная функция, то

а если — нечетная функция, то

Это легко обосновать, опираясь на формулу Ньютона-Лейбница.
Вычислим определенные интегралы:

Подынтегральная функция является четной, то есть поэтому

Применение определенного интеграла в некоторых геометрических и экономических задачах

Длина дуги плоской кривой

Пусть функция является непрерывной и дифференцируемой на отрезке Найдем на этом отрезке длину линии, соответствующей графику данной функции.

Разобьем отрезок произвольным образом на частей точками разделения и впишем в дугу кривой ломаную линию (рис. 24.1) . Длиной дуги называется предел длины вписанной ломаной линии при неограниченном уменьшении длин ее звеньев.

Рис. 24.1

Пусть абсциссами вершин ломаной линии имеет значение Тогда длина одного звена ломаной согласно теореме Пифагора определяется формулой:

где

Отсюда

На каждом частичном отрезке функция удовлетворяет условиям теоремы Лагранжа, поэтому существует точка такая, что

Тогда

Длина всей ломаной линии определяется как сумма длин ее звеньев: и представляет собой интегральную сумму для сложной функции

Следовательно, длина дуги кривой, соответствующей графику функции на отрезке составляет:

Если кривая задана уравнениями в параметрической форме

то длина дуги такой кривой определяется формулой:

где и — значение параметра соответствующие концам дуги.

Наряду с хорошо известной декартовой системой координат в которой каждой точке плоскости соответствует пара чисел — проекций точки на координатные оси, пользуются также полярной системой координат.
Зафиксируем на плоскости некоторую точку — полюс — и луч — полярную ось. Выберем произвольным образом отличную от полюса точку (рис. 24.2).

Расстояние от полюса до точки называется полярным радиусом точки

Угол наклона полярного радиуса к полярной оси называется полярным углом точки В точке полярный угол определен.

Числа и называются полярными координатами точки , и пишут: или
Полюс полярная ось и масштабный (единичный) отрезок определяют полярную систему координат

Полярный угол определяется неоднозначно: при заданном точки с координатами где совпадают. Обычно значение берут из промежутка или и называют их главными значениями полярного угла.

Уравнения является уравнением линии в полярных координатах, если координаты любой точки на линии удовлетворяют его, и наоборот, если пара чисел удовлетворяет уравнению, то и являются координатами точки, принадлежащей линии:

где — закон, который отображает свойство точек линии, и — текущие координаты точек линии.

Связь между координатами точки в полярной и декартовой (рис. 24.3) системах координат легко устанавливается, если полюс совпадает с началом декартовой системы координат, а полярная ось лежит на оси абсцисс, и масштаб систем одинаков.

Рис. 24.3

С получаем формулы перехода от декартовых к полярным координатам:

где или

Если дуга задается уравнением в полярных координатах:

то по формулам (24.2) и (24.4) определяем:

Следовательно, длину дуги в полярных координатах находим по формуле:

где и — значение полярного угла, соответствующие концам дуги.

Вычислить длину дуги кривой

Сначала надо установить пределы интегрирования. для этого найдем область определения данной функции, решив систему неравенств:

Далее находим производную функции

следовательно,

По формуле (24.1) имеем:

Рассмотрим пример нахождения длины дуги, если кривая заданная параметрически. Система уравнений

определяет линию, которая называется астроидом (рис. 24.4). Найдем ее длину.

Рис. 24.4

Кривая симметрична относительно осей и Следовательно, определим длину всей дуги, а именно той части, расположенной в первой четверти. Тогда параметр изменяется от до

Находим производные от и сумму их квадратов:

По формуле (24.2) получаем:

Соответственно, длина всей астроиды равна:

Найдем длину дуги, заданной в полярных координатах уравнением Эта кривая называется кардиоидой (рис. 24.5).

Рис. 24.5

Кардиоида симметрична относительно полярной оси, поэтому найдем половину ее длины. Итак, полярный угол будет изменяться от до
Имеем:

По формуле (24.5) получаем:

Тогда длина всей линии равна:

Вычисление площади геометрической фигуры

Вычисление площади плоской фигуры в декартовых координатах опирается на геометрический смысл определенного интеграла.

Рассмотрим несколько случаев вычисления площадей геометрических фигур.

1. По геометрическому содержанию определенный интеграл от непрерывной функции x на отрезке численно равна площади криволинейной трапеции, ограниченной графиком функции осью и прямыми и при условии , что функция на отрезке является неотъемлемой.
То есть для имеем:

2. Если функция на отрезке неположительные (рис. 24.6), т.е. то определенный интеграл от нее также будет числом неположительные, потому что он является границей интегральной суммы, а значит сохраняет знак подынтегральной функции. Тогда для площадь криволинейной трапеции равна:

Рис. 24.6

3. Если функция на отрезке меняет знак (рис. 24.7), проходя через точки то для нахождения площади фигуры, ограниченной графиком такой функции и осью отрезок надо разбить на три промежутки на которых знак функции остается постоянным, и применить формулы (24.7) и (24.8).
Следовательно, если функция несколько раз меняет знак на промежутке то формулы (24.7) и (24.8) можно объединить в одну:

Рис. 24.7

4. Если надо определить площадь фигуры, ограниченной кривыми по данным на отрезке причем то эта площадь (рис. 24.8) вычисляется по формуле:

Рис. 24.8

5. Если плоская фигура ограничена графиком непрерывной на промежутке функции прямыми и осью ординат (рис. 24.9), то площадь такой фигуры вычисляется по формуле:

Рис. 24.9

Найдем площадь фигуры, ограниченной графиком функции прямой и осью (рис. 24.10).

Рис. 24.10

Устанавливаем пределы интегрирования:
Поскольку функция на отрезке неотъемлемая, то по формуле (24.7) имеем:

Вычислим площадь фигуры, ограниченной линиями: и (рис. 24.11).

Рис. 24.11

Промежутком интегрирования является отрезок
Поскольку подынтегральная функция на отрезке неположительная, то по формуле (24.8) имеем:

Найдем площадь фигуры, ограниченной линиями: (рис. 24.12).

Рис. 24.12

Функция на промежутке интегрирования меняет знак в точке Поэтому по формуле (24.9) имеем:

Найдем площадь фигуры, ограниченной линиями: (рис. 24.13).

Рис. 24.13

Для определения границ интегрирования находим точки пересечения линий:

Откуда получаем:

Согласно формуле (24.10) имеем:

Подчеркнем, что в формуле (24.10) в роли всегда выступает функция, график которой ограничивает фигуру сверху.

6. Пусть фигура ограничена кривой, уравнение которой задано в параметрической форме, то есть зависимость задается параметрически системой уравнений

где которая определяет некоторую кривую на отрезке

Площадь фигуры, как и раньше, вычисляем по формуле (24.7), но в ней сделаем замену переменной: тогда
Следовательно,

Найдем площадь фигуры, ограниченной эллипсом (рис. 24.14), заданным параметрическими уравнениями

Рис. 24.14

Поскольку эллипс симметричен относительно осей координат, то найдем площадь -ой части площади, расположенной в первой четверти.

Определим границы интегрирования. Если изменяется от то по системе уравнений

получаем, что параметр изменяется от

Осуществляем по формуле (24.12) определено интегрирование:

Отсюда площадь всей фигуры равна:

7. Площадь криволинейного сектора

Рассмотрим в полярных координатах геометрическую фигуру, которая ограничена линией и двумя лучами где функция непрерывна при (рис. 24.15). Такую фигуру называют криволинейным сектором для на Вычислим площадь этого сектора.

Рис. 24.15

Выполняем те же шаги, которые осуществлялись при решении задачи нахождения площади криволинейной трапеции:

1) разобьем криволинейный сектор для на произвольным образом на частей с центральными углами

2) выберем на каждом из частичных секторов произвольный луч под углом к полярной оси;

3) вычислим площадь кругового сектора радиуса с центральным углом по известной формуле: площадь криволинейного сектора на приближенно равен сумме всех

которая является интегральной суммой для сложной функции от

4) найдем границу интегральной суммы при условии, что при которая, в случае ее существования, определяет площадь криволинейного сектора:

Вычислим площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда где — положительное число (рис. 24.16).

Рис. 24.16

При чередовании от полярный радиус описывает кривую, ограничивает криволинейный сектор По формуле (24.14) имеем:

Вычисление объемов тел по известным площадям поперечных сечений

Пусть имеем некоторое геометрическое тело, для которого известна площадь любого сечения этого тела плоскостью перпендикулярной к оси (рис. 24.17). Выведем формулу для вычисления объема тела для чего составим соответствующую интегральную сумму как это делалось при определении понятия определенного интеграла:

Рис. 24.17

1) разобьем тело произвольным образом на частей (слоев) плоскостями: (на рисунке показано слой на );

2) выберем на каждом частичном промежутке произвольную точку и для каждой такой точки построим цилиндрическое тело, образующая которого параллельна оси а направляющая является контуром сечения тела плоскостью (на рисунке он не изображен)

3) вычислим объем цилиндра с площадью основания и высотой тогда объем тела на промежутке приближенно равен сумме всех частных объемов

которая является интегральной суммой для функции на промежутке

4) найдем границу интегральной суммы при условии, что при которую, в случае ее существования, принимают за объем тела по площадям поперечных сечений:

Найдем объем тела, ограниченного плоскостями и и однополостным гиперболоидом, который задан уравнением:

Проведем плоскость (рис. 24.18). В сечении получим эллипс:

Перейдем к каноническому уравнению эллипса:

где

Площадь сечения находим по известной формуле площади фигуры, ограниченной эллипсом (24.13):

Следовательно, вычислим объем тела по формуле (24.15) с переменной интегрирования

Вычисление объема тела вращения

Пусть на промежутке задана непрерывная функция Надо определить объем тела, которое образовалось при вращении криволинейной трапеции для на вокруг оси (рис. 24.19). Такое тело называется тело вращения.

Рис. 24.19

При вращении каждая точка дуги кривой описывает круг, а поперечным сечением тела вращения является круг радиуса с центром на оси площадь которого определяется по известной формуле: где

На этом основании расчетную формулу для вычисления объема тела образованного вращением криволинейной трапеции для функции на промежутке вокруг оси получим как частный случай формулы (24.15) при условии, что

Найдем объем шара радиуса Его можно рассматривать как результат вращения вокруг оси криволинейной трапеции, ограниченной полукругом на отрезке

Объем этого шара можно найти по формуле (24.16):

Если в соотношении для формально заменить на то получим формулу объема тела, образованного вращением вокруг оси криволинейной трапеции, ограниченной линиями — функция, обратная к

Приближенное вычисление определенных интегралов

Формула Ньютона-Лейбница как основная формула интегрального исчисления является главным средством вычисления определенного интеграла, если при нахождении первоначальной не возникает трудностей. В случае, если неопределенный интеграл «не берется», то есть первоначальную нельзя представить в виде конечного числа элементарных функции, или подынтегральная функция задана графиком или таблицей, то используют приближенные формулы. Эти формулы основаны на геометрическом смысле определенного интеграла как площади криволинейной трапеции.

Формула прямоугольников

Пусть надо вычислить определенный интеграл от непрерывной на отрезке функции Согласно определению определенного интеграла построим интегральную сумму для функции

Поделим отрезок равных частей длины — точками

Вычислим значение функции в точках а именно

Тогда площадь криволинейной трапеции, изображенной на рис. 24.23, а вместе с тем и определенный интеграл для функции на отрезке приближенно равна сумме площадей прямоугольников с высотами и основами

Рис. 24.23

Полученное выражение (24.24) называется формулой прямоугольников с высотами вычисленным на левой грани частичных интервалов.

Если высоты прямоугольников взять равными значениям функции на правой грани частичных интервалов, то формула прямоугольников иметь вид:

Поскольку для функции непрерывной на существует конечное предел интегральной суммы при и то можно утверждать, что ошибка при вычислении интеграла будет тем меньше, чем больше Абсолютная погрешность при этом вычисляется по формуле:

где

Относительная погрешность определяется как отношение абсолютной погрешности к точному значению интеграла и подается в процентах.

Формула трапеций

Рассмотрим еще один способ приближенного вычисления определенного интеграла.

Как и в предыдущем случае, отрезок делится на равных частей точками и в этих точках вычисляются значения функции (рис. 24.24). Построим прямоугольные трапеции с высотами и основами длиной и

Рис. 24.24

Каждая часть площади под кривой будет приближенно равняться площади прямоугольной трапеции со средней линией и высотой а площадь всей криволинейной трапеции для функции на отрезке приближенно равна площади под ломаной, то есть сумме площадей всех
трапеций, ограниченных сверху отрезками этой ломаной.

Соответственно, получаем:

Это и есть формула трапеций. Формула (24.26), как и в предыдущем случае, будет тем точнее, чем больше число

Можно доказать, что если функция f имеет непрерывную ограниченную производную которая удовлетворяет неравенство (где — постоянная), то для формул прямоугольников и трапеций абсолютная погрешность определяется неравенством:

Для функций, которые имеют ограниченную вторую производную (где — постоянная), для абсолютной погрешности имеет место такая оценка:

Формула Симпсона

Поделим отрезок на четное число одинаковых частей (рис. 24.25). Функцию на отрезке заменим параболой которая проходит через точки и с осью симметрии, параллельной оси

Рис. 24.25

Аналогичные параболы строим и для всех остальных пар частичных отрезков.
Сумма площадей криволинейных трапеций, ограниченных параболами, и даст приближенное значение интеграла.

Покажем, что площадь криволинейной трапеции, ограниченной сверху параболой, проходящей через три точки равна:

где — длина отрезка — промежуток интегрирования (рис. 24.26).

Рис. 24.26

Коэффициенты параболы и значение функции в точках с абсциссами связанные такими соотношениями:

Найдем площадь криволинейной трапеции для на отрезке

С учетом значений функции в точках с абсциссами и следует, что

Итак, то есть получили равенство (24.28). Применяя на каждом отрезке формулу (24.28), при получим:

Если сложить левые и правые части записанных равенств, то получим:

или

— формула Симпсона, или формула парабол.

Если функция имеет непрерывную четвертую производную и где — наибольшее значение y в интервале то абсолютная погрешность формулы парабол определяется неравенством:

Таким образом, формула Симпсона (при одинаковом количестве частичных отрезков разбиения промежутка интегрирования) дает наилучшее приближение к искомому интеграла по сравнению с формулами прямоугольников или трапеций.

Вычислим интеграл применив непосредственное интегрирование.

Сравним этот результат с результатами приближенного вычисления по формулам прямоугольников, трапеций, парабол при и найдем абсолютные и относительные погрешности этих вычислений.

Для применения выведенных формул приближенного вычисления определенных интегралов разобьем отрезок на 10 равных частей. Тогда длина каждого отрезка равна а значение функции в точках разбиения:

Составим таблицу значений функции для каждой границы интервала разбиения.

Таблица 24.1

По формуле прямоугольников (24.24), если принимать высоты прямоугольника значение вычисленное на левой грани частичного интервала, находим:

По формуле прямоугольников (24.25), если принимать высоты прямоугольника значение на правой грани частичного интервала, получаем несколько иное значение:

По формуле трапеций (24.26) имеем промежуточное значение по сравнению с обеими формулами прямоугольников:

По формуле парабол (24.30):

При вычислении интеграла по формуле прямоугольников (24.24) абсолютная погрешность составляет:

а относительная погрешность равна:

При вычислении интеграла по формуле прямоугольников (24.25) абсолютная и относительная погрешности составляют:

или

При вычислении интеграла по формуле трапеций имеем:

При вычислении интеграла по формуле парабол получаем:

Итоговая таблица (табл. 24.2) убедительно подтверждает, что формула парабол действительно дает наибольшую точность при приближенном вычислении определенных интегралов. Конечно, если подынтегральная функция отлична от многочлена второго или третьей степени, то погрешность не будут нулевыми.

Таблица 24.2

По объему вычислительной работы формула Симпсона не имеет преимуществ перед другими формулами.

Лекции:

Замена переменной в определенном интеграле
Формулы тригонометрии и их использование для преобразования тригонометрических выражений
Интегральный признак Коши
Правила дифференцирования
Построение графика функции
Связь между непрерывностью и дифференцируемостью функции
Функции комплексного переменного
Преобразование подобия
Формулы производных
Изометрия

Источник

Вычисление определённых интегралов: базовые алгоритмы

Время на прочтение
13 мин

Количество просмотров 83K

В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают «под капотом», и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.

Определение интеграла

Интегралом (по Риману) от функции $f(x)$ на отрезке $[a;b]$ называется следующий предел:

$int_a^b f(x)dx = lim_{Delta x to 0} sum_{i=0}^{n-1} f(xi_i)(x_{i+1} - x_i),~~(1)$

где $Delta x = maxlbrace x_{i+1} - x_irbrace$ — мелкость разбиения, , , $xi_i$ — произвольное число на отрезке $[x_i; x_{i+1}]$ .

Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким.

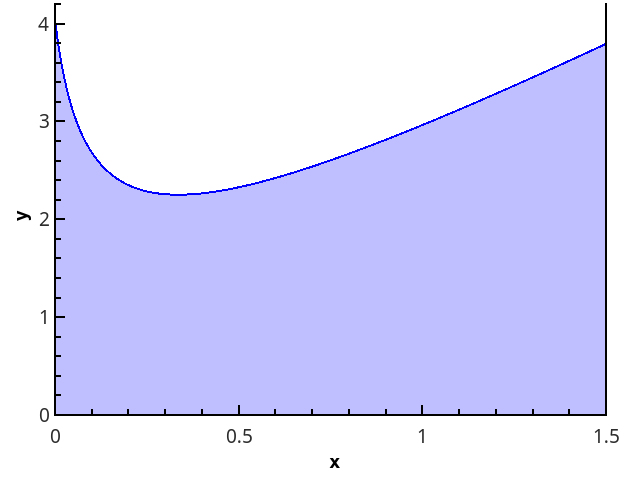
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).

Квадратурные формулы

Определение интеграла (1) можно переписать в виде

$I = int_a^b f(x)dx approx I_n = (b - a)sum_{i=0}^{n-1} w_i f(xi_i),~~(2)$

где $w_i$ — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа $n$ точек, в которых вычисляется функция.

Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки и веса $w_i$ таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.

Вычислительная задача

Задана функция $f(x)$ , для которой есть алгоритм вычисления значений в любой точке отрезка $[a;b]$ (имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).

Требуется найти приближённое значение интеграла .
Решения будут реализованы на языке Python 3.6.

Для проверки методов используется интеграл $int_0^{3/2} left[ 2x + frac{1}{sqrt{x + 1/16}}right]dx = 17/4$ .

Кусочно-постоянная аппроксимация

Идейно простейшие квадратурные формулы возникают из применения выражения (1) «в лоб»:

$I_n = sum_{i=0}^{n-1} f(xi_i) (x_{i+1} - x_i)$

Т.к. от метода разбиения отрезка точками и выбора точек значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1) ; 2) $xi_i = x_{i+1}$ ; 3) $xi_i = (x_i + x_{i+1}) / 2$ .

Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.

Реализация

def _rectangle_rule(func, a, b, nseg, frac):
    """Обобщённое правило прямоугольников."""
    dx = 1.0 * (b - a) / nseg
    sum = 0.0
    xstart = a + frac * dx # 0 <= frac <= 1 задаёт долю смещения точки, 
                           # в которой вычисляется функция,
                           # от левого края отрезка dx
    for i in range(npoints):
        sum += func(xstart + i * dx)

    return sum * dx

def left_rectangle_rule(func, a, b, nseg):
    """Правило левых прямоугольников"""
    return _rectangle_rule(func, a, b, nseg, 0.0)

def right_rectangle_rule(func, a, b, nseg):
    """Правило правых прямоугольников"""
    return _rectangle_rule(func, a, b, npoints, 1.0)

def midpoint_rectangle_rule(func, a, b, nseg):
    """Правило прямоугольников со средней точкой"""
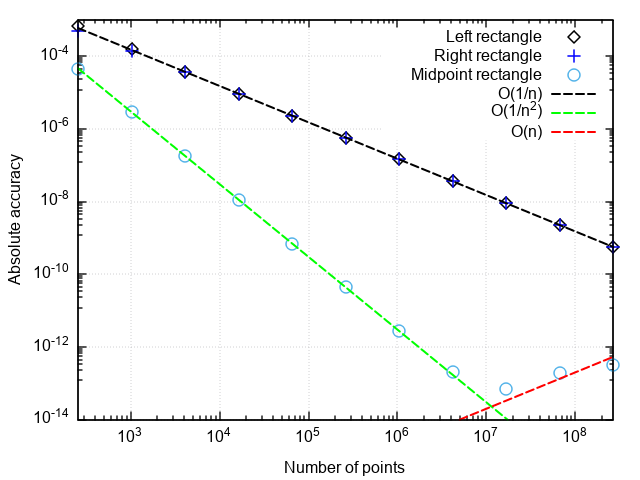
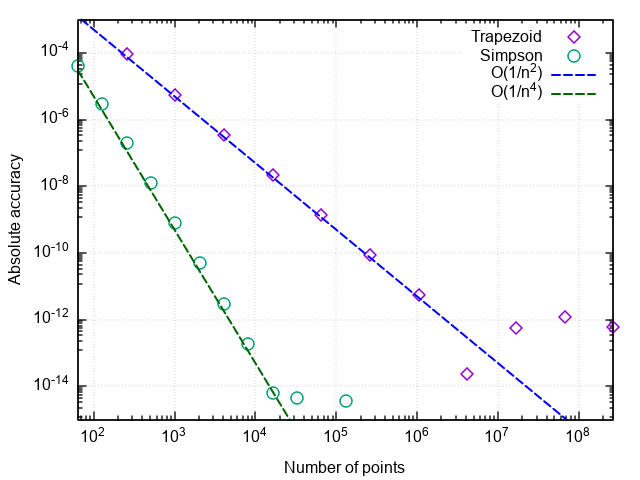
    return _rectangle_rule(func, a, b, nseg, 0.5)

Для анализа производительности квадратурных формул построим график погрешности в координатах «число точек — отличие численного результата от точного».

Что можно заметить:

Формула со средней точкой гораздо точнее, чем с правой или левой точками
Погрешность формулы со средней точкой падает быстрее, чем у двух остальных
При очень мелком разбиении погрешность формулы со средней точкой начинает возрастать
Первые два пункта связаны с тем, что формула прямоугольников со средней точкой имеет второй порядок аппроксимации, т.е. , а формулы правых и левых прямоугольников — первый порядок, т.е. .
Возрастание погрешности при измельчении шага интегрирования связано с нарастанием погрешности округления при суммировании большого числа слагаемых. Эта ошибка растёт как , что не даёт при интегрировании достигнуть машинной точности.
Вывод: методы прямоугольников с правой и левой точками имеют низкую точность, которая к тому же медленно растёт с измельчением разбиения. Поэтому они имеют смысл разве что в демонстрационных целях. Метод прямоугольников со средней точкой имеет более высокий порядок аппроксимации, что даёт ему шансы на использование в реальных приложениях (об этом чуть ниже).

Кусочно-линейная аппроксимация

Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:

$I_n = sum_{i=0}^{n-1} frac{f(x_i) + f(x_{i+1})}{2}(x_{i+1} - x_i)~~(3)$

Иллюстрация метода трапеций для n=1 и n=2.

В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид

$I_n = hleft(frac{f(a) + f(b)}{2} + sum_{i=1}^{n-1} f(a + ih)right),~h=frac{b-a}{n}~~(3a)$

Реализация

def trapezoid_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    dx = 1.0 * (b - a) / nseg
    sum = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        sum += func(a + i * dx)

    return sum * dx

Построив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).

Контроль точности вычисления

Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.

Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: $Delta_{2n} approx |I_{2n} - I_n|$ . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.

Чем ещё хорош метод прямоугольников

Метод прямоугольников не требует вычислять значения функции на концах отрезка. Это означает, что его можно использовать для функций, имеющих на краях отрезка интегрируемые особенности (например, sinx/x или x^-1/2 от 0 до 1). Поэтому показанный далее метод экстраполяции будет работать точно так же и для метода прямоугольников. Отличие от метода трапеций лишь в том, что при уменьшении шага вдвое отбрасывается результат предыдущих вычислений, однако можно утроить число точек, и тогда предыдущее значение интеграла также можно использовать для вычисления нового. Формулы для экстраполяции в этом случае необходимо скорректировать на другое соотношение шагов интегрирования.

Отсюда получаем следующий код для метода трапеций с контролем точности:

def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1):
    """Правило трапеций
       rtol - желаемая относительная точность вычислений
       nseg0 - начальное число отрезков разбиения"""
    nseg = nseg0
    old_ans = 0.0
    dx = 1.0 * (b - a) / nseg
    ans = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        ans += func(a + i * dx)

    ans *= dx
    err_est = max(1, abs(ans))
    while (err_est > abs(rtol * ans)):
        old_ans = ans
        ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) # новые точки для уточнения интеграла
                                                                      # добавляются ровно в середины предыдущих отрезков
        nseg *= 2
        err_est = abs(ans - old_ans)

    return ans

С таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.

Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.

Кусочно-параболическая аппроксимация

Следующим шагом аппроксимируем функцию элементами парабол. Для этого требуется, чтобы число отрезков разбиения было чётным, тогда параболы могут быть проведены через тройки точек с абсциссами {(x₀=a, x₁, x₂), (x₂, x₃, x₄), …, (x_n-2, x_n-1, x_n=b)}.

Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).

Приближая интеграл от функции на каждом из отрезков [x_k;x_k+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (x_k+1=x_k+h), получаем формулу Симпсона:

$I_{Simps, n} = sum_{i=0}^{n/2-1}frac{h}{3}[f(x_{2i})+4f(x_{2i+1})+f(x_{2i + 2})] = \ =frac{h}{3}[f(a)+4f(a+h)+2f(a+2h) + ... +4f(b-h) + f(b)]~~(4)$

Из формулы (4) напрямую получается «наивная» реализация метода Симпсона:

Заголовок спойлера

def simpson_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    if nseg%2 = 1:
        nseg += 1
    dx = 1.0 * (b - a) / nseg
    sum = (func(a) + 4 * func(a + dx) + func(b))
    for i in range(1, nseg / 2):
        sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx)

    return sum * dx / 3

Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.

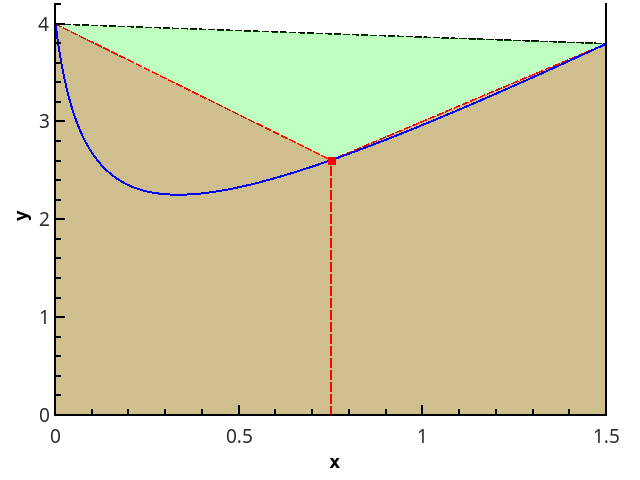
Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам :

$I_{Simps,2} = frac{h}{3}(f_0 + 4f_1 + f_2) = frac{4}{3}hleft(frac{f_0 + f_1}{2} + frac{f_1 + f_2}{2}right) - frac{1}{3}cdot2hfrac{f_0 + f_2}{2} = \ =frac{4I_{trap,2} - I_{trap,1}}{3}$

Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.

Как-то так…

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным числом отрезков разбиения nseg0
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1):
        """Интегрирование методом трапеций с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        ans = Quadrature.__restart(func, x0, x1, nseg0)
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            ans = Quadrature.__double_nseg(func, x0, x1)
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

    def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1):
        """Интегрирование методом парабол с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0)
        new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
        ans = (4 * new_trapez_sum - old_trapez_sum) / 3
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            old_trapez_sum = new_trapez_sum
            new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
            ans = (4 * new_trapez_sum - old_trapez_sum) / 3
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Сравним эффективность метода трапеций и парабол:

>>> import math
>>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 65537
4.250000001385811
>>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 2049
4.2500000000490985

Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!

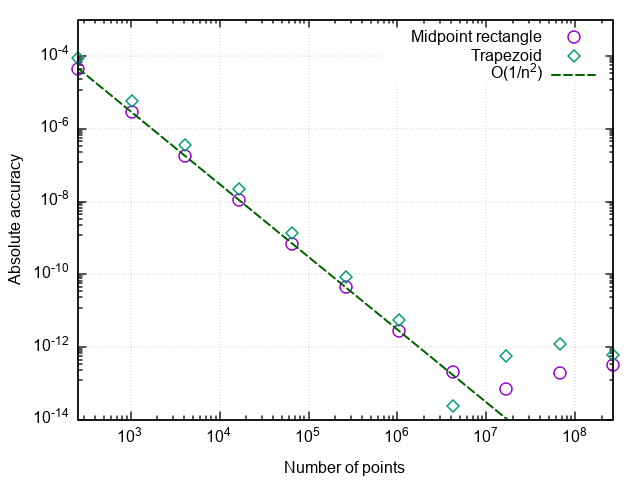
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования $|I_{Simps, n} - I| = O(1/n^4)$ (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).

Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.

Что дальше?

Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов w_i в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.

Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:

$I_{trap,n}[f, a, b] = int_a^b f(x)dx + C_2h^2 + C_4h^4 + C_6h^6 + ...,~h = frac{b-a}{n}~~~(5)$

На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла $I(h)$ строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.

Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.

Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.

$I_{trap,n} - I approx C_2h^2;~I_{trap,2n} - I approx C_2left(frac{h}{2}right)^2$

Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:

$I = I_{trap,2n} - C_2left(frac{h}{2}right)^2 + O(h^4) approx I_{trap,2n} - frac{I_{trap,2n}-I_{trap,n}}{1-2^2} = I_{Simps,2n}$

Повторяя аналогичную процедуру для формулы Симпсона, получаем:

$I_{Simps,2n} - I approx C_4left(frac{h}{2}right)^4;~I_{Simps,n} - I approx C_4h^4$

$I = I_{Simps,2n} - C_4left(frac{h}{2}right)^4 + O(h^6) approx I_{Simps,2n} - frac{I_{Simps,2n}-I_{Simps,n}}{1-2^4}$

Если продолжить, вырисовывается такая таблица:

2 порядок	4 порядок	6 порядок
I_0,0
I_1,0	I_1,1
I_2,0	I_2,1	I_2,2
…	…	…

В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).

Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:

$I_{i,j} = I_{i,j-1} - frac{I_{i,j-1}-I_{i-1,j-1}}{1-left(frac{h_{i-j}}{h_i}right)^2} = I_{i,j-1} - frac{I_{i,j-1}-I_{i-1,j-1}}{1-2^{2j}}~~~(6)$

Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.

$Delta_{i,j} approx I_{i,j} - I_{i,j-1}$

Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.

Реализация

Дополнительный метод добавляется в класс Quadrature

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным разбиением на nseg0 отрезков
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True):
        """Интегрирование методом Ромберга
           nseg0 - начальное число отрезков разбиения
           maxcol - максимальный столбец таблицы"""
        # инициализация таблицы
        Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]]
        i = 0
        maxcol = max(0, maxcol)
        ans = Itable[i][i]
        error_est = max(1, abs(ans))
        while (error_est > abs(rtol * ans)):
            old_ans = ans
            i += 1
            d = 4.0
            ans_col = min(i, maxcol)
            Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1))
            for j in range(0, ans_col):
                diff = Itable[i][j] - Itable[i - 1][j]
                Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0)
                d *= 4.0

            ans = Itable[i][ans_col]
            if (maxcol <= 1): # методы трапеций и парабол обрабатываются отдельно
                error_est = abs(ans - Itable[i - 1][-1])
            elif (i > maxcol):
                error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)])
            else:
                error_est = abs(ans - Itable[i - 1][i - 1])

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Проверим, как работает аппроксимация высокого порядка:

>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) # трапеции
Total function calls: 65537
4.250000001385811
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) # параболы
Total function calls: 2049
4.2500000000490985
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4)
Total function calls: 257
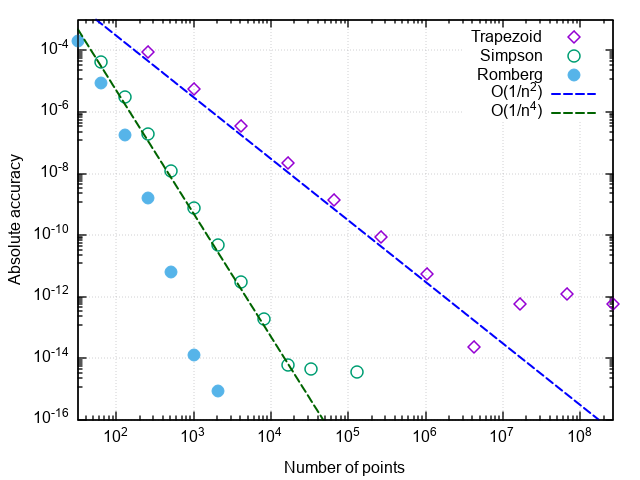
4.250000001644076

Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:

Некоторые замечания

Замечание 1. Количество вызовов функции в этих задачах характеризует число суммирований при вычислении интеграла. Уменьшение числа вычислений подынтегрального выражения не только экономит вычислительные ресурсы (хотя при более оптимизированной реализации и это тоже), но и уменьшает влияние погрешностей округления на результат. Так, при попытке вычислить интеграл тестовой функции метод трапеций зависает при попытке достигнуть относительной точности 5×10^-15, метод парабол — при желаемой точности 2×10^-16(что является пределом для чисел в двойной точности), а метод Ромберга справляется с вычислением тестового интеграла вплоть до машинной точности (с ошибкой в младшем бите). То есть, повышается не только точность интегрирования при заданном числе вызовов функции, но и предельно достижимая точность вычисления интеграла.

Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.

Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:

>>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5)
Total function calls: 9
5.0
>>> Quadrature.simpson(abs, -1, 3, rtol=1e-5)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3)
Total function calls: 33
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4)
Total function calls: 33
5.000001383269357

Замечание 4. Может показаться, что чем выше порядок аппроксимации, тем лучше. На самом деле, лучше ограничить число столбцов таблицы Ромберга на уровне 4-6. Чтобы понять это, посмотрим на формулу (6). Второе слагаемое представляет собой разность двух последовательных элементов j-1-го столбца, поделенную на примерно 4^j. Т.к. в j-1-м столбце находятся аппроксимации интеграла порядка 2j, то сама разность имеет порядок (1/n_i)^2j ~ 4^—ij. C учётом деления получается ~4^-(i+1)j ~ 4^—j². Т.е. при j~7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.

Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла $int_0^1sqrt{x}sin{x}dx$ и эквивалентного ему $int_0^1 2t^2sin{t^2}dt$ . Как говорится, почувствуйте разницу.

Заключение

Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования «обычных» функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.

Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).

Литература

А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука. 1989.
J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.

Источник

Пусть дан подграфик функции f(x)f(x) на участке [a;b][a; b]:

Разобьем отрезок [а;b][а; b] точками x1x_1, x2x_2, x3x_3, xn−1x_{n-1} на nn равных отрезков: [а;x1][а; x_1], [x1;x2][x_1; x_2], [x2;x3],…[xn−1;b][x_2; x_3], …[ x_{n-1}; b].

Построим на первом из этих отрезков прямоугольник с высотой f(x1)f(x_1), на втором — прямоугольник высоты f(x2)f(x_2)… на n-ном — прямоугольник с высотой f(b)f(b). В результате получим восходящий многоугольник, составленный из n прямоугольников. Пусть основание каждого из построенных прямоугольников равно ΔxΔx тогда площадь всего ступенчатого многоугольника составит:

Sn=Δx⋅f(x1)+Δx⋅f(x2)+…+Δx⋅f(b){{S}_{n}}=Delta xcdot f({{x}_{1}})+Delta xcdot f({{x}_{2}})+…+Delta xcdot f(b)

Суммы такого вида называют интегральными суммами. Полученную интегральную сумму можно считать приближенным значением площади SS подграфика функции f(x)f(x) на [a;b][a; b]. При этом если n→∞n → ∞, то Sn→SS_n→S.

Не только задача о нахождении площади подграфика, но и многие другие важные прикладные задачи приводят к вычислению границ подобных интегральных сумм. Поэтому для этого понятия введено специальное название и обозначение.

Границу интегральной суммы Δx⋅f(x1)+Δx⋅f(x2)+…+Δx⋅f(xn),Delta xcdot f({{x}_{1}})+Delta xcdot f({{x}_{2}})+…+Delta xcdot f({{x}_{n}}), если n→∞n → ∞, называют определенным интегралом функции f(x)f(x) от aa до bb.

Его обозначают символом ∫abf(x)dxintlimits_{a}^{b}{f(x)}dx (читают: (определенный) интеграл от aa до bb эф от икс дэ икс). Здесь числа от aa до bb – пределы (границы) интегрирования, ∫∫ – знак интеграла, f(x)f(x) – подынтегральная функция, xx – переменная интегрирования.
Из всего сказанного следует, что площадь подграфика функции f(x)f(x) на [a;b][a; b] равна ∫abf(x)dxintlimits_{a}^{b}{f(x)}dx.

Главная теорема интегрального исчисления

Если у функции f(x)f(x) на отрезке [a,b][a, b] существует первоначальная F(x)F(x), то
I=∫abf(x)dx=F(b)−F(a)I=intlimits_{a}^{b}{f(x)}dx=F(b)-F(a)

Это формула Ньютона-Лейбница, основная формула интегрального исчисления в математическом анализе.

Она дает возможность решать многие важные задачи не вычислением границ интегральных сумм, что достаточно трудно, а с помощью первоначальной.

Свойства определенных интегралов

Рационализировать вычисления интеграла часто помогает знание об их свойствах.
При формулировке определения определенного интеграла мы считали, что a<ba < b. Удобно расширить понятие определенного интеграла, и для случая a>ba > b принять по определению, что

∫abf(x)dx=−∫baf(x)dxintlimits_{a}^{b}{f(x)}dx=-intlimits_{b}^{a}{f(x)}dx

Для случая a=ba = b также по определению будем считать, что

∫aaf(x)dx=0intlimits_{a}^{a}{f(x)}dx=0]

Отметим, что формальное применение формулы Ньютона-Лейбница к вычислению интегралов в данных формулах дает такой же результат. Действительно, если функция F(x)F(x) является первообразной для функции f(x)f(x), то

∫aaf(x)dx=F(x)∣aa=F(a)−F(a)intlimits_{a}^{a}{f(x)}dx=left. F(x) right|_{a}^{a}=F(a)-F(a)

Также

∫abf(x)dx=F(b)−F(a)=−(F(a)−F(b))=−∫baf(x)dxintlimits_{a}^{b}{f(x)}dx=F(b)-F(a)=-(F(a)-F(b))=-intlimits_{b}^{a}{f(x)}dx

С помощью формулы Ньютона-Лейбница легко обосновываются и другие свойства определенных интегралов:

Если F(x)F(x) является первообразной для функции f(x)f(x), то для функции kf(x)kf(x) первоначальной будет функция kF(х)kF(х). Тогда

∫abkf(x)dx=kF(x)∣ab=kF(b)−kF(a)=k(F(b)−F(a))=k∫abf(x)dxintlimits_{a}^{b}{kf(x)}dx=kleft. F(x) right|_{a}^{b}=kF(b)-kF(a)=k(F(b)-F(a))=kintlimits_{a}^{b}{f(x)}dx

Таким образом,

∫abk⋅f(x)dx=k⋅∫abf(x)dxintlimits_{a}^{b}{kcdot f(x)}dx=kcdot intlimits_{a}^{b}{f(x)}dx

Если F(x)F(x) является первообразной для функции f(x)f(x), a G(х)G(х) — первоначальной для функции g(x)g(x), то для функции f(x)+g(x)f(x) + g(x) первоначальной будет функция F(x)+G(х)F(x) + G (х).

Tогда

∫ab(f(x)+g(x))dx=(F(x)+G(x))∣ab=(F(b)+G(b))−(F(a)+G(a))=(F(b)−F(a))+(G(b)−G(a))=∫abf(x)dx+∫abg(x)dxintlimits_{a}^{b}{(f(x)}+g(x))dx=(left. F(x)+G(x)) right|_{a}^{b}=(F(b)+G(b))-(F(a)+G(a))=(F(b)-F(a))+(G(b)-G(a))=intlimits_{a}^{b}{f(x)}dx+intlimits_{a}^{b}{g(x)}dx

Таким образом ∫ab(f(x)+g(x))d=∫abf(x)dx+∫abg(x)dxintlimits_{a}^{b}{(f(x)}+g(x))d=intlimits_{a}^{b}{f(x)}dx+intlimits_{a}^{b}{g(x)}dx

Если F(x)F(x) является первообразной для функции f(х)f(х) и сс на отрезке [a;b][a; b], то

∫ac(f(x))dx+∫cb(f(x))dx=F(x)∣ac+F(x)∣cb=F(c)−F(a)+F(b)−F(c)=F(b)−F(a)=∫ab(f(x))dxintlimits_{a}^{c}{(f(x)})dx+intlimits_{c}^{b}{(f(x)})dx=left. F(x) right|_{a}^{c}+left. F(x) right|_{c}^{b}=F(c)-F(a)+F(b)-F(c)=F(b)-F(a)=intlimits_{a}^{b}{(f(x)})dx

Итак, если функция f(x)f (x) интегрирована на отрезке [a;b][a; b] и с∈[a;b]с ∈ [a; b], то

∫ab(f(x))dx=∫ac(f(x))dx+∫cb(f(x))dxintlimits_{a}^{b}{(f(x)})dx=intlimits_{a}^{c}{(f(x)})dx+intlimits_{c}^{b}{(f(x)})dx

Пример 1

Вычислить ∫0π41cos⁡2xdxintlimits_{0}^{frac{pi }{4}}{frac{1}{{{cos }^{2}}x}}dx.

Поскольку для функции f(x)=1cos⁡2xf(x)=frac{1}{{{cos }^{2}}x} мы знаем первообразную – это F(х)=tgхF(х) = tgх, то заданный интеграл вычисляется непосредственным применением формулы Ньютона-Лейбница I=∫abf(x)dx=F(b)−F(a)I=intlimits_{a}^{b}{f(x)}dx=F(b)-F(a).

Решение

∫0π4dxcos⁡2x=tgx∣0π4=tgπ4−tg0=1−0=1intlimits_{0}^{frac{pi }{4}}{frac{dx}{{{cos }^{2}}x}}=left. tgx right|_{0}^{frac{pi }{4}}=tgfrac{pi }{4}-tg0=1-0=1

Ответ: 1.

Пример 2

Вычислите ∫13(4x−x)dxintlimits_{1}^{3}{left( frac{4}{x}-x right)}dx

Решение
Возможны два пути вычисления заданного интеграла.

Сначала найти первообразную для функции, используя правила исчисления первообразных и таблицу первобытных, а затем найти интеграл по формуле Ньютона-Лейбница.
Использовать правило (∫ab(f(x)+g(x))d=∫abf(x)dx+∫abg(x)dxintlimits_{a}^{b}{(f(x)}+g(x))d=intlimits_{a}^{b}{f(x)}dx+intlimits_{a}^{b}{g(x)}dx и записать заданный интеграл как алгебраическую сумму двух интегралов, каждый из которых можно непосредственно вычислить, как в примере 1.

1 способ
Для функции f(x)=(4/x−x)f(x) = (4/x — x) одной из первообразных является F(х)=4ln∣х∣−x2/2F(х) = 4ln|х| — x2/2. Тогда

∫13(4x−x)dx=(4ln⁡∣x∣−x22)∣13=(4ln⁡∣3∣−322)−(4ln⁡∣1∣−122)=4ln⁡3−4intlimits_{1}^{3}{left( frac{4}{x}-x right)}dx=left. left( 4ln left| x right|-frac{{{x}^{2}}}{2} right) right|_{1}^{3}=(4ln left| 3 right|-frac{{{3}^{2}}}{2})-(4ln left| 1 right|-frac{{{1}^{2}}}{2})=4ln 3-4

2 способ

∫13(4x−x)dx=∫134xdx−∫13xdx=4ln⁡∣x∣∣13−x22∣13=4(ln⁡∣3∣−ln⁡∣1∣)−(322−122)=4ln⁡3−4intlimits_{1}^{3}{left( frac{4}{x}-x right)}dx=intlimits_{1}^{3}{frac{4}{x}}dx-intlimits_{1}^{3}{x}dx=left. 4ln left| x right| right|_{1}^{3}-left. frac{{{x}^{2}}}{2} right|_{1}^{3}=4(ln left| 3 right|-ln left| 1 right|)-(frac{{{3}^{2}}}{2}-frac{{{1}^{2}}}{2})=4ln 3-4

Ответ: 4ln(3)−4.4ln(3) — 4.

Тест по теме “Вычисление определенного интеграла”

Источник

Простое объяснение принципов решения определённых интегралов и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения определенных интегралов

Определённым интегралом функции на отрезке называется разность первообразных функции, вычисленных на концах этого отрезка.

Определённый интеграл вычисляется при помощи формулы Ньютона-Лейбница:

Для нахождения определённых интегралов, используются свойства неопределённых интегралов, правила вычисления определённых интегралов, а также таблица основных неопределённых интегралов.

Таблица основных неопределенных интегралов

Примеры решений определенных интегралов

Задача

Вычислить интеграл:

$[int_0^pi sin{x}dx]$

Решение

По таблице интегралов находим:

$[int_0^pi sin{x}dx = Bigl. -cos{x} Bigr|_0^pi = -(cospi - cos0) = -(-1 - 1) = 2]$

Ответ

$[int_0^pi sin{x}dx = 0]$

Задача

Вычислить интеграл:

$[int_0^pi -cos{x}dx]$

Решение

По таблице интегралов находим:

$[int_0^pi -cos{x}dx = Bigl. -sin{x} Bigr|_0^pi = -(sinpi - sin0) = -(0 - 0) = 0]$

Ответ

$[int_0^pi -cos{x}dx = 0]$

Задача

Вычислить интеграл:

$[int_0^1 e^{kx}dx]$

Решение

По таблице интегралов находим:

$[int_0^1 e^{kx}dx = Bigl. frac{e^{kx}}{k} Bigr|_0^1 = frac{e^{k}}{k} - frac{1}{k}]$

= $frac{e^{k} - 1}{k}$

Ответ

$[int_0^1 e^{kx}dx = frac{e^{k} - 1}{k}]$

Задача

Вычислить интеграл:

$[int_{-1}^{1} frac{1}{1 + x^{2}}dx]$

Решение

$[int_{-1}^{1} frac{1}{1 + x^{2}}dx = Bigl. arctgx Bigr|_{-1}^{1} = arctg(1) - arctg(-1) = frac{pi}{4} - (-frac{pi}{4}) = frac{pi}{2}]$

Ответ

$[int_{-1}^{1} frac{1}{1 + x^{2}}dx = frac{pi}{2}]$

Задача

Вычислить интеграл:

$[int_{0}^{sqrt{3}} frac{1}{1 + x^{2}}dx]$

Решение

$[int_{0}^{sqrt{3}} frac{1}{1 + x^{2}}dx = Bigl. arctgx Bigr|_{0}^{sqrt{3}} = arctg(sqrt{3}) - arctg(0)]$

$[ arctg(sqrt{3}) = frac{pi}{3}, arctg(0) = 0]$

$[ arctg(sqrt{3}) - arctg(0) = frac{pi}{3} - 0 = frac{pi}{3}]$

Ответ

$[int_{0}^{sqrt{3}} frac{1}{1 + x^{2}}dx = frac{pi}{3}]$

Задача

Вычислить интеграл:

$[int_{0}^{frac{pi}{4}} frac{sin{x}}{cos^{2}{x}}dx]$

Решение

Вычислим по частям неопределённый интеграл

$[int frac{sin{x}}{cos^{2}{x}}dx]$

Обозначим: $u = sin{x}, dv = frac{dx}{cos^{2}{x}}, du = cos{x}dx, v = tg{x}$

$[int frac{sin{x}}{cos^{2}{x}}dx = sin{x} tg{x} - int tg{x}cos{x}dx = sin{x} tg{x} - int sin{x}dx]$

$[int_{0}^{frac{pi}{4}} frac{sin{x}}{cos^{2}{x}}dx = Bigl. sin{x} tg{x} + cos{x} Bigr|_{0}^{frac{pi}{4}}]$

$[int_{0}^{frac{pi}{4}} frac{sin{x}}{cos^{2}{x}}dx = (sin{frac{pi}{4}} tg{frac{pi}{4}} + cos{frac{pi}{4}}) - (sin{0} tg{0} + cos{0})]$

$[int_{0}^{frac{pi}{4}} frac{sin{x}}{cos^{2}{x}}dx = frac{sqrt{2}}{2}cdot1 + frac{sqrt{2}}{2} - 1 = sqrt{2} - 1]$

Ответ

$[int_{0}^{frac{pi}{4}} frac{sin{x}}{cos^{2}{x}}dx = sqrt{2} - 1]$

Задача

Вычислить интеграл:

$[int_a^b frac{dx}{x} (a > 0, b > 0)]$

Решение

$[int_a^b frac{dx}{x} = Bigl. ln|x| Bigr|_a^b = ln|b| - ln|a|]$

Т.к. и , то:

$ln|b| - ln|a| = ln{b} - ln{a} = ln{frac{b}{a}}$

Ответ

$[int_a^b frac{dx}{x} = ln{frac{b}{a}}]$

Задача

Вычислить интеграл:

$[int_0^1 frac{dx}{1 + x}]$

Решение

$[int_0^1 frac{dx}{1 + x} = Bigl. ln(1 + x) Bigr|_0^1 = ln2 - ln1 = ln2 - 0 = ln2]$

Ответ

$[int_0^1 frac{dx}{1 + x} = ln2]$

Задача

Вычислить интеграл:

$[int_{5}^{20} frac{1}{x^{3}}dx]$

Решение

$[int_{5}^{20} frac{1}{x^{3}}dx = Bigl. -frac{1}{2x^{2}} Bigr|_{5}^{20} = -frac{1}{800} - (-frac{1}{50}) = frac{-5 + 80}{4000} = frac{3}{160}]$

Ответ

$[int_{5}^{20} frac{1}{x^{3}}dx = frac{3}{160}]$

Задача

Вычислить интеграл:

$[int_{frac{pi}{2}}^{pi}cos{x}dx]$

Решение

$[int_{frac{pi}{2}}^{pi}cos{x}dx = Bigl. sin{x} Bigr|_{frac{pi}{2}}^{pi} = sin{pi} - sin{frac{pi}{2}} = 0 - 1 = -1]$

Ответ

$[int_{frac{pi}{2}}^{pi}cos{x}dx = -1]$

Источник

Изучаем понятие «интеграл»

Неопределенный интеграл

Полная таблица интегралов для студентов

Определенный интеграл

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Свойства определенного интеграла

Примеры решения интегралов

Определённый интеграл

Геометрическое содержание определённого интеграла

Основные свойства определённого интеграла

Непосредственное вычисление определённого интеграла

Вычисление определённого интеграла методом подстановки

Вычисления определённого интеграла частями

Приближённые методы вычисления определённых интегралов

Практическое применение определённого интеграла

Вычисление площадей плоских фигур

Объём тела вращения

Путь, пройденный точкой

Сила давления жидкости

Несобственные интегралы

История определенного интеграла

Определенный интеграл в математике

Геометрический смысл интеграла

Примеры с решением

Пример 1:

Пример 2:

Понятие определенного интеграла

Пример 3:

Пример 4:

Пример 5:

Задачи, приводящие к понятию определенного интеграла

Задача о нахождении площади криволинейной трапеции

Задача об определении пройденного пути материальной точки

Задача о нахождении объема продукции

Основные свойства определенного интеграла

Связь между определенным и неопределенным интегралами

Формула Ньютона-Лейбница

Методы вычисления определенного интеграла

Непосредственное определенное интегрирование

Вычисление интеграла методом подстановки

Интегрирования по частям в определенном интеграле

Длина дуги плоской кривой

Вычисление площади геометрической фигуры

Вычисление объемов тел по известным площадям поперечных сечений

Вычисление объема тела вращения

Приближенное вычисление определенных интегралов

Формула прямоугольников

Формула трапеций

Формула Симпсона

Вычисление определённых интегралов: базовые алгоритмы

Определение интеграла

Квадратурные формулы

Вычислительная задача

Кусочно-постоянная аппроксимация

Кусочно-линейная аппроксимация

Контроль точности вычисления

Кусочно-параболическая аппроксимация

Что дальше?

Некоторые замечания

Заключение

Литература

Главная теорема интегрального исчисления

Свойства определенных интегралов

Пример 1

Пример 2

Тест по теме “Вычисление определенного интеграла”

Алгоритм решения определенных интегралов

Примеры решений определенных интегралов

Не пропустите также: