|
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и |
|
|
Создать новую модель Для расчёта необходимо полностью определить модель (с закреплением и нагрузкой) |
Операции
Узел
С чего начать построение расчётной модели — видео видео откроется в отдельной панели данного окна
| Введите координаты узла |
||
| X, м: | ||
| Y, м: |
Стержень
Для выполнения данной операции необходимо создать как минимум пару узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
С чего начать построение расчётной модели — видео видео откроется в отдельной панели данного окна
| Введите номера | ||
| первого узла: | ||
| второго узла: |
Опора одностепенная
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Развернуть на 180 град.: |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Развернуть на 180 град.: |
Запрет поворота
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Вариант ориентации | ||
| Угол поворота, град.: |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: | ||
| Вариант ориентации | ||
| Угол поворота, град.: |
Опора двухстепенная
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Развернуть на 180 град.: |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Развернуть на 180 град.: |
Опора двухстепенная
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Развернуть на 180 град.: |
Опора двухстепенная
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Вариант ориентации | ||
| Угол поворота, град.: |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: | ||
| Вариант ориентации | ||
| Угол поворота, град.: |
Жёсткая заделка
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Развернуть на 180 град.: |
Сила
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Величина силы, кН: | ||
| для смены направления силы поменяйте её знак | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Вариант изображения |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: | ||
| Величина силы, кН: | ||
| для смены направления силы поменяйте её знак | ||
| Вариант ориентации | ||
| Угол поворота, град.: | ||
| Вариант изображения |
Момент
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Момент, кН·м: | ||
| для смены направления момента измените знак его величины | ||
| Угол поворота, град.: |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: | ||
| Момент, кН·м: | ||
| для смены направления момента измените знак его величины | ||
| Угол поворота, град.: |
Распределённая нагрузка
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Нагрузка, кН/м: | ||
| для смены направления нагрузки поменяйте её знак | ||
| Нагрузка по всей длине стержня |
| Узел для отсчёта смещений: | |
| Cмещения | |
| ближнее, м: | |
| дальнее, м: |
Направление воздействияВариант изображения
Шарнир
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Принадлежность к стержню | ||
| Номер стержня: |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: |
Расчёт перемещения
Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте пункт меню «Узел» в данной панели.
| Номер узла: | ||
| Обозначение точки: | ||
| Тип перемещения | ||
| Примечание. Результат расчёта перемещения будет доступен только в отчёте. |
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
| Номер стержня: | ||
| Узел для отсчёта смещения: | ||
| Смещение, м: | ||
| Обозначение точки: | ||
| Тип перемещения | ||
| Примечание. Результат расчёта перемещения будет доступен только в отчёте. |
Жёсткость
Жёсткость предназначена для определения перемещения, для чего необходимо задать точку расчёта перемещения (диалог «Расчёт перемещения»). Так как точка расчёта перемещения не определена, задание жесткости смысла не имеет.
| Задайте коэффициент жёсткости № 2 : |
| {EJ}2= ∗EJ |
Назначить жёсткость
Жёсткость предназначена для определения перемещения, для чего необходимо задать точку расчёта перемещения (диалог «Расчёт перемещения»). Так как точка расчёта перемещения не определена, задание жесткости смысла не имеет.
| Номер назначаемой жёсткости: | ||
| Номер(а): | ||
| Введите номера стержней, которым необходимо назначить заданную выше жёсткость. В случае нескольких стержней вводите номера через запятую. |
Подбор сечения
| Выполнить подбор сечения |
Параметры расчёта
| Допустимое напряжение [σ], МПа: | |
| Коэффициент запаса: |
Тип сеченияПараметры сечения
| Тип сечения: | |
Параметры сечения
| Соотношение h/w (высота/ширина): |
Примечание. Результат подбора сечения будет доступен только в отчёте.
Настройки
Эпюру изгибающего момента (Mx) строить на
сжатом волокне
растянутом волокне
для строителей
Учёт жёсткости
аналитически
численно
Перемножение эпюр
способ Верещагина
метод Симпсона
Компоновка результата
Состав модели
В данном расчёте не задано ни одного объекта. Для создания объектов модели перейдите в раздел «Операции»
Определение опорных реакций
Построение эпюр поперечных сил и моментов
Просмотр хода решения
Расчет выполняется по следующей методике:
1. Заменяем распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка L, на котором она действует: Fq = q*L.
2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и одну шарнирно-подвижную опоры.
3. Освобождаемся от опор и заменяем их действие на балку реакциями.
Реакции опор при такой нагрузке будут только вертикальными.
4. Составляем уравнения равновесия вида:
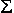
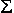
Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).
5. Выполним проверку решения. Для этого составим уравнение равновесия:
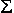
Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.
6. Строим эпюру поперечных сил Qx. Для этого определяем значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Qлев и Qправ.
Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:
а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;
б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.
Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Qx.
7. Строим эпюру изгибающих моментов Мx. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно Млев и Мправ. В точках приложения сил определяется одно значение изгибающего момента.
Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:
а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;
б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.
Пример решения балки:
Данный онлайн калькулятор предназначен для нахождения опорных реакций в простейшей балке, находящейся под воздействием поперечных сил. Простая балка — прямолинейный брус, закрепленная на двух опорах: одной — шарнирно-неподвижной (опора А), другой — шарнирно-подвижной (опора В). Калькулятор выводит опорные реакции VA и VB, уравнения равновесия в символьном виде и показывает модель нагрузок. Обратите внимание, что если требуется задать нагрузку действующую левее опоры A, то расстояние от опоры нужно задать со знаком минус. Теорию и формулы расчета можно найти ниже под калькулятором.
Опорные реакции простой балки
Расстояние между опорами, м
Нагрузка
| Расстояние от опоры A | Нагрузка | Значение | Направление | Направление момента | Протяженность | Изменение | ||
|---|---|---|---|---|---|---|---|---|
Точность вычисления
Знаков после запятой: 2
Положительное направление момента сил
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Реакции опор
Под воздействием нагрузок в опорах балки возникают уравновешивающие силы, называемые реакциями опор. Эти силы зависят от вида нагрузки и типа самих опор.
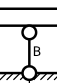
Шарнирно подвижная опора ( в нашей модели обозначена как «B») позволяет балке свободно перемещаться в горизонтальной плоскости и препятствует вертикальному перемещению, поэтому при любой нагрузке она имеет только вертикальную реакцию VB.
Шарнирно неподвижная опора крепится к балке, что препятствует её горизонтальному и вертикальному перемещению. При наличии сил, действующих на балку в горизонтальной плоскости, эта опора дает еще и горизонтальную реакцию. Однако в нашей модели все силы действуют поперечно балке, поэтому горизонтальная реакция опоры A всегда будет равна нулю. Вертикальную реакцию опоры A обозначим VA.
Уравнения равновесия
Как мы знаем из статики, все силы и моменты сил в неподвижной системе, уравновешены. Поэтому суммы сил и моментов в любой точке этой системы равны нулю.
Все силы при поперечной нагрузке на простую балку действуют параллельно оси Y, поэтому можно составить только два независимых уравнения равновесия для проекции сил и моментов на ось Y. Этого вполне достаточно для нахождения двух неизвестных реакций опор VA и VB.
При составлении уравнений у нас есть выбор:
- составить одно уравнение равновесия проекции сил и одно уравнение равновесия моментов в некоторой точке
- составить два уравнения равновесия моментов в двух точках.
Воспользуемся вторым способом, а первый оставим для проверки полученного результата.
Удобнее всего составлять уравнения для точек А и B, в которых находятся опоры:
Напомним, что моментом силы в определенной точке называется произведение силы F на кратчайшее расстояние от этой точки до линии действия силы (плечо) l:
Исходя из этого, уравнения равновесия моментов в точках А и B для системы поперечных сил F1…Fn, действующих на балку приобретают вид:
Где Fi — модуль приложенной силы или реакции опоры в Ньютонах. liA и liB — длина рычага в метрах (кратчайшее расстояние от точки приложения силы i до опоры A и B соответственно). siA и siB — знак момента силы i в точке A и B соответственно.
Правило выбора знаков момента сил: знак положительный (+1) для момента, закручивающего балку вокруг выбранной точки по часовой стрелке ↻ и отрицательный (-1) для противоположного направления ↺. Можно выбрать и противоположные значения. Уравнения примут немного другой вид, но результат от этого не изменится.
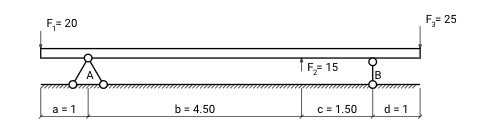
Например, для системы сил, показанной на рисунке выше, уравнения равновесия можно записать следующим образом:
Вычисляя, получаем значения реакций опор: VA = 15.42 и VB = 14.58. Проверим, что сумма всех сил равна нулю (для сил действующих вниз — знак положительный, для действующих вверх — отрицательный):
Составляя уравнения, мы исходили из того, что реакции обеих опор направлены вверх. При расчетах может получиться так, что реакция опоры окажется отрицательной. Это означает, что реакция такой опоры направлена вниз (сумма моментов сил, действующих на балку, пытается оторвать её от опоры).
Распределенная нагрузка
В расчетах, иногда требуется задать нагрузку, которая распределена определенным образом по участку длины a. Для вычисления реакций опор такую нагрузку можно заменить её равнодействующей силой. Точкой приложения такой силы считается центр масс распределенной нагрузки, а модуль вычисляется как интеграл от функции распределения нагрузки на заданном участке. Для простых функций модуль легко выразить через заданную интенсивность нагрузки.
В таблице ниже представлены формулы для модуля сосредоточенной равнодействующей силы и точек её приложения для всех видов распределенных нагрузок, поддерживаемых калькулятором:
В формулах q — это интенсивность нагрузки в Н/м, a — диапазон действия распределенной нагрузки, точка приложения силы отсчитывается от начала диапазона действия распределенной нагрузки. Интенсивность для линейно распределенной нагрузки задается для участка максимума нагрузки ( полагаем, что в точке минимума, интенсивность = 0).
После вычисления модуля и плеча равнодействующей распределенной нагрузки их можно подставить в уравнения моментов, точно так же, как мы это делали с сосредоточенными силами.
Сосредоточенный момент
Еще один способ задания нагрузки в калькуляторе — при помощи момента в Нм, приложенного к некоторой точке. Значение сосредоточенного момента добавляется к уравнениям равновесия со знаком, определяемым направлением момента в соответствии с правилом знаков. Точка приложения сосредоточенного момента для вычисления реакций опор в простой балке значения не имеет.



Укажите тип балки и количество нагрузок:
 Двухопорная балка |
 Двухопорная балка консоль слева |
||
 Двухопорная балка консоль справа |
 Двухконсольная балка |
||
 Заделка слева |
 Заделка справа |
| Количество распределенных нагрузок qi: | |
| Количество сосредоточенных сил Fi: | |
| Количество внешних моментов Mi: |
Единицы измерения (сила / длина):

Инструкция
Новый расчет
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
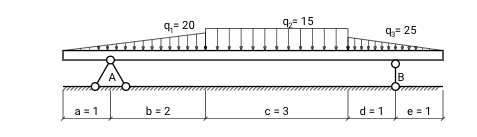
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
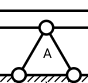
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!







