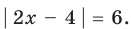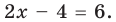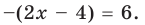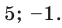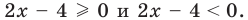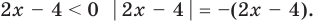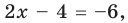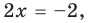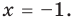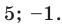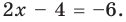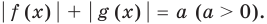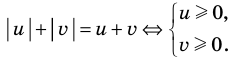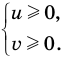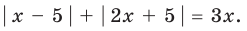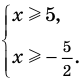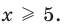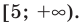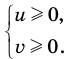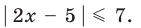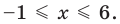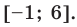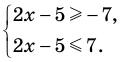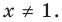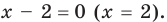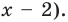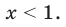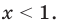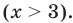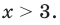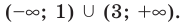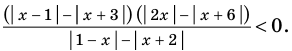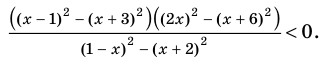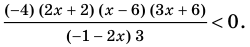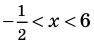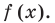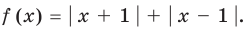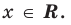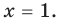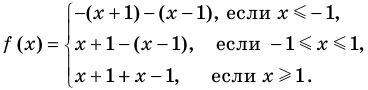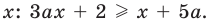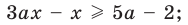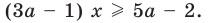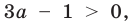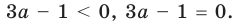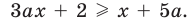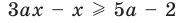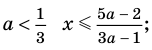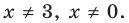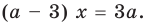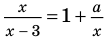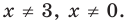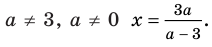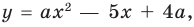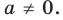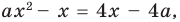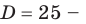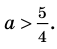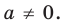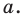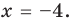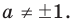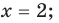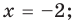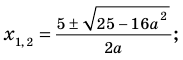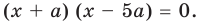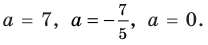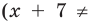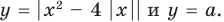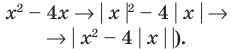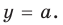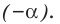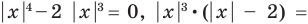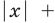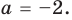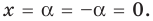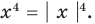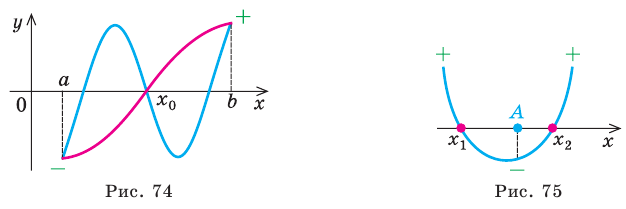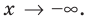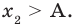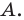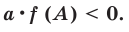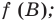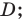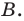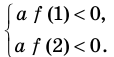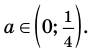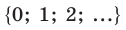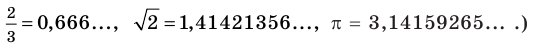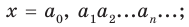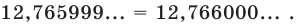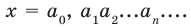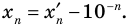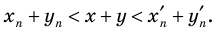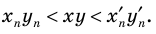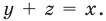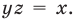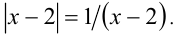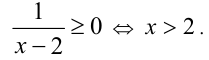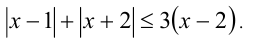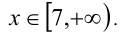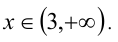Учет области значений модуля при решении уравнения
23 мая 2014
Очень часто в уравнениях под знаком модуля стоят довольно сложные конструкции, которые было бы крайне затруднительно раскрывать, а затем решать «напролом». Для таких случаев существует множество приемов и замечаний, позволяющих значительно ускорить вычисления.
Одним из таких приемов является учет области значений модуля (учителя называют это решение методом следствий). Суть его можно описать одним простым предложением: «Сумма неотрицательных чисел равна нулю тогда и только тогда, когда каждое из этих чисел равно нулю».
Сегодня мы продолжаем изучать конструкции, содержащие знак модуля функции и переходим уже к более сложным конструкциям, когда ихдва, либо само уравнение содержит нестандартную функцию.
Немного теории
Для начала вспомним определение модуля: модулем числа $x$ называется либо само это число (при условии, что оно неотрицательное), либо минус это число, если оно отрицательно:
[left| x right|=left{ begin{align}& x,xge 0 \& -x,x<0 \end{align} right.]
Данная запись является алгебраическим определением, потому что здесь используется только алгебраическая терминология и никак не привлекается геометрия. И именно это определение позволяет нам заключить следующий факт: модуль числа всегда неотрицателен:
[left| x right|ge 0]
Именно поэтому его иногда еще называют абсолютным значением, т.е. расстоянием от 0 до этого числа на числовой прямой. И именно тот факт, что модуль функции всегда является неотрицательным числом, позволяет решить целый класс задач, которые иначе решались бы весьма проблематично.
Решаем реальные задачи
Пример № 1
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Чтобы решить такое выражение, давайте для начала вспомним, как решается простейшая конструкция с модулем, т.е уравнение вида $left| f right|=g$.
Решаются она довольно просто. Рассматривается два случая: в первом случае $f$ неотрицательно — в этом случае модуль функции снимается без всяких изменений и получается, что $f$ равно $g$. А во втором случае $f$ отрицательно — в этом случае модуль раскрывается со знаком «минус», как мы уже знаем из определения. Запишем совокупность систем:
[left| f right|=g=>left[ begin{align}& left{ begin{align}& fge 0 \& f=g \end{align} right. \& left{ begin{align}& f<0 \& -f=g \end{align} right. \end{align} right.]
Но все это работает только при условии, что модуль функции в выражении один, а у нас сегодня сразу два. Что делать в такой ситуации?
Давайте заметим, что при сложении двух модулей возникает выражение, значение которого 0. Но, с другой стороны, мы можем записать следующее:
[left| x-{{x}^{3}} right|ge 0]
[left| {{x}^{2}}+x-2 right|ge 0]
В этом случае сумма вышеописанных двух элементов также будет давать некое число (назовем его $k$), которое больше или равняется 0. При этом от нас требуется, чтобы оно строго равнялось 0. А это значит, что нас устроит только тот вариант, когда каждый из модулей равен 0, т.е. мы можем записать:
[left| x-{{x}^{3}} right|=0]
[left| {{x}^{2}}+x-2 right|=0]
Другими словами, сумма двух чисел, каждое из которых не меньше 0, дает в сумме ноль только в том случае, когда каждое из них равняется 0, т.е. требования должны выполняться одновременно. Поэтому запишем систему:
[left{ begin{align}& left| x-{{x}^{3}} right|=0 \& left| {{x}^{2}}+x-2 right|=0 \end{align} right.]
Модуль функции равен 0, когда подмодульное выражение равно 0, т.е:
[left{ begin{align}& x-{{x}^{3}}=0 \& {{x}^{2}}+x-2=0 \end{align} right.]
Давайте решим каждое из полученных выражений отдельно. Решаем первое:
[xleft( {{1}^{2}}-{{x}^{2}} right)=0]
[xleft( 1-x right)left( 1+x right)=0]
[{{x}_{1}}=0]
[{{x}_{2}}=1]
[{{x}_{3}}=-1]
При трех таких значениях тождество обнуляется.
Теперь разберемся со вторым выражением. Будем решать его при помощи формулы Виета:
[{{x}^{2}}+x-2=0]
[left( x+2 right)left( x-1 right)=0]
[{{x}_{1}}=-2]
[x=1]
А теперь вспоминаем, что мы решаем систему уравнений, т.е. нужно из первого и из второго наборов выбрать корни, которые принадлежат каждому из этих наборов. Очевидно, что такой корень только один — $x=1$.
Итого решением первого выражения является единственный корень $x=1$.
Как видите, такое решение оказалось существенно проще стандартного подхода. Здесь достаточно просто заметить,что сумма двух неотрицательных чисел равняется 0 только тогда, когда каждое из этих чисел имеет значение 0.
Пример № 2
Переходим ко второй конструкции:
[left| x-2 right|=-{{x}^{6}}]
На первый взгляд, можно сказать, что данная конструкция является простейшим уравнением. И, строго говоря, оно хорошо решается по выше записанной формуле, т.е. переходом от выражения с модулем функции к совокупности двух систем. Однако нас смущает степенная функция — степень слишком большая. Поэтому давайте заметим, что функция $fleft( x right)={{x}^{6}}$ является не просто четной, но и еще неотрицательной на всей числовой оси. А это значит, что $-{{x}^{6}}$ всегда будет либо отрицательной, либо равняться 0. Однако с другой стороны от знака равенства у нас стоит модуль функции — а он всегда неотрицателен. Это значит что, слева значение больше или равно нулю, а справа — меньше или равно. И от нас требуется узнать, когда эти значения друг другу тождественны. Очевидно, что такими они могут быть только тогда, когда каждое из них равняется 0, потому что в противном случае они будут лежать по разные стороны от разделяющего 0, т.е. $left| x-2 right|$ будет постоянно отклоняться вправо, а $-{{x}^{6}}$ — влево. Поэтому наше выражением может быть переписано следующим образом:
[left{ begin{align}& left| x-2 right|=0 \& -{{x}^{6}}=0 \end{align} right.]
Давайте решим эти конструкции:
[left{ begin{align}& x-2=0 \& {{x}^{6}}=0 \end{align} right.]
Решаем каждое из этих выражений:
[left{ begin{align}& x=2 \& x=0 \end{align} right.]
Мы получаем, что корень должен быть одновременно равен и 2 и 0. Это невозможно, поэтому решением данного выражения является пустое множество. Пусть вас не смущают подобные ответы при решении задач с модулями. Как и при работе с любыми другими функциями, накладывающими ограничения на область определения или значения в рамках задачи, в процессе решения сложных выражений с модулями функции вполне может оказаться, что этих решений просто не существует.
Ключевые моменты
- Сумма двух неотрицательных чисел равна нулю тогда, когда каждое из этих чисел равно нулю. В результате уравнение, которое само по себе далеко не тривиальное, разбивается на систему из двух отдельных уравнений, каждое из которых решается существенно проще.
- Тот факт, что модуль сам по себе является неотрицательным значением, можно использовать и иначе, например, когда с одной стороны стоит модуль функции (эта сторона неотрицательна), а с другой стороны — функция, которая меньше нуля или равна нулю. В этом случае все уравнение сводится к системе из двух уравнений, каждое из которых легко решается.
Как пример, второе вырадением может быть сведено к равенству первого вида следующим образом:
[left| x-2 right|+{{x}^{6}}=0]
Мы снова видим сумму двух функций, каждая из которых неотрицательна. Запомните этот прием, он очень эффективен при работе со всевозможными функциями, о которых точно известно, что они принимают лишнее отрицательное значение.
Смотрите также:
- Нестандартные уравнения с модулем
- Дробно-рациональные уравнения с модулем
- Тест к уроку «Что такое числовая дробь» (легкий)
- Сводный тест по задачам B15 (2 вариант)
- Как решать простейшие логарифмические уравнения
- Задача B4: вклад в банке и проценты
Содержание:
Уравнения и неравенства, содержащие знак модуля
Объяснение и обоснование:
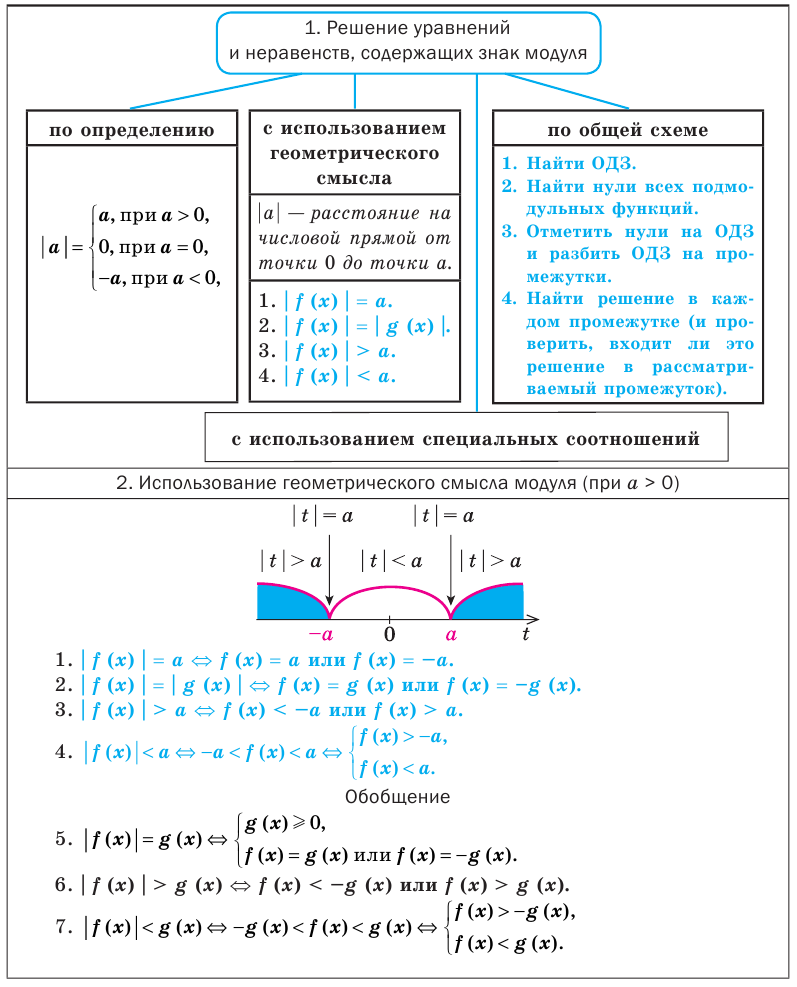
Решать любое уравнение или неравенство, содержащее знак модуля можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства, содержащие знак модуля, могут быть также решены с использованием специальных соотношений (табл. 15).
В зависимости от выбранного способа решения получаем разные записи решения.
Пример №441
Решите уравнение
I способ (по определению модуля)
Решение:
► 1) Если
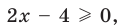
то получаем уравнение
Тогда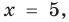
2) Если
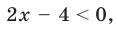
то получаем уравнение
Тогда 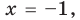
Ответ:
Комментарий:
Чтобы раскрыть знак модуля по определению, рассмотрим два случая:
По определению модулем положительного (неотрицательного) числа является само это число, а модулем отрицательного числа является противоположное ему число. Поэтому при 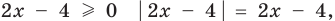
В каждом случае решаем полученное уравнение и выясняем, удовлетворяет ли каждый из найденных корней тому условию, при котором мы его находили.
II способ (использование геометрического смысла модуля)
Решение:
► 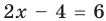
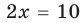
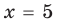
Ответ:
Комментарий:
С геометрической точки зрения 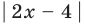

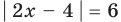
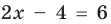
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств, содержащих знак модуля, — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции 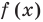
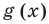
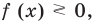
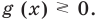
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции 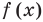
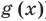
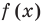
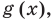
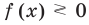
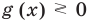
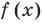
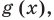
В каждом из полученных промежутков знаки функций 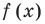
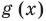
Примеры решения задач:
Пример №442
Решите уравнение
Решение:
► 1. ОДЗ:
2. Нули подмодульных функций:
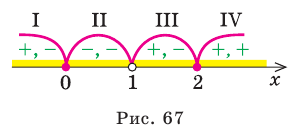
3. Нули 0 и 2 разбивают ОДЗ на четыре промежутка, в которых подмодульные Рис. 67 функции имеют знаки
4. Находим решения данного уравнения в каждом из промежутков (поскольку знаки подмодульных функций одинаковы на промежутках I и III, удобно для решения объединить эти промежутки). Промежутки I и III: 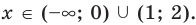
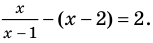
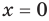
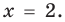
Промежуток II: 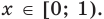
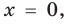
промежутке получаем уравнение 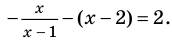
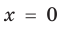
Промежуток IV: 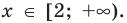
забыть значение 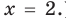
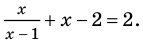
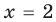
Ответ: 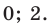
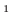
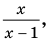
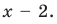
отметить на числовой прямой ОДЗ, а потом нули подмодульных функций на ОДЗ.
Проиллюстрируем также получение и использование специальных соотношений, приведенных в таблице 15.
Обоснуем, например, соотношение 5:
Запишем заданное равенство в виде 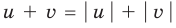
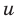
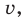
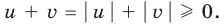
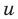
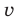
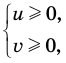
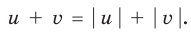
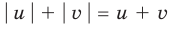
Пример №443
Решите уравнение
Решение:
► Поскольку 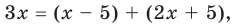
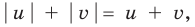
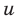
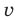
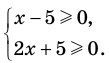
Таким образом,
Ответ:
Комментарий:
Если обозначить 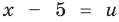
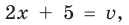
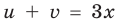
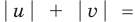
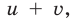
Заметим, что данное уравнение можно решать и по общей схеме, но тогда решение будет более громоздким.
При решении неравенств, содержащих знак модуля, рассуждения, связанные с раскрытием знаков модулей, полностью аналогичны рассуждениям, которые использовались при решении уравнений, содержащих знак модуля.
Пример №444
Решите неравенство
Решение:
► Учитывая геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству
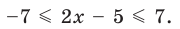
Тогда 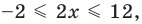
Ответ:
Комментарий:
Неравенство вида 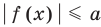
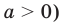
Поскольку заданное неравенство — это неравенство вида 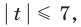
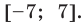
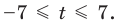
Пример №445
Решите неравенство 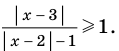
Решение:
► 1. ОДЗ: 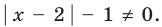
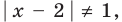
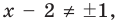
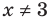
2. Нули подмодульных функций: 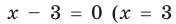
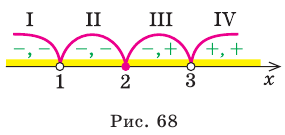
3. Нуль 2 разбивает ОДЗ на четыре промежутка, на которых подмодульные функции имеют знаки, показанные на рисунке 68 (на каждом из промежутков первый знак — это знак функции 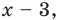
4. Находим решения заданного неравенства в каждом из промежутков (поскольку знаки подмодульных функций являются одинаковыми на промежутках I и II, удобно для решения объединить эти промежутки). Промежутки I и II: 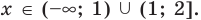
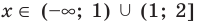
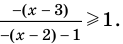
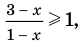
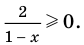
В промежутки, которые мы рассмотрели, входят все значения 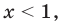
Промежуток III: 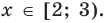
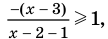
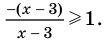
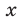
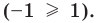
Промежуток IV: 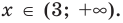
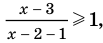
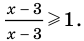
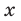
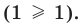
есть любое число из этого промежутка
Объединяя все решения, полученные в каждом из промежутков, имеем решение данного неравенства на всей ОДЗ: 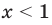
Ответ:
Укажем, что для решения некоторых неравенств, содержащих знак модуля, удобно применять также специальные соотношения, приведенные в таблице 15.
Пример №446
Решите неравенство
Решение:
► Поскольку 
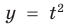
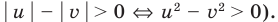
Раскладывая на множители все разности квадратов, имеем:
Далее методом интервалов получаем 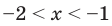
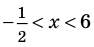
Ответ: 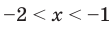
Общая схема, предложенная в таблице 15, может быть использована не только при решении уравнений или неравенств, содержащих знак модуля, но и при преобразовании выражений, содержащих знак модуля.
Например, для построения графика функции 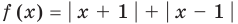
Оформление решения подобного примера может быть таким.
Пример №447
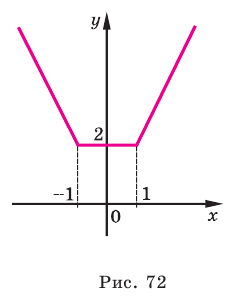
Постройте график функции
► 1. Область определения функции: все
2. Нули подмодульных функций: 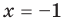
3. Отмечаем нули на области определения и разбиваем область определения на промежутки (на рисунке 71 также указаны знаки подмодульных функций в каждом из промежутков).
4. Тогда
Таким образом,
Строим график этой функции (рис. 72).
Уравнения и неравенства с параметрами
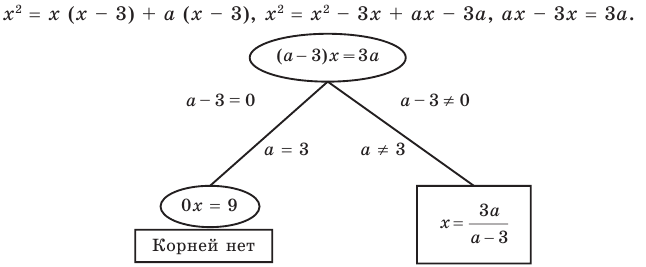
Решение уравнений и неравенств с параметрами
Если в запись уравнения или неравенства, кроме переменной и числовых коэффициентов, входят также буквенные коэффициенты — параметры, то при решении таких уравнений можно пользоваться следующим ориентиром.
Любое уравнение или неравенство с параметрами можно решать как обычное уравнение или неравенство до тех пор, пока все преобразования или рассуждения, необходимые для решения, можно выполнить однозначно. Если какое-то преобразование нельзя выполнить однозначно, то решения необходимо разбить на несколько случаев, чтобы в каждом из них ответ через параметры записывался однозначно.
На этапе поиска плана решения уравнения или неравенства с параметрами или в ходе решения часто удобно сопровождать соответствующие рассуждения схемами, по которым легко проследить, в какой момент мы не смогли однозначно выполнить необходимые преобразования, на сколько случаев пришлось разбить решение и чем отличается один случай от другого. Чтобы на таких схемах (или в записях громоздких решений) не потерять какой-то ответ, целесообразно помещать окончательные ответы в прямоугольные рамки. Записывая окончательный ответ, следует учитывать, что ответ должен быть записан для всех возможных значений параметра.
Пример №448
Решите неравенство с переменной
Комментарий:
Заданное неравенство является линейным относительно переменной 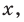
1) переносим члены с переменной 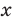
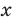
2) выносим в левой части за скобки общий множитель 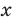
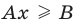
Для решения последнего неравенства мы хотели бы разделить обе его части на 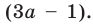
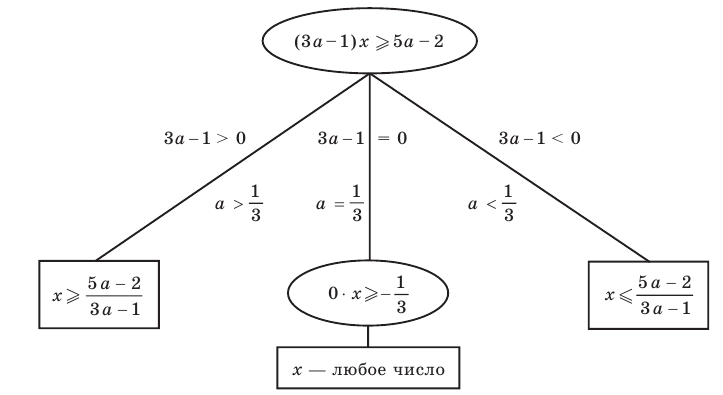
Приведенные выше рассуждения можно наглядно записать так:
Решение:
►
Ответ: 1) при 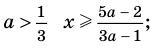
3) при 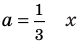
При решении более сложных уравнений или неравенств следует помнить, что уравнения и неравенства с параметрами чаще всего решают с помощью равносильных преобразований, а все равносильные преобразования уравнений или неравенств выполняют на области допустимых значений (ОДЗ) заданного уравнения или неравенства (то есть на общей области определения для всех функций, которые входят в запись уравнения или неравенства). Поэтому, прежде чем записать ответ, нужно обязательно учесть ОДЗ заданного уравнения или неравенства.
Пример №449
Решите уравнение 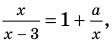
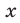
Комментарий:
Заданные дробные выражения существуют тогда и только тогда, когда знаменатели заданных дробей не равны нулю, следовательно, ОДЗ уравнения:
Умножим обе части заданного уравнения на выражение 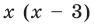
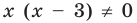
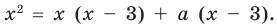
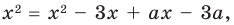
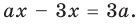
Для того чтобы найти значение переменной 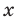
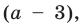
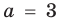
Решение в соответствии с приведенными выше рассуждениями можно наглядно записать в виде схемы.
Решение:
► ОДЗ:
Выясним, при каких значениях 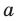
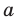
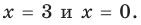
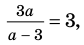
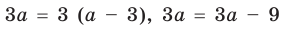
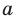
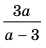
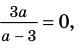
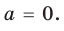
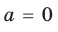
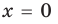
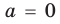
Ответ: 1) при 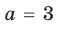
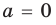
Пример №450
Решите уравнение 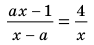
Комментарий:
Будем выполнять равносильные преобразования заданного уравнения. Для этого найдем его ОДЗ (знаменатели дробей не равны нулю). Если теперь обе части уравнения умножить на произведение выражений, которые стоят в знаменателях дробей (и которое не равно нулю на ОДЗ уравнения), то получим уравнение 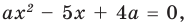
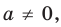
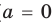
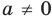
Если 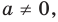
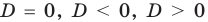
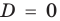
то есть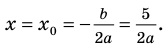

Поскольку корни уравнения (1) записываются достаточно громоздкими формулами (см. решение), то вместо подстановки полученных корней в ограничение ОДЗ можно подставить «запрещенные» значения 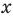
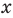
Решение:
► ОДЗ: 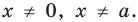
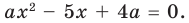
1. Если 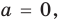
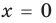
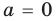
2. Если 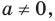
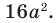
1) 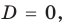
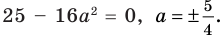
значение корня: 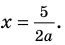
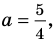
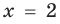
входит в ОДЗ и является корнем заданного уравнения. Если 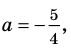
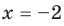
2) 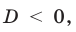
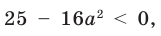
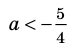
Тогда уравнение (1) не имеет корней.
3) 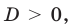
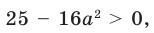
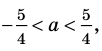
Тогда уравнение (1) имеет два корня:
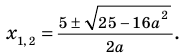
Выясним, при каких значениях 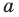
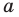
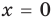
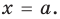
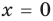
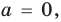
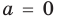
Подставляя в уравнение (1) 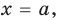

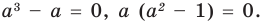
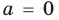
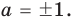
При 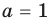
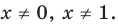
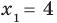
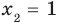
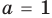
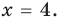
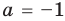
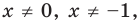
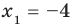
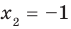
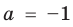
Таким образом, формулу корней (2) можно использовать, если 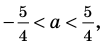
Ответ: 1) если 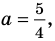
2) если 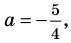
3) если 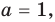
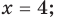
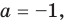
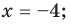
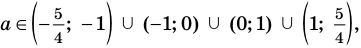
6) если 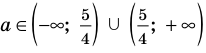
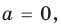
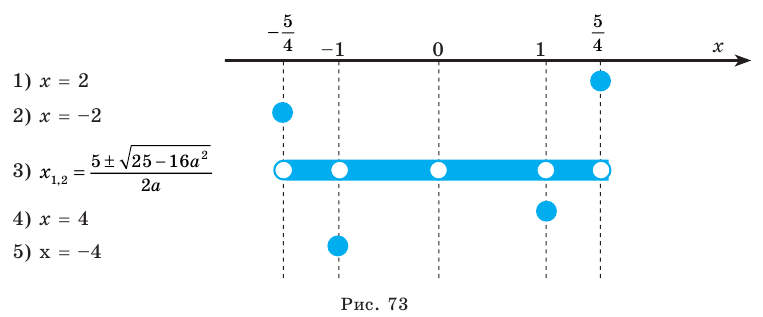
Замечание. Чтобы облегчить запись ответа в этом и аналогичных примерах, можно пользоваться таким приемом. Перед записью ответа в сложных или громоздких случаях изобразим ось параметра (а) и отметим на ней все особые значения параметра, которые появились в процессе решения. Под осью параметра (левее от нее) выпишем все полученные решения (кроме решения «корней нет») и напротив каждого ответа отметим, при каких значениях параметра этот ответ можно использовать (рис. 73). После этого ответ записывают для каждого из особых значений параметра и для каждого из полученных промежутков оси параметра. В частности, перед записью ответа в рассмотренном примере, на черновике удобно изобразить такую схему (рис. 73).
Исследовательские задачи с параметрами
Некоторые исследовательские задачи с параметрами удается решить по такой схеме: 1) решить заданное уравнение или неравенство; 2) исследовать полученное решение.
Пример №451
Найдите все значения 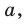
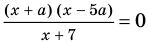
Решение:
► ОДЗ: 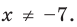
Тогда 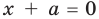
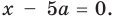
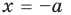
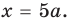
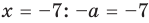
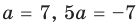
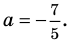
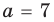
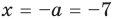
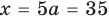
При 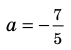
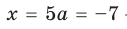
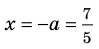
единственный корень. Также заданное уравнение будет иметь единственный корень, если 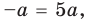
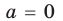
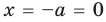
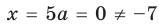
Ответ:
Комментарий:
Поскольку дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю, то на ОДЗ 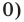
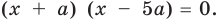
После этого выясним, при каких значениях 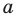
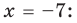
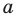
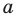
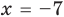
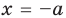
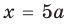
Исследование количества решении уравнении и их систем
При решении некоторых задач с параметрами можно пользоваться таким ориентиром: если в задаче с параметрами речь идет о количестве решений уравнения (неравенства или системы), то для анализа заданной ситуации часто удобно использовать графическую иллюстрацию решения.
Наиболее простым соответствующее исследование является в том случае, когда заданное уравнение можно преобразовать к виду 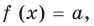
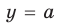
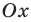
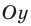
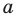
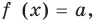
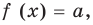
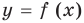
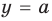
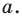
- Заказать решение задач по высшей математике
Пример №452
Сколько корней имеет уравнение 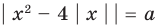
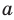
Решение:
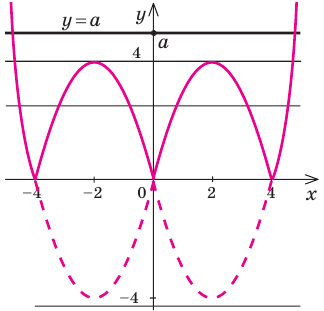
► Построим графики функций
Анализируя взаимное размещение полученных графиков, получаем ответ:
1) при 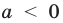
2) при 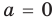
3) при 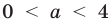
4) при 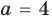
5) при 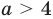
Комментарий:
Поскольку в этом задании речь идет о количестве решений уравнения, то для анализа заданной ситуации попробуем использовать графическую иллюстрацию решения.
1. Строим график функции (учитывая, что 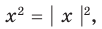
2) Строим график функции
3) Анализируем взаимное размещение полученных графиков и записываем ответ (количество корней уравнения 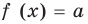
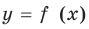
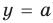
Отметим, что значительное количество исследовательских заданий не удается решить путем непосредственных вычислений (или такие вычисления являются очень громоздкими). Поэтому часто приходится сначала обосновывать какое-то свойство заданного уравнения или неравенства, а затем, пользуясь этим свойством, уже давать ответ на вопрос задачи.
Например, принимая во внимание четность функций, которые входят в запись заданного уравнения, можно использовать такой ориентир.
Если в уравнении 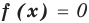
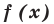
Пример №453
Найдите все значения параметра 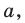
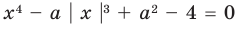
Решение:
► Функция 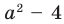
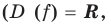
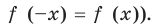
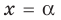
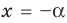
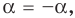
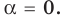
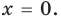
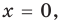
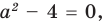
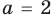
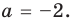
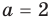
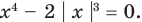
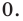
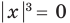
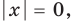
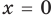
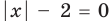
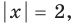
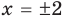
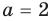
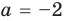
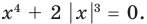
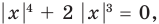
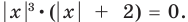
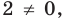
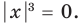
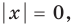
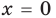
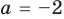
Ответ:
Комментарий:
Замечаем, что в левой части заданного уравнения стоит четная функция, и используем ориентир, приведенный выше. Действительно, если 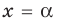
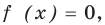
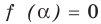
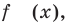
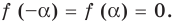
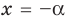
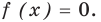
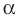
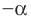
Выясним, существуют ли такие значения параметра 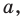
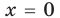
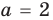
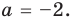
Поскольку значение 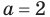
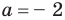
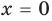
Использование условий расположения корней квадратного трехчлена
Использование условий расположения корней квадратного трехчлена 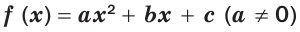
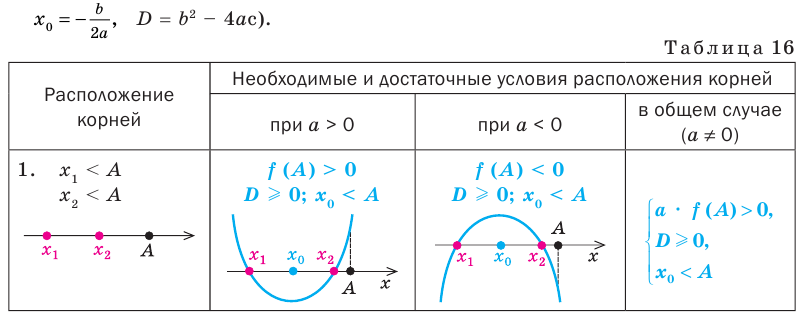
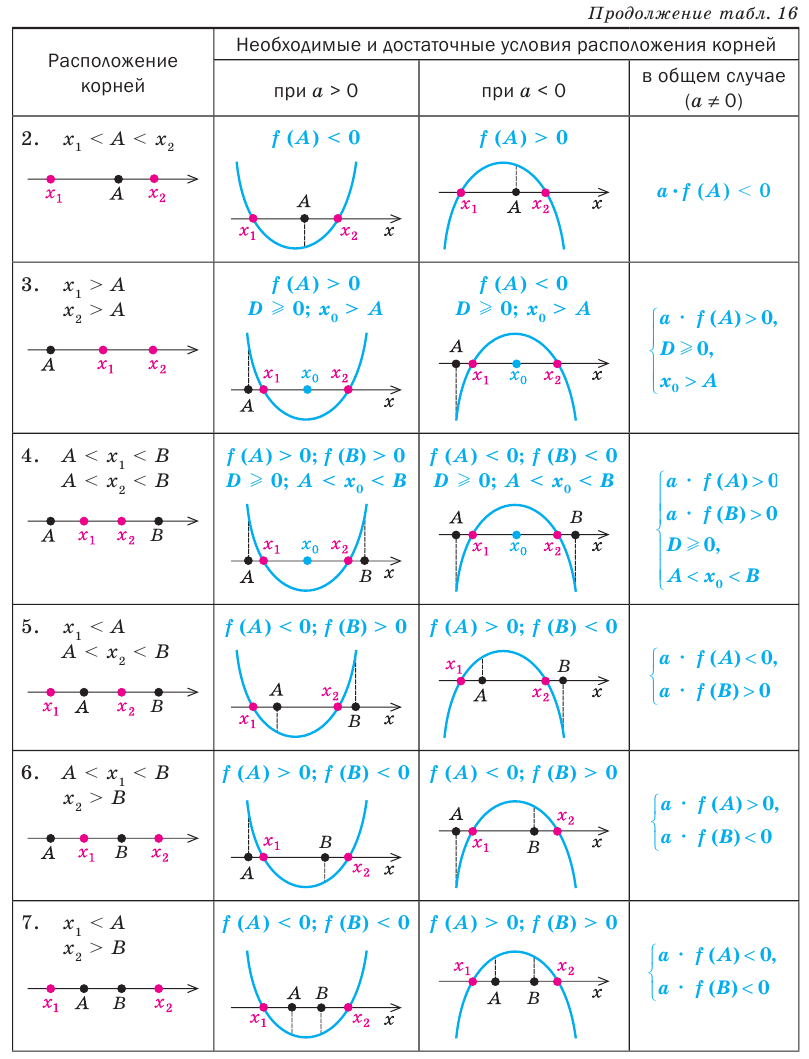
Решение некоторых исследовательских задач с параметрами можно свести к использованию необходимых и достаточных условий расположения корней квадратного трехчлена. Основные из этих условий приведены в таблице 16 (в таблице использованы традиционные обозначения:
Объяснение и обоснование:
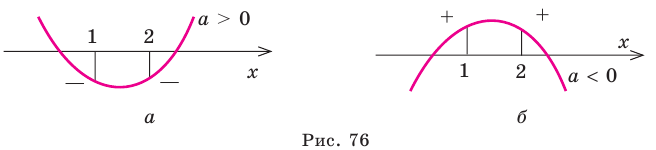
Для обоснования указанных условий достаточно воспользоваться тем, что график функции 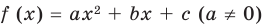
Например, для того чтобы два различных корня квадратного трехчлена 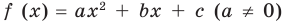

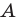
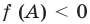
Действительно, график квадратичной функции 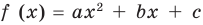
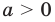
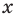

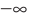
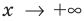
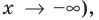
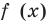
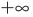
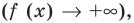
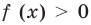
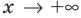
Если выполняется условие 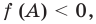
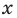
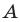
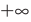
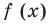
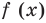
Точно так же с изменением значения аргумента 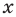
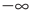
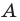
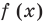
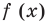
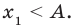
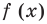

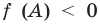
Аналогичные рассуждения при 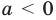
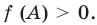
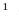
Действительно, 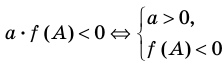
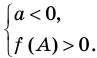
квадратный трехчлен 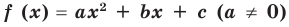
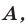
Аналогично можно обосновать и другие условия, приведенные в таблице 16.
Заметим, что приведенные условия не обязательно запоминать: для их записи можно пользоваться графиком квадратичной функции (изображенным для нужного расположения корней) и таким ориентиром.
Для того чтобы корни квадратного трехчлена 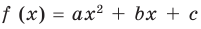
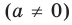
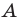
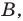
1) знак коэффициента при старшем члене;
2) знаки значений 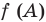
3) знак дискриминанта
4) положение абсциссы вершины параболы 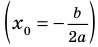
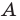
Отметим, что для случаев, в которых хотя бы одно из данных чисел расположено между корнями квадратного трехчлена (см. вторую, пятую, шестую и седьмую строки табл. 16), достаточно выполнения первых двух условий этого ориентира, а для других случаев приходится рассматривать все четыре условия. Заметим также, что, записывая каждое из указанных условий, следует выяснить, будет ли выполняться требование задачи в том случае, когда в этом условии будет записан знак нестрогого неравенства.
Пример №454
Найдите все значения параметра 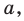
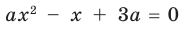
Комментарий:
Поскольку заданное уравнение имеет два различных корня, то оно квадратное (то есть 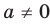
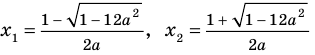
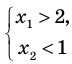
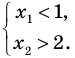
Попробуем воспользоваться условиями расположения корней квадратного трехчлена. Для этого можно непосредственно использовать соответствующие условия, зафиксированные в таблице 16, или получить их с помощью предложенного ориентира. В частности, обозначим 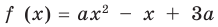
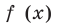
Для того чтобы корни квадратного трехчлена располагались по разные стороны от чисел 1 и 2, необходимо и достаточно выполнения совокупности условий 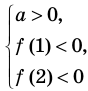
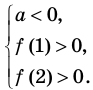
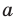
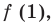
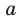
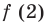
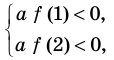
Решение:
► Поскольку заданное уравнение имеет два различных корня, то оно является квадратным (то есть 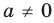
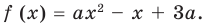
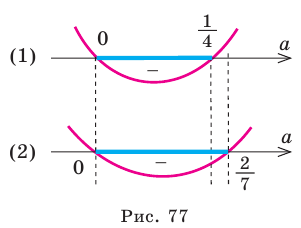
Получаем систему
Решаем неравенства (1) и (2) и находим общее решение системы (рис. 77).
Ответ: заданное уравнение имеет один корень больше двух, а второй — меньше единицы при
Сведения из истории:
Напомним, что алгебра — раздел математики, посвященный изучению буквенных выражений и уравнений. Долгое время алгебра была частью науки о числе — арифметики. Значительное количество задач, возникающих в процессе практической деятельности человека, решают одинаковыми способами. Используя вместо чисел буквы, математики научились решать такие задачи в общем виде. Так и образовалась математическая наука — алгебра.
Исторически зачатки алгебры были известны вавилонянам, египтянам и грекам задолго до нашей эры. Сохранился египетский папирус Ахмеса (XVII в. до н. э.) с решением алгебраических задач. Ученые Вавилона (более 4000 лет назад) умели находить приближенное значение квадратного корня из любого натурального числа, а также решать квадратные уравнения. Это было связано с решением задач на нахождение площадей земельных участков и с развитием астрономии. Однако у вавилонян еще не было понятия отрицательного числа, и поэтому корень квадратного уравнения мог быть только положительным.
Диофант, греческий математик, живший в III в. в Александрии, написал трактат «Арифметика», в котором он уже решал линейные и другие уравнения. В Средние века особенно активно алгебра развивалась в арабских странах и Средней Азии.
Задачи, связанные с квадратными уравнениями, можно найти и в трудах индийских математиков V в. Квадратные уравнения классифицировал в трактате «Алгебра» аль-Хорезми. Он же привел и способы их решения.
В течение многих веков развитие алгебры сильно тормозилось, потому что математикам долго не удавалось ввести в свои исследования удобные обозначения. Поэтому изложение математических работ выглядело громоздко. Только начиная с XVI в. постепенно в математику начали вводить современные обозначения. Символы 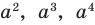
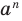
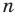
Благодаря исследованиям французского математика Франсуа Виета (1540-1603) уравнения второй степени, третьей и четвертой степеней впервые стали рассматривать в буквенных обозначениях. Он ввел буквенные обозначения для неизвестных величин и коэффициентов уравнений. Особенно ценил открытые им формулы, названные впоследствии формулами Виета. Однако Виет признавал только положительные корни. Лишь в XVII в., после работ Г. Декарта, И. Ньютона и других математиков, решение квадратных и других уравнений приобрело современный вид.
Идея зависимости величин тоже берет начало от древнегреческой науки. Но греки рассматривали лишь величины, которые имеют «геометрическую» природу, и не ставили вопрос об общем изучении разных зависимостей. Графическое изображение зависимостей между величинами широко использовали Г. Галилей (1564-1642), П. Ферма (1601-1665) и Г. Декарт, который ввел понятие переменной величины. Развитие механики и техники привело к необходимости введения общего понятия функции, что сделал немецкий философ и математик Г. Лейбниц (1646-1716). Большие классы функций изучал в ходе своих исследований И. Ньютон.
В 1718 г. ученик Лейбница, И. Бернулли (1667-1748), дал определение функции, лишенное геометрических образов. Следующий шаг в развитии понятия функции сделал его ученик, член Петербуржской академии наук Л. Ейлер (1707-1783).
После работ ряда математиков (Ж. Фурье (1768-1830), М. И. Лобачевский, П. Дирихле и др.) было дано следующее определение: «Переменная величина 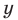
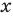
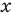
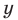
На современном этапе к словам «каждому значению величины л:» добавляют «принадлежащему некоторому множеству», а вместо переменных величин говорят об элементах этих множеств. Такой подход позволяет рассматривать с единой точки зрения как числовые функции, так и, например, геометрические преобразования и т. п.
Несоизмеримость стороны квадрата и его диагонали была открыта в V в. до н. э. в Древней Греции. Это открытие показало, что для измерения геометрических величин недостаточно рациональных чисел. Поэтому греческие математики отказались от обозначения геометрических величин числами и стали развивать геометрическую алгебру (поэтому и сейчас говорят «квадрат числа», «куб числа» и т. п.).
Греческий математик Евдокс (IV в. до н. э.) разработал теорию отношений геометрических величин, которая заменяла для древнегреческих математиков современную теорию действительных чисел. В основе теории Евдокса лежит идея о бесконечной делимости отрезков и других фигур.
Р. Декарт ввел произвольно выбранный единичный отрезок, что позволило ему выразить все действия над числами через действия над отрезками. В сущности, он уже работал с положительными действительными числами. Лишь во второй половине XIX в. теория действительных чисел была приведена к теории натуральных чисел.
О понятии действительного числа
Первые представления о числах формировались постепенно под влиянием практики. С давних времен числа применялись в ходе счета и измерения величин.
Ответ на вопрос «Сколько элементов содержит данное конечное множество?» всегда выражается или натуральным числом, или числом «нуль». Следовательно, множество
всех неотрицательных чисел обслуживает все потребности счета.
Иначе с измерением величин. Расстояние между двумя пунктами может равняться 3,5 километра, площадь комнаты — 16,45 квадратных метра и т. п.
Исторически положительные действительные числа появились как отношение длин отрезков. С открытием несоизмеримости диагонали единичного квадрата с его стороной стало понятным, что отношение длин отрезков не всегда можно выразить не только натуральным, но и рациональным числом. Чтобы числовое значение каждого отрезка при фиксированной единице измерения было определено, необходимо было ввести новые числа — иррациональные.
Все практические измерения величин имеют только приближенный характер. Их результат с необходимой точностью можно выразить с помощью рациональных дробей или конечных десятичных дробей.
Например, измеряя диагональ квадрата со стороной 1 м с точностью до 1 см, мы выясним, что ее длина приближенно равна 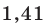
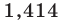
Однако в математике часто уклоняются от приближенного характера практических измерений. Последовательный теоретический подход к измерению длин отрезков приводит к необходимости рассмотрения бесконечных десятичных дробей. (Именно такими дробями являются числа
Отношение длины любого отрезка к длине отрезка, принятого за единицу измерения, всегда можно выразить числом, представленным в виде бесконечной десятичной дроби.
Полная теория действительных чисел достаточно сложна и не входит в программу средней школы. Она обычно рассматривается в курсах математического анализа. Однако с одним из способов ее построения мы ознакомимся в общих чертах.
1. Пусть:
а) каждому действительному числу соответствует (как его запись) бесконечная десятичная дробь:
б) каждая бесконечная десятичная дробь является записью действительного числа.
Но при этом естественно считать десятичную дробь, оканчивающуюся бесконечной последовательностью девяток, только другой записью числа, представленного десятичной дробью, оканчивающей бесконечной последовательностью нулей: 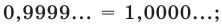
Только исключив из рассмотрения десятичные дроби с девяткой в периоде, получим взаимно однозначное соответствие между множеством действительных чисел и множеством бесконечных десятичных дробей. Число 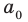
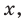
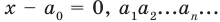
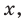
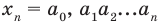
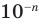
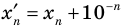
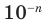
Если число 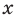
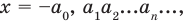
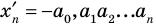
2. Вводят правило сравнения двух действительных чисел. По определению число 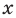
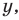
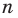
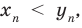
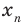
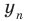
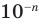
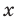
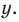
3. Определяют арифметические действия над действительными числами (при этом также пользуются тем, что эти действия уже определены для конечных десятичных дробей).
Суммой двух действительных чисел 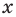
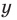
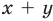
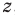
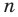
В курсах математического анализа доказывается, что такое число существует и оно единственное.
Аналогично произведением двух неотрицательных чисел 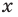
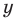
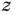
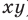
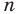
Такое число существует, и оно единственное.
Напомним, что примеры выполнения таким образом определенных действий сложения и умножения действительных чисел было рассмотрено в курсе алгебры 8 класса.
Воспользовавшись тем, что произведение неотрицательных чисел 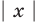
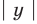
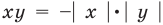
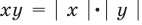
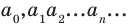
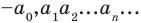
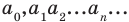
Вычитание определяется как действие, обратное сложению: разностью 
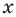
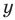
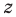
Деление определяется как действие, обратное умножению: частным 
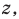
4. Показывают, что неравенства и арифметические операции, определенные выше, сохраняют основные свойства, присущие им во множестве рациональных чисел.
Теория действительного числа была построена сразу в нескольких формах немецкими математиками Р. Дедекиндом (1831-1916), К. Вейерштрассом (1815-1897) и Г. Кантором (1845-1918).
- Уравнение
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Прямые и плоскости в пространстве
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
Раскрытие модулей на ОДЗ
Раскрытие модулей на ОДЗ
При решении задач с модулями не всегда сразу возникает необходимость в применении метода интервалов или каких-либо других способов избавления от модулей. Иногда бывает достаточно провести анализ ОДЗ, и в результате по крайней мере часть модулей удаётся однозначно раскрыть. Рассмотрим три примера.
Пример №274.
Решить уравнение
Решение:
Очевидно, 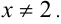
Но при 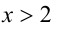
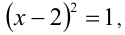
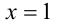
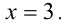
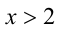
Пример №275.
Решить уравнение
Решение:
Заметим, что левая часть уравнения положительна (как сумма двух неотрицательных слагаемых, одновременно не обращающихся в нуль). Следовательно, 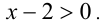
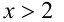
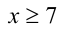
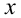
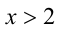
Пример №276.
Решение:
Очевидно,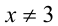
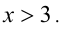
Видно, что при 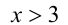
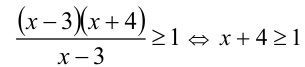
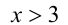
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Способы решения уравнений содержащих модуль
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Способы решения уравнений содержащих модуль.
1. Основные способы, используемые при решении уравнений, содержащих модуль.
Напомним основные понятия, используемые в данной теме.
Уравнением с одной переменной называют равенство, содержащее переменную.
Корнями уравнения называются значения переменной, при которых уравнение обращается в верное равенство.
Решить уравнение – значит, найти все его корни или доказать, что корней нет.
Уравнением с модулем называют равенство, содержащее переменную под знаком модуля.
При решении уравнений, содержащих знак абсолютной величины, мы будем основываться на определении модуля числа и свойствах абсолютной величины числа.
Свойства модуля
Существует несколько способов решения уравнений с модулем. Рассмотрим каждый из них.
1 СПОСОБ. МЕТОД ПОСЛЕДОВАТЕЛЬНОГО РАСКРЫТИЯ МОДУЛЯ.
Пример 1. Решим уравнение |х-5|=4.
Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-5)=4 или х-5= -4. Решая полученные уравнения, находим: х1=9, х2=1.
Ответ: 9; 1.
Решим этим же способом уравнение, содержащее «модуль в модуле».
Пример 2. Решим уравнение ||2х-1|-4|=6.
Рассуждая аналогично, рассмотрим два случая.
1). |2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо 2х-1= -10. Откуда х1=5,5, х2= -4,5.
2). |2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен.
Ответ: 5,5; -4,5.
2 СПОСОБ. МЕТОД ИНТЕРВАЛОВ.
Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять. Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ.
Пример 3. Решим уравнение |х+3|+|х-1|=6.
Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х разбивают числовую прямую на три промежутка:
-3 1
Решим уравнение отдельно в каждом из получившихся промежутков. В первом промежутке (х
Пример 4. |2-х|=2х+1.
Прежде всего, следует установить область допустимых значений. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости этого делать. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом, область допустимых значений – это промежуток [-½; +∞). Найдем нуль выражения, стоящего под знаком модуля: 2-х=0, х=2.
В первом промежутке: 2-х=2х+1, х=⅓. Это значение принадлежит ОДЗ, значит, является корнем уравнения.
Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно не является корнем уравнения. Ответ: ⅓.
3 СПОСОБ. ГРАФИЧЕСКИЙ МЕТОД.
Суть данного метода заключается в использовании графиков функций для нахождения корней уравнения. Этот метод реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.
Преобразуем уравнение: 1 + |x| = 0.5
Графиком функции 

Графики не пересекаются, значит, уравнение не имеет решений.
Ответ: нет решений.
Пример 5. |х+1|=2. Построим графики функций у=|х+1| и у=2.
Для построения графика у=|х+1|, построим график функции у=х+1, а затем отразим часть прямой, лежащую ниже оси ОХ. Абсциссы точек пересечения графиков и есть корни уравнения: х 1 =1, х 2 = -3. Ответ: 1; -3.
Пример 6. |х 2 -1|=|4-х 2 |.
Построим графики функций у=|х 2 -1| и у=|4-х 2 |. Для этого построим графики функций у= х 2 -1 и у=4-х 2 , а затем отобразим часть графиков, лежащую ниже оси ОХ.
х 1 ≈1,6; х 2 ≈-1,6.
4 СПОСОБ. МЕТОД РЕШЕНИЯ ПРИ ПОМОЩИ ЗАВИСИМОСТЕЙ МЕЖДУ ЧИСЛАМИ А И В, ИХ МОДУЛЯМИ И КВАДРАТАМИ ЭТИХ ЧИСЕЛ.
| а |=| в | 
а 2 =в 2 
| а |=| в | 
Пример 7 . Решим уравнение |х 2 -8х+5|=|х 2 -5|.
Учитывая соотношение (1), получим:
х 2 -8х+5= х 2 -5 или х 2 -8х+5= -х 2 +5
Таким образом, корни исходного уравнения: х 1 =1,25; х 2 =0; х 3 =4.
В силу соотношения (2) получаем: (х+3) 2 =(х-5) 2 ;
х 2 +6х+9= х 2 -10х+25;
Пример 9 . (1-3х) 2 =(х-2) 2 .
Учитывая соотношение (2), получаем: |1-3х|=|х-2|, откуда из соотношения (1), имеем:
1-3х=х-2 или 1-3х= -х+2
5 СПОСОБ. ИСПОЛЬЗОВАНИЕ ГЕОМЕТРИЧЕСКОЙ ИНТЕРПРЕТАЦИИ МОДУЛЯ.
Опорная информация: геометрический смысл модуля разности величин – это расстояние между ними. Например, геометрический смысл выражения |х-а| — длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.
Исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой х до двух фиксированных точек с абсциссами 2 и 3. Тогда очевидно, что все точки с абсциссами, принадлежащими отрезку [2;3] обладают требуемым свойством, а точки, расположенные вне этого отрезка – нет. Отсюда, множеством решений уравнения является отрезок [2;3].
Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 2 и 3 равна 1 только для точек, расположенных на координатной оси правее числа 3. Следовательно, решением данного уравнения будет являться луч, выходящий из точки 3, и направленный в положительном направлении оси ОХ.
Обобщением вышеприведенных уравнений 10 и 11 являются следующие равносильные переходы:
|х-а|+|х-в|=в-а, где в ≥ а 
|х-а|-|х-в|=в-а, где в ≥ а 
Проанализировав представленные способы решения уравнений, содержащих модуль, можно сделать вывод, что ни один из них не является универсальным и для получения наилучших результатов необходимо добиваться того, чтобы ученик овладел возможно большим количеством методов решения, оставляя право выбора решения за собой.
Решим аналитически и графически уравнение |x — 2| = 3.
А) Аналитическое решение
Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем
неотрицательно, т. е. x — 2 

Таким образом, получаем, либо x — 2 = 3, либо x — 2 = -3. Решая полученные уравнения, находим:
Ответ:
Теперь можно сделать вывод: если модуль некоторого выражения равен действительному положительному числу a, тогда выражение под модулем равно либо a, либо 
Одним из способов решения уравнений, содержащих модуль, является графический способ. Суть этого способа заключается в том, чтобы построить графики данных функций. В случае, если графики пересекутся, точки пересечений данных графиков будут являться корнями нашего уравнения. В случае, если графики не пересекутся, мы сможем сделать вывод, что уравнение корней не имеет. Этот способ, вероятно, реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.
Другой способ решения уравнений, содержащих модуль — это способ разбиения числовой прямой на промежутки. В этом случае нам нужно разбить числовую прямую так, что по определению модуля, знак абсолютной величины на данных промежутках можно будет снять. Затем, для каждого из промежутков мы должны будем решить данное уравнение и сделать вывод, относительно получившихся корней (удовлетворяют они нашему промежутку или нет). Корни, удовлетворяющие промежутки и дадут окончательный ответ.
Установим, при каких значениях x, модуль равен нулю:
Получим два промежутка, на каждом из которых решим уравнение:
Получим две смешанных системы:
(1) 
Решим каждую систему:
(1) 
(2)
Ответ:
Для решения уравнения графическим способом, надо построить графики функций 
Для построения графика функции 


Графиком функции 
Абсциссы точек пересечения графиков функций дадут решения уравнения.
Прямая графика функции y=3 пересеклась с графиком функции y=|x – 2| в точках с координатами (-1; 3) и (5; 3), следовательно, решениями уравнения будут абсциссы точек:
Ответ:
Практика обучения учащихся способам решения уравнений, содержащих модули, позволила выявить достоинства и недостатки каждого способа, которые для удобства сведены в таблицу.
Метод последовательного раскрытия модулей
1). Объявляя условие раскрытия одного модуля, можно пользоваться им для раскрытия других модуле тем самым, выигрывая время в решении задачи.
2). Последовательность действий, направленных на поиск ответа, позволяет контролировать и проверять промежуточные результаты.
Необходимость раскрытия модуля, что для некоторых заданий приводит к потере темпа в получении ответа.
Самый эффективный способ, так как сопровождается относительно небольшим объемом работы.
В силу необходимости нахождения концов интервалов может возникнуть ситуация, когда соответствующее уравнение либо вызывает серьезные затруднения при определении корней, либо недоступно ученику на данном этапе обучения.
Данный способ имеет очень широкое применение в других темах школьного курса математики.
Ответ определяется приблизительно.
Метод решения при помощи зависимостей между числами, их модулями и квадратами этих чисел
В некоторых случаях применение данного способа позволяет решать уравнения определенного вида на более раннем этапе.
В некоторых случаях выбор данного способа приводит к громоздкому решению, а иногда решение сводится к уравнению, недоступному для ученика на данном этапе обучения.
Геометрическая интерпретация модуля
Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.
Применение данного способа ограничивается уравнениями определенного вида.
Проанализировав достоинства и недостатки каждого из указанных способов, можно с уверенностью сказать, что на мотивационном этапе формирования умения решать уравнения с модулем ученикам следует показывать все, доступные на данном этапе обучения способы решения, и, главное, на конкретных примерах доказывать, что первый этап решения – выбор самого эффективного способа.
Рассмотрим пример |(х-1)(х-3)|=х-3.
Это уравнение можно решить тремя способами.
а) последовательное раскрытие модуля:
Если (х-1)(х-3) ≥ 0, то Если (х-1)(х-3) 2 -4х+3=х-3, х 2 -4х+3= -х+3,
х 2 -5х+6=0, х 2 -3х=0,
х 1 =3, х 2 =2. х 1 =0, х 2 =3.
2 – не удовлетворяет условию. 0, 3 — не удовлетворяет условию.
Ответ: 3.
б) метод интервалов: найдем концы интервалов, решив уравнение (х-1)(х-3)=0, откуда х 1 =1, х 2 =3.
(х-1)(х-3)=х-3, -(х-1)(х-3)=х-3, (х-1)(х-3)=х-3,
х 1 =2, х 2 =3. х 1 =0, х 2 =3. х 1 =2, х 2 =3.
2 (-∞; 1), 0 [1; 3). 2 [3; +∞).
3 (-∞; 1).
Ответ: 3.
в) графический метод: для решения уравнения построим в одной системе координат графики функций у=|х 2 -4х+3| и у=-3.
Построим у=|х 2 -4х+3|. Для этого сначала рассмотрим функцию у=х 2 -4х+3, графиком которой является парабола, ветви направлены вверх. Вершина параболы в точке (2; -1). Строим график и отображаем часть параболы, которая лежит ниже оси ОХ в верхнюю полуплоскость. Далее в этой же системе координат строим график у=х-3. Графики функций пересеклись в точке с абсциссой 3.
Ответ: 3.
Таким образом, можно сделать следующий вывод: систематическое использование различных способов для решения уравнений, содержащих абсолютную величину, приводит не только к повышению интереса к математике, повышению творческой активности школьников, но и повышает уверенность детей в собственных силах, так как у них имеется возможность выбора того способа решения, который наиболее эффективен в каждом конкретном случае.
ТЕСТОВЫЕ ЗАДАНИЯ по теме «Решение уравнений с модулем».
1. Какие числа являются решениями уравнения |х+3|= -4?
а) -7; б) -7; 1; в) нет корней; г) 1.
2. Решите уравнение |х+3|=7:
а) 7; б) -7; в) 0; 7; г) 7; -7.
3. Определите координаты точки пересечения графиков функций у=|2х+1| и у=0:
а) (0;0); б) (-0,5;0); в) (0;-0,5); г) (0,5;0).
4. Решите уравнение |х+3|+|х-1|=6:
а) 3; -2; б) 4; -2; в) -4; 2; г) 2; -3.
5. Сколько точек пересечения имеют графики функций у=||5,5х-4|+2| и у=3?
а) 1; б) 2; в) 3; г) 4.
6. Решите уравнение |3х-7|=1-х:
а) 2; 3; б) -2; 3; в) -3; 2; г) -2; -3.
7. Сколько решений имеет уравнение (2,5х-5)2=(0,5х-6)2:
а) 1; б) 2; в) 3; г) 4.
СИСТЕМА КАРТОЧЕК-ЗАДАНИЙ по теме «Решение уравнений с модулем».
1. ЗАДАНИЯ С УКАЗАНИЯМИ ИЛИ АЛГОРИТМИЧЕСКИМИ ПРЕДПИСАНИЯМИ И ОБРАЗОМ ВЫПОЛНЕНИЯ.
УКАЗАНИЯ ОБРАЗЕЦ ЗАДАНИЕ
Если |х-а|+|х-в|=в-а, где в ≥ а, то
а ≤ х ≤ в
|х-1|+|х-2|=1,
1 ≤ х ≤ 2.
Ответ: [1; 2]
а) |х-4|+|х-5|=1,
б) |х|-|х-1|=1,
в) |х-6|+|х-8|=2,
г) |х-0,5|-|х-4,5|=4.
Если |х-а|-|х-в|=в-а, где в ≥ а, то
х ≥ в
|х-1|-|х-2|=1,
х ≥ 2.
Ответ: [2; +∞).
АЛГОРИТМ ОБРАЗЕЦ ЗАДАНИЯ
1. Отметить все нули подмодульных выражений на числовой прямой. Они разобьют числовую прямую на промежутки, в которых все подмодульные выражения имеют постоянный знак.
2. Из каждого промежутка взять произвольное число и подсчетом определить знак подмодульного выражения, по знаку раскрыть модули.
3. Решить уравнения и выбрать решения, принадлежащие данному промежутку. |х+1|+|х+2|=1.
Решение.
Подмодульные выражения х+1 и х+2 обращаются в нуль при х= -1, х= -2.
1) -3 (-∞; -2]
-х-1-х-2=1; х= -2;
-2 (-∞; -2].
2) -1,5 (-2; -1)
-х-1+х+2=1; 1=1; х — любое число из промежутка (-2; -1).
3) 0 [-1; +∞)
х+1+х+2=1; х= -1;
-1 [-1; +∞).
Ответ: [-2; -1].
1) |14-х|+|х+1|=7;
2) |х|-|х+2|=2;
3) |х2-4|=|2х-1|;
4) | х2-6х+5|+|3-х|=3
2. ЗАДАНИЯ «НАЙДИ ОШИБКУ».
1.
Решить уравнение: |х2-8х+5|=| х2-5|.
Решение.
|х2-8х+5|=| х2-5|
х2-8х+5= х2-5, или х2-8х+5=5- х2,
-8х+10=0, 2 х2-8х=0,
х=1,25. х(2х-8)=0,
х=0, или 2х-8=0,
2х=8,
х=0,25.
Ответ: 1,25; 0,25. ВЕРНОЕ РЕШЕНИЕ
2.
Решить уравнение х2-6х+|х-4|+8=0.
Решение.
Если х-4 ≥ 0, то Если х-4 Решить уравнение |х-1|-2|х+3|+х+7=0.
Решение.
Решим уравнение методом интервалов, для этого найдем концы интервалов, решив уравнения
х-1=0 и х+3=0
х=1 х= -3.
-х+1-2(-х-3)+х+7=0; -х+1-2х-6+х+7=0; х-1-2х-6+х+7=0;
2х+14=0; -2х+2=0; 0=0.
х= -7. х=1. х — любое число.
Ответ: х – любое число. ВЕРНОЕ РЕШЕНИЕ
3. ЗАДАНИЯ С СОПУТСТВУЮЩИМИ УКАЗАНИЯМИ И ИНСТРУКЦИЯМИ.
1.
Решить уравнение |х-2|+|2х-7|=3.
Решение.
Решим уравнение методом интервалов.
1) Найдите нули подмодульных выражений, решив уравнения:
х-2=0 и 2х-7=0.
х1=… х2=…
2) Отметьте полученные значения на координатном луче.
3) Решите исходное уравнение на каждом из интервалов, предварительно определив знак подмодульного выражения. Учитывая знак, раскрыть модули.
4) Проверьте, принадлежат ли найденные корни указанным промежуткам.
Ответ: …………………………………………………….
2.
Решить уравнение ||х-3|-х+1|=6.
Решение.
1) Раскройте внешний модуль, используя определение: |а|=а, если а ≥ 0 и
|а|= -а, если а 4. ЗАДАНИЯ С ПРИМЕНЕНИЕМ КЛАССИФИКАЦИИ.
1.
Выпишите уравнения, которые решаются с помощью зависимостей между величинами, их модулями и квадратами величин. Решите эти уравнения.
1) ||х|+3|=3;
2) |х|+|х+4|=х-1;
3) |х+2|=|3-х|;
4) |х+3|+|х-1|=7;
5) (2х-3)2=(3,5х-1)2;
6) |х2-4х+5|=|х2-9|;
7) |11х-7|= -3;

9) х2-х-2=|5х-3|;
2.
Выпишите уравнения, которые решаются с использованием геометрической интерпретации модуля. Решите эти уравнения.
1) |х|-|х-8|=2;
2) |х 2 -2х-3|=3х-3;
3) |2х-|2х-|2х-3|||=0;
4) |х-1|-2|х+4|+х+11=0;
5) |х-3|+|х-4|=1;
6) (5х-4) 2 =(2х-1) 2 ;
7) |2,5х-11|= -2;

5. ЗАДАНИЯ С ВЫПОЛНЕНИЕМ НЕКОТОРОЙ ЧАСТИ.
1.
Решить уравнение (х 2 -5х+6)2-5•| х 2 -5х+6|+6=0.
Решение.
Пусть | х 2 -5х+6|=t, тогда, учитывая, что (х 2 -5х+6)2=| х 2 -5х+6|2, получим уравнение: t 2 -5t+6=0. Решением этого уравнения являются числа ……. поэтому исходное уравнение равносильно совокупности двух уравнений:
| х 2 -5х+6|=… или | х 2 -5х+6|=…
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
ПРОВЕРОЧНАЯ РАБОТА по теме «Решение уравнений с модулем»
1. Решите уравнение |х-3|=7.
2. Решите графически уравнение |2х+1|=3.
3. Решите уравнение методом интервалов |х+1|+|х-1|=3.
4. Решите уравнение методом последовательного раскрытия модулей |-х+2|=2х+1.
5. Решите уравнение (2х+3) 2 =(х-1) 2 .
6. Решите уравнение самым удобным способом |х 2 +6х+2|=3|х+2|.
7. При каком значении а уравнение можно решить, используя геометрическую интерпретацию модуля: |х-а|+|х-9|=1?
Уравнения с модулем
Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что
Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)
Слева модуль, справа число
Это самый простой случай. Решим уравнение
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Переменная как под модулем, так и вне модуля
Здесь приходится раскрывать модуль по определению. . . или соображать!
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:
Решение первой системы: . У второй системы решений нет.
Ответ: 1.
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения
Стало быть, годятся лишь и .
Ответ:
Квадратные уравнения с заменой |x| = t
Поскольку , удобно сделать замену |x| = t. Получаем:
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Модуль в модуле
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Читайте также о том, как решать неравенства с модулем.
http://infourok.ru/sposobi-resheniya-uravneniy-soderzhaschih-modul-398462.html
http://ege-study.ru/ru/ege/materialy/matematika/uravneniya-i-neravenstva-s-modulem/
Раскрытие модулей на ОДЗ
При решении задач с модулями не всегда сразу возникает необходимость в применении метода интервалов или каких-либо других способов избавления от модулей. Иногда бывает достаточно провести анализ ОДЗ, и в результате по крайней мере часть модулей удаётся однозначно раскрыть. Рассмотрим три примера.
Пример №274.
Решить уравнение
Решение:
Очевидно,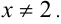
Но при 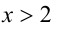
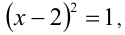
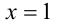
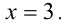
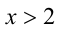
Пример №275.
Решить уравнение
Решение:
Заметим, что левая часть уравнения положительна (как сумма двух неотрицательных слагаемых, одновременно не обращающихся в нуль). Следовательно, 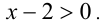
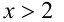
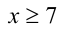
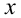
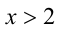
Пример №276.
Решить неравенство
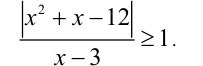
Решение:
Очевидно,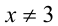
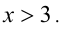
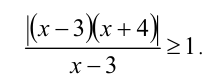
Видно, что при 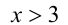
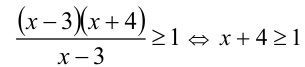
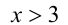
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:
Уравнения и неравенства, содержащие знак модуля
Е.П. Нелин, В.А. Лазарев
АЛГЕБРА
и начала математического
анализа
10 класс
Учебник для
общеобразовательных
учреждений. Базовый и
профильный уровень
§ 5. Уравнения и неравенства, содержащие знак модуля
(Оформление и автор интерактивных технологий Морозова Е.)
Объяснение и обоснование
Решать любое уравнение или неравенство, содержащее знак модуля, можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства с модулем могут быть также решены с использованием специальных соотношений.
В зависимости от выбранного способа решения получаем разные записи решения.
Пример Решите уравнение | 2x – 4 | = 6.
I способ (по определению модуля)
II способ (использование геометрического смысла модуля)
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств, содержащих знак модуля — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
|f (x)| + |g (x)| = a (a > 0).
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции f (x) и g (x) будут положительными, а где — отрицательными. То есть фактически мы должны решить неравенства
f (x) ≥ или ≤0, (1)
g (x) ≥ или ≤0. (2)
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции f (x)), а решение неравенства (2) — с нахождения его ОДЗ (то есть области определения функции g (x)). Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций f (x) и g (x), то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы).
Чтобы продолжить решение неравенств f (x) ≥или≤0 и g (x) ≥или≤ 0 методом интервалов, необходимо найти нули функций f (x) и g (x), то есть найти нули всех подмодульных функций (это и есть второй ориентир).
Если далее применить схему метода интервалов одновременно для двух неравенств, необходимо на ОДЗ отметить нули подмодульных функций и разбить ОДЗ на промежутки (это третий ориентир).
В каждом из полученных промежутков знаки функций f (x) и g (x) не могут измениться. Тогда мы можем найти знаки подмодульных функций на каждом промежутке (в любой точке этого промежутка), раскрыть знаки модулей и найти решение данного уравнения в каждом из этих промежутков (это и есть четвертый ориентир общей схемы).
Обоснование возможности применения приведенной схемы к решению неравенств с модулями проводится аналогично.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Вопросы для контроля
- Объясните, какими способами можно решать уравнения и неравенства, содержащие знак модуля. Проиллюстрируйте эти способы на примерах.
- Обоснуйте специальные соотношения. Проиллюстрируйте их применение к решению уравнений и неравенств, содержащих знак модуля.
- Обоснуйте обобщения использования геометрического смысла модуля. Проиллюстрируйте их применение к решению уравнений и неравенств, содержащих знак модуля.
Упражнения
Решите уравнения и неравенства, содержащие знак модуля (1–15).
Постройте график функции
ТЕСТ
Уравнения и неравенства