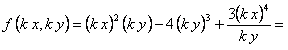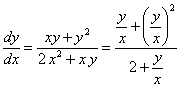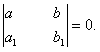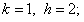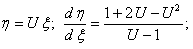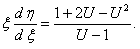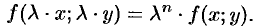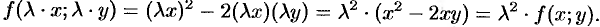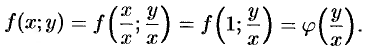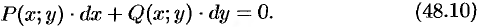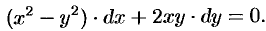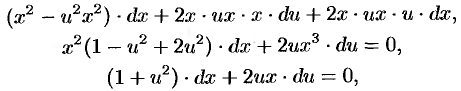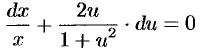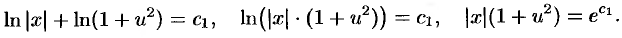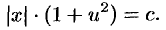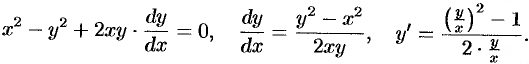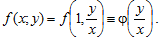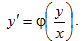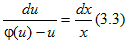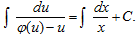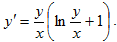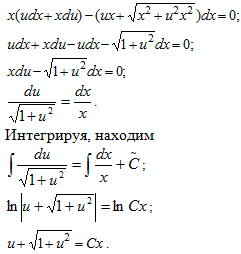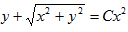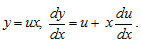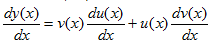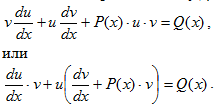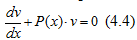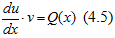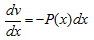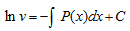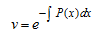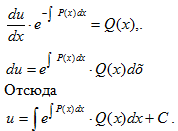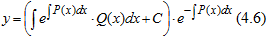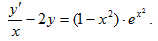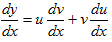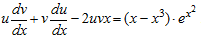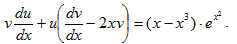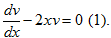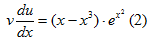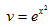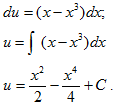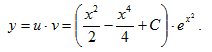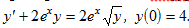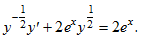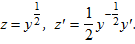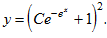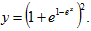Прежде чем давать определение однородного дифференциального уравнения, введем понятие об однородных функциях.
ОПРЕДЕЛЕНИЕ 11.1.8 Функция двух переменных 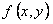
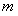
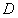
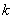
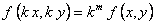
ПРИМЕР 11.1.12 Функция 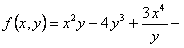
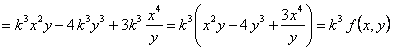
ПРИМЕР 11.1.13 Функция 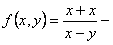
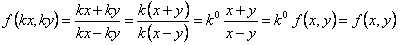
Таким образом, для функции выполняется равенство 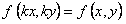
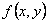
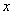
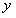
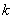
Отношение двух однородных функций одной переменной и того же порядка однородности является однородной функцией нулевой степени.
Однородная функция нулевого порядка может быть записана в виде
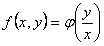
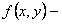
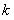
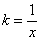
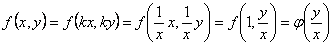
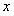
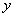
ОПРЕДЕЛЕНИЕ 11.1.9 Дифференциальное уравнение
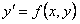
называется однородным, если 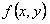
Однородное уравнение можно привести к уравнению с разделяющимися переменными подстановкой
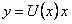
где 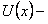
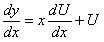
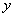
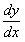
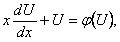
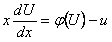

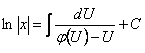
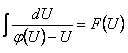
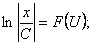
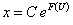
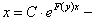
ПРИМЕР 11.1.13
Решение.
Сделаем подстановку: 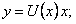
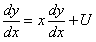
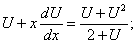
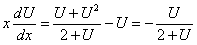
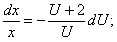
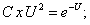
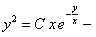
Уравнение вида
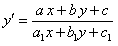
приводится к однородному, если 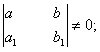
Рассмотрим каждый случай отдельно.
1. Пусть 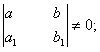
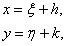
где 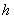
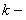
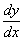
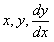
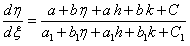
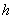
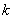
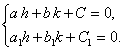
Тогда 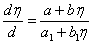
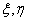
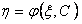
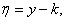
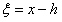
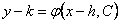
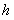
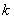
она совместна, так как определитель этой системы 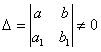
2. Пусть теперь 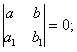
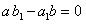
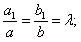
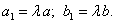
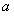
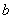
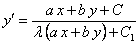
Для разделения переменных введем новую функцию 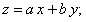
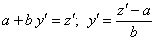
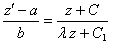
ПРИМЕР 11.1.14 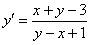
Решение.
Проверим 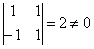
Введем новые переменные 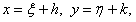
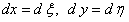
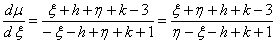
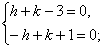
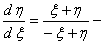
Сделаем подстановку
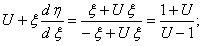
Разделим переменные и проинтегрируем полученное уравнение:
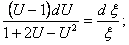
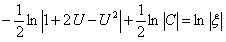
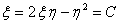
Или возвращаясь к прежним переменны x и y, получим
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
53
Дифференциальные
уравнения 1-го порядка называют
однородными, если для их записи
используются однородные функции. Чтобы
понять особенности записи однородного
уравнения, познакомимся с однородными
функциями, как их определяют в
математическом анализе.
§ 1. Однородные функции.
В алгебре многочленназываютоднородным,
если он состоит из членов одного и того
же измерения. Так, многочлен:=
есть однородный многочлен 2-й степени.
Если в записиумножить переменные
и
на множитель
,
то весь многочлен приобретёт множительво 2-й степени:
=
.
В общем случае, для однородного многочлена
степени,
можем записать:=
.
Для нас важно, что
свойством однородности могут обладать
и функции более сложной природы. Например,
для функции
=
можем записать:
=
,
и её естественно назвать однородной
функцией 2-й степени.
В общем случае для
функции
понятие однородности может быть принято
в таком виде:
|
Определение: (2.1) |
Функция |
Из определения
следует, что возможна запись:
=
.
Это значит, что, в частном случае, функция
может иметь нулевой порядок однородности,
то есть=0.
Замечания:
Показатель степени однородности
может быть любым вещественным числом.
Так, для функции:
=
показатель однородности: .
Так как предполагается
использование однородных функций в
обыкновенных дифференциальных уравнениях,
ограничимся функциями двух переменных:
.
В этом случае для однородной функции
нулевой степени верно:=
,
или=
.
Если положить:=
,
получим:=
=
=
.
Это значит, что функциязависит только от отношения независимых
переменныхи
.
Пусть имеем
однородную функцию:
=
∙
.
Примем:=
.
В этом случае можем записать:=
.
Но,=
=
.
Учитывая все выражения, получаем общую
запись для однородной функции степени:
=
∙
.
Замечания:
Запись:
=
∙
напоминает операцию вынесения общего
множителя за скобку (в данном случае,
за скобку функции).
☺☺
Пример 2–01:
Задана функция:
=
.
Определить является ли эта функция
однородной. Если
–
однородная функция, установить её
порядок.
Решение:
1).
По определению необходимо сделать
замену:
и
,
и посмотреть, что из этого получается.
Итак,
=
=
∙
.
Замечания:
При исследовании однородности функции
достаточно применять значение
:
для рассматриваемого промера это
принципиально важно из-за присутствия
корня!
2).
Полученный результат сразу отвечает
на оба вопроса: а) так как множитель
смогли вынести за скобки функции →
заданная функция – однородная; б)
показатель степени
показывает: заданная функция
–
однородная степени (порядка) =
4.
Ответ:
заданная функция – однородная порядка
=
4.
Пример 2–02:
Задана функция:
=
.
Можно ли представить её в виде выражения
=
∙
?
Решение:
1).
Если бы мы не имели результата предыдущего
Примера, мы бы попробовали вынести все
возможные общие множители
за скобки функции. Но, мы знаем:
=
∙
,
и этим результатом воспользуемся!
2).
Так как общая запись для однородной
функции степени
:
=
∙
,
то в нашем случае сразу получаем ответ:
=
∙
.
Ответ:
для заданной функции запись:
=
∙
возможна.
Пример 2–03:
Заданы пары: функция → число. Выделите
пары, в которых функция – однородная,
а число – ее порядок :
а) f
=
→ =
;
б) f
=
→ =π;
в)
f
=
→ =
.
Решение:
1).
Воспользуемся свойством однородной
функции:
=
∙
,
применяя его к каждой из функций: а)
=
∙
;
б)
=
∙
;
в)
=
∙
.
2).
Следовательно,
в случаях а) и б) пары функция → число,
соответствуют друг другу, в случае в)
неверно указан порядок однородной
функции.
Ответ:
пары а) и б) верно указывают соответствие.
☻
Как найти общее решение однородного дифференциального уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Однородные ДУ первого порядка
-
- Пример 1
- Пример 2
- Пример 3
- Однородные линейные ДУ второго порядка
-
- Пример 4
- Пример 5
Данный тип задачи часто ставит студентов в тупик. Поэтому они присылают их на решение к нам. Мы написали данную статью, чтобы помочь разобраться в этой теме. Итак, прежде, чем приступать решать дифференциальное уравнение, необходимо понять к какому виду оно принадлежит. Сначала определить порядок, затем уже линейность и однородность. В данном материале рассмотрим однородные уравнения первого и второго порядка и как их решать. В зависимости от этого будет разный алгоритм действий. Так как в первом случае однородность уравнения по переменным, а во втором по правой части. Далее разберемся подробнее об этом.
Однородные ДУ первого порядка
Если после подстановки в уравнение вместо $x$ и $y$ соответствующих $lambda x$ и $lambda y$ можно добиться уничтожения всех $lambda$, то уравнение является однородным первого порядка.
Такие уравнения имеют общий вид $$P(x,y)dx+Q(x,y)dy=0,$$ где $P(x,y)$ и $Q(x,y)$ однородные функции одинакового порядка, то есть выполняются условия $P(lambda x,lambda y) = lambda^n P(x,y)$ и $Q(lambda x,lambda y) = lambda^n Q(x,y)$.
Алгоритм решения:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных.
| Пример 1 |
| Решить однородное дифференциальное уравнение первого порядка $$y’=e^frac{y}{x}+frac{y}{x}.$$ |
| Решение |
|
Подставляя $lambda$ перед $x$ и $y$ в исходное уравнение получаем $$y’ = e^frac{lambda y}{lambda x} + frac{lambda y}{lambda x},$$ в котором все $lambda$ сокращаются, и это означает, что перед нами однородное дифференциальное уравнение первого порядка. Выполняем замену $frac{y}{x} = t Rightarrow y’ = t’x + t$ в исходном уравнении и получаем: $$t’x+t=e^t+t$$ $$t’x=e^t.$$ Данное уравнение с разделяющимися переменными. Записываем его соответствующим образом и переносим всё, что содержит $t$ в левую часть, а то что с $x$ в правую: $$frac{dt}{dx} x=e^t$$ $$frac{dt}{e^t}=frac{dx}{x}.$$ Интегрируем обе части уравнения: $$int frac{dt}{e^t}=int frac{dx}{x}$$ $$-e^{-t} = ln|x|+C.$$ Теперь необходимо выполнить обратную замену $t = frac{y}{x}$, чтобы вернуться к $y$ $$-e^{-frac{y}{x}} = ln|x| + C.$$ Записываем ответ в виде общего интеграла $$e^{-frac{y}{x}}+ln|x|=C.$$ |
| Ответ |
| $$e^{-frac{y}{x}}+ln|x|=C$$ |
| Пример 2 |
| Найти решение однородного дифференциального уравнения первого порядка $$(x^2+2xy)dx+xydy=0.$$ |
| Решение |
|
Подставляем перед всеми иксами и игриками дополнительную константу $lambda$, чтобы убедиться в однородности уравнения: $$( (lambda x)^2 + 2lambda x lambda y)d(lambda x) + lambda x lambda y d(lambda y) = 0$$ $$lambda^3 (x^2+2xy)dx+lambda^3 xydy = 0$$ $$(x^2+2xy)dx+xydy=0.$$ Как видно, все $lambda$ уничтожились, поэтому действительно дано однородное ДУ первого порядка. Приведем уравнение к виду $y’ = f(frac{y}{x})$. Разделим уравнение на $x^2$ и $dx$. Получим $$(1+2frac{y}{x})+frac{y}{x}frac{dy}{dx} = 0.$$ Теперь выполняем замену $$frac{y}{x}=t, qquad frac{dy}{dx} = t’x+t.$$ Подставляем это в уравнение и получаем $$(1+2t)+t(t’x+t) = 0, $$ и раскрываем скобки и упрощаем: $$1+2t+t’tx+t^2=0$$ $$t’tx + (t+1)^2=0.$$ Получившееся уравнение является ДУ с разделяющимися переменными. Поэтому начинаем резделять переменные $t$ и $x$ по разные стороны от знака равенства. Записываем уравнение в виде $$frac{dt}{dx}tx = -(t+1)^2.$$ Делим обе части на $(t+1)^2$ и $x$, затем умножаем на $dx$ $$frac{tdt}{(t+1)^2} = -frac{dx}{x}.$$ Последнее равенство нужно проинтегрировать, чтобы вытащить $t(x)$ $$int frac{tdt}{(t+1)^2} = — int frac{dx}{x}.$$ Решаем первый интеграл методом разложения: $$int frac{tdt}{(t+1)^2} = int frac{(t+1)-1}{(t+1)^2}dt = int frac{t+1}{(t+1)^2}dt — int frac{dt}{(t+1)^2} = $$ $$ = int frac{dt}{t+1} — int frac{dt}{(t+1)^2} = $$ $$ = ln|t+1| + frac{1}{t+1} + C.$$ Решаем второй интеграл $$int frac{dx}{x} = ln|x| + C.$$ Возвращаемся к равенству двух интегралов и подставляем полученные решения $$ln|t+1| + frac{1}{t+1} = -ln|x|+C.$$ Вспоминаем, что в начале решения задачи была сделана подстановка $frac{y}{x}=t$, и значит, назад нужно вернуться к $y$ $$ln|frac{y}{x}+1|+frac{1}{frac{y}{x}+1} = -ln|x| + C.$$ Выполняем преобразования последнего уравнения: $$ln|frac{x+y}{x}|+frac{x}{y+x}=-ln|x|+C$$ $$ln|x+y|-ln|x|+frac{x}{y+x}=-ln|x|+C$$ $$ln|x+y|+frac{x}{x+y}=C.$$ Выразить $y$ просто так не получится. Поэтому оставим ответ в таком виде, который называется общий интеграл дифференциального уравнения. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ln|x+y|+frac{x}{x+y}=C$$ |
| Пример 3 |
| Решить однородное дифференциальное уравнение $$xy’ sinfrac{y}{x}+x=ysin frac{y}{x}.$$ |
| Решение |
|
Как всегда начинает с проверки на однородность с помощью подстановки $lambda$ в исходное ДУ $$lambda xy’ sinfrac{lambda y}{lambda x}+lambda x=lambda ysin frac{lambda y}{lambda x}.$$ Видим, что все $lambda$ сокращаются и уравнение приобретает вид из условия задачи. Значит, это однородное ДУ первого порядка. Придадим ему вид $y’=f(frac{y}{x})$ для удобства замены. Для этого разделим обе части уравнения на $x$ $$y’ sinfrac{y}{x}+1=frac{y}{x} sin frac{y}{x}.$$ Теперь делаем подстановку $frac{y}{x}=t$ и $y’=t’x+t$: $$(t’x+t) sin t + 1 = t sin t$$ $$t’x sin t + tsin t+1=tsin t$$ $$t’x sin t=-1.$$ Получили уравнение с разделяющимися переменными. Всё, что с $t$ налево, всё что с $x$ направо: $$frac{dt}{dx} x sin t = -1$$ $$sin t dt = -frac{dx}{x}.$$ Интегрируем обе части равенства: $$int sin t dt = -int frac{dx}{x}$$ $$-cos t = -ln|x|+C.$$ Выполняем обратную замену в последнем уравнении $$cos frac{y}{x} = ln|x|+C.$$ Так как выразить $y$ достаточно тяжело, то запишем ответ в виде общего интеграла $$cos frac{y}{x}-ln|x|=C.$$ |
| Ответ |
| $$cos frac{y}{x}-ln|x|=C$$ |
Однородные линейные ДУ второго порядка с постоянными коэффициентами
Такие уравнения имеют следующий общий вид $$y»+py’+qy=0, $$ где $p$ и $q$ постоянные коэффициенты. Чтобы решить такие уравнения первым делом нужно составить характеристический многочлен $$lambda^2+plambda + q = 0, $$ который получается путем замены всех $y$ на $lambda$ в степенях, соответствующих порядку производной $y$ $$y» Rightarrow lambda^2, quad y’ Rightarrow lambda, quad y Rightarrow 1.$$ Затем в зависимости от найденных корней $lambda_1$ и $lambda_2$ составляется общее решение:
- Если $lambda_1 neq lambda_2$, тогда $y=C_1e^x + C_2e^x$
- Если $lambda_1 = lambda_2$, тогда $y=C_1e^x + C_2xe^x$
- Если $lambda_{1,2} = alpha pm beta i$, тогда $y=C_1e^{alpha x} cos beta x + C_2 e^{alpha x} sin beta x$.
| Пример 4 |
| найти общее решение однородного дифференциального уравнения второго порядка $$y»-9y=0.$$ |
| Решение |
|
Составляем характеристический многочлен путем замены $y$ на $lambda$ в степени, соответствующей порядку производной и находим его корни: $$lambda^2 — 9 = 0$$ $$(lambda — 3)(lambda+3)=0$$ $$lambda_1=3, quad lambda_2=-3.$$ Так как получили действительные корни, отличающиеся друг от друга, то общее решение однородного уравнения будет выглядеть следующим образом $$y=C_1e^{-3x}+C_2e^{3x}.$$ |
| Ответ |
| $$y=C_1e^{-3x}+C_2e^{3x}$$ |
| Пример 5 |
| Решить однородное дифференциальное уравнение второго порядка $$y»-6y’+25y=0.$$ |
| Решение |
| Составим характеристическое уравнение путем замены $y$ на $lambda$ $$lambda^2 — 6lambda + 25 = 0.$$ Решим квадратное уравнение. Вычислим его дискриминант $$D = b^2-4ac = (-6)^2 — 4cdot 1 cdot 25 = 36 — 100 = -64.$$ Теперь найдем значения корней $$lambda_{1,2} = frac{-b pm sqrt{D}}{2} = frac{6pm 8i}{2} = 3pm 4i.$$ В итоге получили комплексно-сопряженные корни, значит, общее решение будет выглядеть $$y = C_1 e^{3x}cos 4x + C_2 e^{3x}sin 4x.$$ |
| Ответ |
| $$y = C_1 e^{3x}cos 4x + C_2 e^{3x}sin 4x$$ |
Однородные дифференциальные уравнения
К уравнению с разделяющимися переменными приводятся одно родные ДУ первого порядка.
Функция 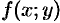
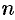
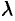
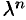
Например, функция 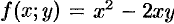
Дифференциальное уравнение
называется однородным, если функция 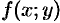
Покажем, что однородное ДУ (48.7) можно записать в виде
Если 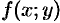
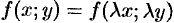
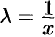
Однороднее уравнение (48.8) преобразуется в уравнение с раздел:
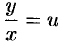
Действительно, подставив 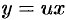
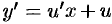
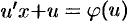
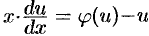
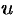
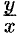
Однородное уравнение част о задается в дифференциальной форме:
ДУ (48.10) будет однородным, если 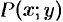
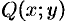
Переписав уравнение (48.10) в виде 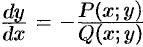
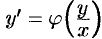
При интегрировании уравнений вида (48.10) нет необходимости предварительно приводить их (но можно) к виду (48.8): подстановка (48.9) сразу преобразует уравнение (48.10) в уравнение с разделяющимися переменными.
Пример №48.6.
Найти общий интеграл уравнения
Решение:
Данное уравнение однородное, т. к. функции 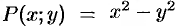
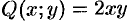
Положим 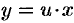
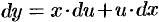
последнее — уравнение с разделяющимися переменными. Делим переменные
и интегрируем
Обозначим 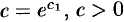
Заменяя 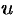
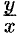
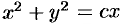
Отметим, что данное уравнение можно было сначала привести виду (48.8):
Затем положить 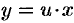
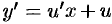
Замечание. Уравнение вида 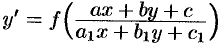
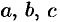
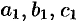
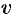
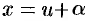
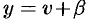
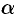
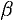
Дополнительный пример №48.7.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Как я и обещал в своей предыдущей статье, сегодня продолжим более детально изучать Дифференциальные уравнения.
§3. Однородные дифференциальные уравнения I-го порядка
Функцию f(x, y) называют однородной функцией порядка mотносительно своих аргументовxиy, если она выполняется тождество
f(tx, ty)= tmf(x, y) (3.1), где t – любой множитель.
Так, например, функции x2y– xy2, 2x2 – 3xy однородные: первая – третьего порядка, вторая – первого.
Определение 3.1. Дифференциальное уравнение y’ = f(x, y) (3.2) называется однородным, если его правая часть функция f(x, y) является однородной функцией нулевого порядка относительно своих аргументов x и y.
Интегрирование однородного уравнения с помощью специальной подстановки сводится к интегрированию уравнения с отделяемыми переменными.
Действительно, учитывая нулевой порядок однородности функции f(x, y), для любого t имеем f(tx, ty)= f(x, y).
В частности, если t = 1/x, получим:
Уравнение (3.2) запишется в виде
Введем вспомогательную неизвестную функцию с помощью подстановки: y = x· u, y’ = u + x· u’.
Уравнение (3.2) записывается в виде u + x· u’ = φ(u),
в котором переменные разделяются:
Отсюда находим общий интеграл уравнения:
где C=const.
Наконец, после вычисления интегралов и замены вспомогательной функции u ее выражением через x и y, найдем решение однородного уравнения.
Пример 3.1. Решить “дифур”
Решения. Это однородное Дифференциальное уравнение I-го порядка. Применим подстановку y = x· u, y’ = u + x· u’.
Тогда получим уравнение с переменными, которые можно разделить, относительно вспомогательной функции u.
u +xu’ = u(ln u + 1)
xu’ = uln u
Решая его, получим
Это ОР уравнения.
Замечания. Уравнение вида P(x, y)dx + Q(x, y)dy = 0 (3.4), в котором функции P(x, y) и Q(x, y) – однородные, относительно своих аргументов x и y функции одного и того же измерения, является однородным и заменой y = ux сводится к уравнению с разделяемыми переменными.
Пример 3.2. Решить “дифур”
Решение. Это однородное уравнение, так как коэффициенты при dxи dy являются однородными функциями I-го порядка. Сделаем замену
y = ux, dy = xdu + udx
Получим “дифур” с переменными, которые можно разделить:
Заменив вспомогательную функцию u = y/x получаем, после преобразований, общий интеграл уравнения:
Пример 3.3. Решить “дифур”
Решения. Произведем следующюю замену
Получим
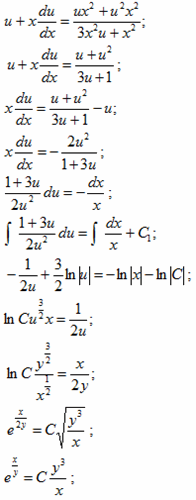
§4. Линейные дифференциальные уравнения I-го порядка. Уравнение Бернулли
Определение 4.1. Дифференциальное уравнение I-го порядка называется линейным, если и сама неизвестная функция и ее производная входят в это уравнение только в первой степени и не содержит их произведения.
В общем виде линейное дифференциальное уравнения I-го порядка:
y’ + P(x)y = Q(x) (4.1)
Используют несколько приемов решения дифференциального уравнений (4.1). Мы рассмотрим здесь метод Бернулли, согласно которому решение в следующем виде y(x) = u(x) · v(x) (4.3).
Тем самым искомыми становятся функции u(x) и v(x), одну из которых можно выбрать произвольно, а вторая – должна определяться уравнением.
Дифференцируем обе части равенства (4.3)
Подставим выражения для y(x) и y‘(x) в уравнение (4.1). Имеем
Подберем функцию v так, чтобы выполнялось равенство
Тогда функция u должна удовлетворять уравнению
Уравнение (4.4) является уравнением с переменными, которые можно разделить,
В результате интегрирования получим.
Если C = 0, получим
Подставляя значение v(x) в уравнение (4.5), получим относительно u(x) дифференциальное уравнение I-го порядка с переменными, которые можно разделить,
Окончательно по формуле (4.3) получим ОР уравнения (4.1) в виде
При решении конкретных линейных дифференциальных уравнений I-го порядка можно пользоваться готовыми формулами (4.6) или использовать прием Бернулли.
Пример 4.1. Решить “дифур”
Решения. Это линейное неоднородное уравнение I-го порядка, решаем методом Бернулли. Сведем его к виду (4.1.) (хотя это необязательно). Для чего обе части уравнения умножим на х. Получим:
y’ – 2xy = (x – x3)· ex2.
Произведем замену
y= u· v.
Дифференцируем это выражение по x:
Заменим в уравнении y’ и y выражениями через u и v, получим
Сгруппируем члены, содержащие функцию u, и вынесем эту функцию за скобки. Получим:
Найдем теперь такую функцию u, чтобы
При этом условии функция u(x) должна удовлетворять уравнению
Решим уравнение (1), разделив переменные:
По определению логарифма
Подставив найденное значение в уравнение 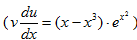
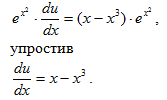
Это “дифур” с переменными, которые можно разделить,. Проинтегрировав его, получим следующее
ОР уравнения получим в виде
Пример 4.2. К линейному уравнению заменой z = y1-α сводят уравнения
y’ + P(x) · y = Q(x) · yα, α≠ 0, α≠ 1 (4.7), которое называется уравнением Бернулли.
Пример 4.3. Решить “дифур” со следующим начальным условием.
Имеем уравнение Бернулли. Разделив наш “дифур” на √y, получим
Сделаем замену
Получим линейное уравнение
Из предыдущего следует
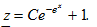
Тогда, искомое ОР “дифура” имеет такой вид
Перейдем к поиску частного решения, удовлетворяющего начальному условию y(0)= 4, отсюда
Тогда частное решение первоначального “дифура” имеет такой вид
Уважаемые студенты, записывайтесь на мои занятия и я помогу Вам разобраться с «Дифурами» раз и навсегда!
Онлайн репетитор Андрей Зварыч.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.