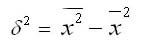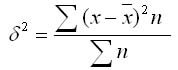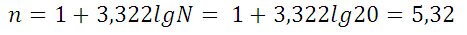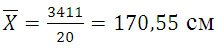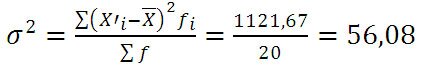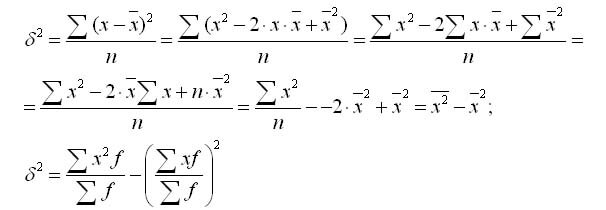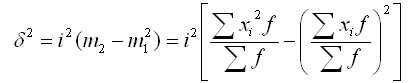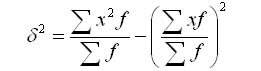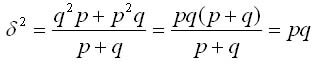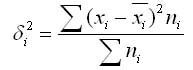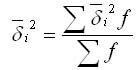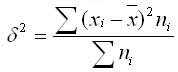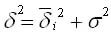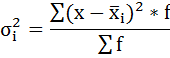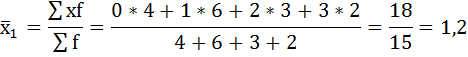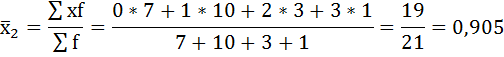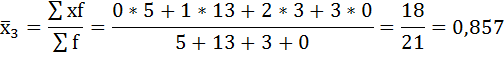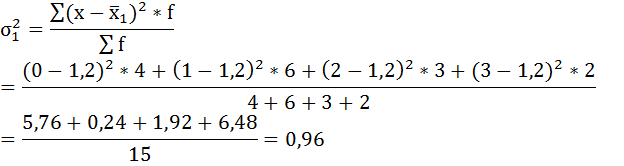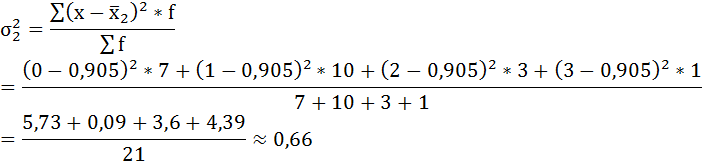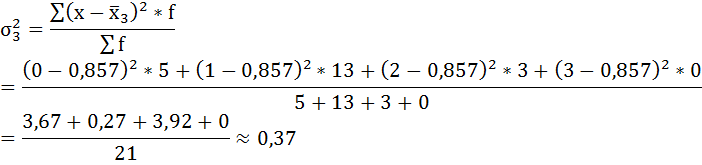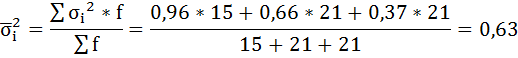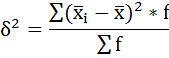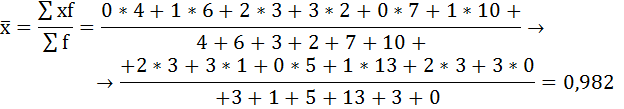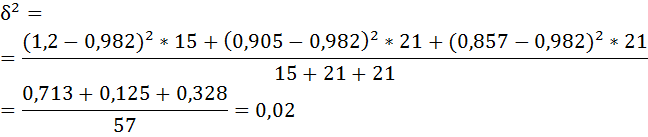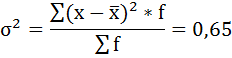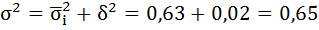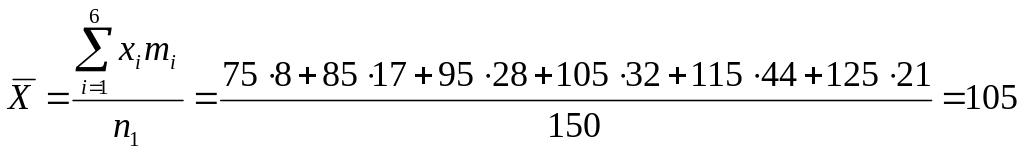Дисперсия, виды и свойства дисперсии
Понятие дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n — частота (повторяемость фактора Х)
Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
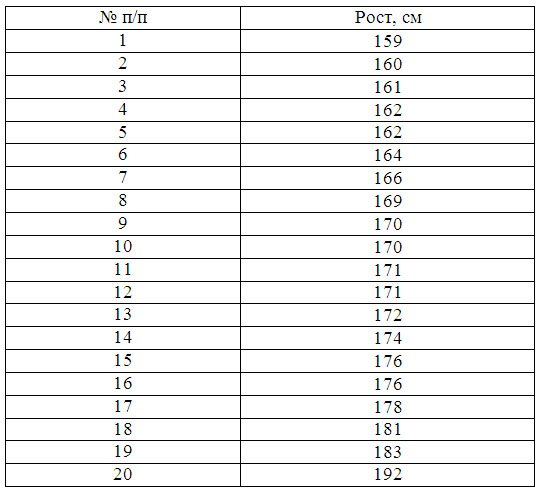
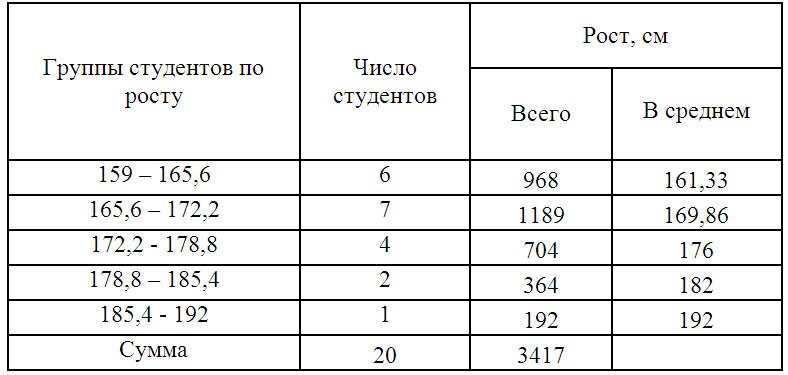
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию
Построим интервальную группировку. Определим размах интервала по формуле:
где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:
Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6
Составим интервальную группировку
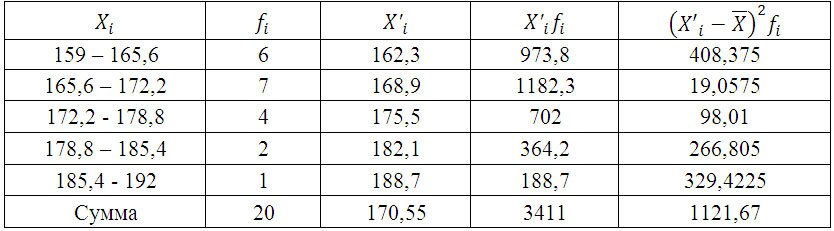
Для дальнейших расчетов построим вспомогательную таблицу:
X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
Определим дисперсию по формуле:
Пример 2. Определение групповой, средней из групповой, межгрупповой и общей дисперсии
Пример 3. Нахождение дисперсии и коэффициента вариации в группировочной таблице
Пример 4. Нахождение дисперсии в дискретном ряду
Формулу дисперсии можно преобразовать так:
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:
Подставляя в данную формулу дисперсии q =1- р, получаем:
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя;
ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.
Свойства дисперсии
1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей | Число семей сотрудников по подразделениям | ||
|---|---|---|---|
| первое | второе | третье | |
| 0 | 4 | 7 | 5 |
| 1 | 6 | 10 | 13 |
| 2 | 3 | 3 | 3 |
| 3 | 2 | 1 | — |
Вычислить:
а) внутригрупповые дисперсии;
б) среднюю из внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию;
Проверьте правильность произведения расчётов с помощью правила сложения дисперсий.
Решение:
Совокупность семей сотрудников финансовой корпорации разбита на три группы по количеству детей.
а) Групповая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы. Внутригрупповые дисперсии вычисляются по формуле:
Нахождению внутригрупповой дисперсии предшествует расчёт средней арифметической по каждой группе.
Рассчитаем внутригрупповые дисперсии:
б) Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых:
в) Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней:
Для её расчета необходимо вычислить общую среднюю:
Определим межгрупповую дисперсию:
Вычислим общую дисперсию обычным способом:
Проверим полученный результат, исчислив общую дисперсию по правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:
Как найти дисперсию?
Полезная страница? Сохрани или расскажи друзьям
Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 — (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 — (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Дисперсия. Формула. Виды дисперсии
Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку, то есть построить аналитическую группировку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами.
Дисперсия результативного признака внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучаемым). Такая дисперсия называется остаточной (та колеблемость, которая осталась при закреплении изучаемого фактора ).
Межгрупповая дисперсия относится на счет изучаемого фактора (и факторов, связанных с ним), поэтому называется факторной.
В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутри групповой.
Общая дисперсия 2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака Х– от общей средней и может быть вычислена как простая дисперсия или взвешенная дисперсия по формуле (6) или (7).
Межгрупповая дисперсия 2 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних , от общей средней
. Межгрупповая дисперсия вычисляется по формуле:
(15)
где mj – численность единиц в группе,
j – номер группы,
– среднее значение признака в j группе,
– общая средняя.
Внутригрупповая (частная) дисперсия , отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы
(групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
,
, (16)
– среднее значение признака в j группе,
– i значение признака (варианта),
– частот i варианты,
п – объем совокупности.
На основании внутри групповой дисперсии по каждой группе, т.е. на основании можно определить общую среднюю из внутригрупповых дисперсий
:
. (17)
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
. (18)
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью — неизвестную, а также судить о силе влияния группировочного признака.
Очевидно, чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак.
Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации (2) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
(19)
Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице.
Эмпирическое корреляционное отношение — это корень квадратный из эмпирического коэффициента детерминации:
оно показывает тесноту связи между группировочным и результативным признаками.
Эмпирическое корреляционное отношение , как и 2, может принимать значения от 0 до 1.
Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.
Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна обшей дисперсии (), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:
|
э |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
|
Сила связи |
Слабая |
Умеренная |
Заметная |
Тесная |
Весьма тесная |
Пример.
Имеются следующие данные о величине кредитов, выданных частным лицам, российскими и иностранными банками, функционирующими на территории РФ:
Таблица 3
|
Банки |
Выдано кредитов частным лицам, млн. руб. |
|
Российские |
2557,3; 2025,1; 1682,2; 1608,5; 1346,3; 1340,2; 1312,4; 1308,6 |
|
Иностранные |
410,1; 273,2; 187,5; 148,1 |
На основании приведенных данных проверить правило сложения дисперсий и определить влияние факторного признака на вариацию величины кредитов, выданных частным лицам.
Решение.
Проанализируем вариацию кредитов частным лицам по всем банкам. Для этого рассчитаем общую дисперсию по следующей формуле:
,
где значение признака по каждой единице;
общая средняя, рассчитанная по всем единицам.
Общая дисперсия характеризует вариацию объема кредитов частным лицам под влиянием всех факторов. Однако из таблицы видно, что вариация объема кредитов частным лицам зависит прежде всего от факторного признака.
Построим групповую таблицу, полученную по результатам аналитической группировки:
Таблица 4
|
Банки |
Число банков, nj |
Средний объем кредитов частным лицам, |
Дисперсия объема кредитов частным лицам в группе, 2j |
|
Российские |
8 |
1647,6 |
173186,45 |
|
Иностранные |
4 |
254,7 |
10105,44 |
|
Итого |
12 |
По каждой группе рассчитывается внутригрупповая дисперсия, характеризующая вариацию объема кредитов частным лицам под влиянием всех прочих случайных факторов (кроме фактора, положенного в основу группировки), по следующей формуле:
,
где j =1k (номер группы)
i = 1n (номер единицы)
Таким образом, имеем:
В целом для всех единиц рассчитывается средняя из внутригрупповых дисперсий:
Для оценки вариации объема кредитов частным лицам под влиянием факторного признака рассчитаем межгрупповую дисперсию:
Общую среднюю () определим по следующей формуле:
(млн. руб.)
Тогда
Общая дисперсия представляет собой сумму межгрупповой и средней из внутригрупповых дисперсий:
, что соответствует общей дисперсии, рассчитанной выше.
Для оценки влияния факторного признака на вариацию объема кредитов частным лицам рассчитаем долю межгрупповой дисперсии в общей, которая называется коэффициентом детерминации (2):
(78,4%)
Следовательно, на 78,4 % вариация объема кредитов частным лицам зависит от факторного признака и на 21,6 % (100-78,4) – от влияния всех прочих факторов.
Таким образом, в сочетании с методом группировок правило сложения дисперсий позволяет выявить факторы, оказывающие наибольшее влияние на вариацию признака в совокупности и дать количественную оценку степени влияния этих факторов.
Пусть некоторая
совокупность объема
разбита на части – на
непересекающихся групп, не обязательно
одинаковых по объему. Группы называются
непересекающимися, если каждый вариант
принадлежит только одной группе. Для
каждой группы вариантов можно вычислить
средние, которые называются групповыми
средними
(
).
Пусть
— количество вариант соответственно в
1-ой, 2-ой, …,
-ой
группах;
— количество вариант всей совокупности;
— объемы данных групп.
Групповая средняя
— ой группы (
)
вычисляется по формуле
(17)
Общей средней
называется средняя арифметическая всей
совокупности:
(18)
Общую
среднюю можно выразить через групповые
средние:
, (19)
где
— объем
-ой
группы.
Если численности
всех групп одинаковые, то общая средняя
может быть получена и как простая средняя
из групповых средних
(20)
Дисперсия для
распределения вариантов
-ой
группы относительно их групповой средней
называется групповой
дисперсией
и
вычисляется по формуле:
, (21)
где
— номер группы,
— значения вариант группы (
),
— частоты значений
,
— групповая средняя
-ой
группы,
— объем
-ой
группы.
Дисперсия по этому
же признаку всей совокупности относительно
общей средней называется общей
средней
(
).
Групповые средние
(
)
могут не совпадать с общей средней (
).
Мерой колеблемости
групповых средних (
)
вокруг общей средней (
)
является межгрупповая
дисперсия
(
),
которая вычисляется по формуле:
. (22)
Межгрупповая
дисперсия характеризует систематическую
вариацию, которая возникает под влиянием
фактора, признака, положенного в основе
группировки.
Для характеристики
среднего рассеяния признака внутри
групп из групповых дисперсий может быть
найдена их средняя арифметическая,
взвешенная по объемам групп, которая
называется внутригрупповой
дисперсией
(
)
и вычисляется по формуле:
. (23)
Внутригрупповая
дисперсия характеризует случайную
вариацию в каждой отдельной группе. Она
возникает под влиянием других,
неучитываемых факторов и не зависит от
условий (или признака-фактора), положенных
в основу группировки.
Общей дисперсией
(
)
называют дисперсию значений признака
всей совокупности относительно общей
средней:
, (24)
где
— частота значения
,
— общая средняя,
— объем всей совокупности.
Между общей
дисперсией, внутригрупповой и межгрупповой
дисперсией существует связь, определяемая
теоремой.
Теорема (правило
сложения дисперсий).
Если
совокупность состоит из нескольких
групп, то общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий.
(25)
Пример 3.
Дано распределение рабочих предприятия
по заработной плате в разрезе цехов:
Таблица №6
|
Заработная плата (в тыс. руб.) |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
|
Цех 1 |
7 |
12 |
15 |
6 |
0 |
0 |
|
Цех 2 |
1 |
5 |
9 |
18 |
12 |
5 |
|
Цех 3 |
0 |
0 |
4 |
8 |
32 |
16 |
Вычислить средние
заработные платы рабочих в каждом цехе
и по предприятию. Вычислить дисперсии
по цехам (групповые дисперсии) и по
предприятию (общую дисперсию). Проверить
правило сложения дисперсий.
Решение.
-
Найдем
объемы групп
и объем всей совокупности
и частоты
для значений
относительно всей совокупности (столбец
«Всего»).
;
;
;
.
-
Найдем
значенияпредставителей интервалов по формуле:
,
где
— начало интервала,
— конец интервала.
;
;
;
;
;
.
Число
вариант в каждой группе
.
-
Вычислим
групповые средние (формула (17)) и общую
среднюю (формулы (18) и (19)).
Число
вариант в каждой группе
.
;
;
;
;
.
-
Вычислим
групповые дисперсии (формула (21)) и общую
дисперсию (формула (24)):


;

-
Вычислим
внутригрупповую (формула (23)), межгрупповую
(формула (22)) и общую (формула (25)) дисперсии:


;
.
Этапы решения задачи оформим в виде
расчетных таблиц №7 и №8(все расчеты
выполним в табличном процессоре Excel):
Таблица №7
|
Заработная (в |
Цех 1 ( |
Цех 2 ( |
Цех 3 ( |
Всего |
(цех |
(цех |
(цех |
(вся |
||
|
70,00 |
||||||||||
|
80,00 |
7,00 |
1,00 |
0,00 |
8,00 |
75,00 |
13,13 |
1,50 |
0,00 |
4,00 |
|
|
90,00 |
12,00 |
5,00 |
0,00 |
17,00 |
85,00 |
25,50 |
8,50 |
0,00 |
9,63 |
|
|
100,00 |
15,00 |
9,00 |
4,00 |
28,00 |
95,00 |
35,63 |
17,10 |
6,33 |
17,73 |
|
|
110,00 |
6,00 |
18,00 |
8,00 |
32,00 |
105,00 |
15,75 |
37,80 |
14,00 |
22,40 |
|
|
120,00 |
0,00 |
12,00 |
32,00 |
44,00 |
115,00 |
0,00 |
27,60 |
61,33 |
33,73 |
|
|
130,00 |
0,00 |
5,00 |
16,00 |
21,00 |
125,00 |
0,00 |
12,50 |
33,33 |
17,50 |
|
|
Всего |
40,00 |
50,00 |
60,00 |
150,00 |
90,00 |
105,00 |
115,00 |
105,00 |
||
|
|
|
|
|
|
|
|||||
|
Таблица №8 |
||||||||||
|
|
|
|
|
|
||||||
|
39,38 |
18,00 |
0,00 |
48,00 |
97,33 |
100,00 |
197,33 |
||||
|
7,50 |
40,00 |
0,00 |
45,33 |
|||||||
|
9,38 |
18,00 |
26,67 |
18,67 |
|||||||
|
33,75 |
0,00 |
13,33 |
0,00 |
|||||||
|
0,00 |
24,00 |
0,00 |
29,33 |
|||||||
|
0,00 |
40,00 |
26,67 |
56,00 |
|||||||
|
90 |
140 |
66,67 |
197,33 |
|||||||
|
|
|
|
Задача 3. Трое
рабочих изготовляли одинаковые детали.
Каждый из них изготовил по 70 деталей.
Для контроля составлены распределения
изготовленных каждым рабочим деталей
по их размеру. Точность измерения 0,01.
Поле допуска 50,04-50,28мм. Сравнением
распределений выяснить, какой рабочий
работает лучше.
Таблица №9
|
Интервалы |
I |
II |
III |
|
50-50,04 |
2 |
0 |
3 |
|
50,04-50,08 |
6 |
2 |
8 |
|
50,08-50,12 |
9 |
5 |
16 |
|
50,12-50,16 |
26 |
9 |
9 |
|
50,16-50,2 |
14 |
14 |
4 |
|
50,2-50,24 |
7 |
19 |
13 |
|
50,24-50,28 |
5 |
8 |
11 |
|
50,28-50,32 |
1 |
5 |
4 |
|
50,32-50,36 |
0 |
5 |
2 |
|
50,36-50,4 |
0 |
2 |
0 |
|
50,4-50,44 |
0 |
1 |
0 |
|
Всего |
70 |
70 |
70 |
Все расчеты
выполнить в табличном процессоре Excel
и оформить в виде расчетных таблиц.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #