Как найти образующий элемент группы - Autoru.top

Думаю оно является достаточным

Если является, то приведите доказательство.

$a^{2^s}$ порождающий элемент $Y$ , значит $(a^{2^s})^r = e$ .

Равенство $(a^{2^s})^r = e$ верно безотносительно к тому, является ли $a^{2^s}$ порождающим элементом для $Y$ .

Это означает, что $a -$ образующий элемент $X$ , если это такое наименьшее натуральное число, что $a$ в его степени равен $e$

Слова «это означает» ни при чем. Это просто определение того, что такое образующий элемент циклической группы.

Пусть $a^k -$ образующий элемент $X$

Так ведь если $a^k$ — образующий для $X$ , то $a$ тоже непременно образующий, в любом случае!

Тогда $(a^k)^{2^sr} = a^{2^srk}$ . Число натуральное. Получается, что $2^sr$ наименьшее такое число, таким образом, утверждение доказано.

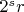
Это вообще нечто невразумительное.

В общем, я думаю, Вы в том, что пишете, и в том, как думаете, сильно путаетесь. У Вас же были в школе уроке геометрии, где среди прочего учат связно рассуждать.

Посмотрите, как в книжках хороших (Кострикин, например, или Калужнин) строят рассуждения. Кроме того, вот в этой теме (ближе к концу) я на примерах (более элементарных) показывал другому человеку, что такое аккуратное рассуждение. Можете также заглянуть в книжку В.А.Успенский, Простейшие примеры математических доказательств.

В общем, Вам стоит стараться рассуждать и писать более аккуратно, а то и обсуждать, по сути, нечего. Такие дела.

Источник

Циклические группы

Определение
6. Группа G
называется циклической, если она состоит
из степеней одного из своих элементов
а, т.е. совпадает с одной из своих
циклических подгрупп (а).

Элемент а
называется образующим элементом
циклической группы (а). Каждая
циклическая группа абелева, т.к.

Пример
1.

– бесконечно циклическая группа. Её
образующий элемент – число 1. Образующим
элементом этой группы является, очевидно,
n-1.

Пример 2.
Мультипликативная группа n-й
степени из 1 является циклической группой
порядка n. Действительно,
корни n-й степени из
1 находятся по формуле:

По формуле Муавра

Т.о. каждый корень
n-й степени из 1 является
определенной степенью корня

₁
и, следовательно, группа n-й
степени из 1 является циклической группой
(
₁),
образующим элементом которой является

Теорема 7.
Каждая бесконечная циклическая группа
изоморфизма аддитивной группы целых
чисел Z.

□ Пусть G=(a)
– произвольная циклическая бесконечная
группа с образующим элементом а.
Каждому элементу а^k
группы G поставим в
соответствие элемента R
Z.
Этим, очевидно, будет задано взаимно
однозначное отображение G
на Z. Это отображение
является изоморфизмом, т.к. из а^k

и а^s

S
следует, что

■

Теорема 8.
Каждая циклическая группа порядка n
изоморфна мультипликативной группе
корней n-й степени из
1.

□ Пусть
G
= (a)
– произвольная циклическая группа
порядка n
с образующим элементом а.
Она состоит из следующих элементов:

Мультипликативная группа корней n
— й степени
из 1 состоит из корней

Рассмотрим
отображение f, заданное
по правилу

.
Очевидно, что из

следует, что

■

Из теоремы 7 и 8
следует, что аддитивной группой целых
чисел и мультипликативной группой
корней n-й степени из
1 по существу исчерпываются все циклические
группы.

Теорема 9.
Каждая группа циклической группы сама
циклическая.

□ Пусть G
= (a) – произвольно
циклическая группы и H
– некоторая ее подгруппа. Будем считать,
что Н отлична от единичной подгруппы
Е, в противном случае не надо
доказывать, что она циклическая.

Среди положительных
степеней элемента а, которые
содержатся в Н, существует наименьшая,
т.к. в произвольном множестве натуральных
чисел всегда есть наименьшее. Пусть
этой наименьшей положительной степенью
является а^к. Покажем, что
если

,
то l делится на k.
Действительно,

Если r>0, то в
подгруппе Н содержится элемент

,
т.е. содержится положительная степень
элемента а, меньшая чем а^k,
что противоречит нашему предположению.
Следовательно, r=0
и k делится на k.■

Разложение группы по подгруппе

Пусть даны группа
G и подмножества А
и В этой группы. Совокупность всех
элементов из G, каждый
из которых можно записать в виде
некоторого элемента из А на некоторый
элемент из В, называется произведением
множества А на множество В и
обозначается АВ.

Если, например,
множество А состоит только из одного
элемента а, то речь идет о произведении
аА элемента а на множество А.

Из ассоциативности
умножения в группе G
вытекает ассоциативность умножения
подмножеств этой группы:

Очевидно, если H
– подгруппа группы G,
то НН=Н.

Покажем это. Для
любых а,b

имеем

и
значит

.
С другой стороны

,
поскольку Н = Не. Значит, НН=Н.

Пусть Н –
произвольная подгруппа группы G.
Используем эту подгруппу для введения
на множестве G бинарное
отношение

,
считая, что

,
где а, b – произвольные
элементы множества G.

Очевидно, что
условие, а

есть
то же самое, что и

,
где h некоторый элемент
подгруппы Н.

Покажем, что

является отношением эквивалентности.

2)

;

Отношение

задает разбиение группы G
на классы эквивалентных элементов.
Выясним, что представляют собой эти
классы эквивалентности. Если H = G,
то разбиение состоит только из одного
класса, т.к.

и, следовательно,

Если

то

является обычным равенством и поэтому
каждый элемент группы G
составляет класс разбиения. Если Н
– подгруппа
отличная от Е
и G
и если В_i
– один из классов разбиения, и пусть
g
.
Тогда

,
где

,
принадлежит

,
т.к.

.
Наоборот, если b
,
то

,
поэтому

.
Следовательно,

Т.о.,
мы доказали, что каждый класс разбиения
группы G
по отношению

,
когда

является произведением gH
произвольного элемента g
этого класса на подгруппу Н.
Эти классы разбиения называют левыми
смежными классами
группы G
по подгруппе Н,
а само разбиение называют левосторонним
разложением
G
по Н.
О смежном классе В_i
= gH
говорят, что он порождается элементом
g.

Если
группа G
конечная, то левостороннее разложение
G
по Н
записывают так:

,
где знаки + и

обозначают объединение множеств, которые
не пересекаются, – левых смежных классов.

На
множестве элементов группы G
можно ввести отношение эквивалентности

В этом случае
приходим к понятию правого смежного
класса Hg группы G
по подгруппе Н, порожденного элементом
g и k
правостороннему разложению G
по Н.

Возникает
вопрос: левостороннее и правостороннее
разложения G
по Н
– это различные разбиения разложения
или нет? Если группа G
– абелева, то, очевидно, левостороннее
и правостороннее разложения G
по Н совпадают,
т.к. gH=Hg
для

Для неабелевой группы разложения по
одной группе могут совпадать, а по другой
могут оказаться различными.

Пример1.

.
G – абелева группа.
Левостороннее и правостороннее разложение
этой группы по подгруппе Н совпадают.
Каждое из этих разложений состоит из k
различных смежных классов, которые
порождаются соответственно числами
0,1,2,3,…,k-1.
Левосторонний смежный класс, порожденный
элементом l имеет вид
l+H,
а правосторонний – H+l.

Пусть
G
– группа невырожденных квадратных
матриц n-го
порядка над полем R,
H
– подгруппа, состоящая из всех матриц
n-го
порядка, определитель каждой из которых
равен 1. Множество всех матриц с равными
определителями составляет левый (а
также и правый) смежный класс. В самом
деле, если

т.е.

,
где

,
то

т.е.

.
Наоборот, если

,
то

т.к.

поэтому

Сгруппировав
в один смежный класс (левый и правый)
все матрицы с равными определителями,
получим разложение (левое и правое)
группы G
по подгруппе Н.

Пример
3. G=S₃

Подмножество
Н={E,A}
группы G
является подгруппой этой группы
(докажите это). Левые смежные группы S₃
по подгруппе Н
следующие:

Видим,
что левые и правые смежные классы
различны. Значит, различны и левостороннее
и правостороннее разложения S₃
по Н.

Для конечных групп
справедливо утверждение.

Теорема
10. (Теорема
Лагранжа)
В каждой конечной группе порядок ее
подгруппы является делителем порядка
группы.

□ Пусть
G
– конечная группа порядка n,
Н – некоторая
ее подгруппа порядка k.
Рассмотрим левостороннее разложение
группы G
по подгруппе Н.
Предположим, что оно состоит из S
смежных классов.

(6)

Подгруппа
Н
состоит из k
элементов, а поэтому и каждый смежный
класс

также состоит из k
элементов,
т.к. если

где

,
то

Следовательно,
из разложения (6) вытекает, что n=ks.
■

Следствие
1. Порядок
каждого элемента а
конечной группы G
является
делителем порядка группы.

Следствие
2. Каждая
конечная группа, порядок которой является
простым числом, является циклической
группой (докажите эти следствия
самостоятельно).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Группоиды, полугруппы, группы

Рассмотрим алгебры, сигнатуры которых состоят из одной. бинарной операции. Эту операцию будем обозначать точкой (,cdot,) и условно называть в этом случае умножением.

Группоидом называют любую алгебру mathcal{G}=(G,cdot) , сигнатура которой состоит из одной бинарной операции. В группоиде на бинарную операцию нет никаких ограничений.

Группоид (G,cdot) называют полугруппой, если его операция ассоциативна, т.е. для любых элементов a,,b,,c носителя выполняется равенство

acdot (bcdot c)= (acdot b)cdot c,.

Пример 2.6. а. Множество V_3 свободных векторов вместе с операцией векторного умножения является группоидом, но не полугруппой, так как векторное умножение не ассоциативно.

б. Множество натуральных чисел вместе с операцией возведения в степень также будет только группоидом, так как $(a^b)^cne a^{(b^c)}$ .

в. Множество 2^A всех подмножеств множества вместе с операцией setminus (разность множеств) тоже только группоид, поскольку указанная операция не ассоциативна.

г. Множество натуральных чисел mathbb{N} вместе с операцией сложения будет полугруппой.

Группоид mathcal{G}=(G,cdot) называют моноидом, если его операция ассоциативна и относительно операции существует нейтральный элемент. Его называют нейтральным элементом моноида или единицей моноида и обозначают bold{1} .

Таким образом, моноид mathcal{G}=(G,cdot) есть полугруппа, в которой для любого а имеют место равенства acdotbold{1}=bold{1}cdot a=a , где bold{1} — нейтральный элемент (единица) моноида.

Поскольку нейтральный элемент относительно любой бинарной операции является единственным, мы можем рассматривать моноид как алгебру (G,cdot,bold{1} , сигнатура которой состоит из двух операций: бинарной операции {}cdot{} (умножение) и нульарной операции bold{1} (нейтрального элемента). Введение bold{1} в сигнатуру моноида удобно тем, что зачастую при рассмотрении конкретных примеров моноидов целесообразно явно указать нейтральный элемент относительно его операции. Например, алгебра $(2^{Atimes A},circ,operatorname{id}A)$ есть моноид всех бинарных отношений на множестве с операцией композиции бинарных отношений, в котором нейтральным элементом является диагональ множества .

Среди полугрупп выделяют полугруппы с коммутативной операцией — коммутативные полугруппы.

Пример 2.7. а. Множество всех бинарных отношений на произвольном множестве с операцией композиции отношений будет моноидом, нейтральным элементом которого служит диагональ множества , поскольку для любых бинарных отношений rho,tau и sigma на множестве имеют место равенства

rhocirc (taucircsigma)= (rhocirctau)circsigma и operatorname{id}Acircrho= rhocircoperatorname{A}=rho. .

б. Множество всех отображений некоторого множества в себя по операции композиции отображений есть моноид.

Напомним, что композиция отображений снова есть отображение и операция композиции имеет нейтральный элемент: тождественное отображение на себя. Поскольку любое отображение множества в себя можно рассматривать как бинарное отношение на этом множестве, а композицию отображений — как частный случай композиции отношений, требуемые свойства операции композиции отображений выполняются (см. пример 2.7.а). При этом тождественному отображению соответствует диагональ operatorname{id}A множества . Этот моноид называют часто симметрическим моноидом или симметрической полугруппой множества .

в. Алгебра $(mathbb{N}_0,+)$ , где носитель — множество $mathbb{N}_0$ неотрицательных целых чисел, а сигнатура состоит из одной операции сложения, есть коммутативный моноид, в котором нейтральный элемент — это число 0. Действительно, сумма двух натуральных чисел есть натуральное число, операция сложения ассоциативна, коммутативна и для любого натурального числа имеет место равенство n+0=n .

Обратим внимание на то, что свойства нейтральных элементов и нулей ассоциируются со свойствами чисел 1 и 0 относительно операций умножения и сложения чисел.

г. Алгебра (mathbb{Z},cdot) , у которой носителем является множество целых чисел, а сигнатура состоит из одной операции умножения, есть коммутативный моноид. Нейтральным элементом этого моноида является число 1.

д. Пусть — конечное множество, а A^n — множество кортежей длины . На множестве всех кортежей $A^{+}= mathop{cup}limits_{ngeqslant1}A^n$ определим операцию соединения (конкатенации) кортежей следующим образом:

(a_1,ldots,a_m)cdot (b_1,ldots,b_k)= (a_1,ldots,a_m,, b_1,ldots,b_k).

Можно видеть, что введенная операция ассоциативна, но не имеет нейтрального элемента. Таким образом, построена полугруппа, но не моноид.

Чтобы превратить эту полугруппу в моноид, расширим носитель полугруппы, введя понятие нулевой декартовой степени A^0 произвольного множества . Под A^0 понимают одноэлементное множество {lambda} , единственный элемент которого называют пустым кортежем. Такое определение множества A^0 объясняется следующим: мощность положительной декартовой степени A^n конечного множества равна |A|^n . При n=0 должно быть |A^0|=|A|^0=1 , откуда заключаем, что A^0 — одноэлементное множество.

Обозначив $A^{ast}=A^{0}cup A^{+}$ , по определению для любого $xin A^{ast}$ полагаем xcdotlambda= lambdacdot x=x . В результате получим алгебру $(A^{ast},cdot)$ , являющуюся моноидом, с нейтральным элементом lambda . Его называют свободным моноидом, порожденным множеством .

Полурешетка в абстрактной алгебре

Полугруппу, операция которой коммутативна и идемпотентна, называют полурешеткой.

Пример 2.8. а. Алгебры (2^A,cup),, (2^A,cap) (для произвольного фиксированного множества ) являются полурешетками, поскольку операции cup и cap ассоциативны, коммутативны и идемпотентны.

б. Алгебра (mathbb{N},operatorname{lcm}) , где — операция вычисления наименьшего общего кратного двух чисел, является полурешеткой. Покажем, что указанная операция ассоциативна. Рассмотрим произвольные натуральные числа m,,n и . Каждое из этих чисел можно разложить на произведение простых чисел и представить в виде

$m=p_1^{alpha_1}cdot ldotscdot p_k^{alpha_k},qquad n=p_1^{beta_1}cdot ldotscdot p_k^{beta_k},qquad l=p_1^{gamma_1}cdot ldotscdot p_k^{gamma_k},$

где набор простых чисел p_1,ldots,p_k выбран одинаковым для всех трех чисел, а некоторые из показателей alpha_i,,beta_i и $gamma_i,~ i=overline{1,k}$ могут быть равными нулю. Тогда для чисел тип имеем

$operatorname{lcm}(n,m)= p_1^{max(alpha_1,beta_1)}cdot ldotscdot p_{k}^{max(alpha_k, beta_k)}.$

Таким образом, ассоциативность операции operatorname{lcm} сводится к ассоциативности операции max вычисления наибольшего из двух натуральных чисел. Ассоциативность последней вытекает из очевидного тождества max(a,max(b,c))= max(max(a,b),c) , верного для любых чисел a,,b и .

Поскольку operatorname{lcm}(n,m)= operatorname{lcm}(m,n) , операция коммутативна, а так как для любого натурального числа справедливо равенство operatorname{lcm}(n.n)=n , то операция идемпотентна.

в. Алгебра (mathbb{N},gcd) , где gcd — операция вычисления наибольшего общего делителя двух целых чисел, также является полурешеткой.

Способы задания группы как алгебры

Группоид mathcal{G}=(G,cdot) называют группой, если операция ассоциативна, существует нейтральный элемент (единица) bold{1} относительно умножения и для каждого xin G существует такой элемент x'in G , называемый обратным к , что xcdot x'=x'cdot x=bold{1} .

Таким образом, группа — это алгебра mathcal{G}=(G,cdot) , в которой для всех a,b,cin G выполняется равенство acdot (bcdot c)=(acdot b)cdot c , существует единственный элемент bold{1}in G , такой, что acdotbold{1}= bold{1}cdot a=a для любого ain G , и для каждого ain G существует такой элемент , что acdot a'=a'cdot a=bold{1} . Короче говоря, группа — это моноид, в котором для каждого элемента существует обратный элемент.

Отметим, что задать группу как алгебру можно несколькими способами в зависимости от состава операций, включенных в сигнатуру.

Во-первых, в сигнатуру может быть включена единственная бинарная операция. В этом случае пишут mathcal{G}=(G,cdot) , а все свойства операции описывают дополнительно.

Во-вторых, в сигнатуру может быть включена нульарная операция — нейтральный элемент группы. В этом случае пишут mathcal{G}=(G,cdot,bold{1}) и дополнительно указывают существование обратного элемента относительно бинарной операции для всех элементов носителя.

Третий способ задания группы как алгебры вытекает из следующей теоремы.

Теорема 2.1. В любой группе mathcal{G}=(G,cdot) для каждого ain G элемент, обратный к , единственный.

Пусть в группе (G,cdot) с единицей bold{1} для некоторого существуют два элемента и a'' , обратных к . Тогда a'=a'cdotbold{1} в силу свойства единицы. Так как bold{1}=acdot a'' , то a'=a'cdot (acdot a'') . Используя ассоциативность и учитывая, что — элемент, обратный к а, получим

a'cdot (acdot a'')= (a'cdot a)cdot a''= bold{1}cdot a''=a''.

Единственность для каждого элемента обратного элемента группы mathcal{G} позволяет обозначать его как $a^{-1}$ и операцию $phantom{A}^{-1}colon amapsto a^{-1}$ вычисления (или взятия) обратного элемента ввести в сигнатуру группы. Таким образом, группу можно рассматривать и как алгебру $mathcal{G}=(G,cdot,phantom{A}^{-1},bold{1})$ , сигнатура которой состоит из бинарной операции умножения, унарной операции взятия обратного элемента и нульарной операции — единицы группы (нейтрального элемента).

В дальнейшем в зависимости от контекста будем использовать все указанные варианты задания группы.

Среди групп также выделяют те, бинарная операция в которых коммутативна, — коммутативные (абелевы) группы. В коммутативных полугруппах и группах бинарную операцию часто обозначают знаком {}+ и называют сложением.

Уместно здесь рассмотреть вопрос о двух формах записи бинарной операции группы. В аддитивной записи операции ее обозначают знаком {}+ , нейтральный элемент — знаком bold{0} , а элемент, обратный к относительно операции {}+ , записывают в виде , называя его при этом противоположным к .

В мультипликативной записи операцию обозначают знаком cdot , нейтральный элемент — знаком bold{1} , а элемент, обратный к , записывают в виде $a^{-1}$ . В этом случае бинарную операцию группы часто называют умножением (также умножением группы или групповым умножением), а элемент acdot b , как правило записываемый в виде , — произведением элементов и .

В алгебраической литературе сложилась такая традиция, что аддитивная запись используется преимущественно для коммутативных групп. Поскольку одним из самых простых, распространенных и вместе с тем важных примеров коммутативной группы служит аддитивная группа целых чисел, то обозначения и термины для произвольной аддитивно записываемой коммутативной группы «скопированы» с терминов для группы (mathbb{Z},+,0) . Аналогично мультипликативная запись произвольной группы » позаимствована» у мультипликативных групп рациональных и вещественных чисел.

Пример 2.9. а. Алгебра (mathbb{Z},+) — коммутативная группа, поскольку на множестве целых чисел операция сложения ассоциативна и коммутативна, число 0 есть нейтральный элемент, и для каждого целого числа существует обратный по сложению элемент, а именно число , противоположное . Рассматриваемую группу называют аддитивной группой целых чисел.

б. Множество всех биекций некоторого множества на себя с операцией композиции отображений есть группа.

Это следует из того, что композиция двух биекций есть биекция, операция композиции ассоциативна, ее нейтральный элемент — тождественное отображение operatorname{id}A — есть биекция, для всякой биекций fcolon Ato A отображение $f^{-1}$ , обратное биекций , определено, является биекцией и выполнены равенства

$fcirc f^{-1}= f^{-1}circ f= operatorname{id}A,.$

Эту группу называют симметрической группой множества , а в том случае, когда множество конечно, — группой подстановок множества . Если множество состоит из элементов, группу подстановок этого множества называют также симметрической группой степени или группой подстановок n-й степени и обозначают S_n (см. пример 2.10).

в. Алгебры (mathbb{Q}setminus {0},cdot) и (mathbb{R}setminus {0}, cdot) есть коммутативные группы. Их называют мультипликативной группой рациональных чисел и мультипликативной группой действительных чисел соответственно. В каждой из них число 1 есть нейтральный элемент (единица) группы, а обратный к числу по операции умножения элемент $x^{-1}$ есть число $x^{-1}=1/x$ .

г. Для произвольно фиксированного множества рассмотрим алгебру (2^A,triangle) , где — операция вычисления симметрической разности множеств. Операция ассоциативна и коммутативна. Для любого Xsubseteq A имеем X,triangle,varnothing=X . Кроме того, X=Y тогда и только тогда, когда X,triangle,Y=varnothing . Поэтому алгебра (2^A,triangle) является абелевой группой, в которой каждый элемент обратен сам себе, а нейтральный элемент — пустое множество.

д. Рассмотрим алгебру $mathbb{Z}_{k}^{+}=({0,1,ldots,k-1},oplus_k)$ , в которой операция oplus_k (сложения по модулю ) определяется так: для любых двух и число $moplus_{k}n$ , называемое суммой чисел и по модулю , равно остатку от деления арифметической суммы m+n на . Можно проверить, что эта алгебра является коммутативной группой. Ее называют аддитивной группой вычетов по модулю . Нейтральным элементом служит число 0, а обратным к числу будет k-n , поскольку $noplus_{k}(k-n)=0$ .

е. Множество всех невырожденных (т.е. имеющих ненулевой определитель) числовых квадратных матриц порядка с операцией умножения матриц является группой. Действительно, произведение двух невырожденных матриц снова есть невырожденная матрица; единичная матрица порядка невырожденная, и матрица, обратная к невырожденной, также является невырожденной. Эту группу будем обозначать $mathcal{M}_n$ .

Из рассмотренных четырех видов алгебр — группоида, полугруппы, моноида и группы — последняя обладает наиболее интересными свойствами. Изучим более подробно операцию вычисления обратного элемента.

Теорема 2.2. Пусть mathcal{G}=(G,cdot) — группа. Для любых элементов a,bin G верны тождества

$(acdot b)^{-1}= b^{-1}cdot a^{-1},qquad (a^{-1})^{-1}=a,.$

В силу ассоциативности умножения группы имеем

$(acdot b)cdot (b^{-1}cdot a^{-1})= bigl((acdot b)cdot b^{-1}bigr)cdot a^{-1}.$

Используя еще раз ассоциативность, определение элемента, обратного к данному, и свойства единицы, получим

$bigl((acdot b)cdot b^{-1}bigr)cdot a^{-1}= acdot (bcdot b^{-1})cdot a^{-1}= acdot a^{-1}= bold{1},.$

Итак, $(acdot b)cdot (b^{-1}cdot a^{-1})=bold{1}$ . Точно так же доказывается, что $(b^{-1}cdot a^{-1})(acdot b)=bold{1}$ . Поэтому элемент $b^{-1}cdot a^{-1}$ является обратным к элементу acdot b . Согласно теореме 2.1, обратный элемент единственный, и поэтому $(acdot b)^{-1}=b^{-1}cdot a^{-1}$ . Второе из доказываемых равенств следует непосредственно из определения элемента, обратного к данному. Действительно, определение элемента $a^{-1}$ , обратного к , равенством $a^{-1}cdot a=acdot a^{-1}=bold{1}$ можно рассматривать как определение $(a^{-1})^{-1}$ — обратного элемента к $a^{-1}$ , которым является, согласно этим равенствам, элемент . В силу теоремы 2.1 он единственный, то есть $a=(a^{-1})^{-1}$ .

Таким образом, мы установили, что элемент, обратный к произведению acdot b , равен $b^{-1}cdot a^{-1}$ , а элемент, обратный к элементу, обратному к , равен .

Теорема 2.3. В любой группе mathcal{G}=(G,cdot,bold{1}) справедливы левый и правый законы сокращения: если acdot x=acdot y , то x=y , и если xcdot a=ycdot a , то x=y .

Пусть acdot x=acdot y . Умножая обе части этого равенства слева на элемент $a^{-1}$ , получаем

$a^{-1}cdot (acdot x)= a^{-1}cdot (acdot y).$

В силу ассоциативности групповой операции последнее равенство можно записать так:

$(a^{-1}cdot a)cdot x= (a^{-1}cdot a)cdot y,.$

Поскольку $a^{-1}cdot a=bold{1}$ , то bold{1}cdot x=bold{1}cdot y , откуда x=y . Тем самым доказан левый закон сокращения. Аналогично доказывается и правый закон.

Пусть mathcal{G}=(G,cdot,bold{1}) — группа, и — фиксированные элементы . Рассмотрим задачу решения уравнений

acdot x=b,

(2.1)

xcdot a=b

(2.2)

в группе mathcal{G} , т.е. поиска всех таких элементов xin G , для которых уравнение (2.1) (или (2.2)) превращается в тождество.

Теорема 2.4. В любой группе mathcal{G} уравнения вида (2.1) и (2.2) имеют решения, и притом единственные.

Покажем, что $x=a^{-1}cdot b$ есть решение (2.1). Действительно, $acdot (a^{-1}cdot b)= (acdot a^{-1}cdot b)=b$ .

Докажем единственность решения. Пусть для фиксированных и и некоторого выполнено равенство acdot x=b . В группе для любого существует и однозначно определен элемент $a^{-1}$ , обратный к . Умножив на него обе части равенства, получим $a^{-1}cdot (acdot x)= a^{-1}cdot b$ . В силу ассоциативности преобразуем последнее равенство к виду $(a^{-1}cdot a)cdot x=a^{-1}cdot b$ . Поскольку $a^{-1}cdot a=bold{1}$ , то $bold{1}cdot x=a^{-1}cdot b$ , откуда $x=a^{-1}cdot b$ . Это решение единственное в силу единственности обратного элемента.

Аналогично из xcdot a=b получаем $x=bcdot a^{-1}$ , и это решение также единственное.

Замечание. При использовании аддитивной записи операции для коммутативной группы mathcal{G}=(G,+,bold{0}) оба написанных выше уравнения сводятся к одному:

a+x=b,,

а его решение есть x=b+(-a) . Правую часть этого равенства в коммутативной группе называют разностью элементов и и обозначают b-a . Саму же операцию, сопоставляющую упорядоченной паре (a,b) разность b-a , называют операцией вычитания. С учетом введенных обозначений решение уравнения в коммутативной группе можно записать так: x=b-a .

В случае коммутативной группы при употреблении для бинарной операции мультипликативной записи решения обоих уравнений имеют вид $x=bcdot a^{-1}$ . Выражение $bcdot a^{-1}$ в коммутативной группе называют частным от деления на и обозначают $tfrac{b}{a}$ (или b/a ), а саму операцию называют операцией деления. Решение уравнения в этом случае записывают в виде $x=tfrac{b}{a}$ (или x=b/a ).

Пример 2.10. Рассмотрим группу подстановок n-й степени S_n всех биекций n-элементного множества {1,2,ldots,n} . Произвольную биекцию sigma из S_n обычно записывают в виде

$begin{pmatrix}1&2& cdots &n\ alpha_1& alpha_2& cdots& alpha_n end{pmatrix}!,$

обозначая тем самым, что образ 1 (при отображении sigma ) есть alpha_1 , образ 2 есть alpha_2,ldots образ есть alpha_n . Биекцию множества {1,ldots,n} на себя называют подстановкой этого множества. Подстановку, которая отображает alpha_1 в alpha_2 , alpha_2 в alpha_3,ldots, , $alpha_{k-1}$ в $alpha_{k}$ , а $alpha_{k}$ в $alpha_{1}$ , где 1leqslant alpha_1,alpha_2, ldots,alpha_k leqslant n и все alpha_j попарно различны, а все элементы, отличные от alpha_1,ldots,alpha_k , отображаются сами в себя, называют циклом длины и записывают ее в виде (alpha_1,alpha_2, ldots,alpha_k) . Например, подстановку из группы S_4

$begin{pmatrix}1&2&3&4\3&2&4&1end{pmatrix}$ можно записать в виде begin{pmatrix}1&3&4end{pmatrix} .

Цикл длины 2 называют транспозицией. Транспозиция представляет такое отображение множества {1,ldots,n} в себя, при котором два элемента меняются местами, а остальные остаются на своих местах. Так, полная запись транспозиции (3~~4) в S_4 будет иметь вид

$begin{pmatrix}1&2&3&4\ 1&2&4&3end{pmatrix}!.$

Подстановка, обратная подстановке $begin{pmatrix}1&2&cdots&n\ alpha_1& alpha_2& cdots& alpha_n end{pmatrix}$ , есть подстановка, которая отображает alpha_1 в 1, alpha_2 в 2, ldots~ alpha_n в . Отметим, что при записи обратной подстановки элементы первой строки тем не менее записываются в обычном порядке: 1,ldots,n .

В группе S_3 решим следующее уравнение:

$begin{pmatrix}1&2&3\3&1&1end{pmatrix}! circ Xcirc! begin{pmatrix}1&2&3\ 2&3&1end{pmatrix}= begin{pmatrix}1&2&3\ 3&2&1 end{pmatrix}!.$

Умножив обе части уравнения слева на

$begin{pmatrix}1&2&3\3&1&2end{pmatrix}^{-1}= begin{pmatrix}1&2&3\ 2&3&1 end{pmatrix}$ , получим $Xcirc! begin{pmatrix}1&2&3\ 2&3&1end{pmatrix}= begin{pmatrix}1&2&3\ 2&1&3end{pmatrix}$ .

Далее, умножив полученное уравнение справа на

$begin{pmatrix}1&2&3\ 2&3&1end{pmatrix}^{-1}= begin{pmatrix}1&2&3\ 3&1&2 end{pmatrix}$ окончательно получим $X=begin{pmatrix}1&2&3\ 1&3&2 end{pmatrix}= begin{pmatrix}2&3 end{pmatrix}$ .

Степень элемента в полугруппе

В полугруппе в общем случае законы сокращения и разрешимость уравнений типа (2.1) и (2.2) могут не иметь места. Например, в полугруппе квадратных матриц фиксированного порядка с операцией умножения матриц из матричного равенства AX=AY , вообще говоря, не следует, что X=Y . Это можно утверждать лишь при дополнительном предположении, что det{A}ne0 . Можно доказать, что в свободном моноиде, порожденном некоторым конечным множеством, оба закона сокращения справедливы, но никаких обратных элементов не существует.

В полугруппе можно умножать любой элемент сам на себя, причем в силу ассоциативности операции полугруппы элемент $overbrace{acdot acdotldotscdot a}^{n~text{times}}$ определен однозначно. Этот элемент называют n-й степенью элемента и обозначают a^n . При этом

$a^1=a,quad a^n=acdot a^{n-1},quad n=2,3,ldots$

В моноиде вводят также нулевую степень элемента, полагая $a^0=bold{1}$ .

Если (A,cdot,bold{1}) — группа, то можно ввести и отрицательные степени элемента согласно равенству

$a^{-n}=(a^{-1})^n,quad n=1,2,ldots$

Без доказательства сформулируем утверждения о свойствах степеней.

Теорема 2.5. Для любой полугруппы $a^mcdot a^n= a^{m+n},~ (a^m)^n= a^{mn}~ (m,nin mathbb{N})$ .

Теорема 2.6. Для любой группы $a^{-n}=(a^n)^{-1},~ a^mcdot a^n=a^{m+n},~ (a^m)^n=a^{nm}~ (m,nin mathbb{Z})$ .

Определение 2.4. Полугруппу (в частности, группу) (A,cdot) называют циклической, если существует такой элемент , что любой элемент полугруппы является некоторой (целой) степенью элемента . Элемент называют образующим элементом полугруппы (группы).

Пример 2.11. а. Полугруппа $(mathbb{N}_0,+,0)$ циклическая, с образующим элементом 1. При аддитивной записи бинарной операции возведение элемента в положительную степень есть сумма этих элементов, и это записывают ncdot a (или , без знака умножения).

б. Группа (mathbb{Z},+,0) также циклическая. Для нее образующими элементами могут быть 1 и –1. Рассмотрим элемент 1. Тогда

$begin{gathered}0cdot1=0,quad 1= underbrace{1+ldots+1}_{n~ text{times}}= n~(n>0), quad (-1)cdot1=-1,\ (-n)cdot1= ncdot(-1)= underbrace{(-1)+ldots+(-1)}_{n~ text{times}}=-n~ (n>0). end{gathered}$

Если в качестве образующего взять элемент –1, то 0cdot(-1)=0 , отрицательные целые числа получаются как положительные «степени» –1, а положительные — как отрицательные «степени» –1. Например, (-2)cdot(-1)=2,~ 4cdot (-1)=-4 .

в. Группа $(mathbb{Z}_3,oplus_3,0)$ вычетов по модулю 3 циклическая, причем любой ее ненулевой элемент является образующим.

Действительно, для 1 имеем 1oplus_31=2,~ 1oplus_3 1oplus_3 1=0 , а для 2 получим

2^2=2oplus_3 2=1,qquad 2oplus_3 2oplus_3 2=0.

Строение конечных циклических групп

Изучим подробнее строение конечных циклических групп, используя мультипликативную запись бинарной операции. Напомним, что конечная алгебра {конечная группа, в частности) — это алгебра, носитель которой — конечное множество.

Порядком конечной группы называют количество элементов в этой группе.

Так, например, аддитивная группа вычетов по модулю имеет порядок . Симметрическая группа степени , т.е. группа подстановок S_n , имеет порядок !. Мультипликативная группа вычетов по модулю , где — простое число, имеет порядок p-1 .

Порядок элемента а циклической группы — это наименьшее положительное , такое, что $a^n=bold{1}$ .

Теорема 2.7. Порядок образующего элемента конечной циклической группы равен порядку самой группы.

Пусть mathcal{G}=(G,cdot,bold{1}) — конечная циклическая группа с образующим элементом и n>0 — порядок этого элемента.

Тогда все степени $a^0=bold{1}, a^1=a,ldots,a^{n-1}$ попарно различны. Действительно, если

a^k=a^l,~ 0<l<k<n , то $a^{k-l}= a^{k+(-l)}= a^ka^l= a^la^{-l}= a^{l-l}= bold{1}$ .

Поскольку k-l<n , получено противоречие с выбором как порядка элемента (ибо найдена степень, меньшая , при возведении в которую элемента получится единица).

Осталось доказать, что любая степень элемента принадлежит множеству ${bold{1},a, ldots, a^{n-1}}$ . Для любого целого существуют также целые n,k , такие, что m=kn+q , где — целое и 0leqslant q<n . Тогда

$a^m= a^{kn+q}= a^{kn}cdot a^q= bold{1}cdot a^q= a^qin {bold{1},a, ldots, a^{n-1}}.$

Поскольку каждый элемент группы mathcal{G} есть некоторая степень элемента , то $G={bold{1},a, ldots, a^{n-1}}$ и порядок группы равен .

Из доказанной теоремы следует, что в бесконечной циклической группе не существует такого n>0 , что для образующего элемента группы выполняется равенство $a^n=bold{1}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Циклические группы

Разложение группы по подгруппе

Группоиды, полугруппы, группы

Полурешетка в абстрактной алгебре

Способы задания группы как алгебры

Степень элемента в полугруппе

Строение конечных циклических групп

Не пропустите также: