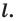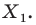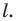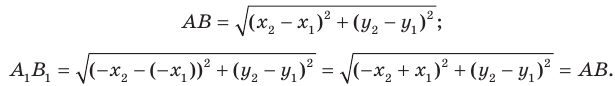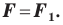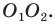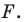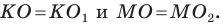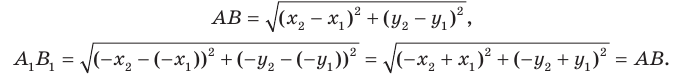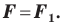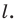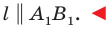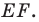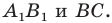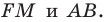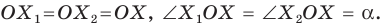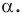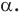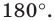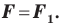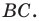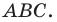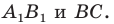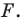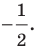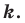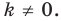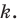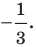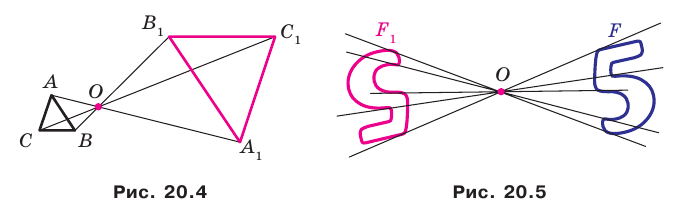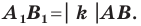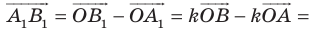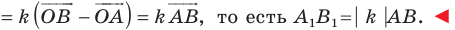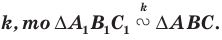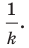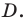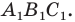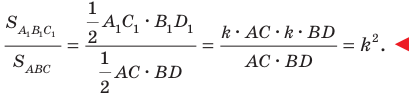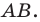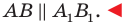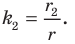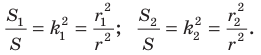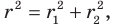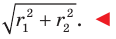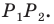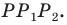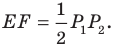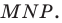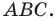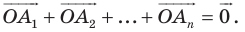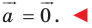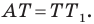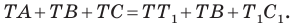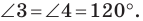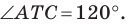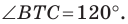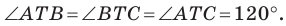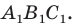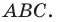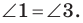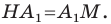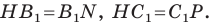Найдите уравнение окружности, являющейся образом окружности (х — 2)^2 + (у + 6)^2 = 36 при параллельном переносе на вектор а (-4; 1).
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,868
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Метод параллельного переноса
Перейдем сразу к решению задач на построение методом параллельного переноса.
Задача 6.34. Даны две окружности Fv F2 и прямая I. Провести прямую, параллельную прямой I, на которой окружности Fr и F2 высекают равные хорды.
Пусть прямая V искомая, т.е. прямая V высекает на данных окружностях равные хорды АВ иА’В’ (рис. 6.34).
Тогда точки АиА’,ВиВ’ можно рассматривать как соответственные при параллельном переносе ОхО<.
Так как точка А’ является образом точки А, принадлежащей окружности Fb то точка Л’ принадлежит образу окружности F,. Следовательно, А’ — общая точка окружности F2 и образа окружности Fj при параллельном переносе 0-[0[. Построив точку А’, находим на окружности F] ее прообраз. _
Если F2 есть образ точки Fx при параллельном переносе OjOf, то задача имеет бесконечное множество решений. В остальных случаях задача имеет не более четырех решений, так как окружность F2 имеет не более двух точек пересечения с окружностью F <и не более двух точек пересечения с окружностью F» (образ окружности Fj при параллельном переносе ОуО<).
Задача 6.35. Между двумя данными окружностями (О, Р) и (Q, г) провести отрезок данной длины (а) параллельно данной прямой (АР).
Анализ. Допустим, что задача решена и отрезок CD является искомым (рис. 6.35). Если мысленно будем перемещать отрезок CD параллельно самому себе, оставляя один из его концов D скользящим по данной окружности (Q, г), то ясно, что другой конец (С) отрезка CD опишет в это время окружность того же радиуса (г), имеющую центр в некоторой точке Р, отстоящей от точки Q на расстояние, равное отрезку а. Отсюда следует, что, построив окружность (Р, г), мы сможем построить и искомые отрезки.
Построение. 1. Проведем из точки Q отрезок QP, который параллелен прямой АВ и равен отрезку а.
- 2. Около точки Р радиусом, равным г, опишем вспомогательную окружность (Р, г).
- 3. Обозначим буквами С и ? те точки, в которых вспомогательная окружность (Р, г) пересечет окружность (О, Р).
- 4. Если из точек С и ? проведем прямые, параллельные прямой АВ, то они пересекут окружность (Q, г) в некоторых точках D и F.
Отрезки CD и ?? — искомые.
Доказательство несложное, а поэтому предлагаем провести самостоятельно.
Исследование. Если вспомогательная окружность (Р, г) пересекает данную окружность (О, К), то задача имеет два решения.
Если окружность (Р, г) будет лишь касаться окружности (О, Р), то задача имеет одно решение.
Наконец, если окружность (Р, г) не будет ни касаться окружности, ни пересекать ее, то задача не имеет решений.
Задача 6.36. Даны окружность и прямая I. На окружности даны две точки А и В. Найти на окружности такую точку М, чтобы прямые МА и МВ пересекали I в точках К и N таким образом, что KN — а, где а — заданный отрезок.
Построим точку А’ (рис. 6.36) так, чтобы NKAA’ был параллелограммом (А’ получается из А при помощи известного параллельного переноса). Поскольку ZBNA’ = ZBMA, а последний известен, то точка N находится как пересечение I с соответствующим геометрическим местом точек. Следует также рассмотреть случай расположения точки М на другой дуге АВ.
Окружность в параллельном переносе
Преобразования декартовой системы координат с примерами решения
Содержание:
Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):
Рис. 46. Параллельный перенос одной системы координат относительно другой системы.
Систему координат
Пример:
Дана точка М(3;2) и начало новой системы координат Вычислить положение точки М в новой системе отсчета.
Решение:
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).
2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол (Рис. 47):
Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода
Найдем обратное преобразование системы координат, найдем матрицу обратную к матрице А:
Найдем алгебраические дополнения всех элементов
Запишем обратную матрицу
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.
Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.
Таким образом, имеем Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:
Пример:
Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол
Решение:
Воспользуемся полученными формулами т.е. в новой системе координат точка имеет координаты М(2; -1).
Рассмотрим применение преобразования координат:
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы
Пример:
Преобразовать уравнение параболы к каноническому виду.
Решение:
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда
следовательно, параметр параболы р = 1/4.
б) Выяснить, какую кривую описывает функция
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение
и новые координаты получим уравнение которое описывает равнобочную гиперболу.
Полярные координаты. Замечательные кривые
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).
Рис. 48. Полярная система координат.
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами
Рассмотрим замечательные кривые в полярной системе координат:
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.
Рис. 49. Спираль (улитка) Архимеда.
2. Уравнение окружности: уравнение описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид
Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.
3. Уравнение описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид
Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.
4. Кардиоиды:
Рис. 52. Кардиоида
Рис. 53. Кардиоида
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.
5. Петля: Величина равна нулю при
Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Параллельный перенос
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса
Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)
то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
Метод параллельного переноса
Перейдем сразу к решению задач на построение методом параллельного переноса.
Задача 6.34. Даны две окружности Fv F2 и прямая I. Провести прямую, параллельную прямой I, на которой окружности Fr и F2 высекают равные хорды.
Пусть прямая V искомая, т.е. прямая V высекает на данных окружностях равные хорды АВ иА’В’ (рис. 6.34).
http://studme.org/245061/matematika_himiya_fizik/metod_parallelnogo_perenosa
http://b4.cooksy.ru/articles/okruzhnost-v-parallelnom-perenose
Содержание:
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
Движение (перемещение) фигуры. Параллельный перенос
Пример:
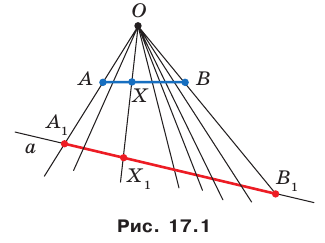
На рисунке 17.1 изображены отрезок
Мы указали правило, с помощью которого каждой точке 
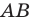
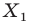
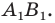
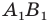
Пример:
На рисунке 17.2 изображены полуокружность 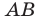
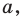
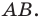
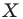
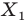
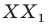
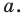
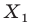
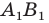
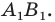
Пример:
Пусть даны некоторая фигура 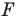
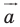
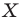
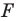
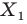
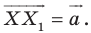
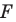
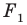
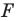
Обобщим приведенные примеры.
Пусть задана некоторая фигура 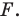
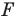
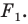
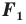
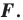
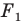
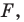
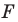
Так, в примере 1 отрезок 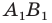
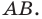
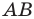
Обратим внимание на то, что в примере 3 фигура 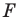
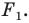
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 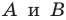
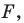
Что такое преобразование фигур
Определение. Преобразование фигуры 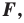
Если каждой точке 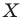
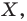
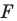
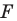
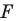
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
Свойства движения подсказывают следующее определение.
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 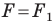
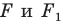
Если существует движение, при котором фигура 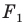
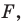
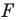
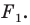
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры 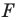
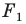
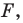
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17.3 фигуры 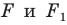
Теорема 17.1 (свойство параллельного переноса). Параллельный перенос является движением.
Доказательство: Пусть 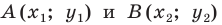
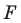
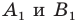
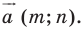
Имеем: 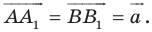
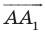
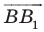
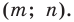
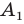
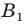
Найдем расстояние между точками
Найдем расстояние между точками
Следовательно, мы показали, что 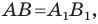
Следствие. Если фигура 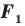
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17.5).
Если фигура 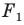
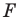
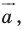
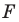
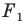
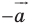
Параллельные переносы на векторы 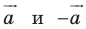
Пример №1
Каждой точке 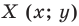
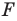
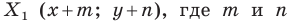
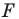
Решение:
Рассмотрим вектор 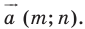
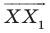
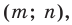
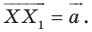
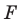
Пример №2
Точка 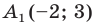
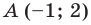
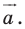
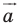
Решение:
Из условия следует, что 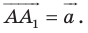
Пусть 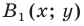
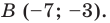
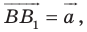
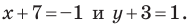
Ответ:
Пример №3
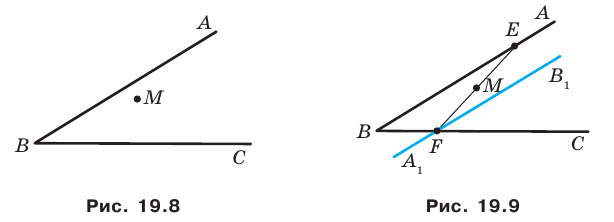
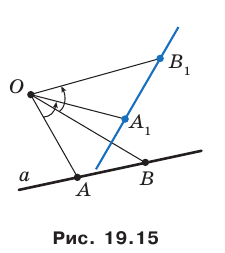
Даны угол 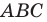
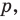
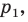
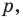
Решение:
Рассмотрим вектор 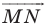

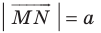
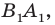
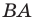
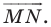
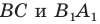
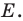
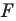
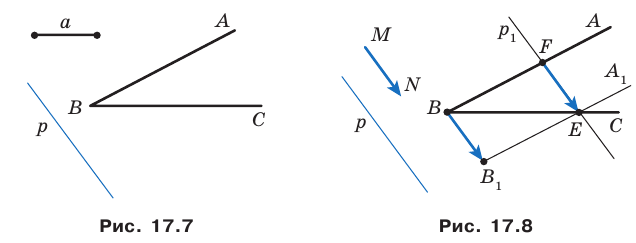
Приведенные рассуждения подсказывают следующий алгоритм построения:
- найти образ луча
при параллельном переносе на вектор
- отметить точку пересечения луча
с построенным образом;
- через найденную точку провести прямую
параллельную прямой
Прямая
будет искомой.
Осевая симметрия
Определение. Точки 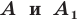
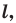
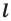
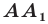
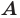
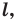
Например, точки 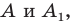
Рассмотрим фигуру 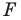
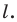
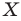
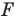
В результате такого преобразования фигуры 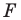
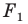
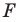
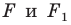
Теорема 18.1 (свойство осевой симметрии). Осевая симметрия является движением.
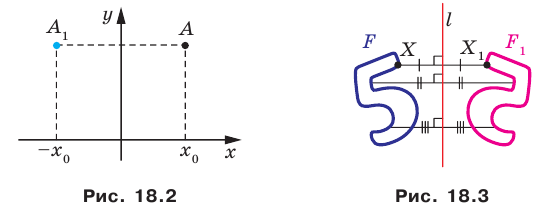
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть 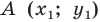
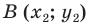
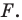
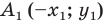
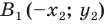
Мы получили, что 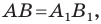
Следствие. Если фигуры 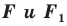
Определение. Фигуру называют симметричной относительно прямой 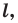
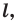
Прямую 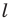
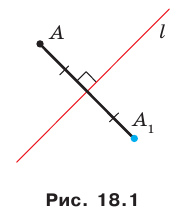
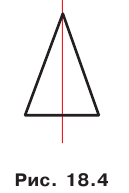
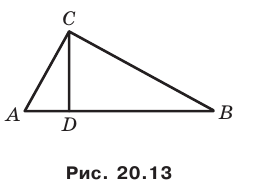
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18.4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
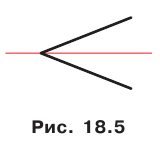
Любой угол имеет ось симметрии — это пря-Рис. 18.5 мая, содержащая его биссектрису (рис. 18.5).
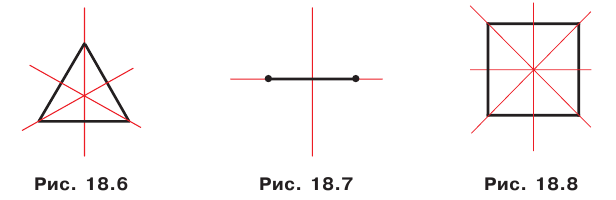
Равносторонний треугольник имеет три оси симметрии (рис. 18.6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18.7).
Квадрат имеет четыре оси симметрии (рис. 18.8).
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18.9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
Пример №4
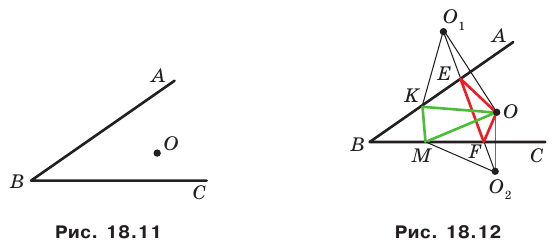
Начертили неравнобедренный треугольник 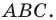
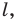
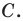
Решение:
Поскольку прямая 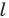
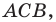
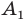
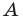
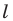
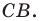
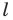
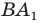
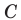
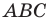
Эти соображения подсказывают, как построить искомый треугольник: строим точку 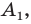
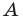
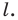
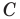
Пример №5
Точка 
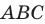
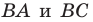
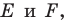
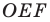
Решение:
Пусть точки 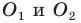
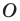
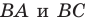
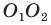
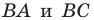
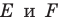
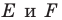
Заметим, что отрезки 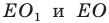
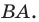
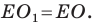
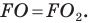
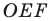
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 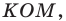
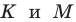
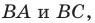
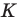
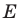
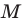
Понятно, что
Тогда периметр треугольника 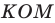
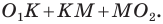
Центральная симметрия. Поворот
Определение. Точки 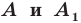
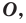
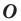
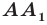
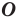
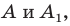
Рассмотрим фигуру 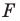
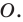
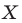
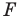
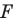
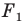
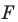
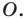
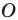
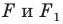
Теорема 19.1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть 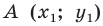
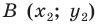
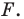
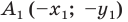
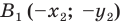
Мы получили, что 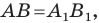
Следствие. Если фигуры 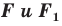
Определение. Фигуру называют симметричной относительно точки 
Точку 
Приведем примеры фигур, имеющих центр симметрии.
Центром симметрии отрезка является его середина (рис. 19.4).
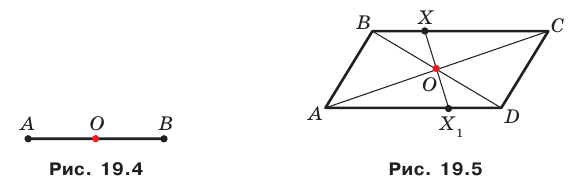
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19.5).
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
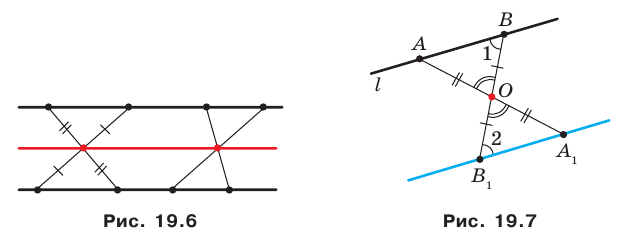
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19.6).
Пример №6
Докажите, что образом данной прямой 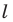
Решение:
Поскольку центральная симметрия — это движение, то образом прямой 
Выберем на прямой 
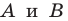
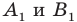
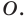
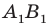
Поскольку 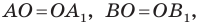
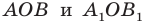
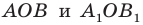
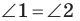
Пример №7
Точка 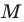
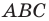
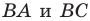
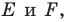
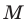
Решение:
Пусть прямая 
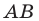
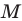
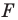
Найдем прообраз точки 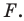
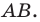
Обозначим эту точку буквой 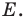
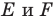
Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19.10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота».
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19.11).
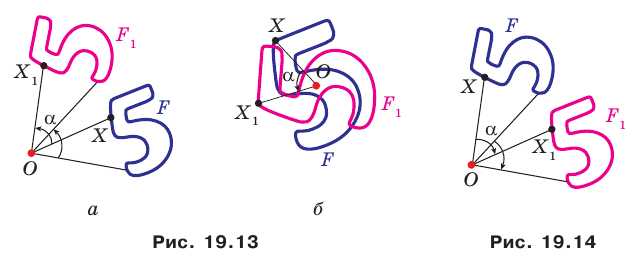
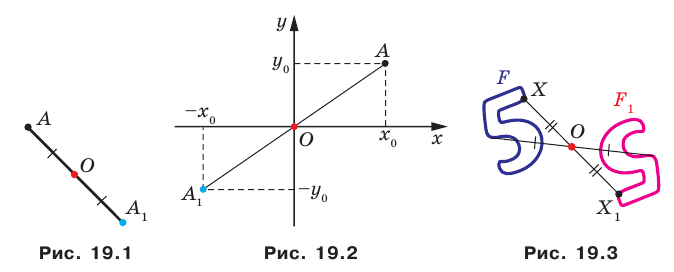
На рисунке 19.12 изображены точки 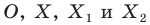
Говорят, что точка 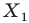
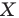
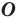
Так же говорят, что точка 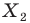
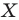
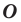
Точку 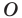
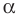
Рассмотрим фигуру 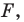
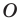
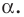
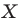
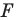
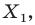
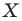
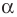
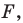
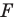
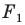
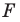
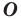
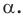
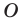
Аналогично определяют преобразование поворота фигуры 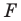
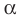
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол
Теорема 19.2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура 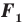
Пример №8
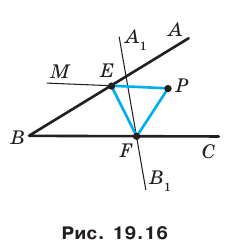
Даны прямая 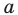
Решение:
Поскольку поворот — это движение, то образом прямой 
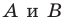
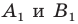
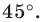
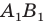
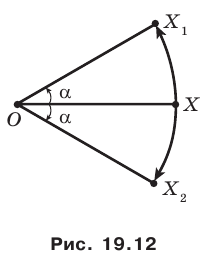
Пример №9
Точка 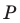
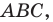
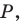
Решение:
Пусть прямая 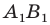
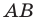
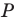
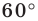
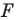
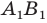
Пусть точка 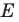
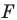
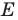
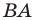
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую 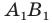
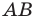
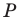
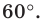
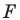
Строим угол 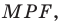
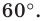
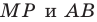
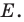
Имеем: 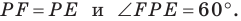
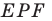
Подобие фигур
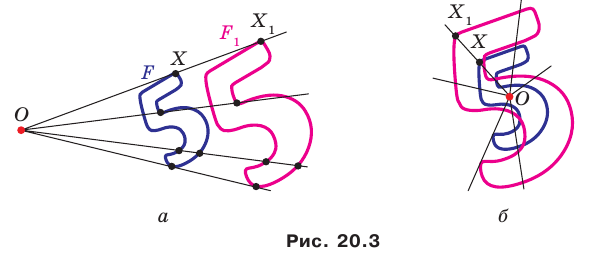
На рисунке 20.1 изображены точки 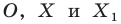
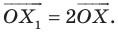
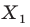
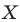
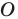
На рисунке 20.2 изображены точки 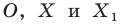
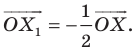
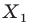
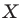
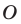
Вообще, если точки 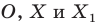
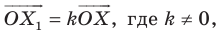
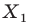
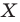
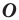
Точку 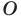
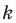
Рассмотрим фигуру 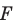
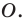
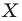
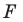
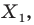
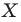
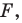
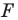
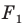
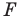
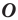
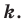
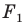
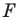
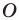
Например, на рисунке 20.4 треугольник 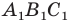
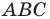
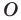
можно сказать, что треугольник 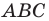
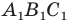
Отметим, что при 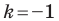
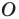
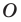
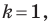
Очевидно, что при 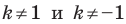
Теорема 20.1. При гомотетии фигуры 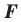
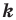
Доказательство: Пусть точка 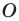
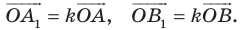
Следствие. Если треугольник 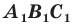
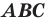
Для доказательства этого утверждения достаточно воспользоваться теоремой 20.1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
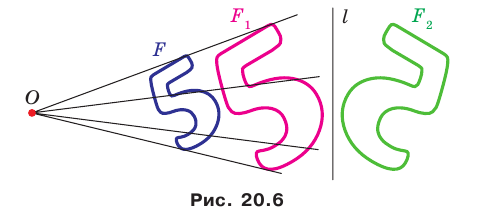
На рисунке 20.6 фигура 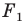
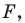
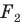
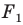
Говорят, что фигура 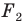
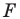
Поскольку 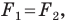
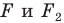
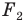
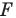
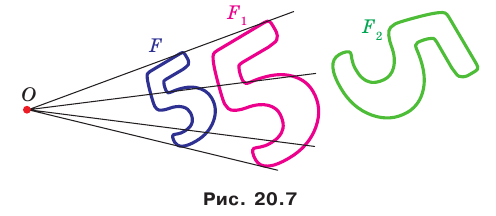
На рисунке 20.7 фигура 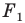
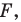
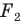
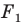
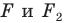
Из сказанного следует, что целесообразно принять такое определение.
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20.8.
Запись 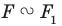
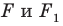
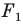
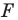
Из приведенного определения следует, что при преобразовании подобия фигуры 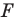
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20.8, следует, что гомотетия — частный случай преобразования подобия.
Пусть 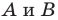
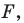
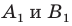
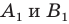
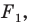
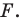
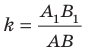
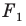
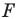
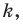
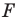
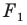
Заметим, что преобразование подобия с коэффициентом 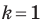
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20.9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия. 
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
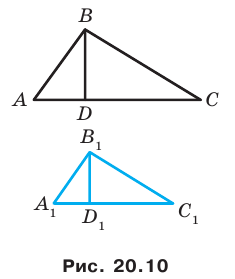
Доказательство: Пусть треугольник 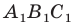
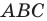
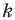
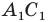
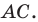
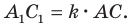
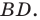
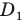
Поскольку при преобразовании подобия сохраняются углы, то отрезок 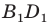
Тогда 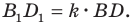
Пример №10
Докажите, что образом прямой 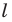
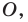
Решение:
Из свойств гомотетии следует, что образом прямой 
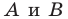
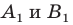
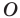
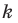
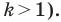
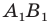
При доказательстве теоремы 20.1 мы показали, что 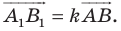
Пример №11
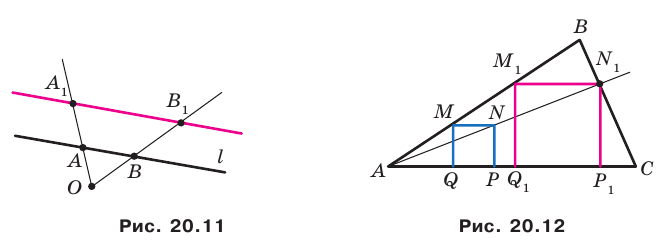
В остроугольный треугольник 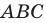
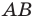
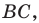
Решение:
Из произвольной точки 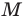
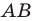
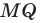
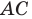
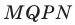
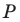
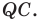
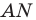
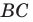
Рассмотрим гомотетию с центром 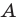
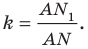
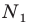
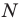
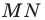
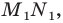
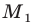
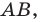
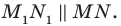
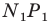
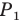
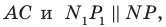
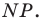
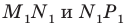
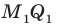
Пример №12
Отрезок 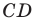
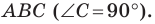
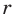

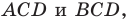
Решение:
Поскольку угол 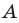
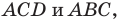
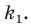
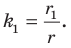
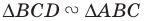
Обозначим площади треугольников 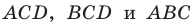
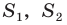
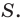
Отсюда 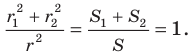
Ответ:
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
Пример №13
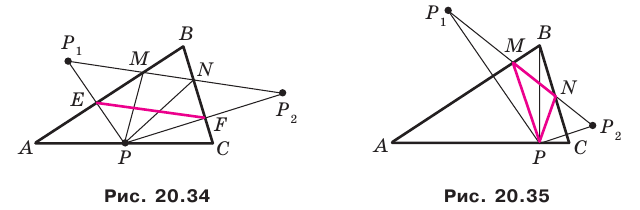
На сторонах 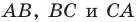
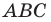
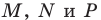
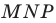
Решение:
Пусть 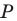
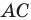
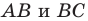
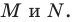
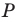
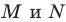
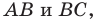
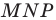
Заметим, что отрезок 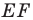
Тогда
Поскольку 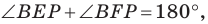
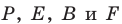
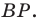
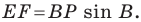
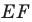
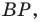
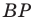
На рисунке 20.35 отрезок 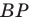
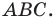
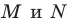
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника 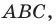
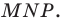
Можно показать (сделайте это самостоятельно), что точки 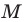
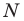
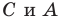
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 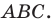
Пример №14
Точка 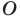
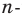
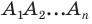
Решение:
Пусть 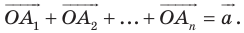
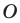
Пример №15
Внутри треугольника 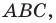
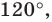
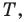
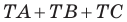
Решение:
Пусть 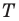
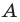
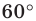
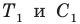
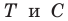
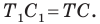
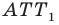
Имеем:
Понятно, что сумма 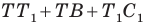
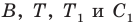
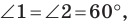
Так как угол 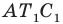
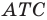
Итак, точки 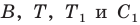
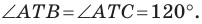
Таким образом, сумма 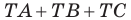
Найти точку 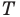
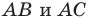
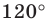
Понятно, что если один из углов треугольника 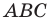
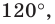
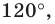
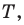
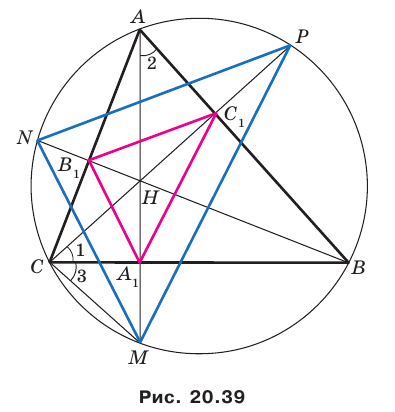
Пример №16
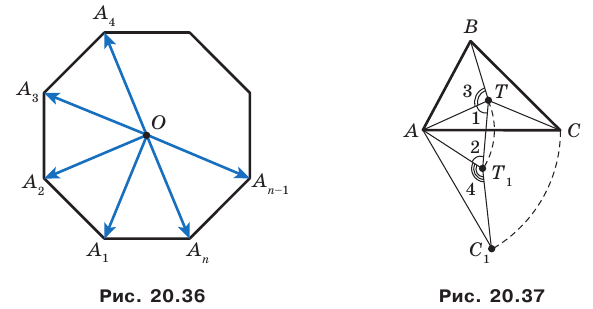
Отрезки 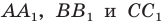
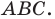
Решение:
Пусть прямые 
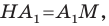
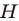
Имеем:
Углы 2 и 3 равны как вписанные, опирающиеся на дугу 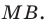
Тогда в треугольнике 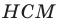
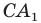
Аналогично можно доказать, что
Теперь понятно, что треугольник 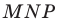
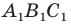
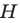
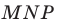
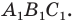
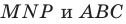
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Параллельный перенос
Введем определение параллельного переноса на вектор. Пусть нам дан вектор $overrightarrow{a}$.
Определение 1
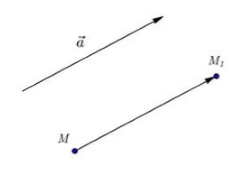
Параллельный перенос на вектор $overrightarrow{a}$ — отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $overrightarrow{{MM}_1}=overrightarrow{a}$ (Рис. 1).
Рисунок 1. Параллельный перенос
Введем следующую теорему.
Параллельный перенос является движением.
Доказательство.
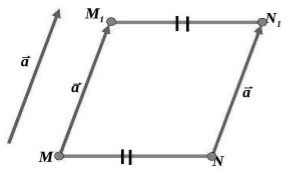
Пусть нам даны точки $M и N$. Пусть при их параллельном переносе на вектор $overrightarrow{a}$ эти точки отображаются в точки $M_1$ и $N_1$, соответственно (рис. 2).
Рисунок 2. Иллюстрация теоремы 1
Так как, по определению 1, $overrightarrow{{MM}_1}=overrightarrow{a}$ и $overrightarrow{{NN}_1}=overrightarrow{a}$, то , $overrightarrow{{MM}_1}=overrightarrow{{NN}_1}$, следовательно, из определения равных векторов получим
Значит четырехугольник ${MM}_1N_1N$ — параллелограмм и, следовательно, $MN=M_1N_1$. То есть параллельный перенос сохраняет расстояние между точками. Следовательно, параллельный перенос является движением.
Теорема доказана.
Поворот
Введем определение поворота вокруг точки $O$ на угол $alpha $.
Определение 2
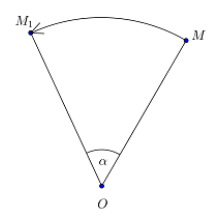
Поворот вокруг точки $O$ на угол $alpha $ — отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что ${OM}_1=OM, angle M{OM}_1=angle alpha $ (Рис. 3).
Рисунок 3. Поворот
«Параллельный перенос и поворот» 👇
Введем следующую теорему.
Теорема 2
Поворот является движением.
Доказательство.
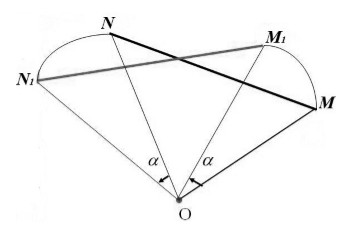
Пусть нам даны точки $M и N$. Пусть при их повороте вокруг точки $O$ на угол $alpha $ они отображаются в точки $M_1$ и $N_1$, соответственно (рис. 4).
Рисунок 4. Иллюстрация теоремы 2
Так как, по определению 2, ${OM}_1=OM, {ON}_1=ON$ и $overrightarrow{{NN}_1}=overrightarrow{a}$, а ,$angle MON=angle M_1ON_1$, то
Следовательно, $MN=M_1N_1$. То есть поворот сохраняет расстояние между точками. Следовательно, поворот является движением.
Теорема доказана.
Примеры задач на параллельный перенос и поворот
Пример 1
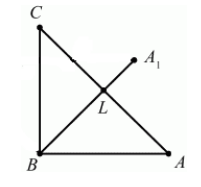
Построить треугольник $A_1B_1C_1$,образованный поворотом вокруг точки $B$ на угол ${45}^0$ равнобедренного прямоугольного (с прямым углом $B)$ треугольника $ABC$.
Решение.
Очевидно, что точка $B$ перейдет сама в себя, то есть $B_1=B$. Так как поворот производится на угол, равный ${45}^0$, а треугольник $ABC$ равнобедренный, то прямая $BA_1$ проходит через точку $L$ — середины стороны $AC$. По определению, отрезок $BA_1=BA$. Построим его (Рис. 5).
Рисунок 5.
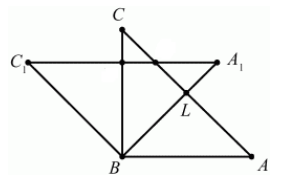
Построим теперь вершину $C_1$ по определению 2:
[angle CBC_1={45}^0, BC=BC_1]
Соединим все вершины треугольника $A_1B_1C_1$ (Рис. 6).
Рисунок 6.
Решение закончено.
Пример 2
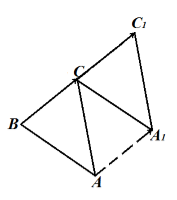
Построить параллельный перенос треугольника $ABC$ на вектор $overrightarrow{BC}$.
Решение.
Перенесем каждую вершину треугольника на вектор $overrightarrow{BC}$. Получаем треугольник $CA_1C_1$ (рис. 7).
Рисунок 7.
Решение закончено.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Сегодня на уроке мы вспомним, какое отображение
плоскости на себя мы называли параллельным переносом, введём понятие
параллельного переноса в пространстве. Проверим, будет ли параллельный перенос
движением пространства.
Вернёмся в планиметрию и вспомним, что параллельным
переносом мы называли преобразование, при котором каждая точка фигуры
перемещается в одном и том же направлении и на одно и то же расстояние. Мы
говорили, что для того, чтобы задать перенос достаточно задать вектор.
Другими словами, параллельным переносом на
вектор называется
отображение плоскости на себя, при котором каждая точка отображается
в такую точку ,
что вектор равен
вектору .
То, что параллельный перенос является примером
движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.
Пусть при параллельном переносе на вектор точки
и
отображаются
в точки и
.
Так как векторы и
,
то значит, эти векторы равны между собой .
То есть они параллельны и
их длины равны, поэтому четырёхугольник –
параллелограмм. Следовательно, ,
то есть расстояние между точками и
равно
расстоянию между точками и
.
Случай, когда точки и
лежат
на прямой параллельной вектору ,
вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между
точками и
будет
равно расстоянию между точками и
.
Таким образом, параллельный перенос сохраняет
расстояние между точками и поэтому представляет собой движение. Это
движение можно представить себе как сдвиг всей плоскости в направлении данного
вектора на
его длину.
В планиметрии мы говорили, что параллельный перенос
обладает некоторыми свойствами.
Свойства параллельного переноса:
·
При
параллельном переносе отрезок переходит в равный ему отрезок.
·
Угол
переходит в равный ему угол.
·
Окружность
переходит в равную ей окружность.
·
Любой
многоугольник переходит в равный ему многоугольник.
·
Параллельные
прямые переходят в параллельные прямые.
·
Перпендикулярные
прямые переходят в перпендикулярные прямые.
Теперь давайте определим, что мы будем понимать под
параллельным переносом в пространстве.
Определение:
Параллельным переносом на вектор называется
такое отображение пространства на себя, при котором любая точка переходит
в такую точку что
.
Проверим, будет ли параллельный перенос в
пространстве примером движения пространства.
При параллельном переносе точки пространства и
переходят
в такие точки и
,
что вектора и
.
Сложим по правилу треугольника векторы
Поскольку левые части равенств равны, значит, равны
и правые части равенств.
Значит, можно записать, что .
Заменим вектора и
на
вектор .
Получим, что .
Отсюда получаем, что вектор .
Поскольку векторы равны, значит, равны и их длины, то есть .
То есть расстояние между точками при параллельном переносе в пространстве
сохраняется, значит, параллельный перенос в пространстве также является
движением, но уже не плоскости, а пространства.
Сформулируем свойства параллельного переноса.
Свойства параллельного переноса:
·
Параллельный
перенос является примером движения пространства.
·
При
параллельном переносе точки смещаются по параллельным или совпадающим прямым на
одно и то же расстояние.
·
При
параллельном переносе прямая переходит в параллельную прямую (или сама в себя).
·
Каковы
бы не были две точки и
,
существует, и притом единственный, параллельный перенос, при котором точка переходит
в точку .
·
При
параллельном переносе в пространстве каждая плоскость переходит либо в себя,
либо в параллельную ей плоскость.
Движение в пространстве обладает теми же свойствами,
что и движение плоскости.
Свойства движения пространства:
·
Движение
сохраняет расстояние между точками.
·
При
любом движении пространства отрезок отображается на отрезок, прямая – в прямую,
плоскость – в плоскость.
Решим несколько задач.
Задача:
начертить отрезок и
вектор .
Построить отрезок ,
который получится из отрезка параллельным
переносом на вектор .
Решение:
для того, чтобы построить отрезок ,
отобразим точку в
точку ,
точку в
точку с
помощью параллельного переноса. Тогда соединив точки ,
мы
получим отрезок .
Задача:
начертить треугольник и
вектор .
Построить треугольник ,
который получится из треугольникa
параллельным
переносом на вектор .
Решение:
отобразим с помощью параллельного переноса точки ,
,
в
точки ,
,
.
Соединив полученные точки, мы получим искомый треугольник .
Задача:
начертить пятиугольник и
вектор .
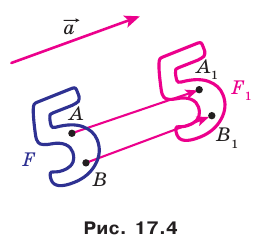
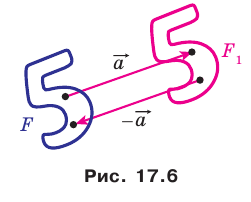
Построить пятиугольник ,
который получится из пятиугольника параллельным
переносом на вектор .
Решение:
решать эту задачу будем аналогично тому, как мы решали предыдущую задачу.
Отобразим каждую вершину пятиугольника с помощью параллельного переноса на
вектор .
Соединим получившиеся точки и получим искомый пятиугольник .
Итоги:
Сегодня на уроке мы вспомнили, что мы понимали под
параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве.
Сформулировали основные свойства параллельного переноса, движения пространства.

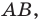
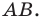
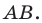
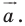
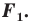
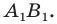
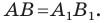
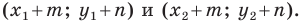
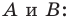
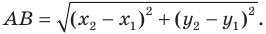
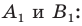
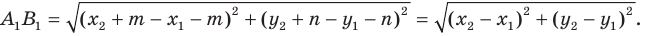

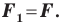

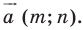

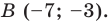
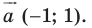
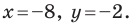
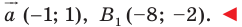
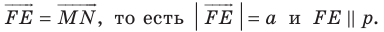
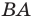 при параллельном переносе на вектор
при параллельном переносе на вектор 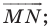
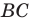 с построенным образом;
с построенным образом;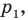 параллельную прямой
параллельную прямой 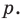 Прямая
Прямая  будет искомой.
будет искомой.