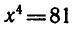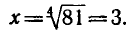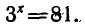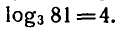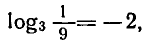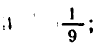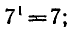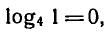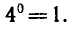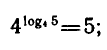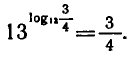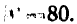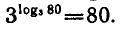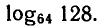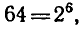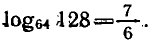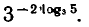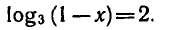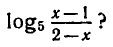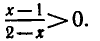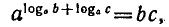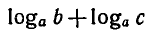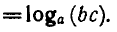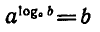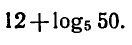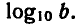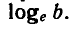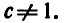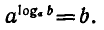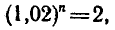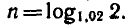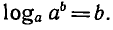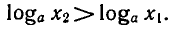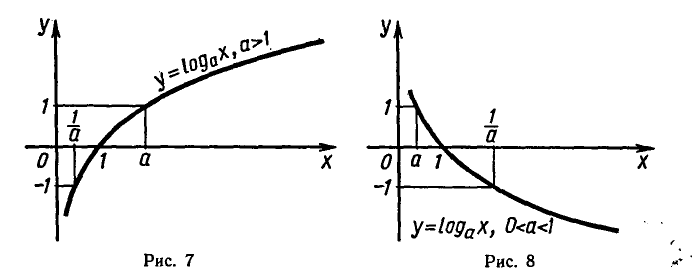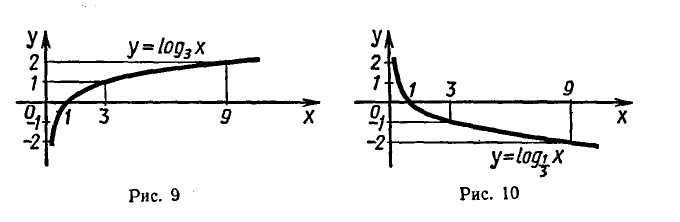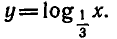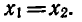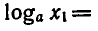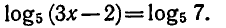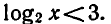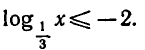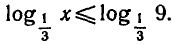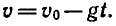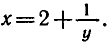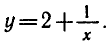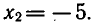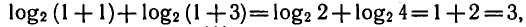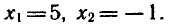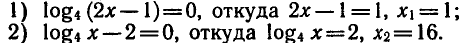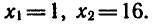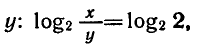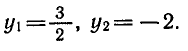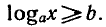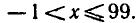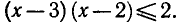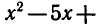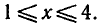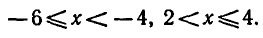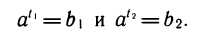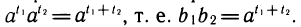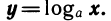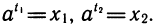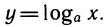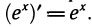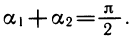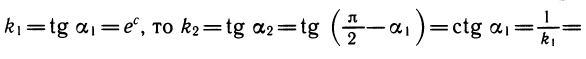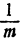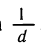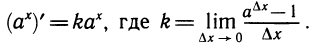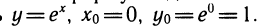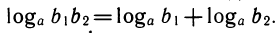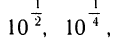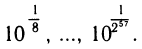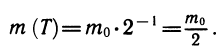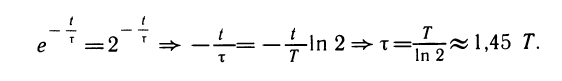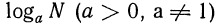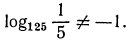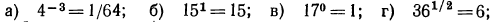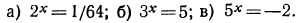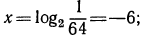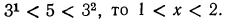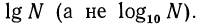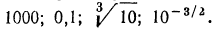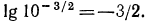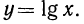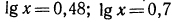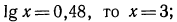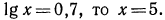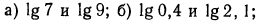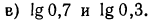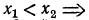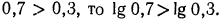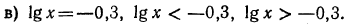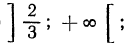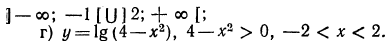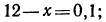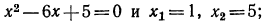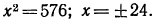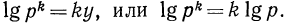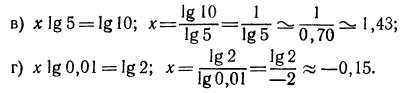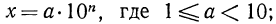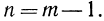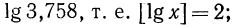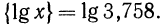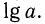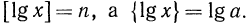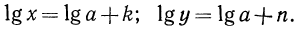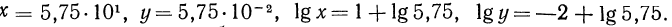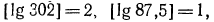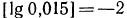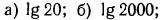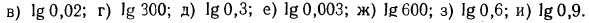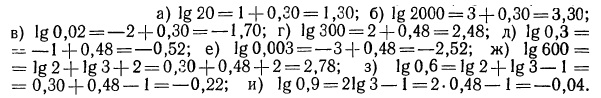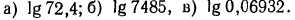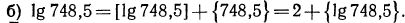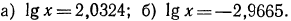Логарифм числа – это показатель степени, в которую нужно возвести одно число, чтобы получить другое.
Если число b в степени y равняется x:
by = x
Значит логарифм числа x по основанию b равен y:
y = logb(x)
Например:
24 = 16
log2(16) = 4
- Логарифм как обратная функция к показательной
-
Натуральный логарифм (ln)
- Обратный логарифм
- Таблица свойств логарифмов
- Логарифмическая функция
- График функции логарифма
Логарифм как обратная функция к показательной
Логарифмическая функция y = logb(x) является обратной функцией к показательной x=b y.
Так что, если мы вычислим показательную функцию логарифма х (х > 0), получится:
f (f -1(x)) = blogb(x) = x
Или если мы вычислим логарифм показательной функции х:
f -1(f (x)) = logb(bx) = x
Натуральный логарифм (ln)
Натуральный логарифм – это логарифм по основанию е.
ln(x) = loge(x)
Число e – это константа, которая может определяться как предел:
или так:
Обратный логарифм
Обратный логарифм (или антилогарифм) числа n – это число, логарифм которого по основанию a равен числу n.
ant logan = an
Таблица свойств логарифмов
Ниже представлены основные свойства логарифмов в табличном виде.
Логарифмическая функция
Функция, которая определена формулой f(x)=loga(x) – это логарифмическая функция с основанием a. При этом a>0, a≠1.
График функции логарифма
График логарифмической функции (логарифмика) может быть двух типов, в зависимости от значения основания a:
Введение в криптографию
Введение в криптографию
|
Ященко В.В. Введение в криптографию. Под общей ред. В. В. Ященко — СПб.: Питер, 2001. — 288 с. Данный учебник по криптографии содержит систематическое изложение научных основ от простейших примеров и основных понятий до современных криптографических концепций. Книга написана специалистами криптографами с целью популяризации основ этой отрасли знания; материал изложен хорошим языком и в доступной форме. Несомненным достоинством книги является то, что все её главы обладают высокой степенью независимости друг от друга. Хотя для понимания некоторой части материала книги всё же желателен определенный уровень математической подготовки, большая часть информации будет полезна массовому читателю. |
|
Оглавление
Предисловие ко второму изданию
Глава 1. Основные понятия криптографии
2. Предмет криптографии
3. Математические основы
4. Новые направления
5. Заключение
Глава 2. Криптография и теория сложности
2. Криптография и гипотеза P != NP
3. Односторонние функции
4. Псевдослучайные генераторы
5. Доказательства с нулевым разглашением
Глава 3. Криптографические протоколы
2. Целостность. Протоколы аутентификации и электронной подписи
Схема аутентификации Шнорра
Схема электронной подписи Шнорра
3. Неотслеживаемость. Электронные деньги
4. Протоколы типа «подбрасывание монеты по телефону»
Протокол подбрасывания монеты
5. Еще раз о разделении секрета
6. Поиграем в «кубики». Протоколы голосования
Протокол Шаума и Педерсена
7. За пределами стандартных предположений. Конфиденциальная передача сообщений
8. Вместо заключения
Глава 4. Алгоритмические проблемы теории чисел
2. Система шифрования RSA
3. Сложность теоретико-числовых алгоритмов
4. Как отличить составное число от простого
5. Алгоритм, доказывающий непростоту числа
Алгоритм, доказывающий непростоту числа
5. Как строить большие простые числа
6. Как проверить большое число на простоту
7. Как раскладывают составные числа на множители
8. Дискретное логарифмирование
9. Заключение
Глава 5. Математика разделения секрета
2. Разделение секрета для произвольных структур доступа
3. Линейное разделение секрета.
4. Идеальное разделение секрета и матроиды
Глава 6. Компьютер и криптография
2. Немного теории
Что надо знать перед написанием программы шифрования
3. Как зашифровать файл?
4. Поучимся на чужих ошибках
5. Вместо заключения
Глава 7. Олимпиады по криптографии для школьников
2. Шифры замены
А. Конан Дойл, «Пляшущие человечки»
Ж. Верн, «Путешествие к центру Земли»
3. Шифры перестановки
4. Многоалфавитные шифры замены с периодическим ключом
5. Условия задач олимпиад по математике и криптографии
6. Указания и решения
Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
3. Способы изображения систем
4. Примеры секретных систем
5. Оценка секретных систем
6. Алгебра секретных систем
7. Чистые и смешанные шифры
8. Подобные системы
Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
10. Совершенная секретность
11. Ненадежность
Логарифмы и теория информации: physic4woman — LiveJournal
Логарифмы
Логарифмы — это существа математической природы, очень красивые и простые в обращении. То есть можно сразу на ты и без церемоний.
Однако порой они особенно кокетливы и куртуазны, и все те степени восторга, которые они выражают в математических формулах, оказываются прикрыты вуалью легкой загадочности (даже, страшно сказать, стыдливости), флёром инфернального кокетства.
Поговорим же подробнее об этих чудесных и загадочных созданиях.
У операции сложения (a+b = c) есть обратная операция (c-b = a, c-a = b).
У операции умножения (a*b = c) есть обратная операция (c/b = a, c/a = b).
А у возведения в степень (ab = c) есть ли обратная операция?
Да, это — логарифмирование (log по основанию a c = b)
Например, тебя интересует, в какую степень b восторга нужно возвести мужчину a, чтобы получить сексуально заинтересованного мужчину c. Ты берешь сексуально заинтересованного мужчину c, логарифмируешь его самым решительным образом, и узнаешь необходимую степень восторга. После чего пускаешь в ход неотразимые женские чары. 🙂
Еще один образный пример применения логарифмов. Представь, что твой папа, король, объявил поиск достойного и знатного жениха для любимой дочери — принцессы, то бишь для тебя. И вот со всех стран приехало множество принцев. Перед тобой собралась толпа восхищенных поклонников, n человек. Тебе предстоит выбрать среди них единственного и лучшего.
Допустим, ты задаешь принцам вопрос: «Кто из вас совершит для меня отважный подвиг?»
Принцы отправляются в разные концы света, и потом n/2 принцев возвращается с трофеями — головами поверженных драконов, скальпами заморских ассасинов и дипломами школы Геракла.
Ты задаешь следующий вопрос: «Кто из вас умеет петь?»
Половина принцев радостно начинает петь красивыми голосами, другая половина хором вздыхает и уезжает восвояси.
Будучи столь же капризной принцессой, сколь и романтичной, ты задаешь следующий вопрос: «Кто из вас способен перебрехать дельфийского оракула?»
Принцы, перебрехавшие оракула, выгоняются тобой прочь, а те, кто потерял дар речи от твоего очарования, продолжают участие.
После каждого испытания число принцев сокращается вдвое, и наконец остается один-единственный, который прошел все испытания, и вас благословляет король.
Теперь вопрос: сколько испытаний ты провела, если изначально принцев было n, и каждое испытание отсеивало половину претендентов на твою руку?
Ответ: х = log 2 n.
После первого испытания принцев осталось n/2. После второго (n/2)/2 = n/(2*2) = n/4. После третьего (n/4)/2 = n/(4*2) = n/8. Наконец остался один принц, что значит, что мы делили количество принцев надвое x раз: n/(2x) = 1. Следовательно,
Следовательно,
n = 2x
х = log 2 n
Теория информации
Логарифмы ужасно любят сплетничать. Именно поэтому на логарифмах основывается теория информации, созданная в 50-х годах 20-го века Клодом Шенноном. Согласно этой теории, единицей информации является 1 бит. Ответ на вопрос «Любите ли вы сыр, мадемуазель?», содержит один бит информации, независимо от того, каким будет ответ — утвердительным или отрицательным. Такое же количество информации содержит и ответ на вопрос «Любите ли вы меня, мадемуазель?», хотя очевидно, что эти два ответа по своему содержанию и значению совершенно различны.
Приведенный выше пример с выбором принца иллюстрирует, как происходит естественный отбор исчисление битов. Каждый твой вопрос приближал тебя к заветному соединению с лучшим из лучших; каждый твой вопрос делал тебя более информированной на 1 бит. Таким образом, чтобы выбрать принца, тебе нужны были всего-то: блеск пламенных очей, одна (зато какая!) очаровательная улыбка, а также log 2 n бит информации. ..
..
Пожалуй, на этом курс для благородных девиц по логарифмам и теории информации можно считать успешно пройденным. Всего тебе доброго, любознательная принцесса, и до новых встреч!
Обратные функции
Математика выполняет операций . В противном случае у нас была бы куча значений и ничего общего с ними; у нас не было бы возможности соединить их. Введите операции.
Операции объединяют строковые значения для получения других значений. Однако иногда нам нужно что-то отменить, поэтому мы создали обратные операции. Обратные операции — это математические уловки: это операции, которые отменяют друг друга. Сложение и вычитание являются операциями, обратными друг другу. Умножение и деление также являются операциями, обратными друг другу. Если вы начали с 3, умножили его на 2, а затем разделили результат на 2, вы сразу же вернетесь к 3.
Угадайте, к чему мы клоним? Экспоненты и логарифмы являются обратными операциями! Итак, если у нас есть это уравнение:
y = x
Мы можем добавить к обеим сторонам…
y + 2 = x + 2
Мы можем выбирать с обеих сторон…
16. y – 2 = x – 2
y – 2 = x – 2
Умножить…
2 y = 2 x
Разделить…
6 6 Также « ЭКОНЕНТИЧЕСКИЙ » Обе стороны:
10 y = 10 x
и, наконец, « Take The Log » с обеих сторон:
6 y = = = = = = = = x
Каждое из приведенных здесь выражений эквивалентно y = x и друг другу. Поскольку вы знаете, что логарифмы и показатели степени являются обратными операциями, как сложение и вычитание, манипулирование уравнениями с показателями степени не составит труда.
Теперь, когда вы знаете, что возведение в степень и получение журнала являются обратными операциями, давайте поговорим об обратных функциях.
Обратные функции
Представьте себе функцию, которая имеет этот набор входов и выходов. Нет, правда, закрой глаза и сосредоточься на своем внутреннем математике:
{(1, 5), (2, 9), (3, 13), (4, 17)}
Если ты на подъеме и вверх, вы можете узнать, что эти числа взяты из линейной функции y = 4 x + 1. Круто. Инверсия этой функции просто переключает все входные и выходные значения:
Круто. Инверсия этой функции просто переключает все входные и выходные значения:
{(5, 1), (9, 2), (13, 3), (17, 4)}
Что это за функция? Никакого обмана, на нас работают роботы.
Очень простой способ найти ответ на этот вопрос — найти x и поменять местами x и y .
Y = 4 x + 1
Y — 1 = 4 x
Затем мы переключаем x и Y .
Бам! Вот ваш ответ: обратно y = 4 x + 1 . Более ясным способом представить это было бы сказать .
Специальное примечание: f -1 ( x ), обратная функция, не такая же, как обратная функция, . Будь осторожен!
Если вы примените функцию и функцию, обратную ей, к входному значению, входные данные останутся без изменений. Докажите это себе: попробуйте поставить 4 в одну из функций, а затем подставьте ответ в другую.
Видишь? Это по-прежнему 4. (Если нет, то что-то пошло не так, и это сообщение самоуничтожится через 3 секунды.) Другими словами, более математическими терминами: )] = x
Вот некоторое доказательство:
Шаг 1, Удивительный шаг: y = 4( 4 ) +1 = 17
Шаг 2, Удивительный шаг0: 9000 Еще шаг:
Это как фокусник, который выходит на сцену, вытаскивает кролика из шляпы и…
ЭТО НЕ КРОЛИК! Он быстро кладет не-кролика обратно в шляпу и пятится со сцены, как будто ничего не произошло. Без возвратов.
В следующем разделе мы попытаемся найти обратную экспоненциальную функцию. Это будет не так просто, как в этом разделе, но вы почувствуете себя еще круче, когда во всем разберетесь.
Инверсия экспоненциальной функции
Примените волшебный урок инверсии к экспоненциальной функции. Во-первых, взгляните на экспоненциальную функцию. Как мы упоминали ранее, экспоненциальные функции проще, чем кажутся: просто вставьте x в экспоненте.
Вот один:
y = 10 x
Верно. Так что насчет обратного? Просто решите для x . Подождите, как это должно работать?
Без логарифмов можно застрять в грязи. Грязная, липкая, неприятная грязь, которая не смоется, сколько бы раз вы ни клали ее в стиральную машину. Математика может все; это может даже сохранить вашу одежду чистой и свежей. (Отказ от ответственности: не пытайтесь положить математику в стиральную машину, это приведет к аннулированию всех гарантий.)
Пройдемте с нами на секунду. Мы собираемся использовать логарифм , чтобы найти x , а затем поменять местами. Как мы говорили в предыдущем разделе, получение логарифма — это операция, обратная возведению в степень, поэтому мы можем использовать ее, чтобы сократить 10 в правой части уравнения. Начните с бревна обеих сторон:
бревно 10 y = бревно 10 10 x
бревно 10 y
17 =
x
Now we swap x and y to get our inverse function:
log 10 x = y
y = log 10 x
Ta-daaa: y = log 10 x , логарифмическая функция, обратная y = 10 x , экспоненциальная функция .
Как найти обратное логарифмическое преобразование в R?
Логарифм данного числа n — это показатель степени, в которую нужно возвести другое фиксированное число по основанию b, чтобы получить это число n. С точки зрения непрофессионала, логарифм подсчитывает количество вхождений одного и того же множителя при повторном умножении. Логарифмическая функция представляется как:
f(x) = log b (x)
Когда основание b логарифма равно 10, мы обычно не упоминаем об этом, т. е. f(x) = log (Икс). Обратная логарифмическая или экспоненциальная функция определяется как:
в общем случае,
Y = log B (x) ⇐ порядка B y = x
для натурального журнала:
Y = LN (x) ⇐ятно = x
Давайте посмотрим на некоторые примеры для лучшего понимания:
Пример 1: , если y = ln (544) = 6,298949
Антилог (y) = E Y = 544
Пример 2 : , если у = log (544) = 2,735598
antilog ( y ) = 10 y = 544
Обратное логарифмическое преобразование в языке программирования R может быть exp(x) и expm010(x) 5) 9010(x) функциями. Функция exp( ) просто вычисляет экспоненциальную функцию, тогда как функция expm1( ) точно вычисляет exp(x) – 1 также и для |x| << 1. Здесь x должен быть числовым или комплексным вектором, а основание должно быть положительным.
Функция exp( ) просто вычисляет экспоненциальную функцию, тогда как функция expm1( ) точно вычисляет exp(x) – 1 также и для |x| << 1. Здесь x должен быть числовым или комплексным вектором, а основание должно быть положительным.
Метод 1: Использование exp()
Синтаксис:
exp ( x )
Где x — числовое значение.
Example:
R
exp (100)
exp (9867528)
exp (0)
exp ( 1.7865)
Вывод:
[1] 2.688117e+43 # exp (100)
[1] Inf # Exp (9867528)
[1] 1 # exp (0)
[1] 5,968526 # exp (1,7865)
Для большего числа, он обычно возвращает «инф», что означает бесконечность.
Метод 2: Использование expm1()
Синтаксис:
expm1 ( x ) = exp (x) – 1
,
Числовое значение.
Пример:
R
expm1 (100)
expm1 (9867528)
expm1 (0)
expm1 (1.7865)
Output:
[1] 2,688117E+43 # expm1 (100)
[1] Inf # expm1 (9867528)
[1] 0 # expm1 (0)
[1] 4.968526 # expm1 (1,7865)
6 [1] 4.968526 # expm1 (1,7865) 6 [1] 4.968526 # expm1 (1,7865) 6 [1]
Для больших числовых значений функции exp() и expm1() возвращают одинаковые значения.
Пример:
Найти положительный корень уравнения
( По определению арифметического корня имеем-
Пример:
Решить уравнение
Запишем данное уравнение так: 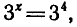
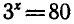
Уравнение 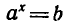
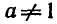
гарифмом числа b по основанию а и обозначают 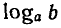
корнем уравнения 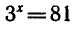
Лаплас Пьер Симон (1749— 1827)— французский математик, физик и астроном, адъюнкт Французской Академии Наук. После Великой Французской революции принимал активное участие в реорганизации системы образования. Важнейшие направления его исследований — математика, небесная механика и математическая физика. Один из создателей теории вероятностей.
Итак, логарифмом положительного числа b по основанию а, где
а > 0, 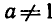
Например, 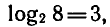
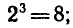
так как 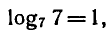
так как
Определение логарифма можно кратко записать так:
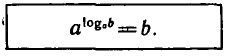
Это равенство справедливо при b > 0, а > 0, 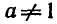
называют основным логарифмическим тождеством.
Например, 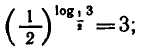
С помощью основного логарифмического тождества можио
показать, например, что 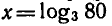
В самом деле,
Действие нахождения логарифма числа называют логарифмированием.
Пример:
Вычислить
Обозначим 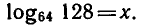
Так как 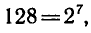
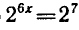
откуда 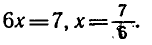
Ответ.
Пример:
Вычислить
Используя свойства степени и основное логарифмическое равенство, находим:
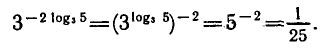
Пример:
Решить уравнение
Но определению логарифма 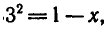
Пример:
При каких значениях х существует
Так как основание логарифма 5 > 0 и 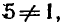
существует тогда и только тогда, когда
Получено неравенство, находим 1 < х < 2.
Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а>0, 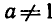
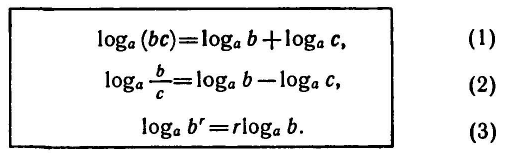
По основному логарифмическому тождеству

1) Перемножая равенства (4) и (5), получаем:
откуда по определению логарифма
Формула (1) доказана.
2) Разделив равенства (4) и (5), получим:
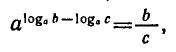
откуда по определению логарифма следует формула (2).
3) Возводя основное логарифмическое тождество
в степень с показателем r, получаем:
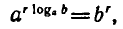
откуда по определению логарифма следует формула (3). •
Приведем примеры применения формул (1) — (3):
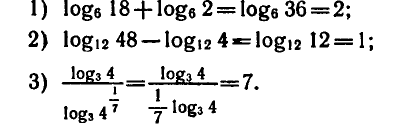
Пример:
Вычислить 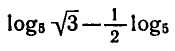
Применяя формулы (1) — (3), находим:
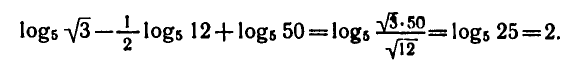
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы
(таблицы логарифмов). Логарифмы вычисляют также с помощью
микрокалькулятора. И в том и в другом случае находятся только
десятичные или натуральные логарифмы.
Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо
Натуральным логарифмом числа называют логарифм этого числа по основанию e, где е — иррациональное число, приближенно равное 2,7. При этом пишут ln e вместо
Иррациональное число е играет важную роль в математике
и ее приложениях. Число е можно представить как сумму:
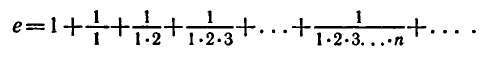
Вычисление числа е на микрокалькуляторе проводится по
программе:
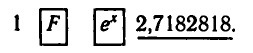
Вычисления на микрокалькуляторе lg b и ln b проводятся
соответственно по программам:
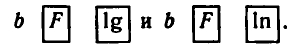
Например, вычисляя lg 13, получаем:
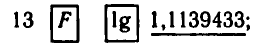
вычисляя ln 13, получаем:
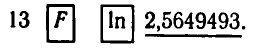
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить
логарифмы чисел по любому основанию. Для этого используется
формула перехода от логарифма по одному основанию к
логарифму по другому основанию:

где b > 0, а > 0 , 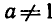
Докажем справедливость формулы (1).
Запишем основное логарифмическое тождество
Возьмем от обеих его частей логарифмы по основанию с:
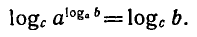
Используя свойство логарифма степени, получаем:
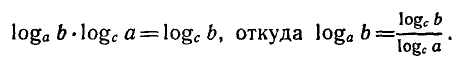
Из формулы (1) при с = 10 и с = е получаются формулы
перехода к десятичным и натуральным логарифмам:
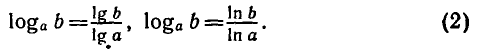
Пример:
С помощью микрокалькулятора МК-54 вычислить
1) С помощью десятичных логарифмов:

2) С помощью натуральных логарифмов:
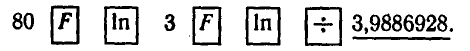
Ответ. 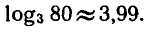
Формула перехода от одного основания логарифма к другому
иногда используется при решении уравнений.
Пример:
Решить уравнение
По формуле перехода
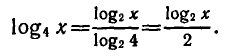
Поэтому уравнение принимает вид 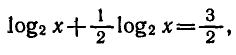
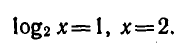
Пример:
Двухпроцентный вклад в Сбербанк, равный
а рублям, через п лет становится равным 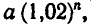
трехпроцентный вклад становится равным
Через сколько лет каждый из вкладов удвоится?
1) Для первого вклада 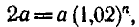
2. Вычисления проведем на МК-54:
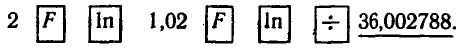
2) Для второго вклада 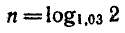
такова:

Ответ. По первому вкладу приближенно через 36 лет, а
по второму — через 23,5 года.
Логарифмическая функция и ее график
В математике и ее приложениях часто встречается
логарифмическая функция
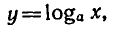
где а — заданное число, а > 0, 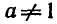
Логарифмическая функция обладает следующими свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
Это следует из определения логарифма, так как выражение 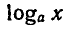
2) Множество значений логарифмической функции — множество R всех действительных чисел.
Это следует из того, что для любого действительного числа
b есть такое положительное число х, что 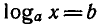
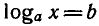
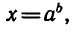
3) Логарифмическая функция 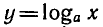
0 < а < 1 .
Пусть а > 1. Докажем, что если 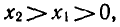

Пользуясь основным логарифмическим
тождеством, условие 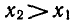

Пусть 0 < a < 1 . Докажем, что если 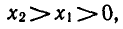
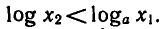

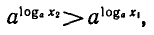
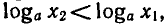
4) Если а > 1, то функция 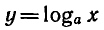
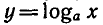
Это следует из того, что функция 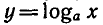
значение, равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если а > 1, и убывающей, если 0 < а < 1 .
Из рассмотренных свойств логарифмической функции 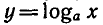
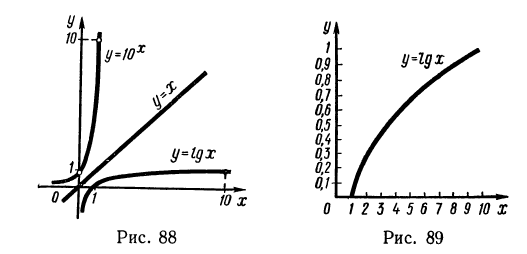
На рисунке 9 изображен график функции 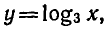
Отметим, что график любой логарифмической функции 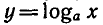
Теорема:
Если 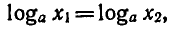
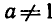
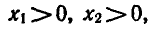
Предположим, что 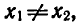
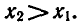


0 < а < 1 , то из неравенства 
В обоих случаях получилось противоречие с условием 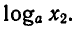
Пример:
Решить уравнение
Используя доказанную теорему, получаем Зх — 2 = 7, откуда Зх = 9,
х = 3.
Пример:
Решить неравенство
Пользуясь тем, что 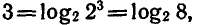
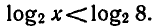
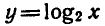
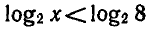
Ответ. 0 < х < 8 .
Пример:
Решить неравенство
Запишем данное неравенство так:
Функция 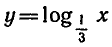
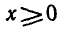
Ответ.
Обратная функция
Известно, что зависимость скорости v от времени t движения
тела, брошенного вверх с начальной скоростью 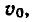
формулой
Из этой формулы можно найти обратную зависимость — времени от скорости: 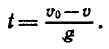
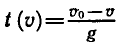
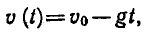
Рассмотрим теперь показательную и логарифмическую
функции. Обозначим символом f(х) показательную функцию,
a g (х) — логарифмическую функцию:
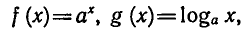
где а — заданное число, а > 0, 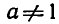
Решим уравнение 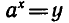
логарифма 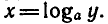
получим логарифмическую функцию 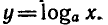
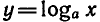
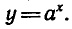
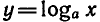
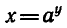
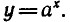
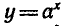
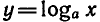
Вообще если функция y = f(x) задана формулой, то для
нахождения обратной функции нужно решить уравнение
f (x) = у относительно х и затем поменять местами х и у.
Если уравнение f(x)= y имеет более чем один корень, то
функции, обратной к y = f (x), не существует.
Например, функция 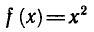
уравнение 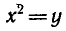
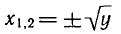
у > 0.
Если функцию 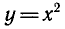
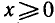
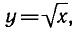
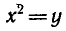
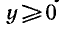
Пример:
Найти функцию, обратную к функции
Решая это уравнение относительно х, получаем
Заменив х на у и у на х, находим
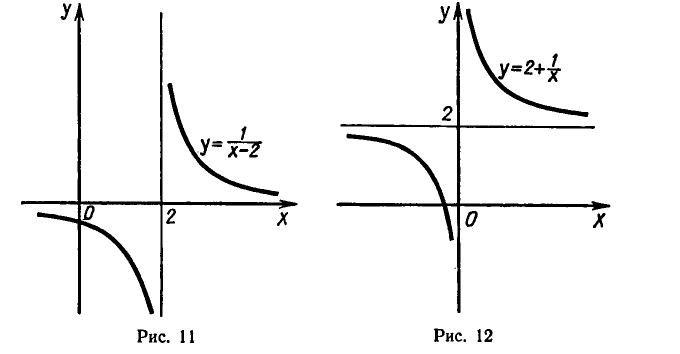
В этой задаче область определения функции 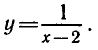
множество действительных чисел, не равных 2, а множество ее значений — все действительные числа, не равные 0. График этой
функции изображен на рисунке 11.
Для обратной функции 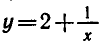
множество действительных чисел, не равных 0, а множество значений — все действительные числа, не равные 2. График обратной функции изображен на рисунке 12.
Вообще область определения обратной функции совпадает
с множеством значений исходной функции, а множество
значений обратной функции совпадает с областью определения
исходной функции.
Можно показать, что если функция имеет обратную, то
график обратной функции симметричен графику данной
функции относительно прямой у = х.
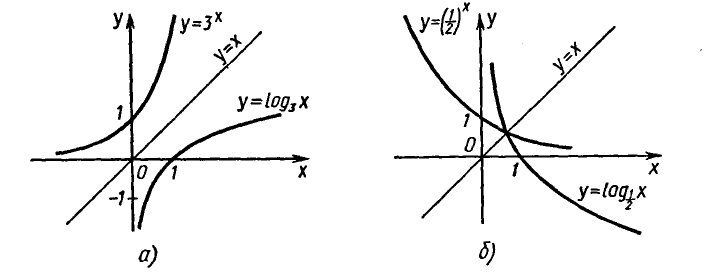
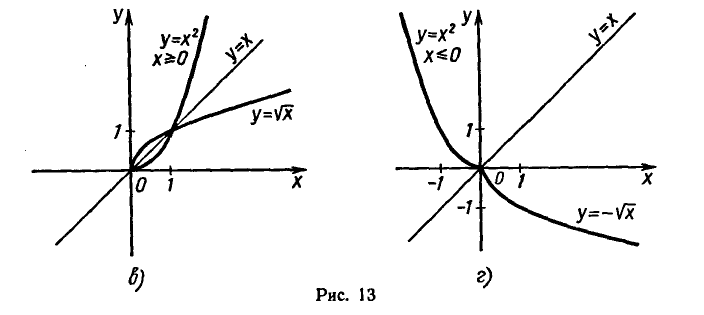
Примеры графиков взаимно обратных функций показаны на
рисунке 13.
Логарифмические уравнения
Пример:
Решить уравнение
( 1 )
Предположим, что х — такое число, при котором равенство ( 1 ) является верным, т. е. х — корень уравнения ( 1 ).
Тогда по свойству логарифма верно равенство
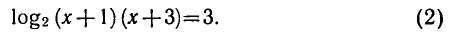
Из этого равенства по определению логарифма получаем:
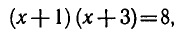
откуда 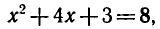
Последнее равенство верно, если 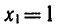
Итак, предположив, что число х — корень уравнения (1),
мы показали, что х может быть равным или 1, или —5.
Проверим, являются ли эти числа корнями уравнения (1).
Подставляя в левую часть данного уравнения х = 1 , получаем
т. е. х = 1 — корень уравнения ( 1 ).
При х = — 5 числа х + 1 и х + З отрицательны, и поэтому
левая часть уравнения ( 1 ) не имеет смысла, т. е. х = — 5 не
является корнем этого уравнения.
Ответ. х = 1 .
Заметим, что х = — 5 является корнем уравнения (2), так
как
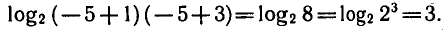
Получилось, что число х = 1 является корнем обоих уравнений
( 1 ) и (2), а число х = — 5 не является корнем уравнения (1 ), но является корнем уравнения (2). Таким образом, при переходе от уравнения (1) к уравнению (2 ) корень х = 1 сохранился и появился посторонний корень х = —5. В этом случае уравнение (2) называют следствием уравнения (1 ).
Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.
Отметим, что в уравнении, которое является следствием
данного, не всегда появляются посторонние корни; важно лишь
то, чтобы корни исходного уравнения не терялись.
В большинстве случаев, как и в задаче 1, уравнения решаются постепенным переходом к более простым уравнениям,
которые являются следствием исходного уравнения. В таких
случаях после нахождения корней необходима их проверка.
Пример:
Решить уравнение
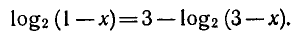
Перенесем логарифм из правой части в левую;
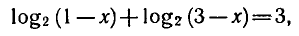
откуда
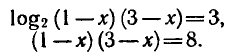
Решая это уравнение, получаем
Число 
как при x = 5 левая и правая части уравнения теряю т смысл.
Проверка показывает, что число х = — 1 является корнем
исходного уравнения.
Ответ. х = — 1. ▲
Пример:
Решить уравнение
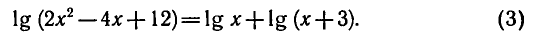
По свойству логарифмов
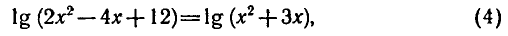
откуда
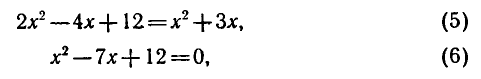
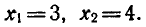
являются корнями исходного уравнения.
Ответ. 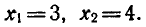
Проверкой можно убедиться в том, что числа 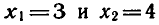
(4) и (5). Все эти уравнения других корней не имеют. Такие
уравнения называют равносильными.
Уравнения, имеющие одно и то же множество корней,
называют равносильными.
В частности, два уравнения, не имеющие корней, являются
равносильными.
Отметим, что любое из двух равносильных уравнений является следствием другого.
Большинство уравнений, с которыми вы встречались в курсе
алгебры, решались с помощью перехода от данного уравнения
к равносильному. Так решались уравнения первой степени с
одним неизвестным, квадратные уравнения, показательные
уравнения.
Напомним, что уравнение заменяется ему равносильным при
следующих преобразованиях:
любой член уравнения можно переносить из одной части
в другую, изменив его знак на противоположный;
обе части уравнения можно умножить или разделить на
одно и то же число, не равное нулю.
Однако не при любом преобразовании уравнение заменяется
на равносильное. Например, при возведении обеих частей
уравнения 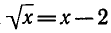
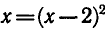
Пример:
Решить уравнение
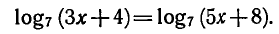
Приравнивая выражения, стоящие под знаком логарифма,
получаем:
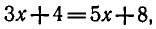
откуда х = — 2. Выполняя проверку, убеждаемся, что при х = — 2
левая и правая части исходного уравнения не имеют смысла.
Ответ. Корней нет.
Здесь посторонний корень появился потому, что при переходе
от равенства логарифмов к равенству чисел не было учтено
требование, чтобы эти числа были положительными.
Рассмотренные примеры логарифмических уравнений
показывают, что при их решении с использованием свойств логарифмов получаются уравнения, которые являются следствиями исходного. Поэтому необходима проверка, которая позволяет
обнаружить посторонние корни. ▲
Пример:
Решить уравнение
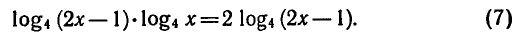
Преобразуем данное уравнение:
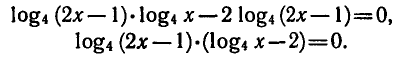
Приравнивая каждый из множителей левой части уравнения
к нулю, получаем:
Проверка показывает, что оба значения х являются корнями
исходного уравнения.
Ответ.
Отметим, что если обе части уравнения (7) разделить на
выражение 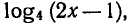
Вообще при делении обеих частей уравнения на выражение, содержащее неизвестное, может произойти потеря корней.
Поэтому уравнение, обе части которого содержат общий
множитель, решают переносом всех членов в одну часть и
разложением на множители.
При решении уравнений главное не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.
Пример:
Решить систему уравнений
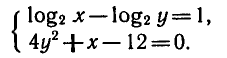
Из первого уравнения выразим х через 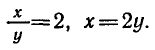
получим 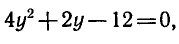
Найдем значения х : 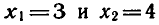
что 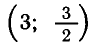
решение.
Ответ.
Логарифмические неравенства
При изучении логарифмической функции рассматривались
неравенства вида 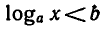
Приведем примеры решения более сложных логарифмических неравенств. Обычный способ решения таких неравенств заключается в переходе от них к более простому неравенству или системе неравенств, имеющей то же самое множество решений.
Пример:
Решить неравенство

Правая часть данного неравенства имеет смысл при всех значениях x, а левая часть — при x + 1 > 0, т. е. при х > — 1.
Промежуток х > — 1 называют областью определения неравенства (1). Так как логарифмическая функция с основанием
10 возрастающая, то неравенство ( 1 ) при условии x + 1 > 0
выполняется, если 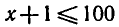
образом, неравенство ( 1 ) равносильно системе неравенств
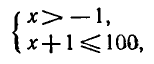
т. е. неравенство ( 1 ) и система (2) имеют одно и то же множество решений. Решая систему (2), находим
Пример:
Решить неравенство
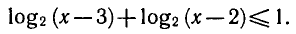
Логарифмическая функция определена при положительных значениях аргумента, поэтому левая часть неравенства имеет смысл при х — 3 > 0 и х — 2 > 0.
Следовательно, областью определения этого неравенства является промежуток х > 3 . По свойствам логарифма неравенство (3)
при х > 3 равносильно неравенству
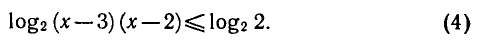
Логарифмическая функция с основанием 2 возрастающая. Поэтому при х > 3 неравенство (4) выполняется, если
Таким образом, исходное неравенство (3) равносильно системе неравенств
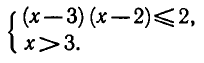
Решая первое неравенство этой системы, получаем 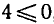
Совмещая этот отрезок с промежутком х > 3 , получаем 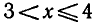
Пример:
Решить неравенство
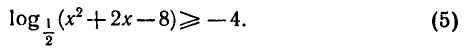
Область определения неравенства находится из условия
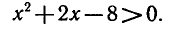
Неравенство (5) можно записать в следующем виде:
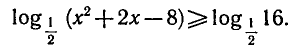
Так как логарифмическая функция с основанием 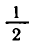
убывающей, то для всех х из области определения неравенства
получаем:
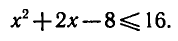
Таким образом, исходное неравенство (5) равносильно системе неравенств
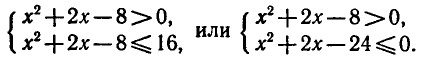

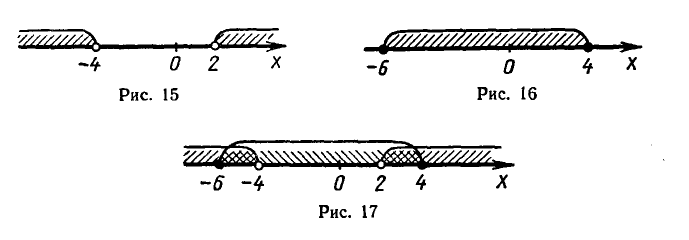
Решая первое квадратное неравенство, получаем х < — 4, х > 2 (рис. 15). Решая второе квадратное неравенство, получаем 
мы выполняются одновременно при 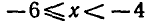
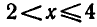
Ответ.
Определение:
Логарифмом числа а по основанию b называется показатель степени, в которую надо возвести а, чтобы получить число b.
В качестве основания мы будем всегда брать положительное число а, отличное от 1.
В записи b = 
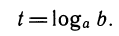
Можно сказать, что формулы 
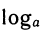
Подставляя в равенство 
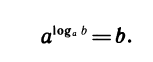
Представляя в равенстве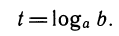
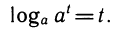
Свойства логарифмов
Теорема:
Верны следующие тождества, выражающие свойства логарифмов:
1)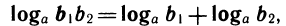
2) 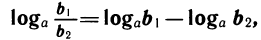
3) 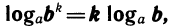
Доказательство:
Свойства логарифмов выводятся из свойств степеней с помощью основного логарифмического тождества, выражающего определение логарифма. Выведем для примера первое свойство.
Обозначим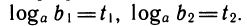
Перемножим эти равенства: 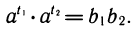
По определению логарифма t1+ t2 = 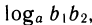
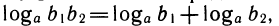
Свойства степеней и логарифмов тесно связаны между собой. Они фактически выражают одно и то же, только один раз мы обращаем внимание на поведение самих степеней, а другой — на поведение показателей:
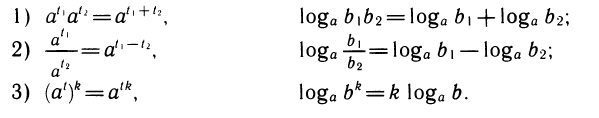
С помощью свойств логарифмов можно логарифмировать выражения, составленные с помощью операций умножения, деления и возведения в степень.
Примеры.
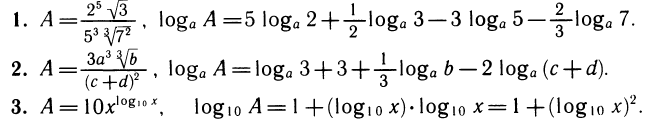
Иногда приходится искать выражение по его логарифму. Такую операцию называют потенцированием.
Примеры:
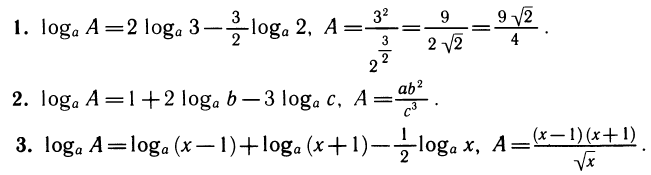
Замечание. Запись 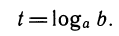
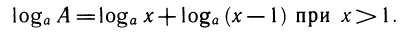
Если же х<0, то оба множителя отрицательны и А нужно разложить на множители так: А =( — x)(1 — x), откуда
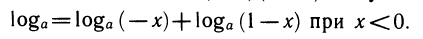
Аналогично 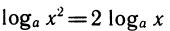
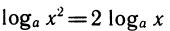
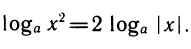
Модуль перехода
В вычислениях в качестве основания а часто берется число а=10. В то же время зачастую необходимы вычисления степеней и логарифмов с разными основаниями. Возникает вопрос: как связать между собой степени и логарифмы с разными основаниями?
Пусть дана степень b = 

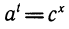
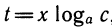
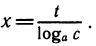
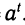
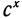
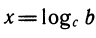
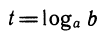
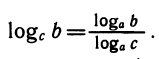
Выведенную формулу называют формулой перехода от одного основания логарифма к другому.
Таким образом, мы видим, что при изменении основания значения логарифмов изменяются пропорционально. Коэффициент пропорциональности 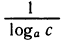
Отметим простые следствия выведенной формулы:
1) 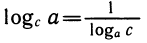
2) 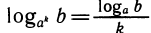
3) 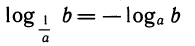
С помощью логарифмов все степени можно привести к одному основанию. Если в качестве основания берется число a =10, то соответствующие логарифмы обозначаются знаком lg и называются десятичными. Можно записать:
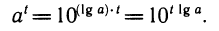
Если в качестве основания берется число е, то соответствующие логарифмы обозначаются знаком ln и называются натуральными:
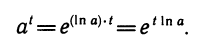
Значения модулей перехода от десятичных логарифмов к натуральным и наоборот таковы:
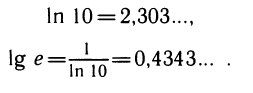
Исследование логарифмической функции
Определение:
Логарифмической функцией называется функция вида
Напомним, что в качестве основания логарифмов выбирается число а> 0, отличное от 1.
Основные свойства логарифмической функции (схема X).
- 1) Область определения: множество всех положительных чисел, т. е. промежуток (0; + ∞).
- 2) Монотонность: если а>1, то логарифмическая функция строго возрастает; если 0<а<1, то она строго убывает.
- 3) Область значений: множество всех вещественных чисел R.
Так как определение логарифмов основано на понятии степени,
то при доказательстве свойств логарифмической функции используют свойства показательной функции.
Свойство 1 в доказательстве не нуждается: оно опирается на определение логарифма числа х, по которому необходимо, чтобы число х было положительным.
Докажем свойство 2. Для этого сначала рассмотрим случай а>1. Возьмем два положительных числа х1 и x2, такие, что x1 <x2, и докажем, что 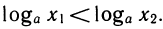
Если бы выполнялось неравенство t1 ≥ t2, то по свойству монотонности показательной функции выполнялось бы неравенство т. е. 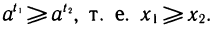
Следовательно, t1<t2, что и требовалось доказать. Случай 0<а<1 рассматривается аналогично.
Свойство 3 утверждает, что всякое вещественное число t может быть логарифмом некоторого числа х. Так как степень 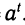
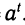
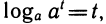
Графики логарифмических функций при различных основаниях показаны на рисунке 108.
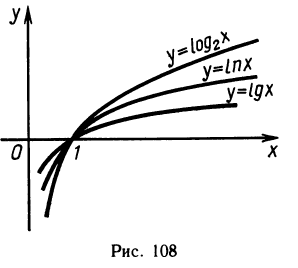
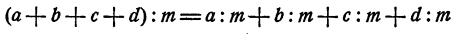
Графики функций 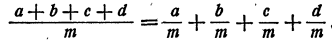
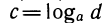
Так как точки Р (с; d) и Q (d; с) симметричны относительно прямой у = х (рис. 109), то симметричны и графики показательной и логарифмической функций.
Вместо логарифмических функций с произвольным основанием удобно рассматривать функции вида у = с ln х. Так как 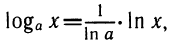
Функция у = ln х растет с ростом х, однако медленнее, чем любая степенная функция вида 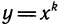
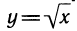
Производная логарифмической функции
Рассмотрим две функции у = 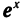
Пусть a1 и а2 — углы, образованные проведенными касательными с осью абсцисс. Из рисунка 109 ясно, что
Так как
Таким образом, производная функции у = ln х в точке x = d равна
Можно написать:
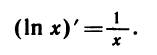
Мы видим, что производная логарифмической функции y = ln х равна степенной функции 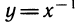
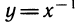
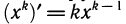
Так как 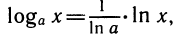
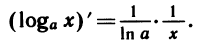
По формулам производной показательной функции 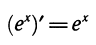
Известно, что ,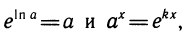
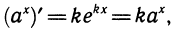
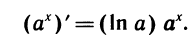
Примеры:
Зная производные экспоненты и логарифма, можно получить приближенные формулы для их вычисления.
Пусть
Разность 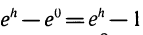
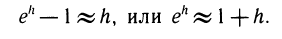
Более точная формула для вычисления экспоненты такова:
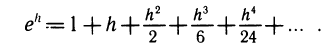
Пусть теперь у =lnх. Выберем дго=1, xо = ln l =0. Положим dx = h и вычислим ln (l+h). Найдем dy при xo=1. Так как
(In то y’ (jc0)= 1 и dy= 1 •dx = h.
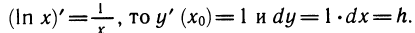
Заменяя ∆y= ln (1+h) — ln l = ln (l+h), получаем приближенную формулу
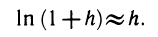
Более точная формула для вычисления логарифма такова:
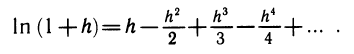
Вычисление логарифмов
Более 300 лет логарифмы использовались для облегчения вычислений. Их основное достоинство — способность сводить умножение к сложению по формуле
Были составлены обширные таблицы логарифмов чисел, с помощью которых можно легко переходить от чисел к их логарифмам и обратно.
Все таблицы логарифмов до 1950 г. являлись перепечаткой или сокращением таблиц Бриггса. Генри Бриггс (1561 —1630) с очень большой точностью (16 знаков после запятой) извлек подряд 57 квадратных корней из 10 и получил значения
Комбинируя эти значения, он получил густую сетку чисел с известными десятичными логарифмами: 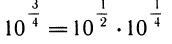
Это огромная работа, и за 300 лет не нашлось никого, кто повторил бы ее. Любопытно, что немного раньше Бриггса таблицу натуральных логарифмов составил Джон Непер (1550—1617).
С появлением ЭВМ ситуация переменилась. Умножение по-прежнему выполняется дольше, чем сложение, но логарифмирование требует еще больше времени. Поиск числа в таблице очень дорогая операция для ЭВМ. Поэтому теперь значение логарифмов как инструмента вычисления резко упало, а с распространением калькуляторов оно сходит на нет. С другой стороны, сами по себе логарифмические зависимости легко обрабатываются и используются при вычислениях на ЭВМ. Например, формула xk = exp(k ln x) служит основным средством возведения в степень (кроме k= l, 2, 3) на всех ЭВМ и на калькуляторах.
На современных ЭВМ (и на калькуляторах) значения In х и 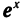
Прикладные примеры
Во вводной беседе мы уже говорили о том, что многие процессы описываются с помощью показательных функций. Почему так происходит, это мы обсудим в следующей главе, а сейчас приведем примеры зависимостей, в которых встречаются экспоненты и логарифмы.
- Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле
, где m0 — масса вещества в начальный момент t = 0, m — масса вещества в момент времени t, Т — некоторая константа, смысл которой мы сейчас выясним.
Вычислим значение m при t — Т. Так,
Это означает, что через время Т после начального момента масса радиоактивного вещества уменьшается вдвое. Поэтому число Т называют периодом полураспада. Период полураспада радия равен 1600 лет, урана-238 — 4,5 млрд. лет, цезия-137 —31 год, иода-131 —8 суток.
Закон радиоактивного распада часто записывают в стандартном виде 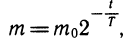
2. Рост народонаселения. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой 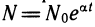
Барометрическая формула. Давление воздуха убывает с высотой (при постоянной температуре) по закону 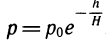
4. Формула Циолковского. Эта формула, связывающая скорость ракеты у с ее массой m, такова: 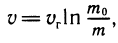
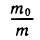
5. Коэффициент звукоизоляции стен измеряется по формуле 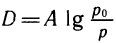
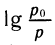
Дополнение к логарифмической функции
Смотрите также:
Предмет высшая математика
Логарифмическая функция
Определение логарифма: Логарифмом числа N по данному основанию а называется такой показатель степени, в который надо возвести основание а, чтобы получить число N; запись
Примеры:

Таким образом, 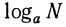
Примеры:
1. Проверить справедливость следующих равенств:
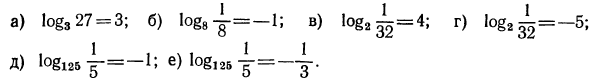
Решение:
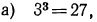
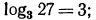
б), г), е) верны; 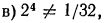
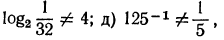
2.Следующие равенства переписать в виде логарифмических равенств:
Решение:
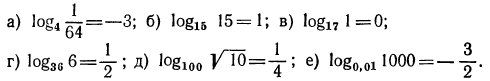
Указать, какие из нижеследующих уравнений имеют решение. Запишите это решение с помощью логарифма:
Решение:
а) Уравнение 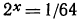
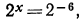
б) Уравнение 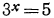
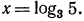
в) Уравнение 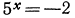
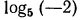
Десятичные логарифмы
Если основанием логарифмов служит число 10, то такие логарифмы называются десятичными. Десятичный логарифм числа N принято обозначать
Примеры:
Найти десятичные логарифмы следующих чисел:
Решение:
Так как 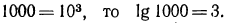
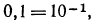
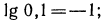
2.Решить следующие уравнения:
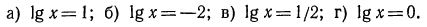
Решение:
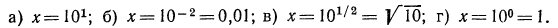
Функция 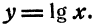
Функция 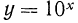
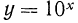
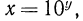
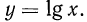
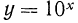
1.Областью определения функции является множество всех положительных чисел.
2.Областью значений функции является множество всех действительных чисел.
Справедливость этих двух свойств вытекает из того факта, что функции 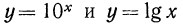
3.Функция 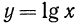
4.При 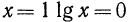
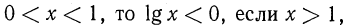
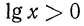
Примеры:
1. На рис. 89 изображен график функции 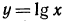
а) найти 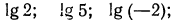
Решение:
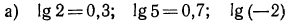
б) если
Если
2.Сравнить значения выражений:
Решение:
а) Функция 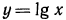
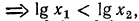
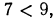
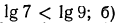
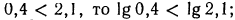
3.Решить уравнения и неравенства:
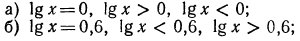
Решение:
Воспользовавшись изображенным на рис. 89 графиком функции 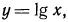
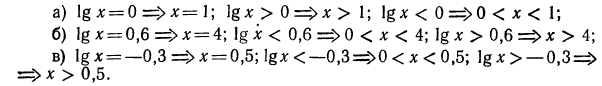
4.Найти область определения функции:
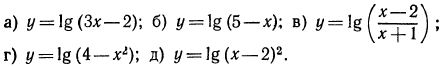
Решение:
При решении этих примеров надо помнить о том, что область определения функции 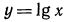
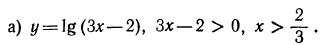
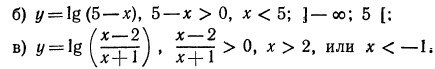
Область определения —объединение двух множеств
Область определения —множество
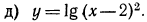
5.Решить уравнения:
Решение:
а) Так как 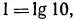
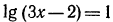
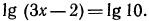
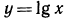
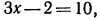
Аналогично решаются и остальные уравнения;
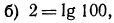
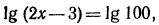
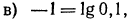
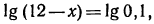
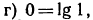
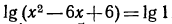
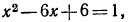
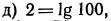
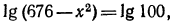
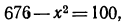
Логарифмирование и потенцирование
Применение логарифмов позволяет во многих случаях значительно упростить вычисления. Чтобы убедиться в этом, прежде всего выясним, как находятся логарифмы произведения, частного, степени и корня.
Теорема:
Логарифм произведения любых двух положительных чисел равен сумме логарифмов множителей, т. е.
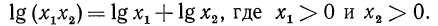
Доказательство:
Пусть 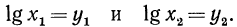
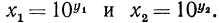
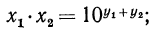
значит,
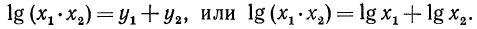
Предлагаем читателю самому доказать, что установленное свойство справедливо для любого числа положительных множителей.
Теорема:
Логарифм степени с положительным основанием равен произведению показателя степени и логарифма ее основания, т. е.
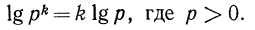
Доказательство:
Пусть 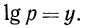
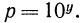
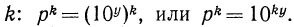
Покажем, что знания этих теорем достаточно для нахождения логарифмов дроби и корня. Действительно, пусть дано выражение 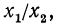
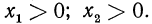
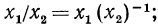
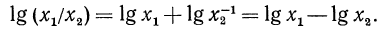
Пусть теперь дано выражение 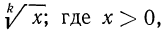
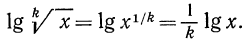
Примеры:
1. Найти приближенные значения следующих логарифмов: 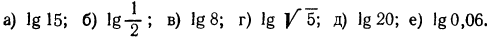
Решение:
Прежде всего, воспользовавшись графиком функции 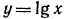
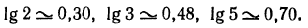
Теперь имеем:
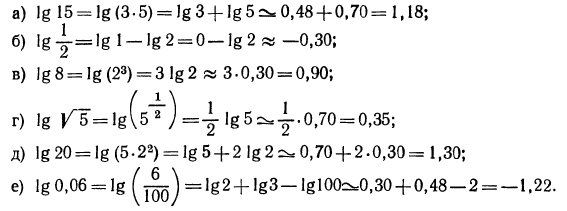
2.Прологарифмировать следующие выражения (буквами обозначены положительные числа):
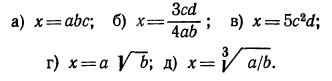
Решение:
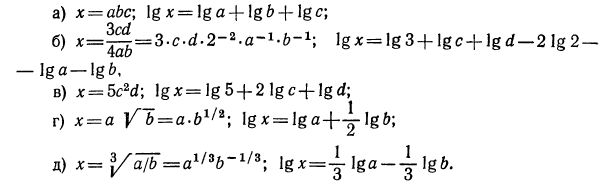
3.Решить уравнения:
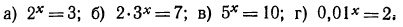
Решение:
а) Прологарифмировав обе части данного равенства, получим 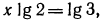
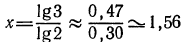
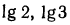
б) в результате логарифмирования имеем равенство 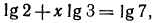
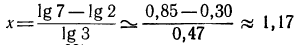
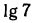
4.Найти x, если:
Решение:
5.Решить уравнения:
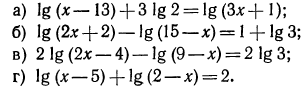
Решение:
а) Потенцируя обе части равенства, получаем уравнение
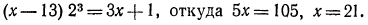
Сделаем проверку. Подставив в уравнение найденное решение х = 21, получим:
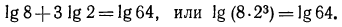
Таким образом, корень данного уравнения x=21;
б) прежде чем потенцировать, заметим, что 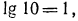
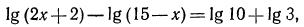
откуда
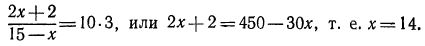
Сделаем проверку: 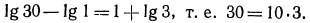
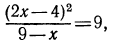
откуда
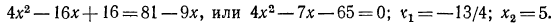
Сделаем проверку. Корень 
Корень x = 5, как легко видеть, удовлетворяет уравнению (Проверьте сами!);
г) уравнение 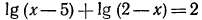
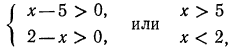
а эта система противоречива и решения не имеет.
Стандартный вид числа. Характеристика и мантисса
Любое положительное число х можно записать в так называемом стандартном виде: 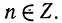
Примеры:
Записать следующие числа в стандартном виде и указать их порядок: а) 273; б) 51,83; в) 0,8912; г) 400012; д) 0,00051; е) 1,002.
Решение:
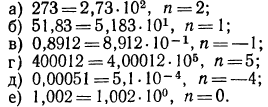
Легко видеть, что если 


Если же число 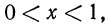
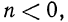
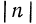
Пример:
Не переходя к стандартному виду записи, найти порядок чисел: а) х = 373,25; б) x: = 0,00085.
Решение:
а) Число 373,25 больше единицы и содержит в целой части три цифры. Следовательно, его порядок n= 2;
б) число 0,00085 меньше единицы и содержит четыре нуля до первой значащей цифры. Следовательно, n =—4.
Пусть х=375,8. Запишем это число в стандартном виде и найдем его логарифм:
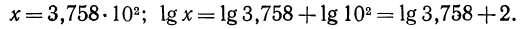
Так как 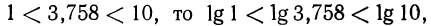
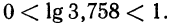
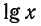
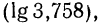
Целая часть логарифма числа называется его характеристикой, а дробная часть — мантиссой.
Теорема:
Характеристика логарифма числа 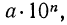
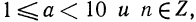
Доказательство:
Пусть 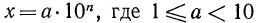
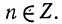
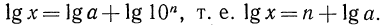
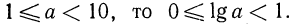
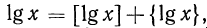
Следствие:
Логарифмы чисел, отличающихся друг от друга только порядком, имеют одну и ту же мантиссу.
Доказательство:
Пусть 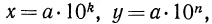
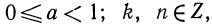
Таким образом,
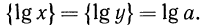
Например, пусть 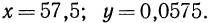
Таким образом, доказанное следствие можно сформулировать иначе: мантисса логарифма числа не зависит от положения запятой в числе.
Примеры:
1. Найти характеристику логарифма числа а) 302;б) 87,5; в) 0,015.
Решение:
Как было доказано Выше, характеристика логарифма числа равна его порядку, а поэтому
2.Зная, что 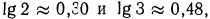
Решение:
Вычисления с помощью таблиц логарифмов
Как известно, характеристика логарифма числа легко находится устно (она равна порядку числа). Значения мантисс приведены в таблице «Четырехзначных математических таблиц» В. М. Брадиса. Приведем часть этой таблицы и укажем как ею пользоваться.
Примеры:
1. Найти логарифмы следующих чисел:
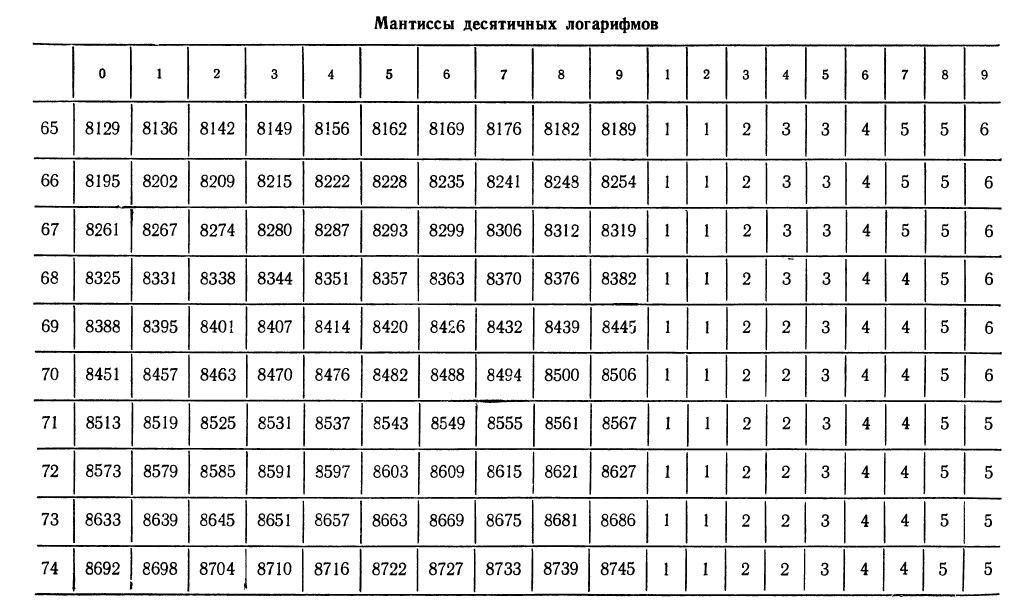
Решение:
а) Характеристика 
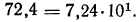
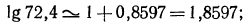
Для отыскания мантиссы мы, прочитав число 8739 на пересечении строки с меткой «74» и столбца с меткой «8», прибавим к этому числу поправку на четвертую цифру. Эта поправка расположена в правой части таблицы на пересечении той же строки и столбца поправок с меткой «5». Поправка равна 3, следовательно, мантисса равна 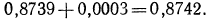
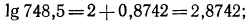
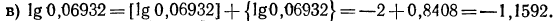
2.Найти x:, если:
Решение:
а) По таблице значений функции 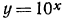
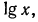
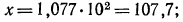
б) представим данный логарифм в виде суммы характеристики и мантиссы:
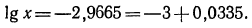
Мантиссу 0,0335 имеет любое число вида 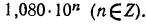
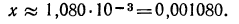
В заключение приведем пример вычисления с помощью таблиц логарифмов.
3.Вычислить значение х, если
Решение:
Логарифмируя, имеем:
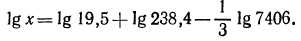
По таблице логарифмов найдем:
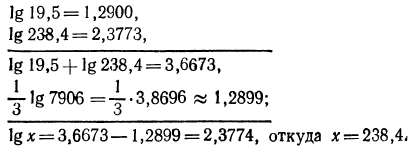
Решение:
а) Характеристика 
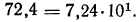
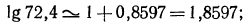
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Загрузить PDF
Загрузить PDF
Математические функции, обычно обозначаемые как f(x) или g(x), можно представить как порядок выполнения математических операций, которые позволяют прийти от «x» к «y». Обратная функция f(x) записывается как f-1(x).[1]
В случае простых функций найти обратную функцию несложно.
Шаги
-
1
Полностью перепишите функцию, заменив f(x) на y. При этом «у» должна находиться на одной стороне функции, а «x» — на другой. Если вам дана функция вида 2 + y = 3x2, вам необходимо изолировать «у» на одной стороне, а «x» — на другой.
- Пример. Перепишем данную функцию f(x) = 5x — 2 как y = 5x — 2. f(x) и «y» взаимозаменяемы.
- f(x) — это стандартная запись функции, но если вы имеете дело с несколькими функциями, то каждой из них нужно будет присвоить свою букву, чтобы их было легче отличать друг от друга. Например, часто функции обозначают как g(x) и h(x).
-
2
Найдите «x». Другими словами, выполните математические операции, необходимые для изолирования «x» по одну сторону от знака равенства. Основные алгебраические принципы: если «x» имеет числовой коэффициент, то разделите обе стороны функции на этот коэффициент; если к члену с «x» прибавляется некоторый свободный член, вычтите его с обеих сторон функции (и так далее).
- Помните, что вы можете применять любую операцию по отношению к одной из сторон уравнения только в том случае, если вы применяете ту же операцию по отношению ко всем членам по обе стороны от знака равенства.[2]
- В нашем примере добавьте 2 к обеим частям уравнения. Вы получите y + 2 = 5x. Затем разделите обе части уравнения на 5 и получите (y + 2)/5 = x. И, наконец, перепишите уравнение с «x» в левой части: x = (y + 2)/5.
- Помните, что вы можете применять любую операцию по отношению к одной из сторон уравнения только в том случае, если вы применяете ту же операцию по отношению ко всем членам по обе стороны от знака равенства.[2]
-
3
Поменяйте переменные, заменив «x» на «y» и наоборот. Результатом будет функция, обратная исходной. Другими словами, если мы подставим значение «x» в исходное уравнение и найдем значение «у», то, подставив это значение «у» в обратную функцию, мы получим значение «x».
- В нашем примере получим y = (x + 2)/5.
-
4
Замените «у» на f-1(x). Обратные функции обычно записывают в виде f-1(x) = (члены с «x»). Следует отметить, что в данном случае -1 — это не показатель степени; это просто обозначение обратной функции.
- Так как «x» в -1 степени равно 1/x, то f-1(x) — это форма записи 1/f(x), что также обозначает функцию, обратную f(x).
-
5
Проверьте работу, вместо «x» подставив постоянное значение в исходную функцию. Если вы правильно нашли обратную функцию, подставив в нее значение «у», вы найдете подставленное значение «x».
- Например, подставьте x = 4. Вы получите f(x) = 5(4) — 2 или f(x) = 18.
- Теперь подставьте 18 в обратную функцию и получите y = (18 + 2)/5 = 20/5 = 4. То есть у = 4. Это подставленное значение «x», поэтому вы правильно нашли обратную функцию.
Реклама
Советы
- Когда вы выполняете алгебраические операции над функциями, вы можете свободно заменять f(x) = y и f^(-1)(x) = y в обоих направлениях. Но прямая запись обратной функции может привести к путанице, поэтому придерживайтесь записи f(x) или f^(-1)(x), которая поможет вам отличить их друг от друга.
- Обратите внимание, что обратная функция обычно (но не всегда) является функциональной зависимостью.[3]
Реклама
Об этой статье
Эту страницу просматривали 63 573 раза.