Как найти область существования функции онлайн - Autoru.top

Областью определения функции
называется множество всех значений аргумента при которых значение функции определено. Иными словами, если у нас задана некоторая функция
,
то область её определения — это все те значения

которые мы можем подставить в уравнение

и получить результат отличный от бесконечности и/или деления на ноль.

Данный калькулятор, построенный на основе системы Wolfram Alpha, находит
область определения функции
в режиме онлайн.

Источник

Область существования функции

Данный сервис используется для нахождения области определения функции в онлайн режиме.

Например, найти область определения функции ln(x²-1).

Примечание: число «пи» (π) записывается как pi; корень квадратный как sqrt, например, sqrt(3); arcsin ≡ asin

В таблице приведены области существования наиболее распространенных функций.

ln(x)	x > 0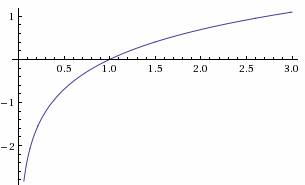
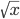	x ≥ 0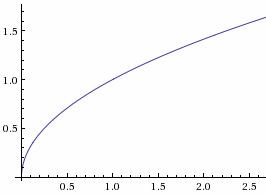
tgx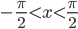
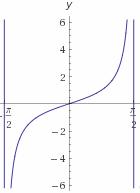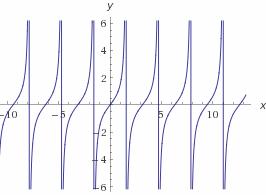ctgx	0 < x< π
arcsinx	-1 ≤ x ≤ 1
arccosx	-1 ≤ x ≤ 1

Пример. Требуется найти область определения функции, для этого нужно знать области определения элементарных функций.

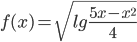
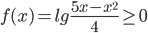
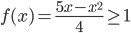
Найдем область определения . Функция определена при тех значениях x, для которых . Это неравенство будет выполнено, если , т.е. x²–5x+4≤0. Решая это неравенство методом интервалов, находим область определения – промежуток [1;4]. Зная f(x), можно найти и т.д.

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Показать Этапы

Номер Строки

Примеры

y=frac{x^2+x+1}{x}
f(x)=x^3
f(x)=ln (x-5)
f(x)=frac{1}{x^2}
y=frac{x}{x^2-6x+8}
f(x)=sqrt{x+3}
f(x)=cos(2x+5)
f(x)=sin(3x)
Показать больше

Описание

Изучите функции шаг за шагом

functions-calculator

Блог-сообщения, имеющие отношение к Symbolab

Functions

A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Подборка онлайн калькуляторов для полного исследования функции и построение графика.
Найти Область определения функции
Вычислить Четность функции
Периодичность функции
Вычисление точек пересечения графика с осью (нули функции)
Промежутки знакопостоянства
Асимптоты функции
Найти экстремумы функции
Точки перегиба, интервалы выпуклости и вогнутости
Построить график функции

even – четная функция;
odd – нечетная функция;
neither even nor odd – функция общего вида;

Для нахождения интервалов на которых функция положительна используйте знак «>»
для интервалов на которых функция отрицательна используйте знак «<«.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»