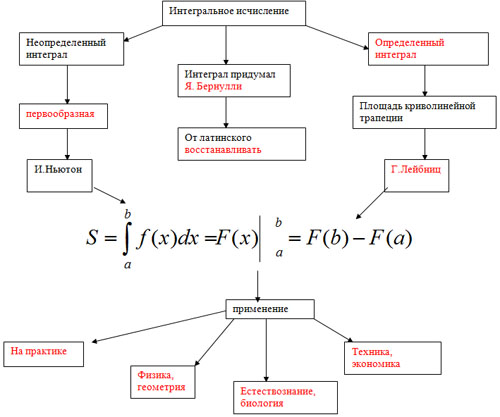
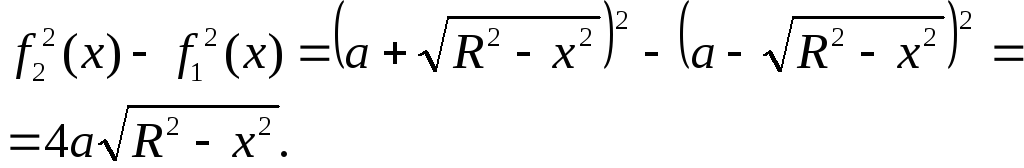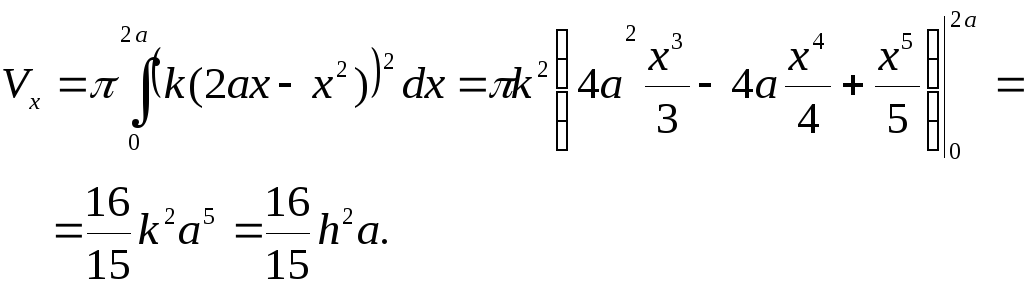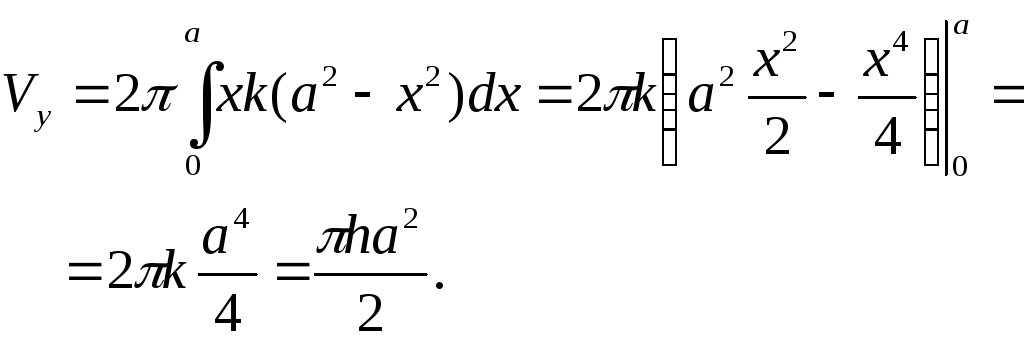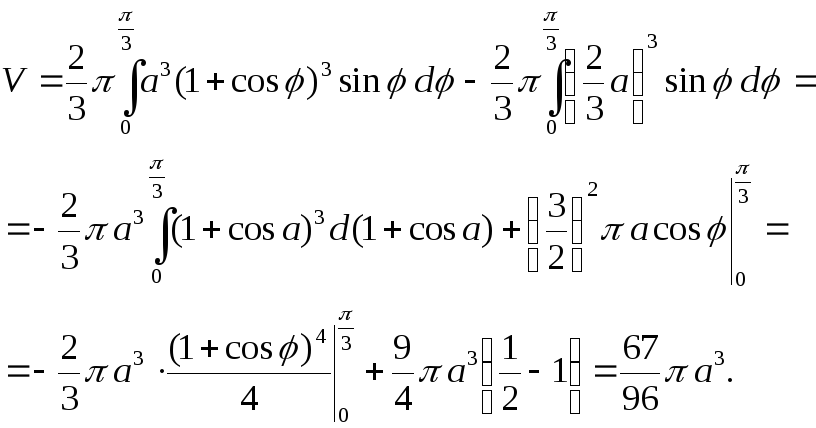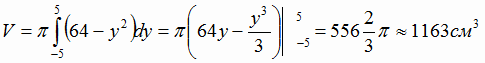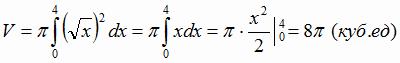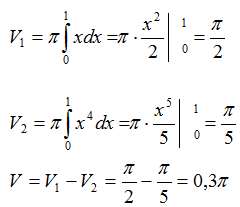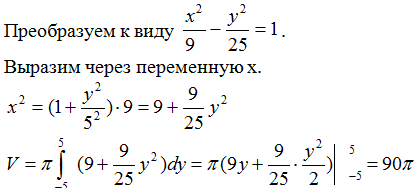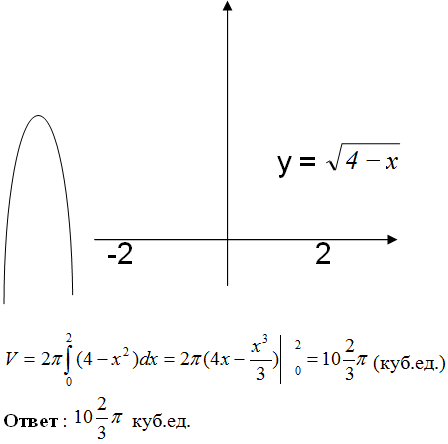Объемы тел вращения
Краткая теория
Объемы тел, образованных вращением
криволинейной трапеции, ограниченной кривой
, осью
и двумя
вертикалями
и
, вокруг осей
и
, выражаются соответственно формулами:
Объем тела, образованного вращением
около оси
фигуры,
ограниченной кривой
, осью
и двумя
параллелями
и
, можно определять по формуле:
Если кривая задана в иной форме
(параметрически, в полярных координатах и т.д.), то в приведенных формулах
нужно сделать соответствующую замену переменной интегрирования.
В более общем случае объемы тел,
образованных вращением фигуры, ограниченной кривыми
и
(причем
) и прямыми
,
, вокруг координатных осей
и
, соответственно равны:
Объем тела, полученного при вращении
сектора, ограниченного дугой кривой
и двумя
полярными радиусами
,
, вокруг полярной оси, может быть вычислен по формуле:
Этой же формулой удобно пользоваться
при отыскании объема тела, полученного вращением вокруг полярной оси фигуры,
ограниченной некоторой замкнутой кривой, заданной в полярных координатах.
Если
– площадь
сечения тела плоскостью, перпендикулярной к некоторой прямой (которую принимаем
за ось
), в точке с абсциссой
, то объем этого тела равен:
где
и
– абсциссы
крайних сечений тела.
Примеры решения задач
Задача 1
С помощью
определенного интеграла вычислить объем тела, полученного вращением фигуры
вокруг указанной оси координат.
вокруг
оси
Решение
Сделаем
чертеж:
Объем
тела, образованного вращением вокруг оси
фигуры можно найти по формуле:
В нашем
случае получаем
Ответ:
Задача 2
Найдите
объем тела, полученного вращением вокруг оси абсцисс криволинейной трапеции,
ограниченной линиями:
и
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Сделаем
чертеж:
Объем
тела можно найти по формуле:
Ответ:
Задача 3
Определить
объем, образованный вращением кривой
вокруг
полярной оси.
Решение
Ответ:
Задача 4
Вычислить
объем тела, ограниченного однополосным гиперболоидом
и
плоскостями
.
Решение
Здесь
удобнее рассмотреть сечения данного тела плоскостями, перпендикулярными к оси
. Тогда объем выразится
формулой:
где
– площадь получаемого сечения, зависящая от
точки с аппликатой
, через которую проходит
секущая плоскость. При пересечении однополосного гиперболоида плоскостью
получается эллипс, который можно определить
уравнениями:
откуда
следует, что полуоси эллипса:
Учитывая, что площадь эллипса с
полуосями
и
равна
, воспользовавшись параметрическим заданием эллипса:
мы можем записать аналитическое
выражение функции
:
Тогда искомый объем:
Ответ:
Объём тела вращения
Пусть — тело вращения, образованное вращением вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми
и
и графиком непрерывной функции
.
Докажем, что это тело вращения кубируемо и его объем выражается формулой
Сначала докажем, что это тело вращения регулярно, если в качестве выберем плоскость
, перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии
от плоскости
, является кругом радиуса
и его площадь
равна
(рис. 46). Поэтому функция
непрерывна в силу непрерывности
. Далее, если
, то это значит, что
. Но проекциями сечений на плоскость
являются круги радиусов
и
с центром
, и из
вытекает, что круг радиуса
содержится в круге радиуса
.
Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объем вычисляется по формуле
Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми
, то
Формулой (3) можно воспользоваться и для вычисления объема тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определенного интеграла.
В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.
Например, найдем объем тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой y#, в основании которого лежит отрезок . Этот объем равен разности объемов двух прямых круговых цилиндров
Но теперь ясно, что искомый объем оценивается сверху и снизу следующим образом:
Отсюда легко следует формула объёма тела вращения вокруг оси ординат:
(4)
Пример 4. Найдем объем шара радиуса .
Решение. Не теряя общности, будем рассматривать круг радиуса с центром в начале координат. Этот круг, вращаясь вокруг оси
, образует шар. Уравнение окружности имеет вид
, поэтому
. Учитывая симметрию круга относительно оси ординат, найдем сначала половину искомого объема
Следовательно, объем всего шара равен .
Пример 5. Вычислить объем конуса, высота которого и радиус основания
.
Решение. Выберем систему координат так, чтобы ось совпала с высотой h (рис. 47), а вершину конуса примем за начало координат. Тогда уравнение прямой
запишется в виде
.
Пользуясь формулой (3), получим:
Пример 6. Найдем объем тела, полученного при вращении вокруг оси абсцисс астроиды (рис. 48).
Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определенного интеграла, найдем для новой переменной пределы интегрирования.
Если , то
, а если
, то
. Учитывая, что
и
, получаем:
Объем всего тела, образованного вращением астроиды, будет .
Пример 7. Найдем объем тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды .
Решение. Воспользуемся формулой (4): , и заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной
от
до
. Таким образом,
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
Ось вращения может
и пересекать фигуру, если это ось
симметрии фигуры.
Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
вращается вокруг оси
.
Тогда объём получающегося тела вращения
можно вычислить по формуле
(2)
Доказательство.
Для такого тела сечение с абсциссой
– это круг радиуса
,
значити формула (1) даёт требуемый результат.
Если фигура
ограничена графиками двух непрерывных
функций
и
,
и отрезками прямыхи
,
причёми
,
то при вращении вокруг оси абсцисс
получим тело, объём которого
Пример
3. Вычислить
объём тора, полученного вращением круга,
ограниченного окружностью вокруг оси абсцисс.
Р
Указанный круг снизу ограничен графиком
функции
,
а сверху –.
Разность квадратов этих функций:
Искомый объём
(графиком
подынтегральной функции является
верхняя полуокружность, поэтому
написанный выше интеграл – это площадь
полукруга).
Пример 4.
Параболический сегмент с основанием
,
и высотой,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
Р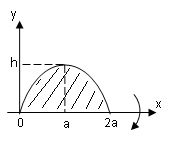
Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем.
Найдём значение параметра:
.
Итак, искомый объём:
Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
,
причём,
вращается вокруг оси.
Тогда объём получающегося тела вращения
может быть найден по формуле
(3)

доказательства.
Разбиваем отрезок
точками
,
на части и проводим прямые.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основаниеми высотой
.
Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами:
,
и
.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
Для получения
точного равенства надо перейти к пределу
при .
Написанная выше сумма есть интегральная
сумма для функции ,
следовательно, в пределе получим интеграл
из формулы (3). Теорема доказана.
Замечание
1. В теоремах
2 и 3 условие
можно опустить: формула (2) вообще
нечувствительна к знаку,
а в формуле (3) достаточнозаменить на
.
Пример
5.
Параболический сегмент (основание
,
высота)
вращается вокруг высоты. Найти объём
получающегося тела.
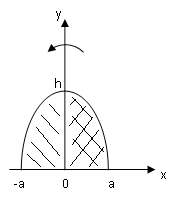
Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем,
значит.
Имеем для объёма:
Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями
,
,
и
,
то можно использовать формулы (2) и (3) с
заменойна
и
на
при измененииt
от
до
.
Пример
6. Фигура
ограничена первой аркой циклоиды
,
,
,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси;
2) оси.
Решение.
1) Общая формула
В нашем случае:
2) Общая формула
Для нашей фигуры:
Предлагаем
студентам самостоятельно провести все
вычисления.
Замечание
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами
,
,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
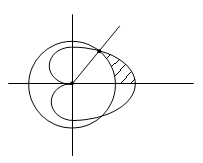
Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой
.
Кривые пересекаются прии
при
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
Задачи
для самостоятельного решения.
1. Круговой сегмент,
основание которого ,
высота
,
вращается вокруг основания. Найти объём
тела вращения.
2. Найти объём
параболоида вращения, основание которого
,
а высота равна.
3. Фигура, ограниченная
астроидой
,
вращает-ся вокруг оси абсцисс. Найти
объём тела, которое получается при этом.
4. Фигура, ограниченная
линиями
и
вращается вокруг оси абсцисс. Найти
объём тела вращения.
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
Тип урока: комбинированный.
Цель урока: научиться вычислять объемы тел вращения с помощью
интегралов.
Задачи:
- закрепить умение выделять криволинейные трапеции из ряда геометрических
фигур и отработать навык вычислений площадей криволинейных трапеций; - познакомиться с понятием объемной фигуры;
- научиться вычислять объемы тел вращения;
- способствовать развитию логического мышления, грамотной математической
речи, аккуратности при построении чертежей; - воспитывать интерес к предмету, к оперированию математическими понятиями
и образами, воспитать волю, самостоятельность, настойчивость при достижении
конечного результата.
Ход урока
I. Организационный момент.
Приветствие группы. Сообщение учащимся целей урока.
Рефлексия.
Спокойная мелодия.
– Сегодняшний урок мне бы хотелось начать с притчи. “Жил мудрец, который знал
все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях
бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или
живая?” А сам думает: “Скажет живая – я ее умертвлю, скажет мертвая – выпущу”.
Мудрец, подумав, ответил: “Все в твоих руках”. (Презентация.
Слайд)
– Поэтому давайте сегодня плодотворно поработаем, приобретем новый багаж
знаний, и полученные умения и навыки будем применять в дальнейшей жизни и в
практической деятельности. “Все в Ваших руках”.
II. Повторение ранее изученного материала.
– Давайте вспомним основные моменты ранее изученного материала. Для этого
выполним задание “Исключите лишнее слово”. (Слайд.)
(Учащийся выходит к И.Д.с помощью ластика убирает лишнее слово.)
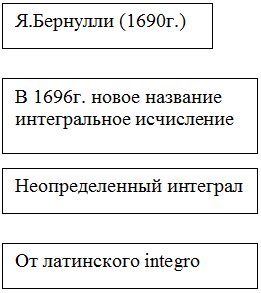
– Правильно “Дифференциал”. Попробуйте
оставшиеся слова назвать одним общим словом. (Интегральное исчисление.)
– Давайте вспомним основные этапы и понятия связанные с интегральным
исчислением..
“Математическая гроздь”.
Задание. Восстановите пропуски. (Студент выходит и вписывает ручкой
необходимые слова.)
– Реферат о применении интегралов мы заслушаем позже.
Работа в тетрадях.
– Формулу Ньютона-Лейбница вывели английский физик Исаака Ньютона (1643–1727)
и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь
математика – язык, на котором говорит сама природа.
– Рассмотрим, как при решении практических заданий используется эта формула.
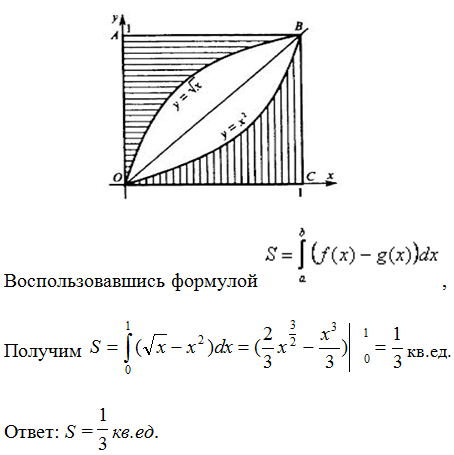
Пример 1: Вычислить площадь фигуры, ограниченной линиями
Решение: Построим на координатной плоскости графики функций
.
Выделим площадь фигуры, которую надо найти.
III. Изучение нового материала.
– Обратите внимание на экран. Что изображено на первом рисунке? (Слайд)
(На рисунке представлена плоская фигура.)
– Что изображено на втором рисунке? Является ли эта фигура плоской?
(Слайд) (На рисунке представлена объемная фигура.)
– В космосе, на земле и в повседневной жизни мы встречаемся не только с
плоскими фигурами, но и объемными, а как же вычислить объем таких тел? Например
объем планеты, каметы, метеорита, и т.д.
– Об объеме задумываются и строя дома, и переливая воду из одного сосуда в
другой. Правила и приёмы вычисления объёмов должны были возникать, другое дело,
насколько они были точны и обоснованны.
Сообщение студентки. (Тюрина Вера.)
1612 год был для жителей австрийского города Линц, где жил тогда известный
астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли
винные бочки и хотели знать, как практически определить их объёмы. (Слайд 2)
– Таким образом, рассмотренные работы Кеплера положили начало целому потоку
исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И.
Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика
переменных величии заняла с этого времени ведущее место в системе математических
знаний.
– Вот сегодня мы с вами и займемся такой практической деятельностью,
следовательно,
Тема нашего урока: “Вычисление объемов тел вращения с помощью определенного
интеграла”. (Слайд)
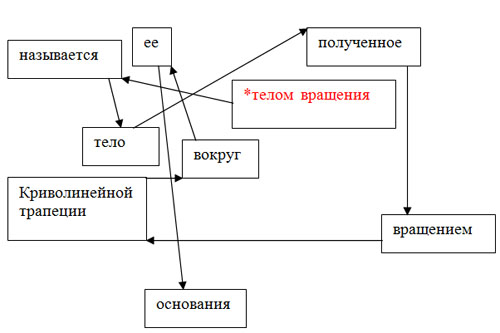
– Определение тела вращения вы узнаете, выполнив следующее задание.
“Лабиринт”.
Лабиринт (греческое слово) означает ход в подземелье. Лабиринт– запутанная
сеть дорожек, ходов, сообщающихся друг с другом помещений.
Но определение “разбилось”, остались подсказки в виде стрелок.
Задание. Найдите выход из запутанного положения и запишите определение.
Слайд. “Карта инструктаж” Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела,
в частности, тела вращения.
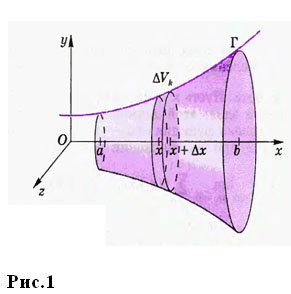
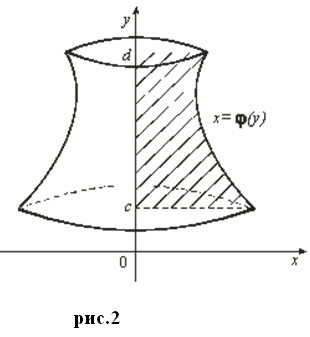
Телом вращения называется тело, полученное вращением криволинейной трапеции
вокруг ее основания (рис. 1, 2)
Объем тела вращения вычисляется по одной из формул:
1.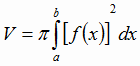
если вращение криволинейной трапеции вокруг оси ОХ.
2. 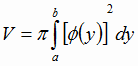
если вращение криволинейной трапеции вокруг оси ОУ.
Карту инструктаж получает каждый студент. Преподаватель подчеркивает основные
моменты.
– Преподаватель объясняет решение примеров на доске.
Пример.
Рассмотрим отрывок из известной сказки А. С. Пушкина “Сказка о царе Салтане,
о сыне его славном и могучем богатыре князе Гвидоне Салтановиче и о прекрасной
царевне Лебеде” (Слайд 4):
…..
И привез гонец хмельной
В тот же день приказ такой:
“Царь велит своим боярам,
Времени не тратя даром,
И царицу и приплод
Тайно бросить в бездну вод”.
Делать нечего: бояре,
Потужив о государе
И царице молодой,
В спальню к ней пришли толпой.
Объявили царску волю –
Ей и сыну злую долю,
Прочитали вслух указ,
И царицу в тот же час
В бочку с сыном посадили,
Засмолили, покатили
И пустили в окиян –
Так велел-де царь Салтан.
(Слайд 5):
Какими же должен быть объем бочки, чтобы в ней поместились царица и её сын?
– Рассмотрим следующие задания
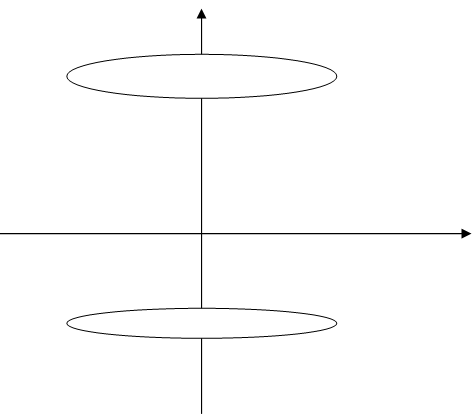
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной
трапеции, ограниченной линиями: x2 + y2
= 64, y = -5, y = 5, x = 0.
Решение.
Ответ : 1163 cm3.
Найти объем тела, получаемого вращением параболической трапеции, вокруг оси
абсцисс y =
, x = 4, y = 0.
Решение .
IV. Закрепление нового материала
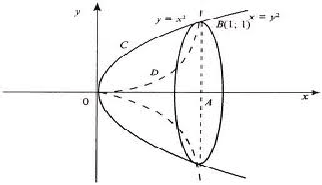
Пример 2. Вычислить объем тела, образованного вращением лепестка, вокруг оси
абсцисс y = x2, y2
= x.
Решение .
Построим графики функции. y = x2, y2
= x. График y2 = x
преобразуем к виду y =
.
Имеем V = V1 – V2
Вычислим объем каждой функции
– Теперь, давайте, рассмотрим башню для
радиостанции в Москве на Шаболовке, построенной по проекту замечательного
русского инженера, почётного академика В. Г. Шухова. Она состоит из частей –
гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных
металлических стержней, соединяющих соседние окружности (рис.8, 9).
– Рассмотрим задачу.
Найти объем тела, получаемого вращением дуг гиперболы
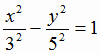
ее мнимой оси, как показано на рис. 8, где
Решение.
куб. ед.
Задания по группам. Учащиеся вытягивают жребий с задачами, рисунки
выполняют на ватмане, один из представителей группы защищает работу.
1-я группа.
Удар! Удар! Ещё удар!
Летит в ворота мячик – ШАР!
А это– шар арбузный
Зелёный, круглый, вкусный.
Вглядитесь лучше – шар каков!
Он сделан из одних кругов.
Разрежьте на круги арбуз
И их попробуйте на вкус.
Найти объем тела, получаемого вращением вокруг оси ОХ функции, ограниченную
Решение.
Ошибка! Закладка не определена.
– Скажите, пожалуйста, где мы встречаемся с данной фигурой?
Дом. задание для 1 группы. ЦИЛИНДР (слайд) .
«Цилиндр – что такое?» – спросил я у папы.
Отец рассмеялся: Цилиндр – это шляпа.
Чтобы иметь представление верное,
Цилиндр, скажем так, это банка консервная.
Труба парохода – цилиндр,
Труба на нашей крыше – тоже,
Все трубы на цилиндр похожи.
А я привёл пример такой –
Калейдоскоп любимый мой,
Глаз от него не оторвёшь,
И тоже на цилиндр похож.
– Задание. Домашняя работа составить график функции и вычислить объем .
2-я группа. КОНУС
(слайд).
Сказала мама: А сейчас
Про конус будет мой рассказ.
В высокой шапке звездочёт
Считает звёзды круглый год.
КОНУС – шляпа звездочёта.
Вот какой он. Понял? То-то.
Мама у стола стояла,
В бутылки масло разливала.
– Где воронка? Нет воронки.
Поищи. Не стой в сторонке.
– Мама, с места я не тронусь,
Расскажи ещё про конус.
– Воронка и есть в виде конуса лейка.
Ну-ка, найди мне её поскорей-ка.
Воронку я найти не смог,
Но мама сделала кулёк,
Картон вкруг пальца обкрутила
И ловко скрепкой закрепила.
Масло льётся, мама рада,
Конус вышел то, что надо.
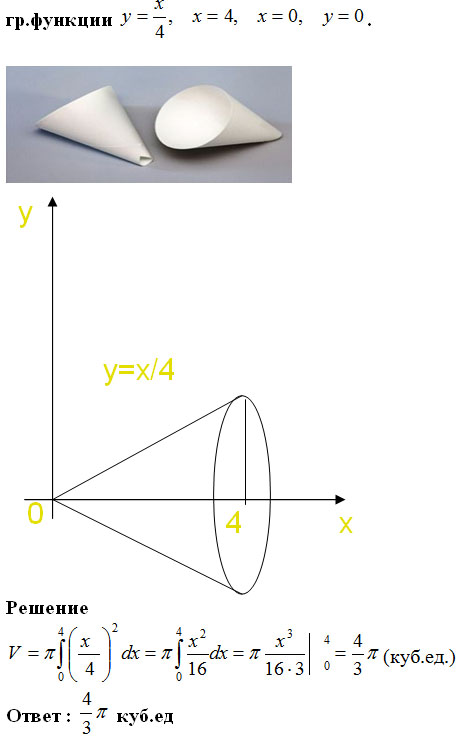
Задание . Вычислить объем тела полученный вращением вокруг оси абсцисс
Дом. задание для 2-й группы. ПИРАМИДА (слайд).
Я видел картину. На этой картине
Стоит ПИРАМИДА в песчаной пустыне.
Всё в пирамиде необычайно,
Какая-то есть в ней загадка и тайна.
А Спасская башня на площади Красной
И детям, и взрослым знакома прекрасно.
Посмотришь на башню – обычная с виду,
А что на вершине у ней? Пирамида!
Задание. Домашняя работа составить график функции и вычислить объем
пирамиды
Вывод.
– Объёмы различных тел мы вычисляли опираясь на основную формулу объёмов тел
с помощью интеграла.
Это является ещё одним подтверждением того, что определённый интеграл есть
некоторый фундамент для изучения математики.
– Ну а теперь давайте немного отдохнем.
Найди пару.
|
|
 |
Математическое домино мелодия играет.
“Дорога та, что сам искал, вовек не позабудется…”
Исследовательская работа. Применение интеграла в экономике и технике.
Тесты для сильных учащихся и математический футбол.
Математический тренажер.
2. Совокупность всех первообразных от данной функции называется
А) неопределенным интегралом,
Б) функцией,
В) дифференциацией.
7. Найти объем тела, получаемого вращением вокруг оси абсцисс криволинейной
трапеции, ограниченной линиями:
Д/З. Вычислить объемы тел вращения.
Рефлексия.
Приём рефлексии в форме синквейна (пятистишия).
1-я строка – название темы (одно существительное).
2-я строка – описание темы в двух словах, два прилагательных.
3-я строка – описание действия в рамках этой темы тремя словами.
4-я строка – фраза их четырёх слов, показывает отношение к теме (целое
предложение).
5-я строка – синоним, который повторяет суть темы.
- Объем.
- Определенный интеграл, интегрируемая функция.
- Строим, вращаем, вычисляем.
- Тело, полученное вращением криволинейной трапеции (вокруг ее основания).
- Тело вращения (объемное геометрическое тело).
Вывод (слайд).
- Определенный интеграл – это некоторый фундамент для изучения математики,
которая вносит незаменимый вклад в решение задач практического содержания. - Тема “Интеграл” ярко демонстрирует связь математики с физикой,
биологией, экономикой и техникой. - Развитие современной науки немыслимо без использования интеграла. В
связи с этим, начинать его изучение необходимо в рамках средне специального
образования!
Выставление оценок . (С комментированием.)
Великий Омар Хайям – математик, поэт, философ. Он призывает быть хозяевами
своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь – одно мгновенье.
Её цени, в ней черпай вдохновенье.
Как проведёшь её, так и пройдёт.
Не забывай: она – твоё творенье.
Приложение 2.
Дополнения
1.О применении определённого интеграла для нахождения объёмов тел вращения
1.1.Формула объёма тела вращения
В п.16.2 дано определение тела вращения.
Получим формулу для вычисления объёма тела вращения, применяя интеграл, о котором вам рассказали в курсе «Алгебры и начал математического анализа».
Пусть f(x) — непрерывная на отрезке [a; b] функция, не принимающая отрицательных значений; А, В — точки графика этой функции (рис. 225).
Рис. 225
Рассмотрим криволинейную трапецию aABb, ограниченную кривой графика функции y = f(x), отрезками aA, bB и отрезком [a; b] координатной оси Ох (см. рис. 225). При вращении этой трапеции вокруг оси Ох образуется тело вращения (рис. 226), которое обозначим Ф и поставим себе задачу: найти объём этого тела.
Рис. 226
Через произвольную точку х = с (a ⩽ с ⩽ b) отрезка [a; b] проведём плоскость, перпендикулярную оси Ox. Сечением тела Ф этой плоскостью является круг, радиус которого равен f(с), а площадь — πf2(с) (или точка (c; 0)).
Объём части тела Ф, заключённой между этой плоскостью и плоскостью х = a, изменяется при изменении x. Обозначим этот переменный объём V(х). Заметим, что V(x) = V(a) = 0 при х = a; при х = b имеем V(x) = V(b) = V — искомый объём тела вращения Ф.
Покажем, что функция V(x) имеет производную V′(х) и V′(х) = πf2(х).
Придадим абсциссе х приращение ∆х > 0, тогда объём V(х) получает приращение ∆V(х) = V(x + ∆x) – V(x). Пусть m и М — соответственно наименьшее и наибольшее значения функции f(х) на промежутке [х; х + ∆х]. Цилиндр, радиус основания которого равен m, содержится в теле вращения объёма ∆V(x), а цилиндр, радиус основания которого равен M, содержит тело объёма ∆V(х); образующие цилиндров параллельны оси Ох и имеют длину, равную ∆х. Объёмы этих цилиндров равны соответственно πm2•∆x и πM2•∆х. На основании свойства 2 объёмов (п. 10.1) получаем
πm2•∆x ⩽ ∆V(x) ⩽ πM2•∆x,
откуда
πm2 ⩽ 
Рассуждения для случая ∆х < 0 проводятся аналогично и дают тот же результат.
Пусть теперь ∆х 





или
πf2(х) ⩽ 
Значит, 

Таким образом, переменный объём V(x) телa вращения представляет собой одну из первообразных для функции πf 2(х) на отрезке [a; b]. Эта первообразная обладает тем свойством, что при х = a она обращается в нуль (V(a) = 0), а при х = b значение функции V(x) равно объёму тела вращения Ф (V(b) = V).
Если F(х) — также некоторая первообразная для функции πf 2(x), то V(x) = F(x) + С, где С — произвольная постоянная. Так как V (a) = 0, то из равенства V(a) = F (a) + C = 0 находим С = –F(a). Значит, V(x) = F(x) – F(a). Toгдa V(b) = F(b) – F(a). Ho V(b) = V — искомый объём тела вращения Ф. Таким образом, V = F(b) – F(a), где F(b) и F(a) — значения первообразной для функции πf 2(х) соответственно при х = b и х = a. Это означает, что
V = 

Вот почему объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = f(x), х = a, х = b, у = 0, вычисляется по формуле
Рис. 227
V = 
ЗАДАЧА. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = 
Решение. Воспользуемся формулой V = π

V = π


Ответ: 4π.
1.2. Объёмы конуса, шара и его частей
Используя формулу V = 
а) Объём конуса и усечённого конуса
Теорема 1 (об объёме полного конуса). Объём V конуса с высотой Н и радиусом основания R равен одной трети произведения площади основания на высоту:
V = 
Рис. 228
Доказательство. Конус с высотой Н и радиусом основания R можно рассматривать как тело, образованное вращением вокруг оси Ox прямоугольного треугольника с вершинами О(0; 0), А(Н; 0) и B(Н; R) (рис. 228). Треугольник АОВ является частным случаем криволинейной трапеции, которая ограничена графиком функции у = 
V = 



где πR2 — площадь основания конуса. Теорема доказана. ▼
Теорема 2 (об объёме усечённого конуса). Объём усечённого конуса с высотой Н и радиусами оснований r и R равен сумме объёмов трёх конусов с высотой Н, радиусы оснований которых соответственно равны r, R и 
V = 
Доказательство. Усечённый конус с высотой H и радиусами оснований r и R можно получить, вращая вокруг оси Oх прямоугольную трапецию OABC, где O(0; 0), A(0; r), В(Н; R), С(H; 0) (рис. 229).

Прямая AВ проходит через точки (0; r) и (Н; R), поэтому её уравнение имеет вид у = 

V = 
Для вычисления интеграла сделаем замену переменных

Тогда 

что и требовалось доказать. ▼
б) Объём шарового слоя
В прямоугольной декартовой системе координат Оху рассмотрим криволинейную трапецию aABb, ограниченную дугой окружности х2 + у2 = R2, –R ⩽ a ⩽ х ⩽ b ⩽ R, отрезком [a; b] оси Ох и отрезками aА и bВ прямых соответственно x = a и х = b (рис. 230, а).

При вращении криволинейной трапеции aАВb вокруг оси Ох образуется шаровой слой (рис. 230, б). Найдём его объём, применяя формулу (*) п. 1.1.
Из уравнения х2 + у2 = R2 имеем у2 = R2 – x2. Поэтому для вычисления объёма V шарового слоя получаем:
Таким образом, объём шарового слоя, отсекаемого от шара x2 + y2 + z2 ⩽ R2 радиуса R плоскостями x = a и x = b, вычисляется пo формуле
V = 
Пусть радиусы оснований шарового слоя равны r1 и r2 (r1 > r2), а высота — H (см. рис. 230, a).
Тогда Н = b – a, 

Формулу (**) преобразуем к виду:
V = 
= 
Из системы равенств (b – a)2 = H2, R2 – a2 = 

R2 – ab = 
Тогда:
V = 
= 
Таким образом, объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле
V = 
в) Объём шара
Рис. 231
При вращении полукруга х2 + у2 = R2 (расположенного в плоскости Оху, рис. 231, а) вокруг оси Ох образуется шар радиуса R (рис. 231, б). Из уравнения окружности х2 + y2 = R2 данного полукруга имеем у2 = R2 – х2. Тогда, полагая a = –R, b = R в формуле (*) п. 1.1, находим объём V шара радиуса R:
Vш = 
= 
Таким образом, имеет место следующая теорема.
Теорема 3 (об объёме шара). Объём шара радиуса R вычисляется по формуле
Vш = 
г) Объём шарового сегмента
Если b = R (см. п. 1.2, б), то получаем криволинейную трапецию aAB (рис. 232, а), при вращении которой вокруг оси Ох образуется шаровой сегмент (рис. 232, б).
Рис. 232
Пусть высота шарового сегмента равна Н, тогда a = R – Н. Так как дуга AВ криволинейной трапеции aАВ является частью окружности x2 + y2 = R2 (в плоскости Оxу), то формулу объёма шарового сегмента получим по аналогии с выводом формулы для вычисления объёма шара, учитывая при этом, что пределы a и b интегрирования равны: a = R – H, b = R, т. е.
Vш. сегм = 
=
Таким образом, имеет место следующая теорема.
Теорема 4 (об объёме шарового сегмента). Объём шарового сегмента, отсекаемого от шара радиуса R и имеющего высоту Н, вычисляется по формуле
Vш. сегм =
Если в формуле (***) п. 1.2, б положить r2 = 0, r1 = r, то получим формулу для вычисления объёма шарового сегмента с радиусом основания r и высотой Н:
Vш. сегм = 
д) Объём шарового сектора
Рис. 233
Шаровой сектор состоит из конуса с вершиной в центре шара и шарового сегмента, имеющего с конусом общее основание (риc. 233). Пусть R = ОА — радиус шара; АС = r — радиус основания шарового сегмента, NC = H — его высота; N — точка сферы (рис. 233).
Найдём объёмы конуса и шарового сегмента, учитывая, что высота h конуса равна OC = ON – CN = R – Н.
Объём Vк конуса равен


Выразим r2 через R и H.
B прямоугольном треугольнике AOC находим r2 = AC2 = ОА2 – OC2 = R2 – (R – H)2 = H(2R – H).
Значит,
Vк = 

Для объёма шарового сегмента имеем:
Vш. сегм = 

= 
Тогда для объёма шарового сектора получаем
Vш. сект = Vк + Vш. сегм =
= 


Таким образом, доказана следующая теорема.
Теорема 5 (об объёме шарового сектора). Объём шарового сектора шара радиуса R вычисляется по формуле
Vш. сект = 
где Н — длина высоты шарового сегмента, соответствующего данному шаровому сектору.
В курсе математического анализа, который вам предстоит изучать в высшей школе, будет дано строгое обоснование применения определённого интеграла не только для нахождения объёмов тел, но и для нахождения площадей поверхностей и длин дуг линий. Решите самостоятельно следующие задачи.
1)Найдите объём тела, которое получается при вращении вокруг оси Ох криволинейной трапеции, ограниченной гиперболой у = 
2)Найдите объём тела, образованного вращением вокруг оси Oх фигуры, ограниченной одной полуволной синусоиды у = sin x и отрезком 0 ⩽ х ⩽ π оси абсцисс. (Ответ: 0,5π2.)
3)Найдите объём тела, полученного при вращении кривой у = 0,25х2 вокруг оси Оу в пределах от у = 1 до у = 5. (Ответ: 48π.)
4)Найдите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2х2 и у = x3.