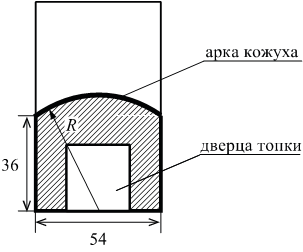
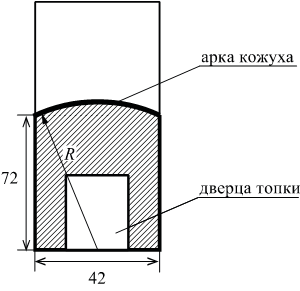
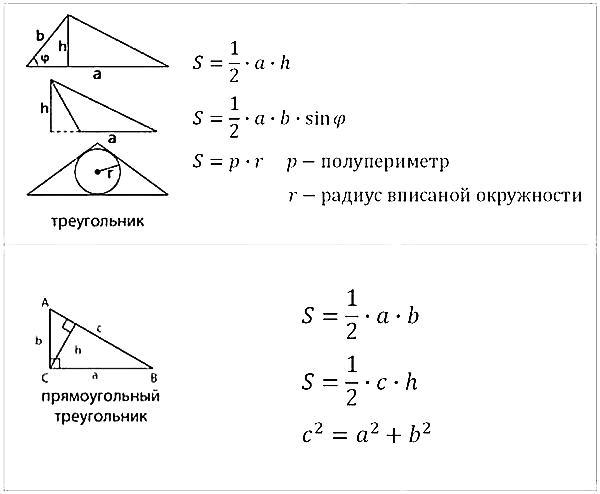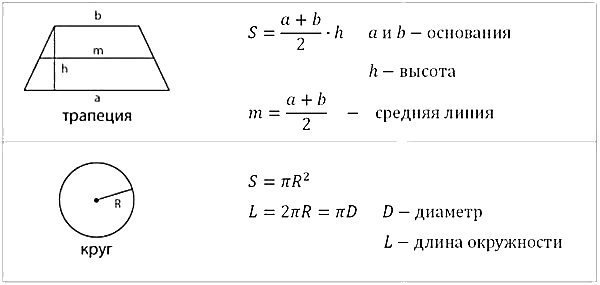1. Расчет объема куба
a
— сторона куба
Формула объема куба, (V
):
2. Найти по формуле, объем прямоугольного параллелепипеда
a , b , c
— стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V
):
3. Формула для вычисления объема шара, сферы
R
—
радиус шара
По формуле, если дан радиус, можно найти объема шара, (V
):
4. Как вычислить объем цилиндра?
h
— высота цилиндра
r
— радиус основания
По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V
):
5. Как найти объем конуса?
R —
радиус основания
H —
высота конуса
Формула объема конуса, если известны радиус и высота (V
):
7. Формула объема усеченного конуса
r —
радиус верхнего основания
R —
радиус нижнего основания
h —
высота конуса
Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V
):
8. Объем правильного тетраэдра
Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.
а
— ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V
):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a
— сторона основания
h
— высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V
):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a
— сторона основания
h
— высота пирамиды
Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V
):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h
— высота пирамиды
a
— сторона основания пирамиды
n
— количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V
):
Все формулы объемов геометрических тел
Геометрия, Алгебра, Физика
Объём геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Формула объема куба
1) Объем куба равен кубу его ребра.
V
— объем куба
H
— высота ребра куба
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V
— объем пирамиды
S
— площадь основания пирамиды
h
— высота пирамиды
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V
— объем конуса
S
— площадь основания конуса
h
— высота конуса
π
— число пи (3.1415)
r
— радиус конуса
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V
— объем цилиндра
S
— площадь основания цилиндра
h
— высота цилиндра
π
— число пи (3.1415)
r
— радиус цилиндра
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V
— объем шара
π
— число пи (3.1415)
R
— радиус шара
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.
Формулы объема
Формулы объема и онлайн программы для вычисления объема
Формула объема
необходима для вычисления параметров и характеристик геометрической фигуры.
Объем фигуры
— это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Параллелепипед
.
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
Цилиндр
.
Объем цилиндра равен произведению площади основания на высоту.
Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
Пирамида
.
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
Правильная пирамида
— это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.
Правильная треугольная пирамида
— это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Правильная четырехугольная пирамида
— это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Тетраэдр
— это пирамида, у которой все грани — равносторонние треугольники.
Усеченная пирамида
.
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S 1 (abcde), нижнего основания усеченной пирамиды S 2 (ABCDE) и средней пропорциональной между ними.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 .
Конус
— это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Усеченный конус
получится, если в конусе провести сечение, параллельное основанию.
V = 1/3 πh (R 2 + Rr + r 2)
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Призма
.
Объем призмы равен произведению площади основания призмы, на высоту.
Сектор шара
.
Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.
Шаровой слой
— это часть шара, заключенная между двумя секущими параллельными плоскостями.
Сегмент шара
— это часть шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом
Формула объема
Формула объема куба, шара, пирамиды, параллелограмма, цилиндра, тетраэдра, конуса, призмы и объемы других геометрических фигур.
В курсе стереометрии один из главных вопросов — как рассчитать объем того или иного геометрического тела. Все начинается с простого параллелепипеда и заканчивается шаром.
В жизни тоже часто приходится сталкиваться с подобными задачами. Например, чтобы рассчитать объем воды, которая помещается в ведро или бочку.
Свойства, справедливые для объема каждого тела
- Это значение — всегда положительное число.
- Если тело удается разделить на части так, чтобы не было пересечений, то общий объем оказывается равным сумме объемов частей.
- У равных тел одинаковые объемы.
- Если меньшее тело полностью помещается в большем, то объем первого меньше, чем второго.
Общие обозначения для всех тел
В каждом из них есть ребра и основания, в них строятся высоты. Поэтому такие элементы для них одинаково обозначены. Именно так они записаны в формулах. Как рассчитать объем каждого из тел — узнаем дальше и применим на практике новые умения.
В некоторых формулах имеются другие величины. Об их обозначении будет сказано при появлении такой необходимости.
Призма, параллелепипед (прямой и наклонный) и куб
Эти тела объединены, потому что внешне очень похожи, и формулы того, как рассчитать объем, идентичны:
V = S * h.
Различаться будет только S . В случае с параллелепипедом она рассчитывается, как для прямоугольника или квадрата. В призме основанием может оказаться треугольник, параллелограмм, произвольный четырехугольник или другой многоугольник.
Для куба формула существенно упрощается, потому что все его измерения равны:
V = а 3 .
Пирамида, тетраэдр, усеченная пирамида
Для первого из указанных тел существует такая формула, чтобы вычислить объем:
V = 1/3 * S * н.
Тетраэдр является частным случаем треугольной пирамиды. В нем все ребра равны. Поэтому снова получается упрощенная формула:
V = (а 3 * √2) / 12, или V = 1/ 3 S h
Усеченной пирамида становится тогда, когда у нее срезана верхняя часть. Поэтому ее объем равен разности двух пирамид: той, которая была бы целой, и удаленной верхушки. Если есть возможность узнать оба основания такой пирамиды (S 1 — большее и S 2 — меньшее), то удобно пользоваться такой формулой для расчета объема:
Цилиндр, конус и усеченный конус
V =π * r 2 * h.
Несколько сложнее обстоит дело с конусом. Для него существует формула:
V = 1/3 π * r 2 * h.
Она очень похожа на ту, что указана для цилиндра, только значение уменьшено в три раза.
Так же, как с усеченной пирамидой, дело обстоит непросто с конусом, который имеет два основания. Формула для вычисления объема усеченного конуса выглядит так:
V = 1/3 π * h * (r 1 2 + r 1 r 2 + r 2 2).
Здесь r 1 — радиус нижнего основания, r 2 — верхнего (меньшего).
Шар, шаровые сегменты и сектор
Это самые сложные для запоминания формулы. Для объема шара она выглядит так:
V = 4/3 π *r 3 .
В задачах часто есть вопрос о том, как рассчитать объем шарового сегмента — части сферы, которая как бы срезана параллельно диаметру. В этом случае на выручку придет такая формула:
V = π h 2 * (r — h/3).
В ней за h взята высота сегмента, то есть та часть, которая идет по радиусу шара.
Сектор делится на две части: конус и шаровой сегмент. Поэтому его объем определяется как сумма этих тел. Формула после преобразований выглядит так:
V = 2/3 πr 2 * h.
Здесь h также высота сегмента.
Примеры задач
Про объемы цилиндра, шара и конуса
Условие:
диаметр цилиндра (1 тело) равен его высоте, диаметру шара (2 тело) и высоте конуса (3 тело), проверить пропорциональность объемов V 1: V 2: V 3 = 3:2:1
Решение.
Сначала потребуется записать три формулы для объемов. Потом учесть, что радиус — это половина диаметра. То есть высота будет равна двум радиусам: h = 2r. Произведя простую замену получается, что формулы для объемов будут иметь такой вид:
V 1 = 2 π r 3 , V 3 = 2/3 π r 3 . Формула для объема шара не изменяется, потому что в ней не фигурирует высота.
Теперь осталось записать отношения объемов и произвести сокращение 2π и r 3 . Получается, что V 1: V 2: V 3 = 1: 2/3: 1/3. Эти числа легко привести к записи 3: 2: 1.
Про объем шара
Условие:
имеется два арбуза радиусами 15 и 20 см, как их выгоднее съесть: первый вчетвером или второй ввосьмером?
Решение.
Чтобы ответить на этот вопрос, потребуется найти отношение объемов частей, которые достанутся от каждого арбуза. Принимая во внимание, что они — шары, нужно записать две формулы для объемов. Потом учесть, что от первого каждому достанется только четвертая часть, а от второго — восьмая.
Осталось записать отношение объемов частей. Оно будет выглядеть так:
(V 1: 4) / (V 2: = (1/3 π r 1 3) / (1/6 π r 2 3). После преобразования остается только дробь: (2 r 1 3) / r 2 3 . После подстановки значений и вычисления получается дробь 6750/8000. Из нее ясно, что часть от первого арбуза будет меньше, чем от второго.
Ответ.
Выгоднее съесть восьмую часть от арбуза с радиусом 20 см.
Про объемы пирамиды и куба
Условие:
имеется пирамида из глины с прямоугольным основанием 8Х9 см и высотой 9 см, из этого же куска глины сделали куб, чему равно его ребро?
Решение.
Если обозначить стороны прямоугольника буквами в и с, то площадь основания пирамиды вычисляется, как их произведение. Тогда формула для ее объема:
Формула для объема куба написана в статье выше. Эти два значения равны: V 1 = V 2 . Осталось приравнять правые части формул и сделать необходимые вычисления. Получается, что ребро куба будет равно 6 см.
Про объем параллелепипеда
Условие:
требуется сделать ящик вместимостью 0,96 м 3 , известны его ширина и длина — 1,2 и 0,8 метра, какой должна быть его высота?
Решение.
Поскольку основание параллелепипеда — прямоугольник, его площадь определяется как произведение длины (а) на ширину (в). Поэтому формула для объема выглядит так:
Из нее легко определить высоту, разделив объем на площадь. Получится, что высота должна быть равна 1 м.
Ответ.
Высота ящика равна одному метру.
Как рассчитать объем различных геометрических тел?
В курсе стереометрии одна из главных задач — как рассчитать объем того или иного геометрического тела. Все начинается с простого параллелепипеда и заканчивается шаром.
Для устройства фундамента, возведения стен и заливки пола применяются бетонные растворы. До начала мероприятий важно выбрать конструкцию фундаментного основания, правильно рассчитать общий уровень затрат и определить необходимое количество строительных материалов. Зная, как рассчитать объем бетона, можно определить сметную стоимость строительных мероприятий, точно спланировать продолжительность выполнения бетонных работ и избежать непредвиденных затрат. Остановимся детально на методике выполнения расчетов для различных , а также стен и пола.
Схема ленточного фундамента
Какими методами можно рассчитать объем бетона
Выполнению строительных работ предшествует разработка проекта. На этом этапе определяется вид фундаментной базы, и рассчитывается требуемый для возведения основания объем бетонного раствора. На проектной стадии вычисляется потребность в растворе для заливки монолитных стен и бетонного пола. Определение кубатуры бетонной смеси, необходимой для выполнения работ, производится по объему бетонируемых конструкций здания.
Для выполнения расчетов используются различные методы
:
- ручной. Он базируется на вычислении объемов фундаментного основания, капитальных стен и пола. Расчет производится на обычном калькуляторе по школьным формулам вычисления объема и не учитывает коэффициент усадки бетона. Полученное значение незначительно отличается от результатов вычислений с помощью программных средств;
- программный. Введенные в программу исходные данные о типе фундаментной основы, ее габаритах, конструктивных особенностях и марке бетона оперативно обрабатываются. В результате выдается довольно точный результат, на который можно ориентироваться, приобретая стройматериал для сооружения фундаментной базы, постройки стен или заливки пола.

Для получения точного результата недостаточно учитывать только внутренний размер опалубки. Второй способ более точен, так как онлайн-калькулятор учитывает все данные: тип фундамента, сечение фундаментной базы, наличие арматурного каркаса и марку раствора.
Готовимся определить объем бетона – как посчитать без ошибок
Готовясь к выполнению расчетов, следует запомнить, что потребность в бетонной смеси определяется в кубометрах, а не в килограммах, тоннах или литрах. В результате ручных или программных расчетов будет определен объем связующего раствора, а не его масса. Одна из главных ошибок, которую допускают начинающие застройщики – выполнение расчетов до того, как будет определен тип фундаментной основы.
Решение о конструкции фундамента принимается после выполнения следующих работ
:
- производства геодезических мероприятий, позволяющих определить свойства грунта, уровень замерзания и расположение водоносных жил;
- вычисления нагрузочной способности базы. Она определяется на основании веса, конструктивных особенностей строения и природных факторов.

- разновидность сооружаемой основы;
- габариты фундамента, его конфигурацию;
- марку смеси, применяемую для бетонирования;
- глубину промерзания грунта.
Точность, с которой посчитан объем бетона, зависит от используемых для расчета данных.
Они разные для каждого типа фундамента
:
- при расчете ленточного основания учитываются его габариты и форма;
- для столбчатой основы важно знать количество бетонных колонн и их размеры;
- рассчитать куб бетона для цельной плиты можно по ее толщине и размерам.
От полноты используемых для расчета данных зависит точность полученного результата.
Как рассчитать бетон в кубах для фундаментной основы
Для всех типов оснований потребность в бетоне определяется по формуле, учитывающей суммарный объем возводимых фундаментных конструкций. При этом в обязательном порядке учитывается и часть фундамента, заливаемая в грунт. Для выполнения расчетов следует руководствоваться размерами, указанными в проектной документации.
- столбчатого;
- ростверкового.
Определение потребности в бетонном растворе для каждого вида фундаментной основы имеет свои особенности.
Как высчитать куб бетона для ленточной базы

Основание ленточного типа достаточно популярно. Оно используется для строительства частных домов, хозяйственных построек и дачных строений. Конструкция представляет собой цельную ленту из бетона, армированную стальными прутками. Монолитная лента повторяет контур строения, включая внутренние перегородки.

Расчет объема бетона для монолитного ленточного фундамента производится по простой формуле V = AхBхP. Расшифруем ее
:
- V – потребность в бетонном растворе, выраженная в кубических метрах;
- A – толщина фундаментной ленты;
- B – высота ленточные базы, включая подземную часть;
- P – периметр формируемого ленточного контура.
Перемножив между собой данные параметры, вычислим суммарную кубатуру бетонного раствора.
Рассмотрим алгоритм вычислений для ленточного основания с размерами 6х8 м, толщиной 0,5 м и высотой 1,2 м. Выполняйте расчет по следующему алгоритму
:
- Рассчитайте периметр, удвоив длину сторон 2х(6+8)=28 м.
- Вычислите площадь сечения, перемножив толщину и высоту ленты 0,5х1,2=0,6 м 2 .
- Определите объем, перемножив периметр на площадь сечения 28х0,6=16,8 м 3 .
Полученный результат имеет небольшую погрешность, связанную с тем, что не учитывается железобетонная арматура и усадка смеси во время вибрационного уплотнения.

Как вычислить куб бетона для основания свайного типа
Основание в виде бетонных колонн является одним из наиболее простых. Оно представляет собой железобетонные опоры, равномерно расположенные по контуру здания, в том числе по углам строения, а также в местах пересечения внутренних перегородок со стенами. Часть опорных элементов расположена в грунте и передает нагрузку от массы строения на почву. Алгоритм расчета предусматривает определение суммарной потребности в бетоне путем умножения объема отдельных колонн на их количество.
Для вычислений используйте формулу – V=Sхn, которая расшифровывается следующим образом
:
- V – количество раствора для заливки колонн;
- S – площадь поперечного сечения опорного элемента;
- n – суммарное количество свайных колонн.
На примере требований проекта, предусматривающего установку 40 свай диаметром 0,3 м и общей длиной 1,8 м, вычисляем требуемое количество бетона
:
- Рассчитайте площадь сваи, умножив коэффициент 3,14 на квадрат радиуса — 3,14х0,15х0,15=0,07065 м 2 .
- Вычислите объем одной опоры, умножив ее площадь на длину — 0,07065х1,8=0,127 м 3 .
- Определите необходимые количество смеси, перемножив объем одной сваи на общее количество опор 0,127х40=5,08 м 3 .

При прямоугольном сечении опорных колонн, для расчета поперечного сечения необходимо перемножить ширину и толщину элемента.
Как посчитать бетон для столбчатой основы с железобетонным ростверком
Для повышения прочностных характеристик столбчатой основы выступающие части опор объединяют железобетонной конструкцией, которая называется ростверком. Он выполняется в виде цельной железобетонной ленты или плиты, в которой забетонированы оголовки колонн.

- Определить площадь сечения ростверка, умножив его толщину на высоту;
- Рассчитать объем ростверка, перемножив площадь сечения на длину конструкции.
Полученное значение соответствует потребности в бетонной смеси для бетонирования ростверковой основы.
Вычисляем объем бетона для фундамента в виде цельной плиты
Основание плитного типа применяется на сложных грунтах с повышенной концентрацией влаги. На нем возводят здания без подвального помещения. Эта конструкция позволяет равномерно распределить нагрузку от массы строения на почву и обеспечить повышенную жесткость и устойчивость возводимого объекта. Применение арматуры позволяет повысить прочность плитного фундамента. Конструкция представляет собой железобетонную плиту в форме прямоугольного параллелепипеда.

Расшифровка обозначений
:
- V – объем бетонного состава для заливки плиты;
- S – площадь плитной основы в поперечном сечении;
- L – длина фундаментной конструкции.
Для фундамента длиной 12 м, шириной 10 м и толщиной 0,5 м рассмотрим алгоритм вычислений
:
- Определите площадь, перемножив ширину плиты на ее толщину 10х0,5=5 м 2 .
- Вычислите объем основы, умножив длину конструкции на площадь 12х5=60 м 3 .
Полученное значение соответствует потребности в бетонной смеси. Если плитный фундамент имеет сложную конфигурацию, то его следует разбить на плане на более простые фигуры, а затем вычислить для каждой площадь и объем.
Как правильно рассчитать куб бетона для возведения стен

Для постройки массивных зданий сооружают прочные коробки из бетона, усиленного стальной арматурой. Для определения потребности в стройматериале, перед строителями возникает задача рассчитать объем бетона для таких конструкций. Для выполнения вычислений используйте следующую формулу – V=(S-S1)хH.
Расшифруем входящие в формулу обозначения
:
- V – количество бетонной смеси для возведения стен;
- S – общая площадь стенной поверхности;
- S1 – суммарная площадь оконных и дверных проемов;
- H – высота бетонируемой стенной коробки.
При выполнении расчетов общая площадь проемов определяется путем суммирования отдельных проемов. Алгоритм расчета напоминает определение потребности в бетоне для плитного основания и легко может быть выполнен самостоятельно с использованием калькулятора.
Как посчитать куб бетона для заливки пола

Для повышения нагрузочной способности пола и обеспечения его плоскостности выполняется бетонная стяжка. После застывания бетона такая поверхность служит основой для укладки напольных покрытий или керамической плитки. Для предотвращения растрескивания толщина формируемой бетонной стяжки составляет 5–10 см. Это связано с тем, что более тонкий материал растрескивается в процессе эксплуатации. Важно правильно рассчитать куб бетона, чтобы сформированная стяжка была прочной и имела предусмотренную проектом толщину.
Формула для определения количества раствора V=Sxh расшифровывается легко
:
- V – количество заливаемого материала;
- S – суммарная площадь бетонируемой стяжки;
- h – толщина бетонной основы.
Разберемся, как выполнить вычисления для помещения с размерами 6х8 м и толщиной бетонной основы 0,06 м
:
- Определите площадь напольной поверхности, перемножив длину и ширину помещения – 6х8=48 м 2 .
- Вычислите объем заливаемого бетонного состава для формирования стяжки, умножив площадь на толщину слоя – 48х0,06=2,88 м 3 .
Руководствуясь приведенным алгоритмом, можно легко определить количество бетонного состава для бетонирования пола. Возникают ситуации, когда черновая поверхность имеет уклон. В этом случае формируемая стяжка имеет разную толщину по площади помещения. В данной ситуации можно использовать усредненную толщину слоя, что снижает точность вычислений.
Заключение – для чего необходимо знать, как рассчитать куб бетона
Занимаясь строительством и планируя самостоятельно изготавливать бетонный раствор или приобретать его на предприятиях железобетонных изделий в необходимом количестве, важно знать, как рассчитать объем бетона. Это позволит спрогнозировать сумму предстоящих расходов, своевременно приобрести стройматериалы, и выполнить работы в запланированные сроки. Произвести расчеты можно как вручную на калькуляторе, так и с помощью программных средств. Главное – овладеть методикой вычислений и использовать для определения количества бетона достоверные данные.
Ученые из разных стран трудились много лет над созданием единой системы. К примеру, в разных странах существовали свои единицы для измерений расстояния: версты, футы, сажени, мили. В единой международной системе расстояние измеряют в метрах. Масса оценивается в килограммах вместо пудов, фунтов и так далее.
Кубический метр является производным, это справедливо и для других единиц.
Кубометр (м 3) — это величина, равная объему куба, имеющего длину ребра в 1 метр. Метрами кубическими измеряются те физические тела, которые характеризуются 3 параметрами измерений:
- длиной;
- шириной;
- высотой.
Чтобы определить величину объема тела, нужно перемножить все 3 параметра.
Для подсчета меньших или больших объектов помимо метров кубических (м 3) используются другие единицы: кубические миллиметры (мм 3), кубические сантиметры (см 3), кубические дециметры (дм 3), кубические километры (км 3), литры. Рассмотрим примеры расчета объемов тел разной конфигурации.
Пример 1. Найти объем коробки с длиной 2 м, шириной 4 м и высотой 3 м. Объем будет равен: 2 м х 4 м х 3 м = 24 м 3
Пример 2. Найти объем цилиндра с диаметром основания 2 м и высотой 4 м. Вычисляем площадь круга, она равна πR 2 . S = 3,14 х (1 м) 2 = 3,14 м 2 . Находим объем: 3,14 м 2 х 3м = 9,42 м 3 .
Пример 3. Найти объем шара с диаметром 3 м. Чтобы посчитать кубические метры в шаре, вспомним формулу.
V = 4/3πR 3. Подставляем заданное значение и находим объем: 4/3 х 3,14 х (1,5 м) 3 = 14,13 м 3.
Соответствия кубического метра
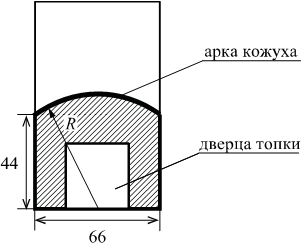
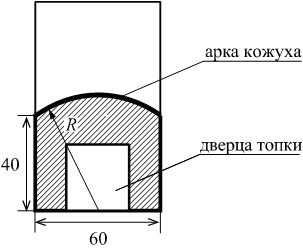
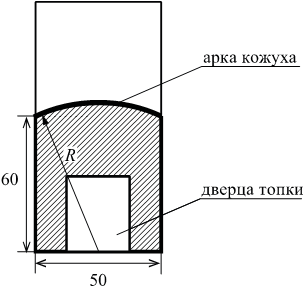
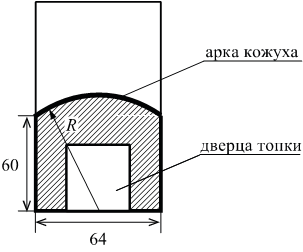
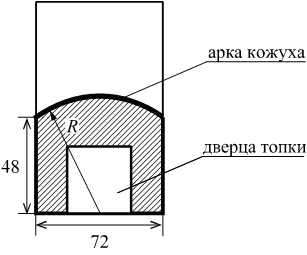
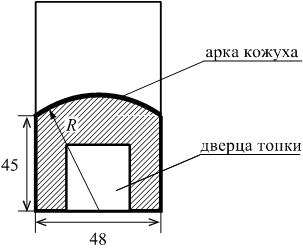
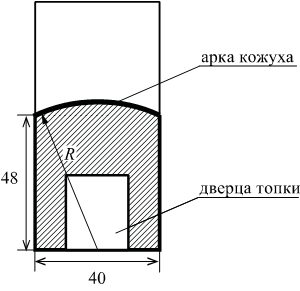
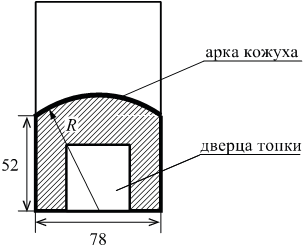
Чтобы найти количество кубов в теле неправильной формы, нужно разделить его на составляющие с правильной формой. Найти их объемы и полученные результаты суммировать. Рассмотрим такой объект, как башня с конусообразной крышей.
Находим сначала кубатуру рабочего помещения, имеющего цилиндрическую форму, затем конусообразной крыши по приведенным выше формулам. Полученные результаты складываем.
Как рассчитать кубатуру материалов?
Чтобы узнать величину объема обрезной доски, следует сделать замеры трех ее величин: длины, ширины и толщины или высоты. Полученные значения перемножаем и получаем кубатуру одной доски. Затем этот объем умножаем на количество досок, находящихся в пачке.
Существует 3 способа подсчета кубатуры:
- пакетно;
- поштучно;
- выборкой.
Выбрав 1 способ подсчета, нужно соблюсти такие условия:
- передние торцы досок в пакете должны быть выровнены;
- величина ширины пакета не должна по всей длине отклоняться от заданной;
- недопустима укладка досок нахлестом;
- недопустимо смещение досок внутрь пакета или наружу на величину, большую 100 мм.
Со стороны выровненных торцов замеряют высоту пакета h 1 . Находим фактическую высоту h. Она будет равна h 1 — ab, где а — количество прокладок между досками, b — толщина одной прокладки.
Ширину пакета меряют по средней линии, разделяющей высоту пополам. Допустимая погрешность замеров — это ±10 мм.
Способ 2 говорит сам за себя. Производится замер каждой доски, подсчитываются все объемы и далее складываются.
Способ 3 применяют для крупных партий древесины. Ее кубатуру вычисляют по усредненным показателям, принятым для всей партии.
Точность расчета кубатуры необрезных пиломатериалов зависит от вида дерева, его типа и степени обработки. Часто бывает, что среди этих досок попадаются и обрезные.
Облегчить задачу подсчета объемов помогут специально разработанные таблицы — так называемые кубатурники.
Способы перевода кубометров в другие кубические единицы
Рассчитывая объемности, необходимо придерживаться одинаковых единиц замеров. Если данные представлены другими единицами, а конечный результат должен быть получен в кубах, то достаточно будет правильно сделать преобразование.
Если V измерен в мм 3 , см 3 , дм 3 , л, то в м 3 переводим соответственно:
- 1 м 3 = 1 мм 3 х х 0, 000000001 = 1 мм 3 х 10 -9 ;
- 1 м 3 = 1 см 3 х 0, 000001 = 1 см 3 х 10 -6 ;
- 1 м 3 = 1 дм 3 х 0,001 = 1 дм 3 х 10 -3. Такой же перевод применяют и для литров, поскольку в 1 л содержится 1 дм 3 .
Чтобы найти кубы вещества, зная его массу, нужно по таблице отыскать его плотность или определить вручную. Разделив заданную массу М (кг) на показатель плотности Р (кг/ м 3), получим V материала (м 3) .
Знания для определения объемов необходимы и специалистам, и обычным людям в повседневной жизни.
Одна из интереснейших задач геометрии, результат решения которой важен и в физике, и в химии, и в других областях — определение объемов. Занимаясь математикой в школе, детки часто задаются мыслью: «Зачем нам это нужно?» Мир вокруг кажется настолько простым и понятным, что определенные школьные знания относят к разряду «ненужных». Но стоит столкнуться, к примеру, с транспортировкой и возникает вопрос о том, как посчитать объем груза. Скажете, что ничего проще нет? Ошибаетесь. Знание расчетных формул, понятий «плотности вещества», «объемной плотности тел» становятся необходимы.
Школьные знания — практическая основа
Учителя школ, преподавая основы геометрии, предлагают нам такое определение объема: часть пространства, занимаемая телом. При этом формулы определения объемов давно записаны, и найти их можно в справочниках. Определить объем тела правильной формы человечество научилось задолго до появления трактатов Архимеда. Но только этот великий греческий мыслитель ввел методику, дающую возможность определить объем любой фигуры. Его умозаключения стали основой интегрального исчисления. Объемными считают фигуры, получаемые в процессе вращения плоских
Евклидова геометрия с определенной точностью позволяет определить объем:
Отличие плоских и объемных фигур не позволяет ответить на вопрос некоторых страдальцев о том, как посчитать объем прямоугольника. Это, примерно, так же, как найти то, не знаю что. Путаница в геометрическом материале возможна, при этом прямоугольником иногда называют прямоугольный параллелепипед.
Что предпринимать, если форма тела не столь четко определена?
Определение объема сложных геометрических конструкций — работа не из легких. Стоит руководствоваться несколькими незыблемыми принципами.
- Любое тело можно разбить на более простые части. Объем равен сумме объемов его отдельных частей.
- Равновеликие тела имеют равные объемы, параллельный перенос тел не меняет его объема.
- Единицей объема считают объем куба с ребром единичной длины.
Наличие тел неправильной формы (вспомним пресловутую корону царя Герона) не становится проблемой. Определение объемов тел вполне возможно. Это процесс непосредственного измерения объемов жидкости с погруженным в нее телом, который будет рассмотрен ниже.
Различные прикладные задачи на определение объема
Вернемся к проблеме: как посчитать объем перевозимых грузов. Каким является груз: фасованным или сыпучим? Каковы параметры тары? Вопросов больше, чем ответов. Немаловажным станет вопрос массы груза, поскольку транспорт отличается грузоподъемностью, а трассы — максимальным весом транспортного средства. Нарушение правил перевозки грозит штрафными санкциями.
Задача 1. Пусть груз представляет собой прямоугольные контейнеры, заполненные товаром. Зная вес товара и контейнера, можно с легкостью определить суммарный вес. Объем контейнера определяем как объем прямоугольного параллелепипеда.
Зная грузоподъемность транспорта, его габариты, можно просчитать возможный объем перевозимого груза. Верное соотношение этих параметров позволяет избежать катастрофы, преждевременного выхода транспорта из строя.
Задача 2. Груз — сыпучий материал: песок, щебень и тому подобное. На этом этапе без знаний физики обойтись может только классный специалист, опыт которого в грузоперевозках позволяет интуитивно определить предельно допустимый к перевозке объем.
Научный метод предполагает знание такого параметра, как груза.
Используется формула V=m/ρ, где m — масса груза, ρ — плотность материала. Перед тем как посчитать объем, стоит узнать плотность груза, что также совсем не сложно (таблицы, лабораторное определение).
Эта методика также замечательно работает при определении объемов жидких грузов. При этом как единицу измерения используют литр.
Определение объемов строительных форм
Вопрос определения объемов играет немаловажную роль в строительстве. Возведение домов, других сооружений — дело затратное, стройматериалы требуют внимательного отношения и предельно точного расчета.
Основа здания — фундамент — представляет собой обычно литую конструкцию, заполняемую бетоном. Перед тем необходимо определить тип фундамента.
Плитный фундамент — плита в виде прямоугольного параллелепипеда. Столбчатое основание — прямоугольные или цилиндрические столбы определенного сечения. Определив объем одного столба и умножив его на количество, можно рассчитать кубатуру бетона на весь фундамент.
Рассчитывая объем бетона для стен или перекрытий, поступают достаточно просто: определяют объем всей стены, умножая длину на ширину и высоту, затем отдельно определяют объемы оконных и дверных проемов. Разность объема стены и суммарного объема проемов — объем бетона.
Как определить объем здания?
Некоторые прикладные задачи требуют знаний об объеме зданий и сооружений. К ним относятся проблемы ремонта, реконструкции, определения влажности воздуха, вопросы, связанные с теплоснабжением и вентиляцией.
Прежде чем ответить на вопрос о том, как посчитать объем здания, делают замеры по внешней его стороне: площади сечения (длина умножается на ширину), высоты здания от нижней части первого этажа до чердака.
Определение внутренних объемов отапливаемых помещений проводят по внутренним обводкам.
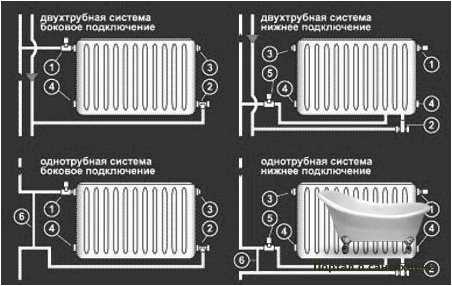
Устройство систем отопления
Современные квартиры и офисы невозможно представить без системы отопления. Основной частью систем являются батареи и соединительные трубы. Как посчитать объем системы отопления? Полный объем всех секций отопления, который указан на самом радиаторе, необходимо сложить с объемом труб.
И на этом этапе встает проблема: как посчитать объем трубы. Представим, что труба — цилиндр, решение приходит само собой: используем формулу цилиндра. В отопительных системах трубы заполняются водой, поэтому необходимо знать площадь внутреннего сечения трубы. Для этого определяем ее внутренний радиус (R). Формула определения площади круга: S=πR 2 . Общая длина труб определяется по их протяженности в помещении.
Канализация в доме — система труб
Закладывая трубы для водоотведения, также стоит знать объем трубы. На этом этапе необходим внешний диаметр, действия аналогичны предыдущим.
Определение объема металла, который идет на изготовление трубы — также интересная задача. Геометрически труба — цилиндр с пустотами. Определить площадь кольца, лежащего в ее сечении — задача достаточно сложная, но решаемая. Более простой выход — определить внешний и внутренний объемы трубы, разность этих величин и будет объемом металла.
Определение объемов в задачах физики
Знаменитая легенда о короне царя Герона стала известной не только вследствие решения задачи выведения «на чистую воду» вороватых ювелиров. Итог сложной мыслительной деятельности Архимеда — определение объемов тел неправильной геометрической формы. Основная мысль, извлеченная философом — объем вытесненной телом жидкости равен объему тела.
В лабораторных исследованиях пользуются мерным цилиндром (мензуркой). Определяют объем жидкости (V 1), погружают в нее тело, выполняют вторичные измерения (V 2). Объем равен разности вторичных и первичных измерений: V т = V 2 — V 1 .
Такой метод определения объемов тел используют при вычислении объемной плотности сыпучих нерастворимых материалов. Он крайне удобен при определении плотности сплавов.
Вычислить объем булавки можно с применением этого метода. Кажется, достаточно сложно определить объем столь маленького тела, как булавка или дробинка. Линейкой его не измерить, мерный цилиндр также достаточно велик.
Но если использовать несколько совершенно одинаковых булавок (n), то можно при помощи мерного цилиндра определить их суммарный объем (V т = V 2 — V 1) . Затем полученную величину разделить на количество булавок. V= V т n.
Эта задача становится понятной, если из одного большого куска свинца необходимо отлить множество дробинок.
Единицы измерения объема жидкости
Интернациональная система единиц предполагает измерение объемов в м 3 . В обыденной жизни чаще используют внесистемные единицы: литр, миллилитр. Когда определяются, как посчитать объем в литрах, используют систему перевода: 1 м 3 = 1000 литров.
Использование в повседневной жизни иных внесистемных мер может вызвать трудности. Англичане используют более привычные для них баррели, галлоны, бушели.
Система перевода:
Задачи с нестандартными данными
Задача 1. Как посчитать объем, зная высоту и площадь? Обычно такую задачу решают, определяя объем покрытия различных деталей гальваническим путем. При этом площадь поверхности детали (S) известна. Толщина слоя (h) — высота. Объем определяют произведением площади и высоты: V=Sh.
Задача 2. Для кубов интересной, с математической точки зрения, может выглядеть задача определения объема, если известна площадь одной грани. Известно, что объем куба: V=a 3 , где а — длина его грани. Площадь боковой поверхности куба S=a 2 . Извлекая из площади, получаем длину грани куба. Используем формулу объема, вычисляем его значение.
Задача 3. Вычислить объем фигуры, если известна площадь и даны некоторые параметры. К дополнительным параметрам можно отнести условия соотношения сторон, высот, диаметров основания и многое другое.
Для решения конкретных задач понадобятся не только знания формул расчета объемов, но и другие формулы геометрии.
Определение объемов памяти
Совершенно не связанная с геометрией задача: определить объем памяти электронных устройств. В современном, достаточно компьютеризованном мире эта проблема не бывает лишней. Точные устройства, какими являются персональные компьютеры, не терпят приблизительности.
Знание объемов памяти флешки или иного накопителя полезно при копировании, перемещении информации.
Немаловажно знать объем оперативной и постоянной памяти компьютера. Часто пользователь сталкивается с ситуацией, когда «не идет игра», «виснет программа». Проблема вполне возможна при низком объеме памяти.
Считается байт и его производные (килобайт, мегабайт, терабайт).
1 кБ = 1024 Б
1 МБ = 1024 кБ
1 ГБ = 1024 Мб
Странность в данной системе перерасчета следует из двоичной системы кодирования информации.
Размер памяти запоминающего устройства является его основной характеристикой. Сравнивая объем переносимой информации и объем памяти накопителя, можно определить возможность его дальнейшей эксплуатации.
Понятие «объема» настолько масштабно, что в полной мере уяснить его многогранность можно только решая прикладные задачи, интересные и увлекательные.
Для простых тел объем — это положительная величина, численное значение которой обладает следующими свойствами:
1. Равные тела имеют равные объемы.
2. Если тело разбито на части, являющиеся простыми телами, то объем этого тела равен сумме объемов его частей.
3. Объем куба, ребро которого равно единице длины, равен единице.
Если куб, о котором идет речь в определении, имеет ребро 1 см, то объем измеряется в кубических сантиметрах; если ребро куба равно , то объем измеряется в кубических
метрах; если ребро куба равно 1 км, то объем измеряется в кубических километрах и т. д.
На рисунке 181 изображено простое тело — четырехугольная пирамида SABCD. Объем этой пирамиды на основании свойства 2 равен сумме объемов пирамид SABC и SADC.
59. Объем параллелепипеда, призмы и пирамиды.
Объем прямоугольного параллелепипеда находится по формуле
где — ребра прямоугольного параллелепипеда. Исходя из этой формулы можно получить формулу для объема куба. Объем куба находят по формуле
где а — ребро куба.
Иногда говорят, что объем прямоугольного параллелепипеда равен произведению его линейных размеров или произведению площади его основания на высоту. Последнее утверждение верно и для любого параллелепипеда.
На рисунке 182 изображен наклонный параллелепипед. Его объем равен , где — площадь основания, а высота наклонного параллелепипеда.
Можно вывести правило нахождения объема любой призмы (в том числе и наклонной).
Объем призмы равен произведению площади ее основания на высоту;
В случае прямой призмы (рис. 183) высота ее совпадает с боковым ребром и объем прямой призмы равен произведению площади основания на боковое ребро.
Объем любой пирамиды находится по формуле
где S — площадь основания, Н — высота пирамиды.
На рисунке 184 изображен правильный тетраэдр SABC с ребром а. Его объем равен
Пример. В наклонном параллелепипеде основание и боковая грань — прямоугольники, площади которых соответственно равны а угол между их плоскостями равен 80°. Одна боковых граней параллелепипеда имеет площадь Найти объем параллелепипеда.
Решение. Пусть в параллелепипеде грани прямоугольники. Тогда ребро AD перпендикулярно грани Дальнейшие вычисления можно выполнить, не находя длин этих отрезков. Имеем Перемножив эти равенства почленно, получим откуда
60. Объем цилиндра и конуса.
Объем любого тела определяется следующим образом. Данное тело нмеет объем V, если существуют содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколь угодно мало отличающимися от V.
Применив это определение к нахождению объемов цилиндра и конуса, можно доказать теоремы.
Объем цилиндра равен произведению площади основания на высоту, т. е.
Если радиус основания цилиндра R, а высота H, то формула его объема такова:
Объем конуса равен одной трети произведения площади основания на высоту» т. е. .
Если радиус основания конуса H, а высота II, то объем его находится по формуле
Объем усеченного конуса можно найти по формуле
где радиусы оснований, Н — высота усеченного конуса. Объем усеченного конуса, изображенного на рисунке 185, находится по формуле
61. Общая формула объемов тел вращения.
Объем шара и его частей. Для вывода формулы объема тела вращения вводят декартовы координаты в пространстве, приняв ось тела за ось Плоскость пересекает поверхность тела по линии, для которой ось х является осью симметрии. Пусть уравнение той части линии, которая расположена над осью х (рис. 186).
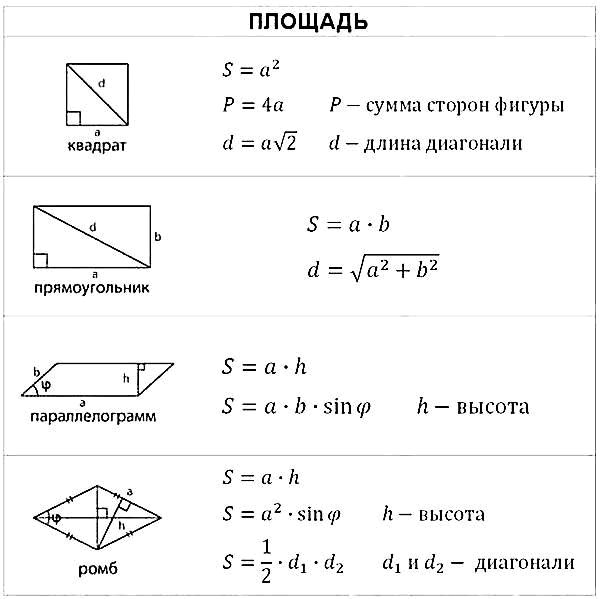
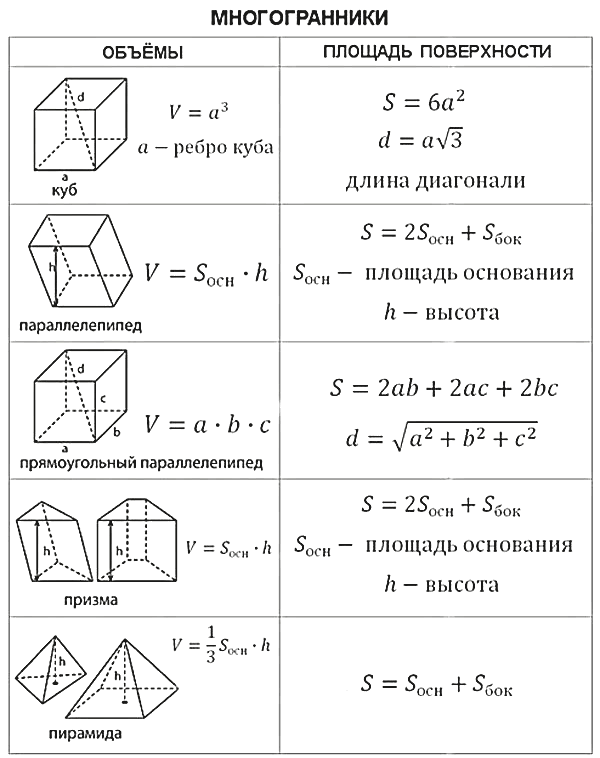
В данной теме выложены вспомогательные картинки для учеников и студентов с формулами площадей и объемов фигур. Ниже расположены основные формулы, которые потребуются при решении задач по геометрии на нахождение объемов и площадей поверхности таких фигур, как квадрат, прямоугольник, параллелограмм, ромб, треугольник, прямоугольный треугольник, трапеция, круг, куб, параллелепипед, прямоугольный параллелепипед, призма, пирамида, цилиндр, конус и шар.
Как рассчитать, посчитать объем помещения.
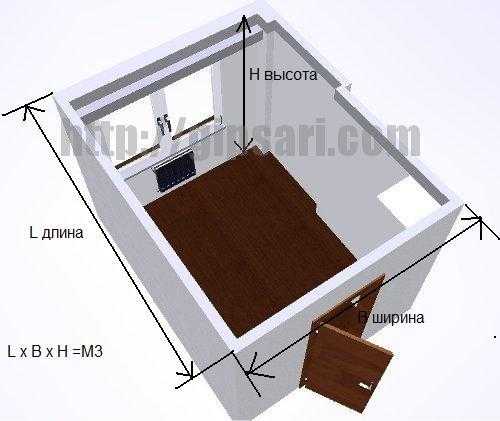
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения.
Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения

Для устройства фундамента, возведения стен и заливки пола применяются бетонные растворы. До начала мероприятий важно выбрать конструкцию фундаментного основания, правильно рассчитать общий уровень затрат и определить необходимое количество строительных материалов. Зная, как рассчитать объем бетона, можно определить сметную стоимость строительных мероприятий, точно спланировать продолжительность выполнения бетонных работ и избежать непредвиденных затрат. Остановимся детально на методике выполнения расчетов для различных , а также стен и пола.
Схема ленточного фундамента
Какими методами можно рассчитать объем бетона
Выполнению строительных работ предшествует разработка проекта. На этом этапе определяется вид фундаментной базы, и рассчитывается требуемый для возведения основания объем бетонного раствора. На проектной стадии вычисляется потребность в растворе для заливки монолитных стен и бетонного пола. Определение кубатуры бетонной смеси, необходимой для выполнения работ, производится по объему бетонируемых конструкций здания.
Для выполнения расчетов используются различные методы
:
- ручной. Он базируется на вычислении объемов фундаментного основания, капитальных стен и пола. Расчет производится на обычном калькуляторе по школьным формулам вычисления объема и не учитывает коэффициент усадки бетона. Полученное значение незначительно отличается от результатов вычислений с помощью программных средств;
- программный. Введенные в программу исходные данные о типе фундаментной основы, ее габаритах, конструктивных особенностях и марке бетона оперативно обрабатываются. В результате выдается довольно точный результат, на который можно ориентироваться, приобретая стройматериал для сооружения фундаментной базы, постройки стен или заливки пола.

Для получения точного результата недостаточно учитывать только внутренний размер опалубки. Второй способ более точен, так как онлайн-калькулятор учитывает все данные: тип фундамента, сечение фундаментной базы, наличие арматурного каркаса и марку раствора.
Готовимся определить объем бетона – как посчитать без ошибок
Готовясь к выполнению расчетов, следует запомнить, что потребность в бетонной смеси определяется в кубометрах, а не в килограммах, тоннах или литрах. В результате ручных или программных расчетов будет определен объем связующего раствора, а не его масса. Одна из главных ошибок, которую допускают начинающие застройщики – выполнение расчетов до того, как будет определен тип фундаментной основы.
Решение о конструкции фундамента принимается после выполнения следующих работ
:
- производства геодезических мероприятий, позволяющих определить свойства грунта, уровень замерзания и расположение водоносных жил;
- вычисления нагрузочной способности базы. Она определяется на основании веса, конструктивных особенностей строения и природных факторов.

- разновидность сооружаемой основы;
- габариты фундамента, его конфигурацию;
- марку смеси, применяемую для бетонирования;
- глубину промерзания грунта.
Точность, с которой посчитан объем бетона, зависит от используемых для расчета данных.
Они разные для каждого типа фундамента
:
- при расчете ленточного основания учитываются его габариты и форма;
- для столбчатой основы важно знать количество бетонных колонн и их размеры;
- рассчитать куб бетона для цельной плиты можно по ее толщине и размерам.
От полноты используемых для расчета данных зависит точность полученного результата.
Как рассчитать бетон в кубах для фундаментной основы
Для всех типов оснований потребность в бетоне определяется по формуле, учитывающей суммарный объем возводимых фундаментных конструкций. При этом в обязательном порядке учитывается и часть фундамента, заливаемая в грунт. Для выполнения расчетов следует руководствоваться размерами, указанными в проектной документации.
- столбчатого;
- ростверкового.
Определение потребности в бетонном растворе для каждого вида фундаментной основы имеет свои особенности.
Как высчитать куб бетона для ленточной базы

Основание ленточного типа достаточно популярно. Оно используется для строительства частных домов, хозяйственных построек и дачных строений. Конструкция представляет собой цельную ленту из бетона, армированную стальными прутками. Монолитная лента повторяет контур строения, включая внутренние перегородки.

Расчет объема бетона для монолитного ленточного фундамента производится по простой формуле V = AхBхP. Расшифруем ее
:
- V – потребность в бетонном растворе, выраженная в кубических метрах;
- A – толщина фундаментной ленты;
- B – высота ленточные базы, включая подземную часть;
- P – периметр формируемого ленточного контура.
Перемножив между собой данные параметры, вычислим суммарную кубатуру бетонного раствора.
Рассмотрим алгоритм вычислений для ленточного основания с размерами 6х8 м, толщиной 0,5 м и высотой 1,2 м. Выполняйте расчет по следующему алгоритму
:
- Рассчитайте периметр, удвоив длину сторон 2х(6+8)=28 м.
- Вычислите площадь сечения, перемножив толщину и высоту ленты 0,5х1,2=0,6 м 2 .
- Определите объем, перемножив периметр на площадь сечения 28х0,6=16,8 м 3 .
Полученный результат имеет небольшую погрешность, связанную с тем, что не учитывается железобетонная арматура и усадка смеси во время вибрационного уплотнения.

Как вычислить куб бетона для основания свайного типа
Основание в виде бетонных колонн является одним из наиболее простых. Оно представляет собой железобетонные опоры, равномерно расположенные по контуру здания, в том числе по углам строения, а также в местах пересечения внутренних перегородок со стенами. Часть опорных элементов расположена в грунте и передает нагрузку от массы строения на почву. Алгоритм расчета предусматривает определение суммарной потребности в бетоне путем умножения объема отдельных колонн на их количество.
Для вычислений используйте формулу – V=Sхn, которая расшифровывается следующим образом
:
- V – количество раствора для заливки колонн;
- S – площадь поперечного сечения опорного элемента;
- n – суммарное количество свайных колонн.
На примере требований проекта, предусматривающего установку 40 свай диаметром 0,3 м и общей длиной 1,8 м, вычисляем требуемое количество бетона
:
- Рассчитайте площадь сваи, умножив коэффициент 3,14 на квадрат радиуса — 3,14х0,15х0,15=0,07065 м 2 .
- Вычислите объем одной опоры, умножив ее площадь на длину — 0,07065х1,8=0,127 м 3 .
- Определите необходимые количество смеси, перемножив объем одной сваи на общее количество опор 0,127х40=5,08 м 3 .

При прямоугольном сечении опорных колонн, для расчета поперечного сечения необходимо перемножить ширину и толщину элемента.
Как посчитать бетон для столбчатой основы с железобетонным ростверком
Для повышения прочностных характеристик столбчатой основы выступающие части опор объединяют железобетонной конструкцией, которая называется ростверком. Он выполняется в виде цельной железобетонной ленты или плиты, в которой забетонированы оголовки колонн.

- Определить площадь сечения ростверка, умножив его толщину на высоту;
- Рассчитать объем ростверка, перемножив площадь сечения на длину конструкции.
Полученное значение соответствует потребности в бетонной смеси для бетонирования ростверковой основы.
Вычисляем объем бетона для фундамента в виде цельной плиты
Основание плитного типа применяется на сложных грунтах с повышенной концентрацией влаги. На нем возводят здания без подвального помещения. Эта конструкция позволяет равномерно распределить нагрузку от массы строения на почву и обеспечить повышенную жесткость и устойчивость возводимого объекта. Применение арматуры позволяет повысить прочность плитного фундамента. Конструкция представляет собой железобетонную плиту в форме прямоугольного параллелепипеда.

Расшифровка обозначений
:
- V – объем бетонного состава для заливки плиты;
- S – площадь плитной основы в поперечном сечении;
- L – длина фундаментной конструкции.
Для фундамента длиной 12 м, шириной 10 м и толщиной 0,5 м рассмотрим алгоритм вычислений
:
- Определите площадь, перемножив ширину плиты на ее толщину 10х0,5=5 м 2 .
- Вычислите объем основы, умножив длину конструкции на площадь 12х5=60 м 3 .
Полученное значение соответствует потребности в бетонной смеси. Если плитный фундамент имеет сложную конфигурацию, то его следует разбить на плане на более простые фигуры, а затем вычислить для каждой площадь и объем.
Как правильно рассчитать куб бетона для возведения стен

Для постройки массивных зданий сооружают прочные коробки из бетона, усиленного стальной арматурой. Для определения потребности в стройматериале, перед строителями возникает задача рассчитать объем бетона для таких конструкций. Для выполнения вычислений используйте следующую формулу – V=(S-S1)хH.
Расшифруем входящие в формулу обозначения
:
- V – количество бетонной смеси для возведения стен;
- S – общая площадь стенной поверхности;
- S1 – суммарная площадь оконных и дверных проемов;
- H – высота бетонируемой стенной коробки.
При выполнении расчетов общая площадь проемов определяется путем суммирования отдельных проемов. Алгоритм расчета напоминает определение потребности в бетоне для плитного основания и легко может быть выполнен самостоятельно с использованием калькулятора.
Как посчитать куб бетона для заливки пола

Для повышения нагрузочной способности пола и обеспечения его плоскостности выполняется бетонная стяжка. После застывания бетона такая поверхность служит основой для укладки напольных покрытий или керамической плитки. Для предотвращения растрескивания толщина формируемой бетонной стяжки составляет 5–10 см. Это связано с тем, что более тонкий материал растрескивается в процессе эксплуатации. Важно правильно рассчитать куб бетона, чтобы сформированная стяжка была прочной и имела предусмотренную проектом толщину.
Формула для определения количества раствора V=Sxh расшифровывается легко
:
- V – количество заливаемого материала;
- S – суммарная площадь бетонируемой стяжки;
- h – толщина бетонной основы.
Разберемся, как выполнить вычисления для помещения с размерами 6х8 м и толщиной бетонной основы 0,06 м
:
- Определите площадь напольной поверхности, перемножив длину и ширину помещения – 6х8=48 м 2 .
- Вычислите объем заливаемого бетонного состава для формирования стяжки, умножив площадь на толщину слоя – 48х0,06=2,88 м 3 .
Руководствуясь приведенным алгоритмом, можно легко определить количество бетонного состава для бетонирования пола. Возникают ситуации, когда черновая поверхность имеет уклон. В этом случае формируемая стяжка имеет разную толщину по площади помещения. В данной ситуации можно использовать усредненную толщину слоя, что снижает точность вычислений.
Заключение – для чего необходимо знать, как рассчитать куб бетона
Занимаясь строительством и планируя самостоятельно изготавливать бетонный раствор или приобретать его на предприятиях железобетонных изделий в необходимом количестве, важно знать, как рассчитать объем бетона. Это позволит спрогнозировать сумму предстоящих расходов, своевременно приобрести стройматериалы, и выполнить работы в запланированные сроки. Произвести расчеты можно как вручную на калькуляторе, так и с помощью программных средств. Главное – овладеть методикой вычислений и использовать для определения количества бетона достоверные данные.
Общий обзор. Формулы стереометрии!
Здравствуйте, Дорогие друзья! В этой статье решил сделать общий обзор задач по стереометрии, которые будут на ЕГЭ по математик
е. Нужно сказать, что задачи из этой группы довольно разнообразны, но не сложны. Это задачи на нахождение геометрических величин: длин, углов, площадей, объёмов.
Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 50% из них решаются элементарно, практически устно.
Остальные требуют небольших усилий, знаний и специальных приёмов. В будущих статьях мы с вами будем рассмотривать эти задачи, не пропустите, подпишитесь на обновление блога.
Для решения необходимо знать формулы площадей поверхности и объёмов
параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Сложных задач нет, все они решаются в 2-3 действия, важно «увидеть» какую формулу необходимо применить.
Все нужные формулы представлены ниже:
Шар или сфера. Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки — центра шара.
Объем шара
равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Круглый конус может быть получен вращениемпрямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называт также конусом вращения. См. также Площадь поверхности круглого конуса
Объем круглого конуса
равен трети произведения площади основания S на высоту H:
(H — высота ребра куба)
Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипедимеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Объем прямоугольного параллелепипеда
равен произведению площади основания на высоту:
(S — площадь основания пирамиды, h — высота пирамиды)

Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.
Объем усеченной пирамиды
равен одной трети произведения высоты h (OS)
на сумму площадей верхнего основания S1 (abcde)
, нижнего основания усеченной пирамиды S2 (ABCDE)
и средней пропорциональной между ними.
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника — основания правильной пирамиды
h — высота правильной пирамиды
Правильная треугольная пирамида — этомногогранник, у которого одна грань — основание пирамиды — правильныйтреугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
Объем правильной треугольной пирамиды
равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC)
на высоту h (OS)
a — сторона правильного треугольника — основания правильной треугольной пирамиды
h — высота правильной треугольной пирамиды

Объем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставитьвысоту тетраэдра и площадь правильного (равностороннего) треугольника.
Объем тетраэдра
— равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра
(h — длина стороны ромба)
Длина окружности
p
составляет примерно три целых и одну седьмую длины диаметра круга. Точное отношение длины окружности к ее диаметру обозначается греческой буквой π
В итоге периметр круга или длина окружности вычисляется по формуле
(r — радиус дуги, n — центральный угол дуги в градусах.)
Измерьте все необходимые расстояния в метрах.
Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.
- 1 мм = 0,001 м
- 1 см = 0,01 м
- 1 км = 1000 м
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу:
объем = L × W × H
(длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
- 4 × 3 × 2,5
- = 12 × 2,5
- = 30. Объем этой комнаты равен 30 м 3
.
- Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L 3 (или W 3 , или H 3).
Для вычисления объема фигур в виде цилиндра используйте формулу:
пи
× R 2 × H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндра. Найдите площадь круглого основания, умножив число пи (3,14) на квадрат радиуса круга (R) (радиус — расстояние от центра окружности до любой точки, лежащей на этой окружности). Затем полученный результат умножьте на высоту цилиндра (H), и вы найдете объем цилиндра. Все значения измеряются в метрах.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
- (3,14) × 0,75 2 × 10
- = (3,14) × 0,5625 × 10
- = 17,66. Объем колодца равен 17,66 м 3
.
Для вычисления объема шара используйте формулу:
4/3 х пи
× R 3 . То есть вам нужно знать только радиус (R) шара.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
- 4/3 х пи × (5) 3
- = 4/3 х (3,14) × 125
- = 4,189 × 125
- = 523,6. Объем воздушного шара равен 523,6 м 3
.
Для вычисления объема фигур в виде конуса используйте формулу:
1/3 х пи
× R 2 × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
- 1/3 х (3,14) × 0,03 2 × 0,15
- = 1/3 х (3,14) × 0.0009 × 0,15
- = 1/3 × 0.0004239
- = 0,000141. Объем конуса мороженного равен 0,000141 м 3
.
Для вычисления объема фигур неправильной формы используйте несколько формул.
Для этого попробуйте разбить фигуру на несколько фигур правильной формы. Затем найдите объем каждой такой фигуры и сложите полученные результаты.
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
- пи × R 2 × H + 1/3 х пи × R 2 × H
- (3,14) × 1,5 2 × 12 + 1/3 х (3,14) × 1,5 2 × 1
- = (3,14) × 2,25 × 12 + 1/3 х (3,14) × 2,25 × 1
- = (3,14) × 27 + 1/3 х (3,14) × 2,25
- = 84,822 + 2,356
- = 87,178. Объем зернохранилища равен 87,178 м 3
.
Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора
гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно. Пример задания и оформления его решения приведен на рисунке ниже.
Примечание 1
. Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).
Примечание 2
. Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
Одна из интереснейших задач геометрии, результат решения которой важен и в физике, и в химии, и в других областях — определение объемов. Занимаясь математикой в школе, детки часто задаются мыслью: «Зачем нам это нужно?» Мир вокруг кажется настолько простым и понятным, что определенные школьные знания относят к разряду «ненужных». Но стоит столкнуться, к примеру, с транспортировкой и возникает вопрос о том, как посчитать объем груза. Скажете, что ничего проще нет? Ошибаетесь. Знание расчетных формул, понятий «плотности вещества», «объемной плотности тел» становятся необходимы.
Школьные знания — практическая основа
Учителя школ, преподавая основы геометрии, предлагают нам такое определение объема: часть пространства, занимаемая телом. При этом формулы определения объемов давно записаны, и найти их можно в справочниках. Определить объем тела правильной формы человечество научилось задолго до появления трактатов Архимеда. Но только этот великий греческий мыслитель ввел методику, дающую возможность определить объем любой фигуры. Его умозаключения стали основой интегрального исчисления. Объемными считают фигуры, получаемые в процессе вращения плоских
Евклидова геометрия с определенной точностью позволяет определить объем:
Отличие плоских и объемных фигур не позволяет ответить на вопрос некоторых страдальцев о том, как посчитать объем прямоугольника. Это, примерно, так же, как найти то, не знаю что. Путаница в геометрическом материале возможна, при этом прямоугольником иногда называют прямоугольный параллелепипед.
Что предпринимать, если форма тела не столь четко определена?
Определение объема сложных геометрических конструкций — работа не из легких. Стоит руководствоваться несколькими незыблемыми принципами.
- Любое тело можно разбить на более простые части. Объем равен сумме объемов его отдельных частей.
- Равновеликие тела имеют равные объемы, параллельный перенос тел не меняет его объема.
- Единицей объема считают объем куба с ребром единичной длины.
Наличие тел неправильной формы (вспомним пресловутую корону царя Герона) не становится проблемой. Определение объемов тел вполне возможно. Это процесс непосредственного измерения объемов жидкости с погруженным в нее телом, который будет рассмотрен ниже.
Различные прикладные задачи на определение объема
Вернемся к проблеме: как посчитать объем перевозимых грузов. Каким является груз: фасованным или сыпучим? Каковы параметры тары? Вопросов больше, чем ответов. Немаловажным станет вопрос массы груза, поскольку транспорт отличается грузоподъемностью, а трассы — максимальным весом транспортного средства. Нарушение правил перевозки грозит штрафными санкциями.
Задача 1. Пусть груз представляет собой прямоугольные контейнеры, заполненные товаром. Зная вес товара и контейнера, можно с легкостью определить суммарный вес. Объем контейнера определяем как объем прямоугольного параллелепипеда.
Зная грузоподъемность транспорта, его габариты, можно просчитать возможный объем перевозимого груза. Верное соотношение этих параметров позволяет избежать катастрофы, преждевременного выхода транспорта из строя.
Задача 2. Груз — сыпучий материал: песок, щебень и тому подобное. На этом этапе без знаний физики обойтись может только классный специалист, опыт которого в грузоперевозках позволяет интуитивно определить предельно допустимый к перевозке объем.
Научный метод предполагает знание такого параметра, как груза.
Используется формула V=m/ρ, где m — масса груза, ρ — плотность материала. Перед тем как посчитать объем, стоит узнать плотность груза, что также совсем не сложно (таблицы, лабораторное определение).
Эта методика также замечательно работает при определении объемов жидких грузов. При этом как единицу измерения используют литр.
Определение объемов строительных форм
Вопрос определения объемов играет немаловажную роль в строительстве. Возведение домов, других сооружений — дело затратное, стройматериалы требуют внимательного отношения и предельно точного расчета.
Основа здания — фундамент — представляет собой обычно литую конструкцию, заполняемую бетоном. Перед тем необходимо определить тип фундамента.
Плитный фундамент — плита в виде прямоугольного параллелепипеда. Столбчатое основание — прямоугольные или цилиндрические столбы определенного сечения. Определив объем одного столба и умножив его на количество, можно рассчитать кубатуру бетона на весь фундамент.
Рассчитывая объем бетона для стен или перекрытий, поступают достаточно просто: определяют объем всей стены, умножая длину на ширину и высоту, затем отдельно определяют объемы оконных и дверных проемов. Разность объема стены и суммарного объема проемов — объем бетона.
Как определить объем здания?
Некоторые прикладные задачи требуют знаний об объеме зданий и сооружений. К ним относятся проблемы ремонта, реконструкции, определения влажности воздуха, вопросы, связанные с теплоснабжением и вентиляцией.
Прежде чем ответить на вопрос о том, как посчитать объем здания, делают замеры по внешней его стороне: площади сечения (длина умножается на ширину), высоты здания от нижней части первого этажа до чердака.
Определение внутренних объемов отапливаемых помещений проводят по внутренним обводкам.
Устройство систем отопления
Современные квартиры и офисы невозможно представить без системы отопления. Основной частью систем являются батареи и соединительные трубы. Как посчитать объем системы отопления? Полный объем всех секций отопления, который указан на самом радиаторе, необходимо сложить с объемом труб.
И на этом этапе встает проблема: как посчитать объем трубы. Представим, что труба — цилиндр, решение приходит само собой: используем формулу цилиндра. В отопительных системах трубы заполняются водой, поэтому необходимо знать площадь внутреннего сечения трубы. Для этого определяем ее внутренний радиус (R). Формула определения площади круга: S=πR 2 . Общая длина труб определяется по их протяженности в помещении.
Канализация в доме — система труб
Закладывая трубы для водоотведения, также стоит знать объем трубы. На этом этапе необходим внешний диаметр, действия аналогичны предыдущим.
Определение объема металла, который идет на изготовление трубы — также интересная задача. Геометрически труба — цилиндр с пустотами. Определить площадь кольца, лежащего в ее сечении — задача достаточно сложная, но решаемая. Более простой выход — определить внешний и внутренний объемы трубы, разность этих величин и будет объемом металла.
Определение объемов в задачах физики
Знаменитая легенда о короне царя Герона стала известной не только вследствие решения задачи выведения «на чистую воду» вороватых ювелиров. Итог сложной мыслительной деятельности Архимеда — определение объемов тел неправильной геометрической формы. Основная мысль, извлеченная философом — объем вытесненной телом жидкости равен объему тела.
В лабораторных исследованиях пользуются мерным цилиндром (мензуркой). Определяют объем жидкости (V 1), погружают в нее тело, выполняют вторичные измерения (V 2). Объем равен разности вторичных и первичных измерений: V т = V 2 — V 1 .
Такой метод определения объемов тел используют при вычислении объемной плотности сыпучих нерастворимых материалов. Он крайне удобен при определении плотности сплавов.
Вычислить объем булавки можно с применением этого метода. Кажется, достаточно сложно определить объем столь маленького тела, как булавка или дробинка. Линейкой его не измерить, мерный цилиндр также достаточно велик.
Но если использовать несколько совершенно одинаковых булавок (n), то можно при помощи мерного цилиндра определить их суммарный объем (V т = V 2 — V 1) . Затем полученную величину разделить на количество булавок. V= V т n.
Эта задача становится понятной, если из одного большого куска свинца необходимо отлить множество дробинок.
Единицы измерения объема жидкости
Интернациональная система единиц предполагает измерение объемов в м 3 . В обыденной жизни чаще используют внесистемные единицы: литр, миллилитр. Когда определяются, как посчитать объем в литрах, используют систему перевода: 1 м 3 = 1000 литров.
Использование в повседневной жизни иных внесистемных мер может вызвать трудности. Англичане используют более привычные для них баррели, галлоны, бушели.
Система перевода:
Задачи с нестандартными данными
Задача 1. Как посчитать объем, зная высоту и площадь? Обычно такую задачу решают, определяя объем покрытия различных деталей гальваническим путем. При этом площадь поверхности детали (S) известна. Толщина слоя (h) — высота. Объем определяют произведением площади и высоты: V=Sh.
Задача 2. Для кубов интересной, с математической точки зрения, может выглядеть задача определения объема, если известна площадь одной грани. Известно, что объем куба: V=a 3 , где а — длина его грани. Площадь боковой поверхности куба S=a 2 . Извлекая из площади, получаем длину грани куба. Используем формулу объема, вычисляем его значение.
Задача 3. Вычислить объем фигуры, если известна площадь и даны некоторые параметры. К дополнительным параметрам можно отнести условия соотношения сторон, высот, диаметров основания и многое другое.
Для решения конкретных задач понадобятся не только знания формул расчета объемов, но и другие формулы геометрии.
Определение объемов памяти
Совершенно не связанная с геометрией задача: определить объем памяти электронных устройств. В современном, достаточно компьютеризованном мире эта проблема не бывает лишней. Точные устройства, какими являются персональные компьютеры, не терпят приблизительности.
Знание объемов памяти флешки или иного накопителя полезно при копировании, перемещении информации.
Немаловажно знать объем оперативной и постоянной памяти компьютера. Часто пользователь сталкивается с ситуацией, когда «не идет игра», «виснет программа». Проблема вполне возможна при низком объеме памяти.
Считается байт и его производные (килобайт, мегабайт, терабайт).
1 кБ = 1024 Б
1 МБ = 1024 кБ
1 ГБ = 1024 Мб
Странность в данной системе перерасчета следует из двоичной системы кодирования информации.
Размер памяти запоминающего устройства является его основной характеристикой. Сравнивая объем переносимой информации и объем памяти накопителя, можно определить возможность его дальнейшей эксплуатации.
Понятие «объема» настолько масштабно, что в полной мере уяснить его многогранность можно только решая прикладные задачи, интересные и увлекательные.
Инструкция
Узнайте плотность (ρ) материала, составляющего физическое тело, объем которого нужно рассчитать. Плотность — одна из двух характеристик объекта, задействованных в формуле вычисления объема. Если речь идет о реальных объектах, в расчетах используется средняя плотность, так как абсолютно физическое тело в реальных условиях представить трудно. В нем обязательно будут неравномерно распределенные хотя бы микроскопические пустоты или вкрапления посторонних материалов. Учитывайте при определении этого параметра и — чем она выше, тем меньше плотность вещества, так как при расстояние между его .
Второй параметр, который нужен для вычисления объема — масса (m) рассматриваемого тела. Эта величина определятся, как правило, по результатам взаимодействия объекта с другими или создаваемыми ими гравитационными полями. Чаще всего приходится иметь дело с массой, выраженной через взаимодействие с силой притяжения Земли — весом тела. Способы определения этой величины для относительно небольших объектов просты — их нужно просто взвесить.
Для вычисления объема (V) тела разделите определенный на втором шаге параметр — массу — на параметр, полученный на первом шаге — плотность: V=m/ρ.
В практических расчетах для вычислений можно использовать, например, объема. Он удобен тем, что не требует искать где-то еще плотность нужного материала и вводить его в вычислитель — в форме есть выпадающий с перечнем наиболее часто используемых в расчетах материалов. Выбрав в нем нужную строку, введите в поле «Масса» вес, а в поле «Точность вычисления» задайте количество знаков после запятой, которые должны присутствовать в результате вычислений. Объем в и вы найдете в помещенной ниже таблице. Там же на всякий случай будут приведены радиус сферы и сторона куба, который должен соответствовать такой объем выбранного вещества.
Источники:
- Калькулятор объема
- объем формула физика
Существуют геометрические объемные фигуры, их объем легко вычислить по формулам. Гораздо более сложной задачей представляется вычисление объема тела
человека, но и ее можно решить практическим путем.
Вам понадобится
- — ванна
- — вода
- — карандаш
- — помощник
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Общий обзор. Формулы стереометрии!
Здравствуйте, Дорогие друзья! В этой статье решил сделать общий обзор задач по стереометрии, которые будут на ЕГЭ по математик
е. Нужно сказать, что задачи из этой группы довольно разнообразны, но не сложны. Это задачи на нахождение геометрических величин: длин, углов, площадей, объёмов.
Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 50% из них решаются элементарно, практически устно.
Остальные требуют небольших усилий, знаний и специальных приёмов. В будущих статьях мы с вами будем рассмотривать эти задачи, не пропустите, подпишитесь на обновление блога.
Для решения необходимо знать формулы площадей поверхности и объёмов
параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Сложных задач нет, все они решаются в 2-3 действия, важно «увидеть» какую формулу необходимо применить.
Все нужные формулы представлены ниже:
Шар или сфера. Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки — центра шара.
Объем шара
равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Круглый конус может быть получен вращениемпрямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называт также конусом вращения. См. также Площадь поверхности круглого конуса
Объем круглого конуса
равен трети произведения площади основания S на высоту H:
(H — высота ребра куба)
Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипедимеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Объем прямоугольного параллелепипеда
равен произведению площади основания на высоту:
(S — площадь основания пирамиды, h — высота пирамиды)

Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.
Объем усеченной пирамиды
равен одной трети произведения высоты h (OS)
на сумму площадей верхнего основания S1 (abcde)
, нижнего основания усеченной пирамиды S2 (ABCDE)
и средней пропорциональной между ними.
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника — основания правильной пирамиды
h — высота правильной пирамиды
Правильная треугольная пирамида — этомногогранник, у которого одна грань — основание пирамиды — правильныйтреугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
Объем правильной треугольной пирамиды
равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC)
на высоту h (OS)
a — сторона правильного треугольника — основания правильной треугольной пирамиды
h — высота правильной треугольной пирамиды

Объем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставитьвысоту тетраэдра и площадь правильного (равностороннего) треугольника.
Объем тетраэдра
— равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра
(h — длина стороны ромба)
Длина окружности
p
составляет примерно три целых и одну седьмую длины диаметра круга. Точное отношение длины окружности к ее диаметру обозначается греческой буквой π
В итоге периметр круга или длина окружности вычисляется по формуле
(r — радиус дуги, n — центральный угол дуги в градусах.)
Как найти объем помещения-Обучение гипсокартонным работам
Строительство и ремонт
Автор: Administrator
08.05.2013 13:44
Найти объем помещения может понадобиться во многих случаях, например, для расчета вентиляции, отопительной системы или кондиционирования. Сделать это не очень сложно. В большинстве случаев достаточно провести простые измерения и элементарные вычисления.
Вычислить квадратуру помещения
В самом простейшем случае нужно узнать объем квадратного или прямоугольного помещения. Обычно это именно так и есть, потому что почти все квартиры и помещения в них делают именно такой простой, но эффективной формы.
Итак, с помощью рулетки или длинной линейки замеряют длину и ширину помещения и выписывают значения на бумагу, чтобы не забыть. Если по каким-то причинам нужно узнать объем помещения очень точно, мало провести по одному замеру длины и ширины, поскольку пол, стены и потолок могут быть не очень ровными. Это может даже не бросаться в глаза, но тем не менее.
Итак, для более точного расчета, нужно провести несколько измерений. Например, замерить ширину комнаты у дальней и ближней стены и по центру. После этого находят среднее арифметическое путем сложения результатов и деления их на три, то есть на количество проведенных замеров.
Те же манипуляции следует провести с длиной и высотой помещения.
Когда будут известны все три необходимых значения, можно узнать объем помещения. Сделать это крайне просто. Для этого их перемножают между собой.
Объем помещения нестандартной конструкции
Если помещение имеет нестандартную конструкцию и форму, придется разбить ее на несколько более удобных для расчета участков. Например, ниши и выступы рассчитываются отдельно, точно по приведенной выше схеме. Затем объем ниш складывают с общим объемом помещения, а выступы наоборот — вычитают из него.
Иногда помещение имеет сложную форму. В этом случае задача усложняется. Нужно опять же разбить такое помещение на отдельные, более удобные для измерений и расчетов участки, затем вычислить их объем отдельно и сложить вместе.
Для расчета площади треугольника подходит одноименная формула площади треугольника, а для расчета площади круга применяют формулу Герона. После того как будет найдена площадь данных фигур, ее умножают на высоту помещения. Тем самым получают объем, занимаемый данным пространством в помещении.
Иногда также нужно знать объем всего сооружения для каких-либо инженерных или архитектурных нужд. Для расчета этого объема, надо следовать общепринятым стандартам. Это так называемый строительный объем здания. Вычисляется он при умножении площади горизонтального сечения на высоту здания. То есть, сначала нужно замерить снаружи здания общую длину стен, затем высоту от земли до верхней части чердачного помещения, после чего оба значения перемножаются.
Читайте также…
gipsari.com
Как найти объем помещения — каталог статей на сайте
При организации вентиляции, кондиционирования, вытяжки и во многих других случаях нужно найти объем помещения. Именно от объема помещения будет зависеть необходимая мощность аппаратуры, которую потребуется установить.
Объем помещения измеряется в «кубах», то есть в кубических сантиметрах и кубических метрах. Конечно же, принято все переводить в кубические метры. Другими словами, 50 кубических сантиметров, записывается как 0,5 кубических метров.
Объем помещения находят по простейшей формуле, которая должна быть знакома каждому еще со школьной скамьи. Нужно узнать линейные размеры данного помещения в трех измерениях и перемножить их между собой.
То есть для начала берут длинную линейку, метр или рулетку и измеряют высоту помещения, длину помещения и его ширину. Эти значения надо записывать на бумагу, чтобы не забыть. Когда размеры будут известны, их умножают друг на друга. В итоге получают искомую цифру в кубических метрах, которая выражает в количественных характеристиках объем помещения.
Можно воспользоваться и другим методом. Найти площадь пола (а возможно, что она уже и так известна), а затем умножить ее на высоту потолка. Результат будет тем же, что и расчеты по предыдущей формуле.
Что делать, если помещение имеет не совсем стандартную форму? К примеру, помещение может состоять из нескольких «кубиков». В таком случае его следует разбить на более удобные для расчетов участки. После этого находят объем каждого из этих участков по отдельности. А когда это будет выполнено, итоги расчетов складывают.
Разумеется, лучше округлять найденные значения объема в большую сторону.
ПО ТЕМЕ:
Как найти площадь стен, потолка и пола: стандарт и нестандарт
Хочу больше статей:
Оставьте Ваш отзыв
Average rating: 0 reviews
Tags:
ламинат обои перепланировка
www.domstoy.ru
Как найти объем помещения |
Как рассчитать, посчитать объем помещения.
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Формула
Пример расчета объема помещения по формуле.
Источник: http://sdelalremont.ru
Метки: Cтроительство домов, дачные дома, деревянные дома, дом из бруса, дома из бруса, евроремонт, загородная недвижимость, загородные дома, земляные работы, как построить дом, котеджи, коттедж, прайс лист строительных работ, продажа готовых проектов, продажа котеджей, продажа коттеджей, проект деревянного дома, проект загородного дома, проект кирпичного дома, проектирование домов, проектирование коттеджей, проекты деревянных домов, проекты домов, проекты загородных коттеджей, проекты кирпичных домов, проекты котеджей, проекты коттеджей, ремонт Киев, ремонт Киевская область, ремонт офисов, ремонт под ключ, снос зданий, строительные компании, строительные компании Киев, строительство в Киеве, строительство дач, строительство дачных домов, строительство деревянного дома, строительство деревянных домов, строительство дома, строительство дома из бруса, строительство загородного дома, строительство загородных домов, строительство катеджей, строительство кирпичных домов, строительство котеджей, строительство коттеджей, стройгрупп, таунхаус, участок с домом, шпунтовое ограждение
remontnew.com
Как посчитать объем помещения — Легкое дело
Как посчитать объем помещения
Объем – геометрический термин, позволяющий измерить количественные характеристики жилого и нежилого пространства.
Определить объемы помещения можно, обладая сведениями о его линейных размерах и характеристиками формы. Объем очень тесно переплетается с характеристиками вместимости. Наверняка каждому знакомы такие термины как внутренний объем сосуда или какой-либо тары.
Единица измерения объема классифицируется в соответствии с всемирными стандартами. Существует специальная система измерений – СИ, в соответствии с которой кубический метр, литр или сантиметр выступает метрической единицей объема.
Любое помещение, будь-то жилая комната или производственное помещение – имеет свои характеристики объема. Если рассматривать любое помещение с точки зрения геометрии, то комната сравнима с параллелепипедом. Это шестигранная фигура, в случае с комнатой грани ее – это стены, пол и потолок. Каждая из сторон комнаты – это прямоугольник. Как известно из геометрии, существует формула нахождения объема прямоугольного параллелепипеда. Объем данной фигуры вычисляется посредством умножения трех главных измерений параллелепипеда – длины, ширины и высоты граней. Также вычислить объем помещения можно по более простой формуле – площадь пола умножают на высоту комнаты.
Как узнать объём комнаты
Итак, каким же образом производят вычисления объема конкретной комнаты? Вначале измеряем длину стены, самой длинной в комнате. Затем определяем длину самой короткой стены в комнате. Все эти измерения проводятся на уровне пола, по линии пролегания плинтусов. При измерениях рулеточная лента должна располагаться ровно. Настал черед измерить и высоту потолка. Для этого необходимо провести рулетку от пола до потолка в одном из углов комнаты.
Все измерения необходимо записывать, с точностью до десятых частей. После этого можно приступить непосредственно к вычислению объемов комнаты. Берем длину самой большой стены, умножаем ее на длину самой маленькой стены, затем полученный результат умножаем на высоту комнаты. В итоге получаем необходимые цифры – объем комнаты.
Вычислить объем помещения бывает нужно в самых разных ситуациях. Так, объем комнаты нужно знать при установке секционного радиатора отопления. Количество секций в нем прямо зависит от объемов комнаты. Если устанавливается кондиционер, также нужно знать объемы помещения, поскольку отдельный кондиционер предназначен только для конкретного объема помещения.
Объём помещения сложной формы
В том случае, когда комната имеет неправильную форму, нужно исходить снова же, из фигуры параллелепипеда. В данном случае комната будет представлена большим и маленьким объемным телом. Так вот, объем нужно измерить отдельно у большого параллелепипеда, а затем – у маленького. После этого два объема складываются между собой. Бывает, что строение комнаты совершенно нестандартное, могут присутствовать арки и ниши полукруглой формации. В данном случае объемы нужно вычислять по другой формуле – объем цилиндра. Объем цилиндра всегда вычисляется по единой формуле – площадь его основания умножается на высоту цилиндрического тела. Полукруглые конструкции в комнате можно представить частью цилиндра, исходя из этого делаются расчеты полного объема цилиндра, а затем из них отнимается лишняя часть, в соответствии с размерами полукруглой ниши.
Как найти объем помещения
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения. Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Как посчитать объем помещения
Объём — количественная черта места. Объём помещения определяется его формой и линейными размерами. С понятием объёма плотно сплетено понятие вместимость, другими словами объём внутреннего места сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр. Для вас понадобится Для измерения объема помещения для вас будет нужно рулетка, лист бумаги, калькулятор, ручка. 1 Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед.
Параллелепипед — это большая фигура, у которой 6 граней. и неважно какая из их есть прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Количество прямоугольного параллелепипеда равен произведению 3-х его измерений. Не считая этой формулы может быть измерить количество помещения умножив площадь пола на высоту.
2 Итак приступайте к вычислениям объема помещения. Определите длину одной стены ,позже определите длину 2-ой стены. Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно.
На данный момент определите высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Приобретенные данные запишите на листочек, чтоб не запамятовать. На данный момент приступайте к вычислениям: умножите длину длинноватой стены на длину недлинной стены, приобретенное произведение умножите на высоту и вы получите требуемый итог.
Объемы помещений вычисляют в различных случаях: 1) в случае приобретения кондюка воздуха, так как кондюки рассчитаны на определенный количество помещений; 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе находится в зависимости от объема помещения. 3 Если у вас комната неверной формы, другими словами складывается из вроде бы огромного параллелепипеда и малеханького. В данном случае необходимо измерить количество каждого из их раздельно, а позже сложить. Если в вашей комнате есть альков. тогда его количество нужно высчитывать по формуле объема цилиндра. Количество всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где. – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота.
Представьте для себя ваш альков как часть цилиндра, вычислите количество вроде бы всего цилиндра, позже поглядите какую часть этого цилиндра занимает ваш альков,отымите от общего объема лишнюю часть.
Как рассчитать площадь комнаты?
Если комната с четырьмя стенами и имеет стандартную геометрическую фигуру с прямыми углами, тогда необходимо измерить две стенки и умножив полученные две цифры друг на друга мы получим площадь помещения, а для объёма нужно умножить полученный результат на высоту. но это только при правильных геометрических фигурах.
Сложнее находить площадь и размеры, когда форма комнаты неправильного размера, например такого.
Тогда нужно применять все знания геометрии, а именно — разделить комнату на несколько правильных фигур и в соответствии с формулами этих фигур найти их площадь, а потом все результаты сложить вместе, тогда получится общая площадь помещения. Для нахождения высоты необходимо полученный результат общей площади умножить на высоту.
Ещё хуже обстоят дела с нестандартными помещениями с неправильными углами стен и крыши. Тогда придётся переносить все размеры помещения на бумагу, разделять его на правильные фигуры и исходя из каждой фигуры находить её площадь и объём, а потом полученные результаты суммировать.
В площадь помещения не входят выступы окон и прочего, что выше пола, но они входят в расчёт объёма помещения.
Как посчитать площадь помещения
В случае измерения комнаты неправильной формы для более точного подсчета площади рекомендуется разбить ее на прямоугольники. Подсчитав площадь каждого такого участка, можно узнать общую площадь комнаты путем простого суммирования всех полученных результатов.
Если же разбить комнату на прямоугольные участки не представляется возможным, то можно попробовать такие фигуры как треугольник либо сектор круга. Площадь треугольника считается по формуле Герона: S=v**).
Р — полупериметр треугольника, который можно рассчитать таким образом: р=/2
http://denisyakovlev.com
legkoe-delo.ru
Как посчитать кубатуру помещения формула. Как посчитать объем помещения
Объём — количественная характеристика пространства. Объём помещения определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр.
Вам понадобится
- Для измерения объема помещения вам потребуется рулетка, лист бумаги, калькулятор, ручка.
Инструкция
Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед. Параллелепипед — это объемная фигура, у которой шесть граней (например комната: 4 стены, потолок, пол), и каждая из них является прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Кроме этой формулы можно измерить объем помещения умножив площадь пола на высоту.
Итак приступайте к вычислениям объема помещения. Измерьте длину одной стены (длинной стены),потом измерьте длину второй стены (короткой стены). Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно. Теперь измерьте высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Полученные данные запишите на листочек, чтобы не забыть. Теперь приступайте к вычислениям: умножите длину длинной стены на длину короткой стены, полученное произведение (число)умножите на высоту и вы получите требуемый результат. помещений вычисляют в различных случаях: 1) в случае покупки кондиционера воздуха, так как кондиционеры рассчитаны на определенный объем помещений- 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе напрямую зависит от объема помещения.
Если у вас комната неправильной формы, то есть состоит из как бы большого параллелепипеда и маленького. В данном случае необходимо измерить объем каждого из них отдельно, а потом сложить. Если в вашей комнате есть альков (ниша полукруглой формы), тогда его объем нужно высчитывать по формуле объема . Объем всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где? – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота. Представьте себе ваш альков как часть цилиндра, вычислите объем как бы всего цилиндра, потом посмотрите какую часть этого цилиндра занимает ваш альков,отнимите от общего объема лишнюю часть.
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
Инструкция
Самый простой случай – когда требуется определить объем помещения
правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения
. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели и вы получите искомый объем.
Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения
на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения
. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части у
piorit.ru
Онлайн калькулятор: Объем геометрических фигур
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Формула:
Объем куба
Длина ребра куба (H)
Точность вычисления
Знаков после запятой: 5
save Сохранить share Поделиться extension Виджет
Объем прямоугольной призмы
Размеры прямоугольной призмы
Формула:
Объем прямоугольной призмы
Точность вычисления
Знаков после запятой: 5
save Сохранить share Поделиться extension Виджет
Объем пирамиды
Размеры пирамиды
Формула:
Объем пирамиды
Площадь основания
Точность вычисления
Знаков после запятой: 5
save Сохранить share Поделиться extension Виджет
Объем усеченной пирамиды
Размеры усеченной пирамиды
Формула:
Объем усеченной пирамиды
Точность вычисления
Знаков после запятой: 5
planetcalc.ru
Как посчитать объем помещения » Белисп
Объём — количественная черта места. Объём помещения определяется его формой и линейными размерами. С понятием объёма плотно сплетено понятие вместимость, другими словами объём внутреннего места сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр. Для вас понадобится Для измерения объема помещения для вас будет нужно рулетка, лист бумаги, калькулятор, ручка. 1 Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед.
Параллелепипед — это большая фигура, у которой 6 граней (например комната: 4 стены, потолок, пол), и неважно какая из их есть прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Количество прямоугольного параллелепипеда равен произведению 3-х его измерений. Не считая этой формулы может быть измерить количество помещения умножив площадь пола на высоту.
2 Итак приступайте к вычислениям объема помещения. Определите длину одной стены (длинноватой стены),позже определите длину 2-ой стены (недлинной стены). Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно.
На данный момент определите высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Приобретенные данные запишите на листочек, чтоб не запамятовать. На данный момент приступайте к вычислениям: умножите длину длинноватой стены на длину недлинной стены, приобретенное произведение (число)умножите на высоту и вы получите требуемый итог.
Объемы помещений вычисляют в различных случаях: 1) в случае приобретения кондюка воздуха, так как кондюки рассчитаны на определенный количество помещений; 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе находится в зависимости от объема помещения. 3 Если у вас комната неверной формы, другими словами складывается из вроде бы огромного параллелепипеда и малеханького. В данном случае необходимо измерить количество каждого из их раздельно, а позже сложить. Если в вашей комнате есть альков (ниша полукруглой формы), тогда его количество нужно высчитывать по формуле объема цилиндра. Количество всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где ? – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота.
Представьте для себя ваш альков как часть цилиндра, вычислите количество вроде бы всего цилиндра, позже поглядите какую часть этого цилиндра занимает ваш альков,отымите от общего объема лишнюю часть.
Наука и техника
belisp.ru
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
| Номер печи | Тип | Объем помещения | Масса | Стоимость |
|---|---|---|---|---|
| 1 | Дровяная | 8-12 | 40 | 18 000 |
| 2 | Дровяная | 10-16 | 48 | 19 500 |
| 3 | Электрическая | 9-15,5 | 15 | 15 000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6500 руб.
1
Найдите объём парного отделения строящейся бани. Ответ дайте в кубических метрах.
2
Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 800 рублей?
3
На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
4
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
5
На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дороже электрической без учёта установки?
2
Найдите объём парного отделения строящейся бани. Ответ дайте в кубических метрах.
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
| Номер печи | Тип | Объем помещения | Масса | Стоимость |
|---|---|---|---|---|
| 1 | Дровяная | 8-12 | 40 | 18 000 |
| 2 | Дровяная | 10-16 | 48 | 19 500 |
| 3 | Электрическая | 9-15,5 | 15 | 15 000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6500 руб.
1
Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
2
Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 800 рублей?
3
На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
4
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
5
На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дороже электрической без учёта установки?
3
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.
Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать
число 51118).
| Мобильный интернет | 2,5 Гб | 3 Гб | 3,25 Гб | 1 Гб |
| Номер месяца |
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
1
Сколько рублей потратил абонент на услуги связи в июне?
2
Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?
3
Абонент хочет приобрести новый смартфон. В трёх салонах сотовой связи этот смартфон продаётся в кредит (сначала делается первоначальный взнос, а потом ежемесячно в течение всего срока кредита вносятся платежи) на разных условиях. Условия приведены в таблице.
| Салон | Стоимость смартфона (руб.) |
Первоначальный взнос (в % от стоимости) |
Срок кредита (мес.) |
Ежемесячный
платёж (руб.) |
| А | 18 000 | 20 | 6 | 2650 |
| Б | 17 500 | 30 | 12 | 1200 |
| В | 17 600 | 25 | 12 | 1300 |
Определите, в каком из салонов покупка обойдётся дешевле всего (с учётом переплаты). В ответ запишите эту сумму в рублях.
4
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ | |
|
А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь |
1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
|---|---|---|---|
| 13 | 14 | 15 | |
| 165 | 165/70 | 165/65 | — |
| 175 | 175/65 | 175/65; 175/60 | — |
| 185 | 185/65; 185/60 | 185/60 | 185/55 |
| 195 | 195/60 | 195/55 | 195/55; 195/50 |
Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
Автомобильное колесо, как правило, представляет собой металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13.
1
На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14?
2
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
3
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/50 R15?
4
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых.
5
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.
| Номер листа | Длина (мм) | Ширина (мм) |
|---|---|---|
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
1
Сколько листов формата А3 получится из одного листа формата А2?
2
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
3
Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.
4
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Пройти тестирование по этим заданиям
. Задание 1 Прочитайте внимательно текст и выполните
задание 1-5
Хозяин дачного участка строит баню с парным отделением. Парное
отделение имеет размеры: длина 3,9 м, ширина 2,1 м, высота 2 м. Для разогрева парного
помещения можно использовать электрическую или дровяную печь. Три возможных
варианта даны в таблице.
|
Номер печи |
Тип |
Объем |
Масса |
Стоимость |
|
1 |
Дровяная |
9-14 |
42 |
19 100 |
|
2 |
Дровяная |
12-18 |
49 |
20 500 |
|
3 |
Электрическая |
10-17 |
16 |
16 000 |
Для установки дровяной печи дополнительных затрат не потребуется.
Установка электрической печи потребует подведения специального кабеля, что
обойдётся в 6200 руб. Кроме того, хозяин подсчитал, что за год электрическая
печь израсходует 2300 киловатт-часов электроэнергии по 3,5 руб. за 1
киловатт-час, а дровяная печь за год израсходует 1,6 куб. м дров, которые
обойдутся по 1700 руб. за 1 куб. м.
1Найдите объём парного отделения
строящейся бани (в куб. м)..
Для нахождения объема парного
отделения бани ,надо перемножить ширину,длину и высоту.
V=aбс
где a — ширина, b — длина, с — высота.
V=2,1*3,9*2 =16,38
Ответ: 16,38.
2. На сколько
рублей дровяная печь, подходящая,по отапливаемому объему парного отделения,
обойдется дешевле электрической с учетом установки?
Объем парного отделения бани 16,38 ,
по таблице подойдет печь №2(отапливаемый объем 12-18 ).
Цена печи №3 20500 руб. , цена электрической
печи с установкой
16000+6200=22200руб.
На сколько рублей дровяная печь, обойдется дешевле электрической
22200-20500= 1700 р
3.На сколько рублей эксплуатация дровяной печи,
которая подходит по отапливаемому объему парного отделения, обойдется дешевле эксплуатации
электрической в течении года?
Эксплуатация дровяной печи №2 за год составит
1700 · 1,6 = 2720
рублей. (1,6 дров
по 1700 руб. за 1 )
Эксплуатация электрической печи за год составит 2300 · 3,5 = 8050 рублей. (2300киловатт-часов
по 3,5 руб. за 1 киловатт-час).
Разница в стоимости эксплуатации:
8050-2720=5330 руб.
Ответ: 5330
4 . Доставка
печи из магазина до участка стоит 700 рублей. При покупке печи ценой выше 19
000 рублей магазин предлагает скидку 5 % на товар и 20 % на доставку. Сколько
будет стоить покупка печи номер 2 вместе с доставкой на этих условиях?.
Стоимость печи №2 20 500 руб. , следовательно за ее покупку
предоставляется скидка 5% на товар и 20% на доставку.
Печь
1-й способ : 100%-5%=95%
20500— 100%
Х—-95% х= = руб. (цена печи со скидкой)
2-й способ :
20500-0,05*20500= 19475 руб. (цена печи со скидкой)
Доставка 700-0,2*700 =560 руб.
Итого за покупку и доставку печи заплатят 19475+560=20035 руб.
Ответ: 20035
5.
5. Хозяин выбрал дровяную печь.
Чертёж печи показан на рис. 1.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха
выполнена в виде арки, приваренной к передней стенке по дуге окружности (см.
рис. 1). Для установки печки хозяину понадобилось узнать радиус закругления
арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус в
сантиметрах.

прямоугольный треугольник со сторонами К, L/2 ,R и выведем формулу для такого
типа задач.
Теорема Пифагора .
Но, K=R-H ,
подставим ,
раскроем скобки ,и упростим
=
R=

R= —
формула, которую нужно запомнить
Н=61-53=8
Подставим данные R=(4*8*8+36*36):8*8 = =24,25
округлить до десятых 24,3
Прочитав внимательно текст, выполните задания № 1 — 5. Хозяин дачного участка строит баню с парным отделением.
Задание 1 (ОГЭ 2020)
Найдите объем парного отделения строящейся бани (в куб. м).
Решение:
Помещение для парного отделения бани — прямоугольный параллелепипед. Его объем равен произведению линейных размеров, то есть длины, ширины и высоты.
V = 2,5 * 2,3 * 2,1 = 12,075(куб. м)
Ответ: 12,075.
Задание 2 (ОГЭ 2020)
На сколько рублей дровяная печь, подходящая по отапливаемому объему парного отделения, обойдется дешевле электрической с учетом установки?
Решение: Объем парного отделения мы вычислили в задании №1. Из таблицы видно, что для данного объема подойдет дровяная печь «Кентавр». Ее стоитмость 25000 рублей. Установка такой печи дополнительных затрат не требует.
Стоимость электрической печи с установкой составляет:
23000 + 6500 = 29500 (рублей).
29500 — 25000 = 4500 (рублей) — разность в стоимости электрической и дровяной печей.
Ответ: 4500.
Задание 3 (ОГЭ 2020)
Решение:
- За год эксплуатации дровяной печи израсходуется 2 кубических метра дров. Стоимость 1700 рублей за куб. Всего уйдет денег: 2 * 1700 = 3400 (рублей).
- Рассчитаем затраты на работу электропечи. 3000 * 5 = 15000 (рублей).
- Выгода в эксплуатации дровяной печки: 15000 — 3400 = 11600 (рублей).
Ответ: 11600.
Задание 4 (ОГЭ 2020)
Доставка печи из магазина до участка стоит 500 рублей. При покупке печи ценой выше 20000 рублей магазин предлагает скидку 3% на товар и 35% на доставку. Сколько будет стоить покупка печи «Кентавр» вместе с доставкой на этих условиях?
Решение:
Печь «Кентавр» стоит 25000 рублей, поэтому магазин сделает скидки на товар и доставку.
- 25000 — 25000 * 0,03 = 24250 (руб.) — стоимость печи с учетом скидки.
- 500 — 500 * 0,35 = 325 (рублей) — доставка.
- 24250 + 325 = 24575 (рублей) — итоговая стоимость печи «Кентавр».
Ответ: 24575.
Задание 5 (ОГЭ 2020)
Хозяин выбрал дровяную печь. Чертеж печи представлен на рисунке 2. Размеры указаны в сантиметрах.
Решение:
На рисунке 2 cделаем дополнительные построения:
- проведем 3 радиуса OA, OB и OD;
- хорду AB.
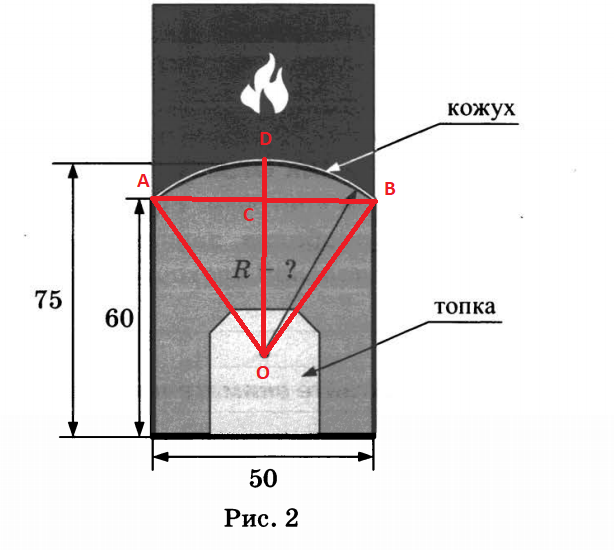
Рассмотрим △OAB. Он равнобедренный. ОС — медиана, проведенная к основанию. ОС также и высота. △OСA — прямоугольный. Воспользуемся теоремой Пифагора. Обозначим радиус за х.
CВ = 75 — 60 = 15.
AB =50. AC = BC = 25.
OC = x — 15.
AO2
= AC2 + CO2;
x2
= 252 + (x — 15)2;
x2
= 625 + x2 — 30x + 225;
30x = 850;
X ≈ 28,3 (см).
Ответ: 28,3.
Подробное решение варианта ОГЭ 2020 — земледелец устраивает на склонах гор терассы — задания 1 — 5.
Страница 5 из 7
Практические задачи №1-5 к ОГЭ по математике
Прочитайте внимательно текст и выполните задания 1–5.
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
|
Номер печи |
Тип |
Объём помещения (куб. м) |
Масса (кг) |
Стоимость (руб.) |
|
1 |
дровяная |
8–12 |
40 |
18 000 |
|
2 |
дровяная |
10–16 |
48 |
19 500 |
|
3 |
электрическая |
9–15,5 |
15 |
15 000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6500 руб.
Задание 1.
Установите соответствие между массами и номерами печей.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Масса (кг) |
15 |
40 |
48 |
|
Номер печи |
Решение:
Ответ: 312
Задание 1.
Установите соответствие между стоимостями и номерами печей.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Стоимость (руб.) |
15 000 |
19 500 |
18 000 |
|
Номер печи |
Решение:
Ответ: 321
Задание 1.
Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наибольшим для отопления помещений.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Объём (куб. м) |
12 |
15,5 |
16 |
|
Номер печи |
Решение:
Ответ: 132
Задание 1.
Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Объём (куб. м) |
8 |
9 |
10 |
|
Номер печи |
Решение:
Ответ: 132
Задание 2.
Найдите объём парного отделения строящейся бани. Ответ дайте в кубических метрах.
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V=a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
Ответ: 15,4
Задание 2.
Найдите суммарную площадь стен парного отделения строящейся бани (без площади двери). Ответ дайте в квадратных метрах.
Решение:
Найдём площадь всех 4-х стен (2 длинных и 2 широких) парного отделения:
Sстен = 3,5·2 + 3,5·2 + 2,2·2 + 2,2·2 = 3,5·4 + 2,2·4 = 22,8 м
Окон нет, есть дверь, найдём её площадь:
Sдвери = 60 см·1,8 м = 0,6 м·1,8 м = 1,08 м
Вычтем от площади стен площадь двери:
S = Sстен – Sдвери = 22,8 – 1,08 = 21,72 м
Ответ: 21,72
Задание 2.
Найдите площадь потолка парного отделения строящейся бани. Ответ дайте в квадратных метрах.
Решение:
S=3,5*2,2=7,7м2
Ответ: 7,7
Задание 2.
Найдите площадь пола парного отделения строящейся бани. Ответ дайте в квадратных метрах.
Решение:
S=3,5*2,2=7,7м2
Ответ: 7,7
Задание 3.
На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дешевле электрической с учётом установки?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V=a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. А электрическая обойдется 15000 печка + потребует подведения специального кабеля, что обойдётся в 6500 руб. 21 500 руб.
21 500 — 19 500=2 000
Ответ: 2000
Задание 3.
На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дороже электрической без учёта установки?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. А электрическая обойдется 15000 печка.
19 500 — 15 000=4500
Ответ: 4500
Задание 3.
Во сколько рублей обойдётся покупка дровяной печи, подходящей по объёму парного отделения, с доставкой, если доставка печи до дачного участка будет стоить 1400 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. Доставка 1400. 19500+1400=20900
Ответ: 20900
Задание 3.
Во сколько рублей обойдётся покупка дровяной печи, подходящей по объёму парного отделения, с доставкой, если доставка печи до дачного участка будет стоить 1200 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. Доставка 1400. 19500+1200=20700
Ответ: 20700
Задание 3.
Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 1000 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть электрическая печка подойдет. 1500+1000=16 000
Ответ: 16 000
Задание 3.
Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 800 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть электрическая печка подойдет. 1500+8000=15 800
Ответ: 15800
Задание 4.
На дровяную печь, масса которой 40 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
Решение:
18000-(18000*10)/100= 18000-1800=16 200
Ответ: 16200
Задание 4.
На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
Решение:
19 500-(19 500*10)/100= 19500-1950=17550
Ответ: 17550
Задание 4.
На электрическую печь сделали скидку 15%. Сколько рублей стала стоить печь?
Решение:
15000-(15000*15)/100=15000-2250=12750 р.
Ответ: 12750
Задание 4.
В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10%, на печь номер 2 — 35%, на печь номер 3 — 25%.
Сколько рублей стоила печь номер 1 в прошлом году?
Решение:
1-я печь сейчас стоит 18000 р., это 100-10=90% от прошлогодней цены,
значит 18000*100:90=20000 р. стоила печь номер 1 в прошлом году
Ответ: 20000
Задание 4.
В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10%, на печь номер 2 — 35%, на печь номер 3 — 25%.
Сколько рублей стоила печь номер 2 в прошлом году?
Решение:
2я печь стоит 19500 р., это 100-35=65% от прошлогодней цены
19500*100:65=30000 р. стоила печь номер 2 в прошлом году
Ответ: 30000
Задание 4.
В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10%, на печь номер 2 — 35%, на печь номер 3 — 25%.
Сколько рублей стоила печь номер 3 в прошлом году?
Решение:
3-я печь стоит 15000 р., это 100-25=75 % от прошлогодней цены
15000*100:75=20000 р. стоила печь номер 3 в прошлом году
Ответ: 20000
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 19 000 рублей магазин делает скидку 5% на товар и 30% на доставку. Сколько рублей будет стоить покупка печи номер 2 с доставкой на этих условиях?
Решение:
2-19500
19500-19500*5/100+1000*70/100=18025+700=18725Ответ: 18725
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 19 000 рублей магазин делает скидку 10% на товар и 25% на доставку. Сколько рублей будет стоить покупка печи номер 2 с доставкой на этих условиях?
Решение:
2-19500
19500-19500*10/100+1000*75/100=17550+750=18300
Ответ: 18300
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 17 000 рублей магазин делает скидку 15% на товар и 20% на доставку. Сколько рублей будет стоить покупка печи номер 1
с доставкой на этих условиях?
Решение:
1-18000
18000-18000*15/100+1000*(100-20)/100=15300+800=16100
Ответ: 16100
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 17 000 рублей магазин делает скидки 5% на товар
и 25% на доставку. Сколько рублей будет стоить покупка печи номер 1 с доставкой на этих условиях?
Решение:
1-18000
18000-18000*5/100+1000*(100-25)/100=17100+750=17850 р.
Ответ: 17850
8889B9
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (442+332)=√ (1936+1089)=√ 3025=55
Ответ: 55
09D7F4
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (402+302)=√ (1600+900)=√ 2500=50
Ответ: 50
59DCD0
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (602+252)=√ (3600+625)=√ 4225=65
Ответ: 65
BE99C7
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (602+322)=√ (3600+1024)=√ 4624=68
Ответ: 68
EF4A79
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (602+322)=√ (3600+1024)=√ 4624=68
Ответ: 68
B65DB1
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (452+242)=√ (2025+576)=√ 2601=51
Ответ: 51
4B7C1D
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (482+202)=√ (2304+400)=√ 2704=52
Ответ: 52
D58214
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (522+392) =√ (2704+1521) =√ 4225=65
Ответ: 65
BEAF28
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (362+272)=√ (1296+729)=√ 2025=45
Ответ: 45
9825C3
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (722+212)=√ (5184+441)=√ 5625=75
Ответ: 75
8EF36E