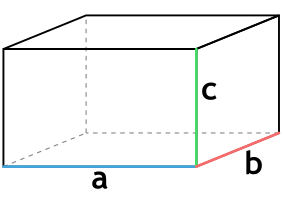
{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
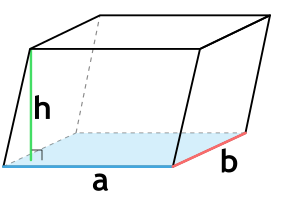
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a — длина параллелепипеда
b — ширина параллелепипеда
c — высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab — это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
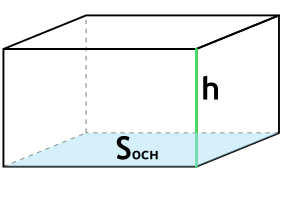
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a — длина основания параллелепипеда
b — ширина основания параллелепипеда
h — высота параллелепипеда
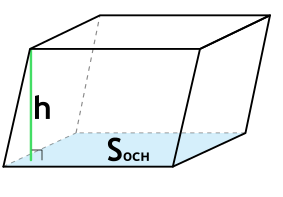
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Формулы объёма и площади поверхности. Многогранники.
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
 Куб |
|
|
 Параллелепипед |
|
|
 Прямоугольный параллелепипед |
|
|
 Призма |
|

|
 Пирамида |
|

|
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат),
(маленький прямоугольник),
Подставим все данные в формулу: 
Ответ: 424.
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник),
(маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно,
большая боковая грань призмы.
Поэтому или
откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда
(по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда
следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как
высота воды
должна быть в 81 раз меньше, чем
Она равна
(см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту
Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, 
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Объёмы многогранников
Куб
V = a3 , где а — ребро куба
Прямоугольный параллелепипед
V = a * b * c, где a, b, c — рёбра фигуры: высота, ширина и длина
Параллелепипед
V = Sоснования * h, где h — высота параллепипеда.
Призма
V = Sоснования * h, где h — высота призмы
Пирамида
V = 1/3 Sоснования * h, где h — высота пирамиды
Объёмы тел вращения
Цилиндр
V = πR2h, где R — радиус основания, h — высота
Конус
V = 13 Sоснования * h
Шар
V = 43πR3 , где R — радиус шара
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
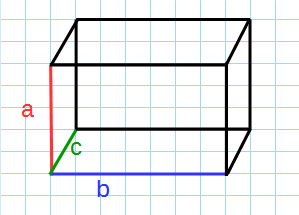
Формула объема параллелепипеда через его ребра:
a,b,c — ребра параллелепипеда.
Через стороны и высоту
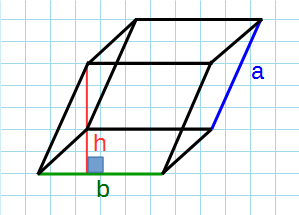
Формула объема параллелепипеда:
a,b — ребра параллелепипеда; h — высота параллелепипеда.
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ — длина;
$b$ — ширина;
$с$ — высота(она же боковое ребро);
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$V$ — объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ — длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ — радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции. - Квадрат.
$S=a^2$, где $а$ — сторона квадрата.
Пример:
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ — стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$