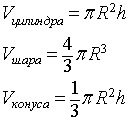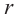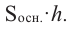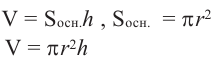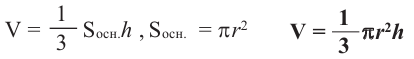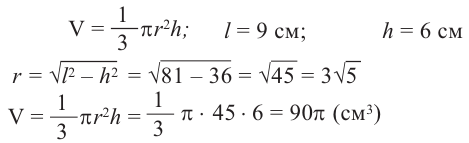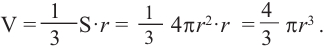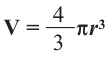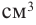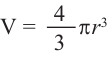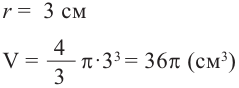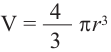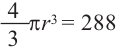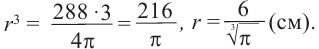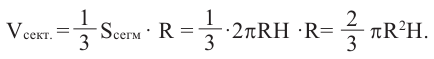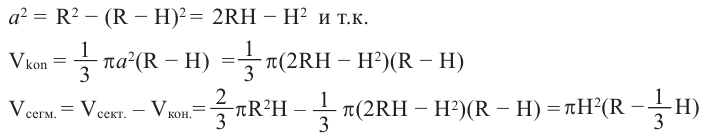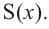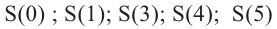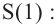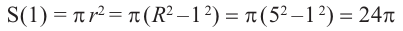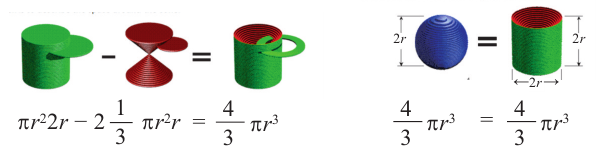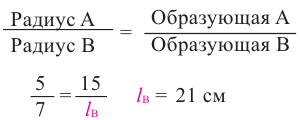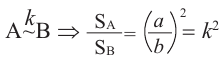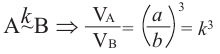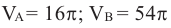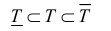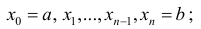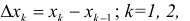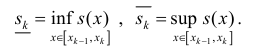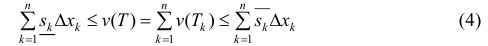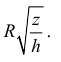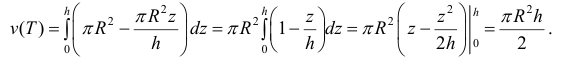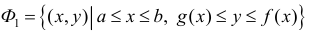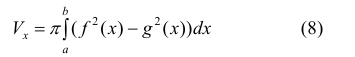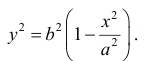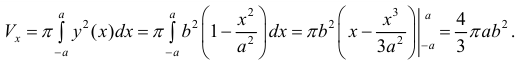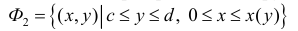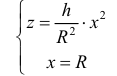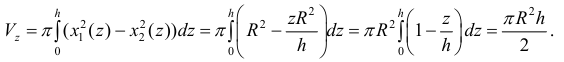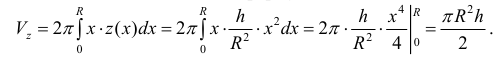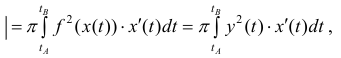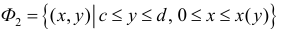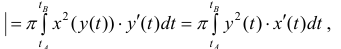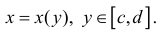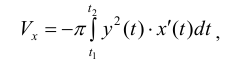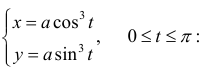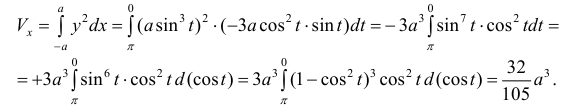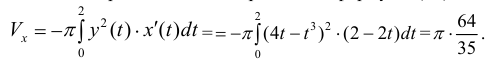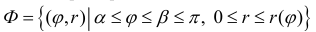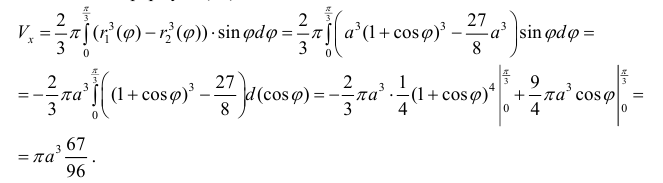Как найти объем конуса зная объем шара

Примечание. Это урок с решениями задач по геометрии (раздел стереометрия, конус). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме.

Задача.

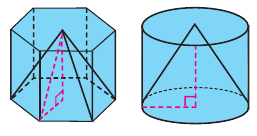
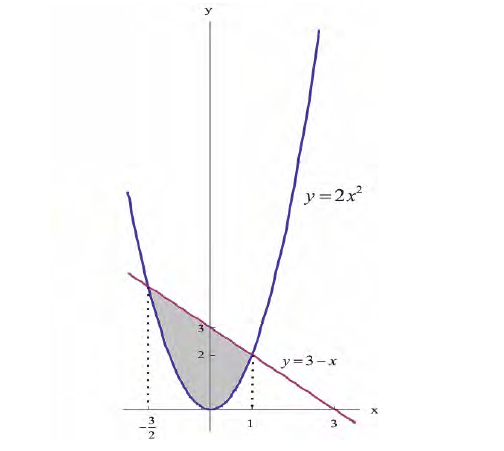
В цилиндр вписаны шар и конус, причём высота цилиндра равна диаметру его основания.

Найти отношение объёма конуса к объёму шара, и к объёму цилиндра.

Решение.

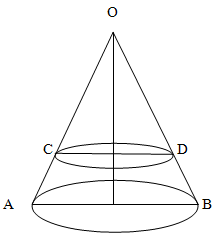
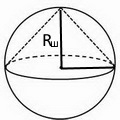
Для решения задачи воспользуемся формулами нахождения объема шара, цилиндра и конуса:

Учтем, что по условию задачи высота цилиндра, а, соответственно и конуса, равны диаметру шара, что следует из построения согласно условию. То есть шар касается обеих оснований цилиндра в их центре. Из чего запишем:

h = 2R

Откуда

Vцилиндра = πR²h =  πR²2R = 2πR³

Vшара = 4/3πR³

Vконуса = 1/3πR²h = 1/3πR²2R = 2/3πR³

Таким образом, соотношение объема конуса к объему шара будет равно:

Vконуса / Vшара =  2/3πR³ / 4/3πR³ = 2/3 / 4/3 = 1/2

А соотношение объема конуса к объему цилиндра будет равно:

Vконуса / Vшара = 2/3πR³ / 2πR³ = 2/3 / 2 = 1/3

Ответ: 1/2 и 1/3

Задача.

Объем конуса равен 27. На высоте конуса лежит точка и делит её в отношении 2:1 считая от вершины. Через точку проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решение.

Обратим внимание, что треугольники AOB и COD — подобны. Из условия задачи определим коэффициент подобия как 2:3.



Объем конуса находится по формуле, указанной в предыдущей задаче.

Vконуса = 1/3πR²h = 27 (по условию)

Тогда объем малого конуса будет равен

Vмал.конуса = 1/3π(2/3R)²(2/3h)

то есть

Vмал.конуса = 1/3π 4/9 R² 2/3 h

Vмал.конуса = 8/27 *1/3π R² h

а так как мы знаем, что 1/3π R² h= 27 (см. выше), то

Vмал.конуса = 8/27 * 27 = 8

Ответ: объем малого конуса равен 8

0
 

 Площадь боковой поверхности конуса |

Описание курса

| Объем конуса (2) 

Воспользуемся формулой для нахождения объема шара: 

V(шара)=4πR3314=4πR3342=4πR310,5=πR3{V(шара)=displaystyle{4pi R^3over3}}\
{14=displaystyle{4pi R^3over3}}\
42=4pi R^3\
10,5=pi R^3  

Теперь напишем формулу для нахождения объема конуса: 

V(конуса)=πR2H3{V(конуса)=displaystyle{pi R^2Hover3}} 

Так как радиус шара равен высоте конуса R(шара)=H(конуса), то 

V(конуса)=πR33{V(конуса)=displaystyle{pi R^3over3}}

подставим найденное значение πR3pi R^3 в формулу для нахождения объема конуса, так радиус основания конуса равен радиусу шара

V(конуса)=10,53=3,5{V(конуса)=displaystyle{10,5over3}=3,5} 

Ответ: 3,5

Задача 11571 Конус вписан в шар. Объём шара равен 14….

Содержание:

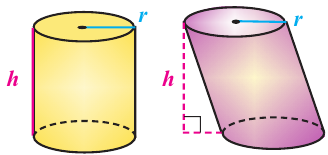
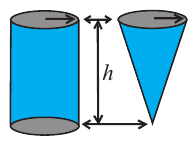
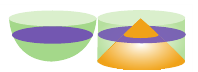
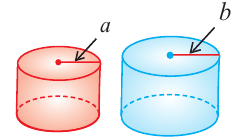
Говоря об объеме, имеют ввиду вместимость пространственной фигуры. Как вы думаете, емкость какого из цилиндров на рисунке больше?

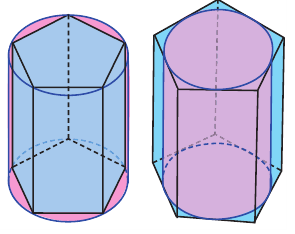
Призмой, вписанной (описанной) в цилиндр, называется призма, основания которой вписаны (описаны) в основания цилиндра.

Объем цилиндра

Пусть в цилиндр с радиусом

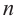
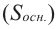
При бесконечном возрастании площадь оснований данных призм приближаются к площади основания цилиндра, а их объемы к объему цилиндра:

Объем цилиндра равен произведению площади основания на высоту.

Практическая работа. Какая связь существует между объемами призмы и пирамиды, если они имеют одинаковые высоты и основания? Можно ли эту связь применить для объемов цилиндра и конуса?

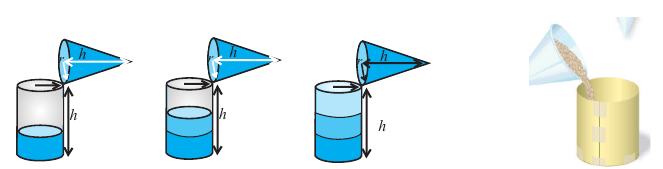
Сделайте из картона модели сосудов в виде конуса и цилиндра, радиусы оснований и высоты которых одинаковы. Заполните цилиндрический сосуд при помощи сосуда в виде конуса (песком, рисом, и т. п.).

Сколько таких сосудов понадобится, чтобы заполнить цилиндрический сосуд? Верно ли утверждение, что цилиндрический сосуд можно заполнить тремя полными сосудами в виде конуса?

Обобщите соответствующую информацию о вычислении объема призмы, цилиндра, пирамиды и конуса, записав ответ в закрашенные ячейки.

Объем призмы и цилиндра:

Объем = площадь основания

Объем пирамиды и конуса:

Объем = объем призмы или цилиндра, имеющих одинаковые

основание и высоту.

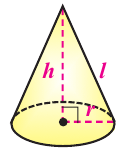
Объем конуса

Объем конуса равен произведению одной третьей площади основания на высоту.

Пример №1

Образующая конуса 9 см, высота 6 см. Найдите объем конуса.

Решение:

Объем шара и его частей

Практическая работа.

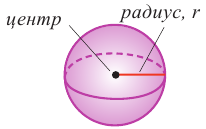
1. Возьмите мяч. Определите его диаметр.

2. Изобразите на бумаге развертку цилиндра, диаметр и высота которого равны диаметру шару.

3. Вырежьте и сверните полученную развертку в цилиндр без верхней крышки. Скрепите развертку при помощи клейкой ленты. Разделите высоту цилиндра на 3 равные части и сделайте соответствующие разметки.

4. Обверните мяч фольгой или плотным материалом и сделайте мешок сферической формы. Наполните его песком.

5. Пересыпьте песок в цилиндр. Какая часть цилиндра заполнится?

Если разделить поверхность шара сеткой из вертикальных и горизонтальных линий и маленький «прямоугольный» кусочек сферы соединить с центром шара, то можно представить, что шар состоит из множества «маленьких пирамид».

Объем шара можно выразить через сумму объемов «маленьких пирамид» 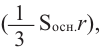высота которых равна радиусу шара. Бесконечно уменьшая размеры оснований, количество пирамид будет бесконечно расти.

Сумма площадей оснований «маленьких пирамид» будет равна площади поверхности шара. Учитывая, что площадь поверхности шара равна 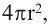получим формулу для нахождения объема шара:

Объем шара:

Объем шара равен произведению 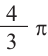и куба радиуса.

Пример №2

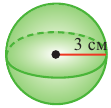
Найдите: а) объем шара радиуса 3 см

b) радиус шара объемом 288

Решение:

а)

b)

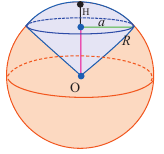
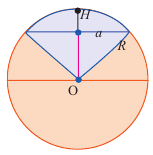
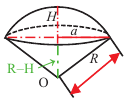
Сектор шара и сегмент шара

Шаровой сектор — это часть шара, ограниченная конической поверхностью с вершиной в центре шара. Шаровой сектор-объеденение конуса и шарового сегмента.

Так как шаровой сектор можно рассмотреть как предел суммы объемов маленьких пирамид, вершины которых находятся в центре шара, а основания касаются его поверхности, то

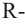
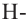
Здесь радиус шара, высота соответствующего сегмента

С другой стороны,

Проектная работа.

Отношение между объемами цилиндра, конуса и шара, которое получил Архимед.

Архимед нашел формулу для нахождения объема шара, исследовав связь между объемом цилиндра, описанного вокруг шара радиуса и объемом конуса, вписанного в данный цилиндр. Попробуйте и вы выполнить это исследование.

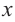
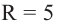
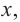
Если — расстояние от центра шара до плоскости сечения, то для шара радиуса представьте зависимость площади сечения от выполнив следующие шаги.

a) Вычислите следующие значения функции

Для примера найдено значение

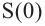
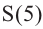
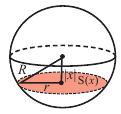
b) Представьте свои суждения о значениях и сечений.

c) Запишите общую формулу для определения площади сечения, расположенного на расстоянии 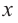от центра шара радиуса

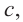
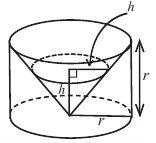
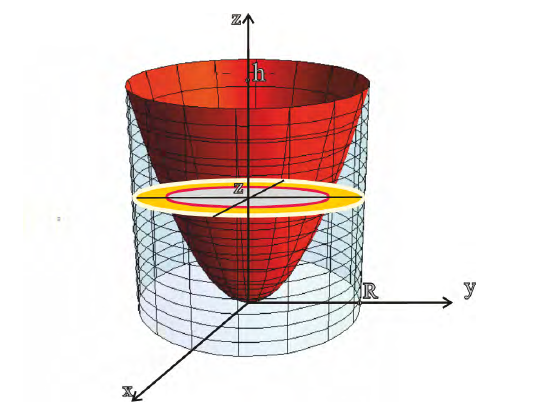
d) Свяжите формулу, полученную в пункте и следующий рисунок.

e) Чтобы понять умозаключения Архимеда, вернемся к начальному рисунку.

При «извлечении» конуса из цилиндра в поперечном сечении получаем кольца, параллельные основанию.

На одном и том же уровне поперечное сечение шара является кругом. Из подобия треугольников можно доказать, что площадь кольца каждого слоя равна 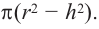Поскольку площади этих плоских сечений равны, по принципу Кавальери равны и объемы этих тел.

Объемы подобных фигур

Отношения соответствующих линейных размеров подобных пространствнных фигур должны быть равны.

По заданным соответствующим размерам подобных пространственных фигур можно найти неизвестные размеры.

Пример №3

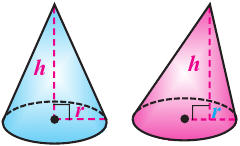
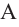
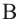
Конусы и подобны. По данным рисунка найдите образующую конуса

Решение: Запишем отношение линейных размеров: Радиус А Образующая А

Известно, что отношение площадей поверхностей двух подобных пространственных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия:

Объемы подобных пространственных фигур

Отношение объемов подобных пространственных фигур и равно кубу отношения соответствующих линейных размеров или кубу коэффициента подобия:

Пример №4

Отношение боковых поверхностей двух подобных цилиндров равно 4:9. Зная, что разность объемов равна 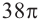куб.ед., найдите объемы цилиндров.

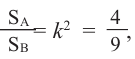
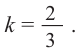
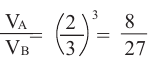
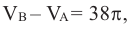
Решение: по условию тогда Значит С другой стороны, принимая во внимание, что получим:

Объемы тел в высшей математике

Под телом Т будем подразумевать ограниченное множество в пространстве.
Будем рассматривать тела, имеющие внутренние точки и границу, которая также принадлежит телу (замкнутые тела), причем такие, что любые две внутренние
точки можно соединить непрерывной линией, проходящей внутри тела.
 

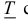
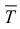
Определение 1. Рассмотрим тело составленное из конечного числа многогранников, содержащихся в Т, и тело , составленное из многогранников и покрывающее тело Т:
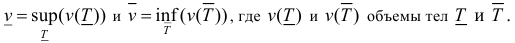
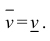
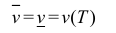
Пусть Тело называется кубируемым, если . При этом число (1) называется объемом тела Т (по Жордану).
 

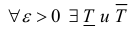
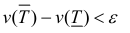
Замечание. Для кубируемости тела Т необходимо и достаточно, чтобы  такие, что  (2)

Пусть для кубируемого тела Т известны площади s=s(x) его сечения плоскостями перпендикулярными оси Ох, проходящими через точки (х, 0, 0),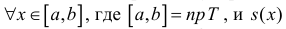 – непрерывна

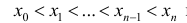
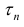
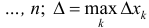
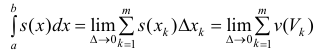
Разобьем отрезок [ a b ] на n частичных отрезков точками и обозначим это разбиение . Пусть 
 – диаметр разбиения, тогда (3)
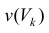
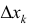
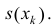
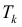
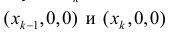
Где это – объем цилиндрического тела высотой  и площадью основания
 Пусть  k − -ый слой тела Т между плоскостями, проходящими через точки и перпендикулярными оси Ох.

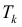
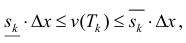
Так как Т – кубируемо, то  – также кубируемо и где

Тогда 
∀n ∈ N, или 

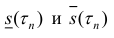
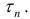
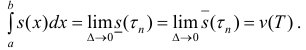
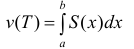
Гдеэто – нижняя и верхняя суммы Дарбу функции s(x) для разбиения
ПоэтомуТаким образом   (6)
 

Замечание. Нужно заметить, что неравенство (4), которое использовалось для вывода формулы (6), выполняется, когда любые два рассматриваемые сечения
тела Т при проекции на плоскость yOz полностью содержатся одно в другом.
Однако формула (6) верна и в общем случае. Для этого достаточно потребовать,
чтобы тело Т было кубируемым и функция s (x) – непрерывной.

Пример №5

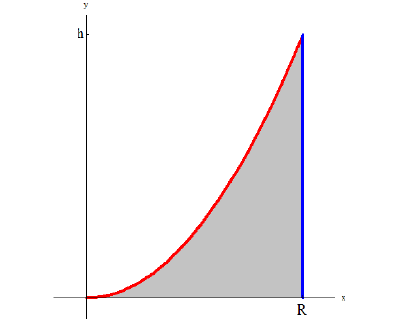
Найти объем тела ограниченного поверхностями 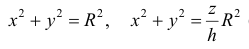 (ниже параболоида).
 

Решение.

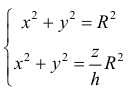
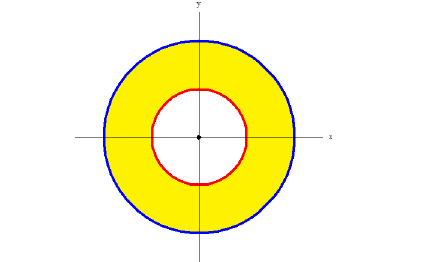
Из системы уравнений   следует, что z=h.

В сечении тела плоскостью проходящей через точку (0, 0, z) перпендикулярно оси Оz получается кольцо

Радиус внешней окружности равен R, радиус внутренней равен 
Поэтому по формуле (6):

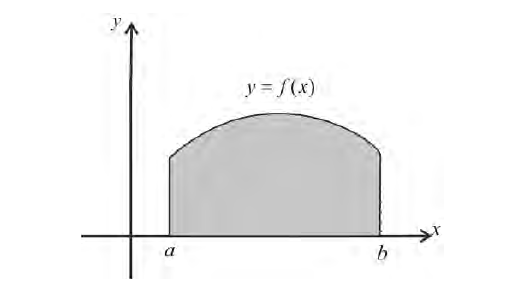
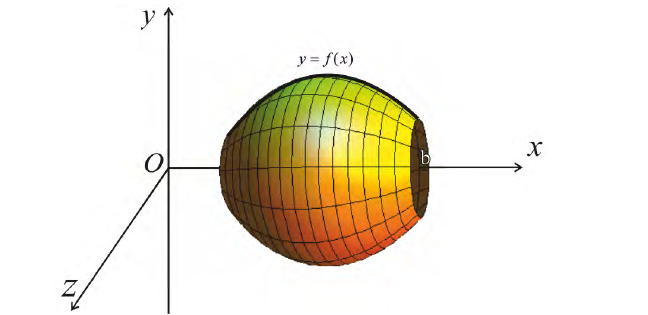
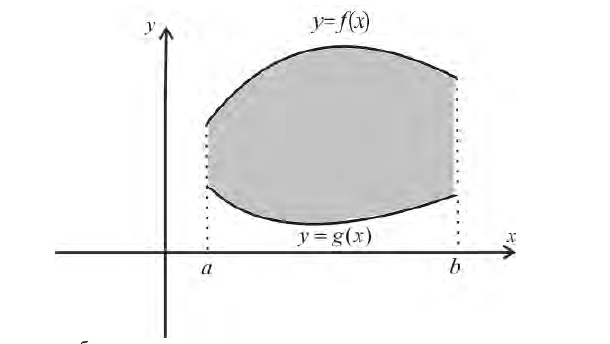
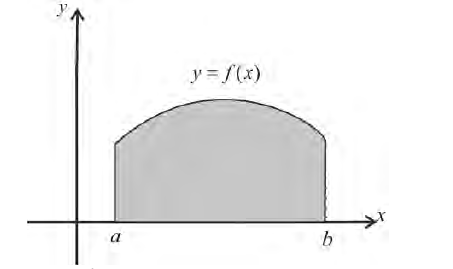
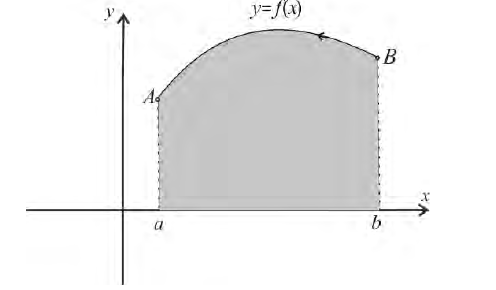
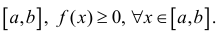
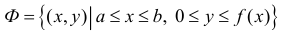
Формулу (6) удобно применять к телам вращения. Пусть y=f(x) – непрерывна на отрезке  Будем вращать криволинейную трапецию
 

вокруг оси Ох. Получим тело:

Тогда сечением полученного тела плоскостью проходящей через точку (х,0,0) и перпендикулярной оси Ох будет круг радиуса 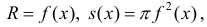 и по формуле (6): 
Где y=f(x).
Аналогично, если 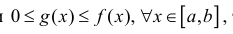то при вращении вокруг оси Ох фигуры

Получим тело, объем которого 
 

Пример №6

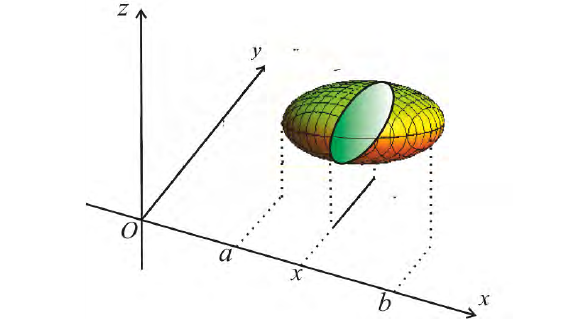
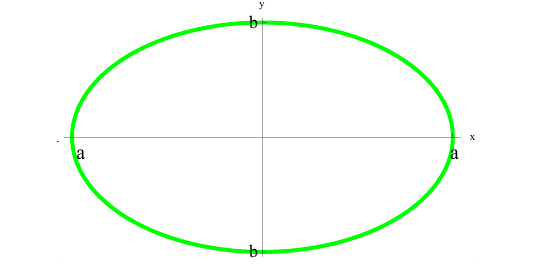
Рассмотрим фигуру Φ ограниченную эллипсом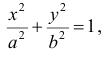  
Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Φ .
 

Решение.

По формуле (7): 
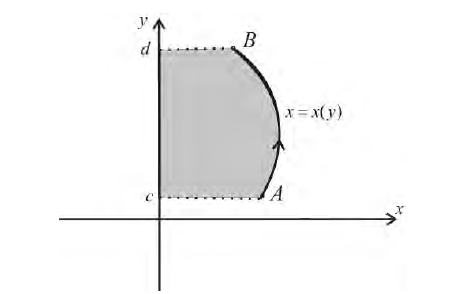
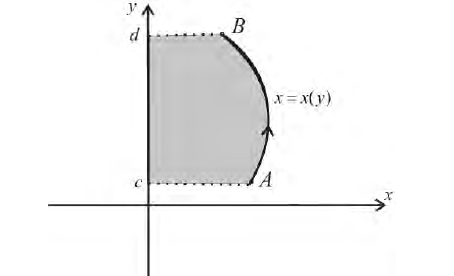
Пусть функция x=x(y) – непрерывна при 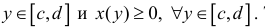Тогда, аналогично, при вращении вокруг оси Оу фигуры 

Получим тело, объем которого 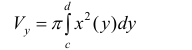(9)
Если же вращать вокруг оси Оу трапецию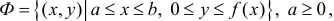  

то 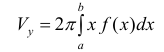(10)
 

Пример №7

Рассмотрим тело Т из примера 1. Оно получается, если вращать вокруг оси Oz фигуру, ограниченную линиями:

Из первого уравнения найдем 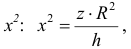поэтому по формуле (9):

 

Пример №8

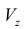
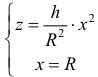
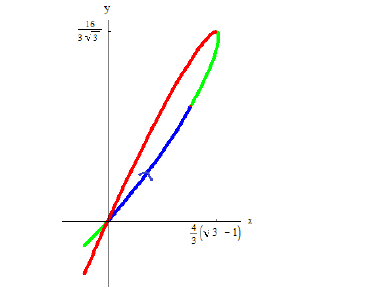
Пример №9

Фигура Ф ограничена линиями 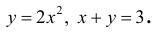 Найти
 

Решение.

Абсциссы точек пересечения: 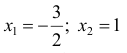 (см. пример 1 § 30). По формуле (8):

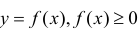
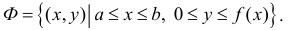
Замечание. Для непрерывной функции рассмотрим криволинейную трапецию  

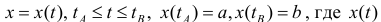
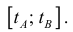
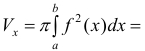
Пусть – непрерывно-дифференцируема на промежуткеТогда по формуле (7): по формуле (1) § 26

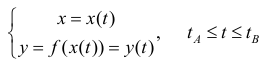
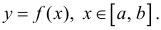
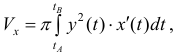
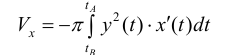
Где – параметрическое задание линии  Таким образом  или (12)
(кривая обходится так, чтобы область Ф оставалась слева).

Аналогично, для непрерывной функции 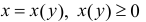рассмотрим криволинейную трапецию 

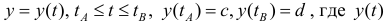
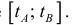
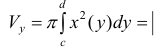
Пусть – непрерывно-дифференцируема на промежутке Тогда по формуле (9): по формуле (1) § 26

Где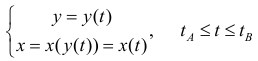 – параметрическое задание линии 

Таким образом 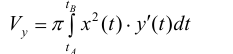(13)   (кривая обходится так, чтобы область Ф оставалась слева).

Рассмотрим область ,ограниченную простой замкнутой кривой
 (кривая лежит по одну сторону от оси Ox ). Тогда объем  можно находить по формуле (12): 
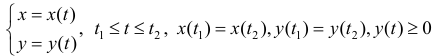
(кривая обходится так, чтобы область оставалась слева).

Аналогично ,для области ограниченной простой замкнутой кривой
 (кривая лежит по одну сторону от оси Oy )объем  можно находить по формуле (13): (кривая обходится так, чтобы область оставалась слева).

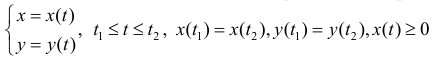
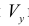
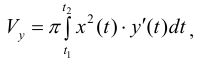
Пример №10

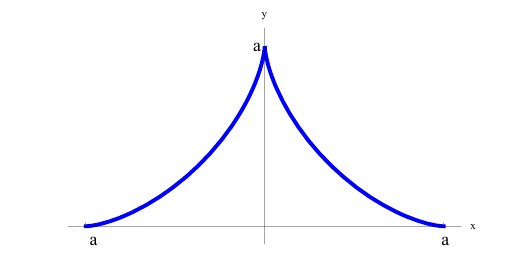
Дана астроида 

Найдем .
 

Решение.

по формуле (12):

 

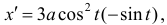
Пример №11

Петля кривой 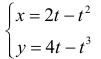вращается вокруг оси Ox .Найти .
 

Решение.

петля обходится против часовой стрелки. По формуле (12):

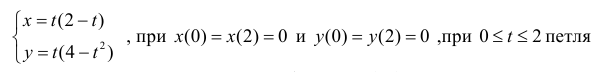
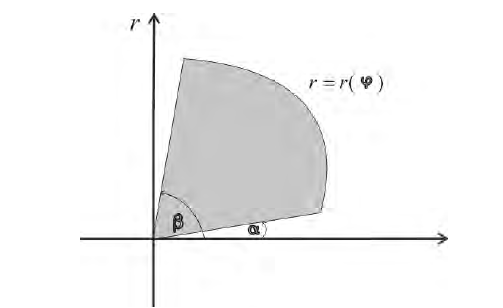
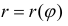
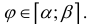
Пусть – кривая в полярной системе координат, r (ϕ) – непрерывна при  Рассмотрим на плоскости хОу криволинейный сектор

Тогда объем тела при вращении фигуры ϕ вокруг полярной оси равен
 (14)

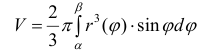
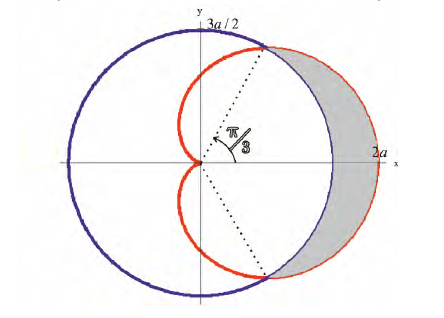
Пример №12

(см. пример 4 § 31).

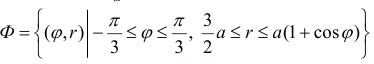
Найдем .
 

Решение.

По формуле (14):

Основанием конуса будет большее сечение шара, так как радиус основания конуса равен радиусу шара по условию. Значит, высота конуса тоже равна радиусу шара.

Объем конуса находят по формуле:

  V = ⅓ * π * R ² * h, где R — радиус основания, h — высота конуса.

Так как высота конуса равна радиусу шара формула примет вид:

 V = ⅓ * π * R ³.

Объем шара: V = (4 * π * R ³) / 3. V = 36 ( по условию )

                         36 * 3 = 4 * π * R ³

                         108 = 4 * π * R ³

                         π * R ³ = 27.

Подставим значение π * R ³ в формулу объема конуса:

          V = ⅓ * 27 = 9.