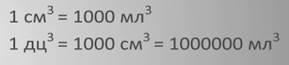Как найти объем формула математика 5 класс

Математика

5 класс

Урок №32

Объём прямоугольного параллелепипеда. Единицы объёма

Перечень рассматриваемых вопросов:

— куб;

— параллелепипед;

— элементы параллелепипеда;

— объём прямоугольного параллелепипеда, куба.

Тезаурус

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.

Высота, длина и ширина – это измерения прямоугольного параллелепипеда.

Единичный куб — куб, ребро которого равно линейной единице.

Обязательная литература

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Как вы думаете, что больше занимает места– 1 кг ваты или 1 кг гвоздей? Чтобы ответить на этот вопрос, нужно знать величину, которая называется объём. В данной задаче ответ очевиден, так как мы можем представить предметы визуально. Но не всегда ответ может быть таким простым. Чаще всего нужно произвести определённые вычисления.

Сегодня мы рассмотрим объём прямоугольного параллелепипеда и научимся его находить.

Объём можно измерить. Его измеряют в кубических миллиметрах, кубических сантиметрах, кубических метрах, литрах и т. д.

Найдём соотношение между единицами измерения объёма.

Так как 1 см = 10 дм, то 1 см³ = 1 000 мм³.

1 дм³ = 1000 см³ = 1 л

1 м³ = 1000 дм³

1 км³ = 1000000000 м³

В древности в разных частях планеты люди по-разному измеряли объём. Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.

На Руси основной мерой жидкостей считалось ведро, в котором 10 кружек или 12 литров. Также для подсчётов объём ведра делили пополам, то есть на два полуведра, которые, в свою очередь, тоже можно было поделить пополам. Для торговли с иностранцами использовали меру объёма, называемую бочка, которая равнялась 40 вёдрам.

Дадим определение единичного куба – это куб, ребро которого равно линейной единице. Его тоже принимают за единицу объёма.

Если прямоугольный параллелепипед можно разрезать на К единичных кубов, то говорят, что его объём V равен К кубическим единицам.

Например, на рисунке объём параллелепипеда равен 24 кубическим единицам.

V = 24 куб. единиц

Введём формулу объёма прямоугольного параллелепипеда.

Объём прямоугольного параллелепипеда равен произведению трёх его измерений, то есть произведению длины а, ширины bи высоты c, или произведению площади основания S на высоту c.

V = а · b · c = S · с

Так как куб является прямоугольным параллелепипедом, у которого все измерения равны, то его объём равен третьей степени длины его ребра а.

V = а³

Решим задачу.

Мальчик купил аквариум в форме прямоугольного параллелепипеда, который имеет площадь дна, равную 1400 см³, и высоту 6 дм. Какой объём воды он налил в аквариум, если уровень жидкости не доходил до края 5 см? Выразите ответ в кубических сантиметрах.

Чтобы решить эту задачу переведём единицы измерения длины в сантиметры.

6 дм = 60 см

Получается, что высота аквариума равна 60 см. Но по условию задачи требуется определить объём налитой жидкости, а её высота соответствует разности между высотой аквариума и уровнем жидкости, не доходящей до края:

с = 60 см – 5 см = 55 см

Получается, что высота жидкости в сосуде соответствует 55 см.

Теперь можно определить объём воды, которая налита в аквариум.

Для этого используем следующую формулу:

V = S · с = 1400 см² · 55 см = 77000 см³

Ответ: мальчик налил в аквариум 77000 см³ воды.

Разбор решения заданий тренировочного модуля

№ 1. Чему равен объём куба, если длина его ребра равна 3 см?

Решение: для нахождения объёма куба нужно воспользоваться формулой.

V = а³ = (3 см)³ = 27 см³

Ответ: 27 см³.

№2. Как изменится объём прямоугольного параллелепипеда, если его длину увеличить в три раза. Подчеркните правильный ответ.

Решение: чтобы ответить на вопрос, нужно воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда.

V = а · b · c, где а – длина прямоугольного параллелепипеда.

Если длина возрастет в три раза, то объём, соответственно, увеличится в три раза, так как, длина – это один из трёх множителей, входящих в формулу объёма прямоугольного параллелепипеда:

V = 3 · а · b · c

Ответ: объём увеличится в три раза.

• Скачать материал

  • 
    18.02.2018
    
    
    24407
    
  • DOCX
    46.6 кбайт
  • 180
    скачиваний
  • Рейтинг:
    5 из 5
  • Оцените материал:

    
    

    
    

    
    

    
    

• Настоящий материал опубликован пользователем Булатова Айгуль Рустемовна. Инфоурок является
  информационным посредником и предоставляет пользователям возможность размещать на сайте
  методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
  сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

  Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
  сайта, Вы можете оставить жалобу на материал.

  Удалить материал

• 

  • На сайте: 5 лет и 7 месяцев
  • Подписчики: 0
  • Всего просмотров: 24524
  • Всего материалов:

    1

Представим себе такую историю…

– Паша, а ты когда-нибудь собирал кубик Рубика? – спросил Саша.

– Конечно! И не один раз, – ответил Паша. –
Кстати, кубик Рубика отличная игрушка-головоломка,
которая развивает логическое мышление.

– Да, мне тоже он очень нравится! – продолжил
Саша. – Я вот сегодня собрал кубик Рубика за 15 минут.
Пока собирал, задумался, а сколько всего маленьких кубиков в нём?

– И в правду, – задумался Паша, – и сколько
же их там?

– Не знаю! – ответил Саша. – Сколько ни
пытался их пересчитать, всё сбивался. В общем, так и не получилось у меня их
сосчитать.

– А давай спросим у Электроши!
– предложил Паша. – Он точно знает, как их посчитать.

– Ребята, прежде чем я вам расскажу о
прямоугольном параллелепипеде, давайте немного разомнёмся и выполним устные
задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас
должно было получиться!

– А теперь вернёмся к вашему вопросу, –
продолжил Электроша. – Только сначала ответьте мне на
вопрос: какую форму имеет кубик Рубика?

– Кубик Рубика
имеет форму прямоугольного параллелепипеда, а точнее – форму куба, – ответили
мальчишки.

– Молодцы! – похвалил ребят Электроша. – Важным свойством любого геометрического тела
является его вместимость, то есть объём фигуры. Величина объёма
даёт нам представление о том, какую часть пространства занимает интересующий
нас объект.

Кстати, с такой величиной, как объём, мы
очень часто встречаемся в нашей жизни. Может, вы сможете привести примеры,
когда мы интересуемся объёмом? – спросил у ребят Электроша.

– Например, объём коробки с соком, объём
бассейна, объём школьного кабинета, – начал Саша.

– Ещё нам нужно знать объём топливного бака
машины, показатели потребления газа или воды на счётчиках, – продолжил Паша.

– Хорошие примеры! – похвалил ребят Электроша. – А как вы думаете, что нужно знать для того,
чтобы измерить объём? – спросил у ребят Электроша.

– Наверное, нужно знать единицу измерения
объёмов, – предположили мальчишки.

– Правильно! – подтвердил Электроша.
– Напомню, что для измерения отрезков мы вводили единичный отрезок, для
измерения углов – единичный угол, а для измерения площадей фигур – единичный
квадрат.

Для измерения объёмов также вводятся единицы
измерения. За единицу измерения объёма выбирают куб, ребро которого равно
единичному отрезку. Такой куб называют единичным.

Например, объём куба с ребром 1 миллиметр
называют кубическим миллиметром. Пишут так: .

Объём куба с ребром 1 сантиметр называют кубическим
сантиметром. Пишут так: .

Объём куба с ребром 1 дециметр называют кубическим
дециметром. Пишут так: .

Всем хорошо известна и такая единица объёма,
как 1 литр. Пишут так  дм³   л. Это другое название кубического
дециметра.

Объём куба с ребром 1 метр называют кубическим
метром. Пишут так: .

Объём куба с ребром 1 километр называют кубическим
километром. Пишут так: .

Легко заметить, что название единицы объёма
получается из названия единицы длины присоединением прилагательного
«кубический».

– Как вы думаете, что значит измерить объём
фигуры? – спросил у ребят Электроша.

– Измерить
объём фигуры – значит подсчитать, сколько единичных кубов в ней
помещается, –
сказали мальчишки.

– Молодцы! – похвалил ребят Электроша. – Проще всего измерить объём прямоугольного
параллелепипеда. Чем мы сейчас и займёмся.

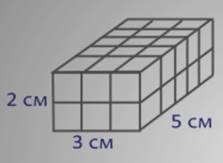
– Посмотрите: на листке бумаги изображён
прямоугольный параллелепипед со следующими измерениями: длина 5 сантиметров,
ширина 2 сантиметра и высота 3 сантиметра. Давайте посчитаем, сколько единичных
кубов может в нём поместиться.

– Начнём укладывать кубики на дно
прямоугольного параллелепипеда, – предложили мальчишки. – Итак, сначала положим
на дно ряд единичных кубиков со стороной 1 сантиметр вдоль длинной стены.
Видим: поместилось 5 таких кубиков. Затем вдоль этих кубиков уложим ещё 1 ряд.
Тоже получим ещё пять кубиков.

– Хорошо! – сказал Электроша.
– Тогда сколько всего кубиков у вас поместилось на дне прямоугольного
параллелепипеда?

– На дне параллелепипеда помещается слой из единичных кубиков, то есть слой из 10 кубов.

– Молодцы! – похвалил ребят Электроша. – А чтобы заполнить
весь прямоугольный параллелепипед, сколько в него нужно вложить таких слоёв?

– Так как высота нашего параллелепипеда 3 сантиметра,
то в него вместится 3 слоя кубиков, в каждом из которых будет по 10 кубиков.
Тогда получается, что весь прямоугольный параллелепипед можно заполнить 30 кубиками.

– Всё правильно! – согласился Электроша. – Мы получили, что всего в нашем параллелепипеде
помещается единичных кубов. Поэтому объём нашего параллелепипеда равен  (см³).

– Электроша,
получается, что три измерения прямоугольного параллелепипеда позволяют
посчитать, сколько всего кубиков в нём поместится? – спросил Паша.

– Да, – ответил Электроша.
– Запомните! Объём прямоугольного параллелепипеда равен произведению
трёх его измерений.

Формулу для вычисления объёма прямоугольного
параллелепипеда в буквенном виде можно записать следующим образом: , где   – объём, , и – измерения прямоугольного параллелепипеда.
При вычислениях обязательно нужно обращать внимание, чтобы все измерения
прямоугольного параллелепипеда были выражены в одинаковых единицах.

– А теперь давайте решим одну задачку, –
предложил Электроша. – Определите объём блока бумаги,
если длина одного листа 20 миллиметров, ширина – 15 миллиметров, а всего в
блоке помещается 500 таких листов (считать толщину листа равной 1 миллиметру).

– Сначала вычислим площадь одного листа, –
сказал Паша, – она будет равна  (мм²).

– А потом площадь этого листа умножим на
количество листов, помещающихся в блоке, – продолжил Саша, – то есть  (мм³).

– Молодцы! – похвалил ребят Электроша. – Обратите внимание: блок бумаги имеет форму
прямоугольного параллелепипеда. Значит, мы с вами сейчас нашли объём
параллелепипеда, но с помощью другой формулы. Запомните! Объём
прямоугольного параллелепипеда равен произведению площади основания на высоту.

В буквенном виде эту формулу записывают так: , где – площадь основания прямоугольного
параллелепипеда,   – его высота.

– А теперь давайте всё же вернёмся к вашему
первоначальному вопросу, – продолжил Электроша. – Вы
хотели выяснить, сколько кубиков содержится в кубике Рубика.
Мы с вами уже определили, что эта замечательная игрушка имеет форму прямоугольного
параллелепипеда, а если быть точнее, то форму куба. Может, вы уже сможете
посчитать количество маленьких кубиков, из которых состоит кубик Рубика?

– Так, – начал рассуждать Саша, – длина
нашего кубика Рубика состоит из 3 маленьких кубиков, точно
такие же ширина и высота. Значит, в нашем кубике Рубика
помещается  маленьких кубиков.

– Всё правильно! – сказал Электроша.
– Изначально кубик Рубика состоял из 27 связных между
собой разноцветных кубиков, но затем его конструкция упростилась до набора из 26
маленьких кубиков, а вместо внутреннего кубика разместился хитроумный
скрепляющий механизм. Кстати, а вы знаете кем, как и когда была придумана эта
замечательная игрушка? – спросил Электроша.

– Не знаем, – ответили мальчишки.

– Скажу вам только, что знаменитый кубик Рубика придумал венгерский преподаватель архитектуры Эрно Рубик в 1974 году.

А вот уже историю его создания и
усовершенствования вы можете изучить на досуге.

– А теперь смотрите, мы с вами определили,
что наш кубик Рубика имеет форму куба. Поскольку у
куба все рёбра равны, то его объём вычисляют по формуле:  , где  – длина ребра куба. Именно поэтому третью
степень числа называют кубом числа.

А теперь, ребята, давайте посмотрим, как вы
всё поняли, и выполним несколько заданий.

Задание первое: объём класса 96 кубических
метров. Найдите высоту стены, если площадь пола 32 квадратных метра.

Решение: класс имеет форму прямоугольного
параллелепипеда. Нам известна площадь пола, то есть площадь основания
прямоугольного параллелепипеда. Значит, можем воспользоваться формулой для
вычисления объёма прямоугольного параллелепипеда через площадь основания и
высоту: . Выразим из этой формулы высоту: . И подставим в получившуюся формулу объём класса и площадь пола:  (м). Получаем, что высота стены равна 3 метрам.

Следующее задание: длина аквариума 80 сантиметров,
ширина 45 сантиметров, высота 65 сантиметров. Сколько литров воды нужно налить,
чтобы уровень воды был ниже верхнего края аквариума на 5 сантиметров?

Решение: высота нашего аквариума 65
сантиметров, а воду нужно налить так, чтобы её уровень был ниже верхнего края
аквариума на 5 сантиметров. Значит, от высоты аквариума отнимем 5 сантиметров: . Получим, что высота уровня воды равна 60 сантиметрам. Воспользуемся
формулой для вычисления объёма прямоугольного параллелепипеда:
. Получим, что в аквариум нужно налить  (см³). Переведём в литры. Мы знаем, что  л  дм³ , а значит, равен  см³ . Тогда получаем, что в
аквариум нужно налить  см³  л.

§ 1  Понятие объема и единицы измерения объема

В этом уроке Вы познакомитесь с таким понятием как объем, узнаете о единицах измерения объёма, а также научитесь находить объем прямоугольного параллелепипеда.

Объем – это количественная характеристика пространства, занимаемого телом. Объем тела или фигуры определяется его формой и размерами.

Единицами измерения объема являются:

кубический миллиметр,

кубический сантиметр,

кубический дециметр,

кубический метр,

кубический километр.

Кубический сантиметр – это объем куба с ребром 1 см, кубический метр – это объем куба с ребром 1 м, кубический дециметр – это объем куба с ребром 1 дм. Между прочим, кубический дециметр также называют литром. Т.е. 1 литр равен одному кубическому дециметру.

Единицы измерения объема связаны друг с другом.

Например,

1 кубический сантиметр = 1000 кубическим миллиметрам,

а 1 кубический дециметр – это 1000 кубических сантиметров или 1 000 000 кубических миллиметров.

§ 2  Объем прямоугольного параллелепипеда

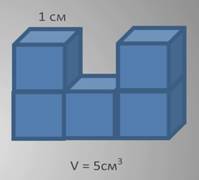
Рассмотрим фигуру, состоящую из 5 кубиков с ребром 1 см.

Так как объем каждого кубика составляет 1 кубический сантиметр, значит, объем всей фигуры равен 5 кубическим сантиметрам.

Т.е. можно сделать вывод, что объем всей фигуры равен сумме объемов ее частей.

Давайте выведем правило для вычисления объема прямоугольного параллелепипеда.

Пусть прямоугольный параллелепипед имеет длину 5 см, ширину 3 см и высоту 2 см.

Разобьём его на два слоя толщиной 1 см каждый.

Т.е. первый слой состоит из 15 кубиков, так как в длину 5 кубиков и в ширину 3 кубика, а 5 умножить на 3, будет 15. Второй слой такой же.

Значит, чтобы найти объем всего параллелепипеда надо 15 умножить на 2.

Т.е. перемножили 5 и 3 – длину и ширину, а затем помножили на 2, т.е. на высоту.

Таким образом, получили правило:

Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.

В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. Volume — «объём» или «наполнение».

Формула объема прямоугольного параллелепипеда имеет вид:

V = авс, где V – это объем, а, в, и с – измерения (т.е. длина, ширина, высота). 

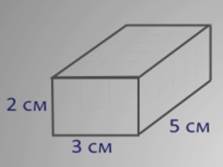
Давайте решим задачу, например, найти объем прямоугольного параллелепипеда, длина которого равна 10 см, ширина 4 см, высота 3 см.

Решение: чтобы найти объем прямоугольного параллелепипеда, нужно перемножить длину, ширину и высоту, т.е. 10 умножить на 4 и умножить на 3, получаем 120.

Ответ: объем равен 120 кубическим сантиметрам.

Таким образом, на этом уроке Вы познакомились с таким понятием как объем, узнали о единицах измерения объёма – кубические миллиметры, кубические сантиметры, кубические метры и так далее. А также получили правило для нахождения объема прямоугольного параллелепипеда: чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.