Как найти объем единицы измерения

У этого термина существуют и другие значения, см. Объём (значения).

Объём
V
Размерность L3
Единицы измерения
СИ м3
СГС см3

Примеры вычисления объёмов:
Куба с помощью перемножения трех сторон[1]

Пирамиды с помощью умножения площади основания пирамиды на её высоту и делению на три[1]

Конуса с помощью умножения площади основания на треть высоты[1]

Цилиндра с помощью перемножения площади на высоту[1]

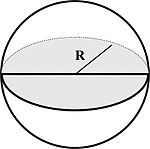
Шара с помощью перемножения четырёх третьих числа Пи на радиус шара в кубе[1]

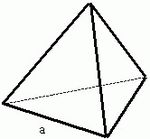
Тетраэдра с помощью произведения длины его ребра в кубе на корень из двух и деления полученного на двенадцать[1]

Объём — количественная характеристика пространства, занимаемого телом или веществом.

Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п..

Единица измерения объёма в СИ — кубический метр; от неё образуются производные единицы, такие как кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель.

В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

Содержание

  • 1 Вычисление объёма
    • 1.1 Математически
    • 1.2 Через плотность
  • 2 Единицы объёма жидкости
    • 2.1 Английские
    • 2.2 Античные
    • 2.3 Древнееврейские[2]
    • 2.4 Русские[3]
  • 3 Единицы объёма сыпучих веществ
    • 3.1 Английские
    • 3.2 Русские
  • 4 Прочие единицы
  • 5 Примечания
  • 6 Литература
  • 7 Ссылки

Вычисление объёма

На практике приблизительный объём тела, в том числе сложной формы, можно вычислить погрузив это тело в жидкость. Объём вытесненной жидкости будет равен объёму измеряемого тела.

Математически

Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром a равен V=a^{3}.

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.

Через плотность

Зная массу (m) и плотность (ρ) тела объём рассчитывается по формуле: V={frac {m}{rho }}

Единицы объёма жидкости

  • 1 л = 1,76 пинты = 0,23 галлона

Английские

  • 1 пинта = 0,58 литра.
  • 1 кварта = 2 пинты = 1,23 литра
  • 1 галлон = 8 пинтам = 4,55 литра
  • 1 галлон (амер.) = 3,785 литра

Античные

  • Котила = 0,275 литра

Древнееврейские[2]

  • Эйфа = 24,9 литра
  • Гин = 1/6 эйфы = 4,15 литра
  • Омер = 1/10 эйфы = 2,49 литра
  • Кав = 1/3 гина = 1,38 литра

Русские[3]

  • Бочка = 40 вёдер = 492 литра
  • Ведро = 12,3 литра

Единицы объёма сыпучих веществ

Английские

  • 1 бушель = 8 галлонов = 36,37 литра
  • 1 баррель = 163,65 литра

Русские

  • Четверик = 26,24 литра (1 пуд зерна)
  • Гарнец = 3,28 литра

Прочие единицы

  • 1 унция (англ.) = 2,841·10−5 м³
  • 1 унция (амер.) = 2,957·10−5 м³
  • 1 кубический дюйм = 1,64·10−5 м³
  • 1 кубический фут = 2,83·10−2 м³
  • 1 кубический ярд = 0,765 м³
  • 1 кубическая астрономическая единица =3,348·1024 км³
  • 1 кубический световой год = 8,466·1038 км³
  • 1 кубический парсек = 2,938·1040 км³
  • 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938·1049 км³

Примечания

  1. ↑ 1 2 3 4 5 6 Вычисление объёма различных тел и пространств
  2. ↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4
  3. ↑ Меры объёма в Древней Руси

Литература

  • Объем // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Ссылки

Источник

Измерение объёма тела по формуле — возможные способы, единицы измерения

Содержание:

  • Понятие объема тела
  • Свойства объема тела
  • Как вычислить объем тела: все формулы
  • Примеры решения задач
  • Задания для самостоятельной работы

Понятие объема тела

Объем является количественным параметром пространства, занятого телом или веществом.

Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:

  • форма;
  • линейные размеры.

Главным свойством объема принято считать аддитивность.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.

Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.

Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.

Свойства объема тела

В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:

  1. Объем тела не может быть отрицательной величиной.
  2. В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
  3. Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
  4. Аналогичные друг другу геометрические тела обладают одинаковыми объемами.
  5. В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: (V1<V2
    )    .

Как вычислить объем тела: все формулы

Существует практический способ определения объема тела, включая тела, обладающие сложной формой и геометрией. Данная методика основана на законе Архимеда и предполагает погружение рассматриваемого тела в некую жидкость. По результатам следует измерить объем вытесненной телом жидкости. Данная величина равна объему измеряемого тела.

Формула расчета объема тела, исходя из известных величин массы и плотности:

(V={frac {m}{rho }})

Здесь m определяется, как масса, а rho является средней плотностью тела.

В том случае, когда тела обладают простыми геометрическими формами, в решении задач допустимо использовать специальные формулы. К примеру, для того чтобы найти объем куба, ребро которого равно а, следует применить такую формулу: (V=a^{3}).

Вычислить объем некого прямоугольного параллелепипеда можно путем умножения длины, ширины и высоты. Запишем другие распространенные формулы для расчета объемов геометрических фигур:

  • куб, формула объема: (V=a^{3}):

куб, формула объема

  • прямоугольный параллелепипед, формула объема: (V=abc) (произведение длин трех сторон):

прямоугольный параллелепипед, формула объема: V=abc

  • призма, формула объема: ( V=Bh) (произведение площади основания и высоты):

призма, формула объема: V=Bh

  • пирамида, формула объема: (V={frac {1}{3}}Bh:)

пирамида, формула объема:

  • параллелепипед, формула объема: (V=abc{sqrt {K}}, {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}:
    )

  • параллелепипед, формула объема

  • тетраэдр, формула объема: (V={{sqrt {2}} over 12}a^{3}:)

тетраэдр, формула объема

  • шар, формула объема: (V={frac {4}{3}}pi r^{3}):

шар, формула объема:

  • эллипсоид, формула объема: (V={frac {4}{3}}pi abc):

эллипсоид, формула объема

  • прямой круговой цилиндр, формула объема: (V=pi r^{2}h):

прямой круговой цилиндр, формула объема

  • конус, формула объема: (V={frac {1}{3}}pi r^{2}h):

конус, формула объема

  • тело вращения, формула объема: (V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x):

тело вращения, формула объема

Источник: ru.wikipedia.org.

В том случае, когда необходимо определить объем, которым обладает некое тело, имеющее сложную форму, нужно разбить мысленно данное тело на отдельные части. Такие части целого должны иметь простую форму. Далее следует сложить вычисленные объемы простых тел. Результат будет являться значением объема начального тела.

Примеры решения задач

Задача 1

Задача

Имеется пара шаров. Радиус первого шара в 5 раз превышает радиус второго шара.

Требуется определить, во сколько раз площадь поверхности второго шара меньше по сравнению с площадью поверхности первого шара

Шар

Источник: shkolkovo.net

Решение

Рассчитать площадь поверхности можно по формуле:

(S=4pi R^2)

Тогда запишем отношения площадей пары шаров:

(dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2})

Сравним радиусы геометрических фигур:

(R_1=5R_2)

В результате:

(dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25)

Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.

Ответ: 25.

Задача 2

На рисунке изображены конусы. Назовем их (K_1) и (K_2).

Полная поверхность (K_1) по площади относится к площади полной поверхности (K_2) как 4:1.

Фигура (K_1) обладает радиусом, который в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2).

Требуется вычислить, как относится образующая (K_2) к образующей (K_1.)

На рисунке изображены конусы

Источник: shkolkovo.net

Решение

Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:

(S=pi R (R+l))

Запишем отношения площадей полной поверхности заданных конусов:

(dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)})

Согласно условию задачи, имеем:

(R_1=4l_1, R_2=frac12R_1=2l_1)

В результате:

(dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)} quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5)

Ответ: 0,5.

Задача 3

Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.

Даны два прямоугольных параллелепипеда.

Источник: shkolkovo.net

Решение

Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:

V=abc

Применительно к нашей задаче, запишем:

(dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2})

Известно, что:

(a_1=7a_2, b_2=2b_1, c_1=3c_2)

В результате:

(dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}= dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot 2}{21}=10)

Ответ: 10.

Задача 4

Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.

Даны два конуса.

Источник: shkolkovo.net

Решение

Составим формулу для расчета площади боковой поверхности конуса:

(S=pi Rl)

Запишем отношения площадей боковых поверхностей для первого и второго конусов:

(dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2})

Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:

(frac{R_1}{R_2}=frac{15}7, то dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2)

Ответ: 0,2.

Задача 5

Имеется пара шаров. Объем первой фигуры составляет 54. Радиус второй фигуры в 3 раза меньше по сравнению с радиусом первой. Нужно определить объем второго шара.

Имеется пара шаров.

Источник: shkolkovo.net

Решение

Запишем формулу, согласно которой можно определить объем шара:

(V=dfrac43 pi R^3)

Составим отношение объемов двух фигур:

(dfrac{54}{V_2}=dfrac{V_1}{V_2}= dfrac{frac43 pi ,R_1^3}{frac43 pi ,R_2^3}=left(dfrac{R_1}{R_2}right)^3)

По условиям задачи:

(R_1=3R_2)

В результате:

(dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad V_2=dfrac{54}{27}=2)

Ответ: 2.

Задача 6

Имеется некая емкость конусообразной формы. Ее заполнили до половины с помощью 75 гр жидкости. Необходимо вычислить вес жидкости, которую нужно добавить в емкость, чтобы заполнить ее до верхнего края.

Имеется некая емкость конусообразной формы

Источник: shkolkovo.net

Решение

Вспомним формулу объема из курса физики:

(V=frac{m}{rho})

Предположим, что O является центром основания большего конуса. Пусть Q — центр основания меньшего конуса, а S обозначает общую вершину данных фигур. В одной плоскости построим радиусы OA и QB:

Имеется некая емкость конусообразной формы.

Источник: shkolkovo.net

В таком случае:

(QBparallel OA)

(triangle SQBsim triangle SOA)

В результате:

(dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21)

Получим, что:

(m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho= dfrac13cdot picdot QScdot QB^2 cdot rho)

Можно сделать вывод, что:

(m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho= dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})

Таким образом, потребуется долить в емкость:

(600-75=525 {small{text{грамм}}})

Ответ: 525.

Задача 7

Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.

Изображена четырехугольная пирамида

Источник: shkolkovo.net

Решение

Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, B’C’, C’D’, D’A’, параллельным соответственно AB, BC, CD, DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой.

Исследуем плоскость ASO. Построим (A’Hparallel SO), где SO представляет собой высоту начальной фигуры. В таком случае:

(A’Hperp ABC)

В результате получилось расстояние, которое равно (frac13SO:)

(triangle AA’Hsim triangle ASO)

(dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad SA=3AA’ quadRightarrowquad SA’=dfrac23SA)

Таким образом:

(SQ=frac23SO)

(triangle ASBsim triangle A’SB’)

Получим, что:

(dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad A’B’=dfrac23AB)

Запишем отношения объемов пирамид:

(dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}= dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot AB^2}=dfrac{SQ}{SO}cdot left(dfrac{A’B’}{AB}right)^2=dfrac23cdot left(dfrac23right)^2=dfrac8{27})

В результате объем малой фигуры составит:

(V_{{small{text{м}}}}=dfrac8{27}cdot 54=16)

Ответ: 16.

Задания для самостоятельной работы

Задание 1

Имеется пара конусов. Вторая фигура обладает радиусом, который в три раза больше по сравнению с радиусом первой фигуры. Второй конус выше первого в шесть раз. Объем второй фигуры равен 18. Требуется вычислить, чему равен объем первого конуса.

Имеется пара конусов

Источник: shkolkovo.net

Решение

Формула определения объема конуса:

(V=frac13pi R^2h)

Запишем отношения объемов двух фигур:

(dfrac{V_1}{18}=dfrac{V_1}{V_2}= dfrac{frac13pi ,R_1^2,h_1}{frac13 pi ,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot dfrac{h_1}{h_2})

Исходя из условий задачи:

(R_2=3R_1)

(h_1=6h_2)

В результате:

(dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}= dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot 18=12)

Ответ: 12
 

Задание 2

Дано два шара. Объем первого шара в 343 раза больше по сравнению с объемом второго шара. Нужно вычислить, во сколько раз радиус первой фигуры больше, чем радиус второй фигуры.

Дано два шара

Источник: shkolkovo.net

Решение

Запишем формулу для нахождения объема шара:

(V=dfrac43 pi R^3)

Составим отношения объемов данных шаров:

(dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}= left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)

Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.

Ответ: 7.

Задание 3

На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.

На рисунке изображены два цилиндра

Источник: shkolkovo.net

Решение

Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:

(S=2pi RH)

Составим отношение площадей боковых поверхностей двух фигур:

(dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}= dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2})

В результате:

(R_2=4R_1, H_1=5H_2)

Таким образом:

(dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}= dfrac14cdot 5=dfrac54)

Получим, что:

(S_2=dfrac{16cdot 4}5=12,8)

Ответ: 12,8.

Задание 4

Имеется некая емкость конусообразной формы. Объем этой емкости составляет 2700 мл. Требуется рассчитать количество жидкости, налитой в емкость, если ее уровень в 3 раза меньше по сравнению с высотой емкости.

Имеется некая емкость конусообразной формы.

Источник: shkolkovo.net

Решение

Введем обозначения, как на рисунке:

Введем обозначения, как на рисунке:

Источник: shkolkovo.net

В таком случае:

(QBparallel OA и triangle SQBsim triangle SOA)

Таким образом:

(dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13)

Соотношение объемов жидкости до определенной линии и емкости:

(dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}= dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27})

В результате:

(V_{small{text{ж}}}=dfrac1{27}V=100)

Ответ: 100.

Задача 5

На рисунке изображены фигуры в виде шаров. Первый шар имеет радиус 6. Второй шар имеет радиус 2. Нужно вычислить, во сколько раз объем первой фигуры превышает объем второй фигуры.

На рисунке изображены фигуры в виде шаров

Источник: shkolkovo.net

Решение

Запишем формулу для расчета объема шара, который не может изменяться:

(V=dfrac43 pi R^3)

Составим отношение объемов двух шаров:

(dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}= left(dfrac62right)^3=27)

В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.

Ответ: 27.

Источник

В древности объём измеряли в сиеках, горстках, тинах, пурах, цибах, штофах, ложках.

(1) тина (= 3) пура (= 9) сиеков (= 720) горсток (= 162) штофа (= 208) литров.

Многие из этих мер давно уже забыты.

В международной системе единиц (СИ) единицей объёма является метр кубический 

м3

.

kub.png

Рис. (1). Кубический метр

В повседневной жизни встречается единица объёма литр 

л

. Она названа именем французского винодела Литра.

Обрати внимание!

Литр является кубическим дециметром:

1 л=1 дм3

.
Деления мензурки обычно выражаются в миллилитрах (мл):

1 мл=1см3

.

В физике важно умение перейти от одной единицы измерения к другой. Рассмотрим следующие соотношения:
 

1м3=10дм⋅10дм⋅10дм=1000дм3;1м3=100см⋅100см⋅100см=1000000см3;1м3=1000мм⋅1000мм⋅1000мм=1000000000мм3.

1 дм3=110м⋅110м⋅110м=11000м3=0,001м3.

1см3=1100м⋅1100м⋅1100м=11000000м3=0,000001м3.1мм3=11000м⋅11000м⋅11000м=11000000000м3=0,000000001м3.

Определение объёма

prjamoug_pallelepiped.png

Рис. (2). Прямоугольный параллелепипед

Объём тела вычисляют по формулам.

Для прямоугольного параллелепипеда:

объём=длина⋅ширина⋅высота.

Если длина равна

l1

, ширина 

l2

, высота 

l3

, тогда объём будет 

V=l1⋅l2⋅l3

.

Объём тел неправильной формы определяют методом погружения.

  1. В мензурку наливают воду и определяют её объём.
  2. В воду погружают тело и определяют общий объём тела и воды.
  3. Объём тела определяют, вычитая из общего объёма начальный объём.

объем-неправильных-тел.gif

Рис. (3). Погружение в жидкость тела неправильной формы  

Некоторые английские неметрические единицы объёма

Акрофут (= 1233,48)

м3

.

Кубический дюйм (= 16,39)

см3

.

Баррель нефти (= 158,99)

дм3

.

Бушель (США) (= 35,24)

дм3

.

Галлон жидкости (США) (= 3,78) 

дм3

.

Источники:

Рис. 1. Кубический метр. © ЯКласс.
Рис. 2. Прямоугольный параллелепипед. © ЯКласс.
Рис. 3. Погружение в жидкость тела неправильной формы. © ЯКласс.

Источник

У этого термина существуют и другие значения, см. Объём (значения).

Объём
{displaystyle V}
Размерность

L3

Единицы измерения
СИ

м3

СГС

см3

Примечания

скалярная величина

Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Синонимом вместимости частично является ёмкость, но словом ёмкость обозначают также сосуды и качественную характеристику конденсаторов.

Принятые единицы измерения — в СИ и производных от неё — кубический метр, кубический сантиметр, литр (кубический дециметр) и т. д. Внесистемные — галлон, баррель.

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

Вычисление объёма

Математически

Основная статья: Объём (геометрия)

В общем случае математически объём тела вычисляется по следующей интегральной формуле:

{displaystyle V=iiint limits _{mathbb {R} ^{3}}chi (x,y,z)dxdydz},

где {displaystyle chi (x,y,z)} — характеристическая функция геометрического образа тела.

Для ряда тел с простой формой более удобным является использование специальных формул. Например, объём куба с длиной стороны, равной a, равен {displaystyle V=a^{3}}.

Через плотность

Объём находится по формуле: {displaystyle V={frac {m}{rho }}}

Единицы объёма жидкости

  • 1 л = 1,76 пинты = 0,23 галлона

Английские внесистемные

  • 1 пинта = 0,57 л
  • 1 Кварта = 2 пинты = 1,23 л
  • 1 галлон = 8 пинтам = 4,55 л (Имперский галлон)

Американские внесистемные

  • 1 американский галлон = 3,785 л (Распространён в США)

Античные внесистемные

  • Котила = 0,275 л

Древнееврейские

  • Эйфа = 24 883 см³ (Эйфа́)
  • Омер = 1/10 эйфы
  • Гин = 4147 см³[1]
  • Кав = 1382 см³

Русские внесистемные

  • Бочка = 40 вёдер = 492 л
  • Ведро = 4 четверти = 8 штофов = 12,3 л
  • Кружка = 10 чарок = 20 шкаликов = 1,23 л
  • Бутылка (винная) = 1/16 Ведра = 0,77 л
  • Бутылка (пивная) = 1/20 Ведра = 0,61 л
  • Мера = 4,7 ведра
  • Чарка = 2 шкалика = 0,123 л
  • Четверть = 4 бутылки = 3,075 л
  • Шкалик (косушка) = пол чарки = 0,0615 л
  • Штоф = 1,54 л

Единицы сыпучих веществ

Английские внесистемные

  • 1 бушель = 36,36872 литров = 8 галлонов = 3,63687×10−2 м³
  • 1 баррель = 0,16365 м³. (для сыпучих веществ)

Русские внесистемные

  • Четверик = 26,238 л
  • Гарнец = 3,2798 л

Молярный объём

Vm — величина, равная отношению объёма V системы (тела) к её количеству вещества n:

Vm = V/n

Молярный объем для газов при нормальных условиях: Vm = 22,4 л/моль

  • Единица: м³/mol; м³/моль

Прочие единицы измерения

  • 1 дюйм кубический = 1,63871×10−5 м³
  • 1 литр = 1×10−3 м³
  • Лямбда 1 λ = 1×10−9 м³
  • 1 унция = 2,841×10−5 м³ (анг.)
  • 1 унция = 2,957×10−5 м³ (амер.)
  • 1 фут кубический = 2,83168×10−2 м³
  • 1 ярд кубический = 0,76455 м³
  • 1 стер = 1 м³
  • 1 ае кубическая =3,348071936e+40 км³
  • 1 км кубический = 1 000 000 000 м³
  • 1 световой год кубический = 8,46590536e+38 км³
  • 1 пк кубический = 2,9379989989648103256576e+40 км³
  • 1 мпк кубический =1 000 000 000 пк³=2,9379989989648103256576e+49 км³

Примечания

  1. ↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4

Литература

  • Объем // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907. (см. ISBN )
  1. Википедия Объём адрес
  2. Викисловарь — адрес
  3. Викицитатник — адрес
  4. Викиучебник — адрес
  5. Викитека — адрес
  6. Викиновости — адрес
  7. Викиверситет — адрес
  8. Викигид — адрес

Выделить Объём и найти в:

  1. Вокруг света адрес
  2. Академик адрес
  3. Астронет адрес
  4. Элементы адрес
  5. Научная Россия адрес
  6. Кругосвет адрес
  7. Научная Сеть
  8. Традиция — адрес
  9. Циклопедия — адрес
  10. Викизнание — адрес
  1. Google
  2. Bing
  3. Yahoo
  4. Яндекс
  5. Mail.ru
  6. Рамблер
  7. Нигма.РФ
  8. Спутник
  9. Google Scholar
  10. Апорт
  11. Онлайн-переводчик
  12. Архив Интернета
  13. Научно-популярные фильмы на Яндексе
  14. Документальные фильмы
  1. Список ru-вики
  2. Вики-сайты на русском языке
  3. Список крупных русскоязычных википроектов
  4. Каталог wiki-сайтов
  5. Русскоязычные wiki-проекты
  6. Викизнание:Каталог wiki-сайтов
  7. Научно-популярные сайты в Интернете
  8. Лучшие научные сайты на нашем портале
  9. Лучшие научно-популярные сайты
  10. Каталог научно-познавательных сайтов
  11. НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов
  • Страница 0 — краткая статья
  • Страница 1 — энциклопедическая статья
  • Разное — на страницах: 2 , 3 , 4 , 5
  • Прошу вносить вашу информацию в «Объём 1», чтобы сохранить ее

Комментарии читателей:

Источник


Загрузить PDF


Загрузить PDF

Объем выражается в кубических единицах измерения. Объем может быть выражен в разных единицах измерения (например, в кубических сантиметрах или в литрах), но любую из них можно преобразовать в кубические метры. Также можно вычислить объем распространенных фигур, таких как прямоугольные параллелепипеды и цилиндры. Чтобы найти объем фигуры в математической задаче или объем какого-то пространства, к примеру, комнаты, надо просто умножить площадь основания на высоту. Также помните, что кубические метры записываются как м3.

  1. Изображение с названием Find Cubic Feet Step 1

    1

    Разделите значение в кубических сантиметрах на 1000000, чтобы преобразовать его в кубические метры. Если объем фигуры или пространства получен в кубических сантиметрах, его можно быстро преобразовать в кубические метры. Обратите внимание, что сантиметр меньше метра, поэтому кубических метров будет меньше, чем кубических сантиметров. Итак, значение в кубических сантиметрах разделите на 1000000.[1]

    • Например, если объем равен 6900000 кубических сантиметров, разделите это значение на 1000000 и получите 6,9. Таким образом, данный объем равен 6,9 кубических метров.

  2. Изображение с названием Find Cubic Feet Step 2

    2

    Разделите значение в кубических ярдах на 1,308, чтобы преобразовать его в кубические метры. Сделайте так, если объем фигуры или пространства получен в кубических ярдах. Обратите внимание, что метр больше ярда, поэтому кубических метров будет меньше, чем кубических ярдов.[2]

    • Например, если объем фигуры или пространства равен 10 кубических ярдов, разделите это значение на 1,308 и получите 7,65. Таким образом, данный объем равен 7,65 кубических метров.

  3. Изображение с названием Find Cubic Feet Step 3

    3

    Умножьте значение в кубических футах на 0,0283, чтобы преобразовать его в кубические метры. Это можно сделать, даже если эти единицы измерения входят в разные системы единиц. Фут меньше метра, поэтому кубических метров будет меньше, чем кубических футов. Итак, значение в кубических футах умножьте на 0,0283.[3]

    • Например, если объем фигуры или пространства равен 500 кубических футов, умножьте это значение на 0,0283 и получите 14,158. Таким образом, данный объем равен 14,158 кубических метров.

  4. Изображение с названием Find Cubic Feet Step 4

    4

    Умножьте значение в кубических дюймах на 0,00001639, чтобы преобразовать его в кубические метры. Конвертировать единицы измерения английской системы в единицы измерения международной системы не так сложно, как кажется. Дюйм меньше метра, поэтому кубических метров будет меньше, чем кубических дюймов. Итак, значение в кубических дюймах умножьте на 0,00001639.[4]

    • Например, если объем пространства или фигуры равен 450000 кубических дюймов, умножьте это значение на 0,00001639 и получите 7,38. Таким образом, данный объем равен 7,38 кубических метров.

    Реклама

  1. Изображение с названием Find Cubic Feet Step 5

    1

    Запомните формулу для вычисления объема прямоугольного параллелепипеда: V = Bh. (В России принято использовать другие буквенные обозначения в формуле: V=S*h.) К прямоугольным параллелепипедам также относятся кубы. В этой формуле V — объем, B (или S) — площадь основания, h — высота. Таким образом, умножьте площадь основания на высоту, чтобы найти объем.[5]

    • Используйте одинаковые единицы измерения. Лучше, если все ребра параллелепипеда будут измерены в сантиметрах или метрах, чтобы получить кубические сантиметры или кубические метры. В противном случае найденное значение объема можно конвертировать в другие единицы измерения.

  2. Изображение с названием Find Cubic Feet Step 6

    2

    Вычислите площадь основания. Для этого умножьте длину на ширину. Чтобы найти площадь прямоугольника, необходимо знать длину (L) и ширину (W). Измерьте каждую сторону или воспользуйтесь данными значениями. Чтобы найти площадь основания прямоугольного параллелепипеда, умножьте длину на ширину.[6]

    • Например, длина комнаты равна 10 м, а ширина — 5 м. Умножьте 10 м на 5 м и получите 50 м2.
    • Обратите внимание, что площадь измеряется в квадратных единицах, в данном случае в квадратных метрах.

  3. Изображение с названием Find Cubic Feet Step 7

    3

    Умножьте площадь основания на высоту, чтобы найти объем. Теперь, когда вы нашли площадь основания, измерьте высоту или воспользуйтесь данным значением. Умножьте площадь основания на высоту, чтобы вычислить объем. [7]

    • Например, если высота комнаты равна 5 м, умножьте 5 м на 50 м2 (площадь основания комнаты). Итак, объем комнаты равен 250 м3.

    Реклама

  1. Изображение с названием Find Cubic Feet Step 8

    1

    Используйте формулу V = Bh для вычисления объема цилиндра. (В России принято использовать другие буквенные обозначения в формуле: V=S*h.) В этой формуле V — объем, B (или S) – площадь основания, h — высота. То есть перемножьте площадь основания и высоту, чтобы найти объем цилиндра. [8]

    • Измерьте стороны в сантиметрах или метрах или конвертируйте значения в указанные единицы измерения, чтобы получить объем в кубических сантиметрах или кубических метрах. Также найденное значение объема можно преобразовать в другие единицы измерения.

  2. Изображение с названием Find Cubic Feet Step 9

    2

    Вычислите площадь основания по формуле В (или S) = πr2. Воспользуйтесь данным значением радиуса или измерьте его. Так как в основании цилиндра лежит круг, вычислите площадь, возведя в квадрат радиус и умножив полученное значение на π, которое равно 3,14.[9]

    • Например, если радиус круглой башни равен 5 м, умножьте 5 на 5 и получите 25 м2. Затем 25 м2 умножьте на 3,14 и получите 78,5 м2.
    • Обратите внимание, что площадь измеряется в квадратных единицах, в данном случае в квадратных метрах.
    • Если дан диаметр, а не радиус круга, разделите диаметр на 2, чтобы найти радиус. Например, если диаметр круга равен 12 м, радиус будет равен 6 м.

  3. Изображение с названием Find Cubic Feet Step 10

    3

    Умножьте площадь основания на высоту, чтобы найти объем. Измерьте высоту цилиндра или воспользуйтесь данным значением. Затем просто перемножьте высоту и площадь основания.[10]

    • Например, высота башни равна 10 м. Таким образом, умножьте 78,5 м2 (площадь основания) на 10 м и получите 785 м3 – это объем башни.

    Реклама

Об этой статье

Эту страницу просматривали 15 835 раз.

Была ли эта статья полезной?

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как составить документ в экселе
  • Как найти кинетическую энергию катящегося шара
  • Как найти бассейн настоящий
  • Пересолила фарш для котлет как исправить куриный
  • Правило как найти расстояние скорость время расстояние

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии