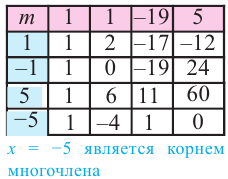
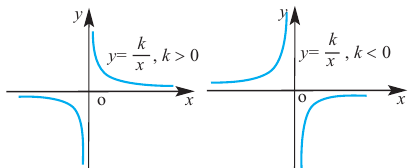
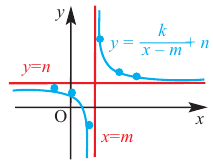
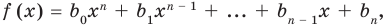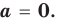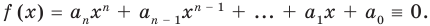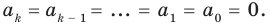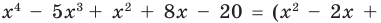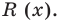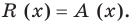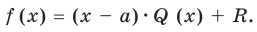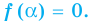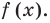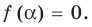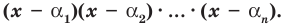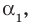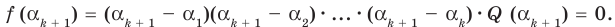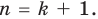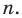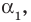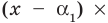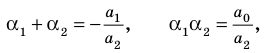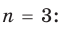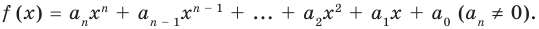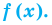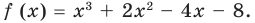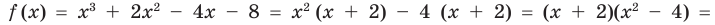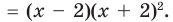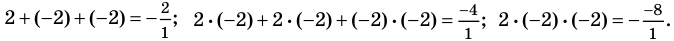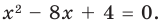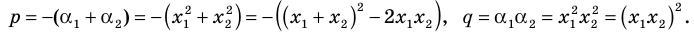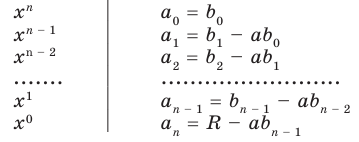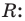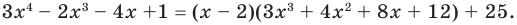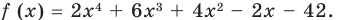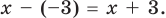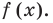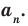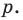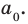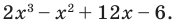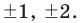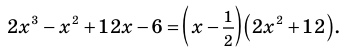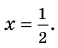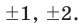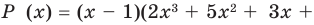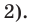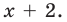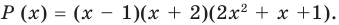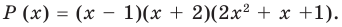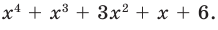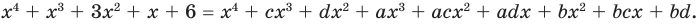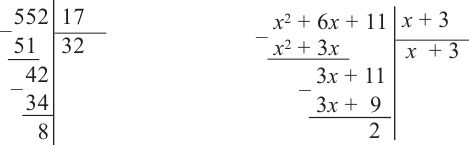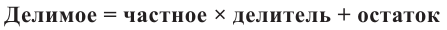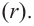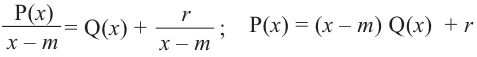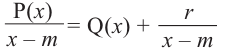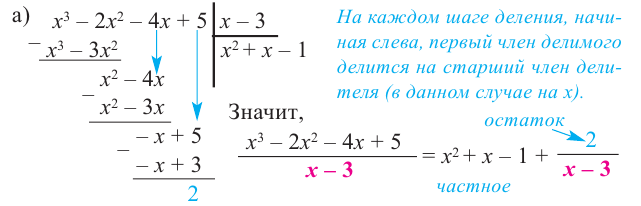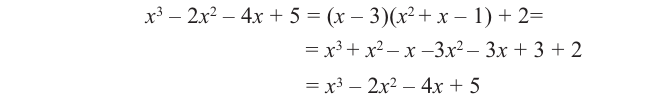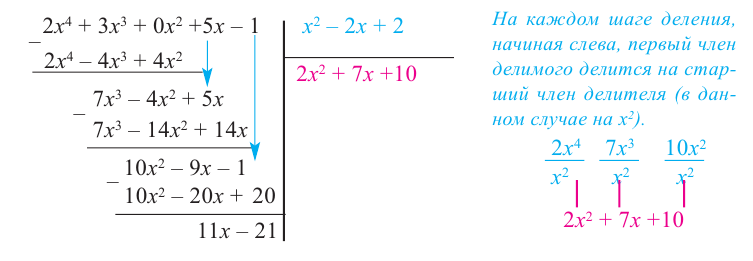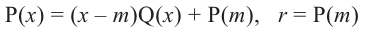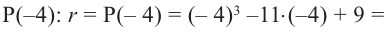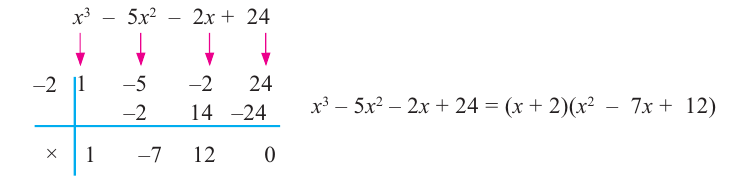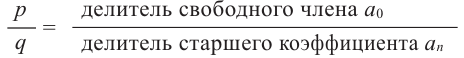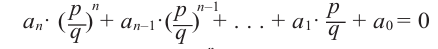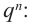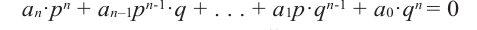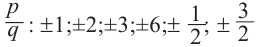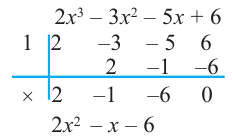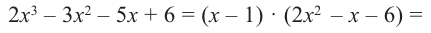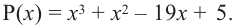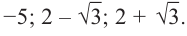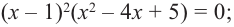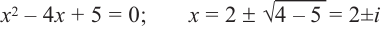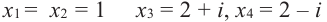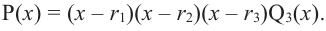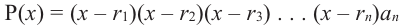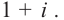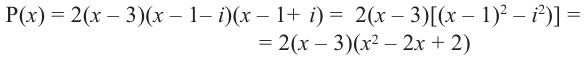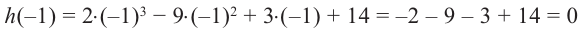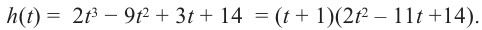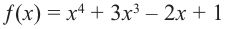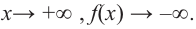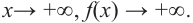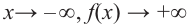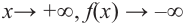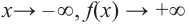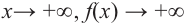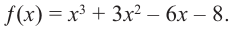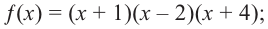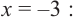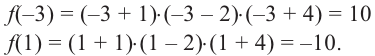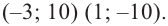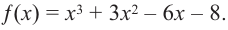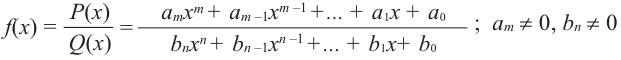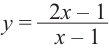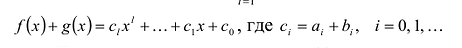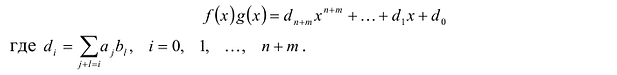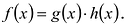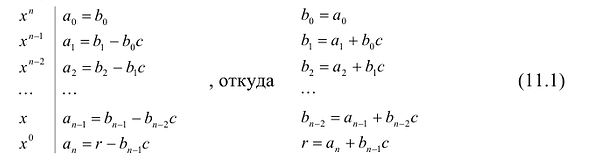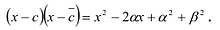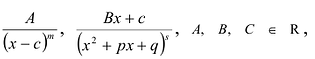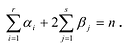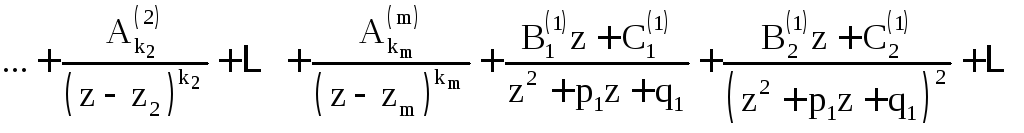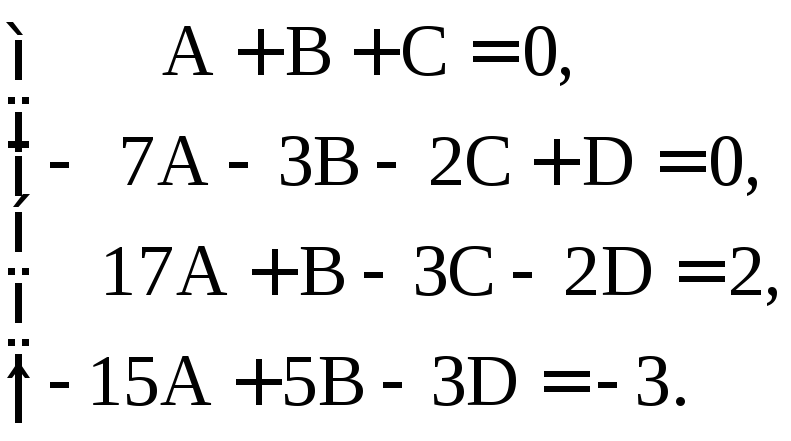Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу
(аналитически). Разберем алгоритм решения
подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.
По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
Вместо « f(x) » подставим ноль.
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель
« x » за скобки.
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x 2 − 4)»
равен нулю.
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.
Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
Подставим вместо « h(x) » ноль.
Перенесем правую часть
в левую, изменив ее знак на минус.
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции
h(x) =
Разбор примера
Найдите нули функции:
Заменим «f(x)» на ноль.
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0)2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.
Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».
Рассмотрим на примере.
Разбор примера
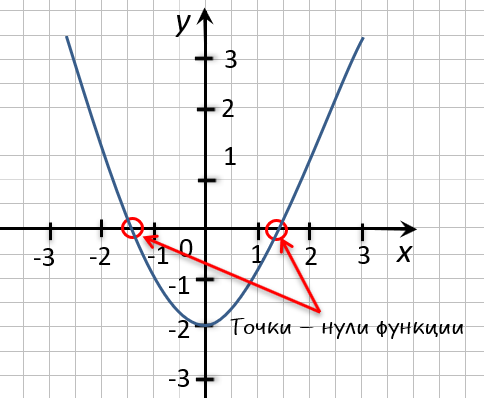
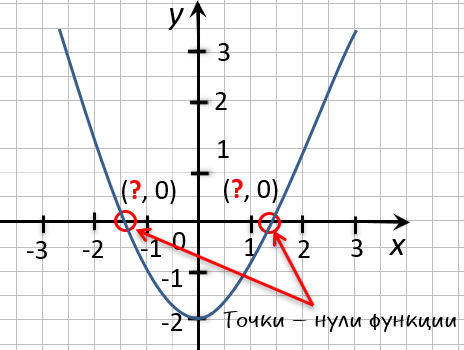
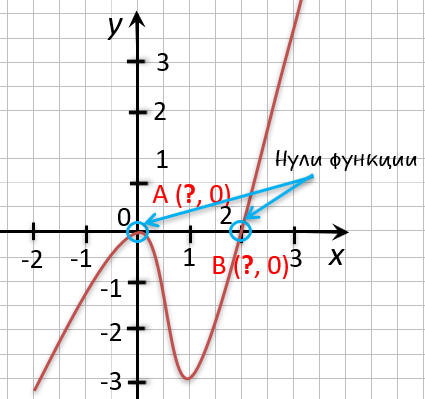
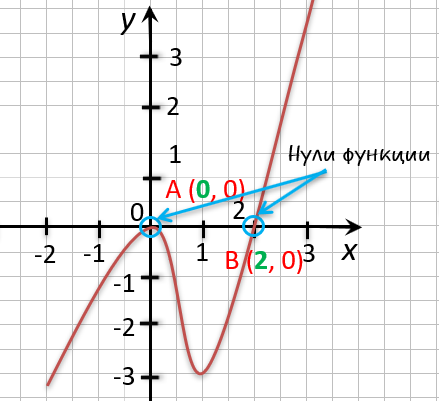
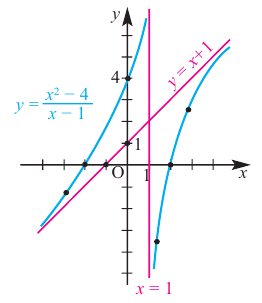
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.
Отметим на графике функции его точки пересечения с осью « Ox ».
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
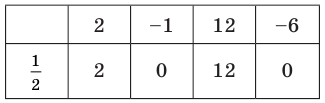
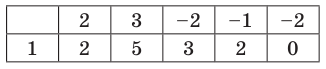
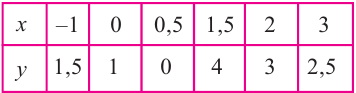
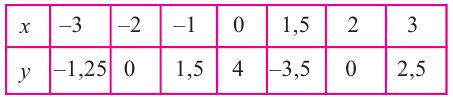
Найдите нули функции, заданной таблицей.
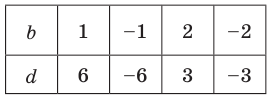
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен — это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 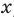
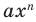
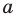
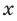
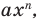
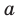
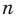
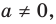
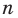
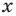
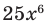
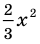
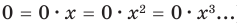
По определению многочлен от одной переменной 
многочленом от одной переменной 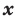
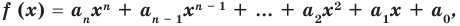
где коэффициенты 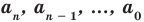
Если 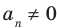
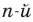
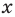
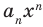
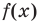
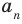
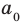
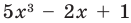
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 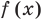
где 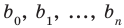
Теорема 1. Одночлены 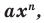
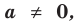
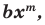
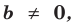
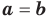
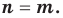
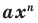
Поскольку равенство одночленов
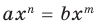
выполняется при всех значениях 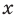
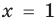
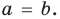
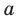
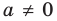
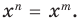
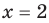
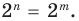
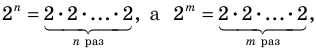
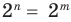
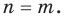
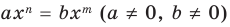
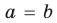
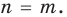
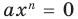
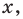
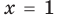
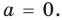
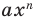
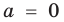
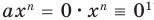
Далее любой одночлен вида 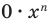
Теорема 2. Если многочлен 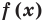
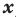
Для доказательства используем метод математической индукции. Пусть
При 
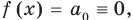
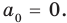
Предположим, что при 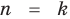
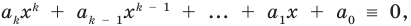
Докажем, что данное утверждение выполняется и при 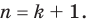
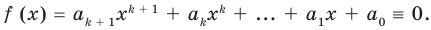
Поскольку равенство (3) выполняется при всех значениях 
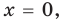
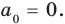
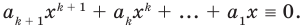

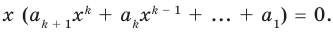
Равенство (4) должно выполняться при всех значениях 
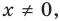
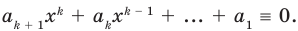
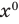
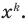
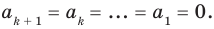
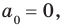
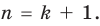
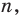
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 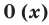
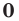
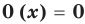
Теорема 3. Если два многочлена 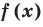
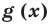
Пусть многочлен 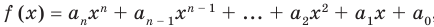
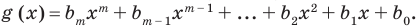
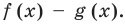
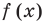
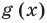
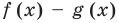
Но 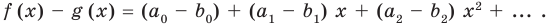
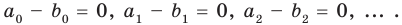
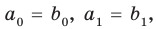
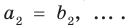
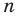
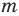
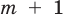
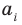
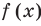
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 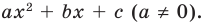
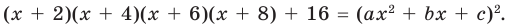
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 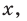
Из первого равенства получаем 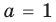
При 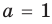
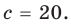
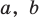
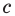
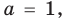
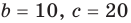
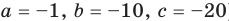
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 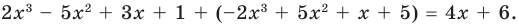
Например, 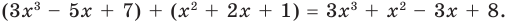
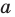
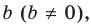
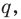
Определение: Многочлен 
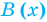
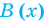

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 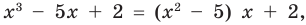
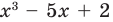
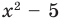
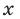
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 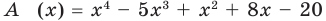
Решение:
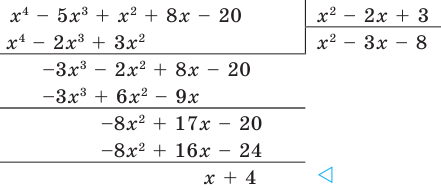
Если обозначить результат выполнения первого шага алгоритма через 
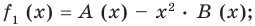
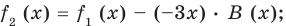
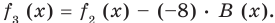
Сложим почленно равенства (1), (2), (3) и получим
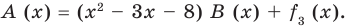
Учитывая, что степень многочлена 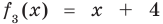
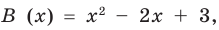
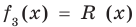
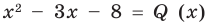
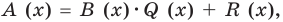
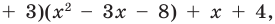
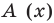
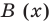
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 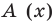
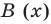
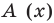
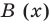
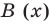
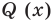
Отметим, что в случае, когда степень делимого 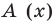
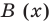
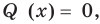
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 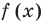
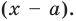
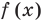
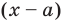
Это равенство выполняется тождественно, то есть при любом значении 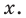
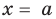
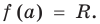
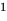
Теорема 1 (теорема Безу). Остаток от деления многочлена 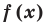
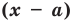
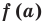
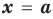
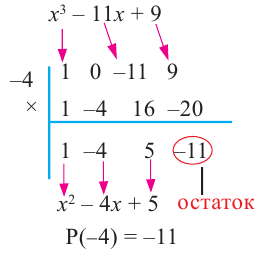
Пример №2
Докажите, что 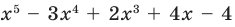
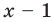
Решение:
► Подставив в 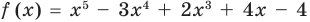
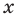
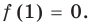
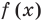

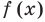

Определение: Число 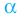
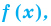
Если многочлен 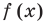

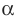
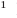
Действительно, если 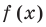
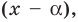

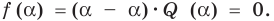
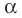
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 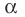
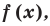
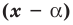
По теореме Безу остаток от деления 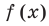

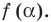
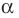
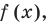
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 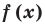
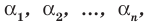
Для доказательства используем метод математической индукции.
При 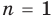
Допустим, что утверждение справедливо при 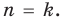
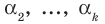
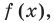
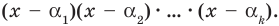
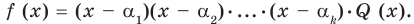
Докажем, что утверждение теоремы справедливо и при 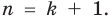
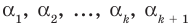
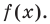
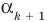
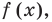
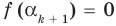
По условию все корни 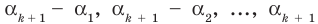
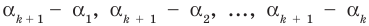
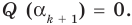
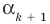
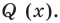
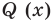
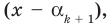
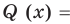
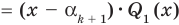
Это означает, что 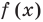
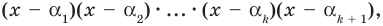
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 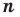
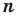
Допустим, что многочлен 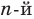
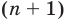
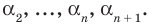
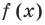
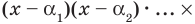
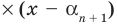
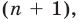
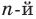
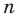
Пусть теперь многочлен 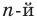
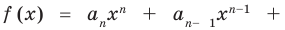
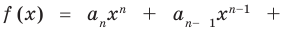
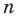
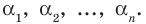
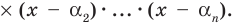
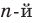
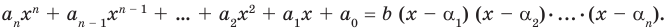
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 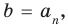
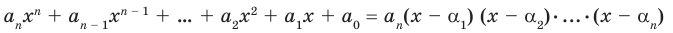
Сравнивая коэффициенты при одинаковых степенях 
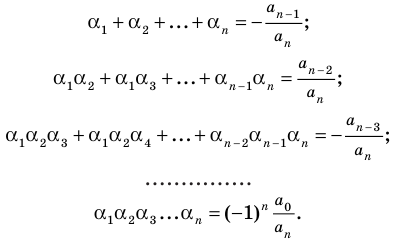
Например, при 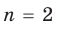
а при
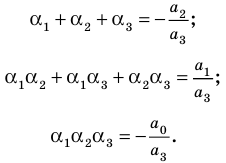
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 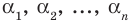
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 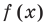
Если многочлен 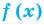
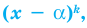
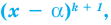


Например, если произведение 
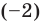
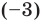
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 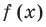
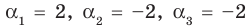
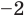
Проверим справедливость формулы (5). В нашем случае: 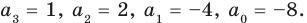
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 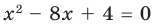
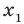
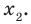
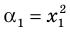
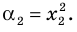
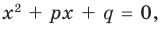
По формулам Виета имеем 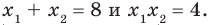
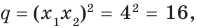
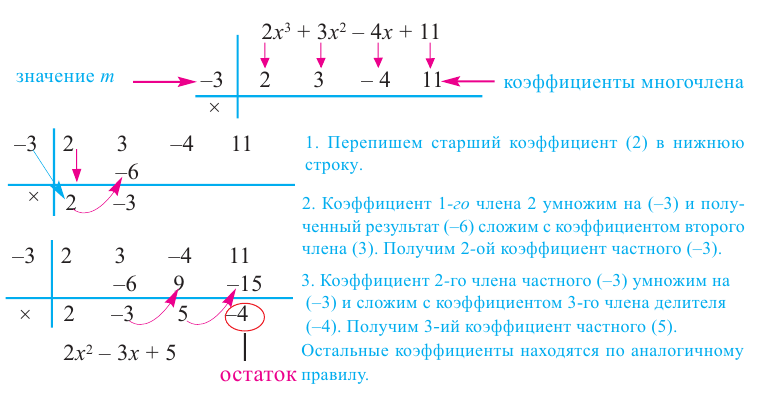
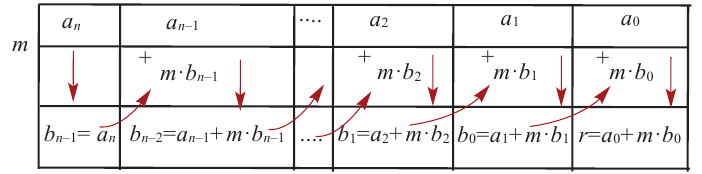
Схема Горнера
Делить многочлен 
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 
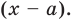
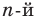
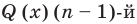
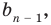
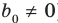
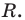
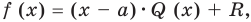
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 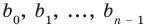
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 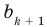
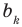
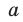
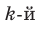
Пример №5
Разделите по схеме Горнера многочлен 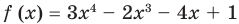
Решение:
► Запишем сначала все коэффициенты многочлена 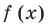
Таким образом,
Пример №6
Проверьте, является ли 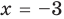
Решение:
► По теореме Безу остаток от деления многочлена 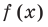
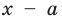
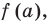
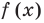
Поскольку 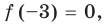
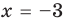
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 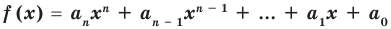
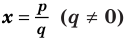
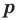
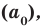
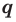
Если 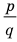
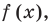
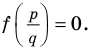
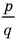
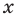
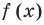
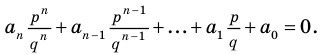
Умножим обе части равенства (1) на 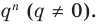
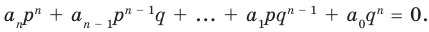
В равенстве (2) все слагаемые, кроме последнего, делятся на 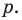
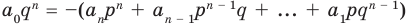
Но когда мы записываем рациональное число в виде 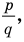
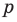
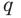
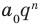
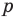
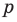
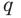
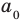
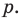
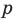
Аналогично все слагаемые равенства (2), кроме первого, делятся на 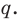
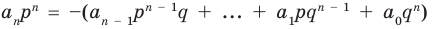
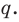
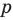
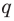
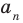
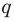
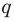
Отметим два следствия из этой теоремы. Если взять 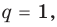
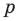
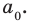
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 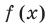
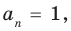
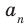
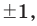
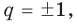
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 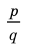
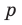
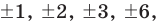
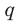
Таким образом, рациональные корни многочлена необходимо искать среди чисел 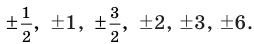
При 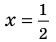
Кроме того, по схеме Горнера можно записать, что
Многочлен 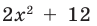
Пример №8
Разложите многочлен 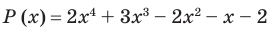
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 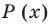

Тогда
Ищем целые корни кубического многочлена 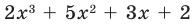
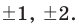
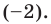
Имеем
Квадратный трехчлен 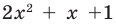
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 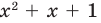
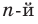
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
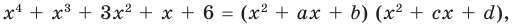
где 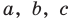
Получаем систему
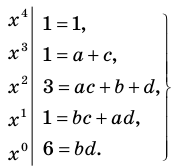
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 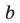
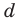
Коэффициенты 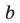
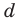
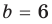
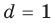
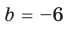
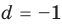
Для каждой пары значений 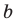
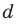
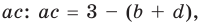
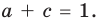
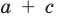
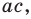
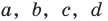
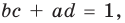
Как видим, системе (4) удовлетворяет набор целых чисел 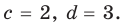
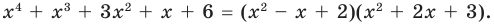
Поскольку квадратные трехчлены 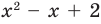
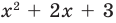
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 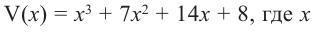
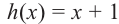
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 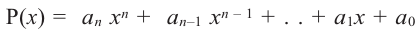
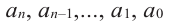
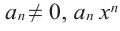
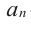
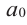
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 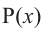
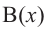
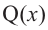
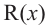
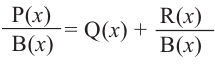
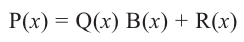
Здесь, степень многочлена 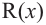
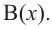
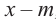
В этом случае:
Пример №10
а) Разделите многочлен 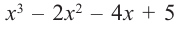
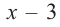
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 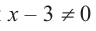
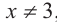
c) Должно выполняться тождество
Пример №11
Разделите 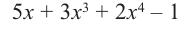
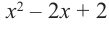
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 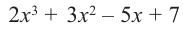
2) На каждом шаге деления делимое делится на старший член делителя, на 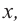
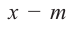
При делении многочлена на двучлен вида 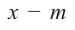
Пример №13
Разделите многочлен 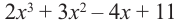
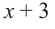
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 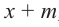
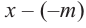
Запишем двучлен 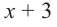
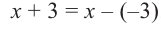
Таким образом, для делимого 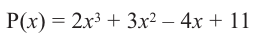
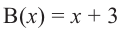
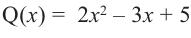
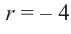
Деление можно записать в виде: 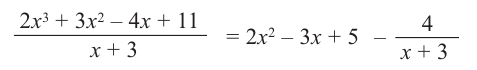
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 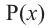
Доказательство: В равенстве 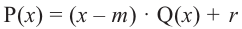
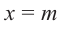
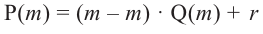
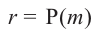
Пример №14
Найдите остаток от деления многочлена 
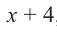
Решение: запишем делитель в виде 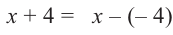
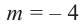
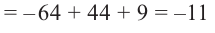
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 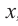
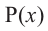
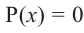
Теорема. Если число 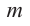
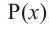
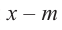
Действительно, если 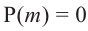
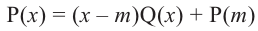
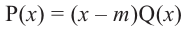
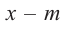
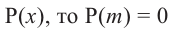
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 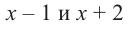
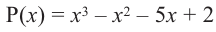
Решение: вычислим значение многочлена 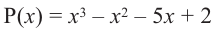
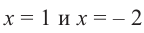
Значит, 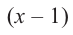
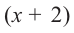
Пример №16
Зная, что 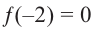
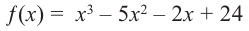
Решение: так как 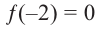
Учитывая, что 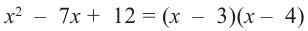
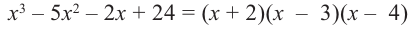
Отсюда получаем, что 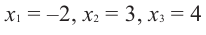
Примечание: Если многочлен задан в виде 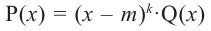
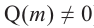
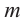
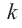
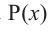
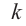
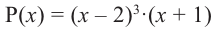
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 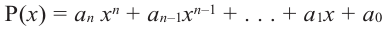
Доказательство. Пусть несократимая дробь 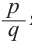
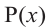
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 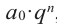
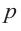
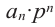
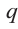
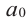
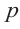
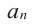
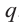
Пример №17
Найдите рациональные корни многочлена 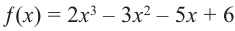
Решение: свободный член 6, старший коэффициент 2.
Для 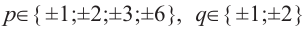
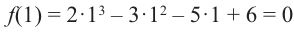
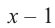
Так как, 
Следствие 1. Если старший коэффициент 
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 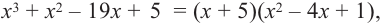
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 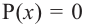
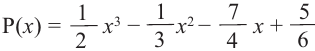
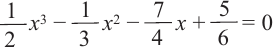
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 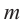
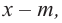
3. Для данного многочлена при помощи синтетического деления на двучлен 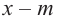
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 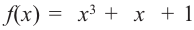
Проверим: 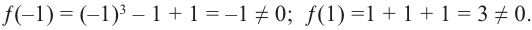
Основная теорема алгебры
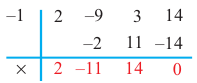
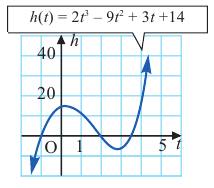
Покажем на примере, что многочлен 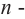
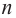
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 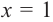
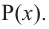
В выражении 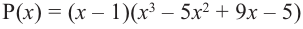
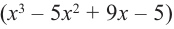
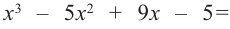
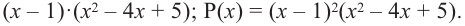
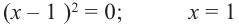
Корни:
Во всех рассмотренных нами примерах уравнение 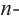
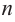
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 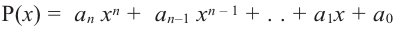
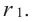
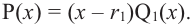
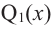
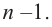
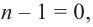
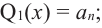
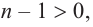
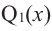
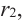
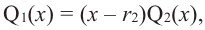
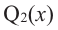
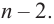
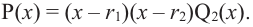
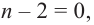
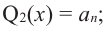
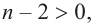
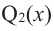
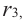
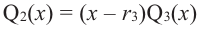
Продолжая процесс 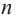
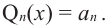
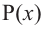
здесь числа 
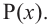
Следствие. Многочлен 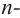
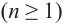
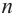
Отметим, что если комплексное число 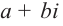
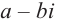
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 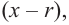
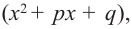
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 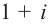
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 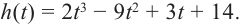
Решение: во всех случаях, кроме значений 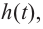
1. Проверим, является ли число 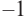
2. Число 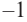
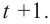
Учитывая, что 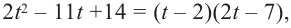
Функция-многочлен
График функции-многочлен
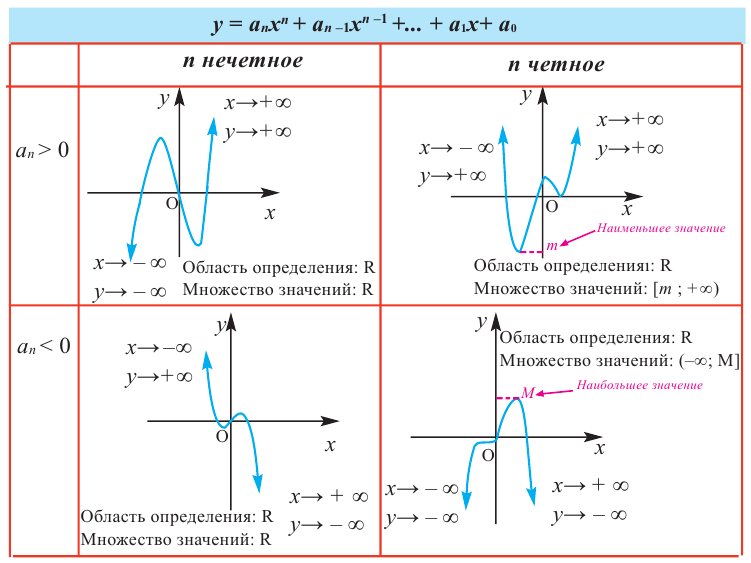
В стандартном виде функция — многочлен записывается как 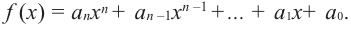
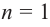
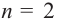
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 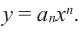
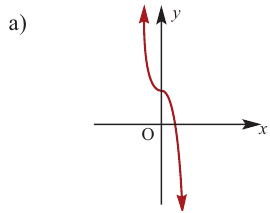
Пример №22
Определите характер поведения функции — многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 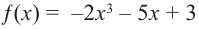
Решение: а) степень многочлена 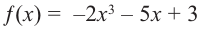
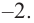
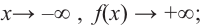
b) степень многочлена 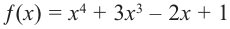
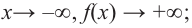
Пример №23
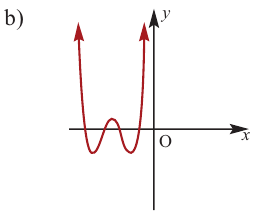
По графику определите как ведет себя функция — многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 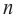
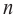
Алгоритм построения эскиза графика функции — многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
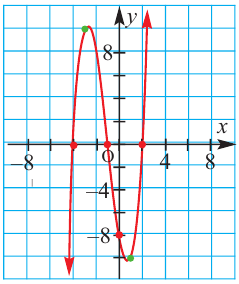
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 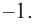
Значит, двучлен 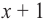
Зная, что 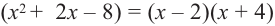
Отсюда находим нули 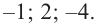
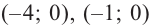
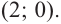
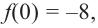
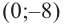
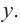
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 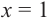
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 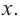
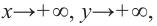
4. Соединим отмеченные точки и получим схематический график функции
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
Самым простым примером рациональной функции является функция
График функции 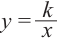
При стремлении значений 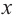
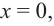
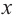
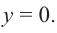
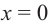
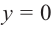
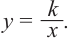
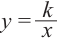
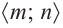
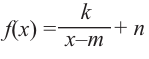
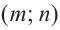
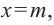
Пример №25
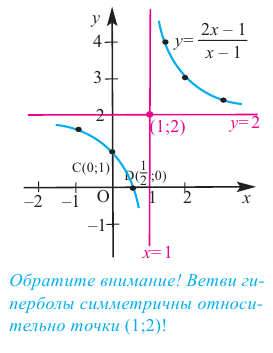
Постройте график функции
Решение: точки пересечения с осью 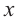
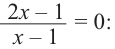
При 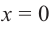
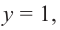
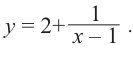
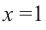
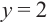
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 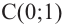
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 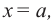
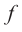
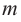
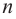
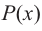
Для 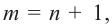
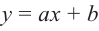
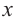
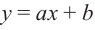
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 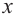
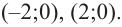
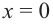
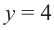
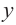
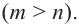
Для больших, но модулю, значений 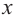
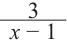
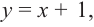
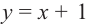
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
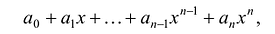
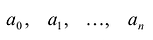
Если коэффициент 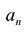
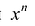
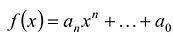
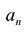
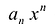
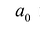
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 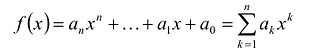
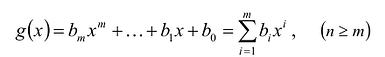
Произведением многочленов 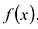
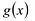
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 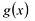
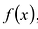
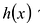
Теорема о делении с остатком
Для любых многочленов 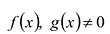
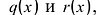
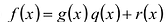
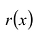
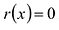
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
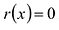
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с — корень многочлена 


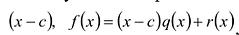
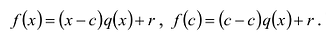

Обратно, пусть (х-с) делит 
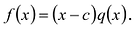
Следствие. Остаток от деления многочлена 
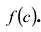
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 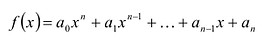
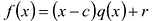
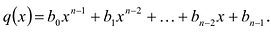
Число с-называется корнем кратности к многочлена 
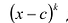

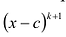

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 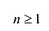
где 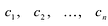

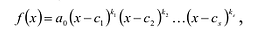
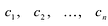

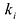
Если многочлен 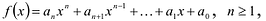
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 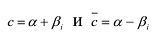


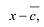
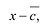

Утверждение 2. Многочлен с действительными коэффициентами степени 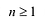
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где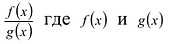
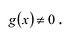

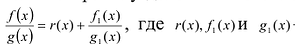
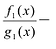
Лемма 1, Если 
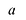
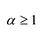
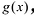
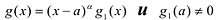
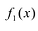
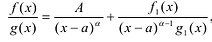
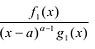
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
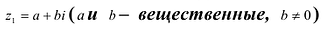
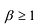
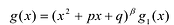
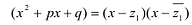
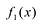
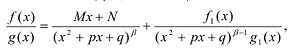
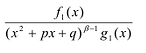
Рациональные дроби вида
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 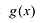
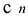
Число неизвестных 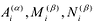
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
Многочленом (или
полиномом) степени
,
называется функция
, (10)
где
– известные комплексные числа
(коэффициенты), при этом старший
коэффициентотличен от 0,z – переменная
комплексная величина. Степень многочлена
f(z)
обозначается deg
f(z).
На
множестве всех многочленов очевидным
образом вводятся операции сложения и
умножения. Число z0
называется нулём многочлена f(z)
, если f(z0)
= 0.
Теорема 1
(о делении
многочленов).
Для любых многочленов f(z) и g(z) существуют
многочлены h(z) и r(z) такие, что:
1)
f(z) = h(z) g(z) + r(z),
2)
deg r(z) < deg g(z).
При
этом h(z)
и r(z)
определяются однозначно.
Многочлен
h(z)
называется частным, а r(z)
– остатком от деления f(z)
на g(z).
При этом оказывается, что deg
f
= deg
g
+ deg
h.
Если r(z)
0, то говорят, что f(z)
делится на g(z).
Теорема 2. Число
z0
является нулём многочлена f(z) в том и
только в том случае,
если f(z)
делится на линейный многочлен (z – z0).
Число
z0
называется нулём кратности m
многочлена f(z),
если f(z)
делится на (z
– z0)m
и не делится на (z
– z0)m+1.
Можно дать другое, равносильное
приведённому, определение: z0
является нулём кратности m
для многочлена f(z),
если f(z)
представим в виде
f(z)
= (z
– z0)m
g(z),
где g(z)
– такой многочлен, что g(z0)
0 .
Теорема 3 (основная
теорема алгебры).
Любой многочлен степени n
1 имеет ровно n нулей, если каждый нуль
считать столько раз, какова его кратность.
Следствием
основной теоремы алгебры является то,
что если z1, z2, … , zm – нули
многочлена (1) кратностей k1, k2, … , km
соответственно, то f(z)
представим в виде
,
при
этом
,
k1
+ k2
+ … +km
= n
.
Для
того чтобы
несократимая дробь
(p – целое, q – натуральное) была нулём
многочлена f(z) с целыми коэффициентами
aj,
необходимо, чтобы число p было делителем
свободного члена a0,
а число q –
делителем старшего коэффициента аn.
В частности, если f(z) имеет целые
коэффициенты aj
и an = 1,
то рациональными нулями такого многочлена
могут быть только целые числа, которые
являются делителями свободного члена
a0
.
Теорема 4. Если
коэффициенты многочлена f(z) – действительные
числа и
– нуль f(z), тоz0 = – i
также является нулём этого многочлена.
Из
последней теоремы следует, что если
f(z) – многочлен с действительными
коэффициентами, то он представим
в виде
,
(11)
где
zj , pj , qj – действительные
числа и квадратичные функции неразложимы
(т.е. имеют отрицательный дискриминант),
при
.
При
этом k1
+ k2
+ … +
km
+ 2(r1
+ r2
+ … + rs)
= n .
Если
f(z),
g(z)
– многочлены, то функция
называется рациональной функцией или
рациональной дробью. Рациональная дробьназывается правильной, еслиdeg
g(z)
< < deg
f(z).
Любую неправильную дробь можно представить
в виде суммы многочлена и правильной
рациональной дроби. Если
– правильная рациональная дробь с
действительными коэффициентами иf(z)
имеет разложение (3), то h(z)
допускает следующее представление в
виде суммы простейших дробей:

Коэффициенты
находятся путём приравнивания
коэффициентов при одинаковых степенях
z у многочлена g(z) и многочлена, который
получается в числителе правой части
(11) после приведения суммы к общему
знаменателю (метод неопределённых
коэффициентов).
Пример 6. Найти
все нули многочлена
и разложить его на неразложимые множители
с действительными коэффициентами, если
известен один его нуль.
Решение.
f(z) имеет действительные коэффициенты,
поэтому наряду с z1
= 2+i нулём f(z) является также z2
=
= 2–i. Значит, f(z) делится на
.
Разделим
f(z) на
уголком
Таким образом,
.
Найдём нули второго множителя: z2
+ 2z + 10 = 0, z3,4
= –1
3i.
Итак, нулями
многочлена f(z) являются: z1
= 2 + i, z2
= 2 – i,
z3 = –1 – 3i,
z4 = –1 + 3i.
Многочлен f(z) разлагается на неразложимые
множители (квадратные функции с
отрицательными дискриминантами)
следующим образом:
z4
– 2z3
+ 7z2
– 30z + 50 = (z2
– 4z + 5)(z2
+2z +10) .
Пример 7. Дан
многочлен f(z) = z4
– 6z3
+ 10z2
+ 2z – 15:
а) подобрать
целые нули многочлена среди делителей
свободного члена;
б) разложить
f(z)
на линейные и неразложимые квадратичные
множители с действительными коэффициентами;
в) разложить
f(z)
на линейные множители с комплексными
коэффициентами;
г) разложить
дробь (2z – 3) / f(z)
на простейшие дроби с действительными
коэффициентами.
Решение.
а) Делителями числа 15 являются: 1,
3,
5,
15.
В
результате проверки убеждаемся, что z1
= –1 является нулём f(z):
f(–1)
= 0. Следовательно, f(z) делится на (z
– z1)
= z
+ 1. Выполним деление
Имеем:
f(z) = (z + 1) (z3
– 7z2
+17z – 15). Найдём
целые нули второго множителя среди
делителей свободного члена (–15): 1;
3;
5;
15.
В
результате проверки убеждаемся, что
является нулём многочлена (z3
– 7z2
+17z
– 15) и, следовательно, многочлена f(z).
Значит, f(z)
делится на (z
– z1)
(z
– z2)
= (z
+ 1) (z
– 3) = z2
– 2z
– 3. Разделим f(z)
на этот квадратный трёхчлен:
Таким
образом, f(z)
= (z2
– 2z
– 3)(z2
– 4z
+ 5). При этом второй множитель (z2
– 4z
+5) не имеет целых (и даже действительных)
нулей. Итак, f(z)
имеет лишь два целых нуля: z1
= –1 и z2
= 3.
б)
Так как z2
– 4z + 5 = 0 имеет лишь комплексные нули
и
,
то искомым разложением будет уже
полученное.
в)
f(z)
имеет 4 однократных (говорят, простых)
нуля: z1
= –1, z2
= 3,
z3
= 2 – i,
z4
= 2 + i.
Старший коэффициент f(z)
равен 1. Поэтому
f(z)
= (z
– z1)(z
– z2
)(z
– z3)(z
– z4)
или f(z)
= (z
+ 1)(z
– 3)
(z
– 2 + i)(z
–2– i).
г)
Дробь (2z
– 3)/f(z)
является правильной. Имеем

Приведём
последнюю сумму к общему знаменателю:

как f(z) равен знаменателю левой части,
то получим равенство
A(z
–3)(z2–
4z +5) + B(z + 1)(z2–
4z +5) + (Cz + D)(z +1)(z – 3)2z
– 3.
Неизвестные
коэффициенты А, В, С, D
можно найти, раскрыв скобки в левой
части, сгруппировав слагаемое по степеням
z
и приравняв соответствующие коэффициенты
в левой и правой частях равенства, при
этом получится система из 4-х линейных
алгебраических уравнений:
(A
+ B + C)z3
+ (– 7A – 3B – 2C + D)z2
+ (17A + B – 3C – 2D)z +
+(–15A
+ 5B – 3D) = 2z – 3.
Приравнивая
коэффициенты при одинаковых степенях
z,
получаем систему
Решая её, находим
A = 1/8, B = 3/8, C = –1/2, D =1. Итак,

Соседние файлы в папке Сборник ч.1 ред 30. 11
- #
- #
- #
- #
- #
- #
I have been told that to find factors of a polynomial (nth degree) we have to find the factors of constant term and that of coefficient of leading term of the polynomial in concern.
The possible integral zeros of the polynomial will be from the factor set of the constant term while rational zeros would be from set of each factor of constant / each factor of coefficient of the leading term.
Now I have to replace one by one value of $X$ for each integral and rational factors founded above and check if the polynomial results to $0$ (zero). The issue is that I go into deep / lengthy calculation if suppose constant term is $140$ and coefficient of leading term is $6$ per say.
Factors of $140 = -1,+1,-2,+2,-4,+4,-5,+5,-7,+7,…..$
Factors of $6 = -1,+1,-2,+2,-3,+3,-6,+6 $
Integral roots of the polynomial (set range) = $-1,+1,-2,+2,-4,+4,-5,+5,-7,+7,…..$
Rational roots of the polynomial (set range)
= $(-1,+1,-2,+2,-4,+4,-5,+5,-7,+7,…..)/ (-1,+1,-2,+2,-3,+3,-6,+6 )$
Taking one by one value and testing for zero is a very lengthy time consuming method — is there a quick easy way to find zeros of the pronominal?
Вычеты и расположение нулей многочлена на комплексной плоскости
Во многих приложениях важное значение имеет задача определения числа нулей данной функции, расположенных в определенной области. Например, при исследовании устойчивости решений дифференциальных уравнений интерес представляют нули характеристического многочлена, расположенные в левой полуплоскости.
Нули функции являются, очевидно, полюсами функции вида
, если
не обращается в нуль в этих точках. В частности, в качестве вспомогательной для исследования нулей функции
можно рассмотреть функцию, полностью определяемую только самой функцией
, а именно
. Из-за очевидного равенства
, эту функцию называют логарифмической произведной функции
. Ее особыми точками являются особые точки и нули
. Поэтому нули функции
можно исследовать как особые точки
. Можно применить аппарат теории вычетов, в частности основную теорему о вычетах. Имеет место следующее утверждение.
Теорема о логарифмическом вычете
Утверждение 4.12 (теорема о логарифмическом вычете).
1. Пусть функция — аналитическая в
за исключением, быть может, конечного числа полюсов, на
— границе области
не имеет ни полюсов, ни нулей. Тогда справедлива формула
(4.37)
где — число нулей,
— число полюсов функции
в области
с учетом их кратностей, т.е. каждый нуль считается столько раз, какова его кратность, а каждый полюс — такое количество раз, каков его порядок.
2. В частности, если функция в
не имеет особых точек и на
не имеет нулей, то
(4.38)
Доказательство формулы (4.37) получается следующим образом. Пусть — нуль порядка
функции
, тогда справедливо равенство
. Дифференцируя это равенство, получаем
. Поэтому для логарифмической производной имеем
. Здесь
— аналитическая в точке
функция, так как
аналитическая и
. Поэтому в последнем равенстве слагаемое
является главной частью разложения
в окрестности
, из чего следует, что
, т.е. вычет логарифмической производной функции
в ее нуле равен кратности этого нуля.
Аналогично, для —
функции
из равенств
и
получаем
,
из чего заключаем, что , т.е. вычет логарифмической производной функции
в ее полюсе равен порядку полюса с противоположным знаком.
Применяя теорему о вычетах к вычислению интеграла устанавливаем справедливость формулы (4.37).
Пример 4.44. Вычислить контурный интеграл с помощью вычетов
а) ; б)
.
Решение
Формула (4.38), очевидно, может быть использована для исследования нулей функции , если удастся получить удобный алгоритм для вычисления интеграла, стоящего слева в (4.38).
Воспользуемся равенством . Так как
— аналитическая на
и на
не имеет нулей, то в некоторой области, содержащей
, возможно выделение однозначных ветвей
, и, следовательно, на
имеем однозначную аналитическую функию
, где
— одно из значений аргумента, в частности главное значение. Запишем интеграл (логарифмический вычет):
Первое слагаемое в правой части равенства равно нулю как интеграл по замкнутому контуру от полного дифференциала функции дву: действительных переменных .
Второе слагаемое определяет приращение аргумента образа точки при отображении в то время, когда точка
совершает полные обход контура
в положительном направлении (рис. 4.9,а), то есть
. Если точка
не совершает обхода вокруг
, то
(рис. 4.9,б) . Если точка
совершает, оборотов, то
(на рис. 4.9,в
), причем в этом равенстве
при положительном обходе (против часовой стрелки) и
при отрицательном (по часовой стрелке). Величина
определяет число оборотов вектора
, а знак — направление обхода.
Приведенные рассуждения отражают геометрический смысл формулы (4.38).
Принцип аргумента
Утверждение 4.13 (принцип аргумента)
1. Разность между числом нулей и полюсов функции в области ограниченной контуром
, равна числу оборотов вектора
при nt ремещении точки
по кривой
— образу
при отображении
и однократном обходе точкой
контура
(4.39)
2. Если функция — аналитическая в
и на
— границе
нет нулей
, то (4.39) принимает вид
(4.40)
т.е. число нулей в области
функции
, аналитической в этой области, равно числу оборотов вектора
вокруг начала координат.
Принцип аргумента, в частности формула (4.40), имеет многочисленные приложения. Приведем, например, следующие две теоремы.
Теорема Руше
Утверждение 4.14 (теорема Руше). Пусть функции и
являются аналитическими в односвязной области
и на ее границе
и в точках границы выполняются условия
. Тогда число нулей функции
и
в области
одинаково.
Приведем доказательство. Прежде всего проверим, что функции и
удовлетворяют условиям применения принципа аргумента, а именно не имеют нулей на контуре
. Действительно, из неравенства
и
получаем
, то есть
. Аналогично для функции
, то есть
.
Далее покажем, что . Для этого запишем функцию
в виде произведения
. Тогда
, где
. На границе
имеем
, т.e. образом кривой
при отображении
является окружность
, из чего следует, что радиус-вектор точки
не обходит начало координат, поэтому
. Таким образом, получаем
.
Основная теорема алгебры
Утверждение 4.15 (основная теорема алгебры). Многочлен степени с комплексными коэффициентами имеет
корней.
Для доказательства представляем многочлен в виде суммы:
, где
и
.
Так как . то найдется такое число
, что для z, удовлетворяющих условию
, выполняется неравенство
. За счет выбора достаточно большого
можно получить, что все нули многочлена расположены в круге
. На границе круга, т.е. на
, выполняется условие
. По теореме Руше многочлен имеет в
, а следовательно, и всюду такое же число нулей, как и функция
. Но
имеет и нулей в круге
, так как
является нулем кратности
.
Замечание 4.8. Во введении мы построили множество комплексных чисел как расширение множества действительных чисел, в котором разрешимо любое квадратное уравнение. Может показаться, что для разрешимости уравнений более высоких степеней понадобится раз за разом расширять множество
. Однако оказывается, что больше никаких новых расширений не нужно. Корни многочлена какой угодно степени принадлежат множеству
, и, значит, новых чисел, не входящих в
, для решения не требуется. Это свойство называется алгебраической замкнутостью множества комплексных чисел.
Практическое применение формулы (4.40) при решении задач определения числа нулей аналитической функции в области заключается в следующем. Строится годограф — кривая, которая является образом границы области
при отображении
. Далее по рисунку определяется число оборотов вектора
при однократном обходе точкой
границы области
. Наконец, по формуле (4.40) определяется число нулей функции
в области
.
Область может быть неограниченной, например полуплоскость
. С задачей определения числа нулей многочлена
в полуплоскости
связана важнейшая проблема механики — проблема устойчивости электрических и механических систем.
В качестве контура в таком случае выбирается полуокружность
и ее диаметр (рис. 4.10,a), число
выбирается достаточно большим, чтобы все нули многочлена, расположенные в правой полуплоскости
, попали в полукруг
, и рассматривается
. Задача определения числа нулей в левой полуплоскости решается аналогично. При этом рассматривается левая полуокружность
и ее диаметр (рис. 4.10,б).
Так как контур состоит из дуги
и отрезка
, то имеем
в случае
и
в случае
.
Для удобства будем считать, что , так как величина коэффициента
не влияет на число корней уравнения
.
Для определения многочлен
записывается в виде произведения
, где
.
Поэтому . При этом
, а из
получаем
. Таким образом, имеем
. Величина
определяется как разность:
, где
— начальная точка на дуге
, a
— конечная. В обоих случаях, изображенных на рис. 4.10,а и 4.10,б,
и
.
Чтобы определить приращение аргумента при перемещении точки
по мнимой оси (отрезок
на рис. 4.10,а или
на рис. 4.10,б при
) строится, как сказано выше, годограф — образ мнимой оси при отображении
. Для этого записываем параметрическое уравнение мнимой оси
, подставляем в
и получаем параметрическое уравнение образа. Чтобы построить годограф, отделяем в полученном уравнении действительную и мнимую части
. Получаем уравнение образа в действительной параметрической форме
.
Для схематичного построения кривой в плоскости достаточно найти несколько значений переменных
и
для различных значений
, в частности нули функций
, а также их значения при
и
. Часто полезно найти угловой коэффициент касательной при
, то есть
. Все данные целесообразно занести в таблицу и по точкам построить кривую. По графику определяем число оборотов вектора
вокруг нуля и приращение аргумента
на мнимой оси. При решении задачи определения числа нулей в правой полуплоскости рассматривается перемещение точки по годографу в направлении от
к
(рис. 4.10,а), а при определении числа нулей в левой полуплоскости — в направлении от
к
(рис. 4.10,б). Результаты рассуждений запишем в виде алгоритма.
Алгоритм применения принципа аргумента для отыскания числа нулей многочлена
1. Определить приращение аргумента на дуге
, где
— степень многочлена
.
2. Определить приращение аргумента на мнимой оси. Для этого:
а) найти и
;
б) построить годограф,
в) определить число оборотов радиуса-вектора вокруг нуля и приращение
. При решении задачи определения числа нулей в правой полуплоскости рассматривается перемещение точки по годографу в направлении от
к
, а при определении числа нулей в левой полуплоскости — в направлении от
к
. При обходе нуля против часовой стрелки
, а по часовой стрелке
.
3. Вычислить .
4. По формуле (4.40) найти — число нулей многочлена
в полуплоскости.
Примеры нахождения нулей многочленов
Пример 4.45. Найти число нулей многочлена в правой полуплоскости.
Решение
1. Определим , так как
.
2. Положим :
а) выделим действительную и мнимую части ;
б) исследуем поведение функций при
при
и
при
— функция нечетная.
Для нахождения нулей — корней биквадратного уравнения
, введем обозначение
. Находим корни
, поэтому
. Так как
, а
, обозначим
и запишем разложение многочлена:
, где
.
Для значений имеем
, вне этого промежутка
.
Так как многочлены и
не имеют общих нулей, то
при
, т.е. на границе области
нет нулей многочлена
. Поэтому можно применить принцип аргумента.
Полученные данные запишем в табл. 4.1 и построим по точкам кривую (рис. 4.11).
в) Из рис. 4.11 видно, что при однократном обходе точкой мнимой оси сверху вниз (
изменяется от
к
), радиус-вектор
поворачивается на
против часовой стрелки, т.е.
.
3,4. Получаем и
. Поэтому по формуле (4.40) находим
.
Заметим, что заданный многочлен можно разложить на множители и выписать все его нули:
. В правой полуплоскости расположены нули
, а в левой — один нуль
.
Заметим, что для определения числа нулей в левой полуплоскости следует изменять в направлении от
к
. При этом обход нуля осуществляется по часовой стрелке и
. Поэтому
.
Пример 4.46. Найти число нулей многочлена в левой полуплоскости.
Решение
Воспользуемся алгоритмом.
1. Находим , так как
.
2. Положим
а) найдем действительную и мнимую части:
б) исследуем поведение функций
при
при
при
и
при
.
Так как , то многочлен
не имеет нулей на мнимой оси и принцип аргумента применим.
Данные занесем в табл. 4.2, причем достаточно провести вычисления только на интервале , так как можно использовать свойства функций:
— четная, a
— нечетная.
в) Из рис. 4.12 видно, что при
и
при
, поэтому
(
, так как годограф обходит нуль, поворачиваясь против часовой стрелки).
3,4. .
Заметим, что для определения числа нулей в правой полуплоскости следует изменять в направлении от
к
. При этом обход нуля осуществляется по часовой стрелке и
. Поэтому
.
Пример 4.47. Найти число нулей многочлена в правой полуплоскости.
Решение
Пример 4.48. Найти число нулей многочлена в области
a)
; б)
.
Решение
Воспользуемся теоремой Руше.
а) Обозначим . На границе области, т.е. для точек, удовлетворяющих условию
, имеем
Условия теоремы Руше выполняются и, следовательно, число нулей данного многочлена в области совпадает с числом нулей функции
в этой области. Так как многочлен
не имеет корней, то заключаем, что многочлен
в области
не имеет нулей.
б) В силу того, что в круге многочлен не имеет нулей, то для нахождения нулей в кольце
достаточно найти их число в круге
. Обозначим
. На границе области, т.е. для
, удовлетворяющих условию
, имеем
Условия теоремы Руше выполняются, и искомое число нулей совпадает с числом нулей многочлена . Так как этот многочлен в области
имеет корень
кратности
, то получаем, что многочлен
в кольце
имеет три нуля.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.