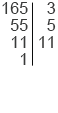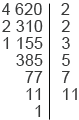Дано: два числа 126 и 126.
Найти: НОД и НОК этих чисел.
Наибольший общий делитель (НОД) целых чисел 126 и 126 — это наибольшее из их общих делителей, т.е наибольшее число, на которое оба делятся без остатка.
Как найти НОД 126 и 126:
- разложить 126 и 126 на простые множители;
- выбрать одинаковые множители, входящие в оба разложения;
- найти их произведение.
Отсюда:
1. Раскладываем 126 и 126 на простые множители:
2. Выбираем одинаковые множители. В нашем случае это: 2, 3, 3, 7
3. Перемножаем эти множители и получаем: 2 · 3 · 3 · 7 = 126
Ответ: НОД (126; 126) = 2 · 3 · 3 · 7 = 126.
Нахождение НОК 126 и 126
Наименьшее общее кратное (НОК) целых чисел 126 и 126 — это наименьшее натуральное число, которое делится на 126 и на 126 без остатка.
Как найти НОК 126 и 126:
- разложить 126 и 126 на простые множители;
- выбрать одну группу множителей;
- добавить к ним множители из второй группы, которые отсутствуют в выбранной;
- найти их произведение.
Отсюда:
1. Раскладываем 126 и 126 на простые множители:
2. Берем множители из первого разложения, добавляем к ним отсутствующие множители со второго разложения и вычисляем произведение.
Ответ: НОК (126; 126) = 2 · 3 · 3 · 7 = 126
Калькулятор нахождения НОД и НОК
Смотрите также
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Наибольший общий делитель
Число 36 имеет такие делители: 1, 2, 4, 6, 9, 12, 18, 36.
Число 126 имеет такие делители: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.
Синим цветом мы выделили числа 1, 2, 6, 9, 18, которые являются общими делителями чисел 36 и 126. Наибольшим из данных множителей является 18.
Наибольший общий делитель чисел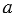 
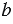
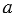
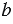
и 
обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.
Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.
Найдем НОД(240; 165).
240 = 2
22235 165 = 3511.
Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.
Найдем НОД(2520; 4620).
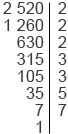
2 520 = 2223357 4 620 = 2235711.
Рассмотрев разложения данных чисел, мы можем заметить, что некоторые простые множители повторяются, например, число 2 в разложении числа 2520 повторяется трижды, а в разложении числа 4620 — дважды. Заметим, что число 4 = 22 является делителем и числа 2520, и числа 4620, а число 8 = 222, является делителем только числа 2520. Так же число 3 является множителем рассматриваемых чисел, а число 9 = 33 является только делителем числа 2520. Кроме чисел 4 и 3, общими делителями данных чисел являются числа 5 и 7.
Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.
Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).
Таким же образом можно найти НОД трех и более чисел.
Чтобы найти НОД нескольких натуральных чисел, надо:
- разложить их на простые множители;
- из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
- найти произведение оставшихся множителей.
Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:
2 520 = 23325171
4 620 = 22315171111.
Тогда НОД мы можем найти по следующему правилу:
- Определить степени, основания которых являются общими простыми делителями данных чисел.
- Из каждой пары степеней с одинаковыми основаниями выбрать степень с меньшим показателем.
- Перемножить выбранные степени. Полученное произведение является искомым наибольшим общим делителем.
Найдем НОД(2520; 4620):
- Выписываем общие основания: 2, 3, 5, 7.
- Выбираем наименьшие показатели данных степеней: 22, 31, 51, 71.
- Находим произведение данных степеней, то есть искомый наибольший общий делитель: НОД(2520; 4620) = 22
315171 = 420.
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 154,
Мерзляк, Полонский, Якир, Учебник
Номер 156,
Мерзляк, Полонский, Якир, Учебник
Номер 224,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 149,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 153,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 171,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 484,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1473,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 190,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Задача: найти НОД и НОК для чисел 126 и 126.
Наибольший общий делитель (НОД) натуральных чисел 126 и 126 — это наибольшее число, на которое 126 и 126 делятся без остатка.
Для нахождения НОД (126;126) необходимо:
- разложить 126 и 126 на простые множители;
- взять те множители, которые входят в разложение каждого из чисел;
- вычислить их произведение.
Таким образом:
Ответ: НОД (126; 126) = 2 · 3 · 3 · 7 = 126.
Подробнее про нахождение НОД смотрите здесь.
Нахождение наименьшего общего кратного (НОК) 126 и 126
Наименьшее общее кратное (НОК) натуральных чисел 126 и 126 — это наименьшее число, которое делится без остатка и на 126 и на 126.
Для нахождения НОК (126;126) необходимо:
- разложить 126 и 126 на простые множители;
- взять множители, входящие в разложение одного из числа;
- добавить к ним те множители, которые отсутствуют в другом числе;
- вычислить их произведение.
Таким образом:
Ответ: НОК (126; 126) = 2 · 3 · 3 · 7 = 126
Подробнее про нахождение НОК смотрите здесь.
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Оцените материал:
Загрузка…
Выберите количество чисел для нахождения НОД
2 числа3 числа4 числа5 чисел6 чисел
Введите числа
Разложим числа 126 и 126 на простые множители
Подчеркнём общие множители
Наибольший общий делитель чисел 126 и 126
Перемножим общие множители
НОД(126, 126) = 2 × 3 × 3 × 7 = 126
Ссылка на результат
https://calc-best.ru/matematicheskie/teoriya-chisel/nod?numbers=126_126
Как найти НОД двух чисел с помощью разложения на простые множители
1) Каждое число нужно разложить на простые множители
2) Потом подчеркнуть множители которые встречаются в обоих числах
3) Перемножить все общие множители
4) Результатом умножения общих множителей будет НОД
Разберём пример
Найдём НОД(16,32)
Разложим числа
16 = 2 × 2 × 2 × 2
32 = 2 × 2 × 2 × 2 × 2
Подчеркнём общие множители
16 = 2 × 2 × 2 × 2
32 = 2 × 2 × 2 × 2 × 2
Перемножим общие множители
НОД(16, 32) = 2 × 2 × 2 × 2 = 16
Похожие калькуляторы
НОД (Наибольший общий делитель) 84 и 126
Наибольший общий делитель (НОД) двух данных чисел 84 и 126 — это наибольшее число, на которое оба числа 84 и 126 делятся без остатка.
НОД (84; 126) = 42.
Как найти наибольший общий делитель для 84 и 126
- Разложим на простые множители 84
84 = 2 • 2 • 3 • 7
- Разложим на простые множители 126
126 = 2 • 3 • 3 • 7
-
Выберем одинаковые простые множители в обоих числах.
2 , 3 , 7
-
Находим произведение одинаковых простых множителей и записываем ответ
НОД (84; 126) = 2 • 3 • 7 = 42
НОК (Наименьшее общее кратное) 84 и 126
Наименьшим общим кратным (НОК) 84 и 126 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (84 и 126).
НОК (84, 126) = 252
Как найти наименьшее общее кратное для 84 и 126
- Разложим на простые множители 84
84 = 2 • 2 • 3 • 7
- Разложим на простые множители 126
126 = 2 • 3 • 3 • 7
- Выберем в разложении меньшего числа (84) множители, которые не вошли в разложение
2
- Добавим эти множители в разложение бóльшего числа
2 , 3 , 3 , 7 , 2
- Полученное произведение запишем в ответ.
НОК (84, 126) = 2 • 3 • 3 • 7 • 2 = 252