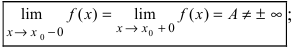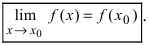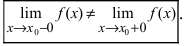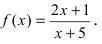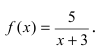Непрерывность функции и точки разрыва
- Приращение аргумента и приращение функции
- Непрерывность функции в точке
- Непрерывность функции на промежутке
- Односторонние пределы
- Классификация точек разрыва
- Точки разрыва первого рода
- Точки разрыва второго рода
- Алгоритм исследования функции на непрерывность
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x= x-x_0 $$ где x — произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
 |
Пусть (y=3x-1) (x_0=1, x=1,1 ) Тогда begin{gather*} triangle x=x-x_0=0,1\ triangle y=(3x-1)-(3x_0-1)=\ =3(x-x_0 )=3triangle x=0,3 end{gather*} В данном случае приращение функции всегда в 3 три раза больше приращения аргумента. |
п.2. Непрерывность функции в точке и на промежутке
Функция (y=f(x)) непрерывна в точке (x_0), если в этой точке малому приращению аргумента (triangle x=x-x_0) соответствует малое приращение функции (triangle y=f(x)-f(x_0)): $$ lim_{triangle xrightarrow 0}triangle y=lim_{xrightarrow x_0}triangle y=0 $$
На «языке ε-δ» определение непрерывности будет следующим:
Функция (y=f(x)) непрерывна в точке (x_0), если для любого (varepsilongt 0) существует такое (delta(varepsilon)gt 0), что для любого (x, |x-x_0|ltdelta) выполняется (|f(x)-f(x_0)|ltvarepsilon:) $$ forall varepsilongt 0 existsdelta=delta(varepsilon)gt 0: forall x, |x-x_0|ltdeltaRightarrow |f(x)-a|ltvarepsilon $$
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль (|x-x_0|) может быть равен 0 для непрерывной функции, т.е. сама точка (x_0) входит в δ-окрестность.
Проанализируем предел приращения функции: begin{gather*} lim_{triangle xrightarrow 0}triangle y= lim_{triangle xrightarrow 0}left(f(x)-f(x_0)right)= lim_{triangle xrightarrow 0}f(x)-lim_{triangle xrightarrow 0}f(x_0)=\ =lim_{triangle xrightarrow 0}f(x)-f(x_0) end{gather*} т.к. (f(x_0)) — величина постоянная и от (triangle x) не зависит.
Для непрерывной функции: $$ lim_{triangle xrightarrow 0}triangle y =0 Leftrightarrow lim_{triangle xrightarrow 0}f(x)-f(x_0)=0Leftrightarrow lim_{triangle xrightarrow 0}f(x)=f(x_0) $$ Учитывая, что (triangle xrightarrow 0Leftrightarrow x-x_0rightarrow 0Leftrightarrow xrightarrow x_0)
получаем (lim{xrightarrow x_0}f(x)=f(x_0).)
Функция (y=f(x)) непрерывна в точке (x_0), если существует предел функции в этой точке и он равен значению функции в точке: $$ lim{xrightarrow x_0}f(x)=f(x_0) $$
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
Функция (y=f(x)) непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
п.4. Односторонние пределы
Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: begin{gather*} lim_{xrightarrow x_0 -0}f(x)=a — text{левый предел}\ lim_{xrightarrow x_0 +0}f(x)=b — text{правый предел} end{gather*}
Рассмотрим гиперболу (y=frac{1}{x-2}).
 |
У этой гиперболы две асимптоты (y=0) и (x=2). Точка (x_0=2) не входит в область определения. Если мы будем приближаться к (x_0=2) слева, начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ lim_{xrightarrow 2-0}frac{1}{x-2}=-infty $$ |
Если же мы будем приближаться к (x_0=2) справа, начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ lim_{xrightarrow 2+0}frac{1}{x-2}=+infty $$ Левый и правый пределы в точке (x_0=2) для данной гиперболы не равны: $$ lim_{xrightarrow 2-0}frac{1}{x-2} ne lim_{xrightarrow 2+0}frac{1}{x-2} $$
Теперь рассмотрим параболу (y=x^2-2)
Областью определения параболы является вся числовая прямая (xinmathbb{R})
 |
В этом случае, если приближаться к (x_0=2) слева, мы получаем: $$ lim_{xrightarrow 2-0}(x^2-2)=2 $$ И если приближаться (x_0=2) справа, мы тоже получаем: $$ lim_{xrightarrow 2+0}(x^2-2)=2 $$ Левый и правый пределы равны: $$ lim_{xrightarrow 2-0}(x^2-2) =lim_{xrightarrow 2+0}(x^2-2) $$ |
Функция (y=f(x)) непрерывна в точке (x_0), если одновременно выполняются следующие три условия:
1) точка (x_0) принадлежит области определения функции (xin D);
2) левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ 3) предел функции в точке (x_0) равен значению функции в этой точке: $$ lim_{xrightarrow x_0}f(x)=f(x_0) $$
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
Точка (x_0) будет точкой разрыва для функции (y=f(x)), если выполняется хотя бы одно из условий:
1) точка (x_0) не принадлежит области определения функции (xnotin D);
2) левый и правый пределы в точке (x_0) не равны или бесконечны: $$ lim_{xrightarrow x_0 -0}f(x) nelim_{xrightarrow x_0 +0}f(x) text{или} lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=pminfty $$ 3) предел функции в точке (x_0) не совпадает со значением функции в этой точке: $$ lim_{xrightarrow x_0}f(x)ne f(x_0) $$
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны |
Устранимые Односторонние пределы равны между собой, но не равны (f(x_0)) |
| Неустранимые (скачок) Односторонние пределы не равны между собой |
||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x)=lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ НО:
либо точка (x_0) НЕ принадлежит области определения функции (xnotin D);
либо предел НЕ равен значению функции в точке (x_0): (lim_{xrightarrow x_0}f(x)ne f(x_0))
Например:
 |
(y=frac{x^2-4}{x-2}, x_0=2) Эта функция эквивалентна системе $$ y=frac{x^2-4}{x-2} Leftrightarrow begin{cases} y=x+2\ xne 2 end{cases} $$ При этом (lim_{xrightarrow 2-0}(x+2)=lim_{xrightarrow 2+0}(x+2)=4) В точке (x_0=2notin D) функция имеет устранимый разрыв. |
Разрыв можно устранить (функцию можно «склеить»), отдельно задав «гладкое» значение в особой точке: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} $$ В таком случае система станет эквивалентна всей прямой, т.е. станет непрерывной функцией: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} Leftrightarrow y=x+2 $$
Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке (x_0) конечны, но не равны: $$ begin{cases} lim_{xrightarrow x_0 -0}f(x)=aneinfty\ lim_{xrightarrow x_0 +0}f(x)=bneinfty\ ane b end{cases} $$ Такой разрыв также называют скачком.
Величина скачка рассчитывается по формуле: $$ triangle y=lim_{xrightarrow x_0 +0}f(x)- lim_{xrightarrow x_0 -0}f(x)=b-a $$
Например:
 |
(y= begin{cases} x+1, xlt 2\ 3-x^2, xgeq 2 end{cases} , x_0=2) Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}f(x)= lim_{xrightarrow 2-0}(x+1)=3\ lim_{xrightarrow 2+0}f(x)= lim_{xrightarrow 2+0}(3-x^2)=-1 end{gather*} Пределы не равны, но конечны. Функция в точке (x_0=2) делает скачок вниз. Величина скачка: $$ triangle y=-1-3=-4 $$ |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
Например:
 |
(y=e^frac1x, x_0=0)
(x_0=0ne D) — точка не входит в ОДЗ Точка (x_0=0) – точка разрыва второго рода. |
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция (y=f(x))
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Пример 1. Исследуйте функцию на непрерывность:
a) ( y=frac{x+3}{x-1} )
ОДЗ: (x-1ne 0Rightarrow xne 1)
(x_0=1notin D) — точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x+3}{x-1}=frac{1-0+3}{1-0-1}=frac{4}{-0}=-infty\ lim_{xrightarrow 1+0}frac{x+3}{x-1}=frac{1+0+3}{1+0-1}=frac{4}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=1) — точка разрыва 2-го рода.
б) ( y=frac{x}{sqrt{x+2}-2} )
ОДЗ: ( begin{cases} x+2geq 0\ sqrt{x+2}-2ne 0 end{cases} Rightarrow begin{cases} xgeq -2\ sqrt{x+2}ne 2 end{cases} Rightarrow begin{cases} xgeq -2\ xne 2 end{cases} )
(x_0=-2) — левая граница ОДЗ
(x_1=2notin D)- точка не входит в ОДЗ
Точки (x_0) и (x_1) — подозрительные на разрыв
Исследуем (x_0=-2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} — text{предел не существует}\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{-2+0}{sqrt{-2+0+2}-2}=frac{-2}{-2}=1 end{gather*} Один из односторонних пределов не существует.
Точка (x_0=-2) — точка разрыва 2-го рода.
Исследуем (x_1=2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} =frac{2-0}{sqrt{2-0+2}-2}=frac{2}{-0}=-infty\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{2+0}{sqrt{2+0+2}-2}=frac{2}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=2) — точка разрыва 2-го рода.
в) ( y=frac{tgx}{3x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{tgx}{3x}=frac13lim_{xrightarrow -0}frac{tgx}{x}=frac13cdot 1=frac13\ lim_{xrightarrow +0}frac{tgx}{3x}=frac13lim_{xrightarrow +0}frac{tgx}{x}=frac13cdot 1=frac13 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
г) ( y= begin{cases} x+1, xlt 3\ x^2+3, xgeq 3 end{cases} )
ОДЗ: (xinmathbb{R})
(x_0=3)- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 3-0}y=lim_{xrightarrow 3-0}(x+1)=3+1=4\ lim_{xrightarrow 3+0}y=lim_{xrightarrow 3+0}(x^2+3)=3^2+3=12 end{gather*} Односторонние пределы конечны, но неравны.
Точка (x_0=3) — точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: (lim_{xrightarrow 3+0}y-lim_{xrightarrow 3-0}y=12-4=8)
Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) ( y=frac{2x^3-x^2}{7x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{2x^3-x^2}{7x}=frac{x^2(2x-1)}{7x}=frac{x(2x-1)}{7}) $$ y=frac{2x^3-x^2}{7x}Leftrightarrow y= begin{cases} frac{x(2x-1)}{7}\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{x(2x-1)}{7}=0, lim_{xrightarrow +0}frac{x(2x-1)}{7}=0 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=0).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{2x^3-x^2}{7x}, xne 0\ 0, x=0 end{cases} $$ б) ( y=frac{1-cos4x}{x^2} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{1-cos4x}{x^2}=frac{2sin^2 2x}{x^2}=frac{2sin^2 2x}{frac{(2x)^2}{4}}=8left(frac{sin2x}{2x}right)^2) $$ y=frac{1-cos4x}{x^2}Leftrightarrow y= begin{cases} 8left(frac{sin2x}{2x}right)^2\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8, lim_{xrightarrow +0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=8).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{1-cos4x}{x^2}, xne 0\ 8, x=0 end{cases} $$
Содержание:
- Точки непрерывности и точки разрыва функции
- Непрерывность элементарных функций. Свойства непрерывных функций
- Непрерывность и разрывы функций
- Определение непрерывности функции в точке. Непрерывность основных элементарных функций
- Разрывы функций и их классификация
- Непрерывность функции на промежутке. Основные теоремы о непрерывных функциях
Точки непрерывности и точки разрыва функции
Важнейшим понятием математического анализа является непрерывность функции.
Определение 1. Функция 




Определение 1 содержит четыре условия непрерывности:
1) функция 

2) должны существовать конечные односторонние пределы 

3) эти пределы должны быть одинаковы;
4) эти пределы должны быть равны 
Определение 2. Если в точке 

Например, функция 


Заметим, что разность между конечными значениями правостороннего и левостороннего пределов называют скачком функции в точке. В данном случае величина скачка равна 2.
Функция 


Непрерывность элементарных функций. Свойства непрерывных функций
Элементарные функции: степенные, показательные, логарифмические, тригонометрические и обратные им, а также их сумма, произведение, частное непрерывны при всяком 
Обратим внимание на свойства непрерывных функций.
Теорема 1. Если функции 







Теорема 2. Непрерывная функция от непрерывной функции является непрерывной функцией.
Определение 3. Функция, определенная на некотором отрезке и непрерывная в каждой его точке, называется непрерывной на отрезке.
Теорема 3. (Вейерштрасс). Всякая непрерывная на отрезке функция ограничена.
Теорема 4. (Вейерштрасс). Всякая непрерывная на отрезке функция имеет на этом отрезке как наибольшее, так и наименьшее значение.
Теорема 5. (Коши). Непрерывная на отрезке функция, принимающая какие-либо два значения, принимает и любое промежуточное.
Следствие из теоремы Коши. Если функция непрерывна на отрезке и на его концах принимает значения разного знака, то на этом отрезке существует точка, в которой функция обращается в ноль.
Заметим, что последний факт полезен при нахождении корней уравнений точно или приближенно.
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
Другие темы которые вам помогут понять высшую математику:
Непрерывность и разрывы функций
Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.
Определение непрерывности функции в точке. Непрерывность основных элементарных функций
Понятие непрерывности функции тесно связано с ее пределом. Оно является характеристикой многих процессов, происходящих непрерывно: непрерывность времени, непрерывность изменения температуры, непрерывность роста дохода и др.
Пусть функция 





Рис. 14.1
Величина, на которую изменилось значение аргумента при переходе от точки 


а соответствующее изменение значения функции называют приростом функции в точке 
или
Приросты могут быть как положительными, так и отрицательными; например, на рис. 14.1 

Функция 

Заметим, что при определении непрерывности, в отличие от границы, функция в точке 
Покажем, что функция 





Найдем границу прироста функции 

Поскольку 


Аналогично можно доказать непрерывность любой из основных элементарных функций
Теорема 14.1 (о непрерывности основных элементарных функций). Основные элементарные функции непрерывные в каждой точке своей области определения.
Доказательство осуществляется для каждой функции отдельно.
Теорема 14.2 (критерий непрерывности «языком границы»). Функция 

Доказательство. Справедливость (14.4) следует из определения непрерывности и свойств предела.
Необходимость. Исходя из (14.3), имеем:
Если обозначить 


Отсюда
Следовательно,
Достаточность. Пусть функция определена в точке 
Тогда в соответствии с определением (14.4)
Таким образом, имеем два определения непрерывности функции в точке, Соответствующие формулам (14.3) и (14 .4):
Функция называется непрерывной на множестве 
Замечания. Если функция непрерывна в точке 

Например, вычислим границу 
Теорема 14.3 (критерий непрерывности «языком односторонних границ»). Функция 

Доказательство. Действительно, соотношение (14.7) базируется непосредственно на теореме существования конечного предела «языком односторонних границ» и определении непрерывности функции в точке (14.4):
Проверить в точке 
Вычислим односторонние пределы этой функции:
то есть предел слева не равен пределу справа, следовательно, функция в точке 
Рассмотрим далее две функции: 


Теорема 14.4 (о арифметические свойства непрерывных функций). Если функции 



Доказательство теоремы осуществляется на основе арифметических свойств предела. Покажем ее справедливость для доли функций.
Согласно (14.4)
Обозначим долю функций через 
Предлагаем другие выводы теоремы доказать самостоятельно.
Относительно функций, образованных из основных элементарных функций с помощью суперпозиции, возникает вопрос, какой с точки зрения «непрерывности» будет составлена функция, если ее составляющие являются непрерывными функциями.
Теорема 14.5 (о непрерывности сложной функции). Если функция 





Доказательство. Обозначим закон связи переменной 







На основании арифметических свойств непрерывных функций, непрерывности сложной функции и теоремы 14.1 (о непрерывности основных элементарных функций) делаем вывод: все элементарные функции непрерывны в каждой точке своей области существования.
Теорема 14.6 (о непрерывности обратной функции). Если функция 





Рис. 14.2
Разрывы функций и их классификация
Если функция 


Различают следующие случаи:
1. Существуют односторонние пределы (конечные), которые равны между собой 


Название разрыва «устранимый» связана с тем, что достаточно в той точке, где исследуется непрерывность функции, задать значение функции, которое бы равнялось значению односторонних границ, или изменить значение функции на значение предела в этой точке, то есть положить
Например, классический устранимый разрыв дает функция 


то есть
то для того чтобы функция была непрерывной, достаточно до определить функцию в точке 
Рис. 14.3
2. Существуют конечные односторонние пределы, но 

3. Не существует хотя бы одного из односторонних пределов, или по крайней мере один из них бесконечен, тогда точка 
Примером функции, имеющей разрыв второго рода, есть функция 
Под исследованием на непрерывность функции 

Если функция элементарная, то исследованию подлежат только точки, в которых функция не определена. При задании функции различными аналитическими выражениями на разных промежутках области существования исследование подлежат точки, которые являются пределами соответствующих промежутков.
Исследовать на непрерывность функцию
Областью определения функции является вся числовая ось, кроме 

1) односторонние границы при 
Следовательно, точка 
2) односторонние границы при
В точке 
Таким образом точка 
Исследуем на непрерывность функцию:
Имеем неэлементарную функцию, которую задано тремя формулами. На каждом из указанных промежутков функция непрерывна, как элементарная на области своего существования, следовательно, область определения этой функции 


1. Односторонние границы при 
Таким образом, функция в точке 
2. Односторонние границы при 
Поскольку f
Рис. 14.4 б
Исследовать на непрерывность функцию
Область определения функции 

Рис. 14.4 в
Непрерывность функции на промежутке. Основные теоремы о непрерывных функциях
В теоретических исследованиях и на практике применяются теоремы, которые отражают свойства непрерывных функций не в отдельно взятой точке, а на множестве точек, то есть на промежутке.
Функцию 






Сформулированные ниже теоремы примем без доказательства. Для лучшего понимания их содержания подадим в каждой теореме соответствующую геометрическую иллюстрацию, которая поможет, надеемся, осознать справедливость теорем на интуитивном уровне.
Сначала приведены определения. Если функция 









Теорема 14.7 (о наименьшем и наибольшем значении непрерывной функции). Если функция 


Если функция 


Рис.14.5
Например, функция 
Для функции 



Функция 




Функция 





Теорема 14.8 (об ограниченности непрерывной функции). Если функция 



Теорема 14.9 (о нуле непрерывной функции). Если 





Рис. 14.6
Теорема 14.10 (о промежуточных значениях функции). Если функция непрерывна на отрезке 





Заметим, что все рассмотренные вопросы непрерывности функции являются по сути применением понятия границ к исследованию функций и построения их графиков.
Лекции:
- Интервал сходимости степенного ряда
- Уравнение прямой через две точки
- Круги Эйлера фигуры, условно изображающие множества
- Тригонометрические комплексные числа
- Непрерывность функции
- Дробные рациональные выражения
- Система линейных уравнений
- Интегрирование тригонометрических функций
- Линии и поверхности уровня
- Дифференциал функции нескольких переменных
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой
-окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
— предел функции в точке 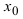
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 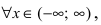
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 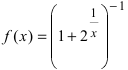
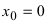
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 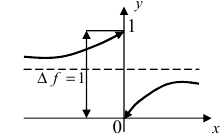
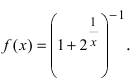
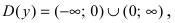
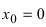
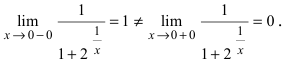
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция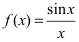
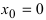
Решение:
В точке 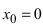
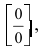
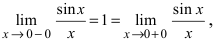
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 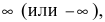
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 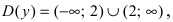
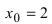
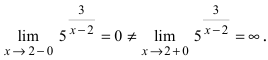
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 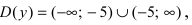
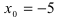
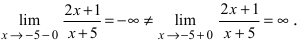
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 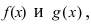
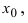
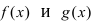
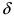
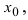
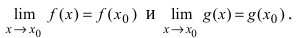
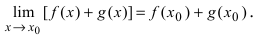
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 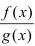
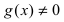
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 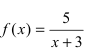
Из рисунка видно, что график функции 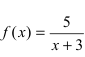
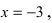
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 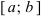
Определение: Замкнутый интервал 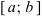
Приведем без доказательства свойства непрерывных функций на сегменте 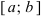
Теорема: Если функция 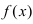
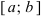
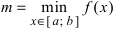
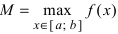
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 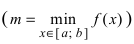
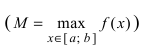
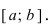
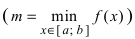
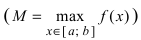
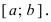
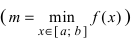
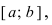
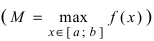
Тб. Если функция 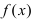
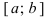
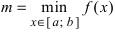
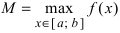
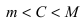
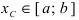
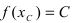
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 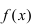
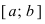
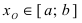
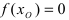
Пример:
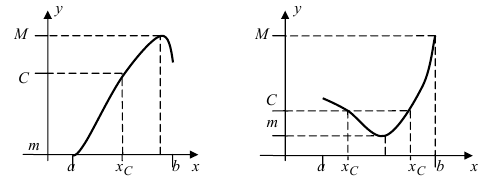
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Непрерывность функции в точке и на промежутке
Непрерывность функции в точке
Пусть функция (
y=f(x)
) определена в некоторой окрестности точки x = a (включая эту точку).
ОПРЕДЕЛЕНИЕ
Функция (
y=f(x)
) называется непрерывной в точке (
x=a
), если в этой точке есть предел (
lim _{x rightarrow a} f(x)
) , равный значению (
f(a)
) функции (
y=f(x) : f(x)
) непрерывна с
(
x=a Leftrightarrow lim _{x rightarrow a} f(x)=f(a)
)
ПРИМЕР
чтобы доказать непрерывность функции (
y=x^{2}-2 x+11
)
Пусть (
x=a
)- некоторая произвольная точка. Найти предел данной функции, поскольку аргумент стремится к точке (
x=a
):
(
lim _{x rightarrow a} f(x)=lim _{x rightarrow a}left(x^{2}-2 x+11right)=a^{2}-2 a+11
)
Затем мы найдем значение функции в точке (
x=a
):
(
y(a)=a^{2}-2 a+11
)
Поскольку
(
lim _{x rightarrow a} f(x)=f(a)
)
то функция (
y=x^{2}-2 x+11
) непрерывна при (
x=a
). Так как точка (
x=a
) — произвольная точка, то доказано, что функция непрерывна при всех значениях (
x
).
Пусть (
Delta x=x
) и (
Delta y=Delta f(x)=f(x)-f(a)
) — приращение функции, соответствующей этому приращению аргумента.
(Необходимое и достаточное условие непрерывности функции в точке). Функция (
y=f(x)
) непрерывна в точке (
x=a
) тогда и только тогда, когда
(
lim _{Delta x rightarrow 0} Delta f(x)=0
)
То есть функция (
y=f(x)
) называется непрерывной в точке (
x=a
), если она определена в точке (
x=a
), а ее окрестность и равенство (
lim _{Delta x rightarrow 0} Delta f(x)=0
) выполняется (инфинитезимальное приращение аргумента соответствует инфинитезимальному приращению функции).
ПРИМЕР
Чтобы исследовать функцию непрерывности (
y=sin x
)
Указанная функция определена для всех (
x in R
) . Возьмем произвольную точку (
x
) и найдем приращение функции (
Delta y
) :
(
Delta y=Delta f(x)=f(x+Delta x)-f(x)=sin (x+Delta x)-sin x
)
Примените формулу «разница синусов»:
(
sin x-sin y=2 sin frac{x-y}{2} cos frac{x+y}{2}
)
Буду иметь:
(
Delta y=2 sin frac{Delta x}{2} cos left(x+frac{Delta x}{2}right)
)
Найдите предел приращения функции при условии, что приращение аргумента стремится к нулю:
(
lim _{Delta x rightarrow 0} Delta y=lim _{Delta x rightarrow 0} 2 sin frac{Delta x}{2} cos left(x+frac{Delta x}{2}right)=2 lim _{Delta x rightarrow 0} sin frac{Delta x}{2} cos left(x+frac{Delta x}{2}right)
)
Поскольку аргумент синуса стремится к нулю, его можно заменить его аргументом (так как эти функции эквивалентны бесконечно малым функциям):
(
lim _{Delta x rightarrow 0} Delta y=lim _{Delta x rightarrow 0} 2 sin frac{Delta x}{2} cos left(x+frac{Delta x}{2}right)=2 lim _{Delta x rightarrow 0} frac{Delta x}{2} cos left(x+frac{Delta x}{2}right)=2 cdot frac{0}{2} cdot cos x=0
)
Тогда по определению функция (
y=sin x
) непрерывна в произвольной точке (
x
).
Функция непрерывна для любого (
x in R
)
Непрерывность функции справа и слева в точке
Рассмотрим функцию (
y=f(x)
), которая определена в полуинтервале (
[a ; a+delta)
)
ОПРЕДЕЛЕНИЕ
Функция (
y=f(x)
) называется непрерывной справа при (
x=a
), если существует односторонний предел
(
f(a+0)=lim _{x rightarrow a+0} f(x)=f(a)
)
Пусть функция (
y=f(x)
) определена в полуинтервале (
(a-delta ; a]
)
ОПРЕДЕЛЕНИЕ
Функция (
y=f(x)
) называется левой непрерывной в точке (
x=a
), если в этой точке есть левый предел
(
f(a-0)=lim _{x rightarrow a-0} f(x)=f(a)
)
Если функции (
f(x) ; quad g(x)
) непрерывны при (
x=a
), то функции в этой точке также будут непрерывными
(
f(x) pm g(x), f(x) cdot g(x), frac{f(x)}{g(x)}, g(a) neq 0
)
Если функция (
t(x)
) непрерывна при (
x=a
), а функция (
f(t)
) непрерывна в соответствующей точке (
t_{0}=f(a)
) , то комплекс (
f(t(x))
) непрерывен при (
x=a
).
Все элементарные функции непрерывны в каждой точке их областей.
(Ограниченность непрерывной функции). Если функция (
y=f(x)
) непрерывна в точке (
x=a
), то существует окрестность этой точки, где данная функция ограничена.
(Об устойчивости знака непрерывной функции). Если функция (
y=f(x)
) непрерывна в точке (
x=a ; quad f(a) neq 0
) , то существует окрестность этой точки, в которой (
f(a) neq 0
) , а знак функции в этой окрестности совпадает со знаком (
f(a)
) .
Функция непрерывности на зазоре
ОПРЕДЕЛЕНИЕ
Функция (
y=f(x)
) называется непрерывной на отрезке (
(a ; b)
) , если она непрерывна в каждой точке этого интервала.
Функция (
y=f(x)
) называется непрерывной на отрезке (
[a ; b]
) , если она непрерывна на отрезке (
(a ; b)
), непрерывном справа в точке а и непрерывном слева в точке (
b
).
Комментарий. Функция, непрерывная на отрезке (
[a ; b]
) , может быть разрывной в точках (
a
) и (
mathrm{b}
).
(Об ограниченности непрерывной функции на отрезке). Если функция (
y=f(x)
) непрерывна на отрезке (
[a ; b]
) , то она ограничена на этом отрезке, т. е. Существует такое число (
M>0
), что для любого (
x in[a ; b]
) неравенства (
|f(x)| leq M
)
(Теорема Вейерштрасса). Если функция (
y=f(x)
) непрерывна на отрезке (
[a ; b]
) , то она достигает на этом отрезке своих наибольших (
mathrm{M}
) и наименьших значений (
mathrm{m}
).
(О существовании нуля на отрезке непрерывности). Если функция (
y=f(x)
) непрерывна на отрезке (
y=f(x)
) , а на концах отрезка принимает ненулевые значения разных знаков, то на интервале (
[a ; b]
) имеется по крайней мере одна точка (
mathrm{C}
), в которой (
f(c)=0
)
(Теорема Больцано-Коши). Если функция (
y=f(x)
) непрерывна на отрезке (
[a ; b]
) , то она принимает на интервале (
(a ; b)
) все промежуточные значения между (
f(a)
) и (
f(b)
)
(О существовании непрерывной обратной функции). Пусть функция (
y=f(x)
) определена, строго монотонна и непрерывна на отрезке (
[a ; b]
) . Тогда на отрезке (
[alpha ; beta]
) , где (
alpha=f(a), beta=f(b)
) , обратная функция (
x=f^{-1}(y)
) строго монотонна и непрерывна на отрезке (
[alpha ; beta]
)

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
го рода. Это – устранимая точка разрыва, т.к. возможно доопределить функцию
|
f(x)= |
sin x |
: |
||||
|
x |
||||||
|
sin x |
, |
при x ≠ 0 |
||||
|
x |
, которая является непрерывной при любом x . |
|||||
|
g(x) = |
||||||
|
при |
x = 0 |
|||||
|
1, |
|
График этой функции: |
|||
|
1 |
|||
|
0 |
.8 |
||
|
0 |
.6 |
||
|
0 |
.4 |
||
|
0 |
.2 |
||
|
-20 |
-10 |
10 |
20 |
|
-0.2 |
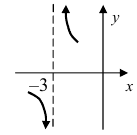
Точка х0 называется точкой разрыва 2-го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы
|
один из них бесконечен. |
1 |
||
|
Пример 5. Функция f(x)= |
имеет в точке х0=0 точку разрыва 2-го рода, т.к. |
||
|
х |
|||
|
lim f (x) = +∞; |
lim f (x) = −∞. |
||
|
x→0+0 |
x→0−0 |
7.5
5
2.5
-2.5
-5
-7.5
Непрерывность функции на интервале и на отрезке
Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом на концах отрезка или интервала необходима только односторонняя непрерывность.
Пример 6. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
117

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
||
|
x + 4, |
x < −1 |
|
|
+ 2, |
−1 ≤ x ≤1 |
|
|
f (x) = x2 |
||
|
x >1 |
||
|
2x, |
Решение. Это составная функция, областью определения которой является вся числовая прямая, которая точками «стыка» x1 = −1 и x2 =1 разбивается на
интервалы, на которых функция меняет свое аналитическое представление. На каждом интервале (−∞, −1) , (-1,1), (1, +∞) функция f(x) определяется
элементарной степенной функцией, которая является непрерывной для любого x . Поэтому на каждом интервале (−∞, −1) , (-1,1), (1, +∞) функция f(x) является
непрерывной. Необходимо проверить непрерывность функции f(x) в точках «стыка» x1 = −1 и x2 =1:
|
lim |
f (x) = 3 |
lim |
f (x) = 3 |
|
x→−1−0 |
x→1−0 |
||
|
lim |
f (x) = 3 |
lim |
f (x) = 2 |
|
x→−1+0 |
x→1+0 |
||
|
f (−1) = (−1)2 + 2 = 3 |
f (1) =12 + 2 = 3 |
Таким образом, в точке х=-1 функция непрерывна, в точке х=1 имеет
разрыв 1-го рода. Так как lim f (x) = 3 = f (1) , то функция f(x) в точке х=1
x→1−0
непрерывна слева.
у
3
2
Пример 7. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
|
cos x, |
x ≤ 0 |
|
|
+1, 0 < x <1 |
||
|
f (x) = x2 |
||
|
x ≥1 |
||
|
x, |
Решение. Это составная функция, областью определения которой является вся числовая прямая, которая точками «стыка» x1 = 0 и x2 =1 разбивается на
интервалы, на которых функция меняет свое аналитическое представление. На
118

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
|
|
каждом интервале |
(−∞,0) , (0,1), (1, +∞) функция f(x) определяется |
элементарными тригонометрической и степенными функциями, которые являются непрерывными для любого x . Поэтому на каждом интервале (−∞,0) ,
(0,1), (1,+∞) функция f(x) является непрерывной. Необходимо проверить непрерывность функции f(x) в точках «стыка» x1 = 0 и x2 =1:
|
lim |
f (x) =1 |
lim |
f (x) = 2 |
|||
|
x→0−0 |
x→1−0 |
|||||
|
lim |
f (x) =1 |
lim |
f (x) =1 |
|||
|
x→0+0 |
x→1+0 |
|||||
|
f (0) = cos0 =1 |
f (1) =1 |
|||||
|
Таким образом, |
т.к. |
lim f (x) = lim f (x) = f (0) , то в |
точке х1=0 функция |
|||
|
x→0−0 |
x→0+0 |
|||||
|
непрерывна. В |
точке |
х2=1 |
lim f (x) ≠ lim f (x) = f (1) , |
поэтому это точка |
||
|
x→1−0 |
x→1+0 |
разрыва 1-го рода. В точке х2=1 функция f(x) непрерывна справа.
у
2
1
Свойства функций, непрерывных на отрезке Свойство 1: (Первая теорема Вейерштрасса ). Функция, непрерывная
на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M≤ f(x)≤ M.
Замечание: Свойство 1 не справедливо для промежутков другого вида, чем отрезок. В этом легко убедиться, построив соответствующие примеры.
Пример 8. Функция y = 1x непрерывна в каждой точке интервала (0,1) и вместе
с тем не ограничена на нем; функция y = x непрерывна на всей вещественной оси и неограниченна на ней.
Свойство 2: Функция, непрерывная на отрезке [a, b], имеет на нем как наибольшее так и наименьшее значение.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
Карл Вейерштрасс (1815-1897) – немецкий математик
119

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
m ≤ f(x) ≤ M
Замечание 1: Отметим, что наибольшее и наименьшее значения функция может принимать на отрезке и несколько раз (например – f(x)=sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Замечание 2: Если функция f непрерывна не на отрезке, а на
промежутке другого типа и даже, кроме того, ограничена на нем, она вообше говоря, не имеет наибольшего и наименьшего значения.
Свойство 3: (теорема Коши). Функция, непрерывная на отрезке [a, b] такая, что f (a) = A, f (b) = B , то для любого значения C , заключенного между
A и B , существует такая точка ξ [a,b], что f (ξ) = C .
Иначе говоря, непрерывная на отрезке функция, принимающая какиелибо два значения, принимает и любое промежуточное.
Свойство 4: Если функция f(x) непрерывна в точке х=х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (теорема Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, в которой функция обращается в нуль.
Т.е. если sign(f(a)) ≠ sign(f(b)), то x0 [a,b] : f(x0)=0.
Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого ε>0 существует δ >0 такое, что для любых точек х1 [a,b] и x2 [a,b] таких, что
|
x1 − x2 |
<δ |
||
|
верно неравенство |
f(x2) – f(x1) < ε |
Отличие равномерной непрерывности от “обычной” в том, что для любого ε существует свое δ , не зависящее от х, а при “обычной” непрерывности δ зависит от ε и х.
Свойство 6: (Теорема Кантора ). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
Замечание: Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.
Кантор Георг (1845-1918) – немецкий математик
120

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|||||
|
1 |
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
|||||
|
Пример 9. |
y = sin |
|||||
|
x |
1 |
|||||
|
0 |
. 5 |
|||||
|
— 3 |
— 2 |
— 1 |
1 |
2 |
3 |
|
|
— 0 |
. 5 |
|||||
|
— 1 |
Функция y = sin 1x непрерывна на интервале (0, а), но не является на нем
равномерно непрерывной, т.к. существует такое число δ >0 такое, что существуют значения х1 и х2 такие, что f(x1) – f(x2) >ε, ε — любое число при условии, что х1 и х2 близки к нулю.
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором (конечном или бесконечном) интервале (a,b) , где
|
c = lim f (x), |
d = lim f (x) , то и обратная ей функция х=g(y) так же |
|
x→a+0 |
x→b−0 |
однозначна, монотонна и непрерывна на интервале с концами c и d .
121
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #




















































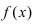
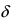 -окрестности;
-окрестности;